Mechanical cooperation between time-dependent and covalent bonds in molecular damage of polymer networks

Abstract

Most covalent polymer networks inherently contain a population of dynamic bonds, such as entanglements and physical associations, that interact with permanent cross-linked chains. This interaction plays a critical role in the mechanical behavior of the material and is evident from experimental observations. However, understanding the underlying nature and mechanisms of this coupling remains a significant challenge. To address this shortcoming, we develop a coarse-grained numerical model that incorporates time-dependent dynamic bonds and permanent covalent bonds. We investigate the effect of temperature, through modification of dynamic bonds intrinsic dissociation rate, and percolation on the mechanical interplay of hybrid networks. We show that high network connectivity constrains the microscopic deformation of local chains ensuring affine deformation, shielding the permanent network from early damage accumulation in the process. Conversely, the gradual erosion of dynamic bonds leads to highly inhomogeneous redistribution of stress and the emergence of structural heterogeneities. Finally, we investigate networks fracture behavior with a single-edge notch defect under varying temperature and network percolation. We demonstrate that the introduction of dynamic bonds explains delocalization of damage from the fracture plane, increasing energy dissipated through bond rupture. This shift can be understood in terms of an increase to the damage zone, where the opening of large-scale heterogeneities leads to an inhomogeneous redistribution of stress from the fracture interface to the bulk.

Introduction

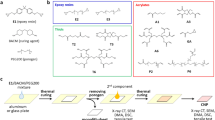
Soft polymers and hydrogels have become essential materials in diverse applications, including healthcare^1,2, soft robotics³, and actuation⁴. These materials are often required to endure repetitive loading and deformation while resisting damage caused by fatigue or mechanical overloading⁵. Cross-linked elastomers, in particular, derive their toughness not only from permanent cross-links but also from chain entanglements, which act as dynamic, load-bearing bonds. These entanglements interact with the permanent network to enhance energy dissipation and shield the material from catastrophic failure. Inspired by this behavior, recent studies^6,7 have explored replicating these toughening mechanisms through engineered dynamic bonds that can break and reform under stress, or through highly entangled networks formed between cross-linking points⁸, as shown in Fig. 1a. The toughening mechanisms in these systems rely on the interplay of two critical processes: (a) chain rupture in the primary network near the crack plane, and (b) energy dissipation in the bulk through rupture, sliding, and bond dynamics, whether from entanglements or engineered dynamic bonds.

Fig. 1: Hybrid networks.

a Illustration of hybrid network architectures which can either: be precisely engineered to have combinations of permanent (blue) and dynamic (red) linkers, or arise naturally due to the presence of many chain entanglements, here shown as dynamic bonds (red). b Hybrid networks are modeled as a 2D network comprised of reversible (yellow) and permanent (purple) bonds bound to nodes (red). Nodes are initially randomly packed with a mesh size ξ and have a fixed number of available sites (n = 8) for bonding. Reversible bonds detach with a force-dependent rate k_d(f) and attach to neighbors within a distance ℓ = 1.25ξ with constant rate k_a. c The normalized dissociation rate ${k}_{d}/{k}_{d}^{0}$ for various decay forces f₀ = [0.0001; 0.0004; 0.004] versus the bonds stretch.

Conceptually, the enhanced fracture toughness of these networks has previously been described by adding a bulk contribution to the intrinsic toughness (Γ₀) of the initial network. As a result, combining a cohesive zone model with a broader viscoelastic framework effectively describes both the intrinsic toughness of the initial network and the properties of the bulk material⁹. The intrinsic toughness component of this combination is often assumed to be constant; however, some models characterize cracks bridged by force-dependent dynamic bonds, yielding a velocity-dependent intrinsic toughness^10,11. The advantage of this description is that scaling laws and semi-analytical relations may be obtained to evaluate the enhanced toughness and its relation with crack speed. This approach is limited by the assumption that damage mechanisms in the process zone (lumped into Γ₀) are decoupled from the viscoelasticity of the bulk. It also assumes that the process zone remains small compared to the crack tip and that bond failure arises directly ahead of the crack tip, along the crack surface. Interestingly, this last hypothesis can now be experimentally investigated using fluorogenic mechanochemistry, where the distribution of bond damage may be visualized via small molecules (mechanophores) that become fluorescent upon damage. Using this technology, Slootman et al.¹² were able to spatially map molecular damage by bond scission in elastomer networks under various strain rates and temperatures. They found, in contrast to modeling assumptions, that bond damage extended far beyond the crack plane, and could be delocalized up to hundreds of micrometers. They also found that this effect strongly depended on temperature, where lower temperatures (i.e. stronger viscoelastic effects) yielded larger delocalization regions. This study therefore suggests a non-trivial coupling between the time-dependent mechanics of the sacrificial network (here provided by entanglements) and bond rupture in the permanent network. In addition to Slootman et al., there has been a growing body of literature that highlights the importance of networks architecture on their fracture toughness. For example, work on perfect versus imperfect polyacrylamide hydrogels, has found that network imperfections (i.e. dangling ends and entanglements) both amplify toughness and make hydrogels tolerant to small cuts¹³. Additionally, a significant improvement to toughness and strength can be realized by allowing one or multiple networks to be grown within another (i.e. multiple network elastomers)^6,14,15. Highly entangled polyacrylamide hydrogels, where entanglements greatly outnumber cross-links, display both high toughness, strength, and fatigue resistance, as the dense entanglements enable transmission of tension to many other chains⁸. It is evident that for many materials, including those just mentioned, the interaction between entanglements and the covalent network plays a critical role in their mechanical behavior. However, understanding the underlying nature and mechanisms of this coupling remains a significant challenge.

In this work, we use a minimalist hybrid network model that combines covalent (permanent) bonds with force-sensitive (reversible) slip bonds, which increase their dissociation rate under applied force. This approach allows us to study how dynamic and permanent bonds cooperate in a time-dependent manner to temporarily shield the network from damage accumulation during deformation. We first perform in silico stress relaxation experiments to uncover the intricate relationship between the microscopic deformation of individual chains and the coordination of the overall network. By analyzing the deviation of chain deformation from the applied loading and mapping the spatiotemporal distribution of bond energy, we explore how network percolation governs the emergence of structural heterogeneities. Our simulations reveal that high network coordination promotes affine deformation, providing time-dependent protection to the permanent network against early damage. This shielding effect is achieved either when the loading rate exceeds the kinetics of the slip bonds, effectively “freezing” their dynamics, or when the network percolation is sufficiently high. Here percolation refers exclusively to that of the permanent network, with the percolation threshold p_c determined by plotting the giant cluster relative size as a function of p. The threshold p_c is taken when the relative size of the largest cluster sharply increases (see Supplementary Note 1). Finally, we investigate the fracture behavior of hybrid networks with a single edge-notch defect under varying temperatures and network percolation levels. Post-mortem analysis of bond rupture, viscous dissipation, and damage patterns, alongside comparisons to the Lake-Thomas model, highlights the intricate coupling between dynamic and permanent bonds and its role in mediating molecular damage during fracture. Importantly, we demonstrate that bond cooperation can explain the delocalization of damage at the front of a propagating crack, a phenomenon that is highly sensitive to strain rate. These findings provide a conceptual framework for understanding how dynamic bonds mediate the coupling between the spatial and temporal damage distribution in these networks, ultimately affecting their intrinsic fracture toughness.

Results and discussion

The time-dependent mechanical response of elastomers can be traced to distinct molecular mechanisms at the network level (Fig. 1a). These include the presence of dangling chains and entanglements that can slowly relax over time, or the effect of temporary junctions formed by physical bonds (i.g. hydrogen bonds or ionic interactions). These effects have been mimicked in engineered polymer networks through the incorporation of dynamic and permanent cross-linkers, allowing a precise design of the network properties. Our methodology focuses on describing a generic network composed of a combination of permanent junctions and dynamic junctions, where the dissociation rate of the latter is sensitive to applied force. We here outline the key features of the proposed model, together with details of its numerical implementation.

Hybrid network model

As shown in Fig. 1b, we here represent “hybrid” networks made of a combination of permanent and dynamic bonds, as a 2D population of randomly packed nodes with a mesh size $\xi \sim {\sqrt{\rho }}^{-1}$ specified by ρ the planar number density. Volume exclusion is enforced on the nodes through a weak purely repulsive Yukawa potential

$${U}_{p}=A\frac{{e}^{-\kappa r}}{r}$$

(1)

where A is a scaling constant, and κ the screening length.

To avoid long-range crystalline order, we fix A = ϵ/50 with ϵ the energy scale governing bond stiffness. Each node has a fixed number of sites (n = 8) from which both permanent and dynamic bonds may connect. The appropriate choice of n depends on the material system of interest, for instance, covalent adaptable networks with chemically programmed bonding dynamics¹⁶, or densely entangled polymer networks where junctions arise from both cross-links and topological constraints⁸. Drawing from prior experience and physical intuition, we adopt n = 8 for two primary reasons: (a) it is sufficiently large to capture the crossover from non-affine to affine deformation regimes, and (b) it ensures robust network connectivity without imposing excessive computational overhead. To model the finite extensibility of a single chain we incorporate a divergent nonlinear bond potential:

$${U}_{b}=\epsilon {(r-{r}_{0})}^{2}/({L}_{c}^{2}-{(r-{r}_{0})}^{2})$$

(2)

where L_c defines the chain’s contour length at which point the force diverges. We set L_c = 5ξ while the equilibrium length r₀ is taken to be equal to the mesh size for simplicity. One could alternatively define parameters for the nonlinear bond potential to mimic other potentials such as the quartic or FENE (finite extension nonlinear elastic) potentials commonly used in coarse-grained polymer simulations. For instance, setting the rest length to ${r}_{0}=\sqrt{N}b$ and the contour length L_c = Nb, with N the number of Kuhn segments and b the Kuhn segment length, one can achieve a decent approximation to the FENE potential by adjusting the stiffness ϵ, as shown in Supplementary Fig. 1. Bonds are added randomly until the network is fully equilibrated and minimal new bonds are added on subsequent timesteps. We set the fraction of permanent bonds p depending on the desired percolation of the permanent network. Unless otherwise specified we set p to be just barely above the percolation threshold p_c ~ 38% (See Supplementary Note 1 for more details) which ensures our network is a solid with a non-zero long-term moduli, but is still very soft, as is common in many weakly cured rubbers. This has an added computational advantage since fewer overall bonding sites are needed.

The kinetic rate of detachment k_d of reversible chains is taken to follow Eyring’s theory, with a base rate ${k}_{d}^{0}$ that is determined by the natural bond frequency η and the unbinding activation energy E_a. Furthermore, to account for the fact that the energy barrier is affected by force, the true dissociation rate k_d increases exponentially with force as described by Bell’s model:

$${k}_{d}={k}_{d}^{0}\exp \left( \, \frac{f}{{f}_{0}}\right)\quad \,{\mbox{where}}\,\quad \ {k}_{d}^{0}=\eta \exp \left(\frac{-{E}_{a}}{kT}\right)$$

(3)

Here, f₀ is the decay force that defines the characteristic length of the bonding interaction, while kT measures the thermal energy (with T the absolute temperature and k the Boltzmann constant). For larger values of f₀ the detachment rate remains relatively constant up to the contour length, whereas for smaller values the kinetics increases rapidly under force as shown in Fig. 1c. We further assume that dynamic segments rebind at rate k_a which is independent of force, but dependent on the availability of potential bonding sites. More specifically, we restrict the rebinding distance l_c = 1.25ξ to low values of stretch enforcing that dynamic bonds re-attach near the stress-free state. This enforces a positive energy dissipation from dynamics^17,18 and, as shown by Lamont et al., this enables the relaxation of the network to remain independent of k_a¹⁹. We set ${k}_{a}=10{k}_{d}^{0}$ to ensure a sufficiently high initial equilibrium concentration of dynamic chains. Both permanent and dynamic bonds are assumed to rupture when stretched beyond a critical length R_crit. Our model is inherently two-dimensional, and we therefore adopt plane stress conditions in the fracture simulations. Due to computational constraints, the height of our in silico specimens is ~100ξ which is significantly smaller than the process zones typically observed in bulk polymer fracture experiments¹⁵. As such, our setup is more representative of fracture in thin adhesive films, such as pressure-sensitive adhesives (PSAs), where the process zone is limited by the specimen height. Beyond the specific case of fracture, our model is intentionally generic and is not calibrated to replicate a particular experiment. Instead, in the following sections, we aim to demonstrate general trends and mechanistic insights, supported by relevant experimental observations and analytical relationships where appropriate.

Simulation methods

Simulations were carried out in LAMMPS, a molecular dynamics codebase²⁰. Networks are loaded in uniaxial tension by adjusting the y-displacement of the top and bottom 3% of atoms with a prescribed engineering strain rate of $\dot{\epsilon }=1 \% {s}^{-1}$. We do not constrain boundary atoms horizontal displacement, allowing them to slide along the x-direction, as illustrated in Supplementary Fig. 2. This creates near stress-free boundaries in the x-direction. Atom positions are then updated using a velocity-Verlet algorithm based on their unbalanced forces, f ^α = ∑_β∇_rU(r^αβ) where r^αβ is the end-to-end distance between atom α and its βth neighbor, and U = U_p + U_b is the total energy provided by Eqs. (1) and (2). To ensure conditions of quasi-static loading, we follow heuristic scaling laws established by Wang anf Mora²¹ selecting a timestep according to:

$$dt=\alpha \sqrt{\frac{m}{{k}_{max}}}$$

(4)

where m is the minimum mass, and k_max is the max stiffness as determined from ∂²U_b/∂r² evaluated at the bonds rupture length L_c, where bonds are at their stiffest. We find a non-dimensional scaling factor α = 0.0005 to be sufficient. At each timestep, bond dynamics proceeds by prescribing a discrete probability for a bond event to occur during each discrete timestep (δt) according to:

$$\delta P=1-\exp {k}_{i}\delta t$$

(5)

where k represents the association or dissociation rate (k_a and k_d respectively). For bond association we assume a Markovian process, such that current events are uncorrelated with prior events. However, since slip bonds are force dependent, breakage events redistribute stress and consequently affect their breakage probability, implying that bond dissociation is a non-Markovian process. All quantities are expressed in terms of reduced units, with length scales expressed in terms of ξ, forces in terms of f₀, and energy in terms of ϵ. Time is expressed in units of the nominal unbinding time ${\tau }_{r}=1/{k}_{d}^{0}$.

In the following sections, we first examine the general behavior of the simulated network, highlighting its ability to capture the interplay between permanent and dynamic junctions under various mechanical conditions, with a particular focus on bond cooperation. We then investigate the mechanisms driving damage evolution in the network, leading to delayed fracture and rate-dependent fracture energy. Finally, we explore how bond cooperation influences these phenomena, including the formation of a non-local process zone whose size scales with the normalized loading rate.

Viscoelastic response and role of permanent network percolation

The relative fraction of permanent to dynamic bonds is expected to play a major role on the viscoelasticity and fracture of hybrid networks. To understand their effects, we first explore how addition of dynamic bonds informs networks viscoelasticity. In most soft polymers and rubbery materials, the complex shear modulus G is a function of both strain-rate (or equivalently frequency ω) and relaxation time at zero-force $\tau =1/{k}_{d}^{0}$ (which depends on temperature) through the simple formula⁹:

$$G(\bar{W})={G}_{0}+\left({G}_{\infty }-{G}_{0}\right)\frac{i\bar{W}}{1+i\bar{W}}$$

(6)

Here the non-dimensional Weissenberg number $\bar{W}=\omega \tau \approx \dot{\epsilon }/{k}_{d}^{0}$ measures the ratio of strain rate and network relaxation through bond dynamics. Equation (6) indicates two distinct regimes in the behavior of the network: a soft solid regime (G = G₀) when $\bar{W} \, \ll \, 1$ and a strong solid regime (G = G_∞) when $\bar{W} \, \gg \, 1$ with a transition occurring at $\bar{W}=1$. To probe this behavior with our discrete model, we simulated networks under uniaxial loading-unloading. We compute the storage modulus ${G}^{{\prime} }$ as the initial stiffness during elastic unloading and the energy lost due to dissipation G^″ from the area between loading-unloading curves (see Supplementary Note 2 and Supplementary Fig. 3 for details). While G^″ is not strictly a moduli (as determined by the imaginary part of G in Eq. (6)) it nonetheless provides a useful measure of hybrid networks ability to dissipate energy during loading. With this in mind, we respectively show in Fig. 2a, b the storage modulus, ${G}^{{\prime} }$ and dissipated energy, G^″ as a function of $\bar{W}$ for networks with three different permanent bond fractions, p. Focusing on p = 0.42 first, we see that ${G}^{{\prime} }$ is highest when $\bar{W} > > 1$, reflecting the combined stiffness of both networks, as dynamic bonds remain effectively frozen during loading. As $\bar{W}$ decreases and dynamic bonds’ kinetics approaches the loading rate, ${G}^{{\prime} }$ decreases, undergoing a sharp transition around $\bar{W}=1$. Below the transition the sacrificial network reforms significantly faster than the loading, giving rise to a soft solid dominated solely by the response of the permanent network. The loss rate, G^″ is observed to peak at the transition point, Fig. 2b. Here both networks are able to sustain stress, however unlike with a stiff solid, the dynamic network relaxes at the same rate as the strain rate, leading to overall large viscous dissipation. For permanent bond fractions p = 0.58 and p = 0.70 the transition in ${G}^{{\prime} }$ from stiff to soft solid becomes less pronounced as networks become less rate-dependent and more elastic. This is also reflected in the loss rate G^″ which decreases as p increases. Modifying the networks permanent bond percolation p therefore serves as a useful parameter to adjust hybrid networks viscoelastic and dissipative character.

Fig. 2: Stress relaxation and viscoelasticity of hybrid networks.

a Storage modulus ${G}^{{\prime} }$ as a function of $\bar{W}$ for networks with three levels of permanent bond fractions (black blue, and red corresponding to p = 0.42, 0.58, 0.7 respectively). The solid black lines correspond to fits predicted by Eq. (6). b Dissipated energy G^″ as a function of $\bar{W}$. Markers correspond to permanent bond fraction p identified in (a). c Log of the normalized stress $\ln (\sigma /{\sigma }_{0})$ versus time for varying held stretch λ_m. Decay forces f₀ = [0.0001; 0.0004; 0.004] are shown with triangles, squares, and circles respectively.

Stress relaxation of hybrid networks

To assess the relaxation of the generated networks, we simulated uniaxial tension to a specified maximum stretch λ_m at a rate $\dot{\lambda } \, \gg \, {k}_{d}^{0}$ that is much faster than the nominal dissociation rate. This effectively freezes the bond kinetics during loading. Networks were then held fixed for 5τ_r to relax. To understand slip bonds role on stress relaxation, we then compared the log of the normalized stress $\ln (\sigma /{\sigma }_{0})$, with σ_o the peak stress following loading, for networks with different decay forces, f₀ and held stretch, λ_m Fig. 2c. Consistent with many adaptable networks, such as hydrazone-²², ionically-²³, and thioester-¹⁶ cross-linked hydrogels, we find that our hybrid networks are well described by a stretched exponential of the form.

$$\sigma -{\sigma }_{\infty }={\sigma }_{0}\exp \left[-{\left(\frac{t}{{\tau }_{k}}\right)}^{\beta }\right]$$

(7)

where τ_k is the macroscopic relaxation time which is on the order of the bond intrinsic relaxation timescale τ_r (although τ_k deviates under different applied stretches), σ_∞ is the long-term stress after relaxation, and β (0 < β < 1) is a measure of how distributed the relaxation times are, with β = 1 implying a single relaxation time. Since our networks are comprised of force-dependent slip bonds, we find that β generally decreases with increasing stretch as the distribution of forces in the network broadens (see Supplementary Fig. 4). This leads to an overall decrease in the average time constant (Supplementary Fig. 5) as computed from the first moment of the stretched exponential 〈τ〉 = (τ_k/β)Γ(1/β), where Γ is the gamma function²⁴. Naturally 〈τ〉 depends on dynamic bonds interaction length-scale with larger decay forces f₀ leading to less deviation in the stress response for different λ_m. As shown in Fig. 1c, larger decay forces lead to a plateau in dynamic bonds unbinding rate, as the force required to overcome the slip barrier increases. In other words, dynamic bonds remain insensitive to the applied force except as chains are stretched close to their contour length. This is observed with the largest decay force Fig. 2c (circle markers) where stress relaxation significantly differs only for λ_m = 3.1 when the network is closest to the macroscopic failure point. In contrast, decreasing the distance to the slip barrier, not only decreases the materials mean relaxation time (Supplementary Fig. 5), but increases the networks sensitivity to held-stretch, as seen for f₀ = 0.0001 (Fig. 2c (triangle markers)). However, since the initial topology remains identical, networks relax to a final stress $\ln (\sigma /{\sigma }_{0})$ that depends only on the held stretch and networks soft solid modulus (i.e. the topology of the permanent network), with f₀ simply driving the timescale for relaxation to occur.

Mechanical cooperation between permanent and dynamic bonds

To examine how dynamic and permanent chains mechanically interact during stress-relaxation we analyze their respective chain populations more closely during deformation. Fig. 3a shows the relaxation modulus E_r(t) = σ(t)/(λ_m − 1) which after loading, decays from an initial short-term modulus ${E}_{r}^{0}$ to a long-term modulus ${E}_{r}^{\infty }$. Visual inspection of networks with bonds colored according to their force, reveal that after relaxation, Fig. 3a (denoted III.), forces are not uniformly distributed across the permanent network. Instead forces are concentrated within a small number of strands which bridge the network. ${E}_{r}^{\infty }$ is as a result therefore much softer and explains the near 80% decrease in E_r, despite the network having over 40% permanent bonds. This is in contrast to the loaded state, Fig. 3a (denoted II.), which shows no discernible force strands and a more uniform distribution of load across the network. These observations are also reflected in chains end-to-end distribution ϕ(r) shown in Fig. 3b separated into permanent (red) and dynamic (blue) bonds. In the loading stage, as the applied deformation rate is well over the detachment rate, dynamic bonds behave as permanent junctions, which leads to an overall high coordination (z > 6) in the network. As shown in Fig. 3b(I-II) this constrains individual chains ensuring that the microscopic deformation closely follows the macroscopic stretch (i.e. affine behavior). As the network relaxes and dynamic bonds dissociate, the reduced connectivity (z < 6) allows chains to rearrange and deform non-uniformly, resulting in local chain motion and the emergence of force strands and other structural heterogeneities like voids, as observed in Fig. 3a. Looking at the distribution ϕ(r), Fig. 3b(II-III), we in fact see that as dynamic bonds relax back to the their initial distribution, the reduced connectivity allows permanent chains to rearrange as well. We find that permanent chains relax into two superimposed chain populations: (1) that relax back to their initial state, and (2) a fraction that remain loaded, albeit with some degree of relaxation. Since chains force is directly related to their stretch we expect to see these two populations also reflected by chains force distribution. Indeed Fig. 3c, shows permanent chains force distribution becomes bimodal as two distinct populations of permanent chains emerge, with the loaded population – responsible for the force strands observed in Fig. 3a – carrying a majority of the stress. Overall, it becomes clear that our simulations show inhomogeneous redistribution of stress within the permanent network, during relaxation. Mechanical cooperation, or networks ability to redistribute stress, thus increases as the percolation level of the main network decreases.

Fig. 3: Mechanical cooperation and non-affinity.

a The relaxation modulus E_r as a function of time for a network loaded to held stretch λ_m = 2.1 with decay force f₀ = 0.0004. Networks relax from the short-term modulus ${E}_{r}^{0}$ characterized by contributions of both networks, to long-term modulus ${E}_{r}^{\infty }$ governed solely by the permanent network. Three snapshots of the network at (I.) λ = 1, (II.) λ = 2.1 just after loading, and (III.) λ = 2.1 after elapsed time 5τ_r are shown above. b Evolution of the chain end-to-end distribution ϕ(r) for the permanent (red) and dynamic (blue) networks for (I.) the initial configuration, (II.) immediately after loading and (III.) after relaxation for 5τ_r. c Probability distribution of force within the permanent network. d The non-affinity Δr² versus time for varying held stretch λ_m. This is normalized by the stretched mesh distance ${(\xi {\lambda }_{m})}^{2}$. e Normalized non-affinity at time τ_r = 5 as a function of the held stretch for decay forces f_o = [0.004; 0.0004; 0.0001] shown with circles, squares, and triangles circles respectively.

Although for our stress-relaxation simulations we observe no local damage accumulation, since the applied stretch remains well below chains’ maximum stretch, we anticipate inhomogeneous load redistribution to play a large role on networks damage and fracture response, similar to in silico experiments on polymer double networks²⁵. For these materials the intranetwork load redistribution did not follow the global deformation, as chains locally deviated from the deformation. Thus, to get a more accurate picture of how local chain motion in hybrid networks progress over time, we introduce a simple quantity to measure the permanent networks deviation from the affine (herein non-affinity) as the difference squared $\Delta {{{{\boldsymbol{r}}}}}^{2}={({{{\boldsymbol{r}}}}-{{{{\boldsymbol{r}}}}}_{aff})}^{2}$ between chains current spatial end-to-end vector r and its end-to-end vector had it deformed affinely r_aff (see Supplementary Note 3 for more details). We normalize this with respect to the stretched mesh distance ${(\xi {\lambda }_{m})}^{2}$ and plot versus time (see Supplementary Fig. 6 for all simulations). Although, most rubbers and polymers deform isochorically, our networks undergo slight volumetric expansion (see Supplementary Fig. 7). Even after accounting for this we find the non-affinity increases linearly during loading Fig. 3d, showing that despite high network coordination during loading, some local motion occurs within the network. As networks relax, however, the decrease in coordination drives a high degree of local chain motion, and permanent chains non-affinity increases sharply, Fig. 3d. The rate of this increase depends on the relaxation timescale of the dynamic network. Thus, once dynamic chains fully relax, further bond kinetics has little impact on the permanent network as evident by the plateau in the non-affinity. We find that the total non-affine motion after relaxation, shown in Fig. 3e is largest in networks with highest held stretch (λ_m), and is largely independent of f₀, further reinforcing that dynamic bonds slip behavior, assuming networks have near-identical topologies, simply drives the timescale at which these processes occur.

So far we have shown how dissociation of dynamic bonds during relaxation, drives local chain motion, and consequently an inhomogeneous redistribution of stress within the permanent network. To see how varying the fraction of dynamic bonds influences these processes, we repeat the above stress relaxation study, now modifying the initial fraction of permanent bonds p to create a network well above the percolation threshold p = 0.6 (Fig. 4d green), at the threshold p = 0.4 (Fig. 4d blue) and below p = 0.36 (Fig. 4d red). We also analyze the spatiotemporal distribution of the bond energy, which provides insight into how forces are redistributed during loading (see Supplementary Fig. 8) and relaxation. For relaxation, starting below percolation (p = 0.36), Fig. 4a shows the evolution over time of the change ΔU_b = U_b(0) − U_b(t) in the stored elastic energy U_b(t) in permanent bonds from their initially loaded state (at energy U_b(0)). Immediately after loading, we observe that this elastic energy increases in localized regions where most dissociation events take place, following a load transfer between dynamic bonds to adjacent permanent chains. Surprisingly, despite these localized spikes in permanent bond energy, the average value 〈U_b〉 decreases, (Fig. 4b) and continues until  ≈80% of the energy has been transferred to the permanent network, Fig. 4c. Initially, stress redistribution is primarily driven by the detachment of dynamic bonds. However, as the network coordination decreases, permanent bonds gain greater degrees of freedom to relax. This relaxation further redistributes stress to adjacent permanent bonds, leading to a highly inhomogeneous force distribution, consistent with previous observations (Fig. 3c). This is also accompanied by the opening of large scale heterogeneities such as voids, with spanning widths, multiple times the mesh size (Fig. 4a III). In most polymers, secondary interactions between chains, such as van der Waals forces, act to resist the formation and growth of cavities. In contrast, our network model does not include a penalty for bulk expansion²⁶. This omission is responsible for the slight volumetric expansion observed in our simulations: in the absence of secondary interactions, cavities can readily form once enough chains dissociate and local connectivity drops below the percolation threshold. These secondary interactions play a critical role in the damage mechanics of polymer networks; once cohesive stability is lost, chains surrounding the cavities undergo pronounced non-affine deformations. While incorporating such interactions in coarse-grained polymer simulations (e.g., via attractive potentials between Kuhn segments) is relatively straightforward, doing so at the network scale remains a significant modeling challenge. Exploring the influence of these interactions on damage initiation and propagation is left for future work. Nonetheless, our results indicate that regions of low coordination are more susceptible to damage initiation, as permanent bonds in these areas disproportionately bear the applied load.

Fig. 4: Role of percolation on bond energy distribution and non-affinity.

a The change in permanent bonds energy ΔU_b within a small subdomain for a network undergoing relaxation. We show snapshots at three intervals in time: (I) immediately after loading, (II) after 2.5τ_r, and (III) at 5τ_r. Dynamic bonds are colored in gray. b The average bond energy for permanent (dotted) and dynamic (dashed) bonds over time. c The fraction of energy ${U}_{b}^{i}/{U}_{b}^{tot}$ stored in network i for permanent (dotted) and dynamic bonds. During loading the relative fraction in bond energy remains roughly unchanged. Following relaxation  ~80% of the energy is carried by the permanent network. Inset shows schematic illustration of load transfer from dynamic to permanent bonds during dissociation events. d The relative size of the largest cluster (see Supplementary Note 1) increases sharply at a permanent bond fraction of p ~ 0.4 indicating the threshold for percolation p_c. Above this, the permanent network spans nearly the entire width of the domain. Insets show corresponding change in bond energy from the loaded to relaxed states. Note that voids remain constrained as the giant cluster size approaches unity. e The non-affinity for networks with three permanent bond fractions as a function of the held stretch λ_m.

Upon visual inspection of the same subdomain presented in Fig. 4a we see that although voids are still present, increasing networks percolation at p = 0.40 or above, (p = 0.60), the permanent network’s higher coordination constrains chain mobility, and prevents the emergence of large-scale voids, Fig. 4d (insets). Looking at the non-affinity, we see that local motion is highest for networks near the percolation limit, and displays the same dependence with the held stretch. However, for highly percolated networks, where the largest cluster spans nearly the entirety of domain, local chain motion not only decreases, as seen by the reduced non-affinity in Fig. 4e, but the non-affinity stabilizes at high stretch. Taking a closer look at stress redistribution (Fig. 4d (insets)) we find that for networks near percolation (p = 0.36 and p = 0.40), the fraction of permanent chains with an increase in energy, ΔU_b following relaxation, is 11.3%, and 12.9% respectively (see Supplementary Fig. 9). This increases to 21.6% for p = 0.70 showing that forces transferred within highly percolated networks are not only distributed across a greater overall number of permanent bonds, but are also more homogeneously distributed. This is in opposition to low percolated networks, where positive ΔU_b is observed across a smaller fraction of the chain population. Stress redistribution in low p networks can therefore become highly inhomogeneous, increasing the probability for loaded chains to rupture.

Dynamic bonds delay rupture under constant stress

We have seen that under fast deformation, dynamic chains not only contribute to the network’s elasticity, but they also take on a portion of the load, shielding the permanent network from sudden rupture. This, however, may only temporarily delay the appearance of damage in the permanent network, until dynamic bonds are fully relaxed. Depending on the applied load, three scenarios can be considered. In the situation where the applied load significantly exceeds the short-term elastic modulus²⁷ (σ ≫ G₀), the network fails immediately, all chains are over-loaded. By contrast, when σ ≪ G₀, the network will creep homogeneously as bonds relax, but will eventually stabilize as the permanent network is capable of carrying the load (i.e. no observed failure). Finally, when σ ~ G₀, the network may exhibit a delay time before ultimate rupture. This phenomena has been observed extensively for soft gels²⁸, glassy materials^29,30, and transient polymer networks²⁷. Two theories to describe delayed fracture nucleation in transient networks have emerged: (1) thermally activated crack nucleation (TAC) model, and (2) activated bond rupture (ABR) model. Both models are built upon Griffith’s theory of brittle fracture, where a critical length for unstable crack growth depends on the applied load³¹. In the TAC model, this length is reached when thermal fluctuations overcome the Griffith free energy cost, whereas for the ABR model, it follows directly from dynamic bonds slip barrier. From these two models, one can derive the average time for a microcrack to reach the critical Griffith length as a function of the applied stress (see Supplementary Note 4 for details). For the TAC model, the barrier to crack nucleation in 2D scales with the stress as U_a ~ 1/σ² such that $\langle {t}_{b}\rangle \sim \exp [{\sigma }^{-2}]$. Meanwhile, for the ABR model, the wait time decreases exponentially with the applied stress giving $\langle {t}_{b}\rangle \sim \exp [-\sigma ]$³².

As pointed out by Ligoure and Mora³³, the range of validity for these two models depends on the magnitude of the applied stress and the network architecture. In the case of the former, when stresses are low, one expects t_b to diverge to infinity, since it is nonphysical for unstressed materials to spontaneously break. While this is captured by the TAC model, it is a clear limitation of the ABR model, which by neglecting creation of new bonds, predicts a finite break time, even under zero stress. Despite these limitations, when applied stresses are high and the bond interaction length-scale δ is on the order of or greater than the mesh size ξ, the ABR model appears to provide a more accurate picture of rupture, as observed in experiments of transient telechelic polypeptide networks,³⁴. Here the authors took δ/ξ as just slightly below unity. For our networks we estimate δ = 1.5ξ, and since we prescribe force-sensitive bond kinetics, we a priori expect networks break time to be well captured by the ABR model. To confirm this we conducted a series of creep simulations by considering networks under constant applied stress, σ. To ensure that a sufficient wait time was observed before fracture, the number of bonding sites was increased to n = 20, with p = 0.3. Figure 5a shows typical creep curves for networks with different applied loads. Initially, networks deform with an elastic modulus G₀ before reaching a secondary creep regime with a roughly constant creep rate $\dot{\epsilon }$ (Fig. 5a inset). Failure, taken when the stretch increases by several decades, occurs after a delay time t_b, with the exception for σ/G₀ = 0.49, which failed immediately. The delay time t_b as a function of the stress is shown in Fig. 5b. The ABR model predicts a rupture time as ${t}_{b} \sim \exp [-\Omega \sigma ]$, where Ω incorporates the factor δ/k_BT but also stress concentration near the crack, which for our networks are voids. For comparison to the TAC model, the inset in Fig. 5b shows the break time as a function of σ⁻². It is clear that the data cannot be fitted by the TAC model. Instead the ABR model fits well (solid line) to the simulation data, with Ω = 9.178G₀. To see how delayed fracture progresses at the network level, we show four snapshots of simulations in Fig. 5c–f with bonds colored according to their non-affinity, a measure of chains local motion. We observe a gradual depletion of dynamic bonds creating sparse regions that precede the nucleation and coalescence of voids. Near these regions, chains undergo local deformation as they maintain local force balance; the consequent stress redistribution creates strongly localized rupture events driving a cascade of damage in the prefracture zone. Voids therefore grow subcritically as a result of strongly localized damage processes due to the gradual erosion of dynamic bonds. This ultimately culminates in nucleation of a critical void followed by propagation of a crack and failure of the network. Recent experiments on rubber, by mapping the micromechanical damage processes through use of Laser Speckle Strain Imaging, also provides strong support for the erosion mechanism of delayed fracture³⁵. In these experiments, a delocalized zone of small strains emerged as a result of local damage processes – via the gradual erosion of bonds – which led to the growth of a prefracture zone, similar to what is observed in our simulations.

Fig. 5: Delayed fracture in hybrid networks.

a Stretch versus time for applied stress σ/G₀. Initially networks respond elastically with a deformation λ ≈ σ/G₀ + 1, before entering a secondary creep phase with constant creep rate $\dot{\epsilon }$, shown in the inset. Networks fail after time t_b, at which point the stretch increases drastically. b Breaking time t_b as a function of the applied stress σ/G₀. Errorbars are on the order of the graph point size. Inset shows t_b as a function of σ⁻².c–f Snapshots of the simulation showing the gradual errision of bonds and growth of the local strain field near the locus of ultimate fracture nucleation. Bonds are colored according to their non-affine square displacement Δr².

Fracture in hybrid networks under constant strain rate

We now turn our attention to damage initiation near a pre-crack, noting that the goal of this study is not to model the complete fracture process, which in soft materials is an inherently multi-scale process^5,36 occurring across length-scales much greater than our simulations could explore. Instead, we seek to understand the role dynamic bonds play on damage initiation, with particular emphasis on the interplay between permanent and transient networks. As discussed in a previous section, decreasing p not only increases the viscoelastic character of hybrid networks, but permits significant redistribution of stress. To see how these combine to influence damage accumulation, we created networks with a single-edge notch  ~ 20ξ in length loaded at a fixed strain rate under uniaxial extension until failure. Figure 6a–d shows the propagation of a crack with bonds colored by force. For the remainder of this study, we vary only the Weissenberg number, $\bar{W}\in [0.1,10]$ and the fraction of dynamic bonds, fixing dynamic bonds decay force to f₀ = 0.0001. We explore three values of p, creating networks close to the percolation threshold p = 0.42, well above p = 0.7, and an intermediary value p = 0.58. Stress-stretch curves for simulations at p = 0.42 are shown in Fig. 6e, and resemble fracture of a brittle solid, characterized by an initial elastic response followed by a precipitous decrease in stress at a critical stretch λ_c, at which point the crack begins to propagate. Both the network stiffness and critical stretch vary with the Weissenberg number. To describe fracture under constant strain rate, we take the approach outlined by Evans³⁷ and Chaudhury³⁸, and modify the ABR model to account for the fact that chains deform linearly in time. This has been done successfully to explain rupture in single bonds³⁷, adhesive failure at polymer-glass interfaces³⁸, and fracture in transient gels³⁴. Again, since we prescribe force-sensitive bond kinetics, we expect our hybrid networks to behave similarly. As a first approximation, we assume affine deformation (the limitation of this becoming apparent later), with chains in the network stretched at a speed $\xi \dot{\epsilon }$, where $\dot{\epsilon }$ is the macroscopic applied strain rate. Further, assuming Gaussian chains with stiffness k_BT/ξ², the force carried by a cross-link increases as $f(t)=K({k}_{B}T/\xi )\dot{\epsilon }t$ where the factor K accounts for stress-intensification that occurs at the pre-notch. Substituting this expression for force into Eq. (3) we obtain the bond-dissociation rate as a function of time. It follows from ref. ³⁷ that the survival probability of a bond P(t) can be written as:

$$P(t)=\exp \left\{-\frac{1}{\tau }\int_{0}^{t}{k}_{d}\left[f(t)\right]dt\right\}$$

(8)

with $\tau =1/{k}_{d}^{0}$. The first moment of P(t) gives the average lifetime 〈τ〉. In the high loading rate limit ($\bar{W} \, \gg \, \xi /K\delta$ and $\bar{W} \, \gg \, 1$), this time can be identified with the time t_b at which fracture occurs²⁷:

$${t}_{b}\approx \int_{0}^{\infty }P(t)dt=\frac{\xi }{K\delta \dot{\epsilon }}\ln \left(\frac{K\delta \bar{W}}{\xi }\right)$$

(9)

This allows us to evaluate the critical strain ${\epsilon }_{c}=\dot{\epsilon }{t}_{b}$ at failure as:

$${\epsilon }_{c} \sim \frac{\xi }{K\delta }\ln \left[\frac{K\delta \bar{W}}{\xi }\right]$$

(10)

The critical stretch is thus λ_c = ϵ_c + 1. This expression indicates a logarithmic dependency on $\bar{W}$, which is confirmed in the high Weissenberg regime (W ≫ 1) by numerical simulations (Fig. 6f) for networks with three different permanent bond fractions.

Fig. 6: Fracture in hybrid networks.

a–d Snapshots of a simulation showing propagation of a crack. Bonds are colored according to their force. e Stress-stretch curves are shown for single-edge notch fracture simulations for $\bar{W}$ = 0.3, 0.6, 10, (from light blue to purple). Crack propagation begins at critical stretch λ_c, indicated by dashed lines. f The critical stretch λ_c as a function of $\bar{W}$ for networks with three levels of permanent bond fractions (black circles, blue triangles, and red squares corresponding to p = 0.42, 0.58, 0.7 respectively). g Images of a crack propagating through a network with bonds colored according to their expected lifetime 1/k_d. Note that we re-map atoms to their initial positions, so that only the network topology changes.

With ξ = 0.0014 and bonds interaction length-scale δ ≈ 1.5ξ, we fit Eq. (10) by adjusting the stress intensity factor finding a value of K ≈ 27 for p = [0.58, 0.7] and K ≈ 11 for p = 0.42, as shown in Fig. 6f by the solid fit lines. This agrees well with experimental fracture of transient telechelic polypeptide networks where K ≈ 35³⁴. Fracture, at least in the high loading rate regime, is therefore well captured by the ABR model, and shows that networks fail according to a stress enhanced bond rupture process, with greater stress intensification (higher K) observed for more brittle networks with higher p values. At low $\bar{W}$ (corresponding to polypeptide gels for instance), we note that the critical strain diverges significantly from that predicted by Eq. (10). This is because at these rates, the network can self-heal through re-association of dynamic bonds. Furthermore, the affine assumption, is likely invalid at low $\bar{W}$ especially for networks with low permanent bond fractions. This in part helps explain why λ_c diverges more sharply for networks with lower p values. For these networks, relaxation of dynamic bonds leads to regions with low coordination resulting in material flow and higher critical stretches.

Figure 6g visualizes the stress-enhanced bond rupture process showing the propagation of a crack from its pre-notch coordinate ${x}^{{\prime} }(0)$ to its current location ${x}^{{\prime} }(t)$ at time t. We show the expected lifetime of dynamic strands, as computed according to Eq. (3), which for visual clarity are remapped back to the undeformed network so that their positions remain fixed. While a common approach for many models of soft elastomers is to restrict fracture to the scission of chains that cross a molecular plane^10,39, our simulations clearly show a larger region with increased chain force (here indicated by decreased bond lifetimes) radially distributed ahead of the advancing crack. As observed by Slootman et al. dissipation and molecular damage in elastomer fracture can occur over much larger length-scales, on the order of 250 μm¹², highlighting the issue in restricting bond scission to the fracture plane. While for our simple hybrid network model simulations, the stress-enhanced region extends no more than  ~5ξ, it nonetheless shows, at least qualitatively, that both dissipation and bond failure extend beyond the crack plane, with more bonds involved in dissipation increasing the networks resistance to fracture.

Rate-dependent fracture of hybrid networks

The propagation of a crack in soft materials involves both the scission of covalent bonds and dissipation due to entanglements and reptation. The classical assumption³⁹ is therefore to express the fracture energy (defined as the energy required to advance a crack by a unit area) as Γ = Γ₀[1 + f(a_Tv_crack)], where Γ₀ is the rate-independent intrinsic fracture energy accounting for bond rupture and Γ_bulk = Γ₀f(a_Tv_crack) captures the rate-dependent viscoelastic dissipation within the bulk. Here, the function f describes the increase in total fracture energy with reduced crack velocity a_Tv_crack³⁹. Even with the addition of bulk hysteretic dissipation Γ_bulk, the bulk dissipation model of fracture still significantly under-predicts the toughness enhancement of many soft materials, including interpenetrating hydrogels⁴⁰, entangled networks⁴¹, and filled⁴² and unfilled rubbers⁴³. To account for this, Lin et al. proposed the addition of near crack-dissipation Γ_tip, which captures the distribution of damage directly surrounding the crack tip, due to mechanisms such as chain entanglements^41,44. The total fracture energy Γ = Γ₀ + Γ_bulk + Γ_tip is thus the sum of these three mechanisms, as schematically depicted in Fig. 7a. While the size of our simulations restricts us from effectively exploring the rate-dependent bulk dissipation, we can, however, address how dynamic bonds influence near-crack dissipation Γ_tip. We hypothesize that introducing dynamic bonds, which in this context can represent entanglements, should lead to an increase in distributed damage. This effect is expected to be especially pronounced in soft networks, which undergo large and non-affine deformations, a key factor in inhomogeneous stress redistribution as discussed earlier. Fig. 7b illustrates how dynamic bonds influence energy dissipation near the crack tip. It shows that when either the permanent network percolation p is high or the normalized strain rate $\bar{W}$ is large, the network deforms predominantly affinely near the crack. As a result, the process zone remains small, and the classical Lake-Thomas model remains applicable in this regime. In contrast, for low values of p and $\bar{W}$, the network becomes highly non-affine and soft and the process zone size increases, leading to a significant amount of distributed damage. This more closely resembles an Irwin-Orowan picture of fracture, with a large process zone traveling ahead of the crack tip, akin to ductile yielding observed in fracture of many metals⁴⁵. To assess whether this hypothesis is true, we extracted the energy dissipated due to scission of bonds. The rupture energy of a single bond U_r is computed from Eq. (2) evaluated at the bonds critical length R_crit. The total energy dissipated due to bond scission, plotted in Fig. 8a as a function of $\bar{W}$, is thus ΣU_r where Σ is the total number of ruptured bonds needed for crack propagation. Note that strictly speaking Γ is an energy per unit area, whereas ΣU_r has units of energy. However, since all networks have identical initial dimensions and notch lengths, we expect both quantities to scale similarly.

Fig. 7: Fracture model.

a Schematic illustration of the three main mechanisms contributing to the fracture energy: intrinsic fracture energy Γ₀ due to chain scission near the crack interface, bulk dissipation Γ_bulk due to interchain friction and reptation, and near-crack dissipation Γ_tip due to distributed damage where L_c is the characteristic length of the process zone. b Schematic illustration showing the effect of non-affinity on the process zone. When networks are affine, the process zone remains close to the network meshsize ξ and the Lake-Thomas model of fracture remains the relevant picture. Chain scission (shown as yellow stars) remains localized. As networks become more non-affine, the damage becomes delocalized leading to an increase in the process zone. The Irwin-Orowan model of fracture is necessary in order to account for the additional near-crack dissipation Γ_tip.

Fig. 8: Rate effects in dissipation and damage.

a The energy dissipated due to irreversible rupture of permanent chains ΣU_r as a function of the Weissenberg number for three levels of permanent bond fractions (black, blue, and red corresponding to p = 0.42, 0.58, 0.7 respectively). b The bulk energy dissipated due to reversible dissociation of dynamic bonds as a function of the Weissenberg number. c The normalized damage Σ/Σ_LT versus Weissenberg number. The gray horizontal dashed line shows the Lake-Thomas threshold.

Contrary to the classical picture of rate-independent strand rupture of permanent bonds, we find that ΣU_r does not remain constant across the probed values of $\bar{W}$. Instead our simulations predict the emergence of two distinct regimes, with the delineation occurring as networks transition from soft to stiff solids around $\bar{W}=1$. Below this transition ($\bar{W} < 1$), the energy dissipated due to bond rupture ΣU_r increases as $\bar{W}$ decreases. This is observed to be steepest for p = 0.42 (Fig. 8a dashed black), consistent with the idea that low network percolation promotes bond cooperation. The effect becomes less pronounced as networks become more percolated and elastic, implying that ΣU_r is strongly coupled to the dynamic network. However, this is only observed when rate-effects are considerable. Above the transition, networks reach a threshold level of damage that does not vary significantly with $\bar{W}$. In this regime, as discussed previously, dynamic bonds freeze, effectively behaving as permanent chains. We observe similar trends for the total energy U_d dissipated due to bond dynamics as shown in Fig. 8b. Unsurprisingly, decreasing p leads to a direct increase in the bulk dissipation U_d. Again for $\bar{W} > 1$ networks display a threshold level of dissipation with U_d remaining roughly constant. For p = 0.42 dissipation peaks just below $\bar{W}=1$ before subsequently decreasing, as at these high rates, dynamic bonds store less elastic energy before dissociating. For p = 0.58 and p = 0.70 bulk dissipation plateaus as $\bar{W}$ decreases instead of decreasing as one might expect. This discrepancy is likely due to the localization of bond kinetics in our model, whereas $\bar{W}$ is a global measure of bond kinetics.

Regardless of $\bar{W}$, the overall energy dissipated due to bond rupture ΣU_r increases with p. This is expected as networks with higher p values have more overall permanent bonds available to rupture. It is therefore instructive to introduce the ratio Σ/Σ_LT where Σ_LT denotes the minimum number of ruptured bonds needed for crack propagation. We note that Σ_LT decreases with decreasing permanent bond fraction p, as network failure requires rupture of fewer permanent bonds, with very little participation from dynamic bonds. We found that due to the slip behavior of dynamic bonds, a very small fraction (below 5%) of dynamic bonds break by bond rupture and thus do not significantly contribute to the intrinsic fracture energy. As a result, Σ_LT is defined only in terms of the permanent bonds within the network. In this context, a ratio Σ/Σ_LT = 1 corresponds to highly localized chain rupture, taking place at the crack interface, consistent with the classical Lake-Thomas model³⁹. Upon rescaling, we see that for $\bar{W} > 1$, networks tend to approach the Lake-Thomas threshold (Fig. 8c dashed line). In this regime, fracture therefore remains highly localized to the fracture plane, irrespective of the dynamic chain population. On the other hand, below the transition, as $\bar{W}$ decreases, the normalized damage increases steadily and depends strongly on p. For the three bond fractions investigated here, p = 0.42, 0.58, 0.7, we find that for $\bar{W} < < 1$ the normalized damage can respectively reach values of, Σ/Σ_LT ≈ 1.67, Σ/Σ_LT ≈ 1.38, and Σ/Σ_LT ≈ 1.15, Fig. 8c. This demonstrates that fracture in the low $\bar{W}$, especially with decreasing p requires rupture of more bonds than approximated by the Lake-Thomas model.

We should point out, that for our model, non-affinity and damage increase with decreasing $\bar{W}$, which is contrary to Slootman et al., where damage was found to increase with $\bar{W}$¹². There are a few likely explanations for these differences. First, is that our hybrid network model does not directly model inter-chain friction that would arise due to sliding of entanglements, instead dissipation depends exclusively on dynamic bonds stored strain energy at the time of dissociation, which peaks at $\bar{W}=1$, Fig. 2. An alternative approach could therefore attempt to model these interactions explicitly, as done in our recent work on entangled polymer networks⁴⁶, however, this significantly increases model complexity. Moreover, due to computational limitations, our simulations are restricted to a small zone around the crack tip, such that the rate-dependent bulk dissipation obtained from simulations is not expected to exactly match fracture in bulk polymers. Differences within our model aside, non-affinity could potentially have a different dependency on $\bar{W}$, as suggested by the work of Slootman et al. This could arise due to the degree of polydispersity, differences in reptation dynamics (e.g. entanglements versus slide rings, etc.), or through varying network architectures (e.g. single versus interpenetrated), whose influence on non-affinity are all subject to future studies. The exact relationship between $\bar{W}$ and non-affinity is expected to depend strongly on both the material and nature of failure. Take pressure sensitive adhesives (PSAs) for example, which despite displaying a considerable amount of interchain friction, which we should point out is absent in our model so that direct comparisons should be reserved for a more detailed future model, their application in thin films most closely resembles our current simulation geometry. With that caveat in mind, varying dependencies of $\bar{W}$ on damage can be observed across different PSAs. For instance, the adhesive fracture energy of poly(2-ethylhexyl acrylate) at first strongly increases with increasing temperature (decreasing $\bar{W}$) due to fibrillation of the adhesive, before eventually peaking and then gradually decreasing with further increase to the temperature⁴⁷. Peeling experiments of a PSA (Scotch 600 tape), on the other hand, show at first an increase to the energy release rate with increasing peel velocity (increasing $\bar{W}$) before subsequently decreasing due to stick-slip dynamics⁴⁸. Interestingly, both experiments found that fracture energies peaked when large deformations through the presence of fibrils and stringing were observed. While strictly speaking our model disallows adhesive failure, such that cracks always propagate through the material (cohesive failure), it is clear that large strain mechanics, where highly non-affine deformations are to be expected, plays an important role in distributing damage, as observed in our simulations.

For $\bar{W} > > 1$, we expect networks to reach a limiting behavior where the normalized damage Σ/Σ_LT includes contributions from both the permanent and the dynamic network. As dynamic bonds freeze, they effectively become permanent cross-links and Σ/Σ_LT should therefore approach an upper Lake-Thomas threshold which requires scission of both chain populations. For our networks this would correspond to normalized damage values of Σ/Σ_LT ≈ 2.5, 1.7, and 1.4 for p = 0.42, 0.58 and 0.7 respectively. These trends are not observed in our simulations, which likely stems from limitations in the current slip bond model. Specifically, the model predicts an infinite kinetic detachment rate (or zero lifetime) under sufficiently high forces. In reality, chain dissociation is limited by other factors including inter-chain friction and viscous effects that should enforce a minimum lifetime for dynamic bonds. Ideally then, chains k_d should plateau under higher forces before ultimately rupturing, something which we will explore in future work. Instead, a propagating crack, regardless of its speed, encounters a local region largely devoid of dynamic bonds, and a network defined exclusive by the topology of the permanent network. On top of this, our hybrid networks are monodispered with bonds that do not extend beyond  ~ 1ξ, the mesh size. Recent studies on multiple network elastomers have shown that introducing networks with different degrees of pre-stretch, (i.e. mesh sizes) greatly improves toughness by increasing the interaction length-scale through which chains can delocalize damage¹⁵. In our case, networks can only redistribute forces directly to their neighbors which leads to more direct localization. These limitations likely explain why Σ/Σ_LT is at most 1.67, contrary to experiments which show Σ/Σ_LT can remarkably reach values ranging from  ≈100 in single network elastomers¹² to upwards  ≈7600 in triple networks¹⁵. Nevertheless, our simulations show that when $\bar{W} < 1$ the normalized damage Σ/Σ_LT increases with addition of dynamic bonds. To rationalize this increase, we next complete our study by analyzing molecular damage patterns that arise during fracture.

Dynamic bonds delocalize damage

Our in silico fracture experiments reveal that networks topology progresses through the nucleation, growth, and coalescence of voids ahead of the crack tip. Here, voids are defined as enclosed regions absent of bonds whose length L_v (see Fig. 9a inset) exceeds 1.4ξ or 1.4 times the mesh size. This ensures that stretched but otherwise damage free regions of the network are not counted. Using image analysis techniques (see Supplementary Note 5 and Supplementary Fig. 10), we extract the void length L_v computed from their area as, $\sqrt{{A}_{v}}$ (see Supplementary Fig. 11) just before the crack begins to propagate. This gives us insight into the damage mechanisms prior to fracture. Fig. 9a shows the average void length 〈L_v〉 versus $\bar{W}$ for the three networks, which shows similar trends to Σ/Σ_LT. Therefore, when bond kinetics are considerable (i.e. $\bar{W} < 1$), formation of heterogeneities depends strongly on both $\bar{W}$ and p. In the stiff solid regime, 〈L_v〉 remains roughly constant, approaching 〈L_v〉 ≈ 1.93ξ,  ≈ 1.76ξ, and  ≈ 1.67ξ for p = 0.42, 0.58, 0.7, respectively. As discussed earlier, the opening of structural heterogeneities is accompanied by increased local chain motion and an inhomogeneous redistribution of stress (Fig. 4). The increase in Σ/Σ_LT then comes as dynamic chains erode, the networks undergo significant rearrangement at the local level. This not only manifests in the nucleation of voids, as shown in Fig. 9a, but critically alleviates tension on surrounding chains, particularly at the crack tip. If networks are close to the percolation threshold, this can even result in blunting of the crack tip as seen in Fig. 9b (uppermost network). Inhomogeneous relaxation of stress therefore delocalizes damage away from the fracture interface to heterogenieties. If this is the case, we speculate that increasing the fraction of dynamic bonds, should also result in an increased damage zone seen through an increased density of voids surrounding the crack tip. Conversely, as networks become purely elastic (i.e. p → 1) opening of voids should remain highly localized to the crack tip, where stresses remain concentrated. Snapshots of three simulations with p = 0.42, 0.58, 0.70 (left to right) taken at λ = 1.55, as in Fig. 5c, show that visually this is indeed the case.

Fig. 9: Molecular damage patterns in hybrid networks.

a The average void length 〈L_v〉 as a function of the Weissenberg number for networks with three levels of permanent bond fractions (black, blue, and red corresponding to p = 0.42, 0.58, 0.7 respectively). b Snapshots of fracture simulations at λ = 1.55 for permanent bond fractions p = 0.42 (black), p = 0.58 (blue), and p = 0.70 (red) shown top to bottom. c The void density ρ_v as function of radially distance r from the crack tip, for $\bar{W}=0.1,0.3,0.6,1.0$. The solid black lines show exponential fits of the form ${\rho }_{v} \sim \exp [-r/{L}_{c}]$ where L_c is the characteristic damage length. d The characteristic damage length L_c as a function of the Weissenberg number.

To provide a more quantitative measure, we extracted the density of voids, ρ_v as a function of the radial distance, r from the crack tip Fig. 9c. We choose void density over extracting the damage distribution simply due to the limited size of our networks which would provide highly noisy radial distributions. Since bond breakage must necessarily precede void opening, we view void density as a reasonable approximate. For low $\bar{W}$, when dynamic bonds intrinsic dissociation rate is largest, ρ_v decays gradually with distance, with voids remaining present far from the crack tip. As $\bar{W}$ increases (Fig. 9c green to purple), void density falls off more rapidly with r, indicating that voids remain localized near the crack. We find that ρ_v can be approximated by an exponential decay of the form ${\rho }_{v}={\rho }_{0}\exp [-r/{L}_{c}]$ with ρ₀ the density at the crack tip. We can extract a characteristic length L_c (schematically illustrated in Fig. 9d), which we interpret as the size of the process zone wherein distributed damage may occur, akin to that found by Slootman et al.¹². Remarkably L_c follows similar trends with Σ/Σ_LT, implying a coupling between bond rupture and the damage length-scale. Looking at networks with the greatest fraction of dynamic bonds (p = 0.42), we see that L_c varies as much as an order of magnitude from a peak of L_c ≈ 90ξ to L_c ≈ 13.6ξ. Above the transition, $\bar{W}=1$, the damage length approaches a roughly constant distance of L_c ≈ 13.6ξ confirming that in this regime, networks freeze into a glassy state with both dynamic and permanent bonds cooperating to resist the opening of voids. Both p = 0.58 and p = 0.70 follow similar trends, respectively reaching L_c ≈ , 10.3, and 7.04 for $\bar{W} > 1$. Taken together, these results indicate that increasing the fraction of dynamic bonds leads to opening of large-scale heterogeneities which inhomogeneously redistribute stress away from the crack tip. This not only reduces stress at the tip, as seen in the reduction of the stress intensity factor K, but also leads to damage away the fracture plane. For highly non-affine networks, fracture could therefore start at a location different from the initial crack tip and suggests that networks in the low $\bar{W}$ regime are not only tougher, but become defect tolerant, see Supplementary Fig. 12. This is similar to the flaw insensitivity trends observed for perfect versus imperfect polyacrylamide hydrogels, for which it is found that network imperfections both amplify toughness and make hydgrogels tolerant to small cuts, in part due to non-affine motion of chains which tend to spatially redistribute damage¹³. Much like our model, this results in damage regions whose characteristic length scales can significantly exceed the mesh size (in our case, reaching up to  ≈ 90ξ) and yield an increased energy dissipation due to bond rupture.

Conclusion

In this work we have presented a framework to study fracture and failure in soft elastomers which consist of permanent and transient cross-links. To assess how these two populations of chains can cooperate to delay and spatially redistribute damage, we performed a suite of in silico mechanical simulations: varying the fraction of permanent bonds p, and dynamic bonds intrinsic detachment rate relative to the applied loading, captured by the nondimensional Weissenberg number $\bar{W}$. Between these two parameters we are not only able to control the viscoelastic character of networks but also elucidate the mechanisms underlying damage and fracture. Our stress relaxation simulations show that stress redistribution becomes highly inhomogeneous across a population of force strands via local non-affine rearrangements within the network. Under constant stress, we demonstrate that our model predicts delayed rupture, a common feature of many soft materials^28,34,35. Again, non-affine deformation of local chains - due to the erosion of dynamic bonds - leads to a gradual cascade of force-induced bond rupture, that culminates in nucleation of a critical void and fracture. While continuum modeling approaches^19,49 could be employed to capture both delayed fracture and stress-relaxation, they would struggle to capture local stress redistribution, which our simulations show, not only leads to further structural relaxation, but also a highly inhomogeneous distribution of forces. An inherent advantage of our discrete model then, is that non-affine deformations and inhomogeneous stresses arise naturally.

In the context of fracture, our model shows, in agreement with simulations of double network elastomers⁵⁰ that inhomogeneous stress redistribution can play a large role on damage processes. This is especially true for $\bar{W} < 1$ when dynamic bonds kinetics becomes considerable. Our simulations predict that below the transition point ($\bar{W}=1$) bond rupture becomes rate dependent. This is in contrast to both existing cohesive zone models^10,38, which assume that bond rupture remains confined to chains that bridge the crack interface within a small cohesive zone ahead of the crack tip, and bulk dissipation models⁵¹ which add a bulk hysteric contribution to the fracture energy. For the former, these models often predict zone lengths on the order of a few nanometers, orders of magnitude less than observed by experimental rupture of single¹² and multiple network¹⁵ elastomers. Both significantly under predict the fracture energy of many soft yet tough materials. Instead, the presented model, in conjunction to recent experimental work¹³, shows delocalization of damage from the crack interface within a process zone that depends on network affinity. In stiff, affine networks (i.e., when $\bar{W} > 1$), our results show that damage remains localized, supporting the applicability of classical cohesive zone models for fracture. However, in soft networks (i.e., when $\bar{W} < 1$) where deformations are highly non-affine, damage becomes significantly delocalized, spreading throughout a broad process zone near the crack tip. These simulations highlight the critical role of non-affine rearrangements in contributing to the high toughness observed in many soft materials. They also emphasize the importance of network-scale models for studying fracture and localization as alternatives to conventional continuum models which can only consider localized stress enhancement at the tip of a crack¹¹.

In spite of these findings, there are obvious limitations to our model which was generic by construction. Among these limitations, we may cite the lack of secondary interactions that would act to restrict defect nucleation or the simplicity of the network, that fails to capture long range interactions from chains that span lengths that considerably exceed the network mesh size. Furthermore, we do not model inter-chain interactions such as friction that would enforce a minimum lifetime for dynamic bonds. Incorporating these interactions are subject to future work. Nevertheless, our simple hybrid network model provides a convenient framework to study other damage processes in highly rate-dependent materials such as improved toughness observed in multiple network elastomers¹⁵, or in materials where entanglements outnumber cross-links including gels⁸ and pressure-sensitive adhesive⁵². In these materials the complex coupling between permanent and dynamic cross-links informs their soft yet tough response, highlighting the need for discrete modeling approaches, which are well suited to capture local rearrangements within the network.