Introduction

Rydberg atom arrays have emerged as a rich playground for quantum simulation of many-body problems1. A key property of these arrays is their high degree of programmability, which enables the realization of multiple Hamiltonians on different lattice geometries and parameter ranges. This programmability facilitates the simulation of a wide array of phases of matter2,3 and enables the solution to challenging combinatorial optimization problems3,4,5. The preparation of spin liquid phases—disordered phases of matter characterized by the presence of anyonic excitations, topological invariants, and long-range entanglement—has been demonstrated in programmable Rydberg arrays, potentially serving as building blocks of future generation of fault-tolerant qubits6,7,8.

Recent numerical studies have investigated the physics of the ground state of Rydberg atom arrays in different lattice geometries, in particular in one9 and two spatial dimensions in various geometries10,11,12,13,14,15,16. In lattices such as ruby and honeycomb lattices, strong numerical evidence favors the existence of a spin liquid phase in agreement with experiments14,16. Another recent example is the kagome lattice, where Density Matrix Renormalization Group (DMRG)17,18 studies provided evidence that Rydberg atom arrays host a liquid-like regime13, while Quantum Monte Carlo (QMC) simulations predicted the existence of a spin glass phase19. These systems display frustration arising from lattice geometry and Hamiltonian interactions, leading to the existence of a large number of quantum states with nearly degenerate energies but markedly different properties. This makes it computationally difficult to accurately approximate the ground state of these systems.

Here we focus on applying recurrent neural network (RNNs) wave functions20,21 to a Rydberg array of atoms on the kagome lattice. The effectiveness of RNNs and Transformer language models has already been demonstrated in Rydberg atom arrays on the square lattice22,23,24. RNNs possess two key properties that make them particularly well-suited for studying frustrated systems. Firstly, their ability to perform exact sampling helps mitigate frustration-induced ergodicity issues in quantum Monte Carlo. Secondly, the ability to define them in any spatial dimension without incurring additional computational intractability helps address challenges faced by techniques like DMRG, such as the increased computational cost stemming from increased entanglement in higher dimensions20,25.

Our findings reveal that in the highly frustrated and highly entangled regimes of the system, the RNN predicts a paramagnetic phase without topological order, consistent with earlier QMC simulations19. However, in contrast to the QMC results in ref. 19, the RNN suggests the absence of a spin-glass phase. Nevertheless, in agreement with QMC, our numerical simulations indicate the emergence of a rugged optimization landscape, necessitating more optimization steps and thermal-like fluctuations to mitigate local minima in the RNN’s parameter landscape.

Overall, our results showcase the remarkable applicability and advantages of machine learning-based wave functions, particularly RNNs, in tackling challenging problems at the forefront of Rydberg atom array physics. These findings pave the way for further exploration of exotic phases and phenomena in highly frustrated quantum systems, harnessing the power of modern machine learning techniques to advance our understanding in this field.

Methods

We focus our attention on an array of neutral atoms on the kagome lattice, interacting via laser excitation to atomic Rydberg states. We consider a lattice with periodic boundary conditions (PBC). The Hamiltonian of this system is given by refs. 1,13:

$$\hat{H}= -{\sum }_{i=1}^{N}\frac{\Omega }{2}\left({\left\vert g\right\rangle }_{i}{\left\langle r\right\vert }_{i}+{\left\vert r\right\rangle }_{i}{\left\langle g\right\vert }_{i}\right)-\delta {\sum }_{i=1}^{N}{\left\vert r\right\rangle }_{i}{\left\langle r\right\vert }_{i}\\ +\frac{1}{2}\sum\limits_{i,j}V(| | {{{{\boldsymbol{x}}}}}_{i}-{{{{\boldsymbol{x}}}}}_{j}| | ){\left\vert r\right\rangle }_{i}{\left\langle r\right\vert }_{i}\otimes {\left\vert r\right\rangle }_{j}{\left\langle r\right\vert }_{j}.$$

Here \({\left\vert g\right\rangle }_{i},{\left\vert r\right\rangle }_{i}\) are respectively the ground and excited states of the Rydberg atom i. Ω is the Rabi frequency and δ is the laser detuning. V(R) = C/R6 is the repulsive potential due to the dipole-dipole interaction between Rydberg atoms, which is responsible for the blockade mechanism1. In practice, we define a blockade radius Rb such that V(Rb/a) = Ω, where a is the distance between two neighboring Rydberg atoms. Finally, we note that the sum over all possible pairs is truncated to a sum over neighbors separated by a distance cutoff Rc = 2 or Rc = 4. The choice Rc = 2 is taken to compare with the DMRG results reported in ref. 13 as well as with the QMC findings in ref. 19

Two dimensional RNNs

The Rydberg Hamiltonian is stoquastic in nature26, which implies that the ground-state wave function contains only positive amplitudes. This offers the opportunity to model the ground state with an RNN wave function with only positive amplitudes20 which we adopt below. Complex extensions of RNN wave functions for non-stoquastic Hamiltonians have been explored in refs. 20,21,25. To model a positive RNN wave function, we can express our ansatz in the computational basis as:

$${\Psi }_{{{{\boldsymbol{\theta }}}}}({{{\boldsymbol{\sigma }}}})=\sqrt{{p}_{{{{\boldsymbol{\theta }}}}}({{{\boldsymbol{\sigma }}}})},$$

such that θ corresponds to the variational parameters of the ansatz \(\left\vert {\Psi }_{{{{\boldsymbol{\theta }}}}}\right\rangle\), and σ = (σ1, σ2, …, σN) is a configuration of the Rydberg atoms. The main advantage of using RNN wave functions is the possibility of estimating observables through autoregressive sampling, which allows obtaining uncorrelated samples by construction20. To do so, we model the joint probability pθ(σ) by constructing the conditionals pθ(σi∣σ<i) by taking advantage of the probability chain rule

$${p}_{{{{\boldsymbol{\theta }}}}}({{{\boldsymbol{\sigma }}}})={p}_{{{{\boldsymbol{\theta }}}}}({\sigma }_{1}){p}_{{{{\boldsymbol{\theta }}}}}({\sigma }_{2}| {\sigma }_{1})\cdots {p}_{{{{\boldsymbol{\theta }}}}}({\sigma }_{N}| {\sigma }_{N-1},\ldots ,{\sigma }_{2},{\sigma }_{1}).$$

These conditional probabilities are obtained through a Softmax layer as follows:

$${p}_{{{{\boldsymbol{\theta }}}}}({\sigma }_{i}| {\sigma }_{ < i})={{{{\boldsymbol{y}}}}}_{i}\cdot {{{{\boldsymbol{\sigma }}}}}_{i}.$$

Here yi = Softmax(Uhi + c) where U and c are, respectively, trainable weights and biases, and ‘Softmax’ corresponds to the normalizing Softmax activation function. Additionally, the memory (hidden) state hi is obtained recursively as ref. 27:

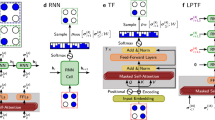
$${{{{\boldsymbol{h}}}}}_{i}=f(W[{{{{\boldsymbol{h}}}}}_{i-1};{{{{\boldsymbol{\sigma }}}}}_{i-1}]+{{{\boldsymbol{b}}}}),$$
(1)

such that [. ; . ] is a concatenation of two vectors, while σi−1 is a one-hot encoding of σi−1. These computations are illustrated in Fig. 1a. W and b are also trainable weights and biases, and f is a user-defined activation function.

Fig. 1: RNN wave functions architecture details.
figure 1

a An illustration of a positive RNN wave function. Each RNN cell receives an input σn−1 and a hidden state hn−1 and outputs a new hidden state hn. This vector is taken as an input to the Softmax layer (denoted S) that computes the conditional probability Pi. b RNN autoregressive sampling scheme: after obtaining the probability vector yi from the Softmax layer (S) in step i, we sample it to produce σi. The latter is taken again as an input to the RNN along with the hidden state hi to sample the following degree of freedom σi+1. c Mapping of a Kagome lattice to a square lattice by embedding three atoms in a larger local Hilbert space. d A two-dimensional (2D) RNN with periodic boundary conditions for a 3 × 3 lattice for illustration purposes. A bulk RNN cell receives two hidden states hi,j−1 and \({{{{\boldsymbol{h}}}}}_{i-{(-1)}^{j},j}\), as well as two input vectors σi,j−1 and \({{{{\boldsymbol{\sigma }}}}}_{i-{(-1)}\,^{j},j}\) (not shown) as illustrated by the black solid arrows. RNN cells at the boundary receive additional hidden states hi,j+1 and \({{{{\boldsymbol{h}}}}}_{i+{(-1)}\,^{j},j}\), as well as two input vectors σi,j+1 and \({{{{\boldsymbol{\sigma }}}}}_{i+{(-1)}^{j},j}\) (not shown), as demonstrated by the blue curved and solid arrows. The sampling path is taken as a zigzag path, as demonstrated by the dashed red arrows. The initial memory states of the 2D RNN and the initial inputs are null vectors, as indicated by the dashed black arrows.

Full size image

By virtue of the ‘Softmax’ activation function, the conditionals pθ(σi∣σ<i) are normalized to one. This property implies that the RNN joint probability pθ is also normalized20. Furthermore, by sampling the conditionals pθ(σi∣σ<i) sequentially, as illustrated in Fig. 1b, we can extract exact samples from the joint RNN probability pθ. An attractive property of this scheme is the possibility to efficiently generate uncorrelated samples from different modes present in pθ, whereas traditional Metropolis sampling scheme may get stuck in only one mode.

The atom configurations of a Rydberg atom array on a kagome lattice can be seen as an L × L × 3 array of binary degrees of freedom where L is the size of each side of the lattice. As illustrated in Fig. 1c, we can map our kagome lattice with a local Hilbert space of 2 to a square lattice with an enlarged Hilbert space of size 23 = 8 which we can study using our two-dimensional (2D) RNN wave function23,28.

To construct a 2D RNN ansatz that can handle PBC, we modify our RNN recursion in Eq. (1) to a two-dimensional recursion relation as:

$${{{{\boldsymbol{h}}}}}_{i,j}=f\,\left(W[\,{{\mbox{Neighbours}}}\,({{{{\boldsymbol{h}}}}}_{i,j});\,{{\mbox{Neighbours}}}\,({{{{\boldsymbol{\sigma }}}}}_{i,j})]+{{{\boldsymbol{b}}}}\right).$$
(2)

hi,j is a memory state with two indices for each atom in the two-dimensional lattice. Here ‘Neighbours(σi,j)’ returns a concatenation of the neighbors of σi,j. The same observation goes for ‘Neighbours(hi,j)’. These neighbors correspond to incoming vectors indicated by the black and blue arrows as illustrated in Fig. 1d. More specifically, we define

$$\,{{\mbox{Neighbours}}}\,({{{{\boldsymbol{h}}}}}_{i,j})\equiv \,[{{{{\boldsymbol{h}}}}}_{i-{(-1)}\,^{j},j};{{{{\boldsymbol{h}}}}}_{i,j-1};{{{\mathbf{0}}}};{{{\mathbf{0}}}}]$$

on the bulk. On the boundaries, we take

$${{\mbox{Neighbours}}}\,({{{{\boldsymbol{h}}}}}_{i,j})\equiv \left[{{{{\boldsymbol{h}}}}}_{i-{(-1)}\,^{j},j};{{{{\boldsymbol{h}}}}}_{i,j-1};\right. \\ \left.{{{{\boldsymbol{h}}}}}_{i+{(-1)}\,^{j},j};{{{{\boldsymbol{h}}}}}_{i,j+1}\right].$$

Note that PBC on the indices is assumed. The additional inputs \({{{{\boldsymbol{\sigma }}}}}_{i+{(-1)}^{j},j}\), σi,j+1 and hidden states \({{{{\boldsymbol{h}}}}}_{i+{(-1)}\,^{j},j}\), hi,j+1 allow to take PBC into account and to introduce correlations between degrees of freedom at the boundaries. During the autoregressive sampling procedure, the input and hidden vectors are initialized to a null vector, if not previously defined, to preserve the autoregressive nature of our scheme, as illustrated in Fig. 1b. Also, note that the particular choice of the indices is motivated by the zigzag sampling path. In this study, we use an advanced version of 2D RNNs incorporating the gating mechanism as previously done in refs. 25,29,30. More details can be found in Supplementary Note 1. Finally, since hi,j is a summary of the history of the generated σ<i,j, it is used to compute the conditional probabilities as follows:

$${p}_{{{{\boldsymbol{\theta }}}}}({\sigma }_{i,j}| {\sigma }_{ < i,j})=\,{{\mbox{Softmax}}}\,(U{{{{\boldsymbol{h}}}}}_{i,j}+{{{\boldsymbol{c}}}})\cdot {{{{\boldsymbol{\sigma }}}}}_{i,j}.$$
(3)

Supplementing RNN optimization with annealing

To reach the ground state of the Rydberg atoms array Hamiltonian on the kagome lattice, we minimize the energy expectation value \({E}_{{{{\boldsymbol{\theta }}}}}=\left\langle {\Psi }_{{{{\boldsymbol{\theta }}}}}\right\vert \hat{H}\left\vert {\Psi }_{{{{\boldsymbol{\theta }}}}}\right\rangle\) using the Variational Monte Carlo (VMC) scheme31 (see Supplementary Note 2). Due to the frustrated nature of the kagome lattice which can induce local minima in the VMC scheme, we leverage annealing with thermal-like fluctuations to mitigate local minima. This technique has been suggested and implemented in refs. 21,25,28,32,33,34. In this case, we obtain a free-energy like cost function, defined as

$${F}_{{{{\boldsymbol{\theta }}}}}(n)={E}_{{{{\boldsymbol{\theta }}}}}-T(n){S}_{{{{\rm{classical}}}}}({p}_{{{{\boldsymbol{\theta }}}}}),$$
(4)

where Fθ is a variational pseudo Free energy and Sclassical is the classical Shannon entropy:

$${S}_{{{{\rm{classical}}}}}({p}_{{{{\boldsymbol{\theta }}}}})=-\sum\limits_{{{{\boldsymbol{\sigma }}}}}{p}_{{{{\boldsymbol{\theta }}}}}({{{\boldsymbol{\sigma }}}})\log \left({p}_{{{{\boldsymbol{\theta }}}}}({{{\boldsymbol{\sigma }}}})\right).$$
(5)

The previous sum goes over all classical Rydberg configurations {σ} in the computational z-basis. Note that Sclassical is a pseudo-entropy that can be efficiently estimated using our RNN wave function as opposed to the quantum von Neumann entropy. Additionally, T(n) is a pseudo-temperature that is annealed from some initial value T0 to zero as follows: T(n) = T0(1 − n/Na) where n ∈ [0, Na] and Na is the total number of annealing steps. We note that for each annealing step, we train our RNN for 5 training steps. We present more details about the hyperparameters of our training scheme in Supplementary Note 3.

Topological entanglement entropy

To investigate the existence of a topological property in the Rydberg atom arrays on the kagome lattice, we compute the topological entanglement entropy (TEE)35,36,37,38,39,40,41. For a gapped phase of matter, where the area law is satisfied, the Renyi-2 entanglement entropy follows the scaling law \({S}_{2}(A)=aL-\gamma +{{{\mathcal{O}}}}({L}^{-1})\), assuming A and B is partition of the system, L is the size of the boundary between A and B and \({S}_{2}(A)\equiv -\log (\,{{\mbox{Tr}}}\,({\rho }_{A}^{2}))\). In this case, γ is the so-called TEE. In this paper, we use the swap trick with our RNN wave function ansatz20,42,43 to calculate the second Renyi entropy S2 to extract the TEE γ.

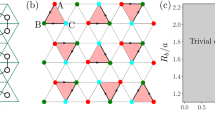
We extract γ using two different strategies, namely the Kitaev-Preskill construction38 and the Levin-Wen construction37, illustrated in Fig. 2.

Fig. 2: Topological entanglement entropy constructions.
figure 2

a A sketch of the parts A, B, and C that we use for Kitaev-Preskill construction to compute the TEE. b Levin-Wen construction using the regions A, B, C and D. For the Rydberg atoms Hamiltonian on a kagome lattice, each dot on the square lattice corresponds to a block of three binary degrees of freedom, as shown in Fig. 1c.

Full size image

The Kitaev-Preskill construction consists of choosing three subregions A, B, C with geometries as shown in Fig. 2a. The TEE can be then obtained by computing

$$\begin{array}{rc}\gamma &=-{S}_{2}(A)-{S}_{2}(B)-{S}_{2}(C)+{S}_{2}(AB)\\ &+{S}_{2}(AC)+{S}_{2}(BC)-{S}_{2}(ABC),\end{array}$$

where S2(A) is the second Renyi entropy of the subsystem A, and AB is the union of A and B and similarly for the other terms. It is worth mentioning that finite size effects on γ can be reduced by extrapolating the size of the subregions38,44. Finally, note that this approach combined with RNN wave functions was successful in extracting a non-zero TEE on the toric code and the hard-core Bose-Hubbard model on the kagome lattice28.

The Levin-Wen construction allows to extract the TEE γ by constructing four different subsystems A1 = A ∪ B ∪ C ∪ D, A2 = A ∪ C ∪ D, A3 = A ∪ B ∪ D and A4 = A ∪ D as illustrated in Fig. 2b such that40:

$$\gamma =\frac{-{S}_{2}({A}_{1})+{S}_{2}({A}_{2})+{S}_{2}({A}_{3})-{S}_{2}({A}_{4})}{2}.$$

Note that finite size effects on γ can be reduced by extrapolating the width and thickness of A1, A2, A3 and A440,44.

Finally, we would like to highlight that our ability to study quantum systems with fully periodic boundary conditions is key to mitigating boundary effects, as opposed to cylinders used in DMRG45,46, which can introduce boundary effects in the TEE value13.

Results

According to the RNN numerics, our results show that the ground state at Rb = 1.95 and δ = 3.3, which is suggested to be in the spin-liquid phase according to ref. 13, is rather a disordered state with no topological order. We first plot the correlations 〈n0nr〉 in Fig. 3a. The results indicate that the extracted state has short-range correlations. To confirm the correctness of our variational implementation, we perform a sanity check and compare our ground state energies with QMC and DMRG as shown in Supplementary Note 4. We found a good agreement between our RNN energies and QMC as well as DMRG energies. Most importantly, we observe that our RNN results using only dh = 100 are more accurate compared to DMRG with a bond dimension χ = 1000 in the highly entangled regime at Rb = 1.95 and δ = 3.3.

Fig. 3: Numerical results of 2DRNNs applied to Rydberg atom arrays on kagome lattice.
figure 3

In these panels, we focus on the Blockade radius Rb = 1.95. a Plot of two point correlations 〈n0nr〉 with δ = 3.3 and for a system size N = 8 × 8 × 3 and Rc = 2. b Plots of the topological entanglement entropy versus δ for two different values of the cutoff radius Rc, using the Levin-Wen (LW) construction and the Kitaev-Preskill (KP) construction, for N = 8 × 8 × 3. c A histogram of the Edwards-Anderson order parameter qEA defined in Eq. (6) as a function of δ for N = 8 × 8 × 3. The inset provides a zoomed-in view close to zero. d A plot of the density overlaps \(\frac{1}{N}{\sum }_{i = 1}^{N}{n}_{i}^{(1)}{n}_{i}^{(2)}\) and the spin overlaps \(\frac{1}{N}{\sum }_{i = 1}^{N}{S}_{i}^{(1)}{S}_{i}^{(2)}\) at δ = 3.3. Here Si = 2ni − 1, and (1) and (2) are labels for two sets of samples obtained from our optimized RNN, that are aggregated from 10 different training seeds, for N = 6 × 6 × 3 and Rc = 2. For each seed, we generate 2 × 105 independent samples and divide them into two sets. The error bars indicate the statistical uncertainty of one standard deviation, calculated across different samples. In this and other plots throughout the Article, error bars may be hidden if they are smaller than the symbol size.

Full size image

To investigate the existence of a spin liquid in this regime, we calculate the TEE γ using the Kitaev-Preskill construction38 for a system size L = 8 (see Fig. 2a), and for different values of δ ∈ [2.0, 3.7] and Rc = 2, 4 at Rb = 1.95. We also do the same using the Levin-Wen construction40 in Fig. 2b. Our results, illustrated in Fig. 3b suggest that the TEE extracted by the RNN is consistent with zero and different from \(\ln (2)\) within error bars. These results suggest the non-existence of a spin liquid within our settings and also suggest that the state we find in this regime is a disordered state. Our findings are further corroborated by a recent QMC study19 and also by previous results in the literature suggesting that the paramagnetic ‘liquid’ phase in Ising systems on the kagome lattice is not exotic47,48,49.

To address the finite-size scaling of the TEE, we compute the TEE at Rb = 1.95, δ = 3.3 for N = 10 × 10 × 3 by pre-training from the RNN optimized at L = 8 and also for L = 12 by starting from the optimized parameters at L = 10. We follow a similar KP construction to Fig. 2 of the regions A, B and C where the size of each subregion is given as 3 × 3 × 3, 3 × 3 × 3, and 6 × 3 × 3 for L = 6 respectively, and 4 × 4 × 3, 4 × 4 × 3, and 8 × 4 × 3 for L = 8. Our estimates γRNN = 0.10 ± 0.26, −0.1 ± 0.22 for L = 6 and L = 8 respectively. These values, which are consistent with zero TEE, corroborate the absence of a Z2 spin-liquid according to the RNN variational calculations. Note that the error bars can be systematically reduced by increasing the number of samples in the swap trick calculations20,28.

In this QMC study19, it was suggested that the region, around Rb = 1.95 and the values of δ used in our study contains an emergent spin-glass phase instead of a paramagnetic state. To verify this claim, we compute the Edwards-Anderson (EA) order parameters50,51, defined as:

$${q}_{{{{\rm{EA}}}}}=\frac{\mathop{\sum }_{i = 1}^{N}{\langle {n}_{i}-\rho \rangle }^{2}}{N\rho (1-\rho )},$$
(6)

where N is the system size, ni is the occupation number of site i and \(\rho =(\mathop{\sum }_{i = 1}^{N}{n}_{i})/N\). Deviations of this order parameter from zero values are signals of the existence of a spin-glass phase. In Fig. 3c, we plot this order parameter as a function of δ with Rc = 2, 4 and Rb = 1.95. We find that the values of the order parameter are consistent with zero, as opposed to the results of QMC in ref. 19. Furthermore, we report in Fig. 3d the density-density overlap \(\frac{1}{N}\mathop{\sum }_{i = 1}^{N}{n}_{i}^{(1)}{n}_{i}^{(2)}\) and the spin-spin overlap \(\frac{1}{N}\mathop{\sum }_{i = 1}^{N}{S}_{i}^{(1)}{S}_{i}^{(2)}\) between different RNN samples at Rb = 1.95, δ = 3.3, and Rc = 2. Here labels (1) and (2) correspond to two independent sets of samples, which are obtained from optimized RNNs with 10 different training seeds. The Gaussian nature of the overlap distribution in both representations is another indicator that there is no static signature of a spin-glass order52.

The discrepancy in our results and previous QMC findings19 could be related to emergent glassy dynamics in the QMC simulations, which results in very long auto-correlations times and thus in a non-ergodic behavior. To corroborate our findings, we run QMC simulations53, based on Stochastic Series Expansion (SSE)54,55, for larger inverse temperatures compared to ref. 19, namely for β ≥ 200 and using 2.2 × 106 Monte Carlo samples. We find that the QMC prediction for the EA order parameter is given as \({q}_{\,{{\rm{EA}}}}^{{{\rm{QMC}}}\,}=0.0000018(5)\) for Rb = 1.95, δ = 3.3, a system size 8 × 8 × 3, and for a radius cutoff Rc = 2. The previous result agrees very well with our RNN findings in Fig. 3c. This result is also confirmed by the good agreement between the RNN energies and the QMC energies as shown in Supplementary Note 4. Our findings are further supported by the results of ref. 56, which suggests the possibility of transition in a quantum dimer model between nematic to paramagnetic to staggered states. In conclusion, our numerical investigation suggests that the long auto-correlation time could be a limiting factor in the QMC results reported in ref. 19.

We note that the emergence of a long autocorrelation time in QMC coincides with the emergence of a rugged optimization landscape, which in our simulations implies a longer number of annealing steps in our RNN simulations to achieve convergence. To demonstrate this point, we compute the structure factor

$$S({{{\boldsymbol{q}}}})=\frac{1}{N}\mathop{\sum}_{i,j}\langle {n}_{i}{n}_{j}\rangle \,{e}^{{{{\rm{i}}}}{{{\boldsymbol{q}}}}\cdot ({{{{\boldsymbol{x}}}}}_{i}-{{{{\boldsymbol{x}}}}}_{j})}$$
(7)

to extract the nature of the states obtained by our RNN ansatz and investigate their dependence on the number of annealing steps Na. We expect the optimization landscape to be rougher as Na required to converge increases. Figure 4a–d at Rb = 1.95 and δ = 3.3 show that the RNN finds different states for different numbers of annealing steps Na, until it converges to a state without ordering peaks, i.e., the paramagnetic state. In contrast, the nematic state at Rb = 1.7, δ = 3.3 can be reached without the need for annealing, as illustrated by the structure factors at different Na in Fig. 4e–h. These observations suggest an emergent rugged optimization landscape when optimizing our ansatz in the highly entangled regime. Finally, to find the optimal number of annealing steps Na in the highly entangled regime, we note that we conduct a scaling study as shown in Supplementary Note 5.

Fig. 4: Structure factor evolution with the number of annealing steps.
figure 4

We illustrate the structure factor for different values of the number of annealing steps Na at Rb = 1.95, δ = 3.3 in (a–d) and at Rb = 1.7, δ = 3.3 in (e–h). The color bars represent the magnitude of the structure factor S(q). Additionally, these results correspond to a system size N = 6 × 6 × 3. Note that we observe convergence to a paramagnetic state without ordering peaks beyond Na = 1000 for Rb = 1.95, δ = 3.3. For Rb = 1.7, δ = 3.3, we find that the nematic state is not affected by the choice of Na and can be obtained without a need for annealing.

Full size image

To indicate the quality of our variational calculations, we use the v-score as a metric57, which we report in Supplementary Note 6. Furthermore, to investigate the effect of parameter sharing in the RNN, illustrated in Eqs. (2), (3), we optimized our RNN using site-dependent parameters at Rb = 1.95, δ = 3.3 and for L = 8 and we find that both TEE and EA order parameters are consistent with zero within errors bars. This result confirms that parameter-sharing in our RNN ansatz does not bias our findings. More details are shared in Supplementary Note 7.

Finally, we report a comparison between RNN and QMC runtimes in Supplementary Note 8. In particular, we find a significant speed-up when training RNNs on an A100 GPU and QMC on a single CPU. This speedup is enabled by GPU hardware in addition to the ability of the 2DRNN to do transfer learning from smaller lattices to larger ones21,25,28,30,58,59.

Conclusion

In this paper, we demonstrate a successful application of recurrent neural network (RNN) wave functions to the task of investigating topological order on Rydberg atom arrays on kagome lattice. We use these architectures to estimate the second Renyi entropies using the swap trick20. The latter allows us to compute the TEEs using the Kitaev-Preskill38 and the Levin-Wen37 constructions. Furthermore, with the possibility of handling periodic boundary conditions in RNNs, the boundary effects on the TEE are reduced compared to DMRG, which has challenges with boundary effects on cylinders46.

Our main finding, suggested by the two-dimensional RNN wave functions results, points out that Rydberg atom arrays on the kagome lattice do not establish a Z2 spin liquid in the highly entangled regime. This observation is also consistent with previous QMC studies19. Our RNN numerics also suggest that the highly entangled region corresponds to a trivial paramagnetic state and that there is no signature for spin glass order as opposed to the observations outlined in ref. 19. We believe that the ability of RNNs to generate uncorrelated samples from a multimodal distribution is a crucial factor for our numerics to indicate the non-existence of the spin-glass phase. Additionally, we find that autocorrelation could be the main factor behind the spin glass phase observed in previous QMC simulations19. In particular, our QMC numerics with more numerical effort compared to ref. 19. suggest the absence of a spin glass phase. Furthermore, supplementing RNNs with annealing turns out to be a valuable tool for mitigating local minima induced by the frustrated nature of the kagome lattice in the highly entangled regime. We highlight that advanced optimization schemes, such as minimal Stochastic Reconfiguration (minSR)60,61, is a potential avenue for enhancing the optimization of our 2DRNN ansätzes. Refs. 62,63 reported that Stochastic Reconfiguration (SR) is not as effective as Adam optimizer when applied to RNN wave functions. As a result, we believe that reconciling SR and RNN wave function optimization is an interesting research direction that deserves a thorough study in the future. Furthermore, studying dynamic properties of Rydberg atoms arrays is another promising research direction that can corroborate our findings by performing time-evolution on our RNN ansatz64,65.

Finally, we note that our method can be generalized to study other systems with potential topological order, such as the Rydberg atom arrays on the Ruby lattice14,66,67. One could also use quantum state tomography with RNNs68 in a wide variety of quantum simulators and also combine data from QMC or quantum simulators with VMC to improve the variational results22,24,69,70. We also believe in the potential of RNN wave functions ansätzes in the discovery of new phases of matter with topological order. Overall, these results highlight the promising future of RNN wave functions20,21, language-model based wave functions, and neural quantum states71, in general, for investigating open questions and discovering new physics within the condensed matter community and beyond.