Towards determining the (2+1)-dimensional quantum electrodynamics running coupling with Monte Carlo and quantum computing methods

Abstract

The solution of strongly-interacting quantum field theories remains a major challenge in theoretical physics, often requiring numerical solutions. A first-principles approach in this direction is the lattice formulation, where spacetime is approximated with a finite grid. In this work, we examine the case of a compact pure-gauge U(1) lattice gauge theory in (2 + 1) dimensions, presenting a strategy to determine the running coupling of the theory and extracting the non-perturbative Λ-parameter. This is achieved by combining Monte Carlo simulations and quantum computing techniques, matching the expectation value of the plaquette operator. We also present results for the static potential and static force, which can be related to the renormalized coupling. The outlined procedure can be extended to other Abelian and non-Abelian lattice gauge theories with matter fields, and might provide a way towards studying lattice quantum chromodynamics utilizing both quantum and classical methods.

Introduction

Quantum field theories are very successful in describing the fundamental laws of nature within the framework of the Standard Model (SM) of particle physics, which unites three of the four known fundamental forces of nature. While many phenomena in the SM can be investigated analytically using perturbation theory, quantum chromodynamics (QCD) is a prominent example of a theory which requires non-perturbative methods in the low-energy regime¹. This concerns, for instance, the hadron spectrum or the QCD energy scale Λ_QCD, which is related to the running coupling of QCD and is generated entirely dynamically². Moreover, the running of the coupling enters all analysis of experimental data of particle accelerators, see e.g., Section 9 in ref. ³. Therefore, first-principle theoretical calculations of such quantities are of high importance. The standard approach for non-perturbative computations in quantum field theories is given by the lattice regularization, see e.g., refs. ^4,5, in combination with stochastic Monte Carlo (MC) methods based on the Euclidean path integral, pioneered by Wilson⁶ and Creutz⁷. In this lattice gauge theory (LGT) approach, the theory is regularized by a finite volume and a discretized space-time. In order to make contact with experimental results, the infinite volume and continuum limits need to be taken. This approach has allowed the computation of many phenomenologically highly relevant quantities, see for instance ref. ⁸, due to significant algorithmic and methodological progress, as well as ever-increasing computer power.

Despite these successes, there are still limitations of the MC approach to LGTs. Among them we recall the sign problem⁹ and critical slowing down. The former prevents from simulating, e.g., real-time evolutions or actions with non-zero matter density, while the latter manifests in a (often exponential) increase of autocorrelation times towards the continuum limit g → 0 (see e.g., refs. ^10,11). In this limit, the non-perturbative calculation of the running coupling on the lattice could, in principle, be matched with perturbation theory, allowing for the determination of Λ_QCD^12,13. Some attempts in this direction have been explored already in e.g., refs. ^14,15,16. In this work, however, we advocate the joint use of MC together with the Hamiltonian formulation of LGTs. In fact, in the latter formulation, one can use, for instance, quantum computing techniques, avoiding the issues related to autocorrelation. Hence, such methods offer the potential of following the approach of working in the regime of very small bare couplings, as proposed in ref. ¹⁷. In recent years, the research field of quantum computing has seen much progress, which resulted in various proof-of-concept demonstrations of lattice gauge theory simulations with quantum technologies^18,19,20.

The goal of this work is to develop a framework to compute the running coupling by utilizing both quantum and classical methods, in order to enable the above-mentioned approach. With present noisy intermediate scale quantum (NISQ) capabilities²¹, it is, however, impossible to study (3 + 1)-dimensional QCD. Therefore, in this paper, we aim at a proof-of-concept for this idea in (2 + 1)-dimensional compact U (1) pure gauge theory, with an eventual extension to (2 + 1)-dimensional QED, which shares important properties with (3 + 1)-dimensional QCD, such as confinement and asymptotic freedom.

The final goal is to compute the Λ-parameter for (2 + 1)-dimensional QED, which sets the scale where perturbation theory breaks down. To give a quantitative value, the perturbative running of the coupling needs to be confronted with a non-perturbative calculation. In principle, this can be already achieved with a perturbative calculation at the one-loop level. This would, however, require very small values of the coupling, where MC calculations are facing severe problems of autocorrelation when considering large volumes. Therefore, to determine the Λ-parameter, higher order loops are included in the corresponding lattice perturbation theory, to be able to go to larger values of g where MC simulations can be performed. This, in turn, requires very demanding perturbative calculations, which can be considered a substantial and independent project in its own right¹². Therefore, it would be a major simplification if we could employ only the one-loop order theory. We propose here to test whether such a scenario can eventually be realized with a quantum computing approach.

A study of (2 + 1)-dimensional QED has been performed perturbatively, with both two and four-component spinors, in refs. ^22,23,24. Here, we propose to combine both quantum computing and MC methods and exploit the respective strengths of these two approaches: first, we perform quantum simulations at small values of the bare coupling to compute the running coupling at small distances. Large volume stochastic simulations¹⁷ then allow to determine the lattice spacing by eventually making contact with experimental or phenomenological results, as it is done for Lattice QCD computations⁸. This work will focus mainly on the aspects of the quantum computing approach and the corresponding numerical techniques. A short description of the MC method, used here, is discussed in Supplementary Note 2. As outlined in a previous work ref. ¹⁷, we employ a quantum variational technique. Variational quantum algorithms, such as the Variational Quantum Eigensolver²⁵, have been extensively used in the past years to study lattice gauge theories, see again refs. ^18,20. A benefit of these methods is the possibility of achieving physically meaningful results already with the current NISQ devices. However, they also present some limitations. A known phenomenon is the appearance of Barren Plateaus, see e.g., refs. ^26,27, which can lead to slow convergence or even complete failure of the optimization process. Another example is their scalability to larger systems, since the variational quantum algorithms involve a classical optimization. Here, we introduce a scheme for designing a quantum circuit that leads to a substantial reduction of the computational cost required in the quantum simulation. In contrast to ref. ¹⁷, here we perform an actual implementation of the proposed strategy, developing a feasible computational method to realize a non-perturbative evaluation of the running coupling.

In this paper, we propose a general procedure, based on a step scaling approach, to compute the running coupling as a function of a physical scale. We then consider a matching between MC and quantum computing, through suitable observables, such as the plaquette expectation value, as we employ in this work. This matching is carried out in a regime of $g \sim {{{\mathcal{O}}}}(1)$, where both methods are reliable. MC can, in principle, be used to obtain the physical value of the lattice spacing from large-volume calculations. The so obtained physical scale can then be transferred to the quantum computing analysis. The step scaling function has been considered, e.g., in O (3) sigma model in (1 + 1) dimensions in refs. ^{28,29,30,31,32}. Here we focus on implementing and testing the feasibility of the method in compact U (1) pure gauge theory at a fixed 3 × 3 lattice volume as an initial demonstration, and propose a follow-up extension to matter fields. The latter, however, goes beyond the scope of the present work. The inclusion of matter fields will lead to a nontrivial β-function, rendering the system physically meaningful. The proposed procedure can be directly generalized to (2 + 1)-dimensional QED but also to non-Abelian lattice gauge theories, and eventually to QCD. Furthermore, to study the continuum limit, large-scale computations are required. This would, in principle, be possible with access to quantum devices with a large number of qubits³³. Moreover, this matching procedure is independent of the way we get the quantum state to compute the expectation value of the physical observables relevant to this work. For example, the quantum simulation could be performed on cold atom quantum simulators or trapped ions quantum simulators³⁴.

Results

Hamiltonian

We consider a lattice discretization of the U (1) LGT using Kogut-Susskind staggered fermions^35,36,37. A naive discretization of the fermionic degrees of freedom leads to the so-called doubling problem^4,38,39, i.e., an incorrect continuum limit of the theory. In the staggered formulation, the spinor components are distributed on different lattice sites to avoid this problem. We present the full Hamiltonian, including matter fields, for completeness, even though it is not used in the present work. The Hamiltonian reads

$${\hat{H}}_{{{{\rm{tot}}}}}={\hat{H}}_{E}+{\hat{H}}_{B}+{\hat{H}}_{m}+{\hat{H}}_{{{{\rm{kin}}}}},$$

(1)

where ${\hat{H}}_{E}$ is the electric energy, ${\hat{H}}_{B}$ the magnetic energy contribution, ${\hat{H}}_{m}$ the fermionic mass term and ${\hat{H}}_{{{{\rm{kin}}}}}$ the kinetic term for the fermions. The electric energy is given by

$${\hat{H}}_{E}=\frac{{g}^{2}}{2}\sum\limits_{{{{\bf{r}}}}}\left({\hat{E}}_{{{{\bf{r}}}},x}^{2}+{\hat{E}}_{{{{\bf{r}}}},y}^{2}\right),$$

(2)

where ${\hat{E}}_{{{{\bf{r}}}},\mu }$ is the dimensionless electric field operator that acts on the link emanating from the lattice site with the coordinates r = (r_x, r_y) in direction μ ∈ {x, y}. The bare coupling g determines the strength of the interaction, playing a pivotal role throughout the work. The second term in ${\hat{H}}_{{{{\rm{tot}}}}}$, the magnetic interaction, reads

$${\hat{H}}_{B}=-\frac{1}{2{a}^{2}{g}^{2}}\sum\limits_{{{{\bf{r}}}}}\left({\hat{P}}_{{{{\bf{r}}}}}+{\hat{P}}_{{{{\bf{r}}}}}^{{{\dagger}} }\right),$$

(3)

with a the lattice spacing and ${\hat{P}}_{{{{\bf{r}}}}}={\hat{U}}_{{{{\bf{r}}}},x}{\hat{U}}_{{{{\bf{r}}}}+x,y}{\hat{U}}_{{{{\bf{r}}}}+y,x}^{{{\dagger}} }{\hat{U}}_{{{{\bf{r}}}},y}^{{{\dagger}} }$ the so-called plaquette operator consisting of a product of the operators ${\hat{U}}_{{{{\bf{r}}}},x}$ acting on the links of a plaquette of the lattice (with the subscripts notation r + x ≡ (r_x + 1, r_y) or r + y ≡ (r_x, r_y + 1)). The unitary operators ${\hat{U}}_{{{{\bf{r}}}},x}$ are related to the discretized vector field ${\hat{A}}_{{{{\bf{r}}}},\mu }$ as

$${\hat{U}}_{{{{\bf{r}}}},\mu }={e}^{iag{\hat{A}}_{{{{\bf{r}}}},\mu }}.$$

(4)

They represent the gauge connection between the fermionic fields, and we choose to work with a compact formulation where $ag{\hat{A}}_{{{{\bf{r}}}},\mu }$ is restricted to (0, 2π). The lattice vector field is the canonical conjugate variable to the electric field, hence one finds for the commutation relations between ${\hat{E}}_{{{{\bf{r}}}},\nu }$ and ${\hat{U}}_{{{{{\bf{r}}}}}^{{\prime} },\mu }$

$$[{\hat{E}}_{{{{\bf{r}}}},\nu },{\hat{U}}_{{{{\bf{r}}}}{\prime} ,\mu }]={\delta }_{{{{\bf{r}}}},{{{{\bf{r}}}}}^{{\prime} }}{\delta }_{\nu ,\mu }{\hat{U}}_{{{{\bf{r}}}},\nu },$$

(5)

$$[{\hat{E}}_{{{{\bf{r}}}},\nu },{\hat{U}}_{{{{{\bf{r}}}}}^{{\prime} },\mu }^{{{\dagger}} }]=-{\delta }_{{{{\bf{r}}}},{{{{\bf{r}}}}}^{{\prime} }}{\delta }_{\nu ,\mu }{\hat{U}}_{{{{{\bf{r}}}}}^{{\prime} },\nu }^{{{\dagger}} }.$$

(6)

The fermionic mass term is given by

$${\hat{H}}_{m}=m\sum\limits_{{{{\bf{r}}}}}{(-1)}^{{r}_{x}+{r}_{y}}{\hat{\phi }}_{{{{\bf{r}}}}}^{{{\dagger}} }{\hat{\phi }}_{{{{\bf{r}}}}},$$

(7)

where m is the bare lattice fermion mass and ${\hat{\phi }}_{{{{\bf{r}}}}}$ a and a single-component fermionic field residing on site r, since we start from a continuum formulation with two-component Dirac spinors (see Supplementary Note 4 for details). The kinetic term corresponds to a correlated fermion hopping between two lattice sites while simultaneously changing the electric field on the link in between,

$${\hat{H}}_{{{{\rm{kin}}}}}= \frac{i}{2a}\sum\limits_{{{{\bf{r}}}}}({\hat{\phi }}_{{{{\bf{r}}}}}^{{{\dagger}} }{\hat{U}}_{{{{\bf{r}}}},x}{\hat{\phi }}_{{{{\bf{r}}}}+x}-{{{\rm{h.c.}}}})\\ -\frac{{(-1)}^{{r}_{x}+{r}_{y}}}{2a}\sum\limits_{{{{\bf{r}}}}}({\hat{\phi }}_{{{{\bf{r}}}}}^{{{\dagger}} }{\hat{U}}_{{{{\bf{r}}}},y}{\hat{\phi }}_{{{{\bf{r}}}}+y}+{{{\rm{h.c.}}}}).$$

(8)

Note that here we consider a different kinetic Hamiltonian compared to a previous work¹⁷, by including an additional phase factor and which corresponds to the original Kogut–Susskind formulation. From now on, we set the a = 1, unless stated otherwise. The physically relevant subspace ${{{{\mathcal{H}}}}}_{{{{\rm{ph}}}}}$ of gauge invariant states is given by those that fulfill Gauss’s law at each site r, which reads

$$\begin{array}{r}\left[\sum\limits_{\mu =x,y}\left({\hat{E}}_{{{{\bf{r}}}},\mu }-{\hat{E}}_{{{{\bf{r}}}}-\mu ,\mu }\right)-{\hat{q}}_{{{{\bf{r}}}}}-{Q}_{{{{\bf{r}}}}}\right]\left\vert {\varPhi} \right\rangle =0\\ \Longleftrightarrow \left\vert \varPhi \right\rangle \in {{{{\mathcal{H}}}}}_{{{{\rm{ph}}}}}.\end{array}$$

(9)

In the above expression, the operators

$${\hat{q}}_{{{{\bf{r}}}}}={\hat{\phi }}_{{{{\bf{r}}}}}^{{{\dagger}} }{\hat{\phi }}_{{{{\bf{r}}}}}-\frac{1}{2}\left[1+{(-1)}^{{r}_{x}+{r}_{y}+1}\right]$$

(10)

correspond to the dynamical charges, and Q_r represent static charges. The static charges will be particularly relevant for the computation of the static potential in the Section “Step scaling approach”. Since in this paper, we are focusing on a U (1) pure gauge theory, we will study only the Hamiltonian ${\hat{H}}_{{{{\rm{tot}}}}}={\hat{H}}_{E}+{\hat{H}}_{B}$.

We remark that instead of working on the full Hilbert space and enforcing Gauss’s law a posteriori, in this work we impose it beforehand and work on a gauge invariant subspace^40,41,42,43.

Implementation of gauge fields

The electric field values on a gauge link are unbounded, which leads to infinite infinite-dimensional Hilbert space for the gauge degrees of freedom. Therefore, for a numerical implementation of the Hamiltonian, the gauge degrees of freedom have to be truncated to a finite dimension. In ref. ⁴⁰, the continuous U(1) group is discretized, in the electric basis, to ${{\mathbb{Z}}}_{2l+1}$, where l introduces a truncation and dictates the dimensionality of the Hilbert space. The discretized gauge fields are constrained to integer values within the range [−l, l], resulting in a total Hilbert space dimension of (2l + 1)^N, where N denotes the number of gauge fields in the system. The eigenstates of the electric field operator, ${\hat{E}}_{{{{\bf{r}}}},\mu }$, form a basis for the link degrees of freedom (see e.g., Section VI C of ref. ⁴⁴),

$${\hat{E}}_{{{{\bf{r}}}},\mu }\left\vert {e}_{{{{\bf{r}}}},\mu }\right\rangle ={e}_{{{{\bf{r}}}},\mu }\left\vert {e}_{{{{\bf{r}}}},\mu }\right\rangle ,\,\,\,{e}_{{{{\bf{r}}}},\mu }\in [-l,l]\,.$$

(11)

The link operators ${\hat{U}}_{{{{\bf{r}}}},\mu }$ (${\hat{U}}_{{{{\bf{r}}}},\mu }^{{{\dagger}} }$) act as a raising (lowering) operator on the electric field eigenstates,

$${\hat{U}}_{{{{\bf{r}}}},\mu }\left\vert {e}_{{{{\bf{r}}}},\mu }\right\rangle =\left\vert {e}_{{{{\bf{r}}}},\mu }+1\right\rangle ,{\hat{U}}_{{{{\bf{r}}}},\mu }^{{{\dagger}} }\left\vert {e}_{{{{\bf{r}}}},\mu }\right\rangle =\left\vert {e}_{{{{\bf{r}}}},\mu }-1\right\rangle .$$

(12)

The link operators have the following form⁴²,

$$\hat{U}\mapsto \left[\begin{array}{cccc}0&\ldots \,&\ldots \,&0\\ 1&\ldots \,&\ldots \,&0\\ 0&\ddots &\vdots &0\\ 0&\ldots \,&1&0\\ \end{array}\right],\,\,\,{\hat{U}}^{{{\dagger}} }\mapsto \left[\begin{array}{cccc}0&1&\ldots \,&0\\ 0&\vdots &\ddots &0\\ 0&\ldots \,&\ldots \,&1\\ 0&\ldots \,&\ldots \,&0\\ \end{array}\right].$$

(13)

With this truncation, unitarity is lost ${\hat{U}}_{{{{\bf{r}}}},\mu }^{{{\dagger}} }{\hat{U}}_{{{{\bf{r}}}},\mu }\ne {\mathbb{1}}$ but is recovered in the l → ∞ limit. The commutation relations between the electric field and link operators from Eqs. (5) and (6) are preserved even for the truncated operators. Other approaches for the definition of the gauge field operators have been considered in refs. ^45,46,47,48 and with qudits⁴⁹. The errors introduced by finite truncation l have been studied in refs. ^50,51.

In Supplementary Note 3, we will explore an alternative representation of the Hamiltonian known as the magnetic basis or dual basis, recently explored in refs. ^40,41,52. This approach becomes relevant when the coupling constant g decreases and the magnetic term of the Hamiltonian becomes dominant. In this regime, the electric basis cannot provide a good approximation of the system with small values of l. However, by exploiting the discrete Fourier transform, we can obtain a diagonal expression for the plaquette terms, thus reducing the resources needed for the calculations. With the magnetic formulation introduced in ref. ⁴⁰, the group under consideration changes to ${{\mathbb{Z}}}_{2J+1}$, where J serves as an additional parameter dictating the discretization. The dimensionality of the Hilbert space remains defined by the truncation parameter l. An alternative formulation for the magnetic basis implementation has been explored in ref. ⁴³. We remark that the Hamiltonian formalism can be extended to non-Abelian gauge groups, like SU(2) (see e.g., refs. ^35,53). For this case, the discretization in the magnetic basis has been investigated more recently in refs. ^54,55,56. Further approaches can be found e.g., in refs. ^57,58,59.

Running coupling and step scaling

The step scaling approach is a computational method employed for the determination of the running coupling, introduced in ref. ¹² and used also for instance in refs. ^60,61. For a general description based on the Schrödinger functional approach see refs. ^62,63. Let us assume we define a running, renormalized coupling α_ren(r_ph) at a physical scale r_ph(g). We then define the step scaling function σ_s in the continuum from

$${\sigma }_{s}({\alpha }_{{{{\rm{ren}}}}}({r}_{{{{\rm{ph}}}}}))={\alpha }_{{{{\rm{ren}}}}}(s{r}_{{{{\rm{ph}}}}})\,,\qquad s\in {{\mathbb{R}}}^{+},$$

(14)

which can be understood as an integrated form of the β-function of the theory. Starting from α_ren(r_ph), we then apply the function in Eq. (14). The step then is repeated, going to α_ren(s²r_ph) and subsequent values, by creating the steps in Fig. 1a.

Fig. 1: Step scaling in the continuum theory and on the lattice.

a Step scaling in the continuum. The method applies the step scaling function σ_s to the renormalized coupling at a physical scale r_ph(g), where g is the bare coupling. The resulting renormalized coupling is at a new scale α_ren(sr_ph). The process is repeated N times and the running coupling is obtained. b Step scaling on the lattice. The method computes the renormalized coupling at a fixed value of the bare coupling g₀ and scales r₁ and r₂ ≡ s ⋅ r₁ in lattice units, α_ren(r₁, g₀) and α_ren(sr₁, g₀). The latter corresponds to σ_s(α_ren(r₁, g₀)) on the lattice. The value where α_ren(r₁, g₁) = α_ren(sr₁, g₀) can be found by tuning g. The steps are repeated to find the sequence in the figure.

This method can be iterated up to arbitrary N + 1 steps, obtaining α_ren(s^Nr_1,ph) and thus getting the running coupling as a function of the physical scale. The goal of this work is to compute the step scaling function non-perturbatively on the lattice, by starting with some distance r in lattice units and with a bare coupling g. The lattice spacing is encoded in the coupling which is an implicit function of a in physical units. We fix two scales, r₁ and r₂ ≡ s ⋅ r₁ in lattice units and compute the renormalized coupling at a fixed value of g, i.e., α_ren(r₁, g₀) and α_ren(sr₁, g₀), which corresponds to σ_s(α_ren(r₁, g₀)) on the lattice. We tune g, finding the value where α_ren(r₁, g₁) = α_ren(sr₁, g₀). The corresponding sequence of steps can be illustrated in Fig. 1b.

In this paper, we consider a lattice calculation and then we convert the lattice distances into physical ones with an artificial value of a in physical units and r_ph = ar (see the Section “Towards defining a physical scale”). Where, as mentioned in the introduction, the numerical value of the lattice spacing can be obtained in principle with large-volume Monte Carlo computations. Since a in physical units is a function of the bare coupling, by decreasing g, we change the physical distance to smaller values. In this way, we get the running of the coupling as a function of the physical scale. Results of the application of this method are discussed in the Section “Towards defining a physical scale”. We use the static force, F(r, g), as the physical quantity of interest, focusing in particular on the dimensionless quantity r²F(r, g), with g the bare coupling at which the force is computed and r the distance between two static charges. The calculation of the static force involves the application of a discrete derivative, approximated as $\frac{\partial V}{\partial r}\simeq \frac{V({r}_{2})-V({r}_{1})}{{r}_{2}-{r}_{1}}$, where V(r_i) denotes the static potential between two static charges separated by r_i. This potential is, for short distances, proportional to a logarithmic Coulomb term $V(r) \sim {\alpha }_{{{{\rm{ren}}}}}\log r$⁶⁴ on the lattice. Thus, r²F(r, g) can be related eventually to the renormalized coupling. For the analysis of the step scaling, we need two values of the static force,

$$F({r}_{2},g)=\frac{V({r}_{3},g)-V({r}_{2},g)}{{r}_{3}-{r}_{2}},$$

(15a)

$$F({r}_{1},g)=\frac{V({r}_{2},g)-V({r}_{1},g)}{{r}_{2}-{r}_{1}}.$$

(15b)

Therefore, it is necessary to involve three distances, namely r₁, r₂, and r₃, in the calculation of the step scaling function. Note that in this paper, we introduce the step scaling method for a pure gauge U(1) theory. Once we will include matter fields, we will have a non-trivial running coupling.

Matching strategy for 3 × 3 PBC system

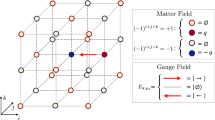
In this section, we describe the matching between the Variational Quantum Eigensolver (VQE) approach and Markov Chain Monte Carlo (MCMC). For our study, we consider the pure gauge case, i.e., the theory without fermionic fields, on a 3 × 3 lattice with periodic boundary conditions (PBC) (see Fig. 2a for an illustration). The quantity we analyze is the expectation value of the plaquette operator,

$$\langle P\rangle =\frac{1}{\tilde{V}}\left\langle \sum\limits_{{{{\bf{r}}}}}\left(\frac{{\hat{P}}_{{{{\bf{r}}}}}+{\hat{P}}_{{{{\bf{r}}}}}^{{{\dagger}} }}{2}\right)\right\rangle ,$$

(16)

where $\tilde{V}$ is the number of plaquettes in the lattice.

Fig. 2: Lattice and plaquette expectation value.

a Illustration of a lattice with periodic boundary conditions. 3 × 3 lattice with PBC. The spheres represent the matter sites, where blue dashed (orange solid) circles indicate sites with even (odd) parity. The lines connecting the vertices represent the gauge links, where the arrows indicate the orientation of the lattice. The links sticking out on top (to the right) indicate the periodic boundary conditions and connect to the vertices on the bottom (left). b Plaquette expectation value for pure-gauge system. Results for a 3 × 3 lattice with PBC found with exact diagonalization with truncation l ∈ [1, 4] (lines with low triangles or solid line) and VQE results (noise-free simulations with infinite shots) with l = 1 (circles). The dotted vertical line corresponds to β matching with MC. We also show the relative error ϵ - comparison between VQE data and exact results. The error depends on the convergence of the optimization reaching a given tolerance and the initial set of parameter values in the quantum gates.

We focus on bare couplings in the interval corresponding to 0.8 ≤ β = 1/g² ≤ 2.6, selected to be in a regime accessible with MCMC methods. We analyze the convergence behavior of the results with exact diagonalization (ED) with respect to the truncation parameter l, as illustrated by the lines in the upper panel of Fig. 2b. The results from ED show that with increasing values of l we observe convergence, and for the range of couplings chosen here l = 3 is sufficient to reliably determine the plaquette expectation value, as the results for l = 3 and l = 4 are essentially indistinguishable. For a truncation l = 2, we see slight deviations for larger values of β. While for l = 1 deviations towards larger values of β are noticeable, the data still qualitatively reproduce the behavior observed for larger values of l. For the VQE approach, we have developed a quantum circuit with an entanglement structure connecting all gauge fields. The resources required for running the circuit are shown in Table 1.

Table 1 Resources required for the variational circuit for Gray encoding

Due to the limited resources available on current quantum devices, we focus on truncation l = 1 for a proof of principle. In order to benchmark the approach, we classically simulate the VQE, assuming a noise-free quantum device. For the optimization, we employ the SLSQP⁶⁵ classical optimizer and infinite shots, i.e., number of measurements, setting as the first goal only the expressivity of the quantum circuit. After applying Gauss’s law, only 10 of the 18 links remain dynamical, thus, we need 20 qubits for the computation. As illustrated in Fig. 2b, the top panel shows the VQE results for this truncation, indicated by circles, along with the relative error with respect to the exact values in the bottom panel. These results are in line with the plaquette curve from ED.

For the future, a closer examination of the entanglement structure could help to improve the accuracy of the data and optimize the scalability of the gate number. Such exploration should focus on three main purposes: to improve our understanding of the interplay between circuit and lattice structure, to extend the results to higher truncation while preserving the depths of the circuits and to prepare for analysis on quantum hardware platforms.

Part of the authors are involved in a MC calculation of the Hamiltonian limit of the theory analyzed in this work, namely the continuum limit in the time direction at fixed spatial lattice spacing, within the Lagrangian formalism. Preliminary account of the latter can be found in ref. ⁶⁶. This procedure returns a β_MC-value for which we know the corresponding bare coupling value of the discretized theory. Thus, the spatial lattice spacing is identical up to lattice artefacts. At this value of the coupling, we can then perform large-volume Monte Carlo simulations and set the physical scale. Since this analysis was still ongoing at the time of writing, in this work we adopt the preliminary value β_MC = 1.4, corresponding to the vertical line in Fig. 2b.

Step scaling approach

In this section, we illustrate the methodology for the pure gauge case on a 3 × 3 lattice with Open Boundary Conditions (OBC). Two static charges of opposite values are placed on two sites, as in Fig. 3. The choice of boundary conditions allows us to obtain more distinct lattice distances than the periodic case. We focus on two sets of distances to generalize any findings regarding the coupling behavior. We have tested all the combinations of the five possible distances for two static charges on a pure gauge lattice, $C(5,3)=\frac{5!}{3!(5-3)!}$, and have chosen the two combinations with more points in the step scaling procedure below a certain threshold for the bare coupling, i.e., β ≤ 10². Note that with a system size of 3 × 3 sites and a range of βs considered here, we always work at distances below the confinement scale, and the correlation length is given by the small system size⁶³.

Fig. 3: Illustration of the static charge configurations.

blue spheres with a− (red spheres with a+ ) correspond to sites carrying a negative (positive) static charge, gray spheres to sites where no static charge is present. The solid arrows indicate the dynamical links, and the dashed arrows are the nondynamical ones. The different panels correspond to different distances of the charges with r = 1.0 (a), $r=\sqrt{2}=1.414$ (b), $r=\sqrt{5}=2.236$ (c), and $r=\sqrt{8}=2.828$ (d). Fig. 4 : Step scaling results for the static forces from the weak coupling region. F(r₁ = 1, g) and $F({r}_{2}=\sqrt{5},g)$ computed in the electric basis at truncation l = 1. Here, we used the smallest truncation to illustrate the method. From the weak coupling regime β = 10², the static forces are computed following a steps procedure, both with ED and VQE (noise-free simulations with shots). ED results for ${r}_{1}^{2}F({r}_{1}=1,g)$ (${r}_{2}^{2}F({r}_{2}=\sqrt{5},g)$) are displayed with circles (squares) and corresponding VQE results with up(down) ward-pointing triangles. In the simulations, a combination of NFT and COBYLA optimizer was considered and a finite number of shots defines the error bars, which are smaller than the markers. These uncertainties (standard deviation) are computed with the combination of the variances of the Pauli terms in the Hamiltonian.

In the following analysis, a variational quantum algorithm is used to calculate the static potential at different distances, and the results are compared with those derived from exact diagonalization. The data presented here are computed with a combination of two classical optimizers: we performed a first minimization with NFT⁶⁷, which gave us fidelities of up to  ~95% (noise-free simulations with $\sim {{{\mathcal{O}}}}(1{0}^{4})$ shots). As the coupling decreases, higher precision in the VQE results becomes necessary. Consequently, we have used the final optimal parameters as a starting point for a new optimization with COBYLA⁶⁸ and a larger number of shots $( \sim {{{\mathcal{O}}}}(1{0}^{6}))$. This aspect is crucial for our objectives, as the values of the static forces in the weak coupling regime are almost equivalent. A better understanding of the entanglement structure may be helpful for increasing the precision with fewer shots. We will consider a more in-depth analysis of this in future work. In Table 2, we show the resource estimation for three values of the truncation parameter l.

Table 2 Resources required for the variational circuit for Gray encoding

Step scaling results for static forces F(r ₁ = 1, g) and $F({r}_{2}=\sqrt{5},g)$

In this section, we focus on illustrating the step scaling method using a variational approach and exact diagonalization as a reference, for the configuration with charges placed as in Fig. 3a, c, d and relative distances on the lattice r₁ = 1, ${r}_{2}=\sqrt{5}$ and${r}_{3}=\sqrt{8}$, respectively.

Illustration of step scaling from β = 10²

We show the step scaling procedure starting from a weak coupling regime. As explained in the Section “Running coupling and step scaling”, we repeat the steps until we reach a certain value of the bare coupling. In Fig. 4, we follow the step scaling procedure starting from β = 10² and moving to the left with a variational Ansatz (up(down)ward-pointing triangles) and exact results (empty circles/squares). One can see that the precision required for small couplings increases because of the small values required in the step scaling function. Considering only the electric basis becomes more difficult, as the superposition within the ground state expands significantly towards weaker couplings. It is thus advisable to start at large β-values with the magnetic basis and monitor the convergence of results throughout the process towards smaller β-values.

Fig. 4: Step scaling results for the static forces from the weak coupling region.

F(r₁ = 1, g) and $F({r}_{2}=\sqrt{5},g)$ computed in the electric basis at truncation l = 1. Here we used the smallest truncation to illustrate the method. From the weak coupling regime β = 10², the static forces are computed following a steps procedure, both with ED and VQE (noise-free simulations with shots). ED results for ${r}_{1}^{2}F({r}_{1}=1,g)$ (${r}_{2}^{2}F({r}_{2}=\sqrt{5},g)$) are displayed with circles (squares) and corresponding VQE results with up(down)ward-pointing triangles. In the simulations, a combination of NFT and COBYLA optimizer was considered and a finite number of shots defines the error bars, which are smaller than the markers. These uncertainties (standard deviation) are computed with the combination of the variances of the Pauli terms in the Hamiltonian.

Start from β = 1.4 to perturbative regime

Here, we discuss the variational results for the step scaling method, starting from the value of the bare coupling where we have a matching with MC, see the Section “Matching strategy for 3 × 3 PBC system,” and continuing towards a weaker regime. We first illustrate the procedure with a fixed truncation, l = 1, and then discuss higher truncations, involving also a magnetic representation. Starting from β_MC = 1.4, we compute ${r}_{1}^{2}F({r}_{1},{g}_{0})$ and ${r}_{2}^{2}F({r}_{2},{g}_{0})$. Next, using the result of the static force at a distance r₁, the bare coupling g is adjusted to a reduced value until a new ${r}_{2}^{2}F({r}_{2},{g}_{1})$ is obtained. This step scaling process is then repeated using a similar approach as in the previous paragraph, but aimed at the weak coupling regime. The comparison between variational results (denoted by up/downward-pointing triangles) and exact results (denoted by empty circles/squares) is illustrated in Fig. 5a.

Fig. 5: Step scaling results for static forces.

a Step scaling results for static forces at low truncation. F(r₁ = 1, g) and $F({r}_{2}=\sqrt{5},g)$, electric basis and l = 1. From β_MC = 1.4 and in a range of couplings within β ≤ 10², the static forces are computed following a steps procedure, both with ED and VQE (noise-free simulations with shots). ED results for ${r}_{1}^{2}F({r}_{1}=1,g)$ (${r}_{2}^{2}F({r}_{2}=\sqrt{5},g)$) displayed with circles (squares) and corresponding variational results with up(down)ward-pointing triangles. In the simulations, a sequential combination of two optimizers NFT and COBYLA was considered and a finite number of shots defines the error bars, which are smaller than the markers. These uncertainties (standard deviation) are computed with the combination of the variances of the Pauli terms in the Hamiltonian. b Step scaling results for static forces at higher truncation. F(r₁ = 1, g) and $F({r}_{2}=\sqrt{5},g)$, electric (magnetic) basis. In contrast to Fig. 5a, we consider here a higher truncation and show ED results with electric basis for ${r}_{1}^{2}F({r}_{1}=1,g)$ (${r}_{2}^{2}F({r}_{2}=\sqrt{5},g)$) with truncation value l = 7 displayed with circles(squares) and with magnetic basis for ${r}_{1}^{2}F({r}_{1}=1,g)$ (${r}_{2}^{2}F({r}_{2}=\sqrt{5},g)$) with l = 3 and discretization values J = 200 displayed with up(down)ward-pointing triangles.

To give physical meaning to the data, it is essential to increase the truncation parameter l applied to the gauge operators until independent solutions are obtained. Given the limited resources, we adopt a strategy involving an interplay between electric and magnetic basis. Starting from the electric formulation, we progressively increase l until convergence is achieved within the desired range, 1.4 ≤ β ≤ 10². Once a reference value is established, we restrict ourselves to l = 7, which will result in a total of 16 qubits, which seems feasible on current quantum hardware. Next, following the procedure described in Supplementary Note 3, we find the value of the bare coupling where the accuracy of the electric basis is not sufficient anymore (i.e., exceeding a relative error of ϵ ≥ 0.01). At this point, we move on to the magnetic basis with l = 3 and discretization J = 200, parameters that give us reliable results. Initially, we conducted tests with l = 7 also for the magnetic basis, maintaining an equal number of qubits for each register as for the electric one. The outcomes proved to be comparable to those obtained with l = 3. Consequently, we can decrease the computational resources required while preserving a high level of accuracy in the solutions. Fig. 5b illustrates the step-scaling method employing the technique described, with exact diagonalization. Similarly, we proceed through the weak coupling regime by increasing β and constructing the steps accordingly.

Step scaling results for static forces $F({r}_{1}=\sqrt{2},g)$ and $F({r}_{2}=\sqrt{5},g)$

In this section, the analysis is repeated for a new set of distances,${r}_{1}=\sqrt{2}$, ${r}_{2}=\sqrt{5}$ and ${r}_{3}=\sqrt{8}$, Fig. 3b–d. Here, we solely explore the step scaling starting from β_MC. The results are then combined in the the Section “Towards defining a physical scale” with the previous set of distances, in order to show the dependence of r²F(r, g) in terms of a physical scale.

Start from β = 1.4 to perturbative regime

The step scaling procedure is illustrated in Fig. 6a in the fixed bare coupling interval. In this case, four steps are observed within the range 1.4 ≤ β ≤ 10².

Fig. 6: Step scaling results for static forces.

a Step scaling results for static forces for the second pairs of distances, low truncation. $F({r}_{1}=\sqrt{2},g)$ and $F({r}_{2}=\sqrt{5},g)$ computed in the electric basis at l = 1. Similar approach as in Fig. 5a, with a different set of distances. From β_MC = 1.4 and in a range of couplings within β ≤ 10², the static forces are computed following a steps procedure, both with ED and VQE (noise-free simulations with shots). ED results for ${r}_{1}^{2}F({r}_{1}=\sqrt{2},g)$ (${r}_{2}^{2}F({r}_{2}=\sqrt{5},g)$) displayed with circles (squares) and corresponding variational results with up(down)ward-pointing triangles. In the simulations, a sequential combination of two optimizers NFT and COBYLA was considered and a finite number of shots defines the error bars, which are smaller than the markers. These uncertainties (standard deviation) are computed with the combination of the variances of the Pauli terms in the Hamiltonian. b Step scaling results for static forces at higher truncation in the electric and magnetic basis. $F({r}_{1}=\sqrt{2},g)$ and $F({r}_{2}=\sqrt{5},g)$ computed in the electric (magnetic) basis. In contrast to we consider here a higher truncation and show ED results with electric basis for ${r}_{1}^{2}F({r}_{1}=\sqrt{2},g)$ (${r}_{2}^{2}F({r}_{2}=\sqrt{5},g)$) with truncation value l = 7 displayed with circles(squares) and with magnetic basis for ${r}_{1}^{2}F({r}_{1}=\sqrt{2},g)$ (${r}_{2}^{2}F({r}_{2}=\sqrt{5},g)$) with l = 3 and discretization values J = 200 displayed with up(down)ward-pointing triangles.

We apply the same technique with higher truncations for this set of distances, Fig. 6b. Also in such a case, we consider l = 7 for the electric basis and l = 3, J = 200 for the magnetic, obtaining a total of five pairs of points.

Towards defining a physical scale

We are not aware of any real experiment which can be described by the effective (2 + 1)-dimensional compact pure gauge theory considered in this paper. Therefore, we cannot extract the physical value of the lattice spacing with large-volume MC calculations. See Section V C in ref. ¹⁷ for the illustration of the principle to determine the value of the lattice spacing. Thus, for the sake of demonstrating our method, we consider an artificial value for the lattice spacing, e.g., a = 0.1 fm, and we use the data in the previous sections to identify the physical value for the scales. With two sets of distances, we have two scale factors s to connect r₁ and r₂, (r₂ = s ⋅ r₁), i.e., ${r}_{2}=\sqrt{5}\cdot {r}_{1}$ and ${r}_{2}=\sqrt{\frac{5}{2}}\cdot {r}_{1}$. We then combine the results in a single plot.

Let us first consider the set r₁ = 1, ${r}_{2}=\sqrt{5}$, ${r}_{3}=\sqrt{8}$. Our aim is to start with β_MC and invert the sequence by changing the scale by s and include the physical value of the lattice spacing, a = 0.1 fm. At β_MC ≡ β_N we have,

$$\hskip 4.6pc {\beta }_{N}\mapsto \left\{\begin{array}{l}{r}_{2,{{{\rm{ph}}}}}={r}_{2}\cdot a=0.223\,{{{\rm{fm}}}},\, \hfill (17{{{\rm{a}}}}) \\ {r}_{1,{{{\rm{ph}}}}}={r}_{1}\cdot a=0.1\,{{{\rm{fm}}}}.\,\qquad\qquad\qquad\qquad(17{{{\rm{b}}}}) \end{array}\right.$$

Then, we go to the next value of the bare coupling, where we have,

$$\hskip 4pc {\beta }_{N-1}\mapsto \left\{\begin{array}{l}{r}_{2,{{{\rm{ph}}}}}={r}_{2}\cdot a/s=0.1\,{{{\rm{fm}}}},\, \hfill (18{{{\rm{a}}}})\quad \\ {r}_{1,{{{\rm{ph}}}}}={r}_{1}\cdot a/s=0.045\,{{{\rm{fm}}}}.\,\qquad\qquad\qquad(18{{{\rm{b}}}})\quad \end{array}\right.$$

The procedure iterates through multiple steps, and eventually, the static force values can be written in terms of a physical scale, as depicted in Fig. 7, with data from Figs. 5a and 6a. Note, for example, that Eqs. (17b) and (18a), correspond to the same physical scale (rightmost full circle and second rightmost full downward-pointing triangle).

Fig. 7: Step scaling results with exact diagonalization (electric basis at low truncation) as a function of physical distances.

Data calculated at l = 1. Set of static forces F(r₁ = 1, g) ($F({r}_{2}=\sqrt{5},g)$) displayed as full circles (full downward-pointing triangles) and for $F({r}_{1}=\sqrt{2},g)$ ($F({r}_{2}=\sqrt{5},g)$) displayed as empty circles (empty downward-pointing triangles).

In compact pure gauge U(1) theory, the β-function of the dimensionful coupling is trivial and therefore there is no renormalization of the coupling. Consequently, there is, in principle, no scale dependence. Nevertheless, in Fig. 7, we observe a non-trivial behavior of the dimensionless quantity r²F(r, g) as a function of the physical distance^22,23,24. However, since the results are at non-zero lattice spacing, we cannot control the uncertainties from a non-zero a and, currently, we cannot compare directly with the continuum perturbation theory.

Note that, when including matter fields, the β-function becomes nontrivial, see again ref. ²².

We can replicate the procedure using the outcomes from the variational quantum algorithm (again Figs. 5a and 6a), as depicted in Fig. 8. Despite fluctuations in the results, attributed in part to the finite number of shots and the limited convergence of the optimization, the data effectively captures the dependence of the coupling as a function of the physical distance.

Fig. 8: Step scaling variational quantum results (electric basis and low truncation) as a function of physical distances.

l = 1 data for set of static forces F(r₁ = 1, g) ($F({r}_{2}=\sqrt{5},g)$) found with the VQE, displayed as full squares (full upward-pointing triangles) and for $F({r}_{1}=\sqrt{2},g)$ ($F({r}_{2}=\sqrt{5},g)$) displayed as empty squares (empty upward-pointing triangles). The error bars (standard deviation) are computed with the combination of the variances of the Pauli terms in the Hamiltonian. They are defined by the finite number of shots and are smaller than the markers.

The procedure is repeated also for the analysis with electric and magnetic basis, using the data from Figs. 5b and 6b and combining them in Fig. 9.

Fig. 9: Step scaling exact diagonalization results (electric basis and magnetic basis) as a function of physical distances.

Data for set of static forces F(r₁ = 1, g) ($F({r}_{2}=\sqrt{5},g)$) displayed as full circles (full downward-pointing triangles) and for $F({r}_{1}=\sqrt{2},g)$ ($F({r}_{2}=\sqrt{5},g)$) displayed as empty circles (empty downward-pointing triangles). l = 7 has been used in the electric basis and l = 3, J = 200 in the magnetic one.

As a final remark, without going into details, we mention a possible strategy to reach the continuum limit for the discussed analysis. The idea is to keep the physical distance between two static charges fixed while changing the lattice size and, correspondingly, the distance of two static charges on the lattice. The step scaling function parameter s is defined by the fixed ratio (s = r₂/r₁). One computes ${r}_{2}^{2}F({r}_{2},g)$ until the same value as in smaller lattice size is found and then applies the step scaling function. The results are studied as a function of ${(a/{r}_{1})}^{2}$. The process is repeated for more steps and the data are subject to a fit, reaching thus the limit ${(a/{r}_{1})}^{2}\to 0$. Carrying out this process will be considered in future work.

Discussion

In a previous work¹⁷, part of the authors outlined the idea of computing the running of the coupling and the Λ-parameter through a step scaling approach in (2 + 1)-dimensional QED. To this end, the combination of MC and quantum computing methods was proposed.

Here, we performed a step towards this final goal by analyzing a compact U(1) gauge theory. We designed tailored quantum circuits for the implementation of gauge degrees of freedom. We showed that our program, based on a variational quantum simulation, can be carried out. This is illustrated in Fig. 8, which shows the dimensionless quantity r²F(r, g), related to the renormalized coupling, as a function of a physical scale. We remark that at the moment an artificial value of the lattice spacing was employed. Our results provide a successful test for the capability of variational quantum simulations for studying the step scaling function on the lattice, with the potential for further applications of this approach in the future, in particular, with existing and emerging quantum hardware.

The Hamiltonian formalism, discussed in this work, can be related to the action formalism by taking the continuum limit in time of the action with a fixed physical condition. This allows us to determine the relation of the bare couplings in both cases by matching, e.g., the corresponding plaquette expectation values. In this work, we used a preliminary value of the bare coupling for this matching, obtained by Monte Carlo simulations for a periodic 3 × 3 system in refs. ^66,69. On the quantum computing side, we were able to achieve results for the expectation value of the plaquette within the same range of bare couplings, see Fig. 2b. In the same figure, it is demonstrated that, employing exact diagonalization, a truncation l = 3 is sufficient to see convergence. There, we also provided VQE results for a truncation l = 1, which could be simulated with current quantum resources.

In Supplementary Note 2, through a detailed finite-size MC study, we demonstrated that with a system size of 6 × 6, matching with the mass gap becomes possible, which opens the road for future quantum computations.

In Supplementary Note 4, we discuss the theoretical details of the fermionic Hamiltonian, building the ground for future calculations, including matter fields. This will then lead to a situation where the running of the coupling is non-trivial and thus can provide a meaningful value of the QED Λ-parameter in (2 + 1) dimensions.

In the work presented here, we set the basis of variational quantum simulation of (2 + 1)-dimensional QED. The methodology developed here can be utilized for extensions of the theory, including, e.g., topological terms or non-zero matter density and even an analysis of real-time evolution.

Methods

Numerical setup for quantum computation

For numerical calculations, it is advantageous to employ a suitable encoding that accurately represents the physical values of the gauge fields. In this work, we consider the Gray encoding (see, e.g., ref. ⁷⁰). With this approach, the minimum number of qubits required per gauge variable is ${q}_{{{{\rm{min}}}}}=\lceil {\log }_{2}(2l+1)\rceil .$. Thus, it will be convenient for the implementation on a quantum circuit to consider a subset of truncation values (l  = 1, 3, 7, 15, . . . ), which allows only a single state to be excluded with the same amount of resources. For instance, three qubits are required for both l = 2 and l = 3. However, with the former, only five configurations are considered physical, whereas with the latter, we can include seven physical states.

The state of a qubit can be defined as a vector in a 2-dimensional complex vector space ${{\mathbb{C}}}^{2}$, with $\left\vert 0\right\rangle ={(1,0)}^{t}$ and $\left\vert 1\right\rangle ={(0,1)}^{t}$ as the computational basis⁷¹. The quantum operations, or gates, on a single qubit can be described by 2 × 2 unitary matrices. Thus, for numerical implementations, we express the Hamiltonian in terms of a sum of Pauli matrices. One can also employ a grouping strategy to identify subsets of Pauli strings present in the Hamiltonian, thereby reducing the necessity for independent circuit evaluations⁷². In the following, we also adopt the convention that the least significant qubit (designated by the zero index, q₀) occupies the rightmost position in the tensor product, as illustrated by $\left\vert {q}_{1}{q}_{0}\right\rangle$ and $\left\langle {q}_{1}{q}_{0}\right\vert$. Let us now consider, as an example, the case of smallest truncation l = 1, where we have the three physical states ${\left\vert j\right\rangle }_{{{{\rm{ph}}}}}$ for j ∈ {−1, 0, 1}. These states can be encoded using only two qubits in a Gray code way, as shown in the following equations:

$${\left\vert -1\right\rangle }_{{{{\rm{ph}}}}}\mapsto \,\left\vert 00\right\rangle ,$$

(19a)

$${\left\vert 0\right\rangle }_{{{{\rm{ph}}}}}\mapsto \,\left\vert 01\right\rangle ,$$

(19b)

$${\left\vert 1\right\rangle }_{{{{\rm{ph}}}}}\mapsto \,\left\vert 11\right\rangle ,$$

(19c)

we then call the state $\left\vert 10\right\rangle$ “unphysical”, since it is outside of this truncated Hilbert space. The expressions for the electric field and link operators then become

$$\hat{E} \, \mapsto -\left\vert 00\right\rangle \left\langle 00\right\vert +\left\vert 11\right\rangle \left\langle 11\right\vert ,$$

(20a)

$$\hat{U} \, \mapsto \left\vert 01\right\rangle \left\langle 00\right\vert +\left\vert 11\right\rangle \left\langle 01\right\vert ,$$

(20b)

$$\hat{{U}^{{{\dagger}} }}\mapsto \left\vert 00\right\rangle \left\langle 01\right\vert +\left\vert 01\right\rangle \left\langle 11\right\vert .$$

(20c)

In this study, we adopt a variational approach to determine the physical quantities of interest. Specifically, we employ the VQE method that aims to find the ground state of a given Hamiltonian. Executing a VQE algorithm requires an input quantum circuit with parametrized gates, called an Ansatz circuit, and a classical optimizer. The optimization starts with an initial set of values for the gate parameters, that can be randomly chosen, and will be optimized in the execution. In the rest of the paper, we consider a set of parameters, where the probability of being in a vacuum state (i.e., ${\left\vert 0\right\rangle }_{{{{\rm{ph}}}}}$) is non-zero for every gauge field. The essence of the approach considered here is to exclude unphysical states directly within the quantum circuit. This is achieved by implementing a customized set of parameterized quantum gates designed to produce the correct final combination of states. With this method, we aim to efficiently identify the desired physical results while reducing the computational overhead. We also considered keeping the state $\left\vert 10\right\rangle$ as a higher physical state ${\left\vert 2\right\rangle }_{{{{\rm{ph}}}}}$ and use a generic variational Ansatz. However, the VQE results did not have a high fidelity. Therefore, we will not describe this option further. It may be considered in future work. For the truncation l = 1, we can use the circuit in Fig. 10 to represent a gauge field. The action of the circuit is straightforward: starting from the state $\left\vert 00\right\rangle$, setting both parameters θ₁ and θ₂ to zero allows for the exploration of the physical state ${\left\vert -1\right\rangle }_{{{{\rm{ph}}}}}$. The introduction of a non-zero value for θ₁ allows the state to change to $\left\vert 01\right\rangle$, which represents the vacuum state${\left\vert 0\right\rangle }_{{{{\rm{ph}}}}}$, with a certain probability. A complete rotation occurs if θ₁ = π, resulting in the exclusive presence of the second state with a probability of 1.0. Subsequently, the second controlled gate operates only when the first qubit is $\left\vert 1\right\rangle$, limiting the exploration to $\left\vert 11\right\rangle$ (i.e., ${\left\vert 1\right\rangle }_{{{{\rm{ph}}}}}$) and excluding $\left\vert 10\right\rangle$.

Fig. 10: circuit for Gray encoding at low truncation.

Results from the variational circuit at l = 1. In the circuit rotational parameterized gates around the y-axis, R_y(θ) have been used. The parameter θ defines the angle of the rotation. With this circuit vacuum state is $\left\vert 01\right\rangle$, and state $\left\vert 10\right\rangle$ is excluded.

This procedure can be expanded to arbitrary l, allowing the exclusion of unphysical combinations, and to multiple gauge fields with entangling gates. For further details, refer to Supplementary Note 1, which provides an extension to three additional values of truncation (l = 3, 7 and 15).