Distinguished role of the laser pulse temporal structure on deuteron acceleration

Abstract

Compared to their conventional counterpart, laser plasma-based ion accelerators offer considerably higher acceleration gradients, opening the way to more compact laser-driven accelerator facilities. In this context, deuteron acceleration has been used for laser-based neutron sources, as deuterons at relatively low kinetic energy can efficiently generate neutrons. While double-pulse and chirp effects have been explored for proton acceleration under radiation pressure and target-normal sheath acceleration schemes, their role in ion acceleration remains unconfirmed, limiting the optimization strategies for neutron sources. Here we clarify the influence of laser pulse temporal shape on ion acceleration from ultrathin targets. We systematically change the temporal structure of the pulse by controlling the group delay dispersion and third-order dispersion (TOD), while pulse energy and focal spot size remain unchanged. The experiments are supported by 2D PIC simulations and analytical modeling. We find that the effect of optimum temporal shape is considerably larger than previously reported: the TOD-induced post-pulses increase the efficiency by 50% and double the deuteron cutoff energy. Our systematic study shows that the performance of laser ion accelerators can be strongly enhanced by matching the dispersion values to the target characteristics.

Introduction

Laser plasma-based proton acceleration has attracted a high interest from the particle physics community, as the acceleration gradient is several orders of magnitude higher than that of conventional linear accelerators¹. Hence, the necessary footprint of a future laser-driven accelerator facility is supposed to be considerably smaller. Along with this, from the dawn of laser ion acceleration, the primary aim was to achieve the highest possible accelerated ion energy. Scaling of proton cutoff energy and efficiency with the laser pulse parameters and target thicknesses was established for various acceleration mechanisms, especially for radiation pressure acceleration (RPA) and target-normal sheat acceleration (TNSA) (see the review papers and references therein:^2,3,4).

Investigations of the role of the temporal characteristics of a laser pulse went in two directions. One is the temporal signal-to-noise ratio of laser pulse, i.e. the intensity temporal contrast, while the second is the duration (FWHM) of the laser pulse. The conclusion of the first studies^5,6,7 was generally accepted that the driving laser pulse should exhibit an ultrahigh temporal contrast - not to destroy the solid target prior to the arrival of the main peak. An early experiment⁸ showed that two femtosecond laser pulses in the close temporal vicinity can enhance the conversion efficiency of TNSA-protons up to 15 percent. Recently, it was also demonstrated for both femtosecond and picosecond pulses that it is even possible to switch between electron and proton acceleration using the same experimental setup by merely varying the energy and timing of the prepulse^9,10.

The first experimental study, supported by 2D PIC simulations, on proton acceleration with the same laser but different pulse duration already showed an improvement of acceleration efficiency and cutoff energy¹¹ for thick targets. Further studies^12,13,14 for both femtosecond and picosecond pulses revealed that proton energy and efficiency could be enhanced with lengthening of the pulse duration via chirping in a pulse compressor. Schreiber et al.¹⁵ also added that the ideal pulse duration depends on the target and target thickness for both the RPA and TNSA regimes.

Regarding the effect of the chirp sign, an early simulation in the RPA regime predicted an enhancement in the number of accelerated ions as well as the cutoff energy when negatively chirped laser pulses were used¹⁶. The acceleration of a proton from a thin foil within the TNSA regime showed that the positively chirped pulse is favorable to the negatively stretched pulse¹⁷. A recent series of simulations confirmed that the optimum choice of the chirp sign still depends on the target thickness and the acceleration mechanism¹⁸.

In most of these experiments, the pulse duration was varied with the change of the grating distance in the pulse compressor of the chirped pulse amplification laser system. In this way, all of the dispersion coefficients were tuned, making it impossible to separate their effects from each other. Recent experimental studies using an acousto-optical programmable dispersion filter (AOPDF) reported an increase in cutoff energy by 15% at a positive linear chirp value of +500 fs², while some increase was also observed at -500 fs²¹⁹. With another laser, the above tendencies were confirmed, although with lower increments²⁰. The variation of the non-linear chirp led to a more dramatic increase in the cutoff energy¹⁹, reaching a duplication of the cutoff energy at positive values, while dropping in a monotone way toward negative values. However, these important findings have not yet been theoretically supported.

Deuteron acceleration with both the TNSA and RPA mechanisms has recently become interesting for creating laser-based neutron sources^{21,22,23,24,25}. Unlike proton-related reactions, most deuteron-induced ones do not have an energy threshold, so a large number of deuterons with low kinetic energy^26,27 spectra can efficiently contribute to neutron generation. To increase efficiency, Sunara et al.²⁸ suggested optimization of the deuteron acceleration for neutron production by optimization of prepulse formation on a CD foil, while another set of simulations showed an increase with multiple laser pulses²⁹.

In this paper we show that in the TNSA regime the characteristics of laser ion acceleration from a given target ultimately depend on the temporal envelope of the driving laser pulse structure. In other words, we show that the double-pulse and chirp effects have the same origin and can be treated together. In a systematic experimental study, both the GDD and TOD of few cycle laser pulses have been varied to optimize deuteron acceleration. Two target types with different thicknesses were investigated to reveal the effect of target material and thickness, as well as to account for the ratio of proton and deuterons. 2D PIC simulations, including for the first time the effect of TOD, have confirmed the physics of all the experimental findings.

Results

Shaping of a pulse temporally

The SEA laser of ELI-ALPS³⁰ delivers 11 fs, p-polarized pulses to the target, with a temporal contrast exceeding 10¹¹. The temporal shape of a laser pulse can be calculated from the measured spectrum (Fig. 1a) and the spectral phase of the pulse. The latter is commonly described with its Fourier coefficients³¹. The second coefficient, called group delay dispersion (GDD), arranges the optical frequencies around the central frequency linearly in time, while TOD does it in a quadratic way³². A pulse is negatively chirped if the high-frequency components propagate at the leading edge of the pulse (GDD < 0), while positive chirp means that the low frequencies come first (GDD > 0). If the spectrum is not symmetrical, the temporal shape of the pulse is determined by the shape of the spectrum and the sign of the GDD. For example, in the case of a negative GDD, the high-frequency components propagating at the leading edge of the stretched pulse make the rising edge steeper than the falling edge (Fig. 1b). A large amount of positive TOD produces a dense series of pulses after the major one (Fig. 1c). Please note that the bottom-bottom durations of the pulses with GDD = −700 fs² and TOD = +10000 fs³ are very similar, but their shapes differ dramatically. If we combine GDD = −300 with TOD, it results in a longer pulse duration and therefore a lower peak intensity (Fig. 1d, e). Furthermore, depending on the sign of the TOD, the pulse starts with a slowly rising front (TOD < 0) (Fig. 1d) or with a long-lasting trailing edge but with a steep front (TOD > 0) (Fig. 1e). Finally, if we stretch the pulse duration a bit longer, the so far multiple-pulse structure starts to fade out (Fig. 1f).

Fig. 1: Influence of GDD and TOD on the temporal shape of the laser pulses.

Measured spectrum corresponding to 11 fs Fourier-transform-limited (FTL) pulse duration (a). Temporal shape with only negative GDD (b) and positive TOD (c). Combined effect of GDD and TOD resulting in a slowly rising leading edge (d) or a fast rising leading edge with a long accelerating tale (e). With large GDD, the TOD-induced post-pulse train becomes smeared (f). The FWHM pulse duration indicates the temporal length of the most intense pulse. Intensities are normalized to the transform-limited pulse shape.

Experimental results

Upon the experiment, first the transform-limited pulse duration was set. The amount and the sign of the spectral phase derivatives (GDD, and TOD) of the generating laser pulses were adjusted by an AOPDF in the front end of the laser system. Further relevant details of the laser system, including the measurement of pulse energy and the setting of the transform-limited pulse duration on the target, can be found in the Methods section.

First, the acceleration of ions from solid-state targets, that is, thin foils, was investigated. Home-made²⁶ deuterated polyethylene films with a thickness of (0.2 ± 0.02 μm) and a density of 1.35 g/cm³ were mounted on a rotating wheel target system, allowing the acceleration of the ions at a repetition rate of 1 Hz in a burst of 75 shots³³. The highest peak intensity of 4 × 10¹⁸ W/cm² was achieved when the off-axis parabola (OAP) with a focal length of 150 mm created a spot size of (3.1 ±  0.2) × (2.6 ± 0.2) μm² on the target with an energy content close to 20% of the total 21 mJ of pulses. However, the commissioning laser operation and its initial alignment procedure resulted in a day-to-day change in peak intensity up to 25%.

In the second experimental campaign, a thin sheet of heavy water (D₂O, with a purity of 99.8 atomic D) was used. Here, two microjets, positioned at an angle, formed a leaf-shaped liquid target. The thickness of the leaf was carefully measured in situ, i.e., in the evacuated interaction chamber³⁴. The orifices with a diameter of 11 μm and 18 μm provided a leaf thickness 210 nm and 430 nm, respectively. This time we used a higher quality OAP coated with hybrid metallic layers, with a focal length of 130 mm. The resulting spot size of (2.07 ± 0.2) × (1.77 ± 0.2) μm² (full width at half maximum, FWHM) encompassed approximately 36% of the total 23 mJ laser energy, providing a peak intensity of 2 × 10¹⁹ W/cm². The improved laser stability and the advanced alignment procedure reduced the day-to-day peak intensity variation below 5%.

Thin foil target  ~200 nm

Due to the composition of the foils, it was possible to accelerate both protons and deuterons in addition to other ions. In the forward direction (Fig. 2a, b), the cutoff energies peak around GDD = −300 fs². The deuteron beam exhibits a second peak around +500 fs², though with larger error margins. It is worth mentioning that the cutoff and bunch energy of the deuteron beam show very similar behavior, with maxima around  −300 fs² (and +300 fs²), and minima at +200 fs². The relation between the cutoff energy and the bunch energy of the proton beam is weak. This is because of the low hydrogen concentration in the foil, meaning that the majority of the protons probably originate from surface contamination of the foil.

Fig. 2: Effect of GDD on the cutoff energy and the bunch energy of accelerated particles.

The cutoff energy and the bunch energy of the accelerated proton and deuteron pulses in the forward (FWD) (a, b) and backward (BWD) directions (c, d), respectively. Each point represents the average of seven shots, while the colored area denotes the standard error of measurement. The blue dashed lines and shaded regions correspond to protons, and the red ones correspond to deuterons.

The situation in the backward direction is similar (Fig. 2c, d). For deuterons, the cutoff energy and bunch energy correlate well, both showing clear minima at 0 fs². For protons, the minimum cutoff energy is also at 0 fs², while the total energy peaks at +100 fs² and  −100 fs². We need to emphasize here that due to the relatively low statistics and the fluctuation of the peak intensity on target, the positions of energy peaks are indicative only. The tendency is the most important one, namely, the minima around zero GDD, while the maxima are nearly symmetric to the zero point to negative and positive GDDs.

The next day of the campaign with lower peak intensity 20%, we scanned the TOD while keeping the GDD at a value of  −300 fs², where the highest deuteron cutoff energy was measured. As seen in Fig. 3a, the dependence of the cutoff energy for both protons and deuterons on the TOD is very similar. In the forward direction, the cutoff energy increases by ~25% when the TOD is tuned to +10000 fs³, while a similar decrease is observed with the opposite sign TOD (−10000 fs³). This behavior is very similar to that observed at much higher peak intensities, but previously only for protons¹⁹.

Fig. 3: TOD dependence of the cutoff energy and the bunch energy of the forward accelerated particles.

The GDD value is kept constant at GDD = −300 fs². a Shows the cutoff energy of forward accelerated particles as a function of TOD, while (b) shows the bunch energy of forward accelerated particles versus TOD. Each point represents the average of seven shots, and the shaded colored areas denote the standard error of the measurement. The blue dashed lines and shaded regions correspond to protons, and the red ones correspond to deuterons.

With respect to the bunch energies of the particles, there is a weak change for protons from negative toward positive TOD. However, for deuterons, the increase is dramatic, as the pulse energy is doubled at +10000 fs³ compared to that at TOD = 0 fs³.

Thin heavy water leaf 210 nm

The liquid-leaf target system allowed us to utilize the full repetition rate of the laser system. At each setting of the AOPDF, 600 shots were recorded at 1-min intervals. It should be noted that the effect of GDD (and TOD) was immediately visible during the experiment (Fig. 4).

Fig. 4: Effect of GDD tuning on the forward accelerated deuterons’ cutoff and bunch energy.

Each point represents the result of a laser pulse interacting a thin heavy water liquid sheet, measured on-the-fly upon tuning the dispersion values. The vertical dashed lines represent the time when the GDD was changed (GDD values are shown in red). Blue dots correspond to cutoff energy, and orange dots indicate bunch energy.

In the case of an ultrathin heavy water leaf (~210 nm), the proton beam produced a signal three orders of magnitude lower than the deuteron beam, when the latter reached the saturation level of the CCD camera. This is due to the inherent lack of surface contamination on the liquid jet as well as the high purity of the heavy water. Hence, it was possible to investigate only the deuteron characteristics.

As seen in Fig. 5a, the cutoff energy of the accelerated deuterons in the forward direction peaks between  −700 fs² and  −900 fs², with a secondary peak around +1000 fs². The energy of the deuteron beam is highest at +600 fs², with a secondary peak between  −800 fs² and  −900 fs². Remarkably, the cutoff energies of the forward- and backward-accelerated deuterons exhibit a very similar behavior as a function of GDD, which was not the case for the foil target.

Fig. 5: GDD dependence of the cutoff energy and bunch energy.

The cutoff energy in forward and backward directions, and the total energy in the forward direction of the accelerated deuterons for a liquid leaf of 210 nm (a), and 430 nm (b), as a function of GDD, while TOD was kept zero. Each mean value is displayed with its standard deviation, but the bar is smaller than the data points. Blue represents the deuteron cutoff energy in the forward (filled square) and backward (open circle) directions, while red indicates the deuteron bunch energy.

Thin heavy water leaf 430 nm

Notably, for a heavy water sheet with double thickness (430 nm), the maximums of the deuteron beam cutoff energy (Fig. 5b) are higher than for the thinner liquid sheet. When we varied the GDD value while keeping the TOD at zero, we observed a clear peak around  −800 fs², close to the peak position of the 210 nm sheet (Fig. 5a). What is even more interesting is that the highest-energy deuteron beam was generated at a lower GDD value than that of the maximum cutoff. This phenomenon is stronger for the thicker liquid sheet, as the maximum bunch energy was reached at GDD = −200 fs², while the maximum cutoff at GDD = −800 fs² (Fig. 5b).

The higher cutoff energy in the case of the thicker target may result from the weaker pre-expansion of the target rear during the picosecond pulse pedestal, which makes the electron heating more efficient.

Next, we varied the TOD while keeping the GDD constant (Fig. 6). Here, the highest overall cutoff energy of 1.5 MeV was measured at GDD = −1000 fs² and TOD = +5000 fs³. In particular, there was a longer plateau at GDD = −700 fs², where the cutoff energy was the least dependent on the absolute amount of TOD. The general trend was very similar to that observed with ultrathin foil (Fig. 3). Specifically, the cutoff energy of the transform-limited pulse can be somewhat lower with a negative TOD. However, it can be increased by 120% with a positive TOD and a negative GDD.

Fig. 6: The effect of TOD on the forward and backward accelerated deuterons from a heavy water leaf at different GDD value.

The deuteron cutoff energy in forward (a) and in backward (b) directions were measured as a function of TOD at various GDD values. Different colors represent different GDD values.

In the backward direction, the cutoff energies follow a very similar trend, though the peak values are lower by a factor of two compared to the forward direction. This further supports our assumption that the target rear and front sides expand differently, leading to a greater difference between the forward and backward directions compared to thinner leaves.

Theoretical results

Our previous work has revealed³⁵ that the backward and forward acceleration of ions differs when high-density solid foils are used. The experimental verification of such a phenomenon is shown in Fig. 2. The explanation is the effect of the picosecond pulse pedestal, which is absorbed more efficiently when the target density is higher. The dominant absorption mechanism is the inverse bremsstrahlung, which relies on the collision between electrons and ions. The density of a liquid material is considerably lower, as is the ionized plasma density, too. Thus, the collision frequency is lower, resulting in less efficient radiation absorption and modest plasma expansion before the main pulse.

The acceleration of ions from a thin liquid leaf (thickness of 200 nm) was simulated for a given laser pulse energy using a one- and two-dimensional particle-in-cell (EPOCH) code³⁶. The laser pulse duration was stretched by spectral phase modulation, keeping the focal spot the same. Therefore, the laser peak intensity was inversely proportional to the pulse duration, which is defined as

$${t}_{L}={t}_{L0}\sqrt{1+{\xi }^{2}}$$

(1)

where $\xi =\frac{{{\rm{GDD}}}{\left(\frac{{{\Delta }}\omega }{{c}_{B}\pi }\right)}^{2}}{2}$, Δω is the bandwidth of the laser pulse, c_B ≈ 0.4413 is a constant and t_L0 is the Fourier-limited pulse duration. For a symmetric power spectrum, the laser frequency depends on the axial position (z) within the pulse according to: ${\omega }_{0}+\frac{\xi (z-{z}_{0})}{c{t}_{L}^{2}}$, where z₀ is the center of the laser pulse and ω₀ is the central wavelength.

a) 1D Lorentz-boosted simulations of laser pulse interaction with thin liquid-leaf targets

In order to reveal the detailed dynamics of electron heating and consequent plasma expansion, a series of one-dimensional (1D) simulations have been performed in a boosted frame³⁷, where all particles drift with a uniform velocity ${v}_{y}=-c\sin \theta$, where θ = π/4 in our case. This simulation technique allows us to take into account the oblique incidence of the laser pulse, and many details of the ion acceleration dynamics become accessible. The drawbacks of using a 1D geometry is the exclusion of transverse expansion of the hot electron cloud and the assumption of a uniform laser intensity profile within the laser spot. The transverse degree of freedom will be considered in the next section, where we show that the electron’s displacement along the target surface is more significant in the case of shorter pulses, i.e. when the GDD is small and the intensity is high.

The temporal evolution of the light-ion density and the hot electron characteristics are shown in Fig. 7 for three GDD values. The maximum ion energy becomes larger as the GDD is increased, which is attributed to the longer acceleration time, since the peak accelerating field is very similar in all cases. Actually, with GDD = 700 fs², in Fig. 7c, the final velocity is higher, although the measured maximum electric field is somewhat lower than in the other cases. The hot electron density is calculated by summing up the number of electrons with energy larger than 2 keV. In such a way, we show the evolution of hot electron concentration in the lower pictures of Fig. 7. The general tendency is that with larger GDD (longer pulses) the electron temperature is lower, but the number of high-energy electrons is larger because the heating lasts longer and more cold electrons from the bulk target can interact with the laser field. The same is also observed in our 2D simulations.

Fig. 7: 1D dynamics of ion acceleration from thin foil.

The temporal evolution of deuteron density (in units of m⁻³) distribution is shown for GDD = 0 (a), GDD = 300 fs² (b) and GDD = 700 fs² (c). The white curves show the electric field at the position of the forward-moving ion front. The final velocity of ions at the ion front is also shown. Below, the evolution of electron energy distribution is shown for the same GDD values. The white line in (a–c) represents the peak electric field near the ion front and the cyan line in (d–f) is the concentration of hot electrons in the target. All color bars are in a logarithmic (log₁₀) scale.

2D Simulations in the laboratory frame

In the experiment, the radiation energy within the central point of the focal intensity distribution was 8 mJ, resulting in a normalized field amplitude a₀ ≈ 1.5 for a spot radius of 3.4 μm. The same normalized laser field amplitude was used in the case of the Fourier-limited pulse in the simulations. The angle of incidence was 45°. The density of all particles at a late time instance is shown in Fig. 8a for GDD = 100 fs², which corresponds to t_L = 27 fs. From the 1D simulations and Fig. 8a, b, it is evident that the plasma expansion is the only mechanism responsible for ion acceleration, which is named target normal sheath acceleration (TNSA).

Fig. 8: Density distribution.

Density distribution (${\log }_{10}$ scale in units of m⁻³) of all particles at t = 200 fs and GDD = 100 fs² (a), where the red arrows represent the incoming and reflected laser pulse. Evolution of the maximum deuteron energy for different chirp parameters (b), where the orange curves represent the temporal shape of the laser pulse. A longer pulse with lower intensity results in a higher cutoff energy. In (c) the deuteron distributions are shown in momentum-space, which shows a very small divergence: basically, all high-energy ions fly almost perpendicularly to the surface with a half cone angle  ~5°. Below, the angular distribution of high-energy (>200 keV − blue lines), mid-energy (100 keV < W_e < 200 keV − red lines) and low-energy (<100 keV − green lines) electrons for GDD = 0 (d), GDD = 300 fs² (e) and GDD = 700 fs² (f).

In agreement with earlier simulations^11,35,38,39, the acceleration lasts much longer than the pulse duration, and the cutoff energy increases asymptotically toward a maximum value. In 2D simulations, the accelerating peak electric field becomes a fraction of its maximum value after 8 t_L (Fig. 8b). Therefore, we chose 8 t_L as the time instance when we determined the value of the ion energy under various dispersion conditions. From the momentum distribution (Fig. 8c) we can infer a very small divergence for all GDD values, which is also in very good agreement with previous experiments⁴⁰.

As we mentioned in the previous section, the main difference between 1D and 2D (or 3D) simulations is the lateral spreading of laser-generated hot electrons along the target surface. This transverse divergence of electrons is less pronounced for larger GDD values, as shown in Fig. 8d–f. It can be explained with the strong v × B component of the Lorentz force when a₀ is larger, thus the electrons are pushed along the laser propagation direction. At lower intensity, the electrons gain momentum from the laser’s electric field, which leads to an electron motion more parallel with the target normal direction. Further details on this electron motion please find in the Methods section.

The total (or absorbed) energy of the particles in the simulation domain is shown in Fig. 9 for three cases. At zero chirp, the interaction is very short, and only 0.5 mJ of laser energy is transferred to the target (Fig. 9a). However, the average energy is the highest in this case, reaching 50 keV. As the pulse duration is increased, the electron’s kinetic energy decreases because of the smaller laser field amplitude. The relation is a bit ambiguous, as the average electron energy also depends on the pulse duration according to a power law, which is discussed in the next section. In the case of GDD = 300 fs², one can observe a sudden change in temperature between 100 fs and 150 fs (Fig. 9b), due to the cold electrons released from the O⁷⁺ level. In the case of GDD = 700 fs², the maximum ionization state is only O⁶⁺ (Fig. 9c). It is important to note that in this case the absorbed energy is 4 times higher than that at GDD = 0 fs², which also contributes to the increase in acceleration efficiency.

Fig. 9: Temporal evolution of the absorbed energy (blue) and electron heating (red) for different chirp parameters along with the theoretical cutoff energy of deuterons as a function of GDD.

The dashed lines in (a–c) show the laser pulse envelope. The temperature is calculated as the average energy of electrons with energies larger than 1 keV. The total energy of hot electrons from the 2D simulation was multiplied by 4 × 10⁻⁶ to take into account the finite spot size in the z-direction. In (d) Blue stars represent cutoff energies for laser pulses with Gaussian spectra, red stars are for the blue-weighted real laser spectra. The analytical calculation of the maximum ion energies with the use of Equation (4), with a₀ = 1.5 (e). The 2D PIC simulated values were taken at t = 8t_L in each simulation.

In our simulations, the Coulomb collision between particles is neglected. The mean free path of electrons with energy around 10 keV (or higher) is on the order of 1 μm (or larger), therefore collisions do not affect the particle dynamics for the target thickness considered here. In our case, collisions might be important for T_h ~ 1 keV, which is relevant for ∣GDD∣ > 1000 fs². This means that for strongly stretched pulses, electron cooling becomes an important factor, resulting in an increase in the thermal energy of the ions instead of an increase in their cutoff energy. This explains the lower cutoff energy measured for GDD larger than 1000 fs². Later, we show that a simple analytical model also predicts a drop in the cutoff energy, albeit less significant than in the experiment.

The cutoff energy of the accelerated deuterons, resulting from simulations with Gaussian laser pulse spectrum, is summarized in Fig. 9d. It shows that plasma expansion with lower electron temperature (higher GDD) leads to a higher cutoff energy because the acceleration time is longer, so that the 1D simulation results shown in Fig. 7 are confirmed. There is a slight preference towards negative GDD, which may be attributed to the high-frequency components on the leading edge of the laser pulse. Due to computational limitations, we performed only one simulation with a large chirp value, GDD = 1500 fs², where the resulting cutoff energy was ~900 keV. This also confirms the experimentally observed drop in cutoff energy for GDD > 1000 fs². For comparison, we also simulated the acceleration with the blue-weighted real spectrum of the laser pulse (asymmetric spectrum), which results in an asymmetric temporal shape of the laser pulse. As one can see from the red stars, the increase of the cutoff energy is larger when negative GDD is used, whereas the cutoff drops with positive stretch, agreeing with the experimental observations. The lesson is that it is preferable to use an asymmetric laser envelope, where the target first interacts with a rapidly increasing intensity profile. Later, the laser intensity slowly decays, but it is sufficiently strong to sustain the hot electron population in the target. These results explain well the measured negative GDD asymmetry in the increase of the cutoff energy (Fig. 5). The explanation is similar to the effect of positive TOD (see the next Subsection), where the asymmetry in the pulse shape is much stronger (see Fig. 1).

It is important to note that the relative cutoff energy enhancement (difference between maximum energy with 0 and optimal GDD) is stronger in 2D than in 1D (see Fig. 9e). This is attributed to the larger transverse divergence of electrons for zero GDD (see Fig. 8), which reduces the TNSA field in 2D. In the case of longer pulses, the motion of high-energy electrons is almost perpendicular to the target surface; therefore, the sheath field is quasi one-dimensional, and the only difference between the simulations is the transversal variation in the laser intensity envelope.

Analytical model

The high temporal contrast of the laser pulse greatly simplifies the modeling process, because pre-plasma formation and its impact on ion acceleration can be neglected. We consider a hot electron cloud, which is continuously heated by the laser field via a stochastic vacuum heating mechanism, as described previously^41,42. If the laser pulse is long enough and the target is thin, then most of the electrons within the focal area can be heated, and thus the acceleration process becomes very efficient.

The isothermal and adiabatic plasma expansion models are well suited for this regime^43,44. According to 1D simulations, the hot electron density is only several times larger than the critical density: ${n}_{{{\rm{cr}}}}=\frac{{\epsilon }_{0}{m}_{e}{\omega }^{2}}{{e}^{2}}$, while in 2D their density is even lower. This means that we have to consider a two-temperature plasma with dominant cold electrons, which only introduces a small change in the analytical expressions for the accelerating electric field⁴⁵.

The electric field acting on the most energetic ions (ion front) in the adiabatic phase (t > t_L) is expressed as^43,44,45

$${E}_{f}^{{{\rm{adi}}}}=\frac{2{E}_{0}{t}_{L}}{t\sqrt{2+{\omega }_{pi}^{2}{t}^{2}}},$$

(2)

where ${\omega }_{pi}=\sqrt{\frac{{e}^{2}{n}_{h}}{{\epsilon }_{0}{m}_{d}}}$ is the ion plasma frequency, ${E}_{0}=\sqrt{\frac{{n}_{h}{T}_{h}}{{\epsilon }_{0}}}$, ${T}_{h}={m}_{e}{c}^{2}({\gamma }_{e}-1){(1+{\xi }^{2})}^{p/2}$ is the hot electron temperature, which depends on the gamma factor associated with the quiver energy of electrons, ${\gamma }_{e}={\left(1+\frac{0.5{a}_{0}^{2}}{\sqrt{1+{\xi }^{2}}}\right)}^{1/2}$ and n_h is the hot electron density. The parameter p depends on the stochasticity of the heating process, which was found to be between 0.3 and 0.6^41,42.

In the isothermal phase (t < t_L), the electric field has a simpler form:

$${E}_{f}^{{{\rm{iso}}}}=\frac{2{E}_{0}}{\sqrt{2+{\omega }_{pi}^{2}{t}^{2}}}.$$

(3)

The final velocity at which the ions can reach is calculated by integrating Equation (3) up to t_L and Equation (2) from t_L up to infinity, which yields the energy

$${W}_{f}={T}_{h}(\xi ){\left(2\ln \left(\frac{\tau }{\sqrt{2}}+\sqrt{{\tau }^{2}/2+1}\right)+\tau \ln \left(\frac{2}{\tau }+\sqrt{1+4/{\tau }^{2}}\right)\right)}^{2}$$

(4)

where $\tau ={\tau }_{0}\sqrt{1+{\xi }^{2}}$ is the normalized pulse duration and τ₀ = ω_pit_L0. In principle ω_pi also depends on time, as is seen in Figs. 9 and 7, but due to the high level of complications, it has to be neglected in the analytical model.

Figure 9 d presents the chirp-dependent cutoff energy from 2D simulations, which agrees well with the experimental results (e.g. Fig. 5a, c), and it can qualitatively reproduce the trend observed in 1D simulations (Fig. 9e). On the other hand, the cutoff energy strongly depends on the value of p. The discrepancy between the 1D results and the analytical curves can be attributed to the fact that the time dependence of n_h and T_h is neglected. In general, the 1D simulations agree better with the model for τ₀ = 1, which corresponds to n_h = 8 × 10²¹ cm⁻³ ≈ 5n_c. This is a rough estimate for the hot electron density considering the concentration measured in Fig. 7e, f.

Simulation of the effect of TOD

In the experiment, we observed a strong dependence on the third-order dispersion (TOD), which can be explained by the following. In the case of a negative TOD, the target interacts with many low-intensity pulses, which generate a low-temperature plasma already half a picosecond before the arrival of the main pulse. This plasma expands, and the scale length of the preplasma increases on both sides of the target; it can be even larger than the initial target thickness. This means that the target density can be significantly altered and become less optimal for TNSA. This leads to a lower acceleration efficiency, as observed in the experiment. This is also confirmed by 1D simulation, which is shown in Fig. 10b, c. In this case, particle collision is also switched on and normal laser incidence is considered because the current implementation of the code does not support collisions in the boosted frame. One can see that with negative TOD at the arrival of the main pulse (around 0.8 ps), the plasma boundary is not sharp, and the maximum accelerating field is very weak.

Fig. 10: The simulated effect of TOD.

a The 2D PIC simulated average electron temperature (black) and maximum deuteron energies (red) resulted from the interaction with a pulse train (blue), taken from Fig. 1d. In (b, c) the results of 1D simulations with θ = 90° (normal incidence) are shown, where the difference is only the sign of the TOD value. The color code represents the deuteron density (log₁₀[n_D(m⁻³)]) and the white line indicates the accelerating field measured at the ion front.

The situation is different with positive TOD (see Fig. 1e, f), where the main pulse reaches the target first, which is not expanded yet (in Fig. 10c). In the 2D simulation, nonlinear vacuum heating⁴⁶ takes place, and the laser field heats the target electrons, as shown by the black curve in Fig. 10a. The interaction with consecutive pulses maintains the electron temperature at a nearly constant level, which in turn enhances ion acceleration. Unfortunately, the simulation time is limited due to boundary conditions, but the maximum energy can still increase and approach 1.5 MeV after an additional 1 ps acceleration time. If we had more “micro-pulses”, as in reality, then the cutoff energy would have been even higher; thus, in the simulations, we would reach higher energies compared to the experiment. It is known that in a 3D simulation (closest to reality), the maximum energy is less than in 2D; therefore, the exaggerated maximum energy would be compensated in the 3D geometry, and more quantitative agreement could be expected with the experiment.

Discussion

We investigated the effect of the temporal shape of the driving laser pulse on the acceleration of protons and deuterons from deuterated foils and heavy-water leaves. The temporal shape of the driving broadband laser pulse was sculptured by systemically changing its spectral phase through tuning the higher-order dispersion values as GDD and TOD.

Our studies revealed that the minimum cutoff energy and yield were obtained with transform-limited pulses, while an increase of up to 100% was achieved with pulses of the same amount of GDD almost regardless of its sign. This increase is considerably higher than previously observed^19,20. The slight asymmetry in favor of a negative-sign GDD in our experiments (Figs. 2a and 5a) and in the simulations (Fig. 9a) can be explained with the blue-weighted asymmetric spectrum of the pulse, which makes the temporal shape asymmetric in favor of the leading edge when negative GDD is applied. A similar effect might be the reason behind the somewhat favorable positive chirp in the other experiments^19,20, but lack of knowledge of their pulse spectra leaves space for other alternative explanations^18,47, too.

At large GDD values, when the pulse duration is stretched to picosecond(s), the peak intensity drops well below the relativistic value. This resembles the situation with picosecond laser pulse TNSA with the difference that our laser has small energy compared to typical picosecond machines⁴⁷. Hence, the electron cloud remains cold, the plasma cannot be considered collisionless anymore, and the cutoff energy of the accelerated ions and the number of ions drop.

With regard to the effect of the third-order dispersion, the cutoff energy increases from a negative TOD toward a positive one, irrespective of the sign and value of GDD. Such findings agree well with recent observations made for protons¹⁹. The record increase in the cutoff energy to 2.4 times compared to transform-limited pulses we measured at GDD = −1000 fs² and TOD = +10000 fs³. This result agrees well with the enhanced acceleration performance with the use of double⁸ and multiple pulses²⁹ with small temporal separation. However, the multiple-pulse structure provided by TOD causes a number of times higher increase than the earlier multiple-pulse approaches.

Further observations show that the optimum chirp values for the highest cutoff and highest bunch ion energies are different. The difference is more pronounced for the thicker liquid target (Fig. 5b), where the cutoff energy peaks at −800 fs², while the bunch energy does around −300 fs². There is a similar effect for protons and deuterons from the dense foil target, since the most intense acceleration occurs also with different chirp values (Fig. 2a, b). These features—which have not been reported so far—open the possibility of optimization of deuteron yield for more sophisticated applications, such as neutron generation via DD (or DT) fusion from solid or liquid targets^26,28,48. For example, we have recently demonstrated a continuous operation laser-driven neutron source with the highest laser-to-neutron conversion efficiency, among the femtosecond laser-driven sources⁴⁹. We believe that this high conversion efficiency was possible due to optimization of the pulse temporal shape via GDD and TOD.

To support such measurements, we extended the analytical models to include the GDD effect³⁵ and simulations to include the higher-order dispersion (TOD) effect, so that we accurately explained the complicated situation with the target preexpansion (negative TOD) and post-acceleration (positive TOD). The latter one can be considered as a staged acceleration, where the hot electron heating done by the post-pulses compensates for the hyperbolic temporal evolution of the accelerating field. In other words, as the plasma expands the energy is transferred from electrons to ions, which results in electron cooling, which is compensated by the post-pulses. Hence, the optimum pulse shape consists of two major parts with different roles: the sharp rising edge reduces the preplasma formation at the target rear, while the long falling edge keeps the acceleration stronger by sustaining the hot electron temperature in the later stage of the TNSA. We need to emphasize that the experimental conditions and the supporting theoretical analyses have stayed within the TNSA regime. A recent paper on ion acceleration from a similar liquid jet, but with pulse energies an order of magnitude higher, also revealed that the dominant mechanism is TNSA⁵⁰.

Finally, we should note that with the use of our findings, the performance of current and future laser ion accelerators can be enhanced and custom-tailored simply by matching the dispersion values to the laser and target characteristics. The simplest way could be to make the broadband laser spectrum (strongly) asymmetric and to add the corresponding linear dispersion (GDD) to the spectral phase. A slightly more complicated option would be to combine the effect of GDD with the tuning of TOD, which could increase the cutoff energy or multiply the efficiency of an ion accelerator by several times. Such an advancement can be done with no additional cost for any laser-ion accelerator working with broadband laser pulses.

Method

Experimental setup

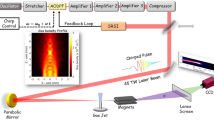
The SEA laser beam enters the purpose-designed and arranged chamber (Fig. 11), and was focused on a target with an off-axis parabola (OAP). The laser-accelerated proton and deuteron beams were recorded and analyzed shot by shot with Thomson ion spectrometers, equipped with micro-channel plate (MCP by Photonis) and CCD camera in both the forward (FWD, target rear side) and the backward (BWD, target front side). The entire Thomson Ion Spectrometer assembly was calibrated for both protons with the use of CR39 plates, detailed as detailed in previous studies^26,51. Hence, the evaluated spectra provide the spectral energy density of the particle beam passing through the 200 μm pinhole.

Fig. 11: Schematics of the experimental setup.

Inset: the temporal contrast measured at the position of the target. The laser enters the target chamber and, after reflection from several mirrors (M), is focused onto the target by an off-axis parabolic (OAP) mirror. Particles such as protons (H⁺), deuterons (D⁺), and other ions are accelerated both forward (FWD) and backward (BWD), reaching Thomson parabola spectrometers positioned in both directions. Each spectrometer is equipped with magnets, electrodes and a microchannel plate (MCP) coupled to a phosphor screen, which is imaged by a CCD camera.

Determination of bunch energy of a particle pulse

The divergence of the proton beams was measured using CR39 particle detectors as discussed in an earlier study⁴⁰. The divergence of the deuteron beam was measured in a similar way only for the liquid sheets. We have found that the divergence angles of the proton and deuteron beams are equal within the accuracy of the measurement, that is, 5° ± 0.3°. As the ion beam divergences are known to change when the target thickness changes through a considerably larger range, we assumed the same divergence angles for both protons and deuterons for all targets. This assumption is also supported by the simulated deuteron beam divergence (Fig. 8c). The particle bunch energy is then calculated from the integrated spectral energy density from 50 keV to the cutoff energy, the divergence angle, the pinhole size, and the distance between the target and the pinhole.

The driving laser

The SEA laser system is based on optical parametric chirped pulse amplification (OPCPA). The amplifier stages are driven by 80 ps pump pulses, so this solution enables a pre-pulse and superfluorescence-free background until 40 ps before the main pulse. The spectrum, which spans 220 nm around a central wavelength of 850 nm (Fig. 1a), supports a transform-limited pulse duration of 11 fs (FWHM). The repetition rate of the SEA laser is adjustable, ranging from shot-on-demand to 10 Hz. The laser beam features a super-Gaussian spatial profile with a full width at half maximum (FWHM) diameter of 65 mm. The low average power, combined with OPCPA, prevents thermal effects, allowing the system to maintain consistent pulse parameters during both single-shot and multiple-shot laser operations. This makes all alignment procedures accurate and straightforward.

Laser pulse characterization on target

In the experimental series, it was of primary importance to know both the pulse duration and the pulse energy at the target position under the laser acceleration conditions, that is, in vacuum, without any vacuum windowed valves between the laser and the target, and at full laser energy.

The SEA laser system has a built-in energy measurement unit, which displays in real time and also logs the energy of each laser pulses, independently of the repetition rate³⁰. The energy of the pulses on the target was then established via measuring the transferred energy from the laser to the target. The calibration was made with laser pulses of 5 mJ, stretched to 50 ps, so that any nonlinear effects in the vacuum window as could be avoided.

The transform-limited pulse duration was established at the focus of the OAP using a chirp scanning method⁵². To reduce the energy below the damage threshold of the second harmonic generation (SHG) crystal, we positioned an uncoated fused silica wedge between the OAP and the focal plane. The beam reflected from the first surface of the wedge was directed onto a 10 μm-thick Type I BBO SHG crystal located in the attenuated focal plane. To further decrease the intensity, a small (5 mm) aperture was installed before the OAP. This ensured that the intensity was low enough to prevent third-order nonlinear effects in the BBO crystal while still being sufficient to generate an adequate second-harmonic signal. The second harmonic signal was collected by a fused silica lens and sent to a spectrometer outside the chamber through a vacuum window. An acousto-optical programmable dispersive filter (AOPDF) installed in a laser system³⁰ was used to adjust the spectral phase of the pulses while recording the second-harmonic spectra. The spectral phase of the pulse was determined from the measured chirp-scan trace using a retrieval algorithm, which provided feedback to the AOPDF to achieve a transform-limited duration at the target. This approach allowed for the compensation of spectral phase distortions introduced by any optical components.

The accuracy of an AOPDF in introducing the set of GDD and TOD values to the spectral phase was investigated earlier. The discrepancy between the set and the measured GDD and TOD values was proven to be within the precision of the measurement itself (that is, a few fs² and a few tens of fs³)⁵³.

Measurement of the temporal shape of a non-transform limited laser pulse would be challenging in the displayed time scale and by femtosecond accuracy (Fig. 1). The reason is that the commercial devices available (D-scan, Wizzler, FROG) work for laser pulses sufficiently close to their transform-limited pulse duration—which is far not the case here. Second, these devices do not measure the temporal pulse shape directly, they deduct it from the spectra and the spectral phase. A possible solution would be to use a cross correlator (e.g., a TUNDRA by Ultrafast Innovation or a SEQUIOA by Amplitude). However, their temporal resolution is not sufficient to show the fine structure of the pre- and postpulses displayed in Fig. 1d, c, e, respectively. We need to mention here that the effect of nonlinear phase shift, especially TOD, on the temporal pulse was investigated and measured for picosecond pulses at the dawn of ultrafast fiber communication (related discussions can be found in earlier work⁵⁴ and in a review on ultrafast laser pulse shaping⁵⁵.). We can then establish that once the transform-limited pulse duration was set on the target, the temporal shape of the laser pulses interacting with the target is the one we can calculate from the pulse spectrum and the added GDD and TOD values³¹.

Please note that optimization of the temporal shape with the introduction of GDD and TOD is a handsome way to find the optimum temporal intensity of the laser pulse. From an optical and laser point of view, other ways are known and possible to sculpt the temporal shape of the pulse, such as the temporal shape of nanosecond laser pulses that drive laser inertial fusion explosions^56,57.

Simulations

Here we summarize the numerical parameters and the setup used in our particle-in-cell simulations³⁶. In the one-dimensional case, the grid size is 2 nm, and the time step is 0.96t_CFL. The target plasma slab has a thickness of 200 nm, consisting of 400 Oxygen, 1000 deuterons, and 1600 electron macroparticles. The initial charge state of Oxygen was set to 5⁺ , and further field ionization was included in the modeling. The electron density at the beginning of the simulations is n_e = 3 × 10²⁹ m⁻³. The initial temperature of electrons is 10 eV, and for ions: 0.5 eV. Because of the high laser intensity contrast and weak pulse pedestal, we consider a preplasma scale length as low as 20 nm at the target front surface in all simulations. The amplitude of the chirped laser field is defined as ${a}_{0,{{\rm{ch}}}}={a}_{0}{\left(1+{\xi }^{2}\right)}^{-\frac{1}{4}}$.

For the 2D parameter scan, we used a 40 × 30 μm² 2D area with a grid spacing as low as 6 nm. In each grid cell, we placed 100 oxygen ions, 400 deuterons, and 200 electron macro-particles. The initial ionization state of oxygen is 5⁺, and further field ionization of higher energy levels is included in the simulation. In one of the simulations, we tracked more than 10,000 electron macroparticles, which were placed after the preplasma in a 20 nm thick region on the front side of the target.

For simulation of the TOD effects, the laser pulse train is represented by consecutive cos² envelopes, which are fitted to the pulse intensity profile seen in Fig. 1, while the main pulse, with the highest intensity, has a Gaussian envelope.

For a deeper insight, we also show here the trajectory of some of the electrons, where the recirculation is clearly recognized (Fig. 12). Furthermore, in the case of high-energy electrons (light-blue, yellow, and red curves in Fig. 12c) it is also visible that their momentum increases each time they return to the front of the target, which means a positive “interference” between the laser field and electron oscillation. For other electrons, the energy could be lost when they interact again with the laser, which means a positive E_x component at the position of the electrons when they return to the target front side. In some cases, even a resonance is possible between the laser and the electron motion, but because of the varying recirculation period, this resonance is only transient. Therefore, electron heating is a stochastic process as previously described^41,42.

Fig. 12: Electron recirculation.

Phase-space trajectories of several electrons with temporal RMS (root mean square) momentum larger than m_ec (a, c) and with RMS momentum between 0.5 m_ec and m_ec (b, d). This is obtained in 2D simulation with GDD=300 fs² and in this case the target is vertically oriented, while the laser’s angle of incidence is the same.