Introduction

Gauge theories are ubiquitous in many areas of physics, ranging from the realm of fundamental interactions1,2, to the low-energy physics of condensed matter systems3,4. Dynamical gauge fields mediate the interactions of quantum matter and are responsible for remarkable non-perturbative phenomena, being confinement a prominent example5. The impossibility of observing isolated particles with a net gauge charge according to the underlying local symmetry group1, first realised in asymptotically-free non-Abelian gauge theories6, can actually also appear in simpler Abelian models, such as quantum electrodynamics in D = 1 + 1 dimensions7. While the dimensional reduction allows for a more detailed quantitative understanding of this phenomenon8,9, a full non-perturbative analysis of finite-density regimes and long real-time propagation lies beyond our current capabilities. The discretization of gauge theories on a space-time lattice does provide a well-defined route to address several non-perturbative problems in the field, such as the phase structure of quantum chromodynamics. However, our most sophisticated numerical analysis of lattice gauge theories (LGTs) is limited by the so-called sign problem10 and the harsh entanglement scaling properties11,12, such that a plethora of quantitative questions remain unanswered.

With the advent of quantum technologies, an alternative strategy has been identified13, which searches for scalable protocols to synthesize LGTs on either digital or analogue quantum simulators14,15,16,17,18,19,20,21,22,23,24,25,26,27,28,29,30,31. Such an endeavour has led to the experimental observation of gauge-invariant dynamics, confinement and string-breaking phenomena32,33,34,35,36,37,38,39,40,41,42,43,44,45,46,47,48,49,50,51,52,53,54,55,56,57,58,59,60. Despite being still far from a fully-fledged quantum simulation of the Standard Model of particle physics, which will likely require a large-scale fault-tolerant quantum computer, these simpler quantum simulators can already provide useful insights, especially when addressing real-time and finite-density phenomena. LGTs built on \({{\mathbb{Z}}}_{2}\) gauge groups constitute a prototypical example of such models, which are of great interest in various contexts, ranging from the understanding of confinement61,62,63,64,65,66,67, to topological phases of matter and spin liquids68,69,70,71, opening the way to new collective effects72,73,74.

Let us consider a D = (1 + 1) dimensional \({{\mathbb{Z}}}_{2}\) LGT in which the dynamical charges correspond to hardcore bosons that can be created or annihilated by \({a}_{i}^{{{\dagger}} },{a}_{i}\) on the lattice sites xi = id, where d is the lattice spacing and \(i\in {{\mathbb{Z}}}_{L}\) with L being the number of sites. The boson operators are constrained by \({a}_{i}^{\,\,2}=0={a}_{i}^{{{\dagger}} 2}\), such that there cannot be double occupancies, and their tunnelling will be mediated by \({{\mathbb{Z}}}_{2}\) gauge fields encoded by Ising spins \({\sigma }_{{i}_{\ell }}^{\alpha }\) on the links \({x}_{{i}_{\ell }}={i}_{\ell }d\) with iℓ = i + 1/2, where α ∈ {x, y, z} specifies the particular Pauli operator. The \({{\mathbb{Z}}}_{2}\) LGT on a chain has been thoroughly studied previously61,63,75,76. In the presence of a non-zero electric field strength h, which leads to a potential between a pair of background test charges growing linearly with their distance V(r) ~ V0r, this model exhibits confinement also when the charges become dynamical61,63. Such property is reflected in the exponential decay of the gauge-invariant one-body Green’s function, indirectly showing that there are no charged quasi-particles in the low-energy spectrum. Confinement in the \({{\mathbb{Z}}}_{2}\) chain has been shown to survive for any particle density76, and even at non-zero temperatures75. For very large electric fields h, the particles get tightly bound into charge-neutral pairs at neighbouring sites connected by a short electric-field string. The emergent dynamics of these bound pairs is governed by an integrable model that, in the continuous limit, has a Luttinger liquid (LL) behaviour with a power-law decay for the corresponding Green’s function61. Hence, in contrast to the charged particles, these charge-neutral \({{\mathbb{Z}}}_{2}\) “mesons” propagate as boson fields with a certain anomalous dimension, governing the physics of the low-energy spectrum of the theory. As one lowers the electric field, even if the confinement is not so tight and the exact mapping to the integrable model is no longer valid, the \({{\mathbb{Z}}}_{2}\) chain remains in a confined LL phase, albeit with an anomalous dimension and power-law decay that change.

In our work, we explore a minimal extension of this model that brings in a neat connection to quantum Hall physics, where the interplay of dynamical matter and static gauge fields has been the object of intense investigations. In this case, the gauge fields provide a background under which the charged particles propagate. A notable effect in such systems is that charged particles in 2d and quasi-1D lattices can localize even in the absence of disorder, as a result of Aharonov-Bohm interference77. This phenomenon is known as Aharonov-Bohm (AB) caging78, as particles are locked inside restricted regions of space. This leads to localised eigenstates and a flat-band spectrum for specific values of the background magnetic flux that pierces each elementary plaquette. The competition of Aharonov-Bohm caging and inter-particle interactions has been widely addressed in the literature: while interactions are disruptive for the stability of cages, they can be responsible for a rich physical phenomenology79,80,81,82,83,84,85,86.

With our work, we introduce the notion of dynamical AB caging, in which gauge fields are no longer static classical configurations, but rather dynamical quantum variables. Indeed, we shall see that a fundamental interplay between AB caging and confinement physics arises. Specifically, also motivated by recent experimental progress in the implementation of a \({{\mathbb{Z}}}_{2}\) loop with trapped-ion devices60, we introduce a minimal LGT generalising the above \({{\mathbb{Z}}}_{2}\) chain, and grounding for the phenomenon of the aforementioned dynamical AB caging through gauge fields. For this purpose, we add an extra Ising spin on each link of the system we sketched above, such that the charges have now two tunnelling paths along the bonds b ∈ {1, 2}, each mediated by the gauge-field parallel transporter \({\sigma }_{b,{i}_{\ell }}^{z}\). This setup can then be naturally represented as a linear chain of loops, with two \({{\mathbb{Z}}}_{2}\) gauge fields living on either arm of each loop - see Fig. 1. These minimal plaquettes thus enclose a dynamical \({{\mathbb{Z}}}_{2}\)-valued flux, whose magnetic energetic contribution stems from a simplified Wilson plaquette term that only requires a two-body Ising interaction to attain gauge invariance. As we shall see, such a \({{\mathbb{Z}}}_{2}\)-flux, taking values 0 or π, can indeed set the sought dynamical AB caging. In the context of fractionalization and \({{\mathbb{Z}}}_{2}\) LGTs with dynamical matter in D = 2 + 1 dimensions, π fluxes are referred to as visons for vortex Ising excitations87,88. They appear as particle-like vortex excitations localised to a single plaquette of the two-dimensional lattice and can only be excited by a non-local string that connects the plaquette to one of the boundaries. By analogy, we shall also refer to these localised π fluxes as visons for our \({{\mathbb{Z}}}_{2}\)-loop chain. While here visons cannot condense to yield confinement-deconfinement transitions, we will demonstrate that phase transitions of a different nature can occur, as arising from the interplay of the particle filling, visons proliferation and AB cages, and dynamical AB caging will emerge as a mechanism of strong-confinement, even in the absence of strong electric field lines binding particles in pairs.

Fig. 1: \({{\mathbb{Z}}}_{2}\) Loop-chain.
figure 1

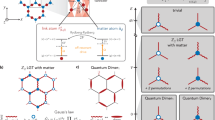
a Hardcore bosons live in the sites of a one-dimensional lattice. Two links depart from each site in a loop geometry and host spin-\(\frac{1}{2}\) gauge-field variables \({\sigma }_{1}^{\alpha }\) and \({\sigma }_{2}^{\alpha }\). Each loop encloses a gauge flux taking values in {0, π} and corresponding to the eigenvalues +1 (0 flux) or -1 (π flux) of  \({\sigma }_{1}^{z}{\sigma }_{2}^{z}\). The hopping amplitude between sites connected by a loop in a π-flux state vanishes due to destructive Aharonov-Bohm interference. b Gauge invariant configurations in the spin-1 reduction of the loop-chain model, where \(| {\Phi }^{\pm }\rangle\) and \(| {\Psi }^{+}\rangle\) are common eigenstates of the spin-1 operators \({({S}^{x})}^{2}\) and \({({S}^{z})}^{2}\), defined at the end of the “Additional local symmetry and reduction to spin-1" subsection in the Methods. Occupied sites are filled in dark blue.

Full size image

Methods

The model

The Hamiltonian of the \({{\mathbb{Z}}}_{2}\)-loop chain, for ℏ = 1, reads

$$H=\frac{t}{2}{\sum}_{i,b}\left({a}_{i}^{{{\dagger}} }{\sigma }_{b,{i}_{\ell }}^{z}{a}_{i+1}+{{{\rm{H.c.}}}}\right)\,+\frac{h}{2}{\sum}_{i,b}\,{\sigma }_{b,{i}_{\ell }}^{x} +\frac{J}{2}\,{\sum}_{i}{\sigma }_{1,{i}_{\ell }}^{z}{\sigma }_{2,{i}_{\ell }}^{z},$$
(1)

where we have introduced the tunnelling strength t, and the electric h and magnetic J couplings. The tunnelling of hardcore bosons is assisted by a Pauli operator along z that acts as a parallel transporter, enforcing the \({{\mathbb{Z}}}_{2}\) gauge invariance of the matter dynamics. Pauli operators along x, instead, play the role of a \({{\mathbb{Z}}}_{2}\) electric field \({E}_{b,{i}_{\ell }}=(1+{\sigma }_{b,{i}_{\ell }}^{x})/2\). In the electric-field basis, the states \(\vert {\pm }_{b,{i}_{\ell }}\rangle =(\vert {\uparrow }_{b,{i}_{\ell }}\rangle \pm \vert {\downarrow }_{b,{i}_{\ell }}\rangle )/\sqrt{2}\) stand for the presence/absence of an electric-field line connecting two neighbouring matter sites. The Ising coupling \({W}_{{\bigcirc }_{{i}_{\ell }}}={\sigma }_{1,{i}_{\ell }}^{z}{\sigma }_{2,{i}_{\ell }}^{z}\) can be interpreted as a Wilson plaquette term that quantifies the ‘magnetic flux’ piercing the loop that connects sites i and (i + 1). Indeed, for a vanishing electric field, the total phase acquired by a boson circulating the loop can be expressed in terms of an effective flux \(\exp \{{{{\rm{i}}}}\Phi_{{{\rm{B}}}}\}=\langle {W}_{{\bigcirc }_{{{{{\rm{i}}}}}_{\ell }}}\rangle\). As a result, ferromagnetic loop orderings are 0-flux configurations, while anti-ferromagnetic ones yield a π-flux. Since π-flux states correspond to vanishing eigenvalues of \({S}_{{i}_{\ell }}^{z}=\frac{1}{2}({\sigma }_{{i}_{\ell },1}^{z}+{\sigma }_{{i}_{\ell },2}^{z})\), such gauge-field loop configurations lead to a perfect destructive AB interference, inhibiting the boson tunnelling to a neighbouring loop. In contrast with the classical AB cages, we note that the interplay of the interference and particle dynamics will be affected by quantum fluctuations and by the specific filling.

The Hamiltonian (1) has a global U(1) symmetry associated to the conservation of the total particle number, which we control through a chemical potential μ via H → H − μ∑ini with \({n}_{i}={a}_{i}^{{{\dagger}} }{a}_{i}\). The \({{\mathbb{Z}}}_{2}\) gauge invariance of the Hamiltonian (1) results from [H,Gi] = 0  ∀i, in which \({G}_{i}={\prod }_{b}{\sigma }_{b,{i}_{\ell }-1}^{x}{(-1)}^{{n}_{i}}{\prod }_{b}{\sigma }_{b,{i}_{\ell }}^{x}\) are the local symmetry generators. When considering an open loop chain terminating with a pair of matter sites, the local generators of the gauge group at its ends should read \({G}_{1}={(-1)}^{{n}_{1}}{\prod }_{b}{\sigma }_{b,{1}_{\ell }}^{x}\) and \({G}_{L}={\prod }_{b}{\sigma }_{b,{(L-1)}_{\ell }}^{x}{(-1)}^{{n}_{L}}\).

Additional local symmetry and reduction to spin-1

Besides its \({{\mathbb{Z}}}_{2}\) gauge symmetry, the Hamiltonian (1) is also invariant under the local exchange of the two Ising operators of each loop: \({\sigma }_{1,{i}_{\ell }}^{\alpha }\leftrightarrow {\sigma }_{2,{i}_{\ell }}^{\alpha }\). Let us define the total spin in a loop as \({{{{\bf{S}}}}}_{{i}_{\ell }}=({{{{\boldsymbol{\sigma }}}}}_{1,{i}_{\ell }}+{{{{\boldsymbol{\sigma }}}}}_{2,{i}_{\ell }})/2\), so that the \({{\mathbb{Z}}}_{2}\)-loop Hilbert space can be seen as the direct sum of a spin-0 (singlet) and a spin-1 (triplet) representation of SU(2). There is thus an additional local conservation of the Casimir operator \({{{{\bf{S}}}}}_{{i}_{\ell }}^{2}\), which has eigenvalues \({s}_{{i}_{\ell }}({s}_{{i}_{\ell }}+1)\), with \({s}_{{i}_{\ell }}\in \{0,1\}\). The total Hilbert space thus decouples into sectors corresponding to each possible set \(\{\ldots ,{s}_{{i}_{\ell }-1},{s}_{{i}_{\ell }},{s}_{{i}_{\ell }+1},\ldots \,\}\). Whenever a loop is in a singlet π-flux configuration, which corresponds to \({s}_{{i}_{\ell }}=0\) and to a loop Bell state \(\vert {\Psi }_{{i}_{\ell }}^{-}\rangle =(\vert {\uparrow }_{1,{i}_{\ell }}{\downarrow }_{2,{i}_{\ell }}\rangle -\vert {\downarrow }_{1,{i}_{\ell }}{\uparrow }_{2,{i}_{\ell }}\rangle )/\sqrt{2}\), the chain gets effectively broken, as the loop resides in a so-called dark state that decouples from the dynamics. Moreover, the associated π-flux inhibits any possible tunnelling connecting the two partitions. Therefore, an arbitrary distribution of singlets leads to the chain being fragmented into a set of independent subchains, which are instead composed only of triplet bonds that allow for non-trivial dynamics.

Without loss of generality, we can thus restrict our analysis to one of these \({s}_{{i}_{\ell }}=1\) subchains. When expressed in terms of the total spin, the Hamiltonian reads

$$H=t{\sum}_{i}\left({a}_{i}^{{{\dagger}} }{S}_{{i}_{\ell }}^{z}{a}_{i+1}+{{{\rm{H.c.}}}}\right)\,+h {\sum}_{i}\,{S}_{{i}_{\ell }}^{x}+J {\sum}_{i}{\left({S}_{{i}_{\ell }}^{z}\right)}^{2},$$
(2)

where we have neglected an irrelevant constant term. The model in Eq. (2) now describes a LGT on a chain, but with gauge degrees of freedom being spin-1 operators. Let us remark that this model differs from the so-called quantum link models89, which can also include a higher-spin representation of the gauge fields to preserve a local U(1) gauge symmetry. In our case, the symmetry is still the discrete \({{\mathbb{Z}}}_{2}\) group, having effective local generators that now read

$${G}_{i}={P}_{{i}_{\ell }-1}^{\,x}{(-1)}^{{n}_{i}}{P}_{{i}_{\ell }}^{x},{P}_{{i}_{\ell }}^{x}=2{({S}_{{i}_{\ell }}^{x})}^{2}-1$$
(3)

together with the corresponding deformations at the edges for open boundary conditions. We will work in the neutral gauge sector, such that the physical space \(\vert \psi \rangle \in {{{{\mathcal{H}}}}}_{{{{\rm{phys}}}}}\subset {{{\mathcal{H}}}}\) is stabilised by Gauss’ law operators \({G}_{i}\vert \psi \rangle =+\vert \psi \rangle \,\forall i\). In this case, considering a finite chain ending with sites, one can see that the total parity of hardcore bosons is actually fixed to be even, as \({P}_{{{{\rm{hb}}}}}={(-1)}^{{\sum }_{i}{n}_{i}}={\prod }_{i}{G}_{i}=1\). We note that the loop chain model (1) is the simplest extension of the \({{\mathbb{Z}}}_{2}\) chain in which the gauge-field dynamics is not entirely fixed by the matter fields. Indeed, the non-linearity of Gauss’ law in terms of the gauge field operators, which is quadratic in the spin-1 reduction of the Hamiltonian, Eq. (2), makes it impossible to integrate them out in favour of a pure matter model, in contrast to the \({{\mathbb{Z}}}_{2}\) chain61.

In the spin-1 language, the Wilson plaquette for each loop becomes \({W}_{{\bigcirc }_{{i}_{\ell }}}=2{({S}_{{i}_{\ell }}^{z})}^{2}-1\), and thus has a \({{\mathbb{Z}}}_{2}\)-valued spectrum  ± 1 corresponding to the 0-flux ( + 1) and π-flux ( − 1) configurations. Equivalently, the total electric field in each loop is controlled by the x component of the total spin \({E}_{{i}_{\ell }}={\sum }_{b}{E}_{b,{i}_{\ell }}=1+{S}_{{i}_{\ell }}^{x}\). From here onward, we will adopt the notation \(\vert {0}_{\Uparrow } \rangle = \vert \uparrow \uparrow \rangle , \vert \pi \rangle =(\vert \uparrow \downarrow \rangle + \vert \downarrow \uparrow \rangle )/\sqrt{2}, \vert {0}_{\Downarrow } \rangle = \vert \downarrow \downarrow \rangle\) for the m = 1, 0, − 1 eigenstates of Sz that label 0-flux and a π-flux states, respectively. For convenience, we also use the Bell pairs

$$\vert {\Phi }^{\pm }\rangle =\frac{1}{\sqrt{2}}(\vert \uparrow \uparrow \rangle \pm \vert \downarrow \downarrow \rangle ),\,\,\vert {\Psi }^{\pm }\rangle =\frac{1}{\sqrt{2}}(\vert \uparrow \downarrow \rangle \pm \vert \downarrow \uparrow \rangle ),$$
(4)

such that \(\vert {\Phi }^{\pm } \rangle =(\vert {0}_{\Uparrow } \rangle \pm \vert {0}_{\Downarrow } \rangle )/\sqrt{2}\) and \(\vert {\Psi }^{+}\rangle =\vert \pi \rangle\), recalling that the missing Bell pair \(\vert {\Psi }^{-}\rangle =(\vert \uparrow \downarrow \rangle -\vert \downarrow \uparrow \rangle )/\sqrt{2}\) is the dark state that is completely decoupled from the dynamics. We note that the role of gauge symmetry and AB interference in these entangled flux states has been realised in recent trapped-ion experiments60. The Bell states are common eigenstates of \({({S}_{{i}_{\ell }}^{x})}^{2}\) and \({({S}_{{i}_{\ell }}^{z})}^{2}\), with \({({S}_{{i}_{\ell }}^{x})}^{2} \vert {\Phi }_{{i}_{\ell }}^{+} \rangle = \vert {\Phi }_{{i}_{\ell }}^{+} \rangle\), \({({S}_{{i}_{\ell }}^{x})}^{2} \vert {\Psi }_{{i}_{\ell }}^{+} \rangle = \vert {\Psi }_{{i}_{\ell }}^{+} \rangle\), \({({S}_{{i}_{\ell }}^{x})}^{2} \vert {\Phi }_{{i}_{\ell }}^{-} \rangle =0\) and \({({S}_{{i}_{\ell }}^{z})}^{2} \vert {\Phi }_{{i}_{\ell }}^{\pm } \rangle = \vert {\Phi }_{{i}_{\ell }}^{\pm } \rangle\), \({({S}^{z})}^{2} \vert {\Psi }_{{i}_{\ell }}^{\pm } \rangle =0\). We also point out that the state \( \vert {\Phi }_{{i}_{\ell }}^{-} \rangle\) is a 0-flux state, which also has a well-defined value of the total electric field \({E}_{{i}_{\ell }} \vert {\Phi }_{{i}_{\ell }}^{-} \rangle = \vert {\Phi }_{{i}_{\ell }}^{-} \rangle\). The gauge-invariant configurations that are allowed by Gauss’ law are depicted in Fig. 1.

DMRG encoding

The interest in low-dimensional LGTs with simplified Abelian groups lies in the expectations that they could be amenable to quantum simulation in the near term and has led to recent experimental progress32,33,34,35,36,37,38,39,40,41,42,43,44,45,47,48,49,50,51,52,53,54,55,56,57,58,59,60. Even if phenomena related to long-time dynamics lie beyond numerical capabilities, the existence of an entanglement area law90 for the reduced dimensionality suggests that one may use numerical simulations based on matrix product states (MPS)91 to explore the full finite-density phase diagram of the model. This will shed light on the role of the dynamical AB cages and the gauge-invariant couplings, guiding our understanding of finite-density effects reported in the following sections. Before delving into the details, let us present our approach to deal with the local \({{\mathbb{Z}}}_{2}\) symmetry using MPS.

The numerical results of this paper are mainly obtained using DMRG algorithms92,93,94 in subspaces of fixed gauge sector Gi = 1 and particle density ν = N/L. A direct use of DMRG for Eq. (2) requires additional Hamiltonian terms to penalize the overlap of a state \(\vert \psi \rangle\) with states not belonging to the physical Hilbert space satisfying the Gauss law \({G}_{i}\vert \psi \rangle =+\vert \psi \rangle \,\forall i\). For instance, one may consider adding Hamiltonian penalty terms such as H → H − λ∑iGi, which suppress unwanted contributions from other gauge-sectors in the low-energy regime, but these are hard to control95.

Another possible strategy would be to integrate out the matter degrees of freedom by making use of Gauss’ law \({G}_{i}\vert \psi \rangle =+\vert \psi \rangle \,\forall i\), with the generators in Eq. (3). In the physical subspace, this would lead to a spin-1 model, in a similar spirit to the spin-1/2 model that arises in the physical subspace of the \({{\mathbb{Z}}}_{2}\) chain61,62, with non-local terms that follow from the mapping of the particle density onto domain-wall operators \({n}_{i}\to (1-{P}_{{i}_{\ell }-1}^{x}{P}_{{i}_{\ell }}^{x})/2\), which count the number of magnetic kinks connecting two neighbouring ferromagnetic domains – see Supplementary Note 1. In this case, a fine-tuning of a chemical potential term \(-\mu (1-{P}_{{i}_{\ell }-1}^{x}{P}_{{i}_{\ell }}^{x})/2\) would be needed to fix the total number of particles in the system.

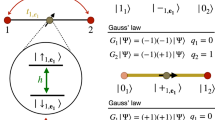
In order to enforce both Gauss’ law and particle number conservation without resorting to penalty or chemical potential terms, we rewrite the model (2) as follows. First, every bond operator is split into two \({S}_{{i}_{\ell }}^{\alpha }\mapsto {\sigma }_{i}^{\alpha },{S}_{i+1}^{\alpha }\). Then, ‘super-sites’ are introduced that enclose the original matter sites of the chain and the neighbouring ‘half-links’. The half-links on the right of each site host Ising spin degrees of freedom, while spin-1 operators live on the left – see Fig. 2. The Hamiltonian is then rewritten as \(H={{{\mathcal{P}}}}\tilde{H}{{{\mathcal{P}}}}\), where

$$\tilde{H}=t {\sum}_{i}({a}_{i}^{{{\dagger}} }{\sigma }_{i}^{z}{S}_{i+1}^{z}{a}_{i+1}+{{{\rm{H.c.}}}})+h {\sum}_{i}{S}_{i}^{x}+J\, {\sum}_{i}{({S}_{i}^{z})}^{2}$$
(5)

still displays a local \({{\mathbb{Z}}}_{2}\) gauge symmetry with generators that are local on the super-sites \({\tilde{G}}_{i}={P}_{i}^{x}{(-1)}^{{n}_{i}}{\sigma }_{i}^{x}\), \({\tilde{G}}_{1}={(-1)}^{{n}_{1}}{\sigma }_{1}^{x}\), \({\tilde{G}}_{L}={P}_{L}^{x}{(-1)}^{{n}_{L}}\). The projectors \({{{\mathcal{P}}}}={\prod }_{i}(1+{\sigma }_{i}^{x}{P}_{i+1}^{x})/2\) impose the condition that \({\sigma }_{i}^{x}={P}_{i+1}^{x}\), ensuring that the dynamics of \(\tilde{H}\) in the subspace constrained by \({\tilde{G}}_{i}=1\,\forall i\) is reduced to that of Eq. (2) in the neutral gauge sector Gi = 1  ∀i(3).

Fig. 2: Schematics of the encoding for DMRG.
figure 2

The bonds of the spin-1 lattice gauge theory in Eq. (2) are broken in half. Super-sites (dashed circles) enclose the original matter sites of the chain and two “half-links", except at the edges, where one “half-link" is dropped as the original chain terminates with sites. In each super-site, the right “half-links" host spin-\(\frac{1}{2}\) degrees of freedom, while spin-1 operators live in those on the left.

Full size image

As detailed in Supplementary Note 2, by exploiting a global symmetry of \({{\mathcal{P}}} {\tilde{H}} {{\mathcal{P}}}\), we show that it is possible to fix both the total number of particles in the system and the Gauss’ law constraints, without resorting to additional Hamiltonian penalties. To the best of our knowledge, other approaches allow to enforce either one of these symmetries, while still relying on energetic penalties for the other. As a figure of merit of the reliability of the above method, in Supplementary Note 2 we show that Exact Diagonalization (ED) results based on Eq. (2) and DMRG results based on Eq. (5) coincide - see Supplementary Fig. 1. In the same figure, further comparison with a different DMRG approach is also presented for a larger system size: there, the results are compared to those obtained for the spin-1 chain that describes the \({{\mathbb{Z}}}_{2}\) loop model in the neutral gauge sector.

Results

Self assembly of Aharonov-Bohm cages at h = 0

For h = 0, the electric field term drops out of the Hamiltonian (2) and the remaining hopping and flux terms locally commute. As a result, \({({S}_{{i}_{\ell }}^{z})}^{2}\) is locally conserved, and the Hilbert space results to be fragmented into sectors labelled by the eigenvalues of \({({S}_{{i}_{\ell }}^{z})}^{2}\) at each link of the chain. Following a similar logic to what has been discussed in the previous section, we conclude that the chain will get partitioned into all possible combinations of AB cages of different lengths, each surrounded by a pair of links in the \(\vert \pi \rangle\) state, which support a perfect AB destructive interference, such that the particles that reside within the cage cannot escape. We will then be left with a set of independent AB cages, each hosting only 0-flux bond states and a number of particles that will search for the minimum energy configuration consistent with the AB constrained length. Every AB cage will only be allowed to host either zero or an even number of particles, as we recall that there is a parity constraint dictated by Gauss’ law. Finding the ground state of the system reduces to a classical problem, which consists of comparing the energies of all the possible different partitionings of the full chain, by allowing for all possible distributions of π fluxes and accounting for all the allowed particle distributions that individually minimize the kinetic energy in each AB cage - see Supplementary Note 3.

The behaviour of the system with changing J/t and μ/t is presented in Fig. 3. The boundaries in red enclose regions of a constant average gauge flux \({\overline{W}}={\sum }_{i}\langle {W}_{{\bigcirc }_{{i}_{\ell }}}\rangle /(L-1)\), which provides indirect information on the nature of the chain partitioning. We find that the lattice does not break into partitions for J < 0, as the magnetic Wilson term favours, in this case, a ferromagnetic ordering of the spins, leading to an overall 0-flux. For positive values, we also find a vanishing flux below a pronged curve that separates the phase with a fully-connected chain from one with AB cages and clustering of particles. Below the transition line, the number of particles decreases in steps of two with decreasing μ. When crossing the curve, we observe the self-assembling of caged configurations favoured energetically: due to destructive AB interference, particles are locked in clusters covering the entire chain according to a periodic crystalline structure. Five main commensurate coverings of the lattice emerge, with cages of sizes ℓAB = 1, 2, 3, 4, 5. Partitions of length ℓAB = 1 correspond to independent empty sites and to a total of zero particles in the lattice, appearing in the bottom right corner of the figure. For all the other values of ℓAB, except for a small area that corresponds to partitions of ℓAB = 5 sites that contain four particles, each ℓAB-sized cage is filled with just two particles. As a result, the filling fraction ν is fixed to the value ν = 2/ℓAB.

Fig. 3: Phase-diagram at h = 0.
figure 3

Contour plot of the filling fraction ν = N/L as a function of J/t and μ/t, for a chain of L = 60 sites. Red lines delimit areas of constant average gauge flux \({\overline{W}}={\sum }_{i}\langle {W}_{{\bigcirc }_{{i}_{\ell }}}\rangle /(L-1)\) in which the chain is divided into clusters of size ℓAB indicated by the red numbers inside each region. For instance, the region on the left corresponds to the un-partitioned chain of ℓAB = L connected sites and no visons, whereas that in the bottom right corner is broken at every site ℓAB = 1 by completely filling the loops with visions. A schematic representation of the flux configurations is depicted in the larger regions, in which the periodic arrangement of visons (red π-flux circles) and 0-flux loops (green circles) with periodicity ℓAB is manifest. Except for the small unlabeled closed area with cages of size ℓAB = 5, which host four particles each, the remaining arrangement of Aharonov-Bohm cages with ℓAB ∈ {2, 3, 4, 5} contain two particles each. Notice that the reference values \({J}^{\star }/t=3\sqrt{3}/\pi -\sqrt{2}\), \(J^{\prime} /t=\sqrt{5}-\sqrt{2}\) and \(J/t=\sqrt{2}\) can be calculated analytically in the thermodynamic limit - see Supplementary Note 3 for details.

Full size image

To the best of our knowledge, and in contrast to the previous results on AB caging in static and homogeneous flux brackgrounds78,79,81, this is the first study reporting a spontaneous fractionalization of the system by the nucleation of π fluxes, sometimes referred to as visons in the context of particle-like deconfined excitations of \({{\mathbb{Z}}}_{2}\) LGTs87,88. Here, these visons get arranged forming ordered patterns with a periodicity that depends on the filling and the competition of the various microscopic terms. We note that, for a chain of finite size L, depending on the number of sites, coverings with a single kind of clusters may become incommensurate with the size of the lattice, resulting in mixed configurations. Such effect is expected to disappear in the thermodynamic limit L → ∞.

Let us now fix the total number of particles and explore this phenomenon in more detail for the specific filling fraction ν = 2/3. Resorting to numerical methods, we find the following behaviour - see Fig. 4: for any J < J⋆, where in the thermodynamic limit \({J}^{\star }/t=3\sqrt{3}/\pi -\sqrt{2}\), the system attains its minimum energy by remaining fully connected without AB cages or visons - see Supplementary Note 3. Strictly at vanishing electric field h = 0, our hardcore bosons hopping on a whole chain then correspond to deconfined excitations in a metallic phase. Increasing the magnetic coupling to \({J}^{\star } < J < \sqrt{2}t\), pairs of particles get caged in three-sites cages (AB trimers) that completely cover the chain. Finally, for even larger couplings \(J\ge \sqrt{2}t\), we find that the system lowers its energy by creating smaller cages of two sites (AB dimers), in which two particles are arranged into a tightly confined ‘meson’. In this case, due to the specific particle number N = 2L/3, one cannot densely cover the lattice with these meson-filled AB dimers, and the ground state shall intersperse AB dimers with other empty sites. We note that this comes with a large degeneracy, corresponding to all the possible arrangements of the diluted AB dimers.

Fig. 4: Chain-partitioning.
figure 4

We plot the averaged expectation value of the magnetic Wilson operators \({\overline{W}}={\sum }_{i}\langle {W}_{{\bigcirc }_{{i}_{\ell }}}\rangle /(L-1)\), which provides a sense on how the number of vison changes with the parameters and, thus, on the formation of Aharonov-Bohm cages at h = 0 and filling \(\nu =\frac{2}{3}\). The fragmented chains contain Aharonov-Bohm cages separated from one another by π-flux loops. By increasing J/t, we observe the transition from a fully-connected chain to an Aharonov-Bohm-trimer covering and, finally, to an Aharonov-Bohm-dimer configuration, in which the cages do not fully cover the chain and can be thus arranged in many degenerate configurations. In the thermodynamic limit, the transition points are given by \({J}^{\star }/t=3\sqrt{3}/\pi -\sqrt{2}\) and \(J/t=\sqrt{2}\).

Full size image

We point out that different values of the filling fraction could set configurations other than the ones discussed above. For instance, for ν = 2/3, it is not commensurable with the total number of particles and sites in the chain to replace any number of trimers with cages of four sites and two particles each. Such AB fourmers configurations can instead be found at half-filling ν = 1/2 - see Supplementary Note 3 and Supplementary Fig. 2 therein.

Interference-assisted tight confinement of mesons

Let us now switch on the electric field h > 0, introducing quantum fluctuations into the loop fluxes that compete with the AB caging and tend to restore the tunnelling among the disconnected partitions of the chain. In particular, visons start to move along the chain, which is accompanied by the rearrangement of AB cages that carry with them the particles that were locked inside. Whilst the effect of h > 0 tends to be disruptive for the AB caging, at small h/t and h/J configurations of constant average gauge flux \(\overline{W}\) and filling fraction ν are resilient to quantum fluctuations and the filling fraction displays a staircase behaviour with changing μ/t - see Fig. 5. Plateaux of fixed ν correspond to incompressible configurations, being characterized by κ = ∂〈N〉/∂μ = 0, at which the average flux \(\overline{W}\) is also constant, indirectly showing the persistence of caged configurations. The size of these plateaux tends to shrink as the strength of the fluctuations controlled by h is increased.

Fig. 5: Staircase behaviour of the filling fraction.
figure 5

We plot the filling fraction ν as a function of the chemical potential μ/t at small values of the electric field strength h/t = 0.05, 0.10, and at J/t = 0.45. The length of the chain is L = 120. Plateaux at the fillings ν = 0, 1/2, 2/3, 1 denote incompressible configurations of the ground state associated to a constant value of the average flux \(\overline{W}\) and thus to the presence of cages of average size ℓAB ~ 1, 4, 3 and 2, respectively, as indicated in the labels above each plateaux.

Full size image

We stress that, at small values of h/t and h/J, most of the incompressible configurations found in the previous semi-classical ground states are still present - see Fig. 6. In fact, we find that cages of size ℓAB = 1, 2, 3, 4 survive quantum fluctuations, while those of size ℓAB = 5 become unstable. As in the semi-classical case, we find that for ground states with single-site AB cages ℓAB = 1, the system has a vanishing particle filling ν = 0. Otherwise, all the remaining AB cages host two particles each, such that ν = 2/ℓAB. We find that all these phases are incompressible since κ = 0 - see Fig. 6, and spontaneously break the lattice translational symmetry down to the subgroup of ℓAB-site translations. This type of transition is reminiscent of the Peierls’ instability in low-dimensional metals, which breaks translational invariance into the subgroup of 2-site translations, leading to an insulator in a dimerised chain96. In our case, we find a periodic arrangement of visons and, in the thermodynamic limit, the ground state is expected to be ℓAB-fold degenerate. This degeneracy corresponds to all the possible non-equivalent coverings of the lattice, namely those that cannot be related by ℓAB-site translations. Being characterized by a staircase behaviour of κ, transitions between different incompressible phases are first-order.

Fig. 6: Incompressible \({{\mathbb{Z}}}_{{\ell }_{{{{\rm{AB}}}}}}\) phases.
figure 6

In a we plot the filling fraction ν at h/t = 0.05, for a chain of L = 120 sites. At small values of the electric field, quantum fluctuations of the flux restore the hopping among separate partitions. Nevertheless, regions of fixed filling fraction ν and flux are stabilized at ν = 0, \(\frac{1}{2}\), \(\frac{2}{3}\) and 1, corresponding to incompressible phases in which the chain is fully partitioned into single empty sites, fourmers, trimers and dimers respectively, as indicated by the labels inside each area that correspond to the average size of the Aharonov-Bohm cages ℓAB. As a result, the lattice translational symmetry is broken to the \({{\mathbb{Z}}}_{{\ell }_{{{{\rm{AB}}}}}}\) subgroup. In b we show the compressibility \(\kappa =\frac{\partial N}{\partial \mu }{| }_{J}\), demonstrating that the caged regions are incompressible areas of fixed filling ν, as indicated by the red labels in each lobe, and are separated by lines of diverging κ, at which the filling fraction changes abruptly.

Full size image

As noted above, in the limit of small h/t, h/J, quantum fluctuations can assist the movement of AB cages and the particles thereby enclosed. This effect can be effectively described via a Schrieffer-Wolff perturbative transformation of Eq. (2): we focus on the caged regimes in which the lattice is broken in clusters of ℓAB sites containing two particles each, far from the values of J/t at which cages of different lengths become degenerate. A non-zero electric field can induce virtual processes that expand and subsequently contract the AB cages by creating and destroying visons through \({S}_{{i}_{\ell }}^{x}\vert {\Phi }_{{i}_{\ell }}^{+}\rangle \to \vert {\Psi }_{{i}_{\ell }}^{+}\rangle\) and \({S}_{{i}_{\ell }}^{x}\vert {\Psi }_{{i}_{\ell }}^{+}\rangle \to \vert {\Phi }_{{i}_{\ell }}^{+}\rangle\). The successive expansion and contraction of an AB cage, which result from creating and destroying visons at its opposite edges, yield an effective hopping process. Conversely, this second-order process taking place at only one of its sides would simply lower the energy. These energy-lowering contributions are suppressed when a single π-flux loop is localised between neighbouring cages, which thus results in an effective repulsive interaction. In this case, second-order processes affecting this boundary vison cause the two ℓAB cages to fuse into a single 2ℓAB cage, and then break apart again. Taking into account both effective hoppings and interactions, we find that this dynamics is described by an extended Bose-Hubbard model, where an additional constraint accounts for the spatial extent of each AB cage - see Supplementary Note 4. The effective Hamiltonian reads

$$\begin{array}{rcl}{H}_{{\ell }_{{{{\rm{AB}}}}}}&=&{{{{\mathcal{P}}}}}_{{\ell }_{{{{\rm{AB}}}}}}{\sum }_{i}\left(-{t}_{{\ell }_{{{{\rm{AB}}}}}}({b}_{i}^{{{\dagger}} }{b}_{i+1}+{{{\rm{H.c.}}}})\right.\\ &&\left.+{V}_{{\ell }_{{{{\rm{AB}}}}}}{n}_{i}{n}_{i+{\ell }_{{{{\rm{AB}}}}}}\right){{{{\mathcal{P}}}}}_{{\ell }_{{{{\rm{AB}}}}}}.\end{array}$$
(6)

In this equation, we have introduced bosonic operators \({b}_{i}^{{{\dagger}} }({b}_{i})\), which create (annihilate) an entire ℓAB-sized AB cage that starts at site i. Hence, they involve the creation (annihilation) of two particles in the lowest two-particle eigenstate available to a ℓAB-site subchain, where all the links enclosed by the cage are forced to 0-flux (π-flux) states according to the Gauss’ law – see Supplementary Fig. 3. Such operators are gauge-invariant meson creators(annihilators) as they can be written as linear combinations of two particle ai, aj (\({a}_{i}^{{{\dagger}} },{a}_{j}^{{{\dagger}} }\)) operators appropriately separated by strings of loop operators to fulfil the Gauss’ law constraints. For instance, in the simplest case of AB dimers ℓAB = 2, we have \({b}_{i}={a}_{i}\,\vert {\Psi }_{{i}_{\ell }}^{+}\rangle \langle {\Phi }_{{i}_{\ell }}^{-}\vert {a}_{i+1}\). Let us also note that the projectors \({{{{\mathcal{P}}}}}_{{\ell }_{{{{\rm{AB}}}}}}\) impose a cluster hardcore constraint \({b}_{i}^{{{\dagger}} }{b}_{i+n}^{{{\dagger}} }=0\) that forbids the occurrence of pairs of doubly-occupied sites within any site in the cage ∀n ∈ {0, ℓAB − 1}. Hence, only a single meson can reside in each AB cage.

In the cases of relevance to our current discussion, namely those in which only two particles are hosted by each cage, the original density ν and the filling fraction of these mesons νm(ℓAB) are related via the expression νm(ℓAB) = ν/2. Due to the constraints imposed by \({{{{\mathcal{P}}}}}_{{\ell }_{{{{\rm{AB}}}}}}\), the specific value \({\bar{\nu }}_{{{{\rm{m}}}}}({\ell }_{{{{\rm{AB}}}}})=1/(1+{\ell }_{{{{\rm{AB}}}}})\) is equivalent to half filling, such that one cage exists on every other site. In a similar way, \({\tilde{\nu }}_{{{{\rm{m}}}}}({\ell }_{{{{\rm{AB}}}}})=1/{\ell }_{{{{\rm{AB}}}}}\) can be regarded as the fully-filled regime, since the projection constraints would not allow for additional clusters to be added. In this last case, the model (6) is forced into one of the configurations discussed above in which the chain is completely covered by the cages and the system is found in an incompressible phase, with the lattice translational invariance being broken to its \({{\mathbb{Z}}}_{{\ell }_{{{{\rm{AB}}}}}}\) subgroup - see Fig. 6.

The model in Eq. (6) can be mapped to a spin-1/2 XXZ chain with a constraint that forbids spin configurations in which two spin-up states are less than ℓAB sites apart. Such models have been exactly solved using the Bethe Ansatz for any value of ℓAB97. The possible phases turned out to be independent of ℓAB, leading to an equal-time Green’s function that displays an algebraic decay \(\langle {b}_{i}^{{{\dagger}} }{b}_{i+r}\rangle \sim {r}^{-\beta }\), with β being dependent on the meson filling νm(ℓAB). At half filling for the mesons, the effect of the above repulsive Hubbard interactions is enhanced, and one finds a quantum phase transition at \({\delta }_{{{{\rm{c}}}}}={V}_{{\ell }_{{{{\rm{AB}}}}}}/2\,{t}_{{\ell }_{{{{\rm{AB}}}}}}=1\) from a gapless Luttinger Liquid phase (δ≤1) to a gapped Mott-insulating phase (δ > 1)61,97.

Below, we will discuss how the above exact results can be exploited to get insights about the phase diagram of Eq. (2), as one departs from the perturbative limit of small electric fields. Let us recall that, at ν = 2/3 filling and h = 0, we found that the system forms AB dimers for \(J > \sqrt{2}\,t\). At small h, we can now make use of the effective description provided by Eq. (6). For ℓAB = 2, the meson density is fixed to \({\nu }_{{{{\rm{m}}}}}(2)=1/3={\bar{\nu }}_{{{{\rm{m}}}}}(2)\) and our effective model in the regime of low quantum fluctuations predicts that we are in the critical regime δc = 1, with \({t}_{{\ell }_{{{{\rm{AB}}}}} = 2}={h}^{2}{t}^{2}/J({J}^{2}-2\,{t}^{2})\). The ground state will then be a LL97, with gapless excitations corresponding to mesons with an anomalous dimension manifested through the exponent of the algebraic decay of the gauge-invariant correlators \(\langle {b}_{i}^{{{\dagger}} }{b}_{i+r}\rangle\) - see Fig. 7 and the analysis reported in Supplementary Note 6 and Supplementary Fig. 6 therein.

Fig. 7: Dimer correlator.
figure 7

The correlator \(g(r)=\langle {b}_{L/2}^{{{\dagger}} }{b}_{L/2+r}\rangle\), with bi corresponding to the annihilator for a dimer, is shown in the opposite regimes of small (0.1) and large (10.0) values of \(\frac{h}{t}\), at the filling \(\nu =\frac{2}{3}\) and at the magnetic coupling J/t = 1.8. To minimize boundary-effects, we evaluate the correlator starting from the middle point of the chain. Notice that, since the model (2) is defined on a chain of length L = 120, dimer operators will be defined on a chain of length L − 1 = 119 and r will be allowed to vary up to 59. The main plot in log-log scale makes it evident that the algebraic decays in the two regimes are almost superimposed and confirms that the effective description provided by Eq. (6) for ℓAB = 2 is valid in both cases. In the inset, the same plot is in linear scale up to r = 30 for a better visualization. The data points are fitted to g(r) = α r−β. For h/t = 0.1(10.0), we find α ~ 0.154(0.154) and β ≈ 1.920(1.925).

Full size image

Up to now, we have observed that interference effects induced by the AB effect on the elementary loops result in a caging that locks particles in pairs inside specific partitions of the chain. The emergent dynamics of the mesons bound inside the AB cages at small h/t and h/J, also emerges for large electric field strength h, where the charges are bound in meson pairs due to a linearly-increasing confining potential and are separated by short electric field lines. The effective model in this regime is still given by Eq. (6) with a 2-site constraint, and we find that the parameters are again fixed to the critical value δc = 1, analogously to what happens for the standard \({{\mathbb{Z}}}_{2}\) chain in this limit of strong electric fields61,63. We stress that, while in the \({{\mathbb{Z}}}_{2}\) chain particles form dimers as a result of strong attractive interactions, controlled by h, penalizing extended configurations of the electric strings, the same effective description applies to our loop model in the absence of strong electric-field lines connecting pairs of particles. Indeed, in the weak-h limit, this is due to the formation of Aharonov-Bohm cages. On the other hand, for h/t ≫ 1, an equivalent situation to the \({{\mathbb{Z}}}_{2}\) chain occurs when h/J ≫ 1 too: in the manifold of the lowest-energy states, all the bonds of the chain are found in eigenstates of the electric-field operator \({E}_{{i}_{\ell }}\), with those binding particles in pairs being characterized by the eigenvalues  + 1, while the others carrying zero electric field. We now show that, as the last condition is relaxed and J is allowed to be comparable to h, not all the bonds of the chain are eigenstates of the electric field operator, but particles are still separated by short electric strings and form dimers, with the same effective dynamics.

For t = 0, the ground-state manifold is obtained by diagonalizing the local Hamiltonian (2)\({H}_{{{{\rm{local}}}}}={\sum }_{i}h\,{S}_{{i}_{\ell }}^{x}+J{({S}_{{i}_{\ell }}^{z})}^{2}\). The three eigenvalues are \({\epsilon }_{\Uparrow }=J/2+\sqrt{{J}^{2}/4+{h}^{2}}\), ϵ0 = J, and \({\epsilon }_{\Downarrow }=J/2-\sqrt{{J}^{2}/4+{h}^{2}}\), with the corresponding eigenstates obtained as combinations of 0 and π-flux states \( \vert {\epsilon }_{\Uparrow } \rangle ={N}_{\Uparrow }\{ \vert {\Psi }^{+} \rangle +(J+\sqrt{{J}^{2}+4{h}^{2}}) \vert {\Phi }^{+} \rangle /2h\}\), \(\vert {\epsilon }_{0}\rangle =\vert {\Phi }^{-}\rangle\) and \(\vert {\epsilon }_{\Downarrow } \rangle ={N}_{\Downarrow }\{\vert {\Psi }^{+} \rangle +(J-\sqrt{{J}^{2}+4{h}^{2}}) \vert {\Phi }^{+} \rangle /2h\}\), N⇑/⇓ being normalization coefficients. By gauge invariance, the ground state at t/h = 0 will be made up of tightly-bound pairs of particles separated by an \(\vert {\epsilon }_{0} \rangle\) link, while all the other links shall arrange in the lowest energy state \( \vert {\epsilon }_{\Downarrow } \rangle\). Despite \({E}_{i\ell }{\vert {\epsilon }_{0} \rangle }_{{i}_{\ell }}={ \vert {\epsilon }_{0} \rangle }_{{i}_{\ell }}\), \({ \vert {\epsilon }_{\Downarrow } \rangle }_{{i}_{\ell }}\) is not an eigenstate of \({E}_{{i}_{\ell }}\) unless J = 0 and, on average, \({i}_{\ell }{\langle {\epsilon }_{\Downarrow }| {E}_{{i}_{\ell }}| {\epsilon }_{\Downarrow }\rangle }_{{i}_{\ell }}=1-2h/\sqrt{4{h}^{2}+{J}^{2}}\). Along the same lines of the previous discussion, we can obtain a bosonic effective theory for composite mesons in which \({\tilde{b}}_{i}={a}_{i}\,{a}_{i+1}{( \vert {\epsilon }_{\Downarrow } \rangle \langle {\epsilon }_{0} \vert )}_{{i}_{\ell }}\) annihilate a dimer at site i. The dynamics of these mesons is then recovered at second order in a Schrieffer-Wolff perturbative expansion98,99. In this formalism, the mesons can move by second-order processes in which one of the charges tunnels such that the electric-field string connecting the pair of charges gets virtually stretched and subsequently compressed. The effective Hamiltonian is again that of Eq. (6) setting ℓAB = 2, albeit in this limit the 2-site constraint refers to the extent of the electric-field string instead of the size of the AB cage. We find again δc = V2/2t2 = 1, with \({t}_{2}={t}^{2}(\sqrt{4{h}^{2}+{J}^{2}}-J)/(4{h}^{2}+{J}^{2}+J\sqrt{4{h}^{2}+{J}^{2}})\) - see Supplementary Note 5. Therefore, following the logic discussed previously for small h/t and h/J, we can conclude that the system lies at the boundary between the LL and a gapped Mott insulating phase for any values of J/t, provided that we are in the strong electric field limit t ≪ h.

In spite of the different mechanisms behind confinement, as reflected in the definitions of the bosonic operators in the two cases, the two meson configurations share correlation functions \(\langle {b}_{i}^{{{\dagger}} }{b}_{i+r}\rangle\) and \(\langle {\tilde{b}}_{i}^{{{\dagger}} }{\tilde{b}}_{i+r}\rangle\) that display the same algebraic decay - see Fig. 7. We can thus infer that tightly confined mesons produced either by AB interference at small h/t and h/J, or by a strong electric field, move with the same anomalous dimension. Indeed, the two regimes are adiabatically connected, as can be inferred by inspection of the spectral gap, which remains closed from \(J > \sqrt{2}t\) and small h/J,h/t to the regime of strong electric field, for any values of J/t – see Supplementary Fig. 4, so that the system remains in a LL phase. Whilst dimers fully populate the ground state only in the limiting regimes of large and small electric field, we can extend the definition of dimer operators \({\tilde{b}}_{i}={a}_{i}\,{a}_{i+1}{(\vert {\epsilon }_{\Downarrow }\rangle \langle {\epsilon }_{0}\vert )}_{{i}_{\ell }}\) to intermediate values of h/t, as the state ϵ⇓ varies with this ratio. Note that, with changing h/t, both the limiting cases are recovered. Inspection of the one-body dimer correlators shows that these mesons display almost the same algebraic decay throughout the whole parameter regime comprised between the two analytical limits, with an anomalous dimension that varies with h/t - see Fig. 8. Moreover, dimers are shown to densely populate the ground state, also at intermediate values of the electric field to hopping amplitude ratio - see Fig. 8.

Fig. 8: Algebraic decay of dimer correlators.
figure 8

a the exponent β of the decay of dimer correlators \(\langle {b}_{i}^{{{\dagger}} }{b}_{j}\rangle \sim | i-j{| }^{-\beta }\), evaluated starting from i = L/2 for a chain of L = 120 sites, at the filling ν = 2/3, is obtained from a best-fit analysis (solid blue line), together with the associated errors ϵβ (shaded blue area between the dashed lines dermarking β ± ϵβ). It is shown that dimers display almost the same algebraic decay throughout the parameter regime between the two limiting cases of small and large electric field. The anomalous dimension η = β − 1 of such composite mesons is seen to vary with the ratio h/t. b we plot the fraction of the total number of particles that form dimers. The ground state results in being densely populated by dimers, even for intermediate values of h/t.

Full size image

\({{\mathbb{Z}}}_{3}\) Mott insulator of mesons locked into AB trimers

In the previous section, we have shown that tightly confined mesons arise either as a result of AB interference at small h/t and h/J, or due to a strong confining interaction at large h/t. At ν = 2/3 filling, the ground state in these two regimes lies at the critical point δc = 1 of the effective perturbative model (6), between a LL of ℓAB = 2 cages and a Mott insulating phase in which such dimers arrange themselves in a configuration that breaks translational symmetry to its \({{\mathbb{Z}}}_{3}\) subgroup. We find that a \({{\mathbb{Z}}}_{3}\) Mott insulating phase can actually be stabilized in our \({{\mathbb{Z}}}_{2}\)-loop chain by lowering the magnetic coupling J. Indeed, in the grand canonical ensemble, we found an incompressible phase in which AB trimers completely cover the chain when \(({J}^{\star } < J < \sqrt{2}\,t)\). When quantum fluctuations are introduced h ≠ 0, and in the regime \(J\approx \sqrt{2}\,t\), the size of the cages fluctuates and ℓAB = 2 and ℓAB = 3 cages can become energetically degenerate. We find that, when lowering the magnetic coupling further, a transition to a different configuration can take place, as AB trimers become energetically favourable, each of them hosting two charges bound in a meson that now extends to the three sites. This forms a \({{\mathbb{Z}}}_{3}\) Mott insulator as reflected by the vanishing compressibility κ = 0 reported earlier, as well as is reflected by the opening of a charge gap \({\Delta }_{c}=\frac{1}{2}[E(N+2)-2\,E(N)+E(N-2)]\). Here, E(N) is the ground-state energy with N particles and the choice N ± 2 is needed to fulfil the even parity requirement in the chosen gauge sector. The numerical results are obtained through DMRG and show that this Mott phase extends to finite values of the electric field strength h. Indeed, both the charge gap and the spectral gap - see Fig. 9 and Supplementary Fig. 4, remain open at finite h, so that the ground state of the system at ν = 2/3 filling is in a \({{\mathbb{Z}}}_{3}\) Mott insulating phase within values of the magnetic coupling comprised between J⋆ and \(\sqrt{2}t\). In order to confirm that the Mott-insulating phase is not washed out in the thermodynamic limit, we have performed a finite-size analysis of the charge-gap showing that it converges to finite values in the limit of L → ∞ - see Supplementary Fig. 4.

Fig. 9: Charge gap Δc.
figure 9

A charge gap opens up at the transition between a Luttinger Liquid and a \({{\mathbb{Z}}}_{3}\) Mott insulator around \(J=\sqrt{2}\,t\), for \(\nu =\frac{2}{3}\). The Mott phase, which at h/t, h/J ≪ 1 spans the range \(\frac{{J}^{\star }}{t} < \frac{J}{t} < \sqrt{2}\) extends in a lobe structure to finite values of the electric field strength h/t. The system size is set to L = 120.

Full size image

To corroborate the previous analysis, we consider a bipartition of the chain in two subchains of length l and L − l and we calculate the von Neumann entanglement entropy (EE) of the bipartition as a function of l - see Fig. 10. We find that, in the \({{\mathbb{Z}}}_{3}\) Mott insulator, the EE nearly vanishes when the bipartition does not intersect any of the sites enclosed in the AB trimer cages, which is when the length of the bipartition l is an integer multiple of 3. This behaviour reflects a quasi-factorized ground state at these specific bipartitions. In the dimer regime, in contrast, the EE displays the conformal field theory (CFT) behaviour, which is consistent with the expectation for a LL with central charge c = 1 in a finite-size system100.

Fig. 10: von Neumann Entanglement Entropy.
figure 10

We plot the entanglement entropy (EE) for bipartitions of the lattice into two subchains of lengths l and L − l, where L = 120 and the filling is fixed to \(\nu =\frac{2}{3}\). The electric field strength is fixed to the value h/t = 0.2. a Trimers Mott regime at J/t = 0.8: the ground state is quasi-factorized in the tensor product of trimer ground states. b Dimer Luttinger Liquid regime at J/t = 1.6: the entanglement entropy follows the conformal field theory behaviour (red solid line) \({S}_{{{{\rm{CFT}}}}}(l)=\frac{c}{6}\log (\frac{2L}{\pi }\sin (\frac{\pi l}{L}))+\tilde{c}\), with central charge c = 1. By fitting the data we find \(\tilde{c} \sim 0.37\).

Full size image

Let us close this section by noting that in the standard \({{\mathbb{Z}}}_{2}\) chain, in order to find these Mott insulating phases, one needs to introduce additional density-density Hubbard-type interactions between charges at neighbouring sites, which can favour a charge-density-wave pattern and effectively lead to δ > 1, favouring the Mott insulator63. In our case, the origin of the Mott insulator is very different: it results from the interplay of the charge dynamics and the dynamical AB caging. We also note that a similar analysis applies to the half-filled case ν = 1/2, as the system can transition from a LL of trimer cages, as described by the effective model (6) with δ < 1, to a Mott insulator of fourmer cages at the full-filling meson density \({\tilde{\nu }}_{b}(4)=1/4\) - see Supplementary Note 4 and Supplementary Fig. 5 therein.

Conclusions

In this paper, we have introduced a minimal quasi-1D geometry in which \({{\mathbb{Z}}}_{2}\) gauge fields can lead to the formation of dynamical Aharonov-Bohm cages. While bearing some resemblance to the ‘static cases’ provided by an external magnetic field79,81,82,84, the physics of dynamical caging in our lattice gauge theory is substantially different. Indeed, our caging arises from the competition of matter and gauge-field dynamics, and is not a consequence of the appearance of flat bands in the single-particle energy spectrum, as it is the case in quantum Hall type systems79. We have shown that these cages self-arrange in periodic structures, separated by π flux loops, providing the analogue of the two-dimensional visons, thus breaking the translational symmetry of the system. Pairs of \({{\mathbb{Z}}}_{2}\) charges get effectively confined inside the cages, forming tightly-confined mesons. In contrast to the standard \({{\mathbb{Z}}}_{2}\) chain, matter is tightly confined even at vanishingly-small values of the electric field h/t. The interplay between caging and confinement results in the different ways in which the chain fragments into subchains of different sizes, which in turn depends on the ratio of the effective magnetic flux and tunnelling strengths J/t. We note that, while at h = 0 confinement arises from the aforementioned chain’s fragmentation (see the “Self assembly of Aharonov-Bohm cages at h = 0" subsection in the Results), quantum fluctuations of the magnetic fluxes induced by a non-vanishing electric field h > 0 actually restore the tunnelling among disconnected clusters; this effect provides the key allowing mesons to propagate in the system – see the “Interference-assisted tight confinement of mesons" subsection in the Results. For small values of h, such dynamics is shown to be integrable and leads to a gapless Luttinger Liquid (LL) of mesons – see Eq. (6) and the discussion below. The LL behaviour at small h/t and h/J, is shown to adiabatically extend to finite values of the electric field strength, up to the limit of large h/t. In the latter case, particles are shown to be also tightly-confined into mesons with a short electric-field line that involves a single link, similar to the case of the standard \({{\mathbb{Z}}}_{2}\) chain. In this regime, confinement does not arise from a destructive interference induced by the gauge flux, but it is due to the linearly-growing attractive interactions between particles separated by electric field strings. In spite of these different origins of confinement, the dimerized regimes at weak and strong electric field h/t showcase the same quasi-long-range behaviour of the dimer correlators – see Fig. 7. We thus find a mechanism for the tight confinement of \({{\mathbb{Z}}}_{2}\) charges where both electric-field penalties and interference effects contribute, this effect persisting also for intermediate values of h/t – see Fig. 8.

For specific values of the filling fraction, we discover that quantum phase transitions to incompressible Mott-insulating phases occur – see the “\({{\mathbb{Z}}}_{3}\) Mott insulator of mesons locked into AB trimers" subsection in the Results. These transitions, which result in the opening of a charge gap (see Fig. 9), arise from quantum fluctuations triggered by the electric field, that aim at modifying the size of the AB cages ℓAB. At a critical value of the magnetic coupling, one finds quasi-degenerate configurations of the clusters characterized by either ℓAB or ℓAB + 1 sites, with the largest cage covering the whole lattice. As the magnetic flux strength is lowered below its critical value, larger cages are favoured and stabilize a Mott insulating configuration with broken translational symmetry. These phases are characterized by a vanishing compressibility κ: changing the chemical potential μ at fixed J/t has no effect, until a new commensurate covering of the lattice with cages of different sizes becomes energetically favourable – see Fig. 6.

In future theoretical studies, different constraints on the particle dynamics (Gauss’ laws) could be explored, as they can lead to different cages’ fillings. Finite temperature effects could also be addressed, as thermal fluctuations are expected to compete with the discussed caging phenomenon.

Our work identifies AB caging as a driving force that can affect confinement, and it would be very interesting to explore it in fully two-dimensional models. Based on the scenario emerged in the present study, our dynamical caging might define a new form of string-net theories3,101,102.

Finally, we note that experimental realizations of the phenomenology described in this paper are in line with current proposals for the quantum simulation of \({{\mathbb{Z}}}_{2}\) gauge theories, for instance, through Rydberg atoms or trapped ions30,31. In the latter platform, real-time dynamics and the interplay of AB interference for a single \({{\mathbb{Z}}}_{2}\) loop have been recently demonstrated60. These experiments exploit a laser-assisted parametric driving between two collective vibrational modes of a 2-ion crystal, in particular by driving a pair of interfering state-dependent forces tuned to the centre-of-mass modes that describe collective in-phase vibrations along two orthogonal axes of the ion trap. The possibility of preparing various gauge-invariant states in trapped ions, as well as the capabilities of measuring both vibrational and internal observables for the \({{\mathbb{Z}}}_{2}\) charges and \({{\mathbb{Z}}}_{2}\) fields, has actually allowed to experimentally demonstrate the relation between the loop dynamics of \({{\mathbb{Z}}}_{2}\) charges and parity oscillations between Bell pairs \(\vert {\Phi }^{\pm }\rangle\) in Eq. (4), as well as the destructive AB interference for a π-flux in the Bell pair \(\vert {\Psi }^{+}\rangle\) in Eq. (4). Although these experiments only constitute a proof-of-principle of the tools that would be required to realise our \({{\mathbb{Z}}}_{2}\) loop model, one could exploit similar ideas as those exposed in previous works31 to extend the gauge-invariant dynamics to larger lattices. In particular, a method to combine various normal modes in a dimerised trapped-ion chain was proposed as a way to make a dimensional reduction from a synthetic ladder to an effective \({{\mathbb{Z}}}_{2}\)-invariant chain31. One can foresee that upgrading the period-2 dimerization to a period-4 modulation of the trapping frequencies can now provide enough resolved collective modes and qubits to generalise the \({{\mathbb{Z}}}_{2}\)-invariant loop tunnelling to a full \({{\mathbb{Z}}}_{2}\)-loop chain. Although this is a challenging experiment requiring extended microscopic control capabilities, we remark that the key ingredients have already been demonstrated in a recent proof-of-principle experiment60. Additionally, the simplified magnetic plaquette interactions corresponding to Ising spin-spin couplings could, in this model, be driven by the vibrational modes not used to encode \({{\mathbb{Z}}}_{2}\) charges, a scheme that has indeed been realised in various laboratories.