Learning integral operators via neural integral equations

Abstract

Nonlinear operators with long-distance spatiotemporal dependencies are fundamental in modelling complex systems across sciences; yet, learning these non-local operators remains challenging in machine learning. Integral equations, which model such non-local systems, have wide-ranging applications in physics, chemistry, biology and engineering. We introduce the neural integral equation, a method for learning unknown integral operators from data using an integral equation solver. To improve scalability and model capacity, we also present the attentional neural integral equation, which replaces the integral with self-attention. Both models are grounded in the theory of second-kind integral equations, where the indeterminate appears both inside and outside the integral operator. We provide a theoretical analysis showing how self-attention can approximate integral operators under mild regularity assumptions, further deepening previously reported connections between transformers and integration, as well as deriving corresponding approximation results for integral operators. Through numerical benchmarks on synthetic and real-world data, including Lotka–Volterra, Navier–Stokes and Burgers’ equations, as well as brain dynamics and integral equations, we showcase the models’ capabilities and their ability to derive interpretable dynamics embeddings. Our experiments demonstrate that attentional neural integral equations outperform existing methods, especially for longer time intervals and higher-dimensional problems. Our work addresses a critical gap in machine learning for non-local operators and offers a powerful tool for studying unknown complex systems with long-range dependencies.

Main

Integral equations (IEs) are functional equations where the indeterminate function appears under the sign of integration¹. The theory of IEs has a long history in pure and applied mathematics, dating back to the 1800s, and it is thought to have started with Fourier’s theorem². Another early application of IEs was found in the Dirichlet’s problem (a partial differential equation (PDE)), which was originally solved through its integral formulation. Subsequent studies, carried out by Fredholm, Volterra, Hilbert and Schmidt, have significantly contributed to the establishment of this theory. IEs appear in many applications ranging from physics and chemistry to biology and engineering^2,3, for instance, in potential theory, diffraction and inverse problems such as scattering in quantum mechanics^2,3,4. Neural field equations, which model brain activity, can be described using IEs and integro-differential equations (IDEs), due to their highly non-local nature⁵. IEs are related to the theory of ordinary differential equations (ODEs) and PDEs; however, they possess unique properties. Although ODEs and PDEs describe local behaviour, IEs model global (long-distance) spatiotemporal relations. Moreover, ODEs and PDEs have IE forms that, in certain circumstances, can be solved more effectively and efficiently due to the better stability properties of IE solvers compared with ODE and PDE solvers^6,7. Another work⁸ provides an example of a PDE system that is solved with high accuracy through an IE method.

Learning non-local operators for dynamics with long-distance relations is an open problem in deep learning. In this Article, we introduce and address the problem of learning non-local dynamics from data through IEs. Namely, we introduce the neural integral equation (NIE) and the attentional neural integral equation (ANIE). Our setup is that of an operator learning problem, where we learn the integral operator that generates dynamics that fit the given data. Often, one has observations of a dynamical system without knowing its analytical form. Our approach permits modelling the system purely from the observations. This model, via the learned integral operator, can be used to generate dynamics, as well as be used to infer the spatiotemporal relations that generated the data. The innovation of our proposed method lies in the fact that we formulate the operator learning problem associated to dynamics in the form of an optimization problem for the solutions of an IE obtained through an IE solver. Unlike other operator learning methods that learn dynamics as a mapping between function spaces for fixed time points, that is, as a mapping $T:{\prod }_{i}{{\mathcal{A}}}_{i}\longrightarrow {\prod }_{j}{{\mathcal{B}}}_{j}$, where ${{\mathcal{A}}}_{i}$ and ${{\mathcal{B}}}_{j}$ are function spaces each representing a time coordinate, NIE and ANIE allow to continuously learn dynamics with arbitrary time resolution. Our solver outputs solutions through an iterative procedure³, which converges to a solution of the IE.

Our contributions

In this Article, we introduce NIE and ANIE, which are neural-network-based methods for learning dynamics, in the form of IEs, from data. Our architectures allow modelling dynamics with long-distance spatiotemporal relations typical of non-local functional equations. Our main contributions are as follows:

• We introduce a method for learning dynamics from data as solutions of IEs of the second kind through an IE solver.

• We implement a fully differentiable IE solver in PyTorch, available via GitHub at https://github.com/emazap7/ANIE.

• We implement a highly scalable version of the solver where integration is done with a self-attention mechanism.

• We derive theoretical results on convergence of the solver and approximation capabilities of our models.

• Our model provides explainable dynamics and meaningful embeddings of these dynamics.

• Finally, we use our method to model and interpret non-local dynamics from brain activity recordings.

Background and related work

IEs in numerical analysis

Due to their wide range of applications, the theory of IEs has attracted the attention of mathematicians, physicists and engineers for a long time. Detailed accounts on IEs can be found elsewhere^3,9,10. Along with their theoretical properties, much attention has been devoted to the development of efficient IE solvers, focusing on rapidly obtaining highly accurate solutions of certain PDE systems^6,7. In fact, it is known that IE solvers yield more accurate solutions than differential solvers for a variety of ODEs and PDEs. The methodology introduced in this work learns a neural integral operator through a numerical IE solver and it, therefore, differs from typical IE solvers where an integral operator needs to be given and fixed.

Operator learning

IE solvers are used to solve given equations through some iterative procedure, as done with other work^3,11. Moreover, machine learning approaches to solve given types of IE have been implemented^{12,13,14,15,16}. In such cases, the IE is known, and we seek its solution. However, in practice, we often do not have access to the analytical form of the equation and we only have data sampled from a system. In such cases, we want to model the system by learning an operator that can reproduce the system. This is the setting of operator learning problems, and several approaches to operator learning, including using deep learning, have been presented^{17,18,19,20,21,22,23,24,25,26,27,28}. Typical operator learning problems are formulated on finite grids (finite difference methods) that approximate the domain of functions. In this case, recovering the continuous limit is a very challenging problem, and irregularly sampled data can completely alter the evaluation of the learned operator. Operator learning for IEs has not been considered thus far, and it constitutes the main novelty of the present Article. This is entailed in the formulation of the operator learning problem through an IE solver. The convenience of this approach lies in the capability of the solver to continuously sample the domain of integration, as well as the capabilities of IEs to model very complex dynamics, due to their highly non-local behaviour. A similar approach for IDEs has been followed in another work²⁹. However, in the present work, our implementation does not include differential solvers, and the reformulation of such dynamical problems in terms of IEs has great benefits in terms of solver speed and stability. Moreover, our version of an IE solver that approximates integrals via self-attention allows for higher-dimensional integrals than those considered in ref. ²⁹.

Learning continuous dynamics

Modelling continuous dynamics from discretely sampled data is a fundamental task in data science. Methods for continuous modelling include those based on ODEs^30,31. Although ODEs are useful for modelling temporal dynamics, they are fundamentally local equations that neither model spatial nor long-range temporal relations. Auxiliary tools³⁰, such as recurrent neural networks (RNNs), have been employed to include non-locality. We point out that RNNs can be seen as performing a temporal integration (in discrete steps), to codify some degree of non-local (temporal) dependence in the dynamics. In this work, we introduce a framework that provides a more general and formal solution to this non-local integration problem. Moreover, the dynamics are not sequentially produced with respect to time, as done by ODE solvers, but are processed in parallel, thereby providing increased efficiency, as we will experimentally demonstrate.

Integration via self-attention

The self-attention mechanism and transformers, introduced elsewhere³², were applied to machine translation tasks. Owing to their initial success, they have since been used in many other domains, including operator learning for dynamics^21,33. Interestingly, the self-attention mechanism can be interpreted as the Nyström method for approximating integrals³⁴. Making use of this connection, we approximate the integral kernel of our model using self-attention, allowing efficient integration over higher dimensions.

NIEs

An IE (Urysohn type) takes the general form given by

$${\bf{y}}(t)=f(t)+\mathop{\int}\nolimits_{\!\!\alpha (t)}^{\beta (t)}G({\bf{y}}(s),t,s){\rm{d}}s,$$

(1)

where variable s is the local time used for integration for each t, which is the global time. Due to their fundamentally non-local behaviour, IEs have been used to model physical and biological phenomena, such as brain dynamics, virus spreading and plasma physics^2,3,5. The case considered in this Article, where the indeterminate function y(t) appears both under the sign of integration and outside it, is termed an equation of the second kind, as opposed to the first kind where the indeterminate function appears only in the integral operator. IEs of the second kind are more stable than of the first kind for reasons rooted in functional analysis (see the ‘Existence and uniqueness of solutions’ section).

We introduce NIEs, a deep neural network model based on IEs. NIEs are IEs as defined by equation (1), where G is a neural network, parameterized by θ, and indicated by G_θ. Training an NIE consists of optimizing G_θ in such a way that the corresponding solution y to equation (1) fits the given data. At each step of training, we perform two fundamental procedures. The first one is to solve the IE determined by G_θ, and the second one is to optimize for G_θ in such a way that solving the corresponding IE produces a function that fits a given dataset. Details on the solver procedure and the training are given in the ‘IEs’ section.

IEs, in contrast to ODEs and PDEs, are non-local equations¹ since to evaluate the integral operator $\mathop{\int}\nolimits_{\alpha (t)}^{\beta (t)}{G}_{\theta }(\bullet ,t,s){\rm{d}}s:{\mathcal{A}}\longrightarrow {\mathcal{A}}$ on a function y, we need the value of y over the full integration domain. In fact, to evaluate the right-hand side of equation (1) at an arbitrary time point t, the function y(s) between α(t) and β(t) is needed. Here α and β are arbitrary functions and common choices include α(t) = a and β(t) = b (called Fredholm equations) or α(t) = 0 and β(t) = t (called Volterra equations). Consequently, solving an IE requires an iterative procedure, based on the notion of Picard iterations (successive approximation method), where the solution is obtained as a sequence of approximations that converge to the solution. Details on the solver implemented in this Article are given in the ‘Generalities on solving IEs’ section, as well as the theory on which it is based and the proofs regarding the convergence of our algorithms to a solution of the given IE (see Theorem 4.1 and Corollary 4.2). We also refer to another work³ for an elementary and computationally driven introduction to the theory behind the methods that motivate this procedure; a more detailed account is also provided elsewhere¹¹.

Interestingly, utilizing NIEs to model ODEs allows to bypass the use of ODE solvers, as the one introduced in other work^30,31. The convenience in this approach is that the IE solver is more stable than the ODE solver³⁵. ODE solver instabilities, induced by equation stiffness, have been previously considered^36,37. The IE solver presented in this work, thus, does not suffer from these problems, and is also considerably faster.

It is often useful to consider a more specific form for IEs, where the function G factors in the product of a kernel K and a generally nonlinear function F as G(y, t, s) = K(t, s)F(y). Here K is matrix valued, and it carries the dependence on time (both t and s), whereas F depends only on the indeterminate function y. Therefore, the form of this IE is

$${\bf{y}}(t)=f(t)+\mathop{\int}\nolimits_{\!\!\alpha (t)}^{\beta (t)}K(t,s)F({\bf{y}}(s)){\rm{d}}s.$$

(2)

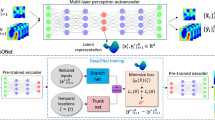
NIEs in this form comprise two neural networks, namely, K and F. We observe that in IEs, the initial condition is embedded in the equation itself, and it is not an arbitrary value to be specified as an extra condition. To solve the IE, we implement a solver that performs an iterative procedure to obtain a solution (see the ‘IEs’ section). During the iterations, Monte Carlo sampling is performed to evaluate the integrals. This procedure allows our deep learning model to be independent of the temporal grid points, thereby resulting in a continuous model, since the model internally uses randomly sampled points to generate the successive iterations, as opposed to using fixed grid points. The general algorithm for training the NIE is given in Algorithm 1, and a diagrammatic overview of it is shown in Fig. 1. Figure 2 shows a visualization of the general solving procedure.

Fig. 1: Diagrammatic representation of the model.

The solver is initialized with f, also called the free function. This initialization is often the first time point of the dynamics. To solve the IE and find the solution y, an iterative procedure is carried out in which at each solver step k, the integral of G_θ(y^k, x, t) is computed and used as the solution y^k+1 in the next step. Integration is done either with Monte Carlo (via torchquad) or with self-attention, representing NIE and ANIE, respectively. The solver integration steps are repeated until convergence of y^k to the IE solution. This solution is then compared with the input data to compute a loss that—via backpropagation—is used to find θ that minimizes the error. The resulting integral operator represents the IE that models the data. Top right: an example of attention weights for calcium imaging dynamics is presented. Bottom right: an example of the dynamical embedding of the Navier–Stokes dataset coloured by velocity is shown.

Source data

Fig. 2: Diagrammatic representation of the IE solver procedure.

The solver is initialized with the free function y⁰ ≔ f. The integral operator is applied to y⁰, and a new guess y¹ is obtained. This is repeated until convergence to a solution. The left panel shows the solution as a function of solver steps. The right panel shows the error of the solution as a function of solver steps.

Source data

Algorithm 1:

NIE method training step: integration is performed using the torchquad module with the Monte Carlo method.

Require: y₀(t)                  ⊳ initialization

Ensure: y(t)           ⊳ solution to IE with initial y₀(t)

 1: y⁰(t) ≔ y₀(t)             ⊳ initial solution guess

 2: While iter ≤ maxiter and error > tolerance do

 3:  Evaluate: ${{\bf{y}}}^{i+1}(t)=f({{\bf{y}}}^{i},t)+\mathop{\int}\nolimits_{\alpha (t)}^{\beta (t)}G(t,s,{{\bf{y}}}^{i}(s)){\rm{d}}s$

 4:  Set solution to be: ryⁱ + (1 − r)yⁱ⁺¹

 5:  New error: error = metric(yⁱ⁺¹, yⁱ)

 6: End while

 7: Output of solver: y(t)

 8: Compute loss with respect to observations: loss(y(t), obs)

 9: Gradient descent step

Space, time and higher-dimensional integration

IEs can have multiple space dimensions in addition to time. Such equations are formulated as

$${\bf{y}}({\bf{x}},t)=f({\bf{x}},t)+\int\nolimits_{\!\!\alpha (t)}^{\beta (t)}\mathop{\int}_{\!\!\varOmega }G({\bf{y}}({{\bf{x}}}^{{\prime} },s),{\bf{x}},{{\bf{x}}}^{{\prime} },t,s){\rm{d}}{{\bf{x}}}^{{\prime} }{\rm{d}}s,$$

(3)

where $\Omega \subset {{\mathbb{R}}}^{n}$ is a domain in ${{\mathbb{R}}}^{n}$ and ${\bf{y}}:\Omega \times I\longrightarrow {{\mathbb{R}}}^{m}$ for some interval $I\subset {\mathbb{R}}$. More commonly, in the literature, one finds a simpler case of higher-dimensional IEs, where the integral component $\int\nolimits_{\!\!\alpha (t)}^{\beta (t)}\mathop{\int}_{\!\!\varOmega }G({\bf{y}}({{\bf{x}}}^{{\prime} },s),{\bf{x}},{{\bf{x}}}^{{\prime} },t,s){\rm{d}}{{\bf{x}}}^{{\prime} }{\rm{d}}s$ is obtained as a sum of terms with only partial integrations. Such an equation takes the form

$${\bf{y}}({\bf{x}},t)=f({\bf{x}},t)+\mathop{\int}\nolimits_{\!\alpha (t)}^{\beta (t)}{G}_{1}({\bf{y}}({\bf{x}},s),{\bf{x}},t,s){\rm{d}}s+{\int}_{\!\varOmega }{G}_{2}({\bf{y}}({{\bf{x}}}^{{\prime} },t),{\bf{x}},{{\bf{x}}}^{{\prime} },t)d{{\bf{x}}}^{{\prime} }.$$

(4)

These equations are the integral counterpart of PDEs, similar to the relation between one-dimensional IEs and ODEs, and they are called partial integral equations (PIEs). With slight abuse of notation, we will still refer to equation (3) as a PIE, as we will, in practice, use such an approach to model PDEs in the case of Burgers’ equation and Navier–Stokes equation.

Attentional NIEs

Training of NIE requires an integration step at each time point, incurring a potentially high computational cost. This integration step is implemented using the torchquad package³⁸, a high-performance numerical Monte Carlo integration method, resulting in the fast integration and high scalability of NIE. For example, solving ODEs using NIE is significantly faster than using traditional ODE solvers (Supplementary Table 1). However, several limitations are associated with the torchquad integration method. In fact, torchquad requires substantially increasing numbers of sampled points with increasing numbers of dimensions. To use NIE for solving PDEs and (P)IEs, we require efficient spatial integration in high dimensions.

To address these challenges, we have employed an approach to NIE where the integral operator is based on a self-attention mechanism. In fact, self-attention can be viewed as an approximation of an integration procedure^34,39, where the product of queries and keys coincides with the notion of a kernel, as the one discussed in the ‘NIEs’ section. In another work²¹, the parallelism between self-attention and integration of kernels was further explored to interpret transformers as Galerkin projections in operator learning tasks.

We have replaced the analytical integral $\mathop{\int}\nolimits_{\alpha (t)}^{\beta (t)}G(t,s,{\bf{y}}(s)){\rm{d}}s$ in equation (1) with a self-attention procedure. The resulting model, which we call ANIE, follows the same principle of iterative IE solving presented in the ‘NIEs’ section but where the neural networks K and F are replaced by attention matrices. It can be shown (see the ‘Generalities on solving IEs’ section) that the successive approximation method is still applicable in this case to obtain a solution for the corresponding equation. Following the comparison between integration and self-attention, we observe that K is decomposed in the product of queries and keys, as described elsewhere²¹. The interval of integration [α(t), β(t)] is determined, in the attentional approximation, by means of the mask. In particular, if there is no mask, we have a Fredholm IE, whereas the causal attention mask⁴⁰ corresponds to a Volterra type of IE.

An iterative procedure similar to the one discussed in Algorithm 1 is implemented to solve the corresponding IE (see the ‘Generalities on solving IEs’ and ‘Implementation of ANIE’ sections). During iterations, we uniformly sample points from the spatiotemporal domain, and the corresponding integral operator does not depend on the grid points of the dataset. Our experiments on the Burgers’ dataset in the Experiments section show that our model is stable with respect to the change in spatiotemporal stamps since the model internally uses randomly sampled points to generate successive iterations, rather than fixed grid points. A detailed description of the integration procedure, along with solver steps and training for ANIE, is given in the ‘Implementation of ANIE’ section. Moreover, Theorem 4.1, Corollary 4.2 and Remark 4.3 show that the solver procedure converges to a solution under certain mild assumptions.

Algorithm 2 summarizes the solving and training procedures for ANIE. A detailed description of the meaning of ${\mathfrak{Att}}$ is found in the ‘Implementation of ANIE’ section. Theoretical considerations on Fredholm generalized equations with general operators, integral operator approximation through self-attention and existence of the solutions for these equations are given in the ‘Existence and uniqueness of solutions’ section. Supplementary Fig. 1 gives a diagrammatic representation of the integration procedure implemented in this Article, and Supplementary Fig. 2 gives a schematic of the solver procedure with space and time.

Algorithm 2:

ANIE method training step: integration here is replaced by a transformer employing self-attention.

Require:y₀(x, t)                ⊳ initialization

Ensure: y(x, t)        ⊳ solution to IE with initial y₀(x, t)

 1: y⁰(x, t) ≔ y₀(x, t)        ⊳ initial solution guess

 2: while iter ≤ maxiter and error > tolerance do

 3:  Concatenate space and time tokens to yⁱ(x, t): ${\tilde{{\bf{y}}}}^{i}({\bf{x}},t)=$${\rm{concat}}({{\bf{y}}}^{i}({\bf{x}},t),s,t)$

 4:  Evaluate with self-attention: ${y}^{i+1}(t)=f({\tilde{{\bf{y}}}}^{i},t)+{\mathfrak{A}}tt({\tilde{{\bf{y}}}}^{i}({\bf{x}},t))$

 5:  Set solution to be ryⁱ + (1 − r)yⁱ⁺¹

 6:  New error: error = metric(yⁱ⁺¹, yⁱ)

 7: end while

 8: Output of solver: y(x, t)

 9: Compute loss with respect to observations: loss(y(x, t), obs)

 10: Gradient descent step

Experiments

Modelling PDEs with IEs: Burgers’ and Navier–Stokes equations

PDEs can be reformulated as IEs in several circumstances, and dynamics generated by differential operators can, therefore, be modelled through an ANIE as a PIE, where integration is performed in space and time. We consider two well-known types of PDE, namely, the Burgers’ equation and the Navier–Stokes equation. Since NIE is implemented only for time integration, we use only ANIE in these experiments, which allows for efficient space and time integration. We observe that our implementation of Algorithm 2 applied to the case of the Navier–Stokes equation closely parallels the IE method employed in another work⁸, with the main difference that we learn the Green’s function through gradient descent, since no knowledge of the underlying Navier–Stokes equations is assumed.

For the Burgers’ equation, we focus on the ability of ANIE to continuously model both space and time and we therefore perform an interpolation task, where the model outputs time points that are not included in the training test, as well as for unseen initial conditions. This is in contrast to other work^19,21 where a ‘static’ Burgers’ equation was considered in which the learned operator maps the initial condition (t = 0) to the final time (t = 1), thereby treating time as a discrete two-point set. In our approach, we continuously model the system over a time interval and randomly sample points during iterations to perform the quadrature of the temporal integrals. In this experiment, the Galerkin model²¹ was not included for the higher-spatial-dimension setting because the amount of memory required exceeded what was available to us during the experiments. The results are reported in Table 1 (right), and an example of the learned dynamics is given in Supplementary Fig. 4.

Table 1 Benchmark on the Navier–Stokes and Burgers’ equations

For the Navier–Stokes equation, we consider an extrapolation task where we evaluate the model on unseen initial conditions. Previous works have shown high performance in the predicting dynamics of Navier–Stokes from new initial conditions, but they require several frames (that is, several time points) to be fed into the model to achieve such performance. We see that since ANIE learns the full dynamics from arbitrarily chosen initial conditions, we achieve good performance even when a single initial condition is used to initialize the system. We train FNO2D, ViT, ViTsmall and ViTparallel with initialization on a single time point, whereas convolutional long short-term memory (LSTM), FNO3D and ViT3D are trained with 2, 2 and 10 times for initialization, respectively. The results are given in Table 1 (left). We note that ANIE even outperforms models that use more data points for initialization. FNO2D did not converge for higher number of points, and therefore, results for time points t = 10 and t = 20 have not been reported, whereas for FNO3D, we have conducted the experiments only for t = 10 and t = 20 since using fewer points for the time dimension would have effectively reduced FNO3D to FNO2D. Example predictions of dynamics with ANIE are shown in Fig. 3, where the convergence of the solver to a solution is represented.

Modelling brain dynamics using ANIE

Brain activity can be modelled as a spatiotemporal dynamical system⁴¹. Although most connections between neurons are localized in space, there are numerous interactions that are long range⁴². As such, brain dynamics can be modelled using IEs⁵ that —unlike PDEs—allow for non-local interactions. Since ANIE allows the efficient learning of integral operators from data, we demonstrate the ability of ANIE to learn non-local brain dynamics from functional magnetic resonance imaging (fMRI) recordings.

To obtain fMRI data that has an arbitrary time duration as well as unlimited trials, we make use of neurolib⁴³, an fMRI simulation package. The data provided by this tool permit for more extensive comparison and statistical power. neurolib simulates whole-brain activity using a system of delay differential equations, which are non-local equations, thereby allowing the testing of ANIE’s ability to model non-local systems. Here we show the performance of ANIE and other models in modelling data generated by neurolib. Details about data generation and preprocessing can be found in the ‘fMRI data generation’ section.

The generated fMRI data comprises neural activity for 80 nodes localized across the cortex. The first half of the data is used for training and the second half is used for testing. For training, the data are divided into segments of 20 time points, where the first time point is used as the initial condition, and the loss is computed over all the 20 points. As such, the models are trained as an initial condition problem. During inference, the models are given points from the test set as new initial conditions and asked to extrapolate for the following 19 points. The mean error per point for 200 new initial conditions is shown in Extended Data Fig. 1 and summarized in Extended Data Table 1. Extended Data Fig. 2 shows the data and model per fMRI recording node over time. We show that ANIE has better performance than other benchmarked methods for medium-time-step (t = 10) and long-time-step (t = 20) predictions, demonstrating its ability to model non-local dynamics. For shorter and more localized dynamics (t = 5), FNO1D shows better performance, which can be explained by the fact that FNO1D outputs the average of the initial points provided as the prediction for the first five time steps. The DeepONet + UNET model (Extended Data Table 1) is implemented similar to that in another work⁴⁴.

Interpretable dynamics

In addition to modelling and generating new dynamics, it is useful to get an insight into the underlying process that generates the dynamics. For example, in neuroscience, a major goal is to understand how specific brain activity patterns give rise to cognition, learning and behaviour. To explore the interpretability of ANIE, we carry out two experiments. For the first experiment, we augment the spacetime integration domain with a Classify (CLS) token⁴⁵, such that each dynamics is projected into a single vector. This vector can then be related to specific properties of the dynamics. Specifically, we embed these vectors for different Navier–Stokes dynamics and find that the resulting manifold (projected using principal component analysis (PCA)) has a highly non-random structure. This is in contrast to the projection of the raw data (Extended Data Fig. 3). To further explore the resulting dynamics manifold, we colour it by the velocities of the dynamics, a property that was not explicitly seen by the model during training. We find that the manifold highly correlates with velocity, whereas the embedding of the raw data has no such correlation. To quantify this, we compute the k-nearest neighbor (kNN) regression error on the embeddings with respect to the velocities and find that the embedding obtained from ANIE has lower error (Extended Data Table 2).

For the second experiment, we inspect the attention weights of the model when predicting brain dynamics (calcium imaging; see the ‘Calcium imaging dataset’ section) to infer which cortical loci drive neuronal dynamics. Extended Data Fig. 4 shows that the motor and visual cortices are the areas of the brain with the highest attention values. We note that the attention plots are not directly correlated with the brain activity inputs, suggesting that they point to new information about the data. To validate this, we compare the performance of predicting the visual stimulus, which was not explicitly provided to the model, from either the raw data or the attention values using a kNN regressor (k = 3) (see the ‘Calcium imaging dataset’ section). In Extended Data Table 3, we show that the attention weights significantly (p = 0.035) outperform the raw data, thereby demonstrating that ANIE can provide insights into the modelled dynamics.

Further experiments

In the ‘Additional experiments’ section, we include several more experiments regarding the training speed of ANIE, showcasing that it is significantly faster than ODE-solver-based models, and hyperparameter sensitivity of the model (Supplementary Fig. 3) and modelling of IE dynamics (Extended Data Fig. 5 and Extended Data Table 4), along with further tables and figures on the experiments in the ‘Modelling PDEs with IEs: Burgers’ and Navier–Stokes equations’, ‘Modelling brain dynamics using ANIE’ and ‘Interpretable dynamics’ sections. In the ‘Solver convergence’ section, we have explored the convergence of the solver to fixed points of the corresponding IE, and Supplementary Fig. 6 shows the dependence of the model with respect to increased solver steps.

Methods

We give here a detailed account of the implementation of the NIE and ANIE models (one-dimensional (1D) and (n + 1)-dimensional IEs, respectively). More specifically, we provide a more thorough description of Algorithms 1 and 2 for solving the IEs associated with neural networks G (feed-forward) and ${\mathfrak{Att}}$ (transformer), and contextualize these algorithms in the optimization procedure that learns the neural networks.

Implementation of NIE

We only consider the case of equation (1), as the case where the function G splits in the product of a kernel K and the (possibly) nonlinear function F is substantially identical. We observe that the main components of the training of NIEs are two. An optimization step that targets G, and a solver procedure to obtain a solution associated with the IE individuated by G, or more precisely, the integral operator that G defines. Therefore, we want to solve equation (1) for a fixed neural network G, determine how far this solution is from fitting the data and optimize G in such a way that at the next step, we obtain a solution that more accurately fits the data. At the end of the training, we have a neural network G that defines an integral operator and, in turn, an IE, whose associated solution(s) approximates the given data.

To fix the notation, let us call X as the dataset for training. This contains several instances of n-dimensional curves with respect to time. In other words, we consider $X={\{{X}_{i}\}}_{i\le N}$, where N is the number of instances and ${X}_{i}=\{{{\bf{x}}}_{0}^{i},\ldots ,{{\bf{x}}}_{m}^{i}\}$, where each ${{\bf{x}}}_{i}\in {{\mathbb{R}}}^{q}$ is a q-dimensional vector, and the sequence of ${{\bf{x}}}_{k}^{i}$ refers to a discretization of the time interval where the curves are defined. For simplicity, we assume that time points are taken in [0, 1]. The neural network G defining the integral operator will be denoted by G_θ, to explicitly indicate the dependence of G on its parameters. The objective of the training is to optimize θ in such a way that the corresponding G_θ defines an IE whose solutions y_i(t) corresponding to different initializations pass through the discretized curves xⁱ(t).

Let us now consider one training step n, where the neural network ${G}_{{\theta }_{n}}$ has weights obtained from the previous training steps (or randomly initialized if this is the first step). We need to solve the IE

$${\bf{y}}=f(t)+\mathop{\int}\nolimits_{\!\alpha (t)}^{\beta (t)}{G}_{{\theta }_{n}}({\bf{y}},t,s){\rm{d}}s$$

(5)

associated with the integral operator $\mathop{\int}\nolimits_{\!\alpha (t)}^{\beta (t)}{G}_{{\theta }_{n}}({\bf{y}},t,s){\rm{d}}s$ corresponding to the weights θ_n at training step n.

For simplicity, we consider a batch size of 1 so that our training curve is given by {x₀,…, x_m}, where we suppress the superscript i because there is only one curve. Then, we select the first vector x₀, and use this to initialize a full curve with repeated instances of this. In other words, we define f(t) = x₀ for all times t. We now apply the IE solver procedure, and set the zero-order solution to the IE to be y⁰(t) = f(t) = x₀. We now apply the integral operator determined by G_θ computing

$${{\bf{z}}}^{0}=f(t)+\mathop{\int}\nolimits_{\!\alpha (t)}^{\beta (t)}{G}_{{\theta }_{n}}({{\bf{y}}}^{0},t,s){\rm{d}}s.$$

Observe that at this stage, we can perform the integration over the interval [α(t), β(t)] for each time t, since y⁰ is given for all times t. We then set y¹ = ry⁰ + (1 − r)z¹, where r is a smoothing factor and 0 ≤ r < 1, which is set beforehand. The function y¹(t) is now the new approximation for the solution of the IE given in equation (5). We can now compute the global error between y⁰ and y¹, which we denote by m(y⁰, y¹). This error is internal to the solver and does not refer to how well the model fits the data. It refers to how far the solver is from converging. We iterate this procedure. Let us assume that this has been done k times. Then, we have a function that approximates a solution of the IE at the kth iteration, denoted by y^k(t). We compute

$${{\bf{z}}}^{k}=f(t)+\mathop{\int}\nolimits_{\!\alpha (t)}^{\beta (t)}{G}_{{\theta }_{n}}({{\bf{y}}}^{k},t,s)ds,$$

where, as before, we can evaluate the integral over the intervals [α(t), β(t)] because the function y^k(t) is defined over the full time length of the dynamics.

This iterative procedure converges to a solution of the IE for the integral operator defined through ${G}_{{\theta }_{n}}$ (ref. ¹¹). To optimize the parameters θ of G, we require gradients on the input of ${G}_{{\theta }_{n}}$ when applying the neural network, we compute the loss between the solution y obtained through the iterative solution and the data, and we then backpropagate.

Implementation of ANIE

We now consider ANIE, which is an IE model where the integral is approximated via self-attention. As the iterative solver procedure to obtain a solution of the IE determined by the integral operator is conceptually the same as in the case of NIE given above, we mostly focus on the details relative to the use of self-attention in this setting. First, we consider an IE with space and time, which takes the form of equation (9). Our dataset now consists of instances of a given dynamics $X={\{{X}_{i}\}}_{i\le N}$, where N is the number of instances in the dataset, and each ${X}_{i}=\{{{\bf{x}}}_{{s}_{1},\ldots ,{s}_{d,\;j}}^{i}\}$ is a family of q-dimensional vectors (where q is the dimension of the dynamics), indexed by the spatial and temporal indices s₁,…, s_d and j corresponding to a discretization (for example, a mesh) of the spatiotemporal domain Ω × [0, T]. Observe that the dimension of the spatial domain Ω here is assumed to be d, thereby implying that each x depends on d indices. Therefore, one can think of each dynamics instance in the dataset as being a temporal sequence of spatial meshes, for example, a sequence of images when d = 2. We will assume that the number of time points in such a sequence is equal to m_T and the total number of space points is equal to m_Ω; we set m = m_Tm_Ω.

For the sake of simplicity, we assume that the attention model approximating the integral operator consists of a single self-attention layer. Let ${\mathfrak{Att}}$ denote a self-attention layer, and assume that ${\mathfrak{Att}}:{{\mathbb{R}}}^{m\times (q+d+1)}\longrightarrow {{\mathbb{R}}}^{m\times (q+d+1)}$. Observe that the attention layer maps sequences of length m of (q + d + 1)-dimensional vectors to sequences of the same type. We, therefore, think of ${\mathfrak{Att}}:{\mathcal{X}}\longrightarrow {\mathcal{Y}}$ as a mapping between two function spaces ${\mathcal{X}}$ and ${\mathcal{Y}}$, whose elements are functions y(x, t) in a discretized form, where x ∈ Ω and t ∈ [a, b]. As discussed in other work^21,34, the self-attention mechanism can be thought of as an approximation of an integral operator where given a discretized function y(x, t), ${\mathfrak{Att}}({\bf{y}}({\bf{x}},t))$ is another discretized function obtained through an approximation of an integration over the variables x and t. This theoretical motivation, and the computational complexity of performing the Monte Carlo integration in higher dimensions, led us to consider an IE solver where instead of learning a simple neural network G as in the setting of NIE, we learn the integral operator in the form of its attentional approximation ${\mathfrak{Att}}$.

As for the detailed description of NIE given above, we assume that the batch size is equal to 1, and the dataset is $X={\{{X}_{i}\}}_{i\le N}$ with ${X}_{i}=\{{{\bf{x}}}_{{s}_{1},\ldots ,{s}_{d,\;j}}^{i}\}$ for a discretization of a spatiotemporal domain Ω × [0, T], as described earlier. Let ${{\mathfrak{Att}}}_{\theta }$ denote the transformer with parameters θ obtained at epoch n of the training session. Here, if n = 0, it simply means that ${{\mathfrak{Att}}}_{\theta }$ is randomly initialized. We want to inspect epoch n + 1. The IE we solve at each training epoch takes the form

$${\bf{y}}=f({\bf{x}},t)+{{\mathfrak{Att}}}_{\theta }({\bf{y}},{\bf{x}},t),$$

(6)

where ${{\mathfrak{Att}}}_{\theta }({\bf{y}},{\bf{x}},t)$ is an approximation of an integral operator $\int\nolimits_{0}^{T}\mathop{\int}_{\Omega }$$G({\bf{y}},{\bf{x}},{{\bf{x}}}^{{\prime} },t,s)d{{\bf{x}}}^{{\prime} }ds$ for some G. The solver is initialized through the free function f(x, t), which plays the role of the first ‘guess’ for the IE solution. Observe that since f is evaluated on the full discretization of Ω × [0, T], then the length m of the sequence of vectors that approximates f(x, t) equates the product of the number of space points s_k for each dimension and time point t_r. The solver, therefore, creates its first approximation by setting y⁰(x, t) = f(x, t). Then, for the first iteration of the solver, we create the new sequence ${\tilde{{\bf{y}}}}^{0}$ by concatenating to each y and the spatiotemporal m coordinates (x_s, t_r). Now, $\tilde{{\bf{y}}}$ consists of a sequence of m = m_Tm_Ω vectors (one per spacetime point), which also possess spacetime encoding (through concatenation). Supplementary Fig. 1 shows a schematic of the integration procedure through a transformer. Then, we set

$${\tilde{{\bf{y}}}}^{1}({\bf{x}},t)=f({\bf{x}},t)+{{\mathfrak{Att}}}_{\theta }({\tilde{{\bf{y}}}}^{0}),$$

where the dependence of ${\tilde{{\bf{y}}}}^{1}$ on spacetime coordinates x and t indicates that we have one vector ${\tilde{y}}^{1}$ per spacetime coordinate. If q is the dimension of the dynamics (that is, the number of channels per spacetime point), then the sequence ${\tilde{{\bf{y}}}}^{1}$ consists of vectors of dimension q + d + 1, where d is the number of space dimensions. This happens because ${\tilde{{\bf{y}}}}^{1}$ is the output of a transformer of a sequence obtained by a sequence of q-dimensional vectors concatenated with a (d + 1)-dimensional sequence. The two simplest options are either to discard the last d + 1 dimensions of the vectors or add an additional linear layer that projects from q + d + 1 dimensions to q. As tests have not shown a significant difference between the two approaches, we have adopted the former. Consequently, we obtain the one-dimensional sequence z¹(x, t). Last, we set y¹(x, t) = ry⁰ + (1 − r)z¹, where r is a smoothing factor that is a hyperparameter of the solver. One, therefore, computes the error m(y⁰, y¹) between the initial step and the second one to quantify the degree of change in the new approximation, where m(•, •) is a global error metric fixed throughout.

Now, we iterate the same procedure and assuming that the approximation yⁱ to the equation has been obtained, we then concatenate the spacetime coordinates to obtain ${\tilde{{\bf{y}}}}^{i}$ and set

$${\tilde{{\bf{y}}}}^{i+1}({\bf{x}},t)=f({\bf{x}},t)+{{\mathfrak{Att}}}_{\theta }({\tilde{{\bf{y}}}}^{i}),$$

which we use to obtain zⁱ⁺¹ (by deleting the last d + 1 dimensions). Then, we set yⁱ⁺¹ = ryⁱ + (1 − r)zⁱ⁺¹ and compute the global error m(yⁱ, yⁱ⁺¹). Supplementary Fig. 2 shows a solver step integration in detail.

In practice, the number of iterations for the solver is a fixed hyperparameter that we have set between 3 and 5 in our experiments. This has been sufficient to achieve good results, as well as to learn a model that is stable under the solving procedure described above. Since the solver is fully implemented in PyTorch and the model that approximates the integral operator is a transformer, we can simply backpropagate through the solver at each epoch, after we have solved for y and compared the solution with the given data ${\{{X}_{i}\}}_{i\le N}$.

We complete this subsection with a more concrete description of the motivations for approximating integration through the mechanism of self-attention. Very similar perspectives have appeared in other sources^21,34, but we provide a formulation of such considerations that more easily fit the perspectives of integral operators for IEs used in this Article. This also serves as a more explicit description of ${\mathfrak{Att}}$ found in Algorithm 2.

We consider an n-dimensional dynamics y(x, t) depending on space x ∈ Ω (for some domain Ω) and time t ∈ [0, 1]. The queries, keys and values of self-attention can be considered as maps ${\psi }_{W}:{{\mathbb{R}}}^{n+1}\times \Omega \times [0,1]\longrightarrow {{\mathbb{R}}}^{1\times d}$, where d is the latent dimension of the self-attention, and W = Q, K and V for queries, keys and values, respectively. Then, (for W = Q, K, V), we have

$$W\,[{\bf{y}}| {\bf{x}}| t]=\left[\begin{array}{c}{\psi }_{W}^{0}[{\bf{y}}| {\bf{x}}| t]\\ \vdots \\ {\psi }_{W}^{i}[{\bf{y}}| {\bf{x}}| t]\\ \vdots \\ {\psi }_{W}^{d-1}[{\bf{y}}| {\bf{x}}| t]\end{array}\right],$$

where [y∣x∣t] indicates the concatenation of the terms in the bracket. Let us now consider the ‘traditional’ quadratic self-attention. Similar considerations also apply for the linear attention used in the experiments, mutatis mutandis. The product between queries and keys gives

$$\left[\left(\cdots {\psi }_{Q}^{i}\left[{\bf{y}}| {\bf{x}}| t\right]\cdots \right)\cdot \left(\cdots {\psi }_{K}^{j}\left[{\bf{y}}| {\bf{x}}| t\right]\cdots \right)^{\rm{T}}\right]_{ij}=\left({\psi }_{Q}^{i}\cdot {\hat{\psi }}_{K}^{j}\right),$$

where T indicates transposition and $\hat{\psi }$ indicates the columns of the transposed matrix. Then, if z is the output of the self-attention layer (observe that this consists of (z_i)_j, where i indicates a spatiotemporal point and j indicates the jth dimension of the n-dimensional dynamics). Then, we have

$${({{\bf{z}}}_{i})}_{j}=\sum _{j}\left({\psi }_{Q}^{i}\cdot {\hat{\psi }}_{K}^{j}\right){\psi }_{V}^{j}\approx {\int}_{\!\Omega \times [0,1]}K({\bf{y}},{\bf{x}},t,{{\bf{y}}}^{{\prime} },{{\bf{x}}}^{{\prime} },{t}^{{\prime} })F({{\bf{y}}}^{{\prime} },{{\bf{x}}}^{{\prime} },{t}^{{\prime} }){\rm{d}}{{\bf{x}}}^{{\prime} }{\rm{d}}{t}^{{\prime} },$$

where the prime symbols indicate the variables we are summing on (this is why the are ‘being integrated’ in the integral), and y is evaluated at x and t whereas y′ is evaluated at x′ and t′.

Additional experiments

Benchmark of (A)NIE training speed

Neural ordinary differential equations (NODEs) can be slow and have poor scalability⁴⁶. As such, several methods have been introduced to improve their performance^{46,47,48,49,50}. Despite these improvements, a NODE is still significantly slower than discrete methods such as LSTMs. We hypothesize that an (A)NIE has significantly better scalability than a NODE, comparable with fast but discrete LSTMs, despite being a continuous model. To test this, we compare NIE and ANIE with the latest optimized version of (latent) NODE⁵¹ and to LSTM on three different dynamical systems: Lotka–Volterra equations, Lorenz system and IE-generated two-dimensional (2D) spirals (see the ‘Artificial dataset generation’ section for the data generation details). During training, models were initialized with the first half of the data and were tasked to predict the second half. The training speeds are reported in Supplementary Table 1. Although all the models achieve comparable (good) fits to the data, we find that ANIE outperforms all the models in two out of the three datasets in terms of speed. Furthermore, ANIE has better MSE compared with all the other models.

Hyperparameter sensitivity benchmark

For most deep learning models, including NODEs, finding numerically stable solutions usually requires an extensive hyperparameter search. Since IE solvers are known to be more stable than ODE solvers, we hypothesize that (A)NIE is less sensitive to hyperparameter changes. To test this, we quantify the model fit, for the Lotka–Volterra dynamical system, as a function of two different hyperparameters: learning rate and L2 norm weight regularization. We perform this experiment for three different models: LSTM, latent NODE and ANIE. As shown in Supplementary Fig. 3, we find that ANIE generally has a lower validation error as well as more consistent errors across hyperparameter values, compared with LSTM and NODE, thereby validating our hypothesis.

Modelling 2D IE spirals

To further test the ability of ANIE in modelling non-local systems, we benchmark ANIE, NODE and LSTM on a dataset of 2D spirals generated by IEs. These data consist of 500 2D curves of 100 time points each. The data were split in half for training and testing. During training, the first 20 points were given as the initial condition and the models were tasked to predict the full 100-point dynamics. Details on the data generation are described in the ‘Artificial dataset generation’ section. For ANIE, the initialization is given via the free function f, which assumes the values of the first 20 points and sets the remaining 80 points to be equal to the value of the 20th point. For NODEs, the initialization is given as the RNN on the first 20 points, which outputs a distribution corresponding to the first time point (details on latent ODE experiments are provided elsewhere³⁰). For the LSTM, we input the data in segments of 20 points to predict the consecutive point of the sequence. The process is repeated with the output of the previous step until all the points of the curve are predicted. During inference, we test the models’ performance on never-before-seen initial conditions. Extended Data Table 4 shows the correlation between the ground-truth curve and the model predictions. Extended Data Fig. 5 shows the correlation coefficients for the 500 curves. In summary, ANIE significantly outperforms the other tested methods in predicting IE-generated non-local dynamics.

Solver convergence

We now consider the convergence of the solver to a solution of an IE for a trained model. Our experiment here considers a model that has been trained with a number of iterations, and we explore whether the solver iterations converge to a solution at the end of the training. These results show that the model learns to converge to a solution of equation (7) within the iterations that are fixed during training. They show that a fixed point for IE is obtained when outputting a prediction.

Supplementary Fig. 5 and Fig. 3 show the convergence error (that is, the value ∥y_n+1 − y_n∥), and the guesses produced by the solver during inference (that is, y_n for n corresponding to the iteration index), respectively.

Fig. 3: Example dynamics of the (2+1)-dimensional Navier–Stokes system, where the model is initialized only with the first frame of the dynamics.

Ground-truth data are given at the bottom. Along with the final prediction (step 7), the subsequent solver guesses are shown. The error during the solution generation are reported on the right. The figure also shows that the solver converges when producing the final output (compare with Supplementary Fig. 5).

IEs

IEs are equations where the unknown function appears under the sign of integral. These equations can be given, in general, as

$$\lambda {\bf{y}}=f+T({\bf{y}}),$$

(7)

where T is an integral operator, for example, as in equations (1) and (3), and f is a known term of the equation. In fact, this functional equations have been studied for classes of compact operators T that are not necessarily in the form of integral operators⁵². We can distinguish two fundamental kinds of equation from the form given in equation (7), which have been extensively studied throughout the years. When λ = 0, we say that the corresponding IE is of the first kind, whereas when λ ≠ 0, we say that it is of the second kind.

In this Article, we formulate our methods based on equations of the second kind for the following important theoretical considerations, which apply to the case where T is bounded over an infinite space (such as the space of functions as we consider in this Article). First, an equation of the first kind can easily have no solution, as the range of a bounded operator T on an infinite space is not the whole space⁵³. Therefore, for choices of f, there is no y such that T(y) = −f, and therefore, equation (7) has no solutions. The other issue is intrinsic to the nature of the equation of the first kind, and does not relate to the existence of solutions. In fact, any compact injective operator T (on an infinite space) does not admit a bounded left inverse⁵³. In practice, this means that if equation (7) has a unique solution for f, then varying f by a small amount can result in very significant variations in the corresponding solution y. This is clearly a potential issue when dealing with a deep learning model that aims at learning operator T from the data. In fact, observations from which T is learned might be noisy, which might result in very considerable perturbations of the solution y and, consequently, considerable perturbations on the operator T that the model converges to. Since equations of the second kind are much more stable, we have formulated all the theory in this setting, and implemented our solver for such equations. The issues relating to the existence and uniqueness of the solution for these equations are discussed in the ‘Existence and uniqueness of solutions’ section.

The theories of IEs and IDEs are tightly related, and it is often the case to reduce problems in IEs to problems in IDEs and vice versa, both in practical and theoretical situations. IEs are also related to differential equations, and it is possible to reformulate problems in ODEs in the language of IEs or IDEs. In certain cases, IEs can also be converted to differential equation problems, even though this is not always possible^9,54. In fact, the theory of IEs is not equivalent to that of differential equations. The most intuitive way of understanding this is by considering the local nature of differential equations, as opposed to the non-local origin of IEs. By the non-locality of IEs, it is meant that each spatiotemporal point in an IE depends on an integration over the full domain of the solution function y. In the case of differential equations, each local point depends only on the contiguous points through the local definition of the differential operators.

IE (1D)

We first discuss IEs where the integral operator only involves a temporal integration (that is, 1D), as discussed in the ‘IEs’ section. In analogy with the case of differential equations, this case can be considered as the one corresponding to ODEs.

These IEs are given by an equation of type

$${\bf{y}}(t)=f(t)+\mathop{\int}\nolimits_{\!\alpha (t)}^{\beta (t)}G({\bf{y}},t,s)ds,$$

(8)

where f is the free term, which does not depend on y, whereas the unknown function y appears both on the left- and right-hand sides under the sign of the integral. The term $\mathop{\int}\nolimits_{\alpha (t)}^{\beta (t)}G({\bf{y}},t,s)ds$ is an integral operator ${\mathcal{C}}(D)\longrightarrow {\mathcal{C}}(D)$ from the space of integrable functions ${\mathcal{C}}(D)$ over some domain of ${\mathbb{R}}$, into itself. We observe that the variables t and s appearing in G are both in D, and they are interpreted as time variables. We refer to them as global and local times, respectively, following the convention used in another work²⁹. The functions α and β determine the extremes of integration for each (global) time t. Common choices for α and β include α(t) = 0 and β(t) = t (Volterra equations) or α(t) = a and β(t) = b (Fredholm equations).

The fundamental question in the theory of IEs is whether solutions exist and are unique. It turns out that under relatively mild assumptions on the regularity of G, IEs admit unique solutions⁹. Furthermore, the proofs in another work⁴ show the close relation between IEs and IDEs, as the existence of uniqueness problems for IDEs are shown to be equivalent to analogous problems for IEs. Then, the fixed-point theorems of Schauder and Tychonoff are used to prove the results.

IEs (n + 1D)

We now discuss the case of IEs where the integral operator involves integration over a multidimensional domain of ${{\mathbb{R}}}^{n}$. This is the IE version of PDEs, and they are commonly referred to as PIEs when integration separately occurs on different components. We will consider equations where the multidimensional integral is obtained through multiple integrations. An equation of this type takes the form

$${\bf{y}}({\bf{x}},t)=f({\bf{x}},t)+\int\nolimits_{\!\!\alpha (t)}^{\beta (t)}\mathop{\int}_{\!\!\Omega }G({\bf{y}},{\bf{x}},{{\bf{x}}}^{{\prime} },t,s)d{{\bf{x}}}^{{\prime} }ds,$$

(9)

where $\Omega \subset {{\mathbb{R}}}^{n}$ is a domain in ${{\mathbb{R}}}^{n}$ and ${\bf{y}}:\Omega \times {\mathbb{R}}\longrightarrow {{\mathbb{R}}}^{m}$. Here m does not necessarily coincide with n.

PIEs and higher-dimensional IEs have been studied in some restricted form since the 1800s, as they have been employed to formulate the laws of electromagnetism before the unified version of Maxwell’s equations was published. In addition, early work on the Dirichlet’s problem found the IE approach proficuous, and it is well known that several problems in scattering theory (molecular, atomic and nuclear) are formulated in terms of (P)IEs. In fact, the Schrödinger equation can be recast as an IE⁵⁵. Bound-state problems have also been treated with the IE formalism⁵⁶.

Generalities on solving IEs

The most striking difference between the procedure of solving an IE and an ODE is that for an IE to evaluate at a single time point, one needs to know the solution for all the time points. This is clearly an issue, since solving for one point requires that we already know a solution for all the points. To better elucidate this point, we consider a simple comparison between the solution procedure of an ODE equation of type $\dot{{\bf{y}}}=f({\bf{y}},t)$ and an IE of type ${\bf{y}}=f(t)+\mathop{\int}\nolimits_{0}^{1}G({\bf{y}},t,s)ds$.

Let us assume that we are solving an ODE of type $\dot{{\bf{y}}}(t)=f({\bf{y}},t)$ and that y is known at time points t₀, t₁,…, t_k−1. Then, one can obtain y at t_k by means of the Euler method by using the known value at t_k−1 by taking small enough steps Δt forward in time. In general, therefore, one starts by the initial condition y₀ and determines the solution y at the points t₀,…, t_n by taking small steps and representing the derivative as Δf/Δt for small intervals Δt. Of course, more sophisticated methods are possible for the numerical solution of the ODE, but they essentially produce the next time point from the previous one in a sequential way. Let us now consider an analogous Fredholm IE to the ODE given above. This is a simple equation of the type ${\bf{y}}=f(t)+\mathop{\int}\nolimits_{0}^{1}G({\bf{y}},t,s)ds$. Suppose we know y at time points t₀,…, t_k−1. To determine y(t_k), we need to compute $f({t}_{k})+\mathop{\int}\nolimits_{0}^{1}G({\bf{y}},{t}_{k},s)ds$, which requires us to know y over the full interval [0, 1], as G is integrated over [0, 1]. It is obvious that knowing a single time point for y (or a sequence of values) does not suffice anymore. In a Volterra type of equation, the integral would be between [0, t_k] (where the unknown value t_k is included), which does not really change the essence of the issue.

Although several methods can be employed to solve IEs, most (if not all) of them are based on the concept of iteration over some initial guess for the solution of the IE. Iterating on the initial guess produces a sequence of functions that then converges to a solution of the IE. More specifically, one can consider the von Neumann series of the integral operator, as discussed below. In fact, let us consider equation (7), which can be rewritten as

$$({\mathbb{1}}-T\;)({\bf{y}})=f,$$

where we assume, for a moment, that T is a linear operator. Observe that if we can find the inverse of ${\mathbb{1}}-T$, then we obtain y as $({\mathbb{1}}-T\;)^{-1}(\;f\;)$. This can be done by writing the von Neumann series for $({\mathbb{1}}-T\;)^{-1}=$$\mathop{\sum }\nolimits_{k = 0}^{\infty }{T}^{\,k}$. This expression makes sense whenever the series $\mathop{\sum }\nolimits_{k = 0}^{\infty }{T}^{\,k}$ converges in the operator norm, which is guaranteed in important cases such as when $\mathop{\sum }\nolimits_{k = 0}^{\infty }\parallel T{\parallel }^{k}$ converges (for example, when ∥T∥ < 1), whereas milder conditions on the convergence of the series exist, too. In such a situation, when the von Neumann series is meaningful, we can then obtain y by iteratively applying T^k to f. The nonlinear case is handled in a similar iterative procedure, which is called the method of successive approximations or Picard’s iterations⁵⁷. It is, in fact, straightforward that under mild conditions, the method will output a solution of the IE. Conditions under which such succession is guaranteed to converge can be found elsewhere⁵⁷. A particularly well-known case is when the integrand of the integral operator is contractive (that is, Lipschitz with a constant between 0 and 1) with respect to the variable y. We give a proof of such an approach for our setting; similar results are available in other work⁵⁷.

Theorem 4.1

Let ϵ > 0 be fixed, and suppose that T is Lipschitz with constant k < 1. Then, we can find y ∈ X such that ∥T(y) + f − y∥ < ϵ, independent of the choice of f.

Proof

Let us set y₀ ≔ f and y_n+1 = f + T(y_n) and consider the term ∥y₁ − y₀∥. We have

$$\parallel {y}_{1}-{y}_{0}\parallel =\parallel T(\;{y}_{0})\parallel.$$

For an arbitrary n > 1, we have

$$\parallel {y}_{n+1}-{y}_{n}\parallel =\parallel T(\;{y}_{n})-T(\;{y}_{n-1})\parallel \le k\parallel {y}_{n}-{y}_{n-1}\parallel .$$

Therefore, applying the same procedure to y_n − y_n−1 = T(y_n−1) − T(y_n−2) until we reach y₁ − y₀, we obtain the inequality

$$\parallel {y}_{n+1}-{y}_{n}\parallel \le {k}^{n}\parallel T(\;{y}_{0})\parallel .$$

Since k < 1, the term kⁿ∥T(y₀)∥ is eventually smaller than ϵ for all n ≥ ν for some choice of ν. Defining y ≔ y_ν for such ν gives the following:

$$\parallel T(\;{y}_{\nu })+f-{y}_{\nu }\parallel =\parallel {y}_{\nu +1}-{y}_{\nu }\parallel < \epsilon .$$

The following now follows easily.

Corollary 4.2

Consider the same hypotheses as above. Then, equation (7) admits a solution. In particular, if the integrand G in equation (8) is contractive with respect to y with constant k such that k ⋅ (b − a) < 1 (where [a, b] is the co-domain of α and β), the iterative method in Algorithm 1converges to a solution of the equation.

Proof

From the proof of Theorem 4.1, it follows that the sequence y_n is a Cauchy sequence. Since X is Banach, then y_n converges to y ∈ X. By continuity of T, y is a solution to equation (7). For the second part of the statement, observe that when G is contractive with respect to y, then we can apply Theorem 4.1 to show that the sequence generated following Algorithm 1is Cauchy, and we can proceed as in the first part of the proof.

Remark 4.3

Observe that the result in Corollary 4.2applies to Algorithm 2, too, under the assumptions that the transformer architecture is contractive with respect to the input sequence y. Also, a statement that refers to higher-dimensional IEs can be obtained (and proved) similar to the second part of the statement of Corollary 4.2, using the measure of Ω × [a, b] instead of the value (b − a).

In practice, the method of successive approximations is implemented as follows. The initial guess for the IE is simply given by the free function f (that is, T⁰(f)), which is used to initialize the iterative procedure. Then, we apply T to y⁰ ≔ T⁰(f) to obtain a new solution z¹ ≔ f(t) + T¹(y⁰). We set y¹ ≔ ry⁰ + (1 − r)z¹ and apply T² to the solution y¹ and repeat. Here r is a smoothing factor that determines the amount of contribution from the new approximation to consider at each step. As the iterations grow, the fractions of the contributions due to the smoothing factor r tend to 1. Observe that when we sum ryⁱ + (1 − r)yⁱ⁺¹ with r = 0, we obtain the terms of the von Neumann series up to degree i applied to f: $\mathop{\sum }\nolimits_{0}^{i}{T}^{\;k}(\;f\;)$. The smoothing factor generally shows good empirical regularization for IE solvers, and we have set r = 1/2 throughout our experiments, even though we have not seen any concrete difference between different values of r. This procedure is shown in Fig. 2.

In another work¹¹, computations on the error bounds for the iterative procedure described above when the integrand function G splits into the product of a kernel (see above) and a linear function F are given. Also, a detailed description of the Nyström approximation for the computation of the error is given. We describe a concrete realization of the iterative procedure discussed above in the ‘IEs’ section, along with the learning steps for the training of our model. Moreover, we additionally observe that the procedure described above does not depend on T being an integral operator or a general operator, and therefore, applying this methodology to the case where we have a transformer instead of T is still meaningful, in the assumption that T is such that the iterated series of approximations is convergent.

Depending on the specific IE that one is solving (for example, Fredholm or Volterra, 1D or (n + 1)-dimensional), the actual numerical procedure for finding a numerical solution can vary. For instance, several studies have showcased such a wide variety of specific methods for the solution of certain types of equation^{35,58,59,60,61}. Such variations on the same theme of iterative procedure depend on finding the most efficient way of converging to a solution, finding the best error bounds, improving stability of the solver and substantially depending on the form of the integral operator. As our method is applied without the actual knowledge of the shape of the integral operator, but it actually aims at inferring (that is, learning) the integral operator from data, we implement an iterative procedure that is fixed and depends only on a hyperparameter smoothing factor. This is described in detail in the next section. However, we point out that since the integrand, and therefore the integral operator itself, is learned during the training, one can assume that the model will optimize with respect to the procedure in a way that our iterations are in a sense ‘optimal’ with respect to the target.

Thus far, our considerations on the implementation of IE solvers seem to point to a fundamental computational issue, since they entail a more sophisticated solving procedure than that of ODEs or PDEs. However, in various situations, even solving ODEs and PDEs through IE solvers presents significant advantages that are not necessarily obvious from the above discussions. The first advantage is that IE solvers are significantly more stable than ODE and PDE solvers, as shown in other work^6,7,35. This, in particular, provides a solution to the issue of underflowing during the training of NODEs that does not consist of a regularization, but of a complete change in perspective. In addition, even though one needs to iterate to solve an IE, in general, the number of iterations is not particularly high. In fact, in our experiments, the total number of iterations turned out to be sufficient to be fixed between 4 and 6. However, when solving, for instance, an ODE, one needs to sequentially go through each time step. These can be in the order of 100 (as that in some of our experiments). On the contrary, our IE solver processes the full time interval in parallel for each iteration. This results in a much faster algorithm compared with differential solvers, as shown in our experiments.

Existence and uniqueness of solutions

The solver procedure described in the previous subsection, of course, assumes that there exists a solution to start with. As mentioned at the beginning of the section, we treat equations of the second kind in this Article also because the existence conditions are better behaved than for the equations of the first kind. We now give some theoretical considerations in this regard. We will also discuss when these solutions are uniquely determined. Existence and uniqueness are two fundamental parts of the well posedness of IEs, the other being the continuity of solutions with respect to the initial data.

A concise and relatively self-contained reference for the existence and uniqueness of solutions for (linear) Fredholm IEs is provided elsewhere⁵³. In fact, it is shown that if a Fredholm equation has a Hermitian kernel, then the IE has a unique solution whenever λ is not an eigenvalue of the integral operator. For real coefficients, which is the case we are interested in, one can simply reduce the case to symmetric kernels, which are kernels for which K(t, s) = K(s, t) for all t and s. In this Article, since we have assumed λ = 1, the condition becomes equivalent to saying that there is no function z such that $\mathop{\int}\nolimits_{0}^{1}K(t,s)z(s)ds=z(t)$ for all t.

For more general (linear) integral operators (bounded on a Hilbert space), a similar result holds. In fact, from ref. ⁵³, we know that a generalized Fredholm IE admits solutions if and only if the free function is orthogonal to each solution of the associated homogeneous adjoint equation. The latter admits the zero function as a solution (therefore, the solution set is not empty), and is obtained from equation (7) by deleting f, and by taking the adjoint of T and the complex conjugate of y. In the real case, the conjugate of y is y itself. Moreover, uniqueness is guaranteed if the associated homogeneous equation has only trivial solutions. In the case of nonlinear integral operators, several existence and uniqueness conditions along with specific formulations can be found in the literature^4,9,57. Generally speaking, such conditions are assumed on the integrand functions that determine the integral operator, in such a way that contractive theorems (such as Schauder and Tychonoff) can be applied.

Observe that such formulations of the existence and uniqueness based on the contractive properties of the operator T are particularly interesting in the case where the integral operator is replaced by a general neural network (between function spaces), which is not necessarily obtained through integration. In practice, when T is a general neural network that is possibly nonlinear on all the entries, except with respect to the function y, T can be approximated by an IE using the following reasoning. It is known that Hilbert–Schmidt operators on the Hilbert space of square integrable functions are approximated by integral operators⁵³. It is reasonable to assume that neural network operators are sufficiently well behaved to be considered Hilbert–Schmidt operators. They, hence, approximate some integral operator, and the training process, therefore, learns an IE.

More generally, for nonlinear IEs of the Urysohn or Hammerstein type, the existence and uniqueness problems are well known under much milder conditions, namely, when the operator is completely continuous^62,63. In this situation, it is sufficient for the operator to have a non-zero topological index to guarantee that the corresponding IE admits a solution, and to study the problem of uniqueness, one can determine the value of the topological index in a bounded subset of the Banach space in consideration, since this is directly related to the number of fixed points of the given IE.

The previous discussion, however, does not directly apply to the case when T is a transformer. Such equations can still be considered generalized Fredholm equations, and conditions on nonlinear operators T being approximated by integral operators can be found in the literature, but the extent to which such equations are equivalent to IEs is a fascinating question, which will not be explicitly considered in this Article.

Informatively, we mention that the general theory ensures the existence and uniqueness of solutions under some (mild) assumptions. Of course, in principle, one should impose constraints to ensure that such assumptions are satisfied and that the results would apply. However, in our experiments, we have observed good stability and good convergence without imposing any additional constraints. This does not apply in general, but we hypothesized that during optimization, the model converges towards operators whose associated IE is well behaved, to avoid regimes of poor stability due to the lack of solutions or the lack of uniqueness of solutions. For different datasets, such behaviour might not be satisfied, and extra care in this regard might be needed.

Initial condition for IEs

NIE does not learn a dynamical system via the derivative of a function y, as is the case for ODEs and IDEs. Therefore, we do not need to specify an initial condition in the solver during training and evaluation. In fact, the initial condition for IEs is encoded in the equation itself. For instance, taking t = 0 in a Volterra or Fredholm equation uniquely fixes y(x, 0) for all x.

Therefore, we can specify a condition for IEs by constraining the free function f(y, t). Hereafter, we will make use of this paradigm several times. There are two immediate ways one could impose constraints on the free function. The simplest is to fix a value y₀ and let f(y, t) be fixed to be y₀ for all t. Alternatively, one could choose an arbitrary function f and keep this function fixed. In practice, the latter is conceptually more meaningful. For instance, in theoretical physics, when transforming the Schrödinger equation into an IE, on the right-hand side, one can choose an arbitrary function ψ(y, t), which corresponds to the wave function of free particles, that is, without potential V. Applications of this procedure are found below in the experiments.

Approximation capabilities

In this section, we consider the capabilities of our models to approximate (nonlinear) integral operators and IEs.

NIE

We consider two settings, where the integral operator is modelled by a single-hidden-layer feed-forward neural network of arbitrary width, or by an arbitrarily deep neural network.

We want to show that when we restrict ourselves to single-hidden-layer feed-forward neural networks of arbitrary depth for our function G_θ in equation (1), we can approximate a wide class of IEs over a suitable subset of the space of functions. In the case of deep neural networks, we will argue that the NIE architecture can approximate any ‘regular enough’ integral operator, where regularity will be described below. We restrict our considerations to the case of function spaces where the domain is ${\mathbb{R}}$, since the higher-dimensional case is easily adapted from this discussion. We will, therefore, use y instead of y to indicate the elements of the domain of the integral operators.

Let T: C([0, 1]) ⟶ C([0, 1]) be an integral operator on the space of continuous functions, defined as $y\mapsto T(\;y)(t):= \mathop{\int}\nolimits_{\alpha (t)}^{\beta (t)}G(\;y(s),t,s)ds$ for continuous functions α and β: [0 1] ⟶ [0, 1] and continuous $G:{\mathbb{R}}\times [0,1]\times [0,1]\longrightarrow {\mathbb{R}}$. In fact, in the following, we could consider G as being Borel measurable, instead of imposing the more restrictive condition of being continuous. However, since in applications, continuity is generally required, we impose this more restrictive condition. Moreover, our discussion easily extends to the case when the definition intervals are [a, b] instead of [0, 1] with simple modifications, and a similar approach also extends to higher-dimensional integrals. We assume that T is such that the corresponding IE of the second kind, that is, equation (1), admits a solution ${y}^{* }:[0,1]\longrightarrow {\mathbb{R}}$ in C([0, 1]). Since y* is continuous, there exists a compact K = [−k, k], for k > 0, such that y*([0, 1]) ⊂ K. Let us now consider a neighbourhood U_K of y* in the compact-open topology such that for all y ∈ U_K, we have the property y([0, 1]) ⊂ K. This could be, for instance, the space of functions y mapping [0, 1] into the open (−k, k) = K°. We can, therefore, restrict G to the domain K × [0, 1] × [0, 1], and we will still indicate this restriction by G and the corresponding integral operator by T (defined over the neighbourhood U_K), for notational simplicity.

For an arbitrarily chosen ϵ > 0, we want to show that we can approximate T(y) with error at most ϵ in the metric induced by C([0, 1]) on U_K through an NIE integral operator ${T}_{\theta }(\;y)(t):= \mathop{\int}\nolimits_{\alpha (t)}^{\beta (t)}{G}_{\theta }(\;y(s),t,s)ds$. To this purpose, let us set $Q=\mathop{\sup }\nolimits_{[0,1]}| \beta (t)-\alpha (t)|$, and observe that by applying the universal approximation theorem for single-hidden-layer feed-forward neural networks⁶⁴ to the function $G:K\times [0,1]\times [0,1]\longrightarrow {\mathbb{R}}$, we can find a single-hidden-layer neural network ${G}_{\theta }:K\times [0,1]\times [0,1]\longrightarrow {\mathbb{R}}$ such that for all t and s ∈ [0, 1], we have ∣G(y(s), t, s) − G_θ(y(s), t, s)∣ < ϵ/Q. With such a G_θ, for all functions y ∈ U_K, we have for any fixed t* in [0, 1],

$$\begin{array}{ll}\left\Vert T(\;y)({t}^{* })-\displaystyle\mathop{\int}\nolimits_{\alpha ({t}^{* })}^{\beta ({t}^{* })}{G}_{\theta }(\;y(s),{t}^{* },s)ds\right\Vert\\\quad\le\mathop{\displaystyle\int}\nolimits_{\alpha ({t}^{* })}^{\beta ({t}^{* })}\Big\Vert G(\;y(s),{t}^{* },s)-\,{G}_{\theta }(\;y(s),{t}^{* },s)\Big\Vert ds\\ \quad < | \beta ({t}^{* })-\alpha ({t}^{* })| \epsilon /Q.\end{array}$$

Therefore, uniformly, in the variable t, we have

$$\left\Vert T(\;y)(t)-\mathop{\int}\nolimits_{\!\!\alpha (t)}^{\beta (t)}{G}_{\theta }(\;y(s),t,s)ds\right\Vert < \epsilon .$$

But this means that d(T(y), T_θ(y)) < ϵ with the metric d on U_K induced by that of C([0, 1]).

We observe that although this approximation does not hold in complete generality, it is valid for a class of integral operators of importance, since we are usually interested in operators whose corresponding IE admits continuous solutions, and we are interested in modelling the operator in the neighbourhood of a solution. Moreover, under mild assumptions (see the ‘Existence and uniqueness of solutions’ section), the dependence of the solution on the initial data is continuous, and therefore, the solutions to the equation for perturbed f lie in a neighbourhood of a solution y* obtained for f. So, our results apply in such important cases. Last, we point out that throughout the previous reasoning, we have implicitly assumed that numerical integration is performed with infinite precision. Of course, this is not the case in practice, but since we can reduce the numerical error in the integration procedure by arbitrarily choosing dense enough samples for a choice of the integration scheme, the error due to numerical integration can be rendered small enough so that the previous inequalities hold.

We now consider the case where we allow deep neural networks⁶⁵. In this case, we argue that for any IE of the second kind as in equation (1) where we set $T(\;y)(t):= \mathop{\int}\nolimits_{\alpha (t)}^{\beta (t)}G(\;y(s),t,s)ds$ for a Lebesgue integral function G, we can approximate the integral operator T with arbitrary precision. As a consequence, there is an NIE model that realizes any IE as in equation (1) with arbitrary accuracy. We can proceed as for the case of single-hidden-layer neural networks above, with the main difference that when applying a theorem from another work⁶⁵, we do not need to restrict ourselves to a neighbourhood U_K of a solution y* of the IE, and the neural integral operator $\mathop{\int}\nolimits_{\alpha (t)}^{\beta (t)}{G}_{\theta }(y(s),t,s)ds$ uniformly approximates T with respect to t for any y ∈ C([0, 1]). Observe that to use the data from ref. ⁶⁵, we need to pre-compose G and G_θ by a characteristic function χ_[0, 1], which does not affect the result.

ANIE

We give some comments on the approximation properties of ANIE with respect to generalized Fredholm equations. For simplicity, we consider the case where the integration is performed only over time, even though the same reasoning can be extended to spatiotemporal domains. Let T: C([0, 1]) ⟶ C([0, 1]) denote a Fredholm integral operator defined through the assignment $T(\;y)(t)=\mathop{\int}\nolimits_{0}^{1}G({\bf{y}}(t),t,{\bf{y}}(s),s)ds$. Observe that this integral form is more general than that considered in equation (1), and it follows the interpretation of integration in terms of self-attention (see the ‘Implementation of ANIE’ section, where the integration approximation used in this Article is given in more detail).

Let us assume that the IE y = f* + T(y) admits a unique continuous solution y* ∈ C²([0, 1]), and that G is regular enough so that the equation admits a unique solution in C([0, 1]) for given functions f in a neighbourhood of f* in the compact-open topology. Observe that such well-posedness conditions are usually relatively mild (see, for instance, the ‘Existence and uniqueness of solutions’ section), and this is the main situation of interest in applications. Then, there exists a compact K = [−k, k] such that y*([0, 1]) ⊂ K and we can choose a neighbourhood U_K of y* in the compact-open topology of C([0, 1]) such that y([0, 1]) ⊂ K for all y ∈ U_K. In fact, one can simply choose U_K ≔ {y ∈ C([0, 1]) ∣ ∣y([0, 1])∣ < k}. Under such a hypothesis, there are numerical integration schemes that can approximate the integral $\mathop{\int}\nolimits_{0}^{1}G({\bf{y}}(t),t,{\bf{y}}(s),s)ds$ for any fixed choice of t with arbitrary precision, on choosing a number of points for evaluation that is sufficiently large. For instance, for any fixed t, the error for trapezoidal rules is bound by a term that goes to zero as n grows, where n is the number of points chosen in [0, 1] for approximating the integral⁶⁶. This term is the modulus of continuity as follows:

$${\omega }_{t}(1/n):= \mathop{\max }\limits_{| {s}_{1}-{s}_{2}| < 1/n}\Big| G({\bf{y}}(t),t,{\bf{y}}({s}_{1}),{s}_{1})-G({\bf{y}}(t),t,{\bf{y}}({s}_{2}),{s}_{2})\Big| .$$

For each choice of n, there exists a compact K_n ≔ [−k_n, k_n] such that y* maps into K_n, and G restricted to K_n × [0, 1] × K_n × [0, 1] has ω_t(1/n) < 1/n for all t ∈ K_n. In this situation, we can choose a neighbourhood of ${y}^{* },{U}_{{K}_{n}}$ such that ω_t(1/n) < 1/n for all t ∈ K_n for each choice of $y\in {U}_{{K}_{n}}$, and this numerical integration approximates the value of T(y)(t) with arbitrarily high accuracy.

We indicate our numerical integration scheme using the formula

$$T(\;y)(t)=\mathop{\int}\nolimits_{\!\!0}^{1}G({\bf{y}}(t),t,{\bf{y}}(s),s)ds\approx \mathop{\sum }\limits_{i=0}^{n}{w}_{i}(t)G({\bf{y}}(t),t,{\bf{y}}({s}_{i}),{s}_{i}),$$

where s_i indicates the ith grid point of {t_i} ⊂ [0, 1]. We can, therefore, obtain the evaluation of T(y) at the grid points t_j as

$$T(\;y)({t}_{j})=\mathop{\int}\nolimits_{\!\!0}^{1}G({\bf{y}}({t}_{j}),{t}_{j},{\bf{y}}(s),s)ds\approx \mathop{\sum }\limits_{i=0}^{n}{w}_{i}({t}_{j})G({\bf{y}}({t}_{j}),{t}_{j},{\bf{y}}({s}_{i}),{s}_{i}),$$

by choosing t to be one of the grid points.

From our regularity assumptions on the derivatives, we can uniformly bound the error on evaluating T(y) at the points t_j such that for sufficiently dense grids, the evaluation error is smaller than ϵ/2 for any choice of ϵ > 0, when evaluating on functions y in a neighbourhood of y*.

Let us now consider a permutation of the input of T(y) for some σ ∈ Σ_n. This means that we permute the grid points {t_i} as {t_σi}. The approximated integration above gives

$$T(\;y)({t}_{i})\approx \sum _{i}{w}_{\sigma i}({t}_{\sigma j})G({\bf{y}}({t}_{\sigma j}),{t}_{\sigma j},{\bf{y}}({s}_{\sigma i}),{s}_{\sigma i})=\sum _{i}{w}_{i}({t}_{\sigma j})G({\bf{y}}({t}_{\sigma j}),{t}_{\sigma j},{\bf{y}}({s}_{i}),{s}_{i}),$$

where the second equality follows from the fact that we are summing over all the permuted indices i. This means that our approximation of the integration, evaluated on grid points, is permutation equivariant. Using results from ref. ⁶⁷, we are able to find a transformer architecture and a weight configuration, which we denote by ${\mathcal{T}}$, such that $\parallel \mathop{\sum }\nolimits_{i = 0}^{n}{w}_{i}({t}_{j})G({\bf{y}}({t}_{j}),{t}_{j},{\bf{y}}({s}_{i}),{s}_{i})-{\mathcal{T}}(\;y({t}_{j})){\parallel }_{p} < \epsilon /2$, as a function of the t_j values. As a consequence, we obtain the approximation

$$\begin{array}{rcl}\left\Vert T(\;y)(t)-{\mathcal{T}}(\;y(t))\right\Vert _{p}&\le &\left\Vert T(\;y)({t}_{j})-\mathop{\sum }\limits_{i=0}^{n}{w}_{i}({t}_{j})G({\bf{y}}({t}_{j}),{t}_{j},{\bf{y}}({s}_{i}),{s}_{i})\right\Vert _{p}\\ &+&\left\Vert \mathop{\sum }\limits_{i=0}^{n}{w}_{i}({t}_{j})G({\bf{y}}({t}_{j}),{t}_{j},{\bf{y}}({s}_{i}),{s}_{i})-{\mathcal{T}}(\;y({t}_{j}))\right\Vert _{p}\\ & < &\epsilon /2+\epsilon /2=\epsilon ,\end{array}$$

for any choice of y in a neighbourhood of y*.

Dependence of the model on iteration steps

Here we explore the dependence of model extrapolation on the initial condition for the Navier–Stokes dataset with respect to the number of iterations of the solver. The results are reported in Supplementary Table 2 and Supplementary Table 3, where the mean squared error and standard deviations are reported. Supplementary Fig. 6 shows the results reported in Supplementary Table 2. We perform our experiments with two different models, one with a much higher number of parameters than the other. We see that for a smaller model, the impact of the number of solver steps becomes much more pronounced. This indicates that although a very large model is able to compensate the effect of the solver steps and reduce the difference in testing quality, a smaller model can greatly benefit from a higher number of iterations. We notice, in particular, that an ANIE model with a single layer performs as well as an ANIE model with four layers and lower number of iterations. In all the cases, a higher number of solver steps gives better evaluations than single-iteration models with statistical significance (P < 0.0001).

Computational cost

We now give more details regarding the computational cost of our models.

The theoretical order of the computation for NIE per iteration is in the order of N × T, where N is the number of Monte Carlo sampling points and T is the number of time points used in the solver. This has to be multiplied by the number of iterations, which, for example, has been taken to be three in the experiments on training speed.

For ANIE, we have performed our experiments using a linear version of self-attention, which requires a linear computational cost in the number of spacetime points used (this changes depending on the resolution of the dataset). So, for a spacetime grid Ω_n ⊂ Ω consisting of n space points, and a grid T_m ⊂ I consisting of m time points, the computational cost is in the order of n × m times the number of solver iterations. The iterations for ANIE varied between three and seven throughout the experiments. We observe that quadratic attention would result in a computational cost of the order of (nm)² × r, where r is the number of iterations of the solver.

Artificial dataset generation

Lotka–Volterra system

Lotka–Volterra equations are a classic system of nonlinear differential equations that model the interaction between two populations. The equations are given by

$$\begin{array}{rcl}\frac{{\rm{d}}x}{{\rm{d}}t}&=&\alpha xy-\beta y\\ \frac{{\rm{d}}y}{{\rm{d}}t}&=&\delta xy-\gamma y\end{array},$$

where α and δ define the population interaction terms, and β and γ are the intrinsic population growth for population x and y. To generate our dataset, 100 values of α, β, δ and γ have been randomly generated and the corresponding system has been solved with a fixed initial condition. Our code was adapted from https://scipy-cookbook.readthedocs.io/items/LoktaVolterraTutorial.html.

Lorenz system

The Lorenz system is a three-dimensional system of ODEs for modelling atmospheric convection. Furthermore, this system is known to be chaotic, which means that small variations in initial conditions can significantly affect the final trajectory. The system is given by

$$\begin{array}{rcl}\frac{{\rm{d}}x}{{\rm{d}}t}&=&\sigma (\;y-x)\\ \frac{{\rm{d}}y}{{\rm{d}}t}&=&x(\;\rho -z)-y\\ \frac{{\rm{d}}z}{{\rm{d}}t}&=&xy-\beta z\end{array}.$$

We have sampled 100 random initial conditions, and have solved the system with the same fixed parameters. Our code was adapted from https://github.com/gboeing/lorenz-system.

IE spirals

The 2D IE spirals have been obtained by solving an IE with the following form:

$$\begin{array}{l}{\bf{y}}(t)=\mathop{\displaystyle\int}\nolimits_{\!\!0}^{t}\left[\begin{array}{cc}\cos 2\uppi (t-s)&-\sin 2\uppi (t-s)\\ -\sin 2\uppi (t-s)&-\cos 2\uppi (t-s)\end{array}\right]\tanh (2\uppi {\bf{y}}(s)){\rm{d}}x+{{\bf{z}}}_{0}\\\qquad\ \ \;+\left[\begin{array}{c}\cos (t)\\ \cos (t+\uppi )\end{array}\right],\end{array}$$

where z₀ was sampled from a uniform distribution.

The equation has been numerically solved through our solver (with analytical functions instead of neural networks) for different known functions f corresponding to different choices of z₀.

fMRI data generation

The simulated fMRI data were generated using neurolib⁴³. This tool encompasses code to generate fMRI data for the resting state with a given structural connectivity matrix and a delay matrix. The code can be found at https://github.com/neurolib-dev/neurolib/blob/master/examples/example-0-aln-minimal.ipynb. We used this code to generate 100,000 time points of data for 80 voxels corresponding to regions of the cortex.

The generated data are normalized via computing the z score of the logarithm of the whole data. These data are then downsampled in time by a factor of 10, thereby resulting in 10,000 time points. In our tests, we use the first 5,000 points, where the first 2,500 points are used for training and the remaining points are reserved for testing. During batching, each point is taken as the initial condition of a curve of length 20 points.

Calcium imaging dataset

C57BL/6J mice were kept on a 12 h light/dark cycle, provided with food and water ad libitum and individually housed following headpost implants. Imaging experiments were performed during the light phase of the cycle. For mesoscopic imaging, brain-wide expression of jRCaMP1b was achieved via postnatal sinus injection, as described elsewhere^68,69.

Briefly, P0–P1 litters were removed from their home cage and placed on a heating pad. Pups were kept on ice for 5 min to induce anaesthesia via hypothermia and then maintained on a metal plate surrounded by ice for the duration of injection. Pups were injected bilaterally with 4 µl of AAV9-hsyn-NES-jRCaMP1b (2.5 × 10¹³ gc ml^–1, Addgene). Mice also received an injection of AAV9-hsyn-ACh3.0 to express the genetically encoded cholinergic sensor ACh3.0 (ref. ⁷⁰). Once the entire litter was injected, pups were returned to their home cage.

Surgical procedures were performed on sinus-injected animals once they reached adulthood (>P50). Mice were anaesthetized using 12% isoflurane and maintained at 37 °C for the duration of the surgery. For mesoscopic imaging, the skin and fascia above the skull were removed from the nasal bone to the posterior of the intraparietal bone and laterally between the temporal muscles. The surface of the skull was thoroughly cleaned with saline and the edges of the incision secured to the skull with Vetbond. A custom titanium headpost for head fixation was secured to the posterior of the nasal bone with transparent dental cement (Metabond, Parkell), and a thin layer of dental cement was applied to the entire dorsal surface of the skull. Next, a layer of cyanoacrylate (Maxi-Cure, Bob Smith Industries) was used to cover the skull and left to cure for 30 min at room temperature to provide a smooth surface for transcranial imaging.

Mesoscopic calcium imaging was performed using a Zeiss Axiozoom with a ×1, 0.25-numerical-aperture objective with a 56 mm working distance (Zeiss). Epifluorescent excitation was provided by an LED bank (SPECTRA X Light Engine, Lumencor) using two output wavelengths: 395/25 nm (isosbestic for ACh3.0, ref. ⁷¹) and 575/25 nm (jRCaMP1b). Emitted light passed through a dual-camera image splitter (TwinCam, Cairn Research) and then through either a 525/50 nm (ACh3.0) or 630/75 nm (jRCaMP1b) emission filter (Chroma) before it reached two sCMOS cameras (Orca-Flash V3, Hamamatsu). Images were acquired at 512 × 512 pixel resolution after 4× pixel binning. Each channel was acquired at 10 Hz with 20 ms exposure using HCImage software (Hamamatsu).

For visual stimulation, sinusoidal drifting gratings (2 Hz, 0.04 cycles per degree) were generated using custom-written functions based on the Psychtoolbox in MATLAB and presented on an LCD monitor at a distance of 20 cm from the right eye. Stimuli were presented for 2 s with a 5 s interstimulus interval.

Imaging frames were grouped by the excitation wavelength (395, 470 and 575 nm) and downsampled from 512 × 512 to 256 × 256 pixels. Detrending was applied using a low-pass filter (N = 100, f_cutoff = 0.001 Hz). Time traces were obtained using (ΔF/F)_i = (F_i − F_{(i, o)})/F_{(i, o)}, where F_i is the fluorescence of pixel i and F_{(i, o)} is the corresponding low-pass filtered signal.

Haemodynamic artefacts were removed using a linear regression accounting for spatiotemporal dependencies between neighbouring pixels. We used the isosbestic excitation of ACh3.0 (395 nm) co-expressed in these mice as the means of measuring activity-independent fluctuations in fluorescence associated with haemodynamic signals. Briefly, given two p × 1 random signals y₁ and y₂ corresponding to ΔF/F of p pixels for two excitation wavelengths ‘green’ and ‘UV’, we consider the following linear model:

$${y}_{1}=x+z+\eta ,$$

(10)

$${y}_{2}=Az+\xi ,$$

(11)

where x and z are mutually uncorrelated p × 1 random signals corresponding to p pixels of the neuronal and haemodynamic signals, respectively. η and ξ are white Gaussian p × 1 noise signals and A is an unknown p × p real invertible matrix. We estimate the neuronal signal as the optimal linear estimator for x (in the sense of the minimum mean squared error):

$$\hat{x}=H\left(\begin{array}{c}{y}_{1}\\ {y}_{2}\end{array}\right),$$

(12)

$$H=\sum _{xy}{\sum _{y}}^{-1},$$

(13)

where $y=\left(\begin{array}{c}{y}_{1}\\ {y}_{2}\end{array}\right)$ is given by stacking y₁ on top of y₂, ∑_y = E[yy^T] is the autocorrelation matrix of y and ∑_xy = E[xy^T] is the cross-correlation matrix between x and y. The matrix ∑_y is directly estimated from the observations, and the matrix ∑_xy is estimated as

$$\sum _{xy}=\left(\sum _{{y}_{1}}-{\sigma }_{\eta }^{2}I-\left(\sum _{{y}_{1}\,{y}_{2}}\left(\sum _{{y}_{2}}-{\sigma }_{\xi }^{2}I\right)^{-1}{\sum _{{y}_{2}}}^{-1}{\sum _{{y}_{1}\,{y}_{2}}}^{{\rm{T}}}\right)^{{\rm{T}}}0\right),$$

(14)

where ${\sigma }_{\eta }^{2}$ and ${\sigma }_{\xi }^{2}$ are the noise variances of η and ξ, respectively, and I is the p × p identity matrix. The noise variances ${\sigma }_{\eta }^{2}$ and ${\sigma }_{\xi }^{2}$ are evaluated according to the median of the singular values of the corresponding correlation matrices ${\sum }_{{y}_{1}}$ and ${\sum }_{{y}_{2}}$. This analysis is usually performed in patches where the size of the patch p is determined by the amount of time samples available and estimated parameters. In the present study, we used p = 9. The final activity traces were obtained by z scoring the corrected ΔF/F signals per pixel. The dimensionality of the resulting video is then reduced via PCA to ten components, which represents ~80% of data variance.

Burgers’ equations

The Burgers’ equation is a quasilinear parabolic PDE that takes the form

$$\frac{\partial u}{\partial t}+u\frac{\partial u}{\partial x}=\nu \frac{{\partial }^{2}u}{\partial {x}^{2}},$$

(15)

where x is a spatial dimension, whereas t indicates time and ν is a diffusion coefficient called viscosity⁷². A very interesting behaviour of the solutions of the Burgers’ equation is evident in the presence of shock waves.

Our dataset is generated using the MATLAB code used in ref. ¹⁹, which can be found at https://github.com/zongyi-li/fourier_neural_operator/tree/master/data_generation/burgers. The solution is given on a spatial mesh of 1,024 and 400 time points are generated from a random initial condition. We use 1,000 curves for training and test on 200 unseen curves, where the interval spans one-fourth of the original time used for testing.

Navier–Stokes equations

The Navier–Stokes equations are PDEs that arise in fluid mechanics, where they are used to describe the motion of viscous fluids. They are derived from the conservation laws (for momentum and mass) for Newtonian fluids subject to an external force with the addition of pressure and friction forces, where the unknown function indicates the velocity vector of the fluid^73,74. Their expression is given by the system

$$\frac{\partial }{\partial t}{u}_{i}+\sum _{j}{u}_{j}\frac{\partial {u}_{i}}{\partial {x}_{j}}=\nu \Delta {u}_{i}-\frac{\partial p}{\partial {x}_{i}}+{f}_{i}({\bf{x}},t),$$

(16)

$${\rm{div}}u=\sum _{i}\frac{\partial {u}_{i}}{\partial {x}_{i}},$$

(17)

where Δ is the Laplacian operator, f is the external force and u is the unknown velocity function. We experiment on the same dataset for ν = 1e−3 (ref. ¹⁹), which is available at https://github.com/zongyi-li/fourier_neural_operator/tree/master/data_generation/navier_stokes. They solved the viscous, incompressible 2D Navier–Stokes equation for vorticity on the unit torus, and with periodic boundary conditions. The initial time point is sampled from a Gaussian distribution. The forcing term is a linear combination of sine and cosine functions depending only on space and independent of time. The numerical method for the solution of the equation is pseudospectral, for the vorticity–streamfunction formulation. The solver scheme follows these steps: (1) solving the Poisson equation, (2) vorticity is differentiated and (3) the nonlinear term is added. A Crank–Nicholson update is used to advance time. Details are provided elsewhere¹⁹.

We use 4,000 instances for training and 1,000 for testing. In our tasks, we utilize a single time point to initialize our model (ANIE) and obtain the full dynamics from a single frame. For comparison, we use the minimal number of time points allowed for the other models for comparison. This is not always possible, for instance, FNO3D cannot be applied on a single time point or few time points, as the time convolution needs several time points to produce significant results. Despite this significant advantage given to FNO3D, ANIE (this work) still performs better on the prediction of 10 and 20 time points.

Additional details on experiments and computational resources

The number of parameters for the models used in the experiments are given in Supplementary Tables 4 and 5. In all the cases, the optimizer ‘Adam’ has been employed. Experiments have been run on a 16 GB NVIDIA A100 GPU.

Reporting summary

Further information on research design is available in the Nature Portfolio Reporting Summary linked to this article.