Introduction

Magnetic frustration is widely known to give rise to a variety of exotic phases, such as quantum spin liquids and spin ice states, which host novel particles such as Majorana fermions and magnetic monopoles1,2,3. Among highly frustrated systems, kagome magnets stand out4. In a kagome lattice, corner-sharing equilateral triangles form perfect hexagons. When these triangles are rotated with respect to each other, they create what is called “twisted kagome lattice”5,6, reducing symmetry and increasing in-plane anisotropy. Additionally, in systems involving rare earth elements, the crystal field splitting introduces an additional energy scale7. In scenarios where the electronic bands near the Fermi energy are derived from the rare earth element, there is a unique opportunity to tune magnetism by manipulating anisotropies through external parameters such as magnetic fields. This tuning becomes even more compelling if the electronic bands exhibit topological features, such as flat bands and Dirac or Weyl points–key areas of interest in condensed matter physics.

HoAgGe features a twisted kagome net formed by a rare earth element Ho8,9. It has a non-centrosymmetric crystal structure \(P\bar{6}2m\), with alternating layers of Ho3Ge and Ag3Ge2 along the [001] direction (Fig. 1a). The equilateral triangles in the lattice are rotated by ≈ 15.6∘ around the c-axis10, forming the twisted kagome network shown in Fig. 1b. Previous studies have revealed that HoAgGe undergoes two successive antiferromagnetic transitions at 11 K (TN1) and 7 K (TN2)9,10,11,12,13. Below TN1, the spins in Ho atoms partially order, while a fully ordered magnetic state emerges below TN210.

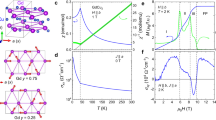
Fig. 1: Crystal and magnetic structures of HoAgGe.
figure 1

a A sketch of the crystal structure of HoAgGe. b A view along the c-axis, highlighting the twisted kagome network of Ho atoms in the ab-plane. c–f The low-temperature magnetic structure of HoAgGe under different magnetic fields applied along the [120] crystallographic direction. The [120] direction, relative to the crystal plane, is indicated by the black arrow. Solid lines represent the crystallographic unit cells. Red arrows in (c–f) denote the spin directions. “U” and “D” refer to up and down spins, respectively. c shows the ground state (B = 0) UDD structure. The numbers 1, 2, and 3 correspond to Ho1, Ho2, and Ho3 atoms, as defined in the main text. At a small magnetic field B1, one down spin (D) of Ho1 flips, leading to the UUD structure (d). As the magnetic field increases to B2, another Ho1 down spin flips, resulting in the UUU structure (e). At the saturated field, B3, spins of all Ho3 atoms flip, producing the UUU(1) structure (f). These magnetic structures were determined in a previous study10. The green dashed lines represent the magnetic unit cell.

Full size image

Given the large single-site magnetic anisotropy energy (MAE) of the f-electrons, the low-temperature ground state has been interpreted as a \(\sqrt{3}\times \sqrt{3}\) kagome spin ice, as shown in Fig. 1c6. There are three distinct types of Ho spins: Ho1 with spins along [120], Ho2 with a positive projection along [120], and Ho3 with a negative projection along [120], as labeled in Fig. 1c.

We refer to the ground-state phase, based on the orientation of the Ho1 spins, as the up-down-down (UDD) phase. When an external field is applied along the [120] direction, the flipping of the two down-oriented Ho1 spins results in the UUD and UUU phases, as shown in Fig. 1d, e. As the magnetic field increases further, Ho2 spins flip, leading to the UUU(1) phase in Fig. 1f. These phases were identified as the 1-in-2-out or 2-in-1-out spin ice states in ref. 10, where each spin flip causes a magnetization jump, creating 1/3 magnetization plateaus.

Additionally, it has been shown6 that within the first (1/3) and the second (2/3) plateaus, time-reversal-like meta-stable ice-rule states—exhibiting identical magnetization but differing in magnetotransport properties—are stabilized, presumably due to the twisting of the Ho-kagome-net. To the best of our knowledge, the magnetic phases developed under an external field along the [100] direction have not been previously studied, despite crystallographic differences between the two cases. Furthermore, the validity of the spin-ice model with infinite MAE has never been put to quantitative tests. There has also been no microscopic explanation proposed for the coupling of these metastable states or for the appearance of the narrow (1/6) and (5/6) phases identified in ref. 10.

In this article, we investigate the impact of an in-plane magnetic field on the electronic band structure using magnetization, Hall effect measurements, and density functional theory (DFT) calculations. We find that the twisted kagome geometry leads to topologically nontrivial features such as quasi-2D bands, which have very narrow dispersion along a particular high-symmetry path in the Brillouin zone, and kagome Dirac crossings. Magnetic ordering into the ground state \(\sqrt{3}\times \sqrt{3}\) supercell state results in the folding of these bands, leading to a change in Fermi surface topology. External magnetic field-induced spin flipping that does not alter the supercell structure has little effect on the electronic structure, even with a substantial change in magnetization. However, when a spin flip transforms the supercell into the 1 × 1 structure, a significant change in Fermi surface topology occurs, causing an abrupt reversal in the Hall conductivity sign thereby regaining the quasi-2D and Dirac bands closer to the Fermi energy and with a significant spin polarization, a much-anticipated outcome of band structure manipulation by an external magnetic field. Even more intriguing, when the external magnetic field is aligned along the crystallographic a-axis, the Hall conductivity exhibits significant changes in Fermi surface topology without a corresponding change in magnetization. This anomalous behavior is attributed to magnetic field-induced frustration caused by the distortion of the perfect kagome geometry. These findings highlight the twisted kagome lattice as an important platform for exploring the interplay between magnetism and band topology.

Results

Magnetic susceptibility and resistivity

The magnetic susceptibility (χ) and longitudinal resistivity (ρ) along the three crystallographic directions [100], [120] and [001] are shown in Fig. 2. A clear antiferromagnetic transition at 11 K (TN1) is observed in χ100 and χ120, while χ001 shows a steady increase down to 1.8 K, the lowest temperature measured [Fig. 2a]. Nevertheless, TN1 is detected in the resistivity along all three directions [Fig. 2b]. Furthermore, both TN1 and TN2 are evident in the derivative of susceptibility [see the inset of Fig. 2a] and of resistivity (Supplementary Fig. 1). This is consistent with previous studies9,10,11,12,13. The in-plane resistivities both along [100] (ρ100) and [120] (ρ120) are almost identical and, in the entire temperature range, larger than the out-of-plane resistivity ρ001, suggesting an anisotropic Fermi surface14. Additionally, in the non-magnetic state, resistivity in either direction above 30 K is approximately linear in temperature, shown by the yellow lines in Fig. 2b.

Fig. 2: Physical properties characterization of HoAgGe.
figure 2

a Magnetic susceptibility measured with an external magnetic field of 0.1 T along [100], [120], and [001] directions using the field-cooled protocol. b Electrical resistivity as a function of temperature, ρ(T), measured with current applied along [100], [120], and [001] directions. The yellow lines represent linear fits to ρ(T) above 30 K. The inset on the left shows an optical image of a polished crystal, illustrating crystallographic directions within the ab-plane. The inset on the right shows a sketch of the hexagonal geometry defining the x, y, and z axes.

Full size image

Magnetization and Hall conductivity

In this study, we focus on comparing Hall conductivity with magnetization, particularly in the magnetic states below TN2. Figure 3a shows the magnetization (M, in blue), and Hall conductivity (−σzx, in red) for magnetic field (B = μ0H) ∣∣[120] at 1.8 K. Description of Hall conductivity calculations from the measured transverse and longitudinal Hall resistivities is presented in the Methods section and the corresponding data are presented in Supplementary Figs. 6 and 7. Here,  −σzx is measured with current I along [100] and Hall voltage along [001]. The magnetization curve exhibits three major jumps at the fields B1 = 0.8 T, B2 = 2.1 T, and B3 = 3.2 T, corresponding to metamagnetic transitions from ground state UDD to UUD, UUU, and UUU(1) states, forming the 1/3 plateaus, as depicted in Fig. 1c–f. Importantly, it does not fully saturate above B3 but keeps increasing at a sizable rate of approximately 0.15 μB/T, suggesting that the assumed Ising MAE is large but not dominant.

Fig. 3: Magnetization and Hall Conductivity measured with magnetic field B and current I applied along different crystallographic directions.
figure 3

Hall conductivity (red curve, plotted on the left axis) and magnetization (blue curve, plotted on the right axis) as a function of magnetic field for magnetic field B∣∣[120] and I∣∣[100] (a), B∣∣[100] and I∣∣[120] (b), and B∣∣[001] and I∣∣[120] (c). The pink colored curve in (b) is the magnetization measured on the Hall bar sample. Hall conductivity as a function of magnetic field at various temperatures for B∣∣[120] and I∣∣[100] (d), B∣∣[100] and I∣∣[120] (e), and B∣∣[100] and I∣∣[001] (f). Dashed lines and shaded regions of different colors serve as guides for the eye, indicating transitions at the magnetic fields B1,  B2, and B3 observed in the magnetization measurements. [100], [120] and [001] are defined as x, y, and z directions as illustrated in the inset of Fig. 2b.

Full size image

In addition, two smaller jumps in M appear just above B1 and B2, corresponding to 1/6 and 5/6 magnetization plateaus, also observed previously6,10. Regarding Hall conductivity,  −σzx shows a positive slope below B3, with slight changes corresponding to each of the M jumps. At B3, −σzx abruptly changes sign and drops by about 1600 S cm−1 before leveling off. Notably,  −σzx(B) is not linear like M in the saturated [UUU(1)] state. In the UUD and UUU states, the plateaus in  −σxz are clearly split, while those in M are not. This hysteretic behavior in Hall conductivity has been attributed in ref. 10 to time-reversal-like metastable toroidal spin-ice structures with opposite chirality, although the microscopic mechanism of coupling toroidicity with the magnetic field is unclear.

When the field is applied along the [100] direction, which is qualitatively different from [120] (see Fig. 3b), three main magnetization steps are again observed at B1 = 0.9 T, B2 =  2.1 T, and B3 = 2.9 T. Notably, between B = 0 and B2, the magnetization along [100], and [120] overlaps (see Supplementary Fig. 3a). However, B3∣∣[100] is ~0.6 T lower than B3∣∣[120], and the magnetization along [100] is about 0.4 μB per F.U. less than that along [120], consistent with the net x and y projection ratio in the twisted kagome geometry, \(2/\sqrt{3}\approx 1.15\). Meanwhile, the differential susceptibility dM/dT above B3 is the same for both the [100] and [120] direction. In Fig. 3b, the pink-colored curve represents the magnetization data measured on the same sample used for the Hall resistivity measurements. This was done to rule out any artifact due to the demagnetizing field, which becomes important when comparing magnetization with the Hall conductivity, particularly in the orientation discussed in the next paragraph. The data indicate that the demagnetizing effect between the larger sample used for magnetization measurements and the Hall-bar sample is ≤0.1 T at 1.8 K.

The Hall conductivity σzy presented in Fig. 3b shows a positive slope below B2, similar to that of  −σzx, and drops sharply above B2, resembling the behavior of −σzx at B3. While  −σzx continues to decrease steadily after the drop at B3, σzy shows a small kink at B3 and completes the sharp drop at 3.1 T. It then increases similarly to  −σzx after the drop at B3, up to about B ≈ 5 T, at which point it rises sharply. There is no corresponding feature in magnetization for this sharp rise in σzy (see Supplementary Fig. 4 for the derivative of magnetization), highlighting a complete decoupling between Hall conductivity and net magnetization. This behavior resembles the  −σzx plateaus in the UUD and UUU states6, but in this case, the change in σyz without any alteration in magnetization is far more pronounced, pointing to a new and significant magnetism effect on the electronic band structure without any effect on magnetization. To the best of our knowledge, such a drastic change in Hall conductivity without any change in the M response has not been reported in any other materials. As the magnetization (pink curve in Fig. 3b) and ρyz were measured on the same sample, any influence of the demagnetizing field on the 5 T upturn observed in σzy can be ruled out. Additionally, the jumps in σzy and ρzy occur precisely at the same field, further eliminating the possibility of artifacts arising during the conductivity calculations from the measured Hall and longitudinal resistivity (see Supplementary Fig. 8).

Finally, when B is applied along [001] direction, the magnetization (M) increases steadily, with a very large slope at small fields, dM/dB ≈ 1.6 μB F.U.−1 T−1. Around 3 T the slope gradually changes, reaching a similar slope to the in-plane response only near 9 T. The implications of this behavior, which are inconsistent with the spin-ice model, are presented below in the Discussion section. The Hall conductivity  −σxy maintains a positive slope across the entire field range from 0 to 9 T, with only a slight slope change near 3 T as depicted in Fig. 3c. It is worth noting that the slope magnitude of  −σzx, σzy, and  −σxy below 2 T remain fairly consistent, ranging from  ~120 to 160 S cm−1 T−1, suggesting that the apparent Hall carrier concentration remains nearly constant in these cases.

To get a deeper insight into the various features observed, particularly in  − σzx and, σzy, we analyzed their temperature dependence for different directions of I and B. Figure 3d illustrates the behavior of  −σzx as the temperature decreases from 16 K to 1.8 K. At 16 K,  −σzx exhibits an overall negative slope, indicating that electrons are the dominant carriers. Just below TN1, −σzx exhibits a slight positive slope, suggesting that holes have become the primary charge carriers, as seen in the 8 K data (extended data with additional temperatures are provided in Supplementary Fig. 5). However, at B3, −σzx drops sharply, and returns to a negative slope, similar to the behavior observed at 16 K data. This trend in  −σzx continues as the temperature decreases to 1.8 K. Above B3, the magnitude of σzx increases progressively as the temperature decreases from TN2 to 4 K. Nevertheless, a significant increase in this magnitude is observed between 4 K and 1.8 K, indicating the emergence of an additional Hall signal at 1.8 K.

The temperature dependence of σzy is depicted in Fig. 3e. After the B2 drop, the magnitude of σzy at 1.8 K does not exceed its value at 16 K, which corresponds to the non-magnetic state. Between B3 and 5 T at 1.8 K, σzy tracks the 16 K data. However, above 5 T, the 1.8  K data turns sharply, followed by a curving off. This upturn and subsequent curving off are observed on warming up to 5 K, but disappear at 6 K. These upturns and the subsequent downturns observed at 4 and 5 K do not have any corresponding features in the magnetization (see Supplementary Figs. 4 and 9) as in the case of 1.8 K-data depicted Fig. 3b. Here, the high-field downturn is not observed at 1.8 K. However, upon performing the measurement up to 14 T (measured in another sample for re-verification), we observed the downturn at 1.8 K at around 13 T (see Supplementary Fig. 10). Above 6 K, σzy shows a monotonic decrease with the magnetic field after the initial drop. Notably, σzy does not display hysteresis at 1.8 K, although significant hysteresis is observed at 4 K during the initial upturn and the subsequent downturn, centered at around 3.2 and 7 T, respectively. At 5 K, the hysteresis is observed only after the first upturn. Similar Hall conductivity behavior is observed when current and voltage directions are reversed, with the magnetic field aligned along ([100]  −σyz), as depicted in Fig. 3f. The behavior below B2 remains consistent, but above B2, the sharp slope changes in  −σyz shift slightly toward higher B.

In summary, Hall conductivity measurements reveal four notable features: (1) The Hall conductivity, which shows electron-like behavior in the non-magnetic state, shifts to hole-like behavior with magnetic ordering below B2 and B3 for magnetic fields aligned along the [100] and [120] directions, respectively. (2) At B2∣∣[100] and B3∣∣[120], there is an abrupt sign change in Hall conductivity, reverting to electron-like behavior. (3) A significant enhancement in Hall conductivity is observed immediately after the B3 sign change, particularly below 4 K, when B is applied along the [120] direction. (4) Below TN2, Hall conductivity below 5 K measured with B along [100] exhibits multiple changes after the B2 drop without any corresponding change in magnetization.

Electronic band structure calculations

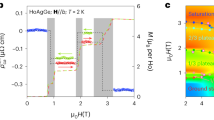
To understand the microscopic origins of these Hall conductivity features, we performed electronic band structure calculations, as depicted in Fig. 4. These calculations were conducted in three states: the non-magnetic state, the magnetic UUD state, and the UUU(1) state. As shown in Fig. 1c–e, the UDD, UUD, and UUU states share the same \(\sqrt{3}\times \sqrt{3}\) magnetic unit cell. However, in the UUU(1) state, the magnetic unit cell is reduced to 1 × 1, the same as in the non-magnetic state, but with ordered spins.

Fig. 4: Calculated electronic structure of HoAgGe.
figure 4

a Band structure in the non-magnetic state. b Electronic structure in \(\sqrt{3}\times \sqrt{3}\) magnetic state UUD. c Electronic structure in 1 × 1 [UUU(1)] stae. d Fermi surface in the UUU(1) state. In the non-magnetic state Fermi surface is very similar, with the main difference being that the orange donuts are disconnected, though they retain the electron character. The colors correspond to those in (c).

Full size image

The band structure in the non-magnetic state, shown in Fig. 4a, reveals a large electron pocket along the hexagonal first Brillouin zone boundary and two smaller hole pockets located along Γ−A. The electron pockets generate the electron-like Hall conductivity, especially for in-plane measurements. Figure 4a shows  ~150 meV above the Fermi energy, these quasi-2D bands hardly changing along MK but highly dispersive along M−Γ and K−Γ, forming a Dirac-like crossing at K.

With the onset of antiferromagnetic ordering, in the UUU state, as shown in Fig. 4b, the band structure becomes considerably more complex due to band folding from the tripled unit cell. The individual pockets, first of all, the electron donuts in Fig. 4d, reconnect, and the topology of the Fermi surface changes dramatically—even though the band’s dispersion changes only moderately. Experimental evidence of hole-like conductivity in this state suggests that the reconnection of the electron pockets makes them hole-like, which, although challenging to quantify, is reflected in the band structure. The small spikes observed in Hall conductivity at B1 and B2 correspond to spin flips at these magnetic fields. However, these spin flips do not significantly alter the magnetic unit cell, resulting in minimal changes to the sign and magnitude of the Hall conductivity. This is further supported by the overall positive slope of  −σxy in Fig. 3c where the magnetic unit cell does not change.

In the UUU(1) state, the magnetic unit cell reduces to 1 × 1, eliminating band folding and resulting in a Fermi surface similar to the non-magnetic state, shown in Fig. 4c. The magnetic ordering induces spin splitting, pushing the quasi-2D bands and Dirac-like crossings to the Fermi energy, which makes the orange donuts touch but does not change their character, restoring the electron-like Hall conductivity. Consequently, above B3, where the UUU(1) magnetic structure stabilizes, the sign of the Hall conductivity changes.

A more rigorous verification of the calculated band structure, particularly the Fermi surface, comes from the longitudinal transport. We calculated the plasma frequency in the paramagnetic state and found that \({\omega }_{pz}^{2}\approx 3.2{\omega }_{px}^{2}\). Using the basic Drude model, where \({\sigma }_{\alpha }={\omega }_{p\alpha }^{2}{\tau }_{\alpha }/4\pi\) (with τα representing the anisotropic relaxation time), we observed that the resistivity shown in Fig. 2 is almost identical for the [120] and [100] directions, as expected. Additionally, above ~30 K, it follows a perfectly linear trend, indicating that the primary scattering agents are excitations with energy ≲ 4 × 30 kB ~10 meV, too low for phonons; the best candidate for this role are, obviously, spin fluctuations. This agrees with the exchange coupling estimate from ref. 10, and our first-principles calculations are presented in detail in the Supplementary Section 1. The resistivity in this range is well described by ρx(T) = 70.6 + 0.82 T μΩ cm, ρz(T) = 30.1 + 0.25 T μΩ cm (see Fig. 2b). The ratio of the slopes is 3.28, which is in excellent agreement with DFT, confirming the accuracy of the calculated Fermi surface. Note that the ratio of the constant terms above is smaller, 2.34, indicating that scattering off defects is anisotropic, with τx about 30% smaller than τz.

Discussion

The experimentally reported magnetic structures for B∣∣[120] account for most of the observed features in the Hall conductivity −σzx, including small spikes during transitions into the UUD and UUU phases and the abrupt sign reversal in the UUU(1) phase. While these changes in the transport and magnetic properties are clearly associated with discontinuous spin reorientations, suggested in ref. 10, several qualitative effects remain unexplained /cannot be explained by the ideal spin-ice model with infinite MAE. Thus, obtaining experimental estimates of both the exchange coupling and the MAE is crucial. To this end, we analyzed magnetization data above B3 for in-plane fields and over the full range for out-of-plane fields. The details are provided in the Supplementary Section 2, where we used slopes and magnetization values in all three directions to find that the in-plane magnetic anisotropy can be described by the lowest-order term \({K}_{| | }{\cos }^{2}\phi\) (with ϕ representing the deviation from the easy axis), and K∣∣ ≈ −5.6 ± 0.6 meV, substantial compared to the exchange coupling but not overwhelmingly larger.

Interestingly, the out-of-plane anisotropy cannot be described as \({K}_{\perp }{\cos }^{2}\theta\) (θ characterizes tilting away from the plane). Instead, it requires higher order terms, such as \({K}_{\perp }^{{\prime} }{\cos }^{4}\theta\) and \({K}_{\perp }^{\prime\prime }{\cos }^{6}\theta\), as seen in similar studies on RMn6Sn6 compounds7. Moreover, the lowest-order term for out-of-plane anisotropy is anomalously soft, with K⊥ ≈ 1 meV, suggesting very strong spin-canting fluctuations. Thus, the ideal spin-ice model is insufficient, and the unexplained features seen in this and previous studies likely arise from deviations from this model.

For B∣∣[100], the magnetic structure remains unknown. However, the Hall conductivity in this configuration suggests that, similar to B∣∣[120], a change in the magnetic unit cell leads to a sign reversal of σzy. The sign change of σzy in the UUU(1) phase, where magnetization increases linearly with B, is unexpected and intriguing. We tentatively attribute it to ordering processes in the Ho1 sublattice. In the limit K ≫ MBx (K representing the in-plane anisotropy and M the Ho moment), the Ho1 spins are perpendicular to x and do not contribute to the total magnetization. In this limit, these spins do not couple either to the external field Bx or to the saturated Ho2,3 sublattices. Instead, they are coupled to each other through weak third-neighbor interaction, potentially mediated by Dzyaloshinskii-Moriya interaction (DMI) (for Ho1–Ho1 bonds, the DMI vector D∣∣z), which couples the x and y projections. Along with the finite stiffness of Ho spins with respect to canting away from the easy directions, this suggests that twisting the kagome lattice introduces a unique mechanism for coupling spins to the transport, driven by the resulting frustration. The irreversible Hall plateaus with the same magnetization, as observed in ref. 10, as well as the sign-flip of the Hall conductivity without a corresponding change in magnetization seen in our work, may also stem from deviations from the ideal Ising spin dynamics and the spin-ice rule. Our additional calculations, which will be the subject of a future publication, have, in fact, successfully reproduced all magnetization features, including the one-third jumps and the two secondary intermediate jumps, resulting in a rich and intriguing spin-ice Heisenberg model.

Here, we clarify the novelty of our findings, as ref. 11 also presents Hall resistivity measurements for B∣∣[100]. However, their data (Supplementary Fig. 5 in ref. 11) differs significantly from our results shown in Supplementary Fig. 7d. In fact, their data closely resembles our  −ρyz measured with B∣∣[120], I∣∣[001], as presented in Supplementary Fig. 11. Examining the Laue data in their Supplementary Fig. 1, it is evident that the applied magnetic field direction in their measurements is apparently [120], not [100]. Therefore, our B∣∣[100] data should not be directly compared to that in ref. 11. Furthermore, we conclude that for B∣∣[120], the abrupt sign change in Hall conductivity (or resistivity) below 6 K is due to a change in carrier concentration caused by the modification of the magnetic structure. This feature has been attributed to the topological Hall effect in ref. 11 (Fig. 4d).

Conclusion

The kagome lattice has been extensively studied for its magnetic frustration and electronic topological properties, including flat and Dirac bands. However, the role of structural twisting in this lattice has been largely overlooked. In this regard, our findings on HoAgGe open a new pathway for investigating the interaction between structural distortion, magnetic frustration, and their influence on electronic topology. This is particularly intriguing as spin-polarized quasi-2D bands and Dirac crossings/anti-crossings are in close proximity to the Fermi energy. Additionally, HoAgGe is a part of the larger RTX family of compounds15,16,17,18,19,20 (where R is a rare earth element, T is a transition metal, and X is either Ge or Si), providing the ability to tune magnetism through different combinations of R,  T, and X atoms.

Methods

Crystal growth and structural characterization

Single crystals of HoAgGe were grown by the flux method considering the eutectic point of Ag-Ge. Ho pieces (Thermo Scientific 99.9%), Ag shots (Thermo Scientific 99.999%), and Ge pieces (Thermo Scientific 99.9999%) were loaded into a 2 ml aluminum oxide crucible in a molar ratio of 1:7.6:2.5. The crucible was then sealed in a fused silica ampule under a vacuum. The sealed ampule was heated to 1175 ∘C over 10 h, kept at 1175 ∘C for 10 h, and then cooled to 825 ∘C over one week. Once the furnace reached 825 ∘C, the tube was centrifuged to separate the crystals in the crucible from the molten flux. Several well-faceted, long crystals [see the inset in Fig. 2b for an optical image of a polished crystal] up to 150 mg were obtained in the crucible. The crystal structure was verified by Rietveld refinement21 of a powder X-ray diffraction pattern collected on a pulverized single crystal using a Rigaku Miniflex diffractometer. The Rietveld refinement was performed using the FULLPROF software22 and is depicted in Supplementary Fig. 12. Selected data obtained from the Rietveld refinement are presented in Supplementary Table 2. Crystal and magnetic structures were drawn using VESTA software23. Before each measurement, every crystal was oriented along the [001], [100], and [120] directions using both an X-ray Laue diffractometer and an X-ray powder diffractometer. The powder diffractometer was used to confirm the [001], [120], and [110] Bragg peaks after the final polishing.

Magnetic property measurements

Most of the DC magnetic susceptibility and magnetization data presented in the manuscript and Supplementary Information were measured using a Quantum Design (QD) Dynacool Physical Property Measurement System (PPMS). The AC Measurement System (ACMS II) option was used for the DC magnetization measurements. The magnetization data presented in Supplementary Fig. 10 was measured using the Vibrating Sample Magnetometer(VSM) option in a QD PPMS equipped with a 14 T magnet. The magnetization measurement on the Hall bar sample, presented in Fig. 3b and Supplementary Fig. 9, was conducted using a QD Magnetic Property Measurement System -3 (MPMS-3) with a 7 T magnet. This measurement was performed after removing the electrical contacts from the sample previously used for ρzy measurements and carefully removing the epoxy used to attach the electrical contacts.

Resistivity and magnetotransport measurements

Resistivity and Hall resistance were measured using the resistivity option of a QD DynaCool PPMS, equipped with either a 9 T or 14 T magnet. All measurements were performed using the four-probe method in a Hall bar geometry. Electrical contacts were made with 25 μm platinum wires, secured using Epotek H20E silver epoxy, resulting in typical contact resistances below 30 Ω. An excitation current of 4 mA was applied for all electrical transport measurements.

The samples were polished to dimensions of  ~1.00 × 0.40 × 0.15 mm, with the long axis oriented along either the [100], [120], or [001] crystallographic direction.

The longitudinal resistivity, ρii, was calculated from the measured longitudinal resistance, Rii, using the relation: ρii = RiiA/l, where A = td is the cross-sectional area (t is the thickness, and d is the width of the sample), and l is the length of the sample between the two voltage contacts.

The Hall resistivity was calculated using the relation: ρij = Rijt, where Rij = Vi/Ij and t represent the measured Hall resistance and the sample thickness, respectively. Here, Vi is the transverse voltage developed along the i-direction in the presence of a magnetic field along k, with current Ij in the j-direction. The indices i, j, and k are mutually orthogonal, representing x, y, or z directions in different measurement geometries.

To account for the contact misalignment, the antisymmetric (Hall) and symmetric (magnetoresistance) contributions to the resistivity and Hall data, respectively, were corrected using symmetrization and antisymmetrization techniques as follows:

$${\rho }_{ii}=\frac{{\rho }_{ii}(+B)+{\rho }_{ii}(-B)}{2},{\rho }_{ij}=\frac{{\rho }_{ij}(+B)-{\rho }_{ij}(-B)}{2}.$$

The longitudinal resistivity and Hall resistivity data were acquired in a four-loop sequence: the magnetic field B was swept from +\({B}_{\max }\) to −\({B}_{\max }\), and then back from −\({B}_{\max }\) to \(+{B}_{\max }\). A similar protocol was used for M vs. B measurements. Symmetrization and antisymmetrization were applied to data obtained during B-field sweeps from \(+{B}_{\max }\) to 0 T and from \(-{B}_{\max }\) to 0 T, as well as from 0 T to \(+{B}_{\max }\) and from 0 T to \(-{B}_{\max }\).

Hall conductivity for various directions was calculated using the following relations:

$${\sigma }_{xy}=\frac{-{\rho }_{xy}}{{\rho }_{xx}^{2}},{\sigma }_{zx}=\frac{-{\rho }_{zx}}{{\rho }_{xx}{\rho }_{zz}},{\sigma }_{yz}=\frac{-{\rho }_{yz}}{{\rho }_{yy}{\rho }_{zz}},{\sigma }_{zy}=\frac{-{\rho }_{zy}}{{\rho }_{zz}{\rho }_{yy}}.$$

Here, ρxx, ρyy, and ρzz represent the longitudinal resistivities for current along the [100], [120], and [001] crystallographic directions, respectively, with the magnetic field applied perpendicularly. The Hall and longitudinal resistivity terms ρyz and ρzz, as well as ρzy and ρyy were measured using two different crystals from the same growth batch and used to calculate σyz and σzy. The terms ρxxρyy and ρyyρzz in the denominators of σxz, σyz, and σzy account for the resistivity anisotropy in the hexagonal system, as shown in Fig. 2. For σxy, ρxx = ρyy is used due to the isotropic in-plane resistivity. The conductivity relations used here are valid under the condition: ρiiρjj ≫ ρijρji.

Electronic structure calculations

Electronic structure calculations were performed using the Vienna ab initio Simulation Package (VASP)24 within the projector augmented wave (PAW) method25. The Perdew-Burke-Enzerhof (PBE)26 generalized gradient approximation was employed to describe exchange-correlation effects. For the ordered states, we added a Hubbard U correction with the fully localized limit double-counting recipe27,28, to account for the strongly correlated Ho 4f states and their localized magnetic moments. The effective parameter U−J = 8 eV was used.

It is well-known that in such cases, when f-states are far removed from the Fermi level, the main challenge in DFT is to reproduce the correct, according to the Hund’s rules, ground state, and when this condition is met, the results are very reliable7. In our case, we verified that the orbital moment on the Ho site obtained from the calculations is consistently 6 μB, which satisfies Hund’s rules and ensures that the electronic structure near the Fermi level is reliable. For the paramagnetic state, the open-core approximation is employed, where the 4f electrons in the Ho pseudopotential are treated as part of the frozen core, simulating the average effect of the disordered magnetic moments. The plasma frequencies are obtained by integration of the Fermi velocity implemented in VASP via the LOPTICS tag29.