Introduction

Ruthenium, an element, which can have oxidation states from −2 to +8, gives rise to a broad range of compounds with many interesting and unique properties1,2. Although it is a relatively scarce element, ruthenium metal and its compounds have a wide range of applications. For example, it is an excellent catalyst in a variety of organic reactions3; it is known to be the best hydrogenation catalyst for nitrogen gas4 and an oxidation catalyst in heterogeneous catalysis5 as well as electrocatalysis6. The high conductivity of ruthenium metal is also widely used in microelectronics devices7. In addition to such practical applications, ruthenium-based compounds particularly, the ruthenium-based oxides also manifest a rich set of fundamental physical phenomena, including unconventional superconductivity in Sr2RuO48, metamagnetism in Sr3Ru2O79, antiferromagnetism in both the Mott insulator Ca2RuO410 and in the strongly correlated metal Ca3Ru2O711, and paramagnetism and ferromagnetism in CaRuO3 and SrRuO3, respectively12.

Although known for many decades, the electronic and magnetic properties of the parent oxide material to these ruthenates – the simple binary oxide RuO2 – have not been extensively explored. It has mainly been used and studied for its electrochemical properties as an electrocatalyst for oxygen and hydrogen evolution13,14,15, an electrode material16, as a pH sensor, and as resistance thermometers17,18. Its high electrical conductivity, comparable to ruthenium metal, and universal pH compatibility make all of the above applications possible.

In recent times, RuO2 itself has gained renewed interest because of the observation of an additional interesting property. Although bulk RuO2 was long considered to be a Pauli paramagnet19, it was found to exhibit antiferromagnetic order up to 300 K with a small room-temperature magnetic moment of approximately 0.05 μB per ruthenium atom20. Anomalous Hall effect, which is a time-reversal symmetry-breaking magneto-electric phenomenon usually observed in ferromagnets, was also observed in RuO2 despite it being an antiferromagnet with antiparallel magnetic ordering21. This is possible because of intriguing predictions and the realization of a new magnetic phase in RuO2 called altermagnetism22. Altermagnetism is characterized by a compensated magnetic order in real space with opposite-spin sublattices connected by crystal-rotation symmetries, and by a corresponding unconventional spin-polarization order in reciprocal space that reflects the same rotation symmetries. The direct-to-reciprocal-space correspondence results in electronic band structures with broken time-reversal symmetry and an alternating momentum-dependent sign of the spin splitting22. In the broader picture, this new altermagnetic phase also allows the realization of d-wave magnetism, a long-anticipated magnetic counterpart of unconventional d-wave superconductivity23.

Although, it has been questioned whether RuO2 is an altermagnet24, interestingly, superconductivity was recently realized in RuO2. In bulk, RuO2 is known to be non-superconducting; measurements down to 300 mK specifically looked for superconductivity, but none was seen25. In contrast, it was shown that by application of epitaxial strain, superconductivity can be realized in RuO2(110) films26. This was the first report of the induction of superconductivity in any material by the application of epitaxial strain. While RuO2 films grown on TiO2(110) oriented substrates (having an in-plane tensile mismatch of  ~ + 2.2% along [1\(\bar{1}\)0] and a compressive mismatch of −4.7% along [001]) were superconducting, the films grown on TiO2(101) oriented substrates (having in-plane tensile mismatch of  ~ + 2.2% along [010] and +0.04% along [\(\bar{1}\)01]) were non-superconducting just like the bulk. The directions given hold for both the film and the substrate as the epitaxial orientation relationships involve parallel crystallographic axes for these rutile-on-rutile epitaxial films. Superconductivity in strained RuO2(110) films has since been confirmed by other groups27,28,29. It has been reported that RuO2 films grown on other crystal orientations of TiO2 and MgF2 single crystal substrates27, yttria-stabilized zirconia (YSZ)(111)30, α-Al2O3(0001)30 and α-Al2O3(1\(\overline{1}\)02)31 single-crystal substrates are non-superconducting. In this work, in contrast to these reports, we predict and realize superconductivity in RuO2 films grown on TiO2(100) substrates. Our density functional theory (DFT) calculations predict commensurately strained RuO2(100) films to be superconducting with a higher superconducting transition temperature Tc than the commensurately strained RuO2(110) films. Our transport measurements along with angle-resolved photoemission studies show that strained RuO2(100) films grown on TiO2(100) substrates are indeed superconducting in agreement with theory. In contrast to the theory predictions, their Tc is lower than the strained RuO2(110) films. To probe the origin of superconductivity in the RuO2 thin films, we performed detailed thickness-dependent transport and structural characterization plus scanning superconducting quantum interference device (SQUID) susceptometry measurements to scan the superconducting Tc locally.

Results and Discussion

DFT calculations: evolution of electronic structure under strain

In our previous work, we showed that epitaxial strain can be used to induce superconductivity in RuO2(110) films26. The reason for the appearance of superconductivity in otherwise non-superconducting bulk RuO2 is attributed to the strain-induced changes in the density of states (DOS) near the Fermi level due to modified occupancy of d-orbitals. In this report, we expand our work by studying the changes in the band structure and DOS for RuO2(100) commensurately strained to an underlying TiO2(100) substrate.

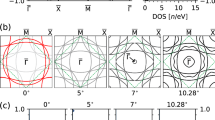
In Fig. 1a we show the DFT-computed band structure and DOS for bulk (unstrained) RuO2, RuO2(110) commensurately strained to a TiO2(110) substrate, and RuO2(100) commensurately strained to a TiO2(100) substrate. From the DOS plot on the right, it can be clearly seen that the DOS for both commensurately strained (110) and (100) RuO2 move closer to the Fermi level, indicating, similar to strained RuO2(110), that strained RuO2(100) can be superconducting too. In addition, we also did electron-phonon coupling calculations. Figure 1b shows that the Fermi surface of the commensurately strained RuO2(100) has contributions from an additional band as compared to the bulk (unstrained) RuO2. Figure 1c shows that in contrast to bulk or unstrained RuO2, both commensurately strained RuO2(110) and (100) have soft phonon modes. This softening of the phonon modes indicates the existence of strong electron-phonon coupling in both these cases. Finally, we did Migdal-Eliashberg calculations to calculate the Eliashberg spectral function α2F(ω) and the electron-phonon coupling λ. The electron-phonon coupling in strained RuO2(100) is slightly larger than strained RuO2(110), even ignoring the imaginary phonon frequencies, suggesting the superconducting temperature could be also slightly larger. Figure 1d shows the difference between the superconducting Tc calculated for commensurately strained (100) and (110) RuO2. It can be clearly seen that the predicted Tc for commensurately strained RuO2(100) is almost 1 K higher than the commensurately strained RuO2(110) case for anticipated values of μ*. Although, the estimated values of Tc are higher in both cases in comparison to our previously determined experimental values of Tc for the commensurately strained (110) case, this can be attributed to several uncontrolled approximations that enter into our Tc calculations. The electronic structure was calculated at the PBEsol level because electron-phonon calculations can only be calculated with this level of approximation with the EPW code at this time, and the electronic structure obtained with the DFT+U approximation better match the experimental results20,26 as discussed below. More importantly, with strain, a portion of the phonon spectra becomes imaginary. While softening of the phonon modes indicate enhanced electron-phonon coupling, imaginary phonon frequencies cannot be included in the calculation of the superconducting Tc. Given that the density of states increases at the Fermi level and there is a comparable and slightly stronger softening of the phonon modes, we predicted that the (100)-strained RuO2 will also become superconducting. Even though we could not accurately calculate the exact superconducting temperature because the phonon modes are imaginary and the correlations in the electronic structure are not fully incorporated, we made a comparison of the difference between the superconducting temperatures of the (110)- and (100)-strained structures considering the similar error exists in both cases. Given the difference in Tc is only about 1 K, we predicted that (100)-strained RuO2 will become superconducting under strain, with comparable or possibly slightly higher Tc than that of (110)-strained RuO2. With the understanding that the exact values of the Tc may not be accurate (Supplementary Fig. 1), here we aimed at capturing the difference in the Tc under different strain conditions. Nonetheless, the trend for superconducting Tc shows commensurately strained RuO2(100) has the potential to have higher Tc than commensurately strained RuO2(110).

Fig. 1: DFT Calculations: Strain induced changes in electronic and phonon band structure and superconducting Tc of RuO2.
figure 1

a The DFT-computed electronic band structure and DOS of bulk (unstrained) RuO2 (black solid line), RuO2(110) (blue dotted line) that is commensurately strained to TiO2(110), and RuO2(100) (red dotted line) that is commensurately strained to TiO2(100). The right panel shows that the DOS for both commensurately strained RuO2(110) and (100) moves closer to the Fermi level, in comparison to bulk. b Calculated Fermi surfaces for the bulk (unstrained) RuO2 and strained RuO2(100). An additional band contributes to the Fermi surface when strained. c Phonon band structure for bulk (unstrained) RuO2 and commensurately strained RuO2(110) and (100) films shown together with the calculated Eliashberg spectral function α2F(ω) and electron-phonon coupling λ. d Difference in the superconducting Tc between the case of commensurately strained RuO2(100) and RuO2(110) as a function of the screening Coulomb potential μ*.

Full size image

Growth and Structural characterization

Motivated by the theoretical calculations, we grew strained (100)-oriented RuO2 thin films. In bulk, RuO2 crystallizes in a tetragonal rutile structure and has lattice constants a = 4.4968 Å and c = 3.1049 Å at room temperature32. Thin films of RuO2 were grown on different surface orientations of TiO2 substrates (Crystec, GmbH) having lattice constants a = 4.5941 Å and c = 2.9589 Å at room temperature33. On TiO2(100) substrates, RuO2 has a lattice mismatch of −4.7% along [001] and +2.2% along [010] as shown in Fig. 2 a. Since, for rutile substrates, (100) is a higher energy surface than the (110) surface34, growth of thin films on this surface requires careful optimization. Reflection high-energy electron diffraction (RHEED) was used to monitor the growth of the films in situ.

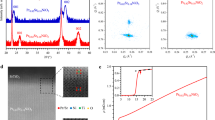
Fig. 2: Structural characterization and electrical transport measurements of epitaxially strained RuO2 thin films.
figure 2

a Schematic diagram of the crystal structure and in-plane lattice mismatch of an RuO2 thin film and the underlying TiO2(100) substrate. Gray and red spheres represent ruthenium and oxygen atoms, respectively. b AFM image (top panel) and RHEED pattern (bottom panel) with the electron beam incident along the [010] azimuth of the RuO2 film and TiO2 substrate of the 9 nm thick RuO2(100) film. c θ-2θ X-ray diffraction scan acquired with Cu-Kα radiation for the same 9 nm thick RuO2(100) film. The Bragg peak arising from the TiO2 substrate is marked with an asterisk, and the peak positions corresponding to unstrained bulk RuO2 and commensurately strained RuO2(100) film are indicated by black and green dashed lines, respectively. d Resistivity vs. temperature curves for a bulk RuO2 single crystal from ref. 25, 18.6 nm thick RuO2(101) film from ref. 26, 24.2 nm thick RuO2(110) film from ref. 26, and a 42 nm thick RuO2(100) film. e Resistance vs. temperature curves of RuO2(100) films with different film thicknesses, normalized to their values at 4 K. The inset shows the value of the superconducting Tc (purple spheres) as a function of the film thickness (t). The non-superconducting films are presented with green spheres. f Resistivity vs. temperature curves acquired at different applied out-of-plane magnetic field for the 42 nm thick RuO2(100) sample. g Upper critical magnetic field Hc⊥ vs. superconducting Tcs extracted from measurements in f. The superconducting Tcs are defined as the temperatures at which the resistance crosses 50% of the normal-state resistance at 4 K.

Full size image

To achieve epitaxial RuO2 films on TiO2(100) substrates, we scanned a growth temperature range from 300 °C to 450 °C keeping the ozone pressure and ruthenium flux constant. The atomic force microscopy (AFM) images for the samples grown at different temperatures are shown in the Supplementary Fig. 2. It was found that 350 °C is the best growth temperature for the films. A ruthenium flux of  ~ 2.0 × 1013 atoms cm−2 s−1 giving a growth rate of RuO2 film of  ~0.063 Å s−1 was used for all the growths. The AFM and the RHEED image of the 9 nm thick sample grown at 350 °C is shown in Fig. 2b. From the flattened line profile along the green arrow on the AFM image, steps of  ~0.25 nm height can be observed on the surface. The root-mean-square (rms) roughness for this film measured across a 1 μm2 area was  ~151 pm.

A θ-2θ x-ray diffraction (XRD) scan of the 9 nm thick RuO2 film is shown in Fig. 2 c. The black dotted line on the plot corresponds to the 200 peak position of bulk (unstrained) RuO2. We calculated the out-of-plane lattice constant that would be expected for a RuO2 film commensurately strained to the TiO2(100) substrate using elasticity theory. Knowing the elastic stiffness tensor coefficients of RuO235, the out-of-plane lattice spacing a⊥ can be calculated from the out-of-plane strain, ϵ11 = (a⊥-\({a}_{Ru{O}_{2}}\))/\({a}_{Ru{O}_{2}}\) by expanding the tensor equation (in Einstein notation): σij = cijkl ϵkl for σ11 and recognizing σ11 = 0, as the film is free of stress in the out-of-plane direction. This gives us:

$${a}_{\perp }={a}_{Ru{O}_{2}}-\frac{{a}_{Ru{O}_{2}}\left[{c}_{12}\left(\frac{{b}_{Ti{O}_{2}}-{b}_{Ru{O}_{2}}}{{b}_{Ru{O}_{2}}}\right)+{c}_{13}\left(\frac{{c}_{Ti{O}_{2}}-{c}_{Ru{O}_{2}}}{{c}_{Ru{O}_{2}}}\right)\right],}{{c}_{11}}$$
(1)

where, c11, c12, and c13 are elastic stiffness tensor coefficients of RuO2 in Voigt notation35 and \({b}_{Ti{O}_{2}}\) (\({b}_{Ru{O}_{2}}\)), and \({c}_{Ti{O}_{2}}\) (\({c}_{Ru{O}_{2}}\)) are the lattice constants of TiO2 (RuO2) along the b and c-axis, respectively. The calculated out-of-plane lattice spacing expected for a commensurately strained RuO2 film on a TiO2(100) substrate is 4.557 Å. The green dotted vertical line in Fig. 2c shows the 2θ value corresponding to this lattice spacing for a commensurately strained film.

To gain a better understanding of the role of epitaxial strain on the superconductivity of RuO2 films, we grew films of thickness varying from 3 nm to 64 nm. Their θ-2θ XRD scans and the rocking curve scans are shown in Supplementary Fig. 3. Supplementary Table 1 gives the growth conditions and the FWHM of the rocking curve of these films. The reciprocal space maps of the films as a function of their thickness are presented in the Supplementary Figs. 4 and 5. Supplementary Table 2 shows the lattice parameters calculated for the RuO2(100) films of different thickness along the three crystallographic directions. The table also includes the longitudinal strain (ϵii) derived from the lattice parameters measured by synchrotron diffraction along the three axes.

From the measured lattice constants, it is evident that the strain along in-plane [010] or b-axis remains commensurate (within experimental error) for all thicknesses investigated. The film is found to relax with increasing thickness, as expected, along the higher strain in-plane [001] direction. The out-of-plane a-axis is the stress-free direction and its length changes as the strain along the c-axis is relaxed with film thickness. As a check to whether the measured out-of-plane a-axis (a⊥) is consistent with the films being commensurately strained along the in-plane [010] direction for all of the film thicknesses studied, we apply linear elasticity theory. The a⊥ expected when RuO2 is strained along the c-axis by the amount indicated in Supplementary Table 2 and commensurately strained (ϵ22 = 2.2%) along the b-axis to the TiO2 substrate is described by Eq. (1) with \({b}_{Ti{O}_{2}}\,\to \,{b}_{Ru{O}_{2}}\) (measured) and \({c}_{Ti{O}_{2}}\,\to \,{c}_{Ru{O}_{2}}\) (measured), so that the measured strains, rather than commensurate strain, are imposed on the RuO2. As shown in Supplementary Fig. 6, the calculated values of a⊥ are in good agreement with the measured values of a⊥ as a function of film thickness.

Electrical and Magneto-transport measurements

Figure 2d shows that as predicted by our theory calculations, both RuO2(110) as well as RuO2(100) films are superconducting. Nonetheless, the superconducting transition temperature for the (100) films (~1.0 ± 0.1 K) is less than that of the (110) films (~2.0 ± 0.1 K) in contrast to our theoretical calculations26. Fig. 1e shows the thickness dependence of superconductivity for RuO2(100) films. It can be seen that similar to what we observed for the (110) RuO2 films, in this case too both our very thin and very thick RuO2(100) films do not superconduct, and there is a region of optimum thickness in which RuO2(100) films superconduct. As discussed in our previous work26, the reason for this observed effect can be attributed to the competition between an intrinsic strain-induced enhancement of Tc that should be maximum for thinner, commensurately strained RuO2 films, versus the disorder-induced suppression of Tc that becomes more pronounced in the ultrathin limit. While the thinnest films experience the largest substrate-imposed strains, as shown in Supplementary Table 2, stronger disorder scattering from interfacial defects reduces Tc below our detection limit. The samples with intermediate thickness, which are partially strained, exhibit superconductivity and have higher Tcs. The fully relaxed films of higher thickness do not host superconductivity.

Figure 2f shows the resistivity vs. temperature curves of a 42 nm thick film acquired for different values of out-of-plane applied magnetic field. Figure 2g shows a plot of the upper critical magnetic field vs. superconducting temperature calculated from Fig. 2f. The upper critical magnetic field and the coherence length calculated for the 42 nm thick RuO2(100) sample is  ~0.4 T and 28.7 nm, respectively. The upper critical magnetic field for the (110) films is roughly two times that of the (100) films, which is expected due to the higher Tc of the (110) films.

We emphasize that the thickness range of the superconducting films observed for the case of (100) films is more broad (inset of Fig. 2e) than the case for (110) films. In the (110) films, superconductivity is observed for films of thickness only up to 25 nm, (ref. 26) whereas (100) films with thickness as high as 46 nm superconduct. This altered behavior can be due to differences in operative strain relaxation mechanisms revealed by the film microstructure.

Although, both (110) and (100) RuO2 have identical lattice mismatch to TiO2, the film microstructure is very different in the two cases. Whereas thick RuO2(110) films had cracks extending from the top of the film to the substrate26 extinguishing the percolative path for current flow and precluding reliable measurements of superconductivity by our 4-point transport method over cm-scale distances, the RuO2(100) films studied here are continuous and uncracked but host other defects driving partial strain relaxation along the [001] direction. Figure 3 shows cross-sectional scanning transmission electron microscopy (STEM) images of the 42 nm thick RuO2(100) film, acquired along the [010] and [001] zone axes. A strain-sensitive large field of view low-angle annular dark-field (LAADF) STEM image on the [010] zone axis shows sharp, highly oriented diagonal defects extending from the interface to the surface of the film, as well as more localized signatures of misfit dislocations (Fig. 3a), both of which are absent from the LAADF image on the [001] zone (Fig. 3c). An atomic-resolution high-angle annular dark-field (HAADF) STEM image on the [010] zone in Fig. 3b shows the presence of diagonal defects. These diagonal defects are comprised of misoriented domains that are a few nanometers wide formed on the (101) and \((10\overline{1})\) planes of the surrounding pristine rutile structure, while the misfit dislocations visible along the film-substrate interface have Burgers vectors pointing in-plane along the [001] direction. These defects explain the partial relaxation of the c-axis observed in X-ray diffraction (Supplementary Fig. 4), while in comparison both the misfit dislocations and extended defects are absent from the HAADF-STEM image on the [001] zone axis (Fig. 3d), consistent with the X-ray diffraction finding that the film is fully strained (within experimental error) along the b-axis. Patchy contrast suggestive of defects along the projection direction and triangular features on the film surface were observed along the [001] zone axis in all RuO2(100) films imaged (Fig. 3c). Here, the surface corrugations replace the higher energy (100) rutile surface34 with termination on lower energy rutile (110) facets. An in-plane lattice constant analysis for three samples –11 nm, 42 nm and 64 nm thick RuO2(100) films, done using HAADF-STEM images is shown in Supplementary Fig. 7 and discussed in Supplementary Note 1.

Fig. 3: STEM structural characterization of 42 nm thick superconducting RuO2(100) film.
figure 3

Large field of view LAADF (a) and atomic resolution HAADF (b) STEM images of the 42 nm thick RuO2(100) sample viewed along the [010] zone axis reveal sharp defects extending from the interface to the film surface as well as misfit dislocations near the film-substrate interface. LAADF (c) and HAADF (d) images of the same film viewed along the [001] zone axis show the absence of these defects in this projection and the presence of a surface corrugation.

Full size image

Angle-resolved photoemission spectroscopy measurements

To further investigate the origin of superconductivity in the RuO2(100) case and explore the role of strain, we performed angle-resolved photoemission spectroscopy (ARPES) measurements on the RuO2(100) films. Figure 4a shows the schematic of the Brillouin zone of RuO2. A Fermi surface map of kx-ky plane at kz = 0.7 π/a (shaded region) of the 30 nm thick RuO2(100) film is shown in Fig. 4b. Figures 4c and d show the band structures and DFT + U calculations (red solid lines) along kx direction ([010]) near the zone center (ky = 0) and zone boundary (ky = π/c), respectively. The dispersive dxz, dyz-derived bands are observed near the zone center, while the flat d∥ bands are observed near the zone boundary. Along the non-high symmetry direction, a dispersive dxz/dyz band, crossing the Fermi energy is observed at ky = 0.51 π/c in Fig. 4g. DFT calculations were performed with the PBEsol+U level of the theory with a Hubbard U = 2 eV and with spin-orbit-coupling, which reproduce the dispersion well and overlap with ARPES measurements in Figs. 4c, d, and g. A comparison of electronic bands calculated by DFT for different values of U parameter is shown in Supplementary Fig. 8 and their comparison with ARPES spectra is shown in Supplementary Fig. 9. To evaluate the evolution of DOS driven by strain, in Fig. 4e, we compare the DOS of d∥ bands for RuO2(100) films of two different thicknesses – 10 nm and 60 nm. To get an estimate of the DOS for these samples, we plot the energy distribution curves of the photoemission intensity averaged over the entire region of k-space probed experimentally. It can be seen that the DOS shifts closer to the Fermi level for the more highly strained 10 nm thick film, which demonstrates that in this case too, the epitaxial strains imposed by TiO2(100) substrates shifts d∥ states towards EF and thereby increase the DOS near Fermi energy. Nonetheless, the observation of no superconductivity in very thin and highly strained films can be attributed to the disorder-induced suppression of superconductivity which becomes prominent in the ultrathin limit. As shown in Figs. 4f–h, the bands are sharp for the thicker films (30 nm and 60 nm) but broadened in the 10 nm film. The reduced particle lifetime in the highly strained 10 nm film indicates the enhanced scattering rate due to the disorder or defects. Supplementary Fig. 10 shows the comparison of the DOS of RuO2(100) with RuO2(110). It can be seen that the DOS shift is more for the strained RuO2(110) than the strained RuO2(100) film, which aligns with the observation of a higher superconducting transition temperature in the strained RuO2(110) films. Supplementary Fig. 11 shows the comparison of the DOS for unstrained (bulk) RuO2, a commensurately strained RuO2(100) film, and RuO2 subjected to the measured strain of the 28 nm RuO2(100) film calculated with the PBEsol functional. From the figure, it is clearly observed that upon applying strain, the DOS at the Fermi level, increases with the shift of peaks towards EF.

Fig. 4: ARPES measurements: Electronic structure of epitaxially strained RuO2 (100) films.
figure 4

a Schematic of Brillouin zone of RuO2. Shaded region corresponds to the measured momentum plane at kz = 0.7 π/a using He-Iα photons (21.2eV). b Fermi surface measured by ARPES for 30 nm thick RuO2(100) film. Energy vs. momentum spectra along c cut 1 and d cut 2 as shown in a for 30 nm thick RuO2(100) film showing the dispersive dxz/dyz and d∥ bands, respectively. The DFT+U calculations with spin-orbit coupling included, overlap on the ARPES spectra (solid red lines). e The energy distribution curves of photoemission intensity averaged over the entire region of k-space. Energy vs. momentum spectra at ky = 0.51 π/c along the kx direction cut 3 for f 10 nm, g 30 nm, and h 60 nm thick RuO2 films.

Full size image

Scanning SQUID Susceptometry

Understanding the local superfluid response is crucial for elucidating the superconducting state, particularly in contexts such as superconducting thin films sensitive to epitaxial strain36, superconductors under applied strain37,38, or multiphase superconductors38,39. To microscopically characterize the uniformity of Tc in the 42 nm thick RuO2(100) thin film, we measured the local susceptibility over an area of 120 × 140μm2 from 0.5 K to 1.2 K (Fig. 5a–d). At 1.1 K, the magnetic susceptibility across the scan area is approximately zero within a range of  ± 0.1Φ0/A. Below 1.0 K, the whole area shows diamagnetic (negative) susceptibility, and the local susceptibility monotonically decreases as temperature decreases, suggesting the Meissner screening effect.

Fig. 5: Scanning SQUID susceptometry on 42 nm thick RuO2(100) film indicates local Tc microscopically varying within 100 mK.
figure 5

a–d Temperature-dependent susceptibility χ(T) images on RuO2. The temperature labels represent the average temperatures during the scanning process. e χ(T) at P1, P2, and P3 denoted in a. f Local Tc is defined as fitted χ(Tc) = − 0.2Φ0/A (dashed line in e). g Local Tc at the cross-section taken along the dashed line in f.

Full size image

We note that in Fig. 5a, the halo-like feature, which indicates weaker diamagnetic susceptibility, is commonly observed in a smaller area than the scale of the scanning SQUID’s field coil. In this area, the penetration depth is significantly longer than in other areas40. The center of the halo was accidentally subjected to strong pressure from the tip of the SQUID chip, which might have created a localized lattice distortion. The size and structure of the halo look similar to the field coil, the outer diameter of which is 7 μm. We also note that the step features in susceptibility at low temperatures, denoted by the arrow labeled ‘scan noise’ in Fig. 5a, are the systematic noise, which depends on the voltages of x and y piezoelectric benders but not on the location. The local Tc map shows the effect of the scan noise, but the noise in Tc is negligible compared to other features.

To obtain the local Tc, we fit the temperature-dependent susceptibility at each location (Fig. 5e). Here, we define the local Tc that satisfies χ(Tc) = −0.2Φ0/A. We used simultaneous temperature and susceptibility measurements for fitting rather than the averaged temperature. Over a 100 μm scale, the local Tc obtained varies from 0.9 K to 1.0 K (Fig. 5f and g), a factor that might account for the observed broadening of the temperature range over which the electrical resistance transitions to zero near Tc (see Fig. 2e). We should ignore the small Tc area near the point-like defect, which is not real. The minimum temperature difference between susceptibility images is 0.05 K, smaller than the local Tc variation. Therefore, our results suggest that the local Tc of the 42 nm thick RuO2 film is microscopically inhomogeneous over a range of 100 mK.

Conclusions

In summary, we show that epitaxially strained RuO2(100) films grown on TiO2(100) single-crystal substrates host superconductivity similar to the previously studied strained RuO2(110) films26. Our theoretical DFT calculations predict the possible realization of superconductivity in the strained RuO2(100) case, but our transport and microscopy measurements reveal that the calculation of the predicted Tc is overestimated. This might be due to the appearance of imaginary phonon modes, which are ignored in the Migdal-Eliashberg calculations for Tc. For accurate prediction of the superconducting transition temperature, these phonon modes should be considered. These imaginary modes could be artifacts of DFT or the signature of some structural changes that are beyond the scope of this work. The latter would be of interest for the subject of a detailed follow-up study. The addition of strain-induced superconductivity in both (110) and (100)-oriented RuO2 films to possible high-temperature altermagnetism reveals that rutile oxides are an exotic and enticing playground for exploration where epitaxial strain can be an empowering tuning knob to alter the stability of competing phases and liberate hidden ground states.

Methods

DFT Calculations

First-principles electronic structure and phonon calculations were performed using the Quantum ESPRESSO software package41,42. The generalized gradient approximation as implemented in the PBEsol functional43 was employed as the exchange-correlation functional with norm-conserving pseudopotentials and plane-wave basis sets, using a kinetic energy cutoff of 160 Ry, an electronic momentum k-point mesh of 16 × 16 × 24, Methfessel-Paxton smearing of 20 meV for the occupation of the electronic states, and a tolerance of 10−10 eV for the total energy convergence. The bulk lattice parameters of RuO2 calculated with the PBEsol functional are a = 4.464 Å, and c = 3.093 Å. The strained RuO2(100) structure is calculated by changing the lattice constants of this bulk crystal by  + 2.2% along [010] and  − 4.7% along the [001]-axis while relaxing the structure along the [100]-axis. Electron-phonon coupling calculations were performed using the EPW code44, using the Wannier interpolation, with an interpolating electron-momentum mesh of 8 × 8 × 12, a phonon-momentum mesh of 2 × 2 × 3, an interpolated electron-momentum mesh of 32 × 32 × 48, and a phonon-momentum mesh of 8 × 8 × 12. The isotropic Eliashberg spectral function α2F(ω) and total electron-phonon coupling constant λ were calculated with a phonon smearing of 0.2 meV. The superconducting transition temperature is then estimated using the semi-empirical McMillan-Allen-Dynes formalism45,46.

Thin film growth and characterization

Strained (100)-oriented RuO2 thin films were grown using a Veeco GEN10 molecular-beam epitaxy (MBE) system. A molecular beam of ruthenium, 99.99% pure ruthenium metal (ESPI Metals), was generated using an electron beam evaporator. A background pressure of 1 × 10−6 torr of distilled ozone (~80% O3 + 20% O2) was used as the oxidant, and a thermocouple behind and not in contact with the back of the substrate was used to measure the substrate temperature. In situ RHEED patterns were recorded using KSA-400 software and a Staib electron source operated at 13 kV and a filament current of 1.52 A. X-ray diffraction, x-ray reflectometry, and preliminary reciprocal space mapping measurements were carried out using a PANalytical Empyrean diffractometer with Cu Kα1 radiation. The morphology of the film surface was characterized using an Asylum Cypher ES environmental AFM.

To determine the relaxation of epitaxial strain as a function of film thickness, reciprocal space mapping was performed using hard X-ray diffraction at the QM2 beam line of the Cornell High Energy Synchrotron Source (CHESS). The samples were mounted on a four-circle Huber diffractometer in reflection geometry with the sample normal oriented along the ϕ-axis. With goniometer tilts of omega = 3 and chi = 88, diffraction images were collected on a Pilatus 6M detector using 15 keV incident X-rays while continuously rotating ϕ through 360 degrees in 0.1 degree steps with a 0.1 second counting time per image. All data were collected at room temperature. Polarization and Lorentz factor corrections were applied to the raw images, which were transformed to a 3D reciprocal space map. From the 3D reciprocal space volume, 2D RSMs were extracted to show the film and substrate Bragg peaks in certain representative planes. Gaps between detector panels result in small sections of missing data in the RSM.

Electrical and magneto-transport measurements

The electrical and magneto-transport measurements were done using Quantum Design Physical Property Measurement System (PPMS) equipped with a 3He insert to measure electrical transport as a function of temperature from 300 K down to 0.4 K. The electrical contacts were made by West-Bond wire bonder in a four-point linear geometry.

STEM measurements

STEM measurements were taken on cross-sectional lamellae prepared via focused ion beam (FIB) lift-out with a Thermo Fisher Helios G4 UX FIB. STEM imaging was performed on a FEI/Thermo Fisher TitanThemis 300 CryoS/TEM operating at 300 kV with a 30 mrad probe convergence semi-angle. The same FIB sample preparation and STEM imaging parameters were used for both the [010] and [001] zone axis experiments, which were performed on the same days. The atomic resolution HAADF datasets were acquired by taking a series of 20 rapid-frame images (1.5 sec. per frame) and rigidly registering them with a method optimized to prevent lattice hops47 to recover high signal-to-noise ratio and high fidelity atomic resolution images. Inter-planar spacing measurements were performed using the technique developed by Smeaton et al.48.

Electronic band structure measurements by ARPES

Our ARPES system consists of a ScientaOmicron R8000 electron analyzer and a Fermi Instruments BL1010s Helium plasma discharge lamp with a monochromator. The ARPES system and MBE system are connected via a transfer chamber with a base pressure of 2 × 10−10 Torr, allowing in situ sample transfer. The in-suit ARPES measurements were performed using He Iα (hν = 21.2 eV) photons at 15 K with a base pressure of 4 × 10−11 Torr. The value of kz was determined by comparing the observed band structures with the DFT + U calculations.

Scanning SQUID Susceptometry

We used SQUID susceptometry to image the magnetic susceptibility of RuO2 films on a micron-scale. Our scanning SQUID susceptometer has two pairs of concentric pickup loops in the SQUID circuit and a field coil configured with a gradiometric structure, canceling non-local background fields and applied fields from the field coils through the SQUID circuit49. The dominant factors in determining the spatial resolution are the effective area of the pickup loop and the scan height, which is the distance between the center of the pickup loop and the sample surface. The inner diameter of the pickup loop is 2 μm, and the scan height is  ~2.5 μm. The pickup loop detects the ac magnetic flux Φac in units of the flux quantum Φ0 in response to the ac magnetic field, which is produced by a current of ∣Iac∣ = 0.2 mA at 877 Hz through the field coil, using an SR830 Lock-in-Amplifier. Here we report the local ac susceptibility χ = Φac/∣Iac∣ in units of Φ0/A.