Rich unconventional Hall effects in a single quasi-kagome Kondo Weyl semimetal candidate Ce₃TiSb₅

Abstract

It is generally believed that electronic correlation, geometric frustration, and topology, individually, can facilitate the emergence of various intriguing properties that have attracted a broad audience for both fundamental research and potential applications. Here, we report a series of unconventional Hall effects observed in a single compound—quasi-kagome Kondo Weyl semimetal candidate Ce₃TiSb₅. In the paramagnetic phase, signature of dynamic c-f hybridization is revealed by a reduction of anomalous Hall effect and is connected to frustration-promoted incoherent Kondo scattering. A large topological Hall effect exceeding 0.2 μΩ ⋅ cm is found at low temperatures, which should be ascribed to the non-collinear magnetic texture. In addition, a peculiar loop-shaped Hall effect with switching chirality is also seen, which is inferred to be associated with magnetic domain walls that pin history-dependent spin chirality and/or Fermi-arc surface states projected from the in-gap Weyl nodes. These exotic results place Ce₃TiSb₅ in a regime of highly-frustrated antiferromagnetic dense Kondo lattice with a nontrivial topology on an “extended” global phase diagram, and highlight the interplay among electronic correlation, geometric frustration and topology.

Introduction

Hall effect, named after Edwin Hall, is a transverse electromagnetic response that occurs when a magnetic field (μ₀H, referred to as H henceforth) is perpendicular to the current. Soon after the discovery of ordinary (or normal) Hall effect (OHE)¹, a more overwhelming Hall signal was observed in magnetic conductors, known as anomalous Hall effect (AHE)². Unlike OHE, which is a consequence of Lorentz-force bending of charge-carrier trajectory induced by an external field, the transverse velocity achieved in AHE can be of multiple origins³, from either extrinsic effect due to skew scattering^4,5 or side jump⁶, or intrinsic effect due to spin-orbit coupling (SOC) induced Berry curvature in filled bands (momentum space)^7,8,9,10. In spite of various mechanisms, a common feature of AHE is that the Hall resistivity ${\rho }_{yx}^{A}(H,T)$ is proportional to the magnetization M(H, T). Of particular interest is that a Berry curvature can also be generated in real space when charge carriers travel across landscapes of non-coplanar or non-collinear spin textures with finite scalar spin chirality, leading to an alternative electromagnetic response—Topological Hall effect (THE)^11,12. These unconventional Hall effects are attractive for both fundamental research and potential applications in advanced electronic and spintronic devices.

Heavy-fermion materials are prototypical strongly correlated systems whose electronic ground states are usually determined by the competition between RKKY (Ruderman-Kittel-Kasuya-Yosida) exchange and Kondo effect¹³: while the RKKY exchange tends to stabilize a long-range magnetic order, the counterpart Kondo effect is to screen the local moments to form a nonmagnetic Fermi liquid. The rich physical properties of heavy-fermion compounds make them an ideal material basis where singular phenomena can be found—e.g., unconventional superconductivity, quantum critical point (QCP), strange metal, etc^14,15,16. Here we report a series of unconventional Hall effects in Ce₃TiSb₅, a candidate of geometrically frustrated Kondo Weyl semimetal with a distorted-kagome structure. The main findings of our work are: (1) In the paramagnetic state well above the Kondo scales, the observed AHE can not be described by a regular incoherent skew scattering (or side jump, either) predicted for most Kondo lattice systems^{17,18,19,20,21,22}; (2) In the magnetically ordered state, on top of the THE that is commonly seen in spin-textured systems, abnormal loop-shaped Hall effect (LHE) with switching chirality is also seen; (3) First-principles calculations suggest Ce₃TiSb₅ as a candidate of magnetic Weyl semimetal. These peculiar results suggest an extended global phase diagram for heavy-fermion systems and thus invoke further consideration about the mechanism of unconventional Hall effects in systems where topology, electronic correlation and geometric frustration meet [Fig. 1a].

Fig. 1: Crystalline structure, magnetic structure and sample characterization of Ce₃TiSb₅.

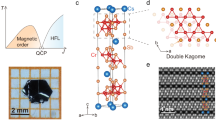
a A cartoon illustration of the interplay among electronic correlation, geometric frustration and topology in Kondo lattices, which can lead to unconventional Hall effects as exemplified by Ce₃TiSb₅. “Correlation” panel: composite heavy quasiparticles in Kondo lattices arising from quantum entanglement of f (red) and itinerant conduction (blue) electrons; “Frustration” panel: kagome structure; “Topology” panel: a pair of Weyl nodes with opposite chiralities. b Left, crystalline structure of Ce₃TiSb₅. Red and blue lines indicate Ce networks on z = 0.25 and 0.75 planes, respectively, as seen also in Fig. 5c. Middle, magnetic structure with wave vector k₁ = [0, 1/2, 1/8] for T_N2 < T < T_N1. Only the Ce sublattice is shown for clarity. Right, magnetic structure with wave vector k₂ = [0, 0, 1/8] for T < T_N2²³. c Temperature dependence of magnetic susceptibility for H∥[1000] (red), $[10\bar{1}0]$ (green) and [0001] (blue). Inset, d(Tχ)/dT plots that exhibit both T_N1 and T_N2. d Field-dependent magnetization at 2K. M(H) for H∥[1000] shows multiple steps hinting field-induced metamagnetic transition. M_1/3 and M_2/3 plateaus are visible for ${{\bf{H}}}\parallel [10\bar{1}0]$. M is nearly linear with H for [0001]. e Electrical resistivity as a function of T, measured with electrical current flowing along [1000] (red) and [0001] (blue), respectively. Onset of incoherent Kondo scattering (${T}_{K}^{on}$) is signified by the minimum of ρ(T). The inset displays a zoom-in plot for the low-temperature region. A tiny trace of superconductivity is visible due to Sn-flux impurity, and can be suppressed by a small field 0.1 T. Kondo coherence (T_coh) established below  ~10 K for both orientations.

Results and discussion

Sample characterization

Ce₃TiSb₅ crystallizes in the anti-Hf₅CuSn₃-type hexagonal structure with space group P6₃/mcm (No. 193, centrosymmetric). The crystalline structure is shown in Fig. 1b. All the Ce atoms reside on the z = 0.25 and 0.75 planes, and in each plane, the nearest neighbors form equilateral triangles, which then build up a 2D network of distorted kagome structure. More details about the chemical composition and crystalline structure are provided in Supplementary Information (SI).

The sample quality of Ce₃TiSb₅ crystals was characterized by magnetic susceptibility (χ) and resistivity (ρ), as shown in Fig. 1c–e. Above  ~100 K, χ_i(T) (i = ab, c) conforms to Curie-Weiss behavior with the fitted effective moment μ_eff = 2.6(1)μ_B, very close to that of a free Ce³⁺ ion, 2.54 μ_B. This demonstrates that the 4f electrons in Ce₃TiSb₅ are highly localized. According to an earlier neutron-scattering work, a commensurate antiferromagnetic (AFM) order with wave vector k₁ = [0, 1/2, 1/8] appears below T_N1 ≈ 5.1 K; further cooled down, a second related AFM order (T_N2~3 K) with k₂ = [0, 0, 1/8] slowly develops with time in the presence of the k₁ phase, and the coexistence of k₁ and k₂ phases persists even for well below T_N1²³. The two proposed magnetic structures are displayed in Fig. 1b. In our magnetic susceptibility measurements, the AFM transition at T_N1 is clearly seen in χ(T), whereas the feature at T_N2 is tiny and can be visible only in the derivative [inset to Fig. 1c]. The anisotropic χ(T) profiles also manifest ab plane as the easy plane, consistent with neutron results and can be well understood by the crystal electric field (CEF) effect²⁴. Field-dependent magnetization for H∥[1000] at 2 K displays multiple metamagnetic transitions, manifested by the discontinuous jumps as shown in Fig. 1d. When the field is along $[10\bar{1}0]$, M_1/3 and M_2/3 plateaus are observable, reminiscent of the kagome spin ice state (2-in-1-out or 1-in-2-out) in HoAgGe²⁵. Such metamagnetic transitions likely are consequences of the competition among magnetic exchange, Zeeman energy and geometric frustration. The magnetization for H∥[0001] is much smaller, and is essentially linear with field, reaffirming c as the hard axis. It should be pointed out that since the local centrosymmetry is broken at Ce (m2m) sites in Ce₃TiSb₅, Dzyaloshinskii–Moriya interaction that arises from non-centrosymmetric SOC would also favor ab as the magnetic easy plane.

Temperature dependence of resistivities is shown in Fig. 1e. For both I∥[1000] and [0001], the ρ(T) curves exhibit clear humps ~100 K, characteristic of scatterings by excitation between CEF levels. A local minimum can be seen at ${T}_{K}^{on} \sim 30$ K, the signature for the onset of incoherent Kondo scattering; and this is followed by a pronounced maximum in ρ near T_coh~10 K below which coherent Kondo liquid comes into being. Previous specific heat measurements revealed an enhanced Sommerfeld coefficient ~600 mJ/mol ⋅ K² (compared to 9.0 mJ/mol ⋅ K² for La₃TiSb₅), confirming a substantial electronic correlation effect. The single-ion Kondo scale was estimated T_K ~ 8 K according to the magnetic entropy²⁴. Altogether, Ce₃TiSb₅ appears as a frustrated AFM Kondo lattice with moderate electronic correlation. Noteworthy that a tiny trace of superconductivity is visible in ρ(T) around 3.5 K, which should be attributed to a small amount of Sn-flux impurity²⁴.

AHE in the paramagnetic phase

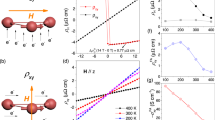
Figure 2a displays the field dependence of Hall resistivity ρ_yx at various temperatures. In these Hall effect measurements, the electrical current flows within the ab plane, and the magnetic field was applied along [0001], the magnetic hard axis [cf. the inset to Fig. 2a]. For all the temperatures measured between 2 K and 300 K, the Hall signal is negative. In the paramagnetic phase (T ≥ 7 K), ρ_yx is essentially linear with H. (Linear ρ_yx(H) was also observed in La₃TiSb₅; all these indicate that the multiband effect is not significant in the ordinary Hall effect for (La,Ce)₃TiSb₅.) At first glance, Hall coefficients can be extracted straightforwardly from the slope of ρ_yx(H), as shown in Fig. 2b. However, we notice that the obtained ρ_yx/H exhibits a significant temperature dependence, rather unusual for a conventional metal. In particular, ρ_yx/H appears inversely proportional to T above 30 K (i.e., Curie–Weiss-like), below which the magnitude of ρ_yx/H falls back. The temperature where ∣ρ_yx/H∣ maximizes coincides with ${T}_{K}^{on}$ observed in ρ(T) [seeing Fig. 1c]. This implies that the asymmetric scattering by magnetic ions is dominant here even in the paramagnetic phase. A conventional expression of Hall resistivity in magnetic conductors consists of two items, ρ_yx = R_HH + R_AM(H), where R_H is the normal Hall coefficient, and the second term is due to AHE. (Note that Ce₃TiSb₅ is a multi-band system; we here avoid relating R_H directly to the carrier density as in single-band cases.) Earlier studies on AHE have revealed that the form of R_A is typically in the form of Aρ^β, where A is a prefactor, and the exponent β depends on specific mechanisms³: β ≈ 1 for skew scattering, and β ≈ 2 for intrinsic and side-jump scattering. We, therefore, describe ρ_yx/H as follows,

$${\rho }_{yx}/H={R}_{H}+A{\rho }^{\beta }{\chi }_{c},$$

(1)

and this is better expressed in a plot of ρ_yx/H vs. ρ^βχ_c with T as an implicit parameter, as shown in the inset to Fig. 2b. We find that only β ≈ 0 fits the data satisfactorily well for $T\ge {T}_{K}^{on}$ [dash line in the inset to Fig. 2b], while both β = 1 and 2 fail in the fitting (Supplementary Fig. 3 in SI). The extrapolation of this fitting to the χ_c → 0 limit results in the normal Hall coefficient of Ce₃TiSb₅, R_H = + 0.6(2) × 10⁻¹⁰ m³/C, meaning that the system actually is hole-like. It should be pointed out that the Hall coefficients of the non-magnetic reference La₃TiSb₅ are  +0.42 × 10⁻¹⁰ m³/C at 2 K and  +0.60 × 10⁻¹⁰ m³/C at 300 K, in close agreement with that of Ce₃TiSb₅ in both sign and magnitude, implying the validity of our analysis. The reason for the negative Hall response in Ce₃TiSb₅ is that the small positive OHE is buried by a large negative AHE. It is worthwhile to mention that opposite signs of OHE and AHE in Ce-contained compounds seem rather common, e.g., our previous work on CeNi_2−δAs₂ revealed a positive AHE, albeit the dominant carriers are electrons²⁶.

Fig. 2: Hall effect of Ce₃TiSb₅ in the paramagnetic state.

a Isothermal field-dependent Hall resistivity ρ_yx at different temperatures. Data of the non-magnetic reference La₃TiSb₅ are also shown for comparison. The inset depicts the schematic of transport measurements. b Hall resistivity divided by field, plotted as a function of T. The inset displays ρ_yx/H vs. χ_c with T as an implicit parameter. The linear fitting for $T > {T}_{K}^{on}$ leads to the normal Hall coefficient R_H = +0.6(2) × 10⁻¹⁰ m³/C. The open squares represent the data of La₃TiSb₅. c Schematic diagrams of Kondo effects: non-screened regime for $T > {T}_{K}^{on}$, incoherent Kondo regime for ${T}_{coh} < T < {T}_{K}^{on}$, and coherent Kondo regime for T < T_coh. The hatched balls signify Kondo entanglement of f (red) and conduction (blue) electrons. The upper panel sketches the skew scattering off a Kondo-screened local moment. d ibid, but in a geometrically frustrated lattice. Geometric frustration adds to the inherent frustration caused by Kondo effect, which further weakens the skew scattering in the frustration-promoted incoherent Kondo regime, viz ${\theta }_{{A}^{{\prime} }} < {\theta }_{A}$.

Anomalous behavior of Hall effect has been extensively studied in many heavy-fermion Kondo lattices, like CeAl₃²⁷, CeCu₆²⁸, CeRu₂Si₂²⁹, Ce(Co,Rh,Ir)In₅³⁰, etc^26,31. Unlike conventional magnetic conductors, in heavy-fermion materials, the hybridization between localized f-electrons and conduction (c) electrons leads to the Kondo effect³², the consequence of which is to screen the local moments. Such a screening may start to set in as a local, incoherent form below the onset Kondo temperature ${T}_{K}^{on}$ [Fig. 2c]. Further cooled down to T < T_coh, the Kondo effect becomes coherent by showing a renormalized Kondo resonance near the Fermi level, and the ground state of the system turns into a Fermi liquid with a large quasiparticle effective mass. Due to the coherent Kondo screening, the asymmetric scattering at the magnetic ions is expected to be reduced, and correspondingly, the strength of AHE will be affected. Previous experimental works revealed a universal temperature dependence in ∣ρ_yx/H∣: it increases substantially with decreasing temperature, passing through a maximum near T_coh, and then decreases rapidly below T_coh^27,28,29. A variety of theoretical models based on modified skew scattering have been proposed for the AHE in heavy-Fermion Kondo lattices^{19,20,21,22,33,34,35}, seeing Table 1.

Table 1 Theories of anomalous Hall effect for heavy-fermion systems

On the whole, our AHE results in Ce₃TiSb₅ are at odds with all the existing theories for heavy-fermion systems. The obtained ρ_yx/H ∝ χρ⁰ shown in Fig. 2b resembles Kontani et al.’s prediction at high temperature on the basis of the periodic Anderson Hamiltonian with degenerate orbitals^33,34,35, however, we notice that this relation is ended up near ${T}_{K}^{on}$, a temperature that is about three times of T_coh [Table 1]. In other words, the suppression of asymmetric magnetic scattering appears prior to the establishment of collective Kondo coherence, which is reminiscent of the hybridization fluctuations (or dynamic Kondo hybridization) in CeCoIn₅ observed by angle-resolved photoemission spectroscopy³⁶ and ultrafast optical pump-probe spectroscopy³⁷ measurements. Our results provide a remarkable sign for this region by the anomalous Hall effect, which has not been reported before. It is likely that geometric frustration adds to the Kondo effect (an inherent frustration to magnetic order), and promotes the incoherent Kondo scattering, reducing local magnetization and thus suppressing the AHE even without Kondo coherence. A schematic illustration is provided in Fig. 2c, d. Indeed, geometric frustration has been found to play a crucial role in the physical properties and quantum phase diagrams of heavy-fermion systems. For instance, in CePdAl, which is also quasi-kagome structured (Supplementary Fig. 9), the involvement of geometric frustration gives rise to a peculiar quantum-critical phase³⁸ that was theoretically predicted to emerge at the high-frustration regime in the “Global phase diagram” of heavy-Fermion systems^39,40. However, we must admit that such a scenario of frustration-promoted dynamic Kondo hybridization still needs to be tested in more heavy-fermion materials, and also that an appropriate description of the influence of geometric frustration on the AHE in heavy-fermion systems is still lacking. Our work strongly suggests this necessity in the future.

Unconventional Hall effects in the AFM phase

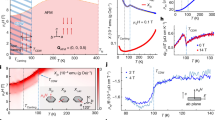
The low-temperature part of Hall effect is displayed in Fig. 3a. When T ≤ 7 K, ρ_yx becomes superlinear with H. Because M(H) is sublinear [cf. Fig. 3b], the superlinear ρ_yx(H) can not be simply understood by a standard AHE, but instead, the high-field part of ρ_yx(H) can be well fit to a H² law; as T decreases, this quadratic regime extends to lower fields, seeing the dashed lines in Fig. 3d. Such a temperature and field dependence mimics the situation in CeIrIn₅⁴¹ and is anticipated as the high-field limit for compensated metals, viz ω_cτ ≫ 1 where ω_c ≡ eH/m^* is the cyclotron frequency, and τ is the scattering time⁴². Another important feature of ρ_yx(H) is that a LHE appears at low temperature, especially below T_N2, i.e., the ρ_yx(H) recorded when field is swept from  +14 T to  −14 T (${\rho }_{yx}^{+-}$) does not overlap with that from  −14 T to  +14 T (${\rho }_{yx}^{-+}$). What attracts us even more is that at 2 K, the base temperature of our measurements, we see the loop twists multiple times, or in other words, the emergent sub-loops are of different chiralities. Such a peculiar LHE has not been observed in other compounds, so far as we know. We tentatively express the total Hall resistivity as follows,

$${\rho }_{yx}(H)={\rho }_{yx}^{O}+{\rho }_{yx}^{A}+{\rho }_{yx}^{T}+{\rho }_{yx}^{L},$$

(2)

where ${\rho }_{yx}^{O}$, ${\rho }_{yx}^{A}$, ${\rho }_{yx}^{T}$ and ${\rho }_{yx}^{L}$ stand for ordinary/anomalous/topological/loop-shaped Hall resistivities, respectively. First, the LHE component can be easily separated out by ${\rho }_{yx}^{L}(H)={\rho }_{yx}^{-+}-{\rho }_{yx}^{+-}$, and the results are presented in Fig. 3c. The sum of the rest components (${\rho }_{yx}-{\rho }_{yx}^{L}$) is shown in Fig. 3d, together with the H² fitting (dashed line) mentioned above. One can clearly see anomalous bumps on top of the smooth H² background in ${\rho }_{yx}-{\rho }_{yx}^{L}$. Since such bumps are absent in M(H) [Fig. 3b], they cannot be attributable to a standard AHE³, but should be categorized as THE. We extract the THE component ${\rho }_{yx}^{T}$ by subtracting the H² background from ${\rho }_{yx}-{\rho }_{yx}^{L}$, and the obtained results are shown in Fig. 3e. Similar results were obtained in other samples [Fig. 3f and Supplementary Fig. 5]. The maximum of ${\rho }_{yx}^{T}$ exceeds 0.2 μΩ ⋅ cm at 2 K, which is comparable with that of MnGe⁴³, and is two orders of magnitude larger than in MnSi^44,45. It is unlikely that such a large THE arises from some extrinsic mechanism such as inhomogeneous current paths, seeing Supplementary Fig. 5. We should note that the components ${\rho }_{yx}^{O}$ and ${\rho }_{yx}^{A}$ in this region are hardly dissolvable; a multiband effect may be also present to cause the nonlinear ρ_yx with respect to field; however, whether ${\rho }_{yx}^{O}$ and ${\rho }_{yx}^{A}$ can be separated, or if multiband effect is indeed active, has little impact on the extracted THE component.

Fig. 3: Hall effect of Ce₃TiSb₅ in the magnetic ordered state.

a Total Hall resistivity as a function of H near and below T_N1. ρ_yx(H) shows clear history dependence. The curves are vertically shifted for clarity. The arrows indicate the direction of the field sweep in the Hall effect measurements. b Field-dependent magnetization is featureless at the same field and temperature. c Loop-shaped topological Hall resistivity ${\rho }_{yx}^{L}$, derived from ${\rho }_{yx}^{-+}-{\rho }_{yx}^{+-}$, where the superscripts “ − + ” and “ + − ” mean the direction of field sweep. d ${\rho }_{yx}-{\rho }_{yx}^{L}$ as a function of H at various T. Note that for 7 and 5 K, ${\rho }_{yx}^{L}$ has no contribution, so ${\rho }_{yx}-{\rho }_{yx}^{L}$ is the same as ρ_yx. The dashed lines indicate the regime of H² dependence that moves to higher fields as T rises. e The extracted topological Hall resistivity ${\rho }_{yx}^{T}$. f Hall resistivity measured on a second Ce₃TiSb₅ sample (S2) grown in the same batch.

To discuss the origin of these peculiar Hall effects seen inside the AFM phase. Apparently, both ${\rho }_{yx}^{T}$ and ${\rho }_{yx}^{L}$ are of magnetic origin in that these signals disappear right above T_N1. Meanwhile, in any case, one can not scale ρ_yx(H) with M(H), suggesting the existence of components other than the standard AHE. Therefore, it is reasonable to attribute the aforementioned ${\rho }_{yx}^{T}$ and ${\rho }_{yx}^{L}$ to the so-called THE. The past decades have witnessed a boost in THE observed in serial materials with non-coplanar or non-collinear spin texture, such as Mn(Si,Ge)^43,44,45,46, GdPtBi⁴⁷, MnBi₄Te₇⁴⁸, Gd₂PdSi₃⁴⁹, YMn₆Sn₆⁵⁰, and EuGa₂Al₂⁵¹. This scenario is likely also applicable to Ce₃TiSb₅, considering the magnetic structures proposed by neutron diffraction²³. For both k₁ and k₂ phases of Ce₃TiSb₅, the moments of Ce are aligned within the ab plane, and the angles spanned by the nearest neighbors are either 120° or 60° [Fig. 1b]. Under field H∥ [0001], these moments are out-of-plane canted and become both non-collinear and non-coplanar; a finite scalar spin chirality χ_ijk = S_i ⋅ (S_j × S_k) is hence accomplished. This makes the observation of THE below T_N1 rather likely. We are impressed that the observed THE here appears across a broad field range, likely due to the slow polarization process when the field is applied along the hard axis of Ce₃TiSb₅.

To the best of our knowledge, the loop-shaped Hall effect—which in our opinion is a special kind of THE—has only been reported in a handful of materials, including Nd₂Ir₂O₇^52,53 and CeAl(Si,Ge)^54,55,56. A major commonality among them is that they are all candidates of magnetic Weyl semimetal with a domain wall (DW) in bulk. In the pyrochlore-type AFM insulator Nd₂Ir₂O₇, the DWs at the boundary between all-in-all-out and all-out-all-in domains pin in-gap Weyl fermions and the projected Fermi-arc surface states, which give rise to an emergent metallic interface⁵⁷ and a loop-shaped electromagnetic response⁵⁸. Our previous work on CeAlGe also suggested an alternative scenario by taking into account the spin chirality in the magnetic DWs⁵⁶. Since DWs are a consequence of meta-stable phases coexisting in the bulk, the magnetization in the DW is usually history dependent. In this context, the loop-shaped Hall response arising from DWs can be understood as follows. Previous neutron experiment revealed two related magnetic orders k₁ and k₂ in Ce₃TiSb₅ below T_N2. More importantly, the transition between k₁ and k₂ seems 1st order with significant hysteresis and phase coexistence²³. DWs are expected to form between these different magnetic phases, which potentially leads to the history-dependent real-space Berry curvature and hence the loop-shaped Hall response. A schematic diagram of this scenario is present in Fig. 4a. Since these DWs are interfaces, conceivably, they are hardly detectable by bulk measurements like magnetic susceptibility. Sample dependence is another feature of DWs, because they are usually pinned by impurities or defects in the crystal. This is indeed true for the LHE in other samples, as shown in Fig. 3f and Supplementary Fig. 5. The scenario can be also supported by the magnetic-force microscopy (MFM) measurements that image the presence of magnetic domains at low temperature for field up to 9 T, seeing Supplementary Fig. 6. However, we must admit that to accurately account for the multiple twists observed in ${\rho }_{yx}^{L}(H)$ at 2 K [Fig. 3a, f], more local, quantitative probes to this interface spin chirality will be needed, which is far beyond our ability at present. Imaging the DW structures by microscopic techniques like vector magneto-optical Kerr effect and scanning superconducting quantum interference device may be informative^59,60.

Fig. 4: Possible mechanisms for the loop-shaped Hall effect.

a Sketch of spin texture for domain wall between the k₁ and k₂ phases. The red and blue arrows stand for the Ce moments on different quasi-kagome networks. Abnormal history-dependent real-space Berry curvature may be picked when carriers travel across this domain wall. b Chiral Fermi arc state (yellow lines) on the domain wall due to the Weyl points (red and blue balls) in the k₂ phase. Such Fermi arcs provide a metallic interface that probably contributes to an abnormal Hall voltage. The time-reversal invariant momenta (TRIM) points of the k₁ phase are also depicted in this panel, while the TRIM points for the k₂ phase are denoted in Fig. 5a for better clarity.

DFT calculations

It is interesting to note that the observed unconventional Hall effects in Ce₃TiSb₅ can also be mediated by nontrivial band topology. This is partly motivated by the topological property in perfect kagome lattices (e.g., see a recent review⁶¹ and the references therein), and can be supported by the density-functional theory (DFT) calculations. We start from La₃TiSb₅, which can be deemed as the non-magnetic reference of Ce₃TiSb₅. The derived Fermi surface and band structure of La₃TiSb₅ are shown in Fig. 5a, b. In the presence of both time reversal (${{\mathcal{T}}}$) and inversion (${{\mathcal{P}}}$) symmetries, all bands are doubly degenerate. Three doubly degenerated bands are found to pass through the Fermi energy (E_F), labeled as 111 (blue), 113 (red) and 115 (red). Band 111 has multiple crossing points with E_F, while bands 113 and 115 are dispersive only along Γ-Z. Correspondingly, the Fermi surfaces show two different topologies, a 3D-like open pocket enclosing the Γ point, and two flat sheets originating from the quasi-1D 113 and 115 bands. Of prime interest is that the bands 113 and 115 cross with each other linearly and give rise to a tilted Dirac node that is about 47 meV above E_F. La₃TiSb₅, therefore, is likely a type-II Dirac semimetal. It is worthwhile to mention here that La₃MgBi₅, isostructural to La₃TiSb₅, was also suggested as a topological Dirac semimetal by quantum oscillations and DFT calculations⁶².

Fig. 5: Density-functional theory (DFT) calculated band structure of La₃TiSb₅ and Ce₃TiSb₅.

a Fermi-surface topology of La₃TiSb₅. The Fermi surface is constituted by a 3D-like pocket (Band 111) and two flat sheets (Bands 113 and 115). b Band structure of La₃TiSb₅. A type-II Dirac node is formed on Γ-Z by the crossing of bands 113 and 115. c ${{{\rm{AFM}}}}_{60/120}^{{{\rm{F}}}}$ magnetic structure that mimics the k₂ phase of Ce₃TiSb₅. The moments of Ce on different layers are distinguished by colors (red and blue), while the net magnetic moment in a Ce₆ polyhegdron is marked by the orange arrows. d Band structure of Ce₃TiSb₅ in ${{{\rm{AFM}}}}_{60/120}^{{{\rm{F}}}}$ calculated with U = 2 eV. The size of the green circles represents the weight of Ce-4f orbitals. Two Weyl points are seen on Γ-Z, depicted by WP1 and WP2, respectively. e AFM − Zigzag^F magnetic structure that mimics the k₁ phase of Ce₃TiSb₅. f Band structure of Ce₃TiSb₅ in AFM−Zigzag^F. The crossing points on Γ-Z near E_F are gapped out, making it a trivial semimetal.

Turning now to the band structure of Ce₃TiSb₅. It is well known that by breaking either ${{\mathcal{T}}}$ or ${{\mathcal{P}}}$ symmetry, a Dirac point splits into two Weyl points with opposite chiralities^63,64. Regarding the situation in Ce₃TiSb₅, it is extremely difficult to calculate its band structure by taking into account the k₁ or k₂ type magnetic structure. Instead, a simpler magnetic unit cell without c-axis modulation was considered in the DFT calculations. Since all the Ce atoms reside in two individual planes that are separated by nonmagnetic Ti-Sb slabs, such a treatment maintains the time-reversal symmetry breaking without qualitatively altering the band topology, seeing EuCuAs⁶⁵ and MnBi₂Te₄⁶⁶ for instance. To make the results closer to the k₂ ground state²³, we imposed two prerequisites: (i) all Ce moments lie inside the ab plane, and (ii) a ferromagnetic interchain coupling exists between the two Ce sublattices. Firstly, a moderate Coulomb U = 2 eV and Hunds coupling J = 0.5 eV were employed. The calculation manifests many magnetic phases with close energy scales (Supplementary Table 3 and Supplementary Fig. 7 in SI), in line with the magnetic frustration exerted by the quasi-kagome lattice. A brief summary of the calculations with different magnetic structures is listed in Table 2. The configuration with the lowest energy (termed as ${{{\rm{AFM}}}}_{60/120}^{{{\rm{F}}}}$) is shown in Fig. 5c, which essentially captures all the features of k₂ only except for the c-axis modulation. In this magnetic structure, there are two moments pointing inside and one moment outside (viz. 2-in-1-out) in one triangle and 1-in-2-out in the adjacent triangle, and the angle between nearest moments is either 60° or 120°; for each Ce6 polyhedron, a net magnetization is found to be along $[10\bar{1}0]$, cf. the orange arrow in Fig. 5c, breaking the ${{\mathcal{T}}}$ symmetry. The band structure of ${{{\rm{AFM}}}}_{60/120}^{{{\rm{F}}}}$ is shown in Fig. 5d. c-f hybridization is obviously seen, and narrow bands with substantial Ce-4f character are found just below E_F, qualitatively consistent with the moderate electronic correlation revealed by specific heat. Due to the ${{\mathcal{T}}}$ symmetry breaking, each doubly degenerate band is split. Two Weyl nodes (denoted by WP1 and WP2) appear on Γ-Z line at the crossing points of the bands with different irreducible representations (LD₃ and LD₄, respectively). To test the robustness of this topological feature to electronic correlation, we considered the situations with different U, and the results are displayed in Supplementary Fig. 8 in SI. As for smaller U = 1 eV, the narrow bands of Ce-4f cross E_F, implying partial delocalization of 4f electrons and that the system probably enters the intermediate-valence regime. For large U = 6 eV, the Ce-4f electrons are fully localized, and the band structure appears similar to that of La₃TiSb₅, whereas the ${{\mathcal{T}}}$ breaking induces a tiny splitting of each band. It is worthwhile to emphasize that in spite of the different energy levels of 4f bands, the Weyl points survive on Γ-Z. Therefore, the ground state of Ce₃TiSb₅ is likely to be a type-II Weyl semimetal.

Table 2 Magnetic space group (MSG), net magnetic moment M, spatial inversion symmetry ${{\mathcal{P}}}$, the combined operation of inversion symmetry and time reversal symmetry ${{\mathcal{P}}}{{\mathcal{T}}}$, and the topological feature of Ce₃TiSb₅ with different imposed magnetic configurations

For comparison, we also attempted to calculate the band structure of Ce₃TiSb₅ with k₁ = [0, 1/2, 1/8] magnetic state. The magnetic unit cell in this case is doubly expanded along b. Here, again, we ignored the c-axis modulation, and the simplified magnetic structure (termed as AFM−Zigzag^F) is shown in Fig. 5e. The calculated band structure with U = 2.0 eV and J = 0.5 eV is displayed in Fig. 5f. In this magnetic structure, the Zigzag-arranged Ce moments cause a net moment M_x in a Ce₆ polyhedron, whereas the adjacent Ce₆ polyhedra along b follow a sequence of M_x, M_x,  −M_x,  −M_x in one expanded unit cell; on the whole, the ${{\mathcal{P}}}{{\mathcal{T}}}$ symmetry is preserved. However, the little group (${2}^{{\prime} }$/m) of Γ-Z cannot protect the Dirac node, which gives the gapped bands along Γ-Z, comparing to the Weyl nodal bands in k₂ phase. Altogether, the k₁ and k₂ phases are potentially of different topological characters. In this context, one may expect that the domain wall between the k₁ and k₂ phases can pin a chiral Fermi arc that connects two Weyl points with opposite chiralities [Fig. 4b]. Such a metallic interface may give a second explanation for the observed loop-shaped Hall effect.

Additional remarks

On the example of Ce₃TiSb₅, we clearly see the interplays among electronic correlation, topology and geometric frustration. Compared with earlier Kondo Weyl semimetal candidates like Ce₃Bi₄Pd₃⁶⁷, YbPtBi⁶⁸ etc, the involvement of geometric frustration sheds new lights to correlated topological materials. On the one hand, geometric frustration can promote the inherent frustration exerted by Kondo coupling, and further weakens the asymmetric skew scattering prior to the establishment of Kondo coherence; on the other hand, it also leads to finite scalar spin chirality and domain walls between quasi-degenerate magnetic orders. All these are reflected in our Hall effect studies.

The frustration-mediated textured AFM orders in Ce₃TiSb₅ remind us of another possible mechanism for the AHE above T_N1. According to H. Ishizuka et al.⁶⁹, an alternative type of skew-scattering via thermally excited spin-clusters with scalar spin chirality can cause a giant AHE whose Hall angle (${\theta }_{H}^{A}$) could be as large as 0.1π, and this has been exemplified in the chiral magnet MnGe⁷⁰. To discuss about this possibility, we show $\tan {\theta }_{H}^{A}$ as a function of T in Supplementary Fig. 4. The Hall angle here is <1%, implying that the scenario of spin-chirality skew scattering originally proposed for weakly-correlated metals is likely non-applicable here, but counter-indicating the important role played by Kondo hybridization⁷¹.

Finally, all these unconventional Hall effects observed in Ce₃TiSb₅ motivate us to discuss further the emergent physics from the standpoint of a heavy-Fermion system. This might be sparked by proposing an “extended” global phase diagram for heavy-Fermion systems, as shown in Fig. 6. The classic global phase diagram³⁹ was proposed to describe the classification of quantum phase transitions in heavy-fermion materials with various frustration parameter (G) and ratio between Kondo coupling and RKKY interaction (J_K/J_RKKY). The green line represents the Kondo-breakdown transition across which the highly localized f electrons become delocalized, and this is accompanied by an abrupt change in the Fermi surface. By convention, we here use the subscripts “S” or “L” to depict the magnetic states with a small or large Fermi surface. Previous studies suggested that Kondo-breakdown type QCP typically occurs in systems with relatively high G (path-II, AFM_S-PM_L), while sequential Kondo-breakdown transition and spin-density-wave (SDW) type QCP were found more often in systems with lower G (path-I, AFM_S-AFM_L-PM_L). Some representative examples include Ce(Cu,Au)₆⁷², YbRh₂Si₂¹⁴, Ce_mM_nIn_3m+2n^73,74,75, CeNiAsO⁷⁶, etc. In a high-frustration limit, a less common quantum phase transition may take place (path-III, AFM_S-PM_S-PM_L), where the magnetic order quenches prior to the Kondo-breakdown transition, and the Fermi surface reconstructs within the paramagnetic state. Recently, this rare case has been exemplified by CePdAl tuned by both pressure and field³⁸. In CePdAl, the high frustration is fulfilled by the quasi-kagome structure, as is the case in our Ce₃TiSb₅. The topological features observed in Ce₃TiSb₅ employ topology—a new degree of freedom that can be switched by SOC—to the classic global phase diagram. Our results place Ce₃TiSb₅ at the highly-frustrated AFM_S regime with non-trivial topology. With this in mind and also taking into account the rich magnetic and topological phases proposed by DFT, natural questions can be further put forward concerning how the ground state evolves when tuned by pressure, chemical doping, or a strong magnetic field, and whether a topological phase transition can entangle with a magnetic quantum phase transition. All these await to be clarified in the future.

Fig. 6: Extended global phase diagram for heavy-Fermion systems.

G parameterizes frustration, J_K characterizes Kondo coupling, and J_RKKY signifies Ruderman-Kittel-Kasuya-Yosida interaction. A new degree of freedom, topology, that can be switched by spin-orbit coupling (SOC), is introduced to the classic global phase diagram³⁹. The abbreviations are: AFM antiferromagnetic, PM paramagnetic, SDW spin-density wave, QCP quantum critical point. The subscript S (or L) denotes a small (or large) Fermi surface. The blue arrows on the topologically trivial plane are the trajectories of quantum phase transition: I, SDW QCP (AFM_S-AFM_L-PM_L), e.g., CeRh_0.58Ir_0.42In₅⁷⁴; II, Kondo-breakdown QCP (AFM_S-PM_L), e.g., Ce(Cu, Au)₆⁷², YbRh₂Si₂¹⁴, CeRhIn₅⁷³, and CeNiAsO⁷⁶; and III, quantum phase transition occurred in highly frustrated systems (AFM_S-PM_S-PM_L) as exemplified by CePdAl³⁸. Our results place Ce₃TiSb₅ at the highly frustrated AFM_S regime with non-trivial band topology.

Conclusion

In all, a series of unconventional Hall effects are observed in a single quasi-kagome Kondo Weyl semimetal candidate Ce₃TiSb₅, suggestive of the intriguing interplay among electronic correlation, topology, and geometric frustration. Our work, therefore, provides a rare paradigm of correlated topological material residing in the regime of highly-frustrated AFM_S, and enriches the classic global phase diagram for heavy-fermion systems.

Methods

Single-crystal preparation and measurements

Single crystals of Ce₃TiSb₅ were grown by a Sn-flux method²⁴. Starting materials Ce:Ti:Sb:Sn = 3 : 1 : 5 : 20 in molar ratio were weighed and placed in an alumina crucible. The mixture was heated up to 1100 °C in 5 h, held for 24 h and then slowly cooled at a rate of 1 °C/h to 650 °C at which temperature the Sn flux was effectively removed by centrifugation. The obtained crystals are of hexagonal prism shape with typical dimensions 1 × 1 × 5 mm³. The chemical composition, the quality of crystallization, and the orientation of the measured sample were verified by energy-dispersive X-ray spectroscopy, Wavelength-dispersive X-ray, single-crystal X-ray diffraction and Laue X-ray diffraction; the results are displayed in Supplementary Figs. 1 and 2 and Supplementary Tables 1, and 2 of SI. Magnetization measurements were carried out in a commercial physical-property measurement system (PPMS-16 T, Quantum Design). For the transport measurements, both in-plane longitudinal resistivity (ρ_xx) and Hall resistivity (ρ_yx) were measured by a lock-in amplifier (SR865A, Stanford Research) equipped with SR554A pre-amplifier. The charge current I was applied parallel with [1000]. For all these measurements, the magnetic field was applied along [0001]. Four samples were measured for the Hall effect, labeled as S1-4, respectively. MFM images were obtained using an Attocube attoDRY2100 closed-cycle cryogenic microscope with a base temperature of 2 K and a magnetic field up to 9 T.

First-principles calculations

First-principles calculations were performed within the DFT formalism as implemented in VASP with the projector augmented wave method. The energy cutoff for wave-function expansion was set as 450 eV, and the k-point sampling was 9 × 9 × 12. The generalized gradient approximation (GGA) of Perdew–Burke–Ernzerhof for the exchange-correlation potential was used in all calculations. The maximally localized Wannier functions were constructed using the WANNIER90 package based on the First-principles calculations. To account for the correlation effects of the Ce-4f electrons, we have adopted the GGA + U method with Hubbard U = 2 eV and Hund’s coupling J = 0.5 eV, which matches the moderate electronic correlation revealed by specific heat. We have also tested different U values, and the results of U = 1 and 6 eV are shown in SI. SOC was implemented in all calculations.