Introduction

Sediment facies is defined as an assemblage of sediments that records specific characteristics of a depositional environment. It hence provides fundamental sedimentological information in space and time, which builds the necessary geological background for studying past surface processes on Earth1. For instance, the change of sediment facies through time assists scientists in reconstructing the evolution of paleoenvironments2,3,4. Moreover, the knowledge of sediment facies makes available a proper selection of geochemical proxies for a better interpretation of paleoclimatic variations5,6,7,8. Exploring geological resources, such as for methane hydrates, oil, and gas, or offshore wind parks also requires regional investigations of sediment facies9,10. Basically, all research initiatives rely on the classification of sediment facies as a preliminary step.

Evolution in computer science and computing power made machine learning (ML) techniques available to various disciplines over the past two decades11. Research has started to include ML to achieve in-depth scientific findings previously constrained by conventional methods and data resolutions12,13. ML applications also have been introduced to the geoscience community, such as support vector machine (SVC), random forest (RF), and artificial neural networks14,15,16,17,18. However, applications are still at an early stage. The data coverage usually remains small, which can be expressed in either the amounts of data (<10 k), target classes (e.g., sediment facies and geochemical zones, <6), or features (e.g., measuring analytes, <10). For instance, input data are mostly geophysical measurements (e.g., seismic profiles and borehole logging data)14,18,19,20,21 or laborious measurements (e.g., grain-size variations and quantitative element concentrations)15,17, which have resolution limits (tens of centimeters to meters in scale). Target classes are thus often homogeneous sediments (e.g., unique tephra layers or sandstones)16,20,21,22 instead of complex units having the sedimentary structure in an mm scale (e.g., laminated stream channel deposits). Furthermore, the ML models’ decision commonly depends on individual data points rather than on comprehensive observations, including adjacent data points, which compare much better to the way how sedimentologists work and investigate. Insua et al.19 determine that their single-point-observation ML models perform worse on composite carbonates than sand layers. All these factors limit the complexity and diversity of applications. The same is true for the fact that developing codes are rarely open-source.

Evolution in core scanning techniques (e.g., X-ray fluorescence (XRF) core scanner, computed tomography (CT), multi-sensor core logger (MSCL), and hyperspectral imaging (HSI)) provide the possibility of acquiring near-continuous (μm-scale resolution), non-destructive and rapid measurements covering both geophysical and geochemical data from natural archives8,23,24,25. A large quantity of sediment investigations is thus integrated with higher spatial resolution and much more measuring detail26. Therefore, data variety and size ascend to a new level, which helps resolve previously unachievable scientific questions (e.g., paleoclimatic variation and anthropogenic interaction with the natural environment)27,28,29. Among these scanning techniques, XRF core scanning is selected for this study as the primary technique to acquire measurements. It is evolved from a well-developed chemometric community30, and its applications have been prosperous since 20008. Its rapid measuring provides a wide range of elemental signals31, which are adopted by the vast Earth and environmental research society (e.g., paleoceanography, paleolimnology, paleoseismology, pollution history29,32,33,34). Besides the chemical properties, XRF core scanning data offer proxies representing physical and biological properties, such as grain size35 and diatom productivity33. Physical measurements, like CT and MSCL techniques, provide more convenient and economical ways to acquire data compared to XRF core scanning, e.g., no core opening is needed. However, they are not direct or sufficient information to describe the sediment composition content21. HSI has a high potential in acquiring high-resolution chemical and physical measurements useful for ML applications, but it can be more precise when coupled with XRF data36. XRF core scanning may give the most comprehensive and reliable information to simulate the sedimentologists’ observational behavior, which includes multiple analyses (e.g., grain size, carbonate content, organic matter, and fossils). Currently, unsupervised ML applications with XRF data are common for data exploration, but not many developments in supervised ML8,30,36.

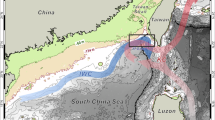
Our approach aims at enhancing the automatic sediment-facies classification by overcoming most restrictions. This is inherited from the successes of two evolutions: ML and core scanning techniques. High-resolution elemental profiles obtained by XRF core scanning were acquired under the interdisciplinary Wadden Sea Archive (WASA) project26 from the UNESCO World Heritage-listed Wadden Sea in Northern Germany. This region belongs to a dynamic geological setting, where the environment varies due to the rapidly rising sea level during the Holocene from glacial (terrestrial) to shallow marine2,37,38. Thus, the studied sediments provide comprehensive geochemical signals and broad coverage (11 sediment facies, 53 core sections, 19k data points, for details: Fig. 1 and Methods), spanning the Late Pleistocene throughout the Holocene37. Instead of effortlessly applying ML algorithms, we tested different feature engineering methods, like data transformations and principal component analysis (PCA), to simulate the sedimentologists’ observational behavior by extending the model’s single-point to a multi-point analysis. Simple (logistic regression (LR)) and complex (kernel SVC, RF) ML algorithms were included to compare their feature engineering-integrated performance. Careful evaluations involving cross-validation (CV), tailor-designed measures, and error analysis were carried out during these steps to guarantee the generalization of the models.

Fig. 1: Sediment facies information.
figure 1

Abbreviation, age, and sedimentary environment for facies occurring in the study area, a tidal flat in the northern German Wadden Sea (adopted from Capperucci et al. (2022)69). Positions of facies in relation to sea level and age are only for illustration. For details, see Supplementary Table S1.

Full size image

The results indicate a noticeable benefit of feature engineering that empowers the use of simple ML algorithms, giving enhanced performance (78% accuracy) and applicability to a standard computer. In addition, the optimal model provides an outcome with a confidence level, which highlights critical parts of the sediment records to allocate more resources for analyzing and saving resources from the remaining sediments. The approach is expected as a blueprint to inspire further studies in Earth and environment communities regardless of data type, region, and objective. More importantly, this brings interdisciplinary scientific research to a new era and scale of capability based on state-of-the-art technological innovations.

Results

Contribution to feature engineering

A series of models were built to classify sediments using the high-resolution elemental profiles automatically. The performances from each combination of feature engineering and ML algorithms were evaluated by the mean accuracy of five-fold CV scores. The output and visualization of the grid search are presented in Supplementary Figs. S3–5. The highest CV scores for each combination are illustrated in Fig. 2a. The CV scores increase after data representations, and the rolling representation results in the best scores. Only 5 out of 9 comparisons between using or not using PCA transformation indicate “including PCA” as the better feature engineering. Thus, there is no clear advantage of using a PCA transformation. After data representation, the complex ML algorithms (SVC and RF), which have the enhanced learning power of non-linearity, provide no noticeable advantage over the simple algorithm (LR).

Fig. 2: Evaluations of built models.
figure 2

a The best cross-validation (CV) score of each combination of feature engineering (data representations and principal component analysis—PCA) and ML algorithms (logistic regression—LR, kernel support vector machine—SVC, random forest—RF classifiers). The CV score is relevant to the mean accuracy during CV iterations. b The fragmentation is quantified by the number of boundaries and accuracy of the optimal model built from each data representation in the test set. c, d The modified confusion matrices describe the performance of the optimal models built from (c) rolling data and (d) raw data when applied to the test set. The y-axis represents the facies from the lithological description by sedimentologists. The x-axis stands for the model-classified facies. The numbers represent the percentages of data in each row, i.e., recall in statistical terminology. For instance, at the top left of (d), only 3% of data points recognized as hcf by sedimentologists are correctly classified by the model, while 51% of these data points are misclassified as mf by the model. For abbreviations, refer to Fig. 1.

Full size image

Furthermore, the best models using each kind of data (Fig. 2a, raw data: SVC with PCA, rolling data: LR without PCA, 2D data: LR with PCA) were evaluated in the test set. Figure 2b shows that the model using rolling data provides the highest accuracy (78%) and fewest boundaries (98). Its boundary amount is about 20 times that sedimentologists gave (5), which is still noticeably lower than the model using raw data output (591). The model using 2D data does not perform as well as the one with rolling data but is still better than raw data. When considering the large size of 2D data (nine times rolling data), creating a burden for computing, the preference for the rolling data approach is confirmed.

The optimal model built on the best ML combination (LR learned from rolling data without PCA) indicates its increasing performance on laminated facies. When comparing the accuracies of channel fill deposits (especially hcf, Fig. 2c) to those of the model using raw data (Fig. 2d), the misclassification to sand and mud flats is remarkably reduced. This points out that the rolling representation describes the laminated characteristic of channel fill deposits well enough, comprising two kinds of homogeneous sublayers (sand and mud). The optimal model does not classify those sediments separately but together as one facies to recognize a specific depositional environment. The simple algorithm is thus allowed to surpass more complex algorithms to the benefit of feature engineering. This finding offers an efficient way of applying automatic sediment-facies classification by demanding less computing power due to less model complexity.

Decision function of the model

Owning to the capability of LR, our optimal model built using LR on the rolling data without PCA transformation gives weights describing which features (rolling mean and standard deviation of elements) are discriminating for each facies (i.e., decision function, Fig. 3). In the following expression, the elements refer to their rolling mean values if without “variance” specification, which represents the essence of standard deviation. Classifying as hsm has (1) substantial negative weights on Ti and Fe, (2) positive weights on Si, Ca, and Sr, and (3) positive weights on the variance of Ca and Ti. The channel fill deposits (hcf and lcf) positively rely on Ca but negatively on Si. To distinguish these two facies, hcf has an evident influence through Si variance, while lcf has a noticeable negative weight on Ba. Furthermore, the decision of lcf is less affected by the variances of elements compared to hcf. sf has substantial positive weights on Si and Ca but negative on Cl, and mf has a positive weight on Ca while negative weights on Rb and Ba. It has an overall negative weight on the variance of elements, especially on S. la has (1) strong negative weights on both Ca and Sr, (2) an apparent positive weight on Br but a negative weight on its variance. pt has a positive weight on S and a negative weight on K. It also has some weights on the variance of Rb and Sr., so has remarkable positive weights on Si, S, and Ba but negative weights on Cl, Ca and Fe. pm has (1) positive weights on K, Fe, Rb, and Ba, (2) negative weights on Ca and Br, and (3) positive weights on the variance of Cl and Fe. pef has noticeable positive weights on Cl and Ba but a negative weight on Ca. mo has the highest (1) positive weights on K, Ti, and Fe, (2) a negative weight on Br, and (3) positive weight on the variance of Br when compared to other facies.

Fig. 3: The optimal model’s discriminating behavior.
figure 3

Weights of features in the decision function of the optimal model built using LR from the rolling data without PCA transformation. The x-axis contains the features of rolling data (i.e., rolling mean and standard deviation of the raw elements). The y-axis is the facies (abbreviations refer to Fig. 1). The darker color, the more decisive that feature is in classifying to a specific facies. A negative coefficient indicates the negative influence of the feature.

Full size image

Misclassification of the model

Besides the improvements that benefited from feature engineering, the optimal model has limitations causing misclassifications. Error analysis summarizes four main error-causing categories (Fig. 4a). The first category, with 63.6% occurrence frequency, describes the situation that the predictions could be correct, but this facies change is omitted to fit a general picture of environmental interpretation by sedimentologists. This is because the capture of composite characteristics is limited by the initially defined (fixed) window size during the rolling representation. For those laminations or sediment sections having a thickness >32 mm (window size: 17 data points), the optimal model cannot identify them as composite facies. These misclassifications are often considered minor sedimentary structures. For instance, minor low-energy channel fill deposits are misclassified to high-energy channel fill deposits in core Sections N31–1 (Fig. 4b), which might reveal a small-scale channel deepening. In fact, sedimentologists have a flexible observation window to identify facies, but our ML-based optimal model can only start from a local measurement and joins with nearby information. Therefore, these misclassifications should be considered as the model looks too detailed rather than classification problems.

Fig. 4: Error analysis results from the test set.
figure 4

a Error categories and their frequency in misclassifications of the test set. The sum of the frequency is not 100% because categories may co-exist. b Comparison (three illustrating cores) between sedimentologists’ descriptions (blue) and predictions (orange) of the optimal model built using LR from the rolling data without PCA transformation. The core images and error category labels (marked in the color code (a) are attached. For abbreviations, refer to Fig. 1.

Full size image

Another error category is the transition boundary problem, having a 41.2% occurrence frequency (Fig. 4a). Figure 2c shows that the accuracies for peat, soil, Pleistocene eolian/fluvial deposits, and Pleistocene marine sediments are relatively low compared to the other facies. In most cases, the boundaries between these facies are gradual and/or indistinct. It is difficult for sedimentologists to draw a clear separation between them via macroscopic observation and elemental variation. For example, soils developed from Pleistocene sediments are similar in their elemental composition and cause confusion in the model. This cause of misclassification can be found in the boundaries of pt-so-pef (lower part of N71-4, Fig. 4b). The relevant transition boundary bias has also been mentioned in a pilot automation study nearby21.

The third category having a 21.4% occurrence frequency (Fig. 4a), is related to the limitation of macroscopic observation by sedimentologists. Sedimentologists describe these misclassified sediments with doubts since they are visually similar to several sediment facies. For instance, in N18-2 (Fig. 4b), around 0.6 m depth, structureless sediments are described as eolian/fluvial deposits like their neighbors by sedimentologists. However, according to their elemental profiles, the optimal model classified them differently from the neighbors as Pleistocene marine sediments. This is reasonable because the Pleistocene sand flat sediments might be visually identical to the structureless eolian/fluvial deposits unless checking their diatom and geochemical data.

Subjective and opposing judgments also happen between sedimentologists. Our model provides a consistent judgment through its fixed and relatively small observation window. Only a few cases, like wood fragments, are misclassified as high-energy shallow marine sediment. But these are out of the model’s ability. This material (3.7% occurrence frequency, Fig. 4a) is not in the facies list of training data for model building. The detailed error-analysis result and comparison results are listed in Supplementary Data 1 and Figs. S6 and 7.

Highlighting critical segments

Our optimal model estimates the confidence level of each classification. Figure 5a demonstrates an example of the probability distribution along the core depth of one selected core section. The probability values are dispersed along the facies if the model lacks confidence in its classification. In contrast, the high probability in specific facies stands for the model’s confident decision. To more conveniently recognize the confidence level of our model, the maximum probability among facies for each data point is extracted (Fig. 5b). The higher the maximum probability value, the more confident the decision is.

Fig. 5: Attributes of the optimal model’s confidence level.
figure 5

a Probability along core Sections N31–1. The probability of each facies in each data point is visualized in bars and projected to a heatmap above (the deeper the blue, the higher the probability). b The maximum probability for each data point is plotted along with the core image. For abbreviations, refer to Fig. 1. c Bi-plots of (1) distribution of the maximum probability in the groups of correct and incorrect classifications and (2) error rate for each interval of the maximum probability in the test set.

Full size image

The relation between the model’s confidence level and its error rate is illustrated in Fig. 5c. The misclassifications (labeled as incorrect) mainly have a low maximum probability, suggesting that the more uncertain our model is, the more likely it is wrong. Empirically, the model’s classification has a higher chance of being wrong when the maximum probability value is <0.3. Therefore, sedimentologists can focus on sediment sections with a low maximum probability to carry out further examinations, such as microscopic observations or quantitative geochemical analyses, while adopting the automatic classification done by the model if the maximum probability is >0.3. This provides a valuable outcome by highlighting the critical part where the expertise and experience of sedimentologists are needed for correct facies classification. When applying the model to the whole dataset of WASA (all 92 cores, 383 sections, 159 k data points), only 1% of the sediments are marked as critical, requiring further analysis.

Discussion

A simple but powerful recipe of feature engineering (centered log-ratio transformation and rolling representation) is proposed to fit the specific needs of sedimentological applications after testing several combinations of feature engineering methods. The best model does not need complex ML algorithms (SVC and RF), thus reducing computation time and model size. A possible reason explaining the usefulness of rolling representation is its combination of measurements (i.e., chemical, physical, and biological-related XRF data) and heterogeneities from the sample and adjacent sediments. This data representation moves from a single-point observation to a multi-point (window-sized) observation, which simulates human observation by considering the context of sedimentary features to define the sediment facies. The rolling mean draws an overall elemental fingerprint of the sediments, while the rolling standard deviation describes heterogeneity within this fingerprint.

By interpreting the optimal model’s decision function (Fig. 3), we can realize the model’s classification behavior and inspect its justifiability. The weights in classifying hsm reflect that the model characterizes the alternating coarse sand (Si) and shell fragments (Ca, Sr) as its standard and has a dominant marine influence39,40,41. The model takes the abundance of shell fragments and relatively few sand grains as the key to discriminating channel fill deposits. Notably, the model recognizes more contrasting sediment properties in hcf than lcf by considering the variances of individual elements. The negative contribution of Ba, which correspondingly happens to mf, may show the lack of this element in finer sediments (clay minerals). Having a high contribution to the elements related to coarse grain (Si) and shell fragment (Ca) and a negative contribution to seawater (Cl) describes the composition of sf and its distance to the sea correctly39,40,41. The model depicts the homogeneous characteristic of mf by giving a negative contribution to the variances of individual elements. la is characteristic of a lower contribution from shell fragments, but more homogeneous organic matter (Br) is recognized by the model34. Interestingly, the model uses the proxy for pyrite (S), less contribution of mineralogical sediments (K), and the slightly heterogeneous composition based on the variance to differentiate pt from la, which is also organic-rich7,42. The weights for distinguishing paleosoils can be related to the leaching (Ca, Fe) process43,44,45, but also the transition boundaries to adjacent sediments, which creates mixed signals and usually leads to bias (e.g., the influence of above peat (S)). Although the sedimentation process of pm is relevant to those Holocene shallow marine sediments, our model learns a major difference between them: lacking carbonate and organic matter due to long degradation. Meanwhile, the abundance of K and Ba is a vital differentiation possibly caused by different sediment provenances46. The distinct characteristics of pef are carbonate-free and structureless, which are well described by the model’s weights. However, the reason for the model considering Cl and Ba is unclear. To classify mo from other facies, the model maps its function in having the highest weights for mineralogical elements (K, Ti, Fe) and a negative contribution of organic matter (Br). Most of the weights in the decision function are sensible. A few of them do not have an appropriate explanation, possibly due to the bias caused by rolling transformation.

The comprehensive evaluation of the model is estimated by using robust CV in the training set as well as boundary amount and balanced accuracy in the test set. Based on a performance of 78% accuracy and the result of detailed error analysis, most misclassifications are summarized as (1) minor structures that were ignored by sedimentologists, (2) confusion caused by transition boundaries, and (3) sediments visually identical to several facies (Fig. 4). These error categories are related to the subjective decision by sedimentologists and thus are described as unavoidable bias47. They can also be considered as opinion variations among sedimentologists, not actual errors. Therefore, it is important for sedimentologists to identify these arguable sediment sections (as quantified by the confidence level, Fig. 5a) from the entire sediment record to concentrate efforts and discussions.

As mentioned for the model’s limitations, our approach has not yet fully simulated the sedimentologist’s behavior. With a flexible observational window and a bigger picture of environmental interpretations in mind, the complex or customized architecture of neural network algorithms, like long short-term memory, may cause improvements. Also, more sediment facies can be considered, which should boost the success of automation. Numerous ML applications use images containing pattern recognition, segmentation, and further well-built deep learning architecture (e.g.,11,48,49). Replacing XRF data with images may be a worthy attempt because it gives higher resolution at a lower measurement cost. Yet, its nature of losing some information that XRF data has needs to be aware.

Our study provides not only a model to automatically classify sediments from the Wadden Sea in Germany, but also can be considered as a methodological blueprint for projects, regardless of the type of data and the region investigated. Compared to other studies developing an automatic classification of geological records15,17,18,21, our approach has elevated the application to a new level, which has (1) input data with comprehensive information that is widely accepted in the Earth and environmental sciences and (2) broader data coverage and facies variability. Scientifically, a large-scale scientific investigation, such as the whole Wadden Sea area (>1500 km2), needs a less time- and labor-consuming research approach to be accomplished21. In industrial terms, cost-efficiency and the capability of managing large-scale exploration data are in demand. Since our model can automatically classify the relatively simple but often vast sediment sections, experts can deal with critical sections and focused analyses. Thus, the resources (time, personnel, material) can be redistributed more efficiently. Our future toward a standard operative procedure of automatically coring, scanning, classifying, and digitally archiving sediments requires further systematic scientific and commercial developments. Hopefully, our advances will assist in exploring new perspectives on Earth and environmental sciences. Furthermore, this evolution shall facilitate the preservation of geoscientific knowledge since investigations will be conducted digitally and promote the findability, accessibility, interoperability, and reusability principles50 (especially reusability).

Methods

Data acquisition

This study was developed under the framework of the interdisciplinary WASA project26. Ninety-two sediment cores (length: up to 6 m, diameter: 8 and 10 cm) were recovered from tidal flats, channels, and offshore around the island of Norderney. A team of sedimentologists carried out lithological descriptions and sediment-facies interpretation through macroscopic observation37. High-resolution elemental profiles were acquired from a COX Itrax-XRF core scanner at the GEOPOLAR lab, University of Bremen, scanned at a fixed setting, and subsequently processed by the Q-spec software (version 2015; COX® Analytical Systems). Twelve elements (Si, S, Cl, K, Ca, Ti, Fe, Br, Rb, Sr, Zr, Ba) were chosen based on signal reliability. All data and information were adopted from a previous study42 that compiled the geochemical and geophysical measurements of the sediment cores. Fifty-three representative sediment core sections (length: <1.2 m, locations: Supplementary Fig. S1a, with 19,823 data points) covering 11 sediment facies (Fig. 1) were selected for this approach in order to constrain computing time. Data points representing cracks and rough or uneven sediment surfaces were excluded. The facies labels extracted from lithological descriptions and elemental profiles were aligned according to their depth.

Feature engineering

The developing scheme of this study is demonstrated in Supplementary Fig. S2a. The dataset was randomly split into training and test sets for a robust evaluation. The test set contains one section for each facies while the remaining sections were used for training. A series of feature engineering methods (i.e., data transformations in ML terminology) were deployed to enhance the performance of the models built by supervised ML algorithms. Then, combinations of these methods were tested to find the most useful one. The steps are the following.

Elemental data were normalized by the geometric mean in each data point to eliminate the variance caused by the machine and the sediment itself, such as XRF tube aging, water content, and grain size, to achieve a better prediction. In addition, the logarithm was applied to free the normalized data from asymmetry and closed-sum effects51,52. Together, this data treatment is called centered log-ratio transformation, which is commonly applied to compositional data53.

To capture the composite character of sediment facies, the neighboring information of each data point needs to be included in the data point. We propose two data representations for comparison. The first is rolling representation, where the dataset is represented by a centered moving mean and its standard deviation (Supplementary Fig. S2b) for each element. The moving window size was set to 17 data points since the step-size resolution of the Itrax XRF core scanner is 2 mm, and the thickness of beddings is predominantly <1 cm for studied sediments42. The second is called 2D representation. It collects adjacent data points as a chunk of data (17 data points * 12 elements) and raveled them to an array of new dimensions (Supplementary Fig. S2c). This approach is common in image analysis, which transforms a 2D pixel data matrix into a 1D array. These representations were implemented for each core section individually to prevent the model building from data snooping54.

In the next step, the represented dataset was standardized to zero mean and unit standard deviation, which is essential for some ML algorithms. PCA with correlation matrix and whitened settings was included in the workflow to discuss its need in feature engineering. Yet, the standardization was not applied to the dataset for the combination of RF classifier without PCA because RF is not sensitive to the variable’s scale difference.

Model building and evaluation

After feature engineering, three algorithms were applied to learn the dataset and to build models to classify sediments into facies by analyzing elemental profiles automatically. LR classifier using ‘lbfgs’ as solver55 and L2 regularization was selected from linear algorithms. LR learns from the data to a model with a linear combination of weights derived from the maximum likelihood convergence. It is a classic soft classifier that produces probability as an outcome in dealing with multi-class problems56. Hence, it quantifies the uncertainty of predictions rather than just classification results. Kernel SVC and RF classifiers were selected from sophisticated non-linear algorithms. The kernel technique of SVC allows for exploring data relations in the infinite space, which includes element ratios. Furthermore, SVC has the ability to tolerate noise due to its soft-margin policy when finding the hyperplane in classification57. RF is an aggregation of decision trees that enforces its non-linear learning capability and decreases the overfitting potential by the nature of randomization (both samples and features). Each decision tree is constructed by a series of decision-making to separate samples into the desired classification, which simulates the human’s intuitive behavior. In addition, the decision tree is free from the scale of data, so there is no need for normalization prior to the implementation, which is more convenient and leads to a difference in the workflow (Fig. S2a)58,59. These three algorithms are well-developed in the ML community and commonly adopted by other disciplines59,60. The algorithms were implemented with the balanced class (i.e., facies) weights61 to deal with our imbalanced facies distribution (Supplementary Fig. S1b).

Prior to the final evaluation, an exhaustive search for parameters using five-fold CV was utilized to (1) assess the usefulness of data representation, (2) evaluate the need of using PCA, and (3) fine-tune parameters (LR: C, SVC: C and \(\gamma\), RF: n_estimators and max_depth) for building models. In brief, those parameters control the regularization strength of algorithms to achieve a better generalization59. C for LR refers to an inverse of regularization strength that penalizes the cost function based on L2 regularization54,60. C for SVC stands for the penalty for SVC’s hyperplane margin in the cost function. A higher C characterizes a harder margin that tolerates fewer misclassifications (potential noise) according to its trained hyperplane. \(\gamma\) for SVC is a parameter in the Gaussian kernel (also known as Radio Basis Function) that defines how effective a single training sample is. These two parameters control the regularization but with a different approach. Both C (for LR and SVC) and \(\gamma\) should be positive floats54,60. We started the searching range from the default 1.0 (C) and 1/n_features (\(\gamma\)) in the log10 interval. n_estimators refer to the number of decision trees composing the forest (RF aggregation). A higher number of trees provides a higher randomization level and thus creates higher regularization. max_depth restricts the size of each decision tree to avoid overfitting54,60. We searched n_estimators from 100 to 5000 with a max_depth from 3 to 15 to find the optimal performance while compromising the computer memory consumption. The details of parameter searching are listed in Supplementary Figs. S3–5.

During each iteration of CV, the training set was split into two sets (second training and validation sets) following the splitting strategy. The 2nd training set was learned by a pipeline composed of feature engineering and algorithm with specific parameters to build a model. The model’s performance was evaluated by its accuracy for the validation set. Instead of using simple accuracy, which calculates the overall percentages of correct predictions, we used balanced accuracy, a macro-average of recall scores per class or, equivalently, the mean of accuracies from 11 facies62,63 for evaluation. This helps with the search for optimal parameters that build models predicting all facies fairly well rather than predicting the dominant facies only. A mean validation accuracy (CV score) was calculated after iterations, which is more robust in facing data heterogeneity. In total, 18 CV scores were collected from the best CV scores of each combination (3 kinds of data, with or without PCA, 3 algorithms).

Once the optimal parameters were decided based on CV results, these algorithms learned the whole training set to build optimal models. The test set was then used for evaluating the models’ performances. The performance was described by balanced accuracy, demonstrated in a modified confusion matrix, and the number of boundaries, describing the fragmentation problem of predicted facies.

Error analysis was also carried out on the test set to investigate the underlying causes of misclassifications and consequently prioritize possible improvements47. Misclassifications were thoroughly checked via both elemental profiles and images to summarize error categories. Each misclassification was given one or multiple error categories. In the end, the occurrence amount of each category was divided by the total amount of misclassification as frequency, i.e., the category’s contribution.

All computations and visualizations were conducted using the SciPy ecosystem in Python60,64,65,66,67,68. The function of providing model probability was adopted from the well-developed Scikit-learn package60.