Abstract
The paleoclimate record provides a test-bed in which climate models can be evaluated under conditions of substantial CO2 change; however, these data are typically under-used in the process of model development and evaluation. Here, we use a set of metrics based on paleoclimate proxy observations to evaluate climate models under three past time periods. We find that the latest CMIP6/PMIP4 ensemble mean does a remarkably good job of simulating the global mean surface air temperatures of these past periods, and is improved on CMIP5/PMIP3, implying that the modern climate sensitivity of the CMIP6/PMIP4 model ensemble mean is consistent with the paleoclimate record. However, some models, in particular those with very high or very low climate sensitivity, simulate paleo temperatures that are outside the uncertainty range of the paleo proxy temperature data; in this regard, the paleo data can provide a more stringent constraint than data from the historical record. There is also consistency between models and data in terms of polar amplification, with amplification increasing with increasing global mean temperature across all three time periods. The work highlights the benefits of using the paleoclimate record in the model development and evaluation cycle, in particular for screening models with too-high or too-low climate sensitivity across a range of CO2 concentrations.
Similar content being viewed by others
Introduction
Climate models are routinely applied to situations outside of the regimes in which they have been evaluated during their development cycle. For example, in the framework of the Coupled Model Intercomparison Project Phase 6 (CMIP6) and the Intergovernmental Panel on Climate Change (IPCC), models are used to project future climates under CO2 concentrations substantially higher than those of the recent observational period.
However, there is potential for traditional model evaluation and development to be expanded to utilise proxy data associated with paleoclimate states e.g.1,2,3,4,5,6. In particular, paleoclimate model simulations test model behaviour under a wide range of forcings, which encompass those expected in the timescale of the next few centuries and beyond7,8. The underlying philosophy is that we would expect to have more confidence in future predictions from a model which has successfully simulated both past and modern climate states, than future predictions from a model which has only successfully simulated the modern climate state.
Here we focus on three time periods, chosen firstly because they were subject to substantial CO2 forcing relative to preindustrial, so are of most direct relevance to future projections, and secondly because they have been part of ongoing international modelling efforts in the framework of the Paleoclimate Modelling Intercomparison Project (PMIP)9, so have simulations available from a variety of different climate models. The time periods are (i) the Last Glacial Maximum (LGM, 21,000 years ago), with a CO2 concentration of ~180 ppmv e.g.10 (compared to ~280 ppmv prior to industrialisation, and ~420 ppmv today), and an increase in ice sheet area and volume compared to today, in particular in the Northern Hemisphere e.g.11, (ii) interglacial KM5c within the mid-Pliocene warm period (MPWP; ~3.2 million years ago), with a CO2 concentration of ~400 ppmv e.g.12, and reduced Greenland and Antarctic ice sheets compared with today e.g.13, and (iii) the early Eocene climatic optimum (EECO; ~53.3–49.1 million years ago), with CO2 concentrations of ~1500 ppmv e.g.14, and no ice sheets. In general, older time periods have fewer locations with proxy data, and greater uncertainty in the proxy data that is available.
When evaluating climate models for the purposes of assessing their ability to project the future, the general approach is to focus on properties of the climate system that are routinely used to quantify the magnitude of future climate change, and which are robust inherent features that persist across a range of climate states15,16. It is also useful to evaluate properties that are determined by the combined effect of multiple components of the climate system (e.g. atmosphere, ocean, cryosphere) so that the integrated effect of the whole system can be assessed. Here, we focus on three large-scale properties: global mean surface temperature, polar amplification, and land–sea warming contrast. Global mean surface temperature (GMST) is the most fundamental metric and is a key focus of international agreements to limit global mean warming e.g.17. Changes in GMST are determined by processes throughout the atmosphere, ocean, and land surface; changes in GMST forced by CO2 alone can be quantified by the Equilibrium Climate Sensitivity (ECS)18. Polar amplification is also a key component of the climate system; the Arctic is currently warming at between 219 and 420 times that of the global mean, with associated impacts including sea level rise21. Polar amplification is determined by a range of processes22, including changes in heat transport23, sea ice/snow feedbacks24, and lapse-rate feedbacks25. Land-sea warming contrast has also been observed over the last 150 years, with 1.6 °C warming over land areas compared with 0.9 °C warming of SSTs, associated with a 1.1 °C GMST warming over the same period26. Land–sea warming contrast is associated with changes to the hydrological cycle and atmospheric circulation e.g.27,28, and the thermal contrast between land and ocean plays a role in monsoon circulations29.
Although these metrics are straightforward to define and quantify in a purely modelling or conceptual framework, estimating them from paleoclimate proxy records is challenging given their sparse distribution and large uncertainties e.g.30. This complicates model-data comparison and means that quantification of model improvements over time is problematic. Here we make use of assessed GMST estimates from the IPCC26, and additionally provide site-specific definitions for all the metrics, that are straightforward to apply in a paleo context (see Online methods, sections “Proxy datasets” and “Definition of metrics”), and apply the metrics to existing simulations from the fourth and third phase of the Paleoclimate Modelling Intercomparison Project (PMIP4, PMIP3). In doing so, we provide a benchmark for paleoclimate model simulations and assess improvements over time, including in some of the very latest CMIP6 models.
Results
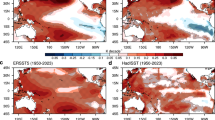
The spatial patterns of ensemble-mean (see Online methods, section “Model simulations”) modelled surface temperature change (near-surface air temperature and SST) are shown in Fig. 1, along with paleoclimate proxy estimates at the locations for which they are available (see Online methods, section “Proxy datasets”). In general, the sparsity of the proxy data increases further back in time. An exception is the terrestrial MPWP data, which is more sparse than the (earlier) EECO; this is because of the relatively narrow time period that is used in the Pliocene terrestrial reconstruction (a window of 30 kyr in the MPWP31 compared with 4120 kyr years in the EECO32; see Discussion section). Polar amplification (more warming in the polar regions than the tropics under increasing CO2) and land–sea warming contrast (more warming over land than over ocean under increasing CO2) are qualitatively apparent for all three time periods. However, in order to quantify these features in proxies and models, and in order to assess model-data comparison, quantitative metrics are required that account for the relative sparsity of the paleo proxy data. Here, we define and use two forms of metrics: firstly, ‘true’ metrics based on the globally defined fields, and secondly ‘site-specific’ metrics, which are defined according to a particular paleo proxy dataset and calculated according to the locations of the proxies (see Online methods, sections “Proxy datasets” and “Definition of metrics”).
Patterns of a, c, e near-surface air temperature (SAT), and b, d, f sea surface temperature (SST), in paleo proxies and models of the a, b last glacial maximum (LGM), c, d the mid-Pliocene warm period (MPWP), and the e, f early Eocene climatic optimum (EECO). Modelled ensemble-mean temperature anomalies compared with pre-industrial are shown in the background colours. Proxy near-surface air temperatures and SST anomalies are shown as coloured circles (see Online methods, section “Proxy datasets”). Note the differing colour scales for each map.
Global mean surface temperature (GMST)
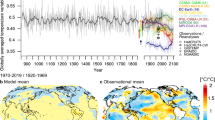
The true GMST metric (l,p,eΔTt) is shown in Fig. 2, for models and observations (see Online methods, sections “Proxy datasets” and “Definition of metrics”), for the three paleo time periods, and also for the Historical (1850–2014) and post-1975 (1975–2014) periods. The paleoclimate observed true GMST metrics are assessed values from the IPCC26; the equivalent site-specific global SAT and SST modelled and observed metrics (l,p,eΔTs) are shown in Supplementary Information, Fig. S1. First of all, it is interesting to note that in the observations, the ratio of mean temperature change to uncertainty in this change (i.e. the signal-to-noise ratio) is similar across the five time periods (Fig. 2, black circles and vertical error bars). The LGM has the largest signal-to-noise ratio for GMST, even larger than the historical record, indicating that it may be the most stringent target for model-data comparisons. This is associated with the fact that the LGM has a greater density of proxy data sites than the other paleo time periods. It is also important to note that the LGM has less uncertainty in the forcing boundary conditions than the other two paleo time periods (in particular CO2, for which ice core records e.g.10,33 give more accurate and precise values than is possible for the MPWP or EECO, where only indirect CO2 proxies are available). As such, the uncertainty in the GMST sensitivity to forcing for the Pliocene and EECO compared to the LGM is greater than would be implied from the uncertainties in GMST alone. However, the 5–7 °C IPCC assessment of LGM GMST cooling may be overly narrow; recent work has suggested a central GMST estimate of 4.5 °C of cooling (Fig. 2, black open circle and dashed range)34.
Global mean true surface temperature (GMST) anomaly, l,p,eΔTt in models and observations from five time periods. a post-1975, b Historical, c Last glacial maximum (LGM, l), d mid-Pliocene warm period (MPWP, p), and e early Eocene climatic optimum (EECO, e). Light grey circles show CMIP6/PMIP4 models with ECS in the very likely range as assessed by Forster et al.18; models in red have an ECS greater than the assessed very likely range (>5 °C); models in blue have an ECS lower than the assessed very likely range (<2 °C). Dark grey large circles show the multi-model ensemble mean for CMIP6/PMIP4. Dark grey small circles show the multi-model ensemble mean for CMIP5/PMIP3. Black circles and very likely ranges show the IPCC-assessed temperature anomaly derived from observations26. For the LGM, the black open circle with a dashed very likely uncertainty range shows the GMST anomaly estimate from Annan et al. 34. The historical anomaly in models and observations is calculated as the difference between 2005–2014 and 1850–1900, and the post-1975 anomaly is calculated as the difference between 2005–2014 and 1975–1984. For the LGM, MPWP and EECO, modelled temperature anomalies are compared with pre-industrial. The square symbol denotes the five simulations carried out by CESM2, and the triangle symbol denotes the three simulations carried out by CESM1.2. A version of this figure with all models labelled is in the Supplementary Information, Fig. S5, and all the models in this plot are listed in order of GMST in the Supplementary Information, Tables S1–S5. A similar plot of the paleo time periods, but also showing the site-specific metric, l,p,eΔTs, is shown in Supplementary Information, Fig. S1.
For each paleo time period, the multi-model mean GMST metric sits within the observed range, which is quite remarkable given that from the LGM to EECO this represents a temperature range of about 20 °C. However, the spread across the ensemble is relatively large, and many individual models sit outside the observed range (78%, 65%, 29% for the LGM, MPWP, and EECO respectively).
Previous studies have not always found a clear correlation between modern ECS and paleo GMST e.g.35,36. Although the ECS of every model in this study is not available, there is some indication that models with an ECS that is known to be greater than the IPCC-assessed range of 2–5 °C simulate too great a change in the paleo time periods (red dots in Fig. 2c–e). Similarly, models with an ECS that is known to be lower than this range simulate too small a change in GMST in the paleo time periods (blue dots in Fig. 2c–e). Only one model, CESM2, carried out simulations across all five time periods. Apart from that, CESM1.2 is the only model that carried out simulations across all three paleo time periods. The results from these two models, highlighted in Fig. 2, indicate consistency in relative GMST changes across the paleo time periods for a particular model. However, more models carrying out simulations across multiple paleo time periods would allow this to be explored further, and allow emergent constraints on ECS37 from multiple time periods to be developed. This would also require all PMIP models to carry out 4 × CO2 simulations alongside their paleo simulations in order to calculate their ECS.
It also appears that both high and low ECS models can simulate the Historical period in good agreement with observations (Fig. 2b), and low ECS models can simulate the post-1970 warming (Fig. 2a). Therefore, paleoclimates may be a better discriminator of high- and low-ECS models than the observational periods (which is consistent with findings from an assessment of ECS that included paleoclimate evidence38). This may be due to the fact that the paleoclimate simulations are close to equilibrium with the CO2 forcing, whereas the Historical simulations are transient and as such, have a GMST that is influenced by a transient pattern effect e.g.39, and/or it may be related to uncertainties in the aerosol forcing over the historical period40. However, more paleo simulations are required to further confirm this relation. In particular, there is a need for more paleo model simulations to be carried out with the same models that carry out the Historical CMIP simulations (this lack of consistency between the CMIP6 and PMIP4 model ensembles arises, at least in part, due to the long integration lengths required for full equilibrium of paleoclimate simulations).
It is also apparent that for all three paleo time periods, there has been an improvement in the modelled GMST in the PMIP4/CMIP6 paleoclimate model simulations compared with the previous CMIP5/PMIP3 simulations (large versus small dark grey dots in Fig. 2c–e). This improvement is likely due to a combination of updated boundary conditions, and improvements to the models themselves. Key changes in boundary conditions in PMIP4 compared with PMIP3 include updated ice sheets for the LGM41, updated palaeogeography and representation of ocean gateways for the Pliocene42, and a consistent experimental design for the EECO including a new palaeogeography43. It is harder to robustly identify particular model improvements that may be relevant, because there is no clear lineage between the models in PMIP3 and PMIP4, but, for some models at least, improvements in model representation of cloud microphysics are playing an important role e.g.44,45.
Polar amplification
The site-specific polar amplification metric (see Online methods, section “Definition of metrics”), (l,p,eΔPs), is shown in Fig. 3a. Because the MPWP and EECO are warmer than the preindustrial whereas the LGM is colder, the observed site-specific metric from proxies is positive for the EECO and MPWP but is negative for the LGM (black circles in Fig. 3; in the Online methods, see the subsection “Proxy datasets” for a description of how the error bars are calculated). For all three time periods, this indicates a polar amplification associated with increasing temperature (i.e. a decrease in meridional temperature gradient with increasing temperature).
Site-specific metrics for a SST polar amplification (l,p,eΔPs) and b land–sea warming contrast (l,p,eΔLs), for last glacial maximum (LGM, l), mid-Pliocene Warm Period (MPWP, p), and early Eocene climatic optimum (EECO, e). Black circles and very likely ranges show the observed site-specific metric (s), dark grey circles show the model ensemble mean site-specific metric (large circles for CMIP6/PMIP4 and small circles for CMIP5/PMIP3), and light-grey/red/blue circles show the individual CMIP6/PMIP4 model site-specific metric. The EECO observed metric shown with an open circle and dotted error bar excludes SST data from the southwest Pacific. All metrics are calculated relative to the preindustrial. See Supplementary Information, Fig. S2, for a version that also includes the site-specific metrics.
For the LGM, the proxies indicate a site-specific SST polar amplification of about −0.4 °C, whereas the model ensemble mean indicates a greater amplification of −0.7 °C (large dark grey circles in Fig. 3a). The proxy value sits within the model range, but the model range is large compared with the uncertainty range from the proxies, from 0.1 °C (IPSLCM5A2) to −1.4 °C (CESM2). For the MPWP and EECO, the polar amplification indicated by the proxies is greater than in any of the models, although for the MPWP two models do get close to the observed value of 1.7 °C and are within the uncertainty range of the proxy metric. For the EECO, the model-data disagreement is much starker, with nearly double the polar amplification in the proxies (12 °C) than in the model with the greatest value (CESM2; 7 °C). This discrepancy is primarily because of exceptionally warm proxy temperatures in the southwest Pacific. Many reasons for possible warm biases in the proxy temperatures in this region have been proposed, including a seasonal bias in mid- and high-latitude SST proxies32,46, and/or uncertainties in the functional form of different paleo-temperature proxies (e.g., TEX86) in the upper-temperature range47,48. Since data from this region represent a large number of the high latitude records available from the EECO, they bias the proxy-based metric towards extremely high values. With the SSTs from the southwest Pacific excluded, the proxy polar amplification decreases from 12 to 4 °C, and the model and data are in closer agreement (see Supplementary Information, Fig. S2a). Note that our site-specific proxy-based metrics are not comparable with previous estimates of Eocene polar amplification e.g.44,49, which were based on Mg/Ca estimates of deep ocean temperatures, and designed to be comparable with true model metrics.
There has been little change in the ensemble mean LGM or EECO SST polar amplification between PMIP4 and PMIP3 (Fig. 3a, compare large and small dark grey circles), although improvements in cloud parameterisations since PMIP3 have been shown to improve the simulation of polar amplification in the EECO for individual models44,50. However, for the Pliocene, there has been a substantial improvement. At least some of this improvement is likely related to the closure of the Bering Strait in the PMIP4 experimental design, which has been shown to increase Pliocene temperatures in the North Atlantic51. However, the proxies still indicate greater amplification than the models (0.8 °C for PMIP4 and 0.25 °C for PMIP3, compared with 1.7 °C in the proxies).
For all three time periods, the site-specific polar amplification metric (l,p,eΔPs) has a similar value to the true metric l,p,eΔPt for most models (see Supplementary Information, Fig. S2a). Across the ensemble, the true metric is greater than the site-specific metric in the MPWP (by 0.05 °C), and less than the site-specific metric in the EECO (by 0.4 °C); indicating that despite the sparsity of the proxy data, there is enough data for the site-specific polar amplification metric to be meaningful. However, the exception to this is for the CESM2 model at the LGM (red dot and star in the LGM panel of Supplementary Information, Fig. S2a), where the site-specific metric (−1.4 °C) is very different, and even of opposite sign, to the true metric (0.3 °C). This is because although the CESM2 LGM ΔT metric is greater than any other model (Fig. 2), the LGM polar SSTs can not drop below the freezing point of seawater, resulting in relatively low polar amplification in the true metric (see Supplementary Information, Fig. S3b).
There is not enough proxy SAT data in the tropics to define an SAT polar amplification metric for the MPWP or the EECO, and there is not enough data in the Southern Hemisphere to define a global SAT polar amplification metric for the LGM. However, it is possible to quantify the absolute changes in high-latitude SATs for all three time periods (see Supplementary Information, Fig. S4a–c), and for the LGM a Northern Hemisphere-only polar amplification metric can be defined (see Supplementary Information, Fig. S4a). This shows that the Northern Hemisphere LGM polar amplification is very well simulated by the PMIP4 model ensemble mean (−4.1 °C) compared with the proxies (−4.2 °C). For the Pliocene, the model ensemble is colder than the proxies in general in the Northern Hemisphere high latitudes, related to less warmth in the Eurasian and Northern America continental interiors than indicated by the proxies. It has been suggested that the warm proxy temperatures in this region may be related to seasonal biases and/or the lack of modern analogues for the associated pollen records52. For the EECO, the Southern Hemisphere high latitude terrestrial temperatures are well simulated by the ensemble mean, which further supports that the Southwest Pacific SSTs proxy temperatures are biased too warm. For the Northern Hemisphere, the models simulate a greater polar amplification than the proxies, but this is largely due to a set of proxy temperatures at 45°N in North America, which are relatively cold and may be influenced by the local topography of the Rockies.
Land-sea warming contrast (LSWC)
The site-specific land–sea warming contrast (LSWC) metrics, (l,p,eΔLs), are shown in Fig. 3b. The proxies indicate a negative (positive) LSWC for the LGM (MPWP), indicating that for both these time periods the land surface SAT warms more than the ocean SST under warming GMST. However, for the EECO the proxies indicate a negative LSWC under warming GMST. Again, this is related to the super warm southwest Pacific proxy SST temperatures, and discounting SSTs from that region results in a positive LSWC for the EECO (see open circle and dotted error bars in Fig. 3b, and see Supplementary Information, Fig. S2b). The terrestrial proxies for the Eocene are from a wider time window (56.0–47.8 Ma) than the marine proxies (53.3–49.1 Ma)32, and in many cases have uncertain paleoaltitude, and so this may also be playing a role. For both the LGM and MPWP, the model ensemble has a lower magnitude LSWC than the proxies, and this discrepancy is greater in the PMIP4/CMIP6 models than in the PMIP3/CMIP5 models. For the MPWP, the proxy SAT locations are all in the mid-latitudes of the Northern Hemisphere, and as discussed above, in this region the models simulate colder temperatures than indicated by the proxies (see Supplementary Information, Fig. S4b), and it is this discrepancy which leads to the discrepancy in land–sea warming contrast. The model site-specific and true metrics differ from each other quite considerably (see Supplementary Information, Fig. S2b), with the true metrics being lower than the site-specific metrics for all time periods by 70%, 50%, and 40% for the LGM, MPWP, and EECO, respectively.
Discussion
There is a remarkable relationship between the modelled GMST metric, ΔT, and the polar amplification metric, ΔP, across the three time periods, in both the site-specific and true metrics (Fig. 4a). This is also supported in the proxies, in particular when the southwest Pacific sites are excluded from the EECO; in this case, both models and proxies point to an approximately linear relationship between the two metrics. The fact that this relationship is so linear is surprising given the greatly reduced (or non-existent) sea ice in the EECO, indicating that other mechanisms of polar amplification (for example related to cloud feedbacks) are compensating for each other across different time periods, resulting in the linear relationship. This relationship is also seen in proxy estimates of global mean temperature and meridional temperature gradient from across the last 95 million years53.
Relationship between metrics for a GMST (l,p,eΔTt,s) and polar amplification (l,p,eΔPt,s), and b GMST and land–sea warming contrast (l,p,eΔLt,s), for the last glacial maximum (LGM; blue, l), mid-Pliocene warm period (MPWP; orange, p), and early Eocene climatic optimum (EECO; red, e). Large circles and very likely ranges show the observed site-specific metric (s), small circles show the model site-specific metric for all CMIP6/PMIP4 models, and stars show the true model metric (t) for all CMIP6/PMIP4 models. The square shows the preindustrial. The EECO observed metric shown with an open circle excludes SST data from the southwest Pacific.
In the models, there is also a clear relationship between the GMST metric and the LSWC metric (Fig. 4b). In this case, there is a non-linear relationship, with LSWC increasing at lower GMST, but then flattening out under the high temperatures of the EECO. This relationship, including saturation, is consistent with a theory based on contrasting surface humidities and lapse rates over land and ocean28. The LGM proxy data is consistent with this relationship, but Pliocene LSWC in the proxies is greater than in the models, even accounting for the error bars in the proxy metric. In the EECO, the proxies indicate a complete reversal in this relationship, but when the EECO southwest Pacific sites are excluded again, the models and proxies are more consistent, especially accounting for the large error bars of the EECO proxy estimates of GMST and LSWC.
In this paper, we have used metrics derived from paleo proxy data to evaluate climate model simulations of the LGM, MPWP, and EECO. We find that model ensemble mean GMSTs are in exceptionally good agreement with the proxy data for all three paleo time periods, and that this agreement has improved in CMIP6/PMIP4 compared to CMIP5/PMIP3. The LGM is shown to be a very stringent target for model evaluation and development due to its large signal-noise ratio, and well-defined boundary conditions. There are indications that model evaluation using the paleo proxy record can be a better discriminator of models with very high or very low climate sensitivity than using the Historical observational period. Models also simulate polar amplification, and the relationship between GMST and polar amplification, in reasonable agreement with proxies. However, there are uncertainties associated with the proxy records in (i) the MPWP within the northern hemisphere continental interiors, and ii) during the EECO, particularly in the southwest Pacific. In addition, some proxy terrestrial sites are from high-elevation regions that are not resolved in the models, or, for the EECO, are from regions for which the paleoelevation is uncertain. Furthermore, the relatively wide temporal window of the EECO (~4.1 Myr) means that the proxy signal is affected by orbital forcing and temporal variations in CO2. All of these proxy uncertainties should be further explored in future work in order to maximise the utility of the paleoclimate proxy record for model development. Land-sea warming contrast is reasonably well simulated at the LGM, but less so at the MPWP and EECO. The models indicate an increasing but saturating relationship between GMST and LSWC, consistent with theory.
Overall, the paper provides a framework for paleo model evaluation that can be used for future model development in the framework of CMIP7 and beyond6,8,54. The framework also provides a traceability to previous model generations, allowing a robust assessment of model improvements over time, through successive model development cycles.
Online methods
Model simulations
The most recent experimental designs for the three time periods above are described in detail in ref. 41 for the LGM, ref. 42 for the MPWP, and ref. 43 for the EECO. These experimental designs describe standard boundary conditions (e.g. CO2, non-CO2 greenhouse gases, ice sheets, and vegetation) to be implemented in models and protocols for the simulations themselves (e.g. run length and initial conditions). Simulations carried out using these experimental designs are all classified here as PMIP4/CMIP6 simulations. The models that carried out these PMIP4 simulations are of varying complexity and include models developed for use in CMIP6, as well as earlier iterations of CMIP. The large-scale features of these PMIP4 simulation results are discussed in ref. 4 for the LGM, ref. 1 for the MPWP (as part of the PlioMIP2 project), and ref. 3 for the EECO (as part of the DeepMIP project). Simulation results are also presented for previous model simulations in the framework of PMIP3/CMIP5, described in ref. 4 for the LGM31, for the MPWP, and ref. 55 for the EECO. Tables listing all the simulations used in this paper are given in Supplementary Information, Tables S1–S5.
Note that for the EECO, the NorESM1_F model uses palaeogeography with a different reference frame than the other models and, as such, is only included in the GMST metric and not in the polar amplification or land–sea warming contrast metrics, which are reference frame-specific. Also for the EECO, there are fewer models presented here than in ref. 3. This is because here we only include those models that carried out simulations in the range ×4–×8 preindustrial levels of CO2, in accordance with CO2 proxy estimates for the EECO3. The exception is CESM2.1slab, which we include for context and which was run at ×3.
Proxy datasets
In order to evaluate the model simulations, we use existing syntheses and compilations of paleo proxy data for all three time periods.
For the GMST metric, we make use of the IPCC AR6 assessments of GMST change for the three paleo time periods26. These are based on a thorough review of the literature and are designed to be global metrics directly comparable with the global mean output from models (i.e., they are ‘true’ metrics, see Online methods, section “Definition of metrics”). For the LGM, we also include the GMST metric of ref. 34.
For the polar amplification and land–sea warming contrast metric, we use site-based data; for the LGM, we use ref. 56 for the sea surface temperatures (SSTs) and ref. 57 (at the locations defined in ref. 58, which are the actual proxy locations that inform the global assimilated dataset of ref. 57) for the land air temperatures (LATs). For the MPWP we use ref. 59 for the SSTs and ref. 60 for the LATs. For the EECO we use ref. 61 for the SSTs and LATs.
Definition of metrics
For changes in GMST, polar amplification, and land-sea warming contrast, we can define two types of quantitative metrics. Firstly, ‘true’ quantities, Qt, which in theory require SST, LAT and near-surface air temperature (SAT) values to be defined over the entire ocean and globe respectively (i.e. at all gridcells of a model or global gridded observational dataset). SSTt is the ocean-only true global mean SST; LATt is the land-only true global mean SAT; and SATt is the true global mean SAT. Secondly, ‘site-specific’ means; SSTs, LATs, and SATs. These are similar to the true quantities, but rather than averaging over all gridcells they are defined according to a particular paleo proxy dataset and are averaged only over those cells/locations that include at least one proxy data point in that dataset. True quantities, Qt, can, in theory, only be defined for globally gridded output, whereas site-specific quantities, Qs can be defined either for global model output or for proxy datasets. In practice, the IPCC-assessed paleoclimate GMST metrics are also considered to be ‘true’ metrics, as discussed in the section “Proxy datasets”. Site-specific quantities are simply the average of the temperatures at each site in the proxy dataset. All quantities can be defined for a particular time period (x, where x can be e for EECO, p for MPWP, l for LGM, or pi for preindustrial) and can also be defined for selected latitude ranges (r), \(\scriptstyle{{x}\atop{\rm {r}}}Q\), so that, for example, the site-specific mean SST in the range 90S to 30S during the EECO, is written \(\scriptstyle{\hskip14pt{{\rm{e}}}\atop{{-90:-30}}}{\rm{SST}}^{s}\).
We then define three key metrics as a function of these quantities. In particular, the change in true or site-specific (t,s) mean temperature relative to the preindustrial (ΔT), for the LGM (l), MPWP (p), or EECO (e) is
for SAT, and similarly for SST and LAT. The polar amplification metric (ΔP) is
for SST, and similarly for LAT. The land–sea warming contrast metric (ΔL) is
The proxy compilations that we use are published with associated uncertainties in temperature for each individual site. However, the meaning of these uncertainty ranges is unclear in some cases, and inconsistent across different time periods. Here we interpret all published uncertainties as representing a range of uniformly distributed uncertainty. In order to estimate the associated uncertainty in the polar amplification and land-sea warming contrast site-specific proxy metrics that we present, we use Monte Carlo sampling to generate 100 proxy datasets and use these to generate 100 associated metrics, from which we report a mean and a 90% uncertainty range (consistent with the IPCC ‘very likely’ range).
Developments since IPCC AR6
IPCC AR6 includes a figure showing ensemble mean maps and zonal means of the SST and SAT data analysed in this paper (ref. 18, Fig. 7.13 therein). Compared with the IPCC figure, here we have carried out some developments, and incorporated these into our overall analysis: (1) Here, in Supplementary Information, Fig. S4, the horizontal lines showing the banded mean SSTs, and the values given in the plot for the values of the polar amplification associated with these bands, are calculated using the ensemble mean SSTs only for those gridboxes where all models have an ocean grid ocean (cdo operator ‘ensaver’). In the equivalent IPCC plot, the values given are the same as in Fig. S1, but the horizontal lines were calculated using the mean of the models for all gridboxes for which at least one model had ocean (cdo operator ‘ensmean’). (2) Here, for extracting the modelled SST at the location of a proxy, for SST proxy locations that are defined as land in the models, the nearest ocean gridcell is used to define the model value. In the IPCC, due to a coding error, the nearest-but-one ocean gridcell was used. (3) Here, we assign an uncertainty of ±5 °C for any proxy data that does not have an associated uncertainty in the original reference. In the IPCC, due to a coding error, an error of zero was assigned. (4) Here, with the exception of NorESM stated above, all models are used to calculate all three metrics. In the IPCC, the EECO CESM2.1slab simulation was not included in the map of the ensemble mean map or in the plot of the zonal mean.
Data availability
All model outputs and proxy data used in this study are available from the IPCC AR6 Data Distribution Centre (https://www.ipcc-data.org/), in the archive for Fig. 7.13 of WG1 (https://ipcc-browser.ipcc-data.org/browser/dataset/7509/0; https://doi.org/10.5285/4dbd3ccb85d747188586735133f1d3d9).
Code availability
The code for carrying out the analysis and making the plots is available from https://github.com/danlunt1976/ipcc_ar6/blob/master/patterns/fgd/plot_all_metrics.pro, version fb09c5e.
References
Haywood, A. et al. What can palaeoclimate modelling do for you? Earth Syst. Environ. 3, 1–18 (2019).
Haywood, A. M. et al. The Pliocene Model Intercomparison Project Phase 2: large-scale climate features and climate sensitivity. Clim. Past 16, 2095–2123 (2020).
Lunt, D. J. et al. DeepMIP: model intercomparison of early Eocene climatic optimum (EECO) large-scale climate features and comparison with proxy data. Clim. Past 17, 203–227 (2021).
Kageyama, M. et al. The PMIP4 Last Glacial Maximum experiments: preliminary results and comparison with the PMIP3 simulations. Clim. Past 17, 1065–1089 (2021).
Zhu, J. et al. LGM paleoclimate constraints inform cloud parameterizations and equilibrium climate sensitivity in CESM2. J. Adv. Model. Earth Syst. 14, e2021MS002776 (2022).
Burls, N. & Sagoo, N. Increasingly sophisticated climate models need the out-of-sample tests paleoclimates provide. J. Adv. Model. Earth Syst. 14, e2022MS003389 (2022).
Burke, K. D. et al. Pliocene and Eocene provide best analogs for near-future climates. Proc. Natl Acad. Sci. USA 115, 13288–13293 (2018).
Tierney, J. E. et al. Past climates inform our future. Science 370, eaay3701 (2020).
Kageyama, M. et al. The PMIP4 contribution to CMIP6—part 1: Overview and over-arching analysis plan. Geosci. Model Dev. 11, 1033–1057 (2018).
Luthi, D. et al. High-resolution carbon dioxide concentration record 650,000–800,000 years before present. Nature 453, 379–382 (2008).
Peltier, W. R., Argus, D. F. & Drummond, R. Space geodesy constrains ice age terminal deglaciation: the global ICE-6G_C (VM5a) model. J. Geophys. Res.: Solid Earth 120, 450–487 (2015).
Vega, E. D. L., Chalk, T. B., Wilson, P. A., Bysani, R. P. & Foster, G. L. Atmospheric CO2 during the mid-Piacenzian warm period and the M2 glaciation. Sci. Rep. 10, 1–8 (2020).
Dolan, A., de Boer, B., Bernales, J., Hill, D. & Haywood, A. High climate model dependency of Pliocene Antarctic ice-sheet predictions. Nat. Commun. 9, 2799 (2018).
Anagnostou, E. et al. Proxy evidence for state-dependence of climate sensitivity in the Eocene greenhouse. Nat. Commun. 11, 4436 (2020).
Izumi, K., Bartlein, P. J. & Harrison, S. P. Consistent large-scale temperature responses in warm and cold climates. Geophys. Res. Lett. 40, 1817–1823 (2013).
Drost, F., Karoly, D. & Braganza, K. Communicating global climate change using simple indices: an update. Clim. Dyn. 39, 989–999 (2012).
United Nations Framework Convention on Climate Change (UNFCCC). The Paris Agreement https://unfccc.int/sites/default/files/resource/parisagreement_publication.pdf (United Nations Framework Convention on Climate Change (UNFCCC), 2016).
Forster, P. et al. The Earth’s Energy Budget, Climate Feedbacks, and Climate Sensitivity 923–1054 (Cambridge University Press, Cambridge, UK and New York, NY, USA, 2021).
Walsh, J. E. Intensified warming of the Arctic: causes and impacts on middle latitudes. Global Planet. Change 117, 52–63 (2014).
Rantanen, M. et al. The Arctic has warmed nearly four times faster than the globe since 1979. Commun. Earth Environ. 3, 168 (2022).
Fox-Kemper, B. et al. Ocean, Cryosphere and Sea Level Change 1211–1362 (Cambridge University Press, Cambridge, UK and New York, NY, USA, 2021).
Previdi, M., Smith, K. L. & Polvani, L. M. Arctic amplification of climate change: a review of underlying mechanisms. Environ. Res. Lett. 16, 093003 (2021).
Armour, K. C., Siler, N., Donohoe, A. & Roe, G. H. Meridional atmospheric heat transport constrained by energetics and mediated by large-scale diffusion. J. Clim. 32, 3655–3680 (2019).
Graversen, R. G., Langen, P. L. & Mauritsen, T. Polar amplification in ccsm4: contributions from the lapse rate and surface albedo feedbacks. J. Clim. 27, 4433–4450 (2014).
Pithan, F. & Mauritsen, T. Arctic amplification dominated by temperature feedbacks in contemporary climate models. Nat. Geosci. 7, 181–184 (2014).
Gulev, S. et al. Changing State of the Climate System, 287–422 (Cambridge University Press, Cambridge, United Kingdom and New York, NY, USA, 2021).
Joshi, M. & Gregory, J. Dependence of the land-sea contrast in surface climate response on the nature of the forcing. Geophys. Res. Lett. 35, https://agupubs.onlinelibrary.wiley.com/doi/abs/10.1029/2008GL036234 (2008).
Byrne, M. P. & O’Gorman, P. A. Link between land-ocean warming contrast and surface relative humidities in simulations with coupled climate models. Geophys. Res. Lett. 40, 5223–5227 (2013).
Zuo, Z. & Zhang, K. Link between the land–sea thermal contrast and the Asian summer monsoon. J. Clim. 36, 213–225 (2023).
Gebbie, G., Streletz, G. J. & Spero, H. J. How well would modern-day oceanic property distributions be known with paleoceanographic-like observations? Paleoceanography 31, 472–490 (2016).
Haywood, A. et al. On the identification of a Pliocene time slice for data-model comparison. Philos. Trans. R. Soc. Lond. A 371, 20120515 (2013).
Hollis, C. J. et al. Early Paleogene temperature history of the southwest Pacific Ocean: reconciling proxies and models. Earth Planet. Sci. Lett. 349-350, 53–66 (2012).
Monnin, E. et al. Atmospheric CO2 concentrations over the last glacial termination. Science 291, 112–114 (2001).
Annan, J. D., Hargreaves, J. C. & Mauritsen, T. A new global surface temperature reconstruction for the last glacial maximum. Clim. Past 18, 1883–1896 (2022).
Renoult, M., Sagoo, N., Zhu, J. & Mauritsen, T. Causes of the weak emergent constraint on climate sensitivity at the last glacial maximum. Clim. Past 19, 323–356 (2023).
Hargreaves, J. C. & Annan, J. D. Could the Pliocene constrain the equilibrium climate sensitivity? Clim. Past 12, 1591–1599 (2016).
Renoult, M. et al. A Bayesian framework for emergent constraints: case studies of climate sensitivity with PMIP. Clim. Past 16, 1715–1735 (2020).
Sherwood, S. C. et al. An assessment of Earth’s climate sensitivity using multiple lines of evidence. Rev. Geophys. 58, e2019RG000678 (2020).
Dong, Y. et al. Intermodel spread in the pattern effect and its contribution to climate sensitivity in CMIP5 and CMIP6 models. J. Clim. 33, 7755–7775 (2020).
Bellouin, N. et al. Bounding global aerosol radiative forcing of climate change. Rev. Geophys. 58, e2019RG000660 (2020).
Kageyama, M. et al. The PMIP4 contribution to CMIP6—Part 4: scientific objectives and experimental design of the PMIP4-CMIP6 Last Glacial Maximum experiments and PMIP4 sensitivity experiments. Geosci. Model Dev. 10, 4035–4055 (2017).
Haywood, A. M. et al. The Pliocene Model Intercomparison Project (PlioMIP) Phase 2: scientific objectives and experimental design. Clim. Past 12, 663–675 (2016).
Lunt, D. J. et al. The DeepMIP contribution to PMIP4: experimental design for model simulations of the EECO, PETM, and pre-PETM (version 1.0). Geosci. Model Dev. 10, 889–901 (2017).
Zhu, J., Poulsen, C. J. & Tierney, J. E. Simulation of Eocene extreme warmth and high climate sensitivity through cloud feedbacks. Sci. Adv. 5, eaax1874 (2019).
Feng, R., Otto-Bliesner, B. L., Brady, E. C. & Rosenbloom, N. Increased climate response and earth system sensitivity from CCSM4 to CESM2 in mid-Pliocene simulations. J. Adv. Model. Earth Syst. 12, e2019MS002033 (2020).
Davies, A., Hunter, S. J., Gréselle, B., Haywood, A. M. & Robson, C. Evidence for seasonality in early Eocene high latitude sea-surface temperatures. Earth Planet. Sci. Lett. 519, 274–283 (2019).
Cramwinckel, M. J. et al. Synchronous tropical and polar temperature evolution in the Eocene. Nature 559, 382–386 (2018).
Inglis, G. & Tierney, J. E. The TEX86 Paleotemperature Proxy (Cambridge University Press, 2020).
Evans, D. et al. Eocene greenhouse climate revealed by coupled clumped isotope-mg/ca thermometry. Proc. Natl Acad. Sci. USA 115, 1174–1179 (2018).
Kiehl, J. T. & Shields, C. A. Sensitivity of the palaeocene–eocene thermal maximum climate to cloud properties. Philos. Trans. R. Soc. A 371, 20130093 (2013).
Otto-Bliesner, B. L. et al. Amplified North Atlantic warming in the late Pliocene by changes in Arctic gateways. Geophys. Res. Lett. 44, 957–964 (2017).
Tindall, J. C., Haywood, A. M., Salzmann, U., Dolan, A. M. & Fletcher, T. The warm winter paradox in the Pliocene northern high latitudes. Clim. Past 18, 1385–1405 (2022).
Gaskell, D. E. et al. The latitudinal temperature gradient and its climate dependence as inferred from foraminiferal δ18O over the past 95 million years. Proc. Natl Acad. Sci. USA 119, e2111332119 (2022).
Zhu, J., Poulsen, C. J. & Otto-Bliesner, B. L. High climate sensitivity in CMIP6 model not supported by paleoclimate. Nat. Clim. Change 10, 378–379 (2020).
Lunt, D. J. et al. A model-data comparison for a multi-model ensemble of early Eocene atmosphere-ocean simulations: EoMIP. Clim. Past 8, 1717–1736 (2012).
Tierney, J. E. et al. Glacial cooling and climate sensitivity revisited. Nature 584, 569–573 (2020).
Cleator, S. F., Harrison, S. P., Nichols, N. K., Prentice, I. C. & Roulstone, I. A new multivariable benchmark for Last Glacial Maximum climate simulations. Clim. Past 16, 699–712 (2020).
Bartlein, P. et al. Pollen-based continental climate reconstructions at 6 and 21 ka: a global synthesis. Clim. Dyn. 37, 775–802 (2011).
McClymont, E. L. et al. Lessons from a high-Co2 world: an ocean view from ~3 million years ago. Clim. Past 16, 1599–1615 (2020).
Salzmann, U. et al. Challenges in quantifying Pliocene terrestrial warming revealed by data-model discord. Nat. Clim. Change 3, 969–974 (2013).
Inglis, G. N. et al. Global mean surface temperature and climate sensitivity of the early Eocene Climatic Optimum (EECO), Paleocene–Eocene Thermal Maximum (PETM), and latest Paleocene. Clim. Past 16, 1953–1968 (2020).
Acknowledgements
D.J.L. acknowledges NERC grants NE/P01903X/1 (SWEET: Super-Warm Early Eocene Temperatures and climate: understanding the response of the Earth to high CO2 through integrated modelling and data) and NE/X000222/1 (PaleoGradPhan: Paleoclimate meridional and zonal Gradients in the Phanerozoic). G.N.I. is supported by a GCRF Royal Society Dorothy Hodgkin Fellowship (DHF/R1/191178) with additional support via the Royal Society (RF/ERE/231019, RF/ERE/210068). U.S. acknowledges NERC grant NE/P019137/1. The CESM project is supported primarily by the National Science Foundation (NSF). This material is based upon work supported by the National Center for Atmospheric Research, which is a major facility sponsored by the NSF under Cooperative Agreement No. 1852977. Computing and data storage resources, including the Cheyenne supercomputer (doi:10.5065/D6RX99HX), were provided by the Computational and Information Systems Laboratory (CISL) at NCAR. DJL acknowledges support provided through an NCAR affiliate scientist appointment. All authors acknowledge CMIP6/PMIP4 and the associated infrastructure that makes model intercomparisons possible, and all the modelling groups that contributed to simulations that have been included in this study.
Author information
Authors and Affiliations
Contributions
D.J.L. carried out the analysis and wrote the first draft of the paper. B.L.O.B., C.B., A.H., G.N.I., K.I., M.K., D.K., T.M., E.L.Mc.C., U.S., S.S., J.E.T., A.Z., and J.Z. discussed the paper and provided edits.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests.
Peer review
Peer review information
Communications Earth & Environment thanks Thomas Chalk and the other, anonymous, reviewer(s) for their contribution to the peer review of this work. Primary Handling Editors: Olivier Sulpis and Carolina Ortiz Guerrero. A peer review file is available.
Additional information
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Lunt, D.J., Otto-Bliesner, B.L., Brierley, C. et al. Paleoclimate data provide constraints on climate models' large-scale response to past CO2 changes. Commun Earth Environ 5, 419 (2024). https://doi.org/10.1038/s43247-024-01531-3
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s43247-024-01531-3
This article is cited by
-
Ocean drilling makes for more robust climate modelling of the future
Nature Geoscience (2024)