Introduction

Sandy lakes in deserts or desert transition zones provide important ecological functions for regional climate regulation, species habitat and migration, and biodiversity maintenance1. Owing to consumptive water use and increased frequency and severity of droughts in arid and semiarid regions with climate change, some sandy lakes are shrinking at alarming rates, with subsequent changes in chemical (e.g., salinization) and biological (e.g., reduced biodiversity) characteristics, threatening the ecosystem services of sandy lakes and even leading to the disappearance of lakes, such as the Lop Nor and the Aral Sea2,3,4. Studying the structure and dynamics of lake ecosystems under multiple stressors, including warming, anthropogenic nutrient enrichment, and shrinkage, has increased fundamental understanding of how global change alters lake ecosystems, as well as how to save shrinking sandy lakes1,5. Many lake ecosystems experiencing warming reach a critical state in which slight increases in nutrient levels can trigger drastic ecosystem changes6,7. However, we still lack a comprehensive perspective on the nonlinear responses of multitrophic biodiversity and the dynamics of ecological networks in lake ecosystems under multiple stressors.

Understanding of the dynamics of lake ecological networks under multiple, continuous stressors is partially limited by the scarcity of long-term, well-organized time series of complete multitrophic ecological interactions5,8. Most studies focus on only one or few groups (e.g., bacteria, algae, or fish) and thereby ignore cascade effects of food webs, such as the loss of some important species causing the extinction of others9,10,11,12. Furthermore, a biological community is not a simple arithmetic sum of species but an ecological network formed by interactions of species within a community13,14. Most studies examine single types of interactions (e.g., trophic, mutualistic, or competitive) or interactions between two functional groups, such as bipartite herbivore–plant networks15. This partiality may be due to methodological constraints, because it is difficult to measure interactions in a standardized and comparable manner across a wide range of taxonomic groups, let alone across environmental gradients in an ecosystem in the field. Recently, the combination of a meta-web with empirical species cooccurrence has been used as an efficient tool to study multitrophic ecological networks13. The advantage of this approach is that network links or nodes are built on a knowledge-based regional meta-web (based on literature and expert knowledge)16,17. However, this practice often assumes that species interactions are fixed and constant over time. Therefore, an equation-free modeling approach may be more conducive to reveal the nonlinear, dynamic responses of ecological networks under multiple environmental stressors5,18.

The effects of simultaneous environmental stressors on lake communities often differ in intensity or direction, depending on differences in spatial diffusion constraints and species interaction strengths16,18,19. For example, on one hand, high nutrient concentrations can promote primary producer biomass and energy transfer across trophic levels, whereas on the other hand, they can act as a strong filter factor, leading to a reduction in biodiversity or keystone species5,20. Because ecological metabolism theory predicts that activity of individual metabolic processes and organism growth increase with increasing temperature, warming can stimulate various biological interactions (predation, parasitism, competition, symbiosis) and thus increase the complexity of species associations21,22. By contrast, increases in temperature and associated environmental changes (e.g., increased evaporation) can act as powerful filters against existing species, leading to reductions in lake biodiversity and even possible collapse of ecological networks, as recently reported in artificial pond food webs17,23. In the case of shrinking sandy lakes, evaporation of water is greater than recharge, resulting in decreased water volume and increased salinity. However, understanding of the combined effects of changes in nutrient load, warming, and lake shrinkage on the multitrophic ecological networks of sandy lakes remains elusive.

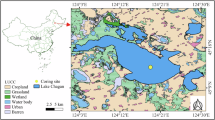
Recent advances in the meta-barcoding of sedimentary DNA (sedDNA) greatly improve insights into the complete taxonomic biodiversity across multiple trophic levels at a wide range of time scales24,25,26. Here, we used a sedDNA approach to address the gap in understanding of the dynamic responses of biodiversity and ecological networks to multiple stressors in Lake Hongjiannao, the largest desert freshwater lake in China, at high taxonomic resolution (Fig. 1A). First, we reconstructed multitrophic biodiversity of invertebrates, protozoa, fungi, algae, and bacteria using sedDNA developed since the formation of Lake Hongjiannao in 1929. Second, to study ecological network dynamics, we used an equation-free model, called empirical dynamics model (EDM), and in particular, a nonlinear causality test referred to as convergent cross mapping to estimate changes in network properties (number of realized links and strength of those links) over time. Third, the direction and intensity of the influence of warming, shrinking, and nutrient load on the ecological networks over time, as well as the influence paths, were analyzed by generalized additive models (GAM) and structural equation models (SEM), respectively. Based on the intermediate disturbance hypothesis27, we hypothesized that species diversity and the connectance and strength of ecological networks would decrease first, then increase, and then decrease again under low–medium–high stress gradients, respectively (Fig. 1B). This study was conducted on a typical natural lake ecosystem, which has experienced low, medium, and high levels of stress, and thus, we expect the findings to be of general significance and comparable to other similar ecosystems.

Fig. 1: Methods summary and hypothesize diagram of this study.
figure 1

A Methods summary: using sedimentary DNA metabarcoding, we derived an abundance matrix for invertebrates, protozoa, fungi, algae, and bacteria. Species were classified into 13 functional groups based on taxonomy and trophic roles, forming a conceptual network defined by predation, mutualism, and competition. Employing empirical dynamic models with convergent cross mapping, we simulated annual ecological networks, calculating key parameters: connectance and interaction strength. Generalized additive models and structural equation modeling were then applied to assess the impact of environmental factors—lake area, nutrients, and temperature—on network characteristics and to elucidate the pathways through which these factors influence ecological diversity and network structure. B Hypothesize diagram: we hypothesized that species diversity and the connectance and strength of ecological networks would decrease first, then increase, and then decrease again under low–medium–high stress gradients, respectively.

Full size image

Results

Effects of environmental stressors and meteorological factors on diversity

A reliable dating series of the Lake Hongjiannao core (No. HJN) ranging from 1929 to 2021 was provided by the 137Cs and 210Pbex dating model (Supplementary Fig. 1). Contents of sedimentary total nitrogen (TN) and total organic carbon (TOC) increased significantly after 2010 (p < 0.05), with the average contents increasing from 1.67 g kg−1 and 15.58 g kg−1, respectively, before 2010 to 3.70 g kg−1 and 41.30 g kg−1, respectively, after 2010 (Supplementary Fig. 2). Sedimentary total phosphorous (TP) contents increased to the maximum of 0.83 g kg−1 in 1963 and began to increase again after 2010. The mean annual air temperature (MAT) increased significantly after 1965, from a mean value of 7.56 °C before 1965 to 8.47 °C after 1965 (Supplementary Fig. 2). The mean annual daily precipitation (MAP) was relatively constant throughout the time period, with no consistent changes observed since 1929. The average annual precipitation of 338 mm was characteristic of the arid and semiarid climate in the Hongjiannao basin. Lake area reached its maximum in 1968 with 61.11 km2, followed by a decrease in area (Supplementary Fig. 2). Therefore, Lake Hongjiannao has experienced three stages: (1) stage I, characterized by low stressors during the period of lake area expansion from 1929 to 1965; (2) stage II, marked by medium stressors as the lake area decreased and the MAT increased from 1965 to 2010; and (3) stage III, defined by high stressors with the lake area continuing to decrease, along with increases in salinity, nutrient levels, and MAT from 2010 to the present.

Total numbers of reads obtained by the sedDNA meta-barcoding method were the following: invertebrates, 2,567,219; protozoa, 373,417; fungi, 421,401; algae, 1,184,784; and bacteria, 6,764,046. Reads were assigned to 179 invertebrate Amplicon sequence variants (ASVs), 327 protozoan ASVs, 348 fungal ASVs, 548 algal ASVs, and 10,460 bacterial ASVs (Supplementary Tables 1–5). The comparison of the number and sequences of ASVs among samples showed no remarkable biases towards selective degradation, such as the loss of ASVs associated with specific taxa with sediment age. Invertebrate communities were dominated by Copepods (37.29%), Ostracoda (26%), and Monogononta (21.12%) (Supplementary Table 1). After 2007, Copepods and Ostracods were dominant and Monogononta decreased (Supplementary Fig. 3a). The dominant groups in protozoan communities were Ciliophora (41.91%), Cercozoa (18.52%), Stramenopiles (16.54%), and Euglenozoa (9.3%) (Supplementary Table 2 and Supplementary Fig. 3b). The most abundant taxa of fungal communities were Ascomycota (69.17%), Cryptomycota (36.33%), Oomycota (8.17%), and Chytridiomycota (7.9%) (Supplementary Table 3 and Supplementary Fig. 3c). Eukaryotic algal communities were dominated by Bacillariophyceae (50.71%), Chlorophyceae (17.17%), and Trebouxiophyceae (11.41%), and the community composition changed from Chlorophyta-dominant to Bacillariophyta-dominant in ~1963 (Supplementary Table 4 and Supplementary Fig. 3d). The cyanobacteria community was dominated by the genera Cyanobium_PCC_6307 (58.05%), Synechococcaceae (15.29%), and Planktothrix (7.98%), and the relative abundance of Synechococcaceae increased after 2011 (Supplementary Fig. 3e). The most abundant taxa of bacteria were Chloroflexi (26.74%), Desulfobacterota (9.89%), Firmicutes (9.71%), and Proteobacteria (8.2%) (Supplementary Table 5 and Supplementary Fig. 3f). According to the constrained incremental sums of squares analysis, the time points of changes in community composition of invertebrates, protists, fungi, algae, and bacteria were generally consistent with the successional stages of the lake environment in ~1965 and ~2010 (Supplementary Fig. 3).

Regarding temporal diversity, species richness (i.e., ASV richness) of invertebrates, protozoa, fungi, algae, and bacteria increased from 1929 to 2021, whereas species turnover decreased (p < 0.05) (Fig. 2). Species stability increased in the three successional stages (except for bacteria), whereas species synchrony decreased for high-trophic invertebrates and protozoa and increased for low-trophic algae, fungi, and bacteria (Fig. 2).

Fig. 2: Temporal patterns of species diversity, synchrony and stability across invertebrate, protozoa, fungi, eukaryotic algae, cyanobacteria, and bacteria communities in Lake Hongjiannao.
figure 2

a Species richness, b mean rank shifts, c turnover and d community change over time for species of multiple groups. Slide straight lines indicate the relationship by linear regression fit, dot line represents the 95% confidence interval. Species synchrony (e) and stability (f) across the three succession stages. Stages 1, 2 and 3 refer to 1929–1965, 1966–2010, and 2011–2021, respectively.

Full size image

The influence of seven explanatory variables, namely, nutrient factors (TN, TP, and TOC), meteorological factors (MAT and MAP), lake area, and chlorophyll a (Chl a) level, on communities of the five taxonomic groups was tested by redundancy analysis (RDA). The explanatory variables explained 44.12% of the total variance in invertebrates, 44.81% in protozoa, 44.35% in fungi, 42.59% in algae, and 68.55% in bacteria (Fig. 3). The first axis (RDA 1) of invertebrate, protozoan, and algal communities explained 28.1%, 28.92%, and 24.92% of the total variance, respectively, and temporally separated stage I from stages II and III. Among all explanatory variables, TP, Chl a, and lake area were the most significant factors affecting the composition of all five taxonomic groups, with respective Mantel test r = 0.148, 0.127, and 0.206 for invertebrates, r = 0.389, 0.287, and 0.233 for protozoa, r = 0.423, 0.319, and 0.269 for fungi, r = 0.518, 0.386, and 0.250 for algae, and r = 0.684, 0.542, and 0.386 for bacteria, with p = 0.001 for all r values (Fig. 3f). Mean annual temperature strongly affected bacterial community composition (Mantel test r = 0.290, p = 0.001), and MAP significantly affected the composition of invertebrate and protozoan communities (r = 0.064 and 0.087, respectively, p < 0.05) but did not affect the composition of other communities. In aggregated boosted tree analysis, we added water salinity and land use (data available since 1990) as explanatory variables to rank the relative influence of factors on the five taxonomic groups. Among all explanatory variables, TP, Chl a, lake area, and salinity had the greatest relative influences on community composition of the five taxonomic groups (Supplementary Fig. 4).

Fig. 3: Community structure and environmental factors relationships.
figure 3

Ordination plots of invertebrates (a), protozoa (b), fungi (c), algae (d) and bacteria (e) community structure with environmental factors. Community composition was correlated to each environmental factor or biodiversity index by Mantel tests (f). “Bact”, “Inver” and “Protz” present the bacteria, invertebrates, and protozoa, respectively. TN total nitrogen, TOC total organic carbon, TP total phosphorus, Chla chlorophyll-a, MAP mean annual daily precipitation in the watershed, MAT mean annual temperature in the watershed.

Full size image

Disruption of ecological network by nutrient fluctuation, lake area, and warming

The alpha diversity of different taxonomic groups was correlated with the composition of the other communities, according to Mantel tests (Fig. 3f), indicating the cascade effect of ecosystem food webs28. Thus, the dynamics of multitrophic ecological networks were studied further. We examined the structural properties (i.e., connectance and strength) of complete ecological networks, as well as the network properties of different trophic types and trophic directions. For the complete ecological networks, piecewise linear regression analysis of connectance showed trends of first decrease, then increase, and then decrease (R2 = 0.49, p < 0.01), which is consistent with our hypothesis. The inflection points of temporal variation in connectance were in 1954 and 1983 (Fig. 4). For network strength, there were two cycles of first decrease and then increase (R2 = 0.46, p < 0.01), with the temporal inflection points of network strength in 1966, 1976, and 2011 (Fig. 4). For the network structure of different trophic types, the mean network connectance of nontrophic types over time (64.63 ± 14.71) was lower than that of trophic (72.21 ± 10.70) and hybrid-trophic types (72.82 ± 17.20; p < 0.05) (Fig. 4 and Supplementary Fig. 5). The strength of species interaction for nontrophic connections was also significantly lower than that of trophic connections (p < 0.05). Moreover, for the network structure of different trophic directions, the network connectance of the bottom-up effect (72.67 ± 12.14) was significantly higher than that of the top-down effect (35.95 ± 5.05; p < 0.0001) (Fig. 4).

Fig. 4: Conceptual model of ecological network and the temporal changes in connectance (%) and strength between nodes of ecological network of Lake Hongjiannao.
figure 4

Empirical trophic classification (a) and paradigm of metaweb generated by sedDNA data (b). Trophic links represents predator–prey interactions. Non-trophic links encompass facilitation and competition. Hybrid links can be both trophic and non-trophic. All species or genera were classified into one of 13 guilds, then these links were used to constructed a conceptual ecological network. c, d Connectance (%) and average strength between the realized links of the whole ecological network. All lines are drawn based on the central point of a moving window of 6 years, used for causality detection via convergent cross mapping. e, f Connectance (%) and average strength of trophic, non-trophic and hybrid interactions. g, h Connectance (%) and average strength of bottom-up (BU) and Top-down (TD) interactions. The significant level between groups were calculated using pairwise comparisons via non-parametric Wilcoxon test.

Full size image

The nonlinear patterns of network properties and the three drivers TP, lake area, and MAT determined in the GAM analysis are shown in Fig. 5. The two GAM models explained 31.0% and 71.2% of the variation in network connectance and interaction strength, respectively (Supplementary Table 6). The contribution of lake area to connectance and strength in the ecological network reached 32.88% and 22.96%, respectively, and its contributions increased with the decrease in lake area (Supplementary Table 6 and Fig. 5). The contribution of MAT to network connectance and strength was 9.9% and 43.24%, respectively, and the influence on network structure increased with the increase in MAT. TP explained 13.8% and 16.96% of the variation in network connectance and strength, respectively, and the influence on the strength of species interaction tended to be unimodal (Supplementary Table 6 and Fig. 5). Before the 1950s, the influence of TP on network connectance was relatively high, but with the increase in TP over time, its influence on connectance decreased.

Fig. 5: Generalized additive models for the connectance and strength of ecological network in Lake Hongjiannao.
figure 5

a, b show the temporal changes contribution of TP, lake area, and mean annual air temperature (MAT) for connectance and strength, respectively. The dotted line indicates a 95% confidence interval. Changes in the effects of TP, lake area, and tm changes on connectance (c–e) and strength (f–h) are shown. The gray bands represent 95% confidence intervals.

Full size image

Mechanisms of diversity-mediated stressors on ecological networks

The SEMs revealed that nutrients, climate change, lake area, primary production, species richness, and turnover exerted direct or indirect effects on the structural properties of ecological networks during the three successional stages (Fig. 6). Specifically, the direct influence of nutrient level on ecological network structure changed from a relatively large positive effect in stage I (significant path coefficient = 34.61) to a small negative effect in stages II and III (significant path coefficient = −0.24 and −0.37, respectively). The MAT increase in stages II and III promoted increases in network connectivity and strength, with significant path coefficients of 0.73 and 0.01, respectively (Fig. 6). The increase in primary productivity in stages I and II had positive effects on ecological network structure (significant path coefficient = 9.02 and 0.03, respectively), whereas the decrease in primary productivity in stage II had a negative effect (significant path coefficient = −0.33). The direct effect of species richness on ecological network structure was negative in the three stages, whereas that of species turnover changed from positive in stage I to negative in stages II and III. The stressors that provided the greatest direct influence on network structure were nutrients in stage I, climate in stage II, and turnover in stage III (Fig. 6).

Fig. 6: Structural equation modeling shows the direct and indirect effects of environmental (nutrients, salinity, and lake area) and meteorological factors on lake biodiversity and ecological network.
figure 6

We hypothesized that environmental and meteorological indirectly affects ecological network characteristics by changes in biodiversity, that is, richness and turnover. Structural equation models for the succession stage 1 (a), stage 2 (b), and stage 3 (c) were constructed separately. The block represents the observed variable and the ellipse represents the latent variable. The orange and blue arrows indicate the negative and positive coefficients, respectively. And the dash arrows represent non-significant effects. The numbers on the arrows are the standardized coefficients, which represent the strength of the effect of one factor on another. The width of arrows is weighted according to standardized path coefficients.

Full size image

Discussion

Using nearly 100 years of sedDNA data on multitrophic biodiversity in shrinking, sandy Lake Hongjiannao, we gained multifaceted insights into how multiple persistent stressors drive multitrophic biodiversity and ecological network dynamics in an aquatic environment. The data suggest that changes in ecological network structure mainly depended on the direct effects of stressors under low or medium stress conditions and a diversity-mediated pathway under high stress conditions. The diversity and synchrony of all species within the ecological network, the temporal stability of multitrophic groups, and the nonlinear influence patterns of different component stressors among multiple stressors can explain these results5,16,17.

Species richness and stability increased and species turnover decreased under the gradients of increasing stress, whereas species synchronicity decreased for high-trophic invertebrates and protozoa and increased for low-trophic algae, fungi, and bacteria (Fig. 2). First, the contrasting responses between species richness and rate of species turnover with time could be explained from two aspects embedded in the theories of community assembly, compensatory dynamics, and species coexistence29. On one hand, richness may directly affect species turnover when niche differences among species interact with rates of colonization and extinction at local or regional scales30. On the other hand, species turnover may change with richness in relation to how environmental change affects species coexistence through time31,32. Second, species richness was associated with higher temporal stability, which is consistent with the classic positive diversity–stability relation17,33. Recently, a sublinear population growth model exhibited a form of population self-regulation analogous to the individual ontogenetic model and confirmed the conclusion that diversity begets stability34. Third, the synchrony of high-trophic species decreased and that of low-trophic species increased with the increasing stress gradients, suggesting that destabilizing effects of environmental stressors on biodiversity are related to compensation dynamics among species. In addition, high-trophic species may be more likely to provide an insurance effect, i.e., a decrease in the abundance of some species is compensated for by an increase in the abundance of others16,19. However, the expected decline in species richness was not observed under the high stress gradient, either because we only explored five taxa of organisms and did not cover all species in the aquatic environment, such as fish (which disappeared around 2010), or because the stress intensity did not reach the tipping point for species richness decline35.

We also provide evidence that the nonlinear patterns of influence of different component stressors among multiple stressors affect the connectance and strength of ecological networks (Figs. 3 and 5). Network connectance and strength trends decreased–increased–decreased over time, which provided the signals of ecosystem change, indicating potential ecosystem adaptation, resistance, and degradation processes with increases in stress gradients5,36. By disentangling the independent influence patterns of different component stressors on ecological networks, we found a negative response between nutrient gradients and network connectivity, suggesting that species interactions were strongest at low nutrient concentrations because of resource constraints and weakest at high nutrient concentrations because of abundant nutrient resources10,11. Additionally, warming increased the intensity and uncertainty of temperature influence on ecological networks, which are results consistent with those of recent studies in which temperature alters temporal stability of ecological networks by disproportionate changes in specific trophic groups (e.g., producers, consumers, and predators)22,23,37. Warming can also indirectly affect the nutrient supply of deep-water lakes through water stratification, resulting in lake-specific responses of ecological networks to warming5,17. Furthermore, shrinking lake areas associated with increased temperature and evaporation are linked to greater effects on ecological networks, which may be caused by increasing water salinity filtering more predators (i.e., fish), tightening bottom-up trophic control13.

Ecological network connectance and strength of species interaction mainly depended on a diversity-mediated pathway (i.e., the decrease in temporal turnover) in the high stress conditions rather than on the direct effects of environmental stressors (Fig. 6), suggesting a strong biotic driver of community stability under relatively high stressors16. Species in high-trophic layers of ecological networks (such as top predators) can promote primary productivity via top-down effects, leading to more complementary selections in resource utilization by primary producers38. Moreover, the loss of top predators (i.e., the fish disappeared in ~2010 in Lake Hongjiannao) can trigger a breakdown in the mechanisms that support coexistence of interacting species, reducing the connectance of ecological networks and resulting in secondary species extinctions39. Therefore, the loss of top predators can be regarded as an alert signal of ecosystem degradation, and rich species diversity and complex network structure can be important regulators of maintaining trophic cascade effects, which determine ecosystem productivity, structure, diversity, and dynamics14,38,39.

SedDNA-based and empirical observations-based records of taxa occurrences and trophic interactions in the lake have enabled us to comparatively evaluate realistic food webs across extended time scales, which eliminates the need to base the construction of local food webs on continuous, unbiased observations and calculations of species co-occurrence probabilities5,13. Although there are additional species in the historical succession of this lake ecosystem (i.e., fish), our current species coverage is relatively extensive, encompassing functional groups of predators, producers, and decomposers that are of high importance. Future work may need to expand to cover a broader range of species and their interactions to achieve ecological networks with greater completeness and higher temporal resolution.

In conclusion, on the basis of nearly 100 years sedDNA data, we identified the underlying mechanisms by which multiple stressors drive the biodiversity and ecological network dynamics in a shrinking sandy lake. We found that changes in ecological network structure mainly depended on the direct effects of stressors (nutrients and temperature) under low or medium stress conditions and a diversity-mediated pathway under high stress conditions. These findings have certain implications for the development of effective management and conservation strategies, because environmental stressors are reshaped by global changes. Although the multitrophic communities and ecological networks might not be reconstructed completely over the past 100 years, our findings highlight the importance of maintaining the complexity and integrity of ecological network structures in lake ecosystems and in particular, top predators. In addition, ensuring adequate ecological water quantity and low nutrient levels under climate change may mitigate the effects of multiple stresses on lake ecological networks. Especially for the shrinking sandy lakes in arid or semiarid areas, scientific ecological water replenishment would save the lakes from disappearing.

Methods

Study site and sediment coring

Lake Hongjiannao (39°04′–39°08′N, 109°49′–109°56′E), the largest freshwater desert lake in China, is in the arid and semiarid regions of the transitional zone between the Loess Plateau and the Inner Mongolian Plateau, at the intersection of the Mu Us Desert and the Ordos Basin. The lake was formed from low-lying land in 1929 with an area of 1.3 km2, which expanded to 60–67 km2 during the 1960s and then gradually decreased to 35 km2 recently40. Lake pH was approximately 7 in the 1960s, about 7.2 in the 1980s, and about 8.2 in the 1990s. In the 2010s, owing to the reduction in lake area and increase in lake salinity, the pH reached 9.6, which greatly exceeds the limit for fish survival, resulting in the disappearance of fish41. The annual average temperature in the basin has increased since the 1960s. After remediation for desertification, the area of grassland and forest land in the Lake Hongjiannao basin increased and the area of sandy land decreased substantially since the 2000s. Simultaneously, owing to the intensification of human activities, the nutrient load into the lake increased. Thus, Lake Hongjiannao was chosen for this study because it has clear stress gradients developing over time.

A sediment core (No. HJN) was collected by a gravity corer fitted with a polymethyl methacrylate tube (inner diameter = 8 cm, length = 100 cm) in the center of Lake Hongjiannao in April 2023. The water environment at the sampling site was measured by multiparameter water quality analyzer (YSI, USA) and had the following properties: temperature, 11.8 °C; dissolved oxygen, 7.69 mg L−1; electrical conductivity, 8242 uS cm−1; pH, 9.28; salinity, 6.11 ‰; transparency, 125 cm (Secchi disk depth). The overlying water was removed by siphon, and the 68.5 cm-long sediment core was divided into 137 slices with 0.5-cm spacing in sterile conditions42. Approximately 1.0 g of sediment from the center of each slice was stored in a sterile tube for DNA extraction, with the remaining sediment used for dating and geochemical analysis. After samples were transported to the laboratory on dry ice, they were stored at −80 °C away from light.

Sediment core dating, proxy analysis, and data source

The age–depth model of core HJN was established by excess 210Pb (210Pbex) and 137Cs radioactivity values, which were determined by a gamma ray spectrometer coupled with a DSPEC jr 2.0 multi-channel spectrometer and a GWL-120-15 well detector (ORTEC, USA). The standard was provided by the Institute of Atomic Energy, Chinese Academy of Sciences (catalog no. 7137, source no. 586-26-2). Radiometric dates were calculated using 137Cs stratigraphic records and validated using a constant rate supply 210Pb dating model11,42. The nutrient proxies were sedimentary TOC, TN, and TP, and the primary productivity index was sedimentary Chl a, with nutrients and Chl a measured by previously reported methods43. The meteorological factors of MAT and MAP of the Lake Hongjiannao basin were extracted from the CN05.1 data set by the anomaly approach44. The land-use data set of the basin with a resolution of 30 m × 30 m was obtained from the Institute of Geographic Sciences and Natural Resources Research, Chinese Academy of Sciences (http://www.resdc.cn/Default.aspx). Data on Lake Hongjiannao area from 1929 to present and on salinity from 1980 to present were collected from literature40,41.

Molecular analyses and data processing

Sedimentary DNA was extracted from 0.5-g sediment samples (dry weight) using a PowerSoil DNA Isolation kit (MoBio Laboratories, USA). To detect invertebrates, protozoa, fungi, and algae, a universal eukaryotic primer pair (960F and NSR1438) was selected to amplify the V7 region of the 18S rRNA gene, and to detect bacteria, a universal bacteria primer pair (515F and 806R) was chosen to amplify the V4 region of the 16S rRNA gene16,42. All PCRs were conducted in 50-μL reaction mixtures, which contained ddH2O, 24 μL; buffer, 10 μL; dNTPs, 1.0 μL; primers (10 μM), 1.5 μL; High GC Enhancer, 10 μL; and Q5 high-fidelity DNA polymerase, 2 μL. The PCR protocol was as follows: initial denaturation at 94 °C for 10 min, followed by 35 cycles of 94 °C at 1 min, 1 min at the primer annealing temperature, and 72 °C for 30 s, with a final extension at 72 °C for 10 min11. Three PCR replicates were performed on all samples and blank controls (nuclease-free water as the DNA template) to minimize PCR bias. The PCR products were purified by a D6492-02 Cycle Pure kit (Omega, USA) and then quantified using a NanoDrop ND-2000 spectrophotometer (Thermo Fisher Scientific™, USA). Sequencing templates were sequenced in an Illumina HiSeq 2500 sequencer (Illumina, USA).

Raw reads were filtered and cleaned in strict quality control steps using the FASTX Toolkit and UCHIME tool in Mothur (v.1.35.1)11. ASVs were identified using DADA245. Taxonomic annotation of all eukaryotic ASVs was assigned against the Greengenes databases46 and the Protist Ribosomal Reference database47. Bacterial taxonomic identity was determined using the Silva 138.1 database48. The ASV counts were rarefied to control the difference in sequencing depth11. Alpha diversity (i.e., Chao1 richness) was determined using the “vegan” package for R software (v4.1.0). Temporal changes in relative abundances of invertebrates, protozoa, fungi, algae, and bacteria were displayed using Tilia (v2.2.1) and clustered using constrained incremental sums of squares analysis.

Temporal diversity analysis

To study the temporal diversity and stability of the composition of invertebrate, protozoan, fungal, algal, and bacterial communities over time, we calculated species turnover, mean rank shifts (MRS), species synchrony, and species stability using the R package “codyn”49. Species turnover is the change in species composition over time in an ecological community and is determined using the following formula Eq. (1):

$${{{Total}}\; {{turnover}}}=\frac{{{{Species}}\; {{gained}}}+{{{Species}}\; {{lost}}}}{{{{Total}}\; {{species}}\; {{observed}}\; {{at}}\; {{both}}\; {{time}}\; {{points}}}}$$
(1)

Mean rank shifts is a temporal analogue of species rank-abundance distribution and represents the analogue degree of species recorded between two time points, determined using the following equation Eq. (2):

$${{{MRS}}}={\sum}_{i=1}^{N}\left(\left|{R}_{i,t+1}-{R}_{i,t}\right|\right)/N$$
(2)

where N is the number of species in common at both time points, t is the time point, and Ri,t is the relative abundance rank of species i at time t49.

Species synchrony φ was calculated to compare the aggregated abundances of species to summed variance of individual species and was determined by using the following formula Eq. (3):

$$\varphi =\sigma {({x}_{T})}^{2}/{\left({\sum}_{i}\sigma ({x}_{i})\right)}^{2}$$
(3)

where xi is the vector of abundance of species i over time and xT is the \({\sum }_{i}^{N}{x}_{i}\)50. Species synchrony φ ranges from 0 to 1, indicating a range from perfectly asynchronized to synchronized species fluctuation, respectively17. Then, species stability was determined as the temporal mean divided by the temporal standard deviation of species abundance within different periods49.

Ecological network analyses

To explore dynamic processes in ecological networks under persistent stressors over time, and to control potential biases in taxa classification, abundances of all taxa were aggregated into a conceptual network based on taxonomic classification and feeding behavior51. This method can overcome the limitation that the frequency of observational data is lower than the time of biological generation and account for the inherent changes in species interactions and thus can well reflect the transition of interannual networks5. The conceptual network consisted of up to 13 nodes comprising the following: invertebrate predators, omnivores, and herbivores, herbivore rotifers, ciliates, mixotrophic flagellates, Chlorophyta, Chrysophyta, diatoms, Cryptophyta, Cyanobacteria, fungi, and heterotrophic bacteria28. We considered the direct and indirect links between nodes, including trophic (predator–prey relations), nontrophic (i.e., mutualisms and competition), and hybrid. All links were in two directions: bottom–top links (e.g., from a primary producer to a grazer) and top-down links (e.g., from a grazer to a primary producer).

Considering that the chaos and nonlinear dynamic of lake aquatic communities could exhibit state dependent ubiquitously52, EDM, an equation-free approach, was performed for state–space reconstruction of ecological networks. In EDM, the attractor is a description of the rules governing a system and is reconstructed through a time series of the same dynamic system without any prior assumptions5. For example, if large herbivores (H) are affected by phytoplankton (P) and invertebrate predators (C2), then the attractors of the system can be reconstructed as H(t), P(t), C2(t), that is, H(t), H(t–E(τ)), H(t-E(τ)), where E is the ideal embedding and τ is the time lag. Convergent cross mapping was used to test the mapping between two univariate attractor reconstructions to judge whether the two variables belong to the same system and share a causal relationship53. Network connectance (%) was calculated by dividing the total possible links for a network at this time point by all causal links throughout the time series. Taxa interaction strength over time was calculated by multiplying the average strength of each link by its prevalence. All analysis were conducted using the “rEDM” package in R (https://github.com/SugiharaLab/rEDM).

Statistical analyses

The stressor variables were standardized by Z-score transformation before statistical analysis, to overcome the effect of dimensionality and variable value ranges among indices. Ordinations of invertebrate, protozoan, fungal, algal, and bacterial communities with stress variables were evaluated by RDA analysis using the rda function of the “vegan” package. To assess significant correlations between communities and stressor variables, a Mantel test was performed using the “Pearson” correlation method, incorporating 999 permutations. Aggregated boosted tree analysis was performed to assess the relative effects of nutrients, meteorological factors, lake area, and land use change on the composition of invertebrate, protozoan, fungal, algal, and bacterial communities based on ASVs tables using the “gbm” packages in R54.

To separate and quantify the effects of nutrients, lake area, and meteorological factors on properties of ecological networks, GAMs were constructed using the “mgcv” package in R. The GAM formula was the following Eq. (4):

$$g\left(\mu \right)={\beta }_{0}+{\sum}_{i=1}^{k}{s}_{i}\left({x}_{i}\right)+\varepsilon$$
(4)

where μ represents the response variable, β0 is the constant intercept term, si(xi) is the smooth function of explanatory variable xi, and ε is the residual. Bayesian information criterion (BIC) and generalized cross validation (GCV) scores were used to select explanatory variables and evaluate their parameters in models10.

To further explore how changes in diversity mediated the effects of multiple stressors on ecological networks (including connectance and strength), SEMs were developed to infer the direct and indirect pathways by which environmental stressors affected ecological networks by using the “lavaan” package in R. Collinearity analysis was performed to exclude redundant variables (Pearson’s r > 0.7). We proposed a priori hypotheses based on known effects of nutrients, lake area, and meteorological factors on biodiversity and ecological networks. The goodness-of-fit of SEMs was evaluated using the following indices: ratio of chi-square value to degrees of freedom (χ2/df), goodness-of-fit index (GFI, >0.9), and the root of mean square error of approximation (RMSEA, <0.05)8.

Reporting summary

Further information on research design is available in the Nature Portfolio Reporting Summary linked to this article.