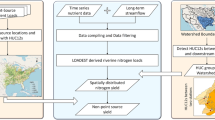
Abstract
Accurate contaminant yield estimation in rivers is essential to developing water quality policies and monitoring their effectiveness over time. We assessed the contribution of high-flows (≥90th percentile) to total yields of nitrate-nitrogen, total nitrogen, total phosphorus, and E. coli calculated from monthly data over 15 years (310–325 sites) in New Zealand, and at 24 sites with high-frequency (30-min) nitrate-nitrogen and total phosphorus. High flows contributed 51–74% of annual contaminant yields at long-term sites and 48% of nitrate-nitrogen and 63% of total phosphorus in the high-frequency sites. Mean uncertainties in annual yields estimated from monthly monitoring data (compared to the true yield, calculated from high-frequency records) were 29% for nitrate-nitrogen and 52% for total phosphorus. Daily sampling was needed to reduce uncertainty to <10% especially in catchments with a high proportion of agricultural land use.
Similar content being viewed by others
Introduction
Annual loads of contaminants like nutrients (nitrogen (N) and phosphorus (P)), sediment and the faecal indicator bacteria Escherichia coli (E. coli) in rivers are strongly influenced by high flows1,2,3. Management of land at the property (i.e. farm) scale typically focuses on reducing losses of these contaminants to water as a load—the amount of contaminant transported by a river, or more commonly as a yield—amount of contaminant transported over a period (commonly a year), per unit area of the farm or catchment. Assuming flow is measured continuously, yields cannot be accurately estimated if concentrations during high-flows are poorly characterised (for example if high-flow events are poorly represented in monthly concentration monitoring datasets). Therefore, if farms are in a catchment where high flows are a strong driver of contaminant yield, it can be difficult to establish accurate yields and the effect of on-farm management actions to reduce farm and catchment yields. This inaccuracy can erode trust in the process that implements on-farm management actions to reduce contaminant loads and meet water quality objectives.
The concentration and form (dissolved or total) of nutrients can also influence the likelihood of water quality impairment from algal growth in rivers or lakes4,5,6, what algal species proliferate, and their effects on trophic interactions and human health7. Much work has shown that the yield and concentration of particulate-bound N and P and E. coli increase with storm size owing to greater inputs from contaminants concentrated or deposited (e.g., via animal dung) onto topsoil and lost via surface runoff or artificial drainage networks8,9,10. Owing to shorter residence times, dissolved nutrients are thought to be more available to algae in smaller rivers than particulate-bound nutrients, but long residence times mean all nutrient forms can become available to algae in lakes and larger rivers. Hence, to understand the risk to river or lake water quality, it is necessary to understand if nutrients are being preferentially lost in particulate form at high flows as it will enable the better targeting of strategies to mitigate particulate losses (such as filter strips or sediment retention ponds)11.
We have a good understanding of the factors that influence the proportion of contaminant yields associated with high river flows from studies that have looked at a few catchments of similar characteristics. However, our understanding is poor when we have tried to elucidate common factors across multiple catchments12. For example, snow melt is well understood as a consistent cause of contaminant losses from frozen fields, especially those receiving manure in agricultural catchments13,14. However, across a range of agricultural and forested catchments, both positive and negative, correlations have been found between nitrate concentrations and antecedent soil moisture conditions15,16. Hence, an improved understanding of how climate, hydrology and land use factors influence the contribution of high-nutrient flows to yields, their timing and their location, is critical to determine the strategies that may be put in place to reduce total nutrient yields in freshwaters and evaluate their success over time.
The frequency of sampling is a key factor that determines the accuracy of contaminant yield estimates. Here, ‘accurate’ yield estimates are defined to be as close as possible to the ‘true’ yield. Although continuous records of contaminant concentrations and hence the true yield do not exist, high-frequency sampling, often only a few minutes apart, is seen as the closest proxy for continuous measurement and therefore can be combined with high-frequency river flow measurements to give the most accurate estimates of the ‘true’ yield. High-frequency contaminant monitoring is becoming more common, and the data can be used to inform our understanding of the interactions between catchment and stream process such as nutrient cycling and stream metabolism and the effects of different lithologies, soil types, management practices and flow paths on contaminant transfers17. Bieroza, et al.17 also point out that high-frequency sampling can be used to detect changes in load that infrequent sampling may miss. For example, Shore, et al.18 showed that the underprediction of nutrient loads was exacerbated if high flows coincided with, or were soon preceded by, an application of a contaminant in a highly available form (e.g., slurry). Moreover, we argue that high-frequency sampling can be used to estimate the contribution of high flows to the ‘true’ yield.
The aims of this study were two-fold. The first aim was to calculate the contribution of catchment average yields coming from high flows and total flows for monitored sites and use these with catchment characteristics to predict the contribution of high flows to total yields for unmonitored river sites. These outputs were combined in an interactive national map showing both yields at monitored sites and the percentage of average annual total contaminant yield that is associated with high flows at rivers ≥4 order in the New Zealand digital stream network (DN 2.4). The map provides users with information of where high flows make a large contribution to total yield, and thus, for example, where to target mitigation actions that are more effective at mitigating the risk of contaminant losses during runoff events. The second aim was to assess the effect of different sampling frequencies on the accuracy of high flow and total flow yield estimates. This will provide managers with information to adjust monitoring strategies in catchments where the percentage of high flow yield is high, for example by targeting water quality sampling during high river flow events to improve the accuracy of total yield estimations.
Results and discussion
To derive national maps of contaminant yields and components of yields associated with high flows, we used nationally available monthly sample results of the nutrient forms nitrate-nitrogen (nitrate-N), total nitrogen (TN), dissolved reactive phosphorus (DRP) and total phosphorus (TP) and the microbiological indicator E. coli. We selected these contaminants because of their control of water quality attributes (either via direct toxicity or of other attributes like algal growth), and their inclusion in many policies and remedial efforts to improve water quality, worldwide19,20,21. We chose to present data as yields as they standardise losses by area enabling comparisons between catchments (and farms). To assess the effect of different sampling frequencies, we used locally available high-frequency (30-min) nitrate and turbidity (matched to TP) measurements and ‘sub-sampled’ the data series to determine the error in estimating yields from data of differing sample frequencies (varying from 2-hourly to monthly). Finally, we used insights from the study to provide a commentary on the suitability of different monitoring strategies and frequencies to improve the accuracy of contaminant yield estimates and to detect the effectiveness of actions to mitigate mobile and immobile contaminant loss from land to water.
Behaviour and distribution of yields at monthly sampled sites
Across the 310–325 sites with monthly contaminant concentration and river flow data, estimated median yields of nitrate-N and TN were, respectively, 3.4 and 6.0 kg N ha−1 yr−1, for DRP and TP the respective median yields were 0.1 and 0.6 kg P ha−1 yr−1, and for E. coli the median yield was 1.1 × 106 cfu ha−1 yr−1. The distribution of yields is shown in Supplementary Fig. 1. The estimated median yields were slightly lower than published median estimates of TN (9.0 kg ha−1 yr−1), TP (0.8 kg ha−1 yr−1), and E. coli (5.0 × 1010 cfu ha−1 yr−1) lost from 55 agricultural catchments in New Zealand22 but this was expected given that these published studies were dominated by almost 100% agricultural land use and the 310–325 monitored sites used in our study contained 26.8% non-agricultural land23.
The median percentage of yield associated with high flows (≥90th flow percentile) was 51%, 55%, 42%, 66%, and 74% for nitrate-N, TN, DRP, TP and E. coli of total yields, respectively (Fig. 1). On average, there were 16 samples per site taken during high flows over the 15-year study period, equivalent to ~9% of monthly samples and close to the 10% of samples expected if flows ≥90th flow percentile were sampled randomly. This implies that flows ≥90th percentile were, on average, representatively sampled - numerically. Indeed, the ratio of observed (daily yield calculated from monitoring data) to expected daily yields (from Weight Regression over Time, Discharge and Season [WRTDS] estimates for the same day) (Fig. 2) were close to one for nutrient forms for most flow percentiles. Furthermore, the ratio converged towards one at higher flows, suggesting that, on average, yields were estimated reasonably well at higher flows by WRTDS. The same tendency was true for E. coli, but overall predictions were farther from one compared with those for nutrients (Fig. 2).
Box plots showing the percentage of total yield accounted for by flows greater than each percentile (upper and lower end of the box are the 75th and 25th percentiles, with the median in the middle and the 95th and 5th percentiles as whiskers, and outliers shown as dots). The mean number of samples per site greater than each percentile is given along the top.
The percentage of average total yields associated with high flows was greater than estimated in some other studies overseas, but can be explained by a high percentage (73.2%) of catchments in agricultural land use (of which 10% is estimated to be artificially drained)24, and steep slopes (mean slope = 4%) that tend to be characterised by flashy hydrological responses. For instance, in Illinois, Kelly et al.8 found the load of soluble (viz. dissolved) reactive P associated with high flows was only 19% of total yield. This was likely caused by flat cropping land with conservation tillage that would likely promote soil water and nutrient storage. In contrast, heavily tile-drained land in the mid-west region of the United States exhibits flashy hydrology25, and high flows were found to transport 50-80% of total yield26,27,28. Similarly, headwater catchments with steeper slopes and frequent rainfall led to 80% of TP losses in high flows in Northwest England29.
Spatially, the sites with a high percentage of total yields associated with high flows were widely distributed across both of New Zealand’s main islands (Fig. 3). High percentages were associated with intensive agricultural activity, whereas, lower percentages were more evident for all contaminants in the central North Island and in some basins in the central parts of the South Island. Lower percentages in the central North Island are likely caused by high infiltration into porous soils and aquifers of volcanic lithology leading to stable flows30, and in both areas by large areas of low-intensity land use (often including conservation land31) that reduce the availability of N, P and E. coli to be lost from land to waterways during rainfall events32.
Total contaminant yields associated with high flows, at monthly sampled and high-frequency (bottom right map) sites. Numbers in the bottom right map refer to high-frequency sites listed in Table 2. Basemap from GAGM (https://gadm.org/data.html).
To further investigate the percentage of total yields associated with high flows, we combined both yield types with catchment characteristics to predict them (and the percentage of total yields associated with high flows) for unmonitored rivers ≥4th order. The performance of these models, as measured by the coefficient of determination, was classed (as per Moriasi et al.33) as satisfactory (R2 > 0.6) for all but E. coli for both yield types, and for the TP yields associated with high flows (Table 1). Performance, estimated by the root mean square error, was classed as good (0.75–1.0) to satisfactory (1–2) for all analytes. Estimated yields from unmonitored ≥4th order rivers were lower than for the monitored sites, owing to the higher percentage of native and exotic forestry in unmonitored catchments (median = 34.1 vs 26.8%, respectively23).
Across ≥4th order rivers the percentage of total yields associated with high flows was 46% (nitrate-N), 48% (TN), 45% (DRP), 66% (TP) and 74% (E. coli) (Table 2). Consistent with the effect of catchment characteristics on high-flow hydrology34, variables such as elevation and mean flow tended to be more important for models of high flow yield than for total yield (Supplementary Figs. 2 to 21). However, there were differences in the effect of hydrology and/or catchment characteristics between contaminants. For instance, stocking density was important for nitrate-N (Supplementary Figs. 2 and 4), TN (Supplementary Figs. 6 and 8) and E. coli (Supplementary Figs. 18 and 20), commensurate with the importance of urine and dung deposits by grazing animals on the loss of nutrients and faecal bacteria in New Zealand35. In contrast, DRP (Supplementary Figs. 10 and 12) and TP (Supplementary Figs. 14 and 16) appeared to be more responsive to hydrological variables such as mean flow (Supplementary Figs. 13 and 14).
High-frequency data
Across the 24 sites with high-frequency nitrate-N, turbidity (converted to TP) and flow data, we calculated loads using different sub-sampling of the original high frequency data to determine if lower sampling frequencies could accurately estimate the ‘true’ yield (the continuous record). Owing to lower spatial coverage of high-frequency data, a preliminary analysis investigated if using WRTDS outputs from the monthly sampling sites could be used as a surrogate for ‘true’ yields and compare them against yields from weekly or monthly sub-samplings. However, because the WRTDS outputs are smoothed, minimising variability in daily loads, such a comparison is not possible (see Supplementary Note 1 and Supplementary Fig. 28). Instead, we only examined the influence of sub-sampling frequencies using the 24 continuous sites with high-frequency data.
Like the results obtained at the monthly sites, the high-frequency data showed a high percentage of total yield was associated with high flows (Supplementary Fig. 29). A Mann-Whitney test indicated that the median yields of nitrate-N and TP in high flows and all flows, were slightly greater (P = 0.026) for the continuous sites (0.9 kg P ha−1 yr−1) compared to the long-term sites (0.6 kg P ha−1 yr−1). Owing to the presence of some extreme outliers from equipment failure in the high-frequency nitrate-N record for the Kakanui River at McCones, calculated yields for sub-sampled frequencies from six-hourly to fortnightly were erroneous (Supplementary Fig. 30). We therefore filtered-out these sub-sampling frequencies for this site from further analysis. As a check of the validity of sub-sampling after filtering, the mean number of sub-samples was within 10% of the expected number for each sub-sampling frequency for both nitrate-N and TP (e.g., 11 vs 12 for monthly sampling; Figs. 4 and 5).
Absolute percentage difference between nitrate-nitrogen (NO3-N) yields estimated by different sampling frequencies (2-hourly, 6-hourly, 12-hourly, daily, weekly, and monthly) and the ‘true’ yields (calculated from high-frequency data), for high flow yields (top graph) and total (All flows) yields (bottom graph) The different number of samples reflect variation in flow at each site.
Absolute percentage difference between total phosphorus (TP) yields estimated by different sampling frequencies (2-hourly, 6-hourly, 12-hourly, daily, weekly, and monthly) and the ‘true’ yields (calculated from high-frequency data), for high flow yields (top graph) and total (All flows) yields (bottom graph). The different number of samples reflect variation in flow at each site.
For nitrate-N, the mean percentage of total yield associated with high flows was 48%, varying from 20% in the spring-fed Kaiapoi River to 70% in the steep Shag River (Table 3). The absolute difference to the true yield for high flows (only) and for total flows increased to >10% for weekly and monthly sampling (Table 4), with the Kakanui River at Gemmels exhibiting the greatest mean differences across all sampling frequencies (44.1 and 20.9% for high flows and all flows, respectively; Fig. 4). For TP, the mean absolute difference to the true yield for high flows was 63%, varying from 39% in the Wakapuaka River to 81% in the smaller Pauatahanui and Porirua Streams (Table 3). Like nitrate-N, the absolute difference to the true yield of TP for high flows and total flows increased to >10% for weekly and monthly sampling (Table 4), with the Tangahoe River exhibiting the greatest mean differences across all sampling frequencies (32.3 and 23.7% for high flows and total flows, respectively; Fig. 5).
Several other studies have compared the uncertainty that regular but infrequent sampling can cause when compared to high-frequency sampling and estimates of the true yield. For instance, Bieroza et al.36 also showed that the median uncertainty in the estimating TP load was −0.02% for daily sampling and 16% for weekly sampling (compared to the ‘true’ load estimated from hourly measurements) but varied across both sampling frequencies depending on the time of sampling (12 p.m. to 4 a.m.) from −10 to 9% and on the day of sampling from −69 to 77%. We didn’t vary time of the day in our analysis, as regular sampling in New Zealand is usually conducted between 10 am and 4 pm, but we did vary the day of sampling (up to seven days), yielding similar absolute errors to Bieroza et al.36. Cassidy and Jordan37 examined sub-sampling in three small Irish catchments dominated by pasture (3–5 km2; compared to a mean of 535 km−2 studied here, Table 3). The mean error compared to the true TP load was 60% (close to the 63% we estimated). However, some of this error was associated with the method of load estimation, which was also the case for uncertainties in nutrient loads from tile-drained landscapes in the US and Canada38. Although not the aim of our work, which focuses only on sub-sampling frequency, subsequent work has shown WRTDS tends to produce outputs closer to the true load than models like Beale’s Ratio Estimator that use average flows, and therefore are highly influenced by high flows39,40.
Limitations and caveats
We used high-frequency data to determine if lower-frequency sampling regimes would introduce uncertainty in yield estimates. High-frequency data are not without uncertainty, which could be caused by sensor fouling and drift41, data loss due to sensor damage, and poor correlations between sensor data and other contaminants (e.g., between turbidity and TP)42. In our study, we lost <5% of data owing to equipment failure, which did not coincide with high flows and hence is unlikely to have affected our findings. In general, relationships between turbidity and TP were good (mean R2 = 0.81). Furthermore, few trends in concentrations were observed over the period of record43 that could have changed relationships42. However, we accept that there is a possibility that uncertainty estimates for deriving TP from turbidity at sites with lower coefficients of determination (e.g., Waingongoro River R2 = 0.27) may themselves be prone to large error.
Accepting these factors as minor limitations of the high-frequency data, it is important to note that sites were restricted to pastoral land uses in five out of 16 regions of New Zealand. No differences were noted between the proportion of sites (χ2 test) in the climate (P = 0.616), land cover (P = 0.494), geology (P = 0.238) and source of flow (P = 0.907) River Environment Classes between high-frequency and monthly sampled sites. While this implies that the high-frequency sites were representative of the proportion of long-term sites in these classes, they are unlikely to be representative of sites in other regions (n = 11). Furthermore, too few sites were present for there to be significant correlations between the contribution of biophysical characteristics and error in either high or total flows or to make robust predictions about their influence on error (Supplementary Tables 1 and 2).
Policy impact
Many jurisdictions, both in New Zealand and internationally have developed water quality improvement policies that link catchment sources of contaminants to acceptable water quality and/or ecological conditions in downstream receiving environments such as rivers, estuaries and lakes19,44. The development of water quality improvement targets, and related controls and regulations on resource use (point-source and diffuse discharges) within the catchment, typically relies on catchment models, which are generally calibrated to estimates of mean annual in-river loads derived from monitoring data45,46,47. In New Zealand, much like other jurisdictions, authorities have also set regulations requiring the reduction of contaminant losses from farms, for example, nitrate-N yields from farms by 5–20% over 10 years48 or 36% (to 20 kg N ha−1 yr−1) by 203549. Although these regulations apply at the farm level, the water quality outcomes are measured in the catchment at the downstream receiving water body (river, lake, or estuary). In all these applications, obtaining accurate estimates of in-river loads and yields is central to supporting the development of robust water quality policies and evaluating whether water quality outcomes (e.g., an overall 30% reduction in nitrogen load being delivered to an estuary) are met or being progressed towards over time. Developing and implementing water quality monitoring strategies enabling more accurate estimates of loads and yields are therefore critical to developing water quality policy and evaluating, and reporting on, their success over time as is required by law in New Zealand19. Understanding how hydrology, in particular high flows, influence the temporal distribution of in-river loads is one important consideration when developing or improving water quality monitoring strategies to improve our ability to accurately characterise in-river loads and yields.
Our data shows that yields are strongly influenced by high flows, and that there is considerable uncertainty in estimating the true yield (both high flow and total) from monthly data sets. Excluding the influence of attenuation processes that may alter farm yields before they reach a river, our data suggests that the present standard water quality monitoring based on monthly sampling will result in a mean uncertainty of 29% in the estimation of in-river annual yields. This uncertainty is the same as, or greater than, the overall reductions required on farm by some policy targets. A similar conclusion was reached by Neal et al.50 who suggested seven-hourly sampling as the optimal frequency for estimating loads/yields. Progress towards or actual achievement of yield reduction targets is likely to be difficult to evaluate unless different sampling strategies aiming at reducing the uncertainty in load estimates, including more frequent sampling, are implemented. Assuming sampling is optimised to detect the signal of N losses from farms and that the lag time between N being lost and detected in the receiving freshwater body is short (note the mean lag time in New Zealand rivers is about 5 years51), our data suggests daily sampling would give a mean uncertainty of ~6% for N and P. We suggest that this magnitude of uncertainty would improve confidence that progress towards achieving targets is being measured appropriately. For instance, high-frequency sampling would increase the likelihood of detecting the effect of 15 out of 24 strategies developed in New Zealand to mitigate the loss of nutrients and E. coli from land to freshwater (Supplementary Table 3). However, it should be mentioned that like monthly sampling, yields determined from high-frequency sampling will not be immune to variation caused by climate and hydrology52,53,54. It is therefore also important to consider the influence of climate on uncertainty in calculating yields, irrespective of the frequency of sampling. Such considerations are now being explored with adaptations to common methods to calculate yield such as WRTDSplus55.
Higher frequency sampling will increase the cost to regulatory authorities. Indeed, a recent study of sampling in New Zealand suggested that the variation inherent with monthly sampling would require an increase in monitoring costs by 4–5 times over the current costs to detect water quality changes required to meet national bottom lines for nutrients, sediment, and E. coli. Recent advances in real-time sensors have quickly decreased the cost of analyses56. We do not suggest that all water quality sampling be replaced by high-frequency sensors as (1) the cost of doing so may be large, (2) operationally ready, high-frequency monitoring technologies are not available for all key water quality variables, and (3) such increased monitoring effort is unlikely to be required at every existing monitoring station. Instead, where accurately characterising contaminant yields is critical to policy development or policy effectiveness evaluation, it may be prudent to use our interactive map of the degree to which high flows are influencing total yields to guide a review of current monitoring practices, and potentially replace some manual low-frequency sampling with high-frequency sensors, especially in streams that are strongly influenced by agricultural land use. Doing so will enable poor practices, such as the runoff of dairy shed effluent, to be quickly detected, processed, and the practice corrected18,57.
Materials and methods
Monthly river water quality data
We obtained daily mean flow and monthly water quality data (nitrate-N, TN, DRP, TP, and E. coli concentration results from grab samples) from New Zealand’s 16 regional authorities via the Land, Air, Water Aotearoa website (www.lawa.org.nz), and from the National Institute of Water and Atmospheric Research’s (NIWA) National River Water Quality Network (NRWQN) (see Supplementary Table 4 for descriptive statistics). The analysis was restricted to water quality sites where flow is also monitored. We used monthly data for the period 2006–2021. Sampling for this data was done on the same weekday ±1 day, four weeks apart for each site. Fifteen years of data are long enough to account for trends caused by short-term climatic variation58. A description of the sites, and the methods used to create a consistent data set are available elsewhere52,59,60,61. To determine if the sites were representative of those across the national river network we first placed sites into a series of six hierarchical River Environment Classes62 (or New Zealand’s Digital River Network 2.5) that group sites according to factors like climate, topography, hydrology and geology. We then used a chi-square test if the homogeneity of the proportion of sites within 25 out of 30 classes was like the proportion of river segments per class across the drainage network (Supplementary Table 5).
Estimating loads from monthly sample data
Daily loads for each site were estimated using the Weighted Regression on Time, Discharge and Season (WRTDS)63 using the EGRET package in R64. The WRTDS model uses a dynamic regression between concentrations and a daily flow record, to impute daily concentration, and load as the product of daily (estimated) concentration and flow. The performance of these models by contaminant is presented in Supplementary Table 6. Although we concluded that their performance was, on average, good, we were not confident that they produced realistic loads for some sites with very high loads and could not be explained by, for example, widespread intensive agriculture in the catchment. These sites had estimated loads that, when converted to yields by dividing by their catchment areas and period of record, were greater than the mean plus three times the interquartile range. They represented 6%, 3% and 5% of the data for DRP, TP and E. coli, respectively and were removed from our database. Following removal and due to variations in contaminants sampled over time, the number of sites in our database varied from 310 for DRP to 325 for nitrate-N.
Predicting the proportion of annual yields associated with high flows
Using continuous flow data, we inspected the daily mean flow for each site and calculated the 1, 5, 10, 20, 30, 40, 50, 60, 70, 80, 90, 95, and 99th percentiles of flow. We then used WRTDS predictions of daily mean concentrations and multiplied these by daily mean flow to generate daily mean load. We isolated and summed the daily loads for those days when flow was greater than each percentile and for all days (thereafter called ‘total’ load or yield). Both the total and percentile loads were divided by catchment area and 15 years to generate annual average yields. We used the estimated site annual yields as response variables for models of total yields and yield that occurs during flows ≥90th flow percentile across New Zealand, hereafter, ‘high flow’ yield65,66. We present predictions of both yields, and as the percentage of high flow yield associated with total yield.
To model total and high flow yields nationally, we used predictor variables (Table 5) extracted from the national drainage network database (Digital Network DN2.5), and subsequent hydrological modelling67, which contained data for each river reach (as 560,000 segments between upstream and downstream confluences) and their catchments62. The predictors were chosen based on their ability to predict nutrient concentrations and flow characteristics61,68,69. We natural log-transformed the total and high flow yields and used 70% of the data along with the predictors in Table 5 to train a Random Forest model in Minitab70 with 300 trees, a minimum internal node size of five, and six as the number of predictors for internal node splitting. We used the remaining 30% of the data to test the performance of the models outputting the coefficient of determination (R2), root mean squared error (RMSE), mean absolute deviation (MAD), and mean absolute percent error along with plots of the relative importance of each variable (see Supplementary Figs. 2 to 21). We used a Random Forest model because they are able to handle non-normally distributed and categorical data, non-linear relationships and high order interactions with high prediction accuracy71.
The final model outputs were restricted to estimates of segments of rivers ≥4th order or greater in the digital river network. We limited our modelling to these ‘larger’ rivers after inspecting the dataset for representativeness and finding that very few (<10%) of the 310-325 sites were in smaller order streams, which meant that there was a greater proportion of lowland streams present in our database than expected in the network (Supplementary Table 5). Predictions for each contaminant were back-transformed and corrected for retransformation bias72 and used in an interactive map.
Interactive map
The interactive map application (https://www.monitoringfreshwater.co.nz/rivers) allows the user to explore the percentage of total average contaminant yield associated with high flows in ≥4th order rivers. The user chooses a contaminant and can then either click on individual existing monitoring sites or segments of rivers of fourth order or greater in the digital river network. The map was developed in the Python programming language using the Dash web application framework (https://dash.plotly.com/).
Short-term, high-frequency water quality data
High-frequency nitrate-N data, measured using TriOS Opus UV spectral sensors, were obtained from seven regional authorities for nine sites (Table 1). These sites were installed by regional authorities to be representative of local land use, but because of budget constraints were not able to be installed at more sites, giving better geographical coverage.
High-frequency turbidity data, measured using VisoTurb® 700 IQ WTW sensors, were provided by four regional authorities for 15 sites. All data were supplied at either 5-, 10- or 15-min intervals but were matched and averaged with flow to the nearest 30-min interval to make a consistent 30-minute concentration and flow data set. The high-frequency sites had data records varying from 0.4 to 11.4 years (Table 1). Although smaller (620 km2) on average than monthly sampling sites (1039 km2), the mean stream order was the same (4th order). Data were checked and periods of corrupt or missing data were removed (<1% of data).
For turbidity data, we matched log-transformed observations of turbidity to the log-transformed concentration of contaminants (N and P fractions, and E. coli) from monthly grab samples for the period 2006-2021. This analysis (see Supplementary Figs. 22– 27) indicated that TN and TP were very strongly related to turbidity (R2 > 0.82, averaged across all sites). Total P tended to have the strongest relationships and hence we used the regression relationship for each site to estimate a synthetic high-frequency TP record. Although other researchers have used more sophisticated techniques like Random Forests regression to predict TP from turbidity and catchment characteristics, the coefficient of determination was no better (74%) than our simple linear approach73.
Influence of sampling frequency on the accuracy of yields
To assess the effect of different sampling frequencies on the accuracy of high flow and total flow contaminant yield estimates, we sub-sampled the high-frequency data records. The ‘true’ yield was taken as the product of 30-min contaminant concentration and flow observations, summed across the entire data set for which full years (January–December) were available, then divided by catchment area and annualised. Sub-sampling was performed at monthly, weekly, daily, and 12-, 6-, and 2-hourly intervals. The daily and sub-daily data sets were generated by filtering the existing data set to match the required sampling rate; for example, daily samples were those taken at 12 a.m., 12-hourly at 12 a.m. and 12 p.m., 6-hourly at 12 and 6 am and 12 and 6 pm, and so on. Weekly samples were randomly selected to occur on a weekday (commensurate with current regional authority sampling regimes) at 12 p.m., and this was repeated seven times to obtain an average of the sub-sampled yield estimate. Monthly samples were similarly selected on a random day of the month, which was then taken throughout the term of the time series, at 12 p.m., and again repeated seven times to obtain an average sub-sampled yield. The absolute percentage difference of sub-sampled total yields and high flows yields to the total and high flow ‘true’ yields was then calculated and annualised so that the time series were able to be plotted on a standardised scale for each sub-sampling frequency.
Reporting summary
Further information on research design is available in the Nature Portfolio Reporting Summary linked to this article.
Data availability
Filtered load and high-frequency data can be found at23: https://figshare.com/s/b9c0972f4e84f056173d.
References
Pionke, H. B., Gburek, W. J., Schnabel, R. R., Sharpley, A. N. & Elwinger, G. F. Seasonal flow, nutrient concentrations and loading patterns in stream flow draining an agricultural hill-land watershed. J. Hydrol. 220, 62–73 (1999).
Cozzi, S., Ibáñez, C., Lazar, L., Raimbault, P. & Giani, M. Flow regime and nutrient-loading trends from the largest South European watersheds: implications for the productivity of Mediterranean and Black Sea’s coastal areas. Water 11, 1 (2019).
Sigleo, A. & Frick, W. Seasonal Variations in River Flow and Nutrient Concentrations in a Northwestern USA Watershed. 7 (United States Environmental Protection Agency, Washington DC, 2003).
O’Neill, A., Foy, R. H. & Phillips, D. H. Phosphorus retention in a constructed wetland system used to treat dairy wastewater. Bioresour. Technol. 102, 5024–5031 (2011).
Schindler, D. W. The dilemma of controlling cultural eutrophication of lakes. Proc. R. Soc. London B Biol. Sci. 279, 4322–4333 (2012).
Francoeur, S. N., Biggs, B. J. F., Smith, R. A. & Lowe, R. L. Nutrient limitation of algal biomass accrual in streams: seasonal patterns and a comparison of methods. J. N. Am. Benthol. Soc. 18, 242–260 (1999).
Elser, J. J. et al. Global analysis of nitrogen and phosphorus limitation of primary producers in freshwater, marine and terrestrial ecosystems. Ecol. Lett. 10, 1135–1142 (2007).
Kelly, P. T., Renwick, W. H., Knoll, L. & Vanni, M. J. Stream nitrogen and phosphorus loads are differentially affected by storm events and the difference may be exacerbated by conservation tillage. Environ. Sci. Technol. 53, 5613–5621 (2019).
Jiang, X. et al. High flow event induced the subsurface transport of particulate phosphorus and its speciation in agricultural tile drainage system. Chemosphere 263, 128147 (2021).
Oliver, D. M., Heathwaite, L., Haygarth, P. M. & Clegg, C. D. Transfer of Escherichia coli to water from drained and undrained grassland after grazing. J. Environ. Qual. 34, 918–925 (2005).
Frazar, S. et al. Contrasting behavior of nitrate and phosphate flux from high flow events on small agricultural and urban watersheds. Biogeochemistry 145, 141–160 (2019).
Winter, C. et al. Explaining the variability in high-frequency nitrate export patterns using long-term hydrological event classification. Water Resourc. Res. 58, e2021WR030938 (2022).
Reid, K., Schneider, K. & McConkey, B. Components of phosphorus loss from agricultural landscapes, and how to incorporate them into risk assessment tools. Front. Earth Sci. 6. https://doi.org/10.3389/feart.2018.00135 (2018)
Wiens, J. T., Cade-Menun, B. J., Weiseth, B. & Schoenau, J. J. Potential phosphorus export in snowmelt as influenced by fertilizer placement method in the Canadian prairies. J. Environ. Qual. 48, 586–593 (2019).
Knapp, J. L. A., von Freyberg, J., Studer, B., Kiewiet, L. & Kirchner, J. W. Concentration–discharge relationships vary among hydrological events, reflecting differences in event characteristics. Hydrol. Earth Syst. Sci. 24, 2561–2576 (2020).
Blaen, P. J. et al. High-frequency monitoring of catchment nutrient exports reveals highly variable storm event responses and dynamic source zone activation. J. Geophys. Res. Biogeosci. 122, 2265–2281 (2017).
Bieroza, M. et al. Advances in catchment science, hydrochemistry, and aquatic ecology enabled by high-frequency water quality measurements. Environ. Sci. Technol. 57, 4701–4719 (2023).
Shore, M. et al. Incidental nutrient transfers: Assessing critical times in agricultural catchments using high-resolution data. Sci. Total Environ. 563, 404–415 (2016).
Ministry for the Environment. National Policy Statement for Freshwater Management 2020 amended October 2024. 70 (2020). https://environment.govt.nz/assets/publications/Freshwater/NPSFM-amended-october-2024.pdf.
Ministry for the Environment. 41 (Ministry for the Environment, 2022).
McDowell, R. W., Macintosh, K. A. & Depree, C. Linking the uptake of best management practices on dairy farms to catchment water quality improvement over a 20-year period. Sci. Total Environ. 895, 164963 (2023).
McDowell, R. W. & Wilcock, R. J. Water quality and the effects of different pastoral animals. N. Z. Vet. J. 56, 289–296 (2008).
McDowell, R. (figshare, 2025).
Manderson, A. Mapping the extent of artificial drainage in New Zealand. 40 (Manaaki Whenua, Landcare Research, Palmerston North, 2018).
Miller, S. A. & Lyon, S. W. Tile drainage causes flashy streamflow response in Ohio watersheds. Hydrol. Process. 35, e14326 (2021).
Liu, W. et al. Processes and mechanisms controlling nitrate dynamics in an artificially drained field: Insights from high-frequency water quality measurements. Agric. Water Manage. 232, (2020). 106032.
Basu, N. B. et al. Nutrient loads exported from managed catchments reveal emergent biogeochemical stationarity. Geophys. Res. Lett. 37 https://doi.org/10.1029/2010GL045168 (2010).
Pace, S., Hood, J. M., Raymond, H., Moneymaker, B. & Lyon, S. W. High-frequency monitoring to estimate loads and identify nutrient transport dynamics in the Little Auglaize River, Ohio. Sustainability 14 https://doi.org/10.3390/su142416848 (2022).
Ockenden, M. C. et al. Changing climate and nutrient transfers: evidence from high temporal resolution concentration-flow dynamics in headwater catchments. Sci. Total Environ. 548–549, 325–339 (2016).
Larned, S. T., Snelder, T., Unwin, M. J. & McBride, G. B. Water quality in New Zealand rivers: current state and trends. N. Z. J. Mar. Freshwat. Res. 50, 1–29 (2016).
Manaaki Whenua—Landcare Research. LCDB v5.0 - Land Cover Database version 5.0, https://lris.scinfo.org.nz/layer/104400-lcdb-v50-land-cover-database-version-50-mainland-new-zealand/ (2020).
Larned, S. T., Moores, J., Gadd, J., Baillie, B. & Schallenberg, M. Evidence for the effects of land use on freshwater ecosystems in New Zealand. N. Z. J. Mar. Freshwat. Res. 54, 551–591 (2020).
Moriasi, D. N. et al. Model evaluation guidelines for systematic quantification of accuracy in watershed simulations. Trans. ASABE 50, 885–900 (2007).
Sharpley, A. N. et al. Phosphorus loss from an agricultural watershed as a function of storm size. J. Environ. Qual. 37, 362–368 (2008).
Scarsbrook, M. R. & Melland, A. R. Dairying and water-quality issues in Australia and New Zealand. Anim. Prod. Sci. 55, 856–868 (2015).
Bieroza, M. et al. Hydrologic extremes and legacy sources can override efforts to mitigate nutrient and sediment losses at the Catchment Scale. J. Environ. Qual. 48, 1314–1324 (2019).
Cassidy, R. & Jordan, P. Limitations of instantaneous water quality sampling in surface-water catchments: comparison with near-continuous phosphorus time-series data. J. Hydrol. 405, 182–193 (2011).
Williams, M. R. et al. Uncertainty in nutrient loads from tile-drained landscapes: effect of sampling frequency, calculation algorithm, and compositing strategy. J. Hydrol. 530, 306–316 (2015).
Park, D. et al. Insights from an evaluation of nitrate load estimation methods in the Midwestern United States. Sustainability 13, 7508 (2021).
Lee, C. J. et al. An evaluation of methods for estimating decadal stream loads. J. Hydrol. 542, 185–203 (2016).
Huebsch, M. et al. Technical Note: Field experiences using UV/VIS sensors for high-resolution monitoring of nitrate in groundwater. Hydrol. Earth Syst. Sci. 19, 1589–1598 (2015).
Leigh, C. et al. Predicting sediment and nutrient concentrations from high-frequency water-quality data. PLOS ONE 14, e0215503 (2019).
Ministry for the Environment & Stats NZ. Our Freshwater 2023. 52. https://environment.govt.nz/assets/publications/our-freshwater-2023.pdf (2023).
European Parliament (European Union, 2000).
Snelder, T. et al. Land-use suitability is not an intrinsic property of a land parcel. Environ. Manag. 71, 981–997 (2023).
Elliott, A. H. et al. A heuristic method for determining changes of source loads to comply with water quality limits in catchments. Environ. Manag. 65, 272–285 (2020).
Larned, S. T. & Snelder, T. H. Meeting the growing need for land-water system modelling to assess land management actions. Environ. Manag. 73, 1–18 (2024).
Environment Canterbury. Decision on provisions of proposed plan change 7 to the Canterbury land and water regional plan. 179 (Environment Canterbury, 2023).
Environment Canterbury. Hinds Plan Change Summary. 5 (Environment Canterbury, 2018).
Neal, C. et al. High-frequency water quality time series in precipitation and streamflow: from fragmentary signals to scientific challenge. Sci. Total Environ. 434, 3–12 (2012).
McDowell, R. W., Simpson, Z. P., Ausseil, A. G., Etheridge, Z. & Law, R. The implications of lag times between nitrate leaching losses and riverine loads for water quality policy. Sci. Rep. 11, 16450 (2021).
Snelder, T. H., McDowell, R. W. & Fraser, C. E. Estimation of catchment nutrient loads in New Zealand using monthly water quality monitoring data. J. Am. Water Resourc. Assoc.53, 158–178 (2017).
Murphy, C. et al. Climate change impacts on irish river flows: high resolution scenarios and comparison with CORDEX and CMIP6 ensembles. Water Resour. Manage. 37, 1841–1858 (2023).
Murphy, J. C. Changing suspended sediment in United States rivers and streams: linking sediment trends to changes in land use/cover, hydrology and climate. Hydrol. Earth Syst. Sci. 24, 991–1010 (2020).
DeCicco, L., Diebel, M. W., Podzorski, H. L., Murphy Blair, J. C. & Hirsch, R. M. WRTDSplus: extensions to the WRTDS method. https://code.usgs.gov/water/wrtdsplus (2024).
Meng, F., Fu, G. & Butler, D. Cost-effective river water quality management using integrated real-time control technology. Environ. Sci. Technol. 51, 9876–9886 (2017).
Han, F. et al. Assimilating low-cost high-frequency sensor data in watershed water quality modeling: a Bayesian approach. Water Resourc. Res. 59 https://doi.org/10.1029/2022WR033673 (2023).
Snelder, T. H., Larned, S. T., Fraser, C. & De Malmanche, S. Effect of climate variability on water quality trends in New Zealand rivers. Mar. Freshwat. Res. 73, 20–34 (2022).
Smith, D. G., McBride, G. B., Bryers, G. G., Wisse, J. & Mink, D. F. J. Trends in New Zealand’s national river water quality network. N. Z. J. Mar. Freshwat. Res. 30, 485–500 (1996).
Julian, J. P., de Beurs, K. M., Owsley, B., Davies-Colley, R. J. & Ausseil, A. G. E. River water quality changes in New Zealand over 26 years: response to land use intensity. Hydrol. Earth Syst. Sci. 21, 1149–1171 (2017).
Snelder, T. H., Whitehead, A. L., Fraser, C., Larned, S. T. & Schallenberg, M. Nitrogen loads to New Zealand aquatic receiving environments: comparison with regulatory criteria. N. Z. J. Mar. Freshwat. Res. 54, 527–550 (2020).
Ministry for the Environment. Freshwater classification system: River environment classification, https://www.mfe.govt.nz/environmental-reporting/about-environmental-reporting/classification-systems/fresh-water.html (2013).
Hirsch, R. M., Moyer, D. L. & Archfield, S. A. Weighted regressions on time, discharge, and season (WRTDS), with an application to Chesapeake Bay River inputs1. J. Am. Water Resourc. Assoc. 46, 857–880 (2010).
Hirsch, R. M. & De Cicco, L. A. in Book 4, Hydrologic Analysis and Interpretation Vol. Section A, Statistical Analysis Techniques and Methods 4–A10 Ch. Chapter 10, (U.S. Geological Survey—U.S. Department of the Interior, 2015).
Banner, E. B. K., Stahl, A. J. & Dodds, W. K. Stream discharge and riparian land use influence in-stream concentrations and loads of phosphorus from central plains watersheds. Environ. Manag. 44, 552–565 (2009).
van Vliet, M. T. H. et al. Global river discharge and water temperature under climate change. Glob. Environ. Chang.23, 450–464 (2013).
Booker, D. J. & Snelder, T. H. Comparing methods for estimating flow duration curves at ungauged sites. J. Hydrol. 434-435, 78–94 (2012).
Whitehead, A. Spatial modelling of river water-quality state. Incorporating monitoring data from 2013 to 2017. 41 (NIWA, Christchurch, New Zealand, 2018).
McMillan, H. K., Booker, D. J. & Cattoën, C. Validation of a national hydrological model. J. Hydrol. 541, 800–815 (2016).
Minitab 21.3 Statistical Software (State College, PA., 2022).
Breiman, L. Random Forests. Mach. Learn. 45, 5–32 (2001).
Hicks, M., Watson, B. & Rose, M. National Environmental Monitoring Standards: Turbidity, Measurement, Processing and Archiving of Turbidity Data. 65 (Wellington, New Zealand, 2017).
Harrison, J. W., Lucius, M. A., Farrell, J. L., Eichler, L. W. & Relyea, R. A. Prediction of stream nitrogen and phosphorus concentrations from high-frequency sensors using Random Forests Regression. Sci. Total Environ. 763, 143005 (2021).
Acknowledgements
We are grateful to Regional Authorities and the National Institute for Water and Atmospheric Research for providing the data. Funding to write this manuscript was provided by the Our Land and Water National Science Challenge (contract C10X1507 from the Ministry of Business, Innovation and Employment).
Author information
Authors and Affiliations
Contributions
R.W.M. conceived the idea and wrote the manuscript. E.M., A.N., and R.W.M. analysed the data and derived the models. M.K. provided their high-frequency data. O.A., L.K., and T.S. co-wrote the manuscript. C.D. provided additional geographic data.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests.
Peer review
Peer review information
Communications Earth & Environment thanks Vincent Cloutier and the other, anonymous, reviewer(s) for their contribution to the peer review of this work. Primary Handling Editors: Rahim Barzegar, Somaparna Ghosh. A peer review file is available
Additional information
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution-NonCommercial-NoDerivatives 4.0 International License, which permits any non-commercial use, sharing, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if you modified the licensed material. You do not have permission under this licence to share adapted material derived from this article or parts of it. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by-nc-nd/4.0/.
About this article
Cite this article
McDowell, R.W., Meenken, E., Noble, A. et al. High flows contributed a large part of annual contaminant yields in New Zealand’s rivers. Commun Earth Environ 6, 335 (2025). https://doi.org/10.1038/s43247-025-02238-9
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s43247-025-02238-9