Waterline responses to climate forcing along the North American West Coast

Abstract

Understanding waterline variability at seasonal to interannual timescales is crucial for predicting coastal responses to climate forcing. However, relationships between large-scale climate variability and coastal morphodynamics remain underexplored beyond intensively monitored sites. This study leverages a newly developed 25-year (1997–2022) satellite-derived waterline dataset along the North American West Coast. Our results reveal distinct latitudinal patterns in seasonal waterline change, with excursions exceeding 25 m in the Pacific Northwest, decreasing to less than 10 m in Southern California and farther south. Waterline fluctuations strongly follow wave power in the Pacific Northwest (R = −0.78), northern California (R = −0.75), and Baja California (R = −0.62), while Baja California Sur aligns more with sea-level variations (R = −0.42). Interannually, waterline change exhibits latitudinal dependence: south of southern California, variability is low, with major erosion confined to strong El Niño-Southern Oscillation (ENSO) events, while northern regions show mixed responses. ENSO-driven storm track shifts modulate winter wave climate, resulting in enhanced (attenuated) erosion from southern California to Baja California Sur during El Niño (La Niña). However, further north, ENSO impacts are less consistent, reflecting a complex interplay of storm track displacement and intensification. These findings highlight the spatial complexity of ENSO-driven morphodynamics and provide a framework for assessing climate-induced coastal vulnerability.

Introduction

Coastal morphodynamics have long been the subject of scientific study^1,2,3,4, because of their implications for coastal ecosystems and human activities. For decades, coastal researchers have used various in-situ and remote methods to monitor coastal indicators, such as changes in waterline, shoreline⁵, vegetation line, and the overall topography-bathymetry continuum (e.g., refs. ^6,7,8). These indicators provide insights into the evolving nature of coasts and highlight potential threats to both natural areas and human settlements. Monitoring efforts have provided valuable data in recent decades, but their application has often been limited to local scales⁹, limiting the ability to capture broader regional and global patterns of coastal change. In recent years, however, new monitoring methods have emerged, notably with the advent of Earth observation satellites, which allow the acquisition of some coastal indicators on greatly larger spatiotemporal scales. Satellite-derived methods, whose application has been facilitated by the development of turnkey tool-kits (e.g., CoastSat¹⁰, SAET¹¹ derived from SHOREX¹², CASSIE¹³) and cloud-computing platforms¹⁴, seem particularly relevant for regional^15,16, continental^17,18, and global^19,20,21 coastal monitoring, generally through linear (i.e., 2D) indicators. These indicators are commonly referred to as satellite-derived shorelines (SDS) or satellite-derived waterlines (SDW), the former supposedly representing a morphological (e.g., volumetric changes, subsidence) coastal indicator while the latter integrates both morphological and hydrodynamic (e.g., tide, wave runup, non-tidal residuals) information.

Few studies have examined indicators of coastal change at regional, continental, and global scales, largely due to the computational resources and time required for automated extraction of waterline positions from extensive satellite imagery. Moreover, the automated nature of these methods limits the ability to visually inspect the quality of each image and resulting waterline, sometimes raising concerns about the reliability of these derived products^22,23. Despite obvious limitations, the few studies conducted at such scales have consistently provided insightful information about the nature of coastal change, such as ref. ¹⁹ who found that ∼30% of the world’s coastline is sandy and quantified trends in shoreline change for all of these beaches, thereby highlighting the largest hotspots of accretion/erosion around the world and revealing that about 50% of the world’s sandy coastline exhibit a long-term linear trend of change greater than 0.5 m/yr, either erosion or accretion. Studies of long-term coastal change have mainly been limited to historical trend analyses, due to data scarcity, which often precludes the study of seasonal and interannual variability and response to variability in hydrodynamic forcing. Most of the fluctuations in wave power operate over relatively short timescales, from the event to the seasonal cycle, and are well known to be a primary driver of shoreline variability²⁴. Equilibrium-based models, linking variations of wave power to shoreline position changes^25,26, have proven to be effective for prediction²⁷. Wave-driven equilibrium behavior has been widely observed, particularly at seasonal scales, where shorelines tend to erode in response to high-energy winter waves and accrete during lower-energy summer conditions, across many sites, such as the northern California (NCA) Coast²⁸. In some locations, shoreline variability does not consistently mirror wave-power fluctuations, challenging the assumption that cross-shore wave forcing is the dominant driver of shoreline change. For instance, the sandy beach of Duck, North Carolina, experiences dominant interannual shoreline variability despite a relatively weak interannual variance in wave energy²⁹. Beaches along the U.S. Pacific Northwest exhibit a mix of seasonal and interannual shoreline responses despite experiencing a highly seasonal wave climate¹⁶. These discrepancies suggest that additional factors (such as shoreface-related processes³⁰ contribute to shoreline variability beyond wave-power variability. Longshore sediment transport driven by wave-direction changes can induce beach rotation and complex shoreline adjustments²⁶, and sea-level fluctuations, whether event-driven, seasonal, or longer term, can amplify or dampen shoreline excursions, as theorized by ref. ³¹, further complicating the relationship between wave forcing and shoreline position^32,33.

Added to these considerations is the influence of low-frequency climatic modes that modulate atmospheric and oceanic conditions, influencing hydrodynamics at the coast and therefore shoreline forcing. In particular, El Niño-Southern Oscillation (ENSO) is the most prominent mode of interannual climate variability. It is a coupled ocean-atmosphere phenomenon that strongly interacts with the weather-climate continuum, influencing both the global Earth system and its regional subsystems, especially in the Pacific Ocean, with widespread societal and economic impacts^34,35. ENSO oscillates between warm (El Niño) and cold (La Niña) phases, with a typical return period of 2–7 years. El Niño events are characterized by a weakening of the trade winds, leading to anomalous warming of sea surface temperatures (SSTs) in the central and eastern equatorial Pacific. These changes disrupt atmospheric circulation patterns, intensifying and deviating storm activity, and strengthening wave climates in the eastern subtropical Pacific. Conversely, La Niña events are associated with stronger trade winds, cooling SST anomalies in the central and eastern Pacific, and typically reduced storminess in the region³⁴). Several indices, such as the Oceanic Niño Index (ONI³⁶), Southern Oscillation Index (SOI³⁷), and Multivariate ENSO Index (MEI³⁸) provide a first-order description of ENSO phases and intensity by averaging SST and/or sea-level pressure anomalies within specific oceanic regions. Although significant progress has been made in understanding ENSO³⁹, new layers of complexity have emerged, with important implications for its predictability⁴⁰. One key aspect of ENSO complexity is its spatial diversity. El Niño events occur along a continuum but are often classified into two dominant types, or flavors: Eastern Pacific (EP) El Niño and Central Pacific (CP) El Niño. These classifications refer to the location of the strongest positive SST anomalies, with EP El Niños centered in the far EP and CP El Niños peaking farther west^{41,42,43,44,45,46}. EP El Niños, such as the strong 1997/1998 event, are characterized by a stronger, more zonal subtropical jet, enhancing storm intensity in the central and EP. This results in larger, longer-period swells propagating eastward. In contrast, CP El Niños, like the 2009/2010 event, shift increased storminess westward into the CP, generating stronger swells toward Hawaii and generally smaller and less frequent long-period swells reaching the U.S. West Coast and Mexico, compared to EP El Niños^47,48,49. This spatial diversity in ENSO events plays a crucial role in reorganizing global atmospheric circulation and modulating extratropical and tropical storm activity^50,51,52. These shifts can have major impacts on coastal ecosystems, particularly through the modulation of wave direction and extreme wave events⁵³, which in turn influence coastal erosion and shoreline change^54,55,56 through different mechanisms as enhanced cross-shore sediment transport, longshore-sediment transport and sediment by-passing^57,58,59.

The recent development of remote sensing methods, powered by cloud-based platforms, has considerably advanced coastal monitoring techniques, enabling more detailed studies of coastal responses to climate forcing using satellite-derived waterline/shoreline data, particularly those related to the seasonal cycle²⁸, and interannual climate variability^17,21,18 specifically investigated the influence of ENSO on shoreline change using satellite-derived data, revealing its widespread influence on coastlines across the Pacific Basin with El Niño phases generally resulting in erosion (accretion) of the shoreline in the eastern (western) part of the Pacific Basin, and conversely during La Niña.

Building upon these pioneering large-scale remote sensing studies applied to climate-related coastal morphodynamics, this study specifically focuses on the North American West Coast (NAWC), a 4000-km-long coastal region spanning mid-latitudes, from Northern Washington (48°N) in the USA to Baja California Sur (BCS) (23°N) in Mexico. Using a newly generated product of waterline positions derived from optical satellite imagery over a 25-year period, we analyze the coastal response to environmental forcing from seasonal to interannual scales, with particular attention to ENSO-related behavior. This approach leverages sub-kilometric spatial resolution data (250 m spaced transects), allowing for a fine-scale investigation of coastal dynamics along the NAWC.

The NAWC faces the Pacific Ocean, with its northern half roughly oriented westward and its southern half trending southwestward. More than half of its coastline is covered by sandy beaches, with most of the non-sandy, rocky coastlines concentrated between central California and northern Washington¹⁹. To better account for its heterogeneity, the NAWC is subdivided into five distinct subregions, shown in Fig. 1:

• 1. The U.S Pacific Northwest (PNW)—Extending from northern Washington to NCA, this region is strongly influenced by extratropical storms. During winter, storm tracks shift south, offshore of the PNW, leading to more frequent and intense storms that drive a high-energy coastal wave climate^6,60. This results in a strongly seasonal wave climate, as illustrated at Long Beach, WA, where monthly averaged significant wave height oscillates between 1.5 m in summer to 3–4 m in winter, reaching above 5 m during strong El Niño events⁶⁰. The seasonal variation in monthly mean sea-level (MMSL) also reflects this dynamic environment, with MMSL rising (falling) by 0.25 m in winter (summer) as shown in Fig. 1b and described in ref. ⁶. Also, the PNW is situated along the Cascadia subduction zone, exposing the area to hazards associated with active tectonics.

• 2. Northern California (NCA)—This region, spanning from NCA to Point Sur, south of Monterey, CA, experiences a strong seasonality of its wave climates, similar to and also impacted by extratropical storms but slightly weaker than in the PNW^61,62. Monthly averaged significant wave heights at Monterey, CA, range from ∼1.5 m in summer to over 2.5–3.0 m in winter, with strong El Niño events amplifying these extremes. MMSL are slightly driven by the seasonal cycle, making the mean sea-level varying over ∼10 cm over the year, peaking in late fall and at the lowest in spring (Fig. 1c).

• 3. Southern California (SCA)—Extending from Point Sur to the U.S.-Mexico border, this region is characterized by a wave climate dominated by a mix of North Pacific winter swells and Southern Hemisphere swells in summer. The south-southwest orientation of the coast and the presence of the Channel Islands attenuate North Pacific swell along most of the southern part of its coastline⁶³. Mean significant wave heights range from ∼1 m in summer to 2 m in winter, though its complex geomorphic settings lead to a high spatial variability of coastal wave climate⁶⁴. MMSL follows a seasonal cycle, rising (falling) by up 0.2 m in fall (spring), illustrated in Fig. 1d at Torrey Pines, CA.

• 4. Baja California (BC)—Spanning from the U.S.-Mexico border to the southern administrative boundary with Baja California Sur, this region features arid coastal plains and is influenced by both North Pacific swells in winter and Southern Hemisphere swells in summer, along with occasional tropical cyclones from the EP. Monthly averaged significant wave heights generally range between 1.0–2.0 m, but regularly reach above 3.0 m during winter storms^65,66.

• 5. Baja California Sur (BCS)—This region, extending to the southern tip of the BC Peninsula, includes southwest-facing coastlines and experiences a wave climate influenced by three primary sources: North Pacific winter swells, Southern Hemisphere swells in summer, and tropical cyclones from the EP⁶⁷. The southernmost part of BCS is highly exposed to hurricane-generated waves. Monthly averaged significant wave heights typically range from 1.0–2.0 m, with seasonal increases in the winter months. MMSL also exhibits a slight seasonal rise, reaching 15 cm above (below) the yearly mean during fall (spring), as shown on Fig. 1e).

Fig. 1: Study area overview with hydrodynamic forcings and beach morphology states.

a Map of the North American West Coast, the monitored coastline is shown in light yellow. Dashed boxes delineate the different subregions of the study area. Pie charts show the regional distribution of advancing/retreating waterline trends during 2000–2022 derived from the dataset presented in this study. b–e Time series of monthly averaged significant wave height (H_s, red) and sea level anomaly (SLA, blue) at Long Beach, WA, Monterey, CA, Torrey Pines, CA and Playa el Suspiro, Baja California Sur (from top to bottom) between 2000–2020, with wave data from ERA5 dataset (ECMWF, 2020¹⁰¹) and sea-level provided by NOAA^102,103,104 tide gages (replaced by AVISO (CNES, 2020¹⁰⁵) data at Playa el Suspiro). Black circles (blue squares) on (a) indicate locations of the four sites (closest ERA5 wave model nodes) described on the right panels. The lateral boundaries of the rectangles delineating the subregions are intended solely to visually illustrate the extent of each subregion and should not be interpreted as representing the offshore or nearshore limits of the coastal system. We use the ESRI World Imagery layer as the background map.

By focusing on a coastal zone as diverse as the NAWC, our study aims to better understand the regional-scale impacts of climate variability on coastal hydrodynamics and morphodynamics. In particular, we investigate the specific responses of these subregions to seasonal cycles and ENSO phases, assessing how varying storminess, wave climates and sea-level drive waterline evolution. This large-scale, fine-resolution, region-specific approach complements and extends previous studies^17,21 by focusing on a narrower geographical area and utilizing a high spatial resolution to explore regional heterogeneity in waterline responses to seasonal and interannual ENSO-driven variability, offering critical information for coastal management and adaptation strategies.

Results

We collected time series of the waterline contours along the NAWC from publicly available satellite imagery and projected onto 250 m spaced transects to get cross-shore waterline position time series. We then sampled the dataset at a monthly resolution to reduce issues with temporally-variable data density. Due to the limited availability of data from the early Earth observation satellites, we restricted our analysis to the period 2000–2022 (7182 transects). At each transect, the time series of the waterline position, X_w, can be divided as follows:

$${X}_{w}(t)={X}_{seasonal}(t)+{X}_{trend}(t)+{X}_{residuals}(t),$$

(1)

where X_seasonal and X_trend represent the seasonal cycles and trends in waterline change seasonal, respectively, and X_residuals accounts for the remaining variability, predominantly driven by interannual fluctuations. The trend was derived from the monthly sampled time series of waterline change using the Theil-Sen estimator^68,69, which calculates the slope as the median of the slopes of all lines passing through pairs of points in the time series. The seasonal cycle was estimated for each month m ∈ {1, 2, …, 12} by averaging the monthly sampled detrended waterline positions for each corresponding month m over the period from 2000 to 2022. This 12-month cycle was then repeated to cover the entire period from 2000 to 2022. Further details on the data acquisition and processing are provided in the Methods section. A graphical depiction of the waterline position dataset, along with its associated trend, seasonal cycle, and anomalies, is presented on Fig. S1 in the Supplementary Material.

The long-term evolution of the NAWC’s sandy beaches

Figure 1 shows the regional distribution of waterline change trends along the NAWC. Over the 7182 transects of sandy coast considered in this study, 75% of them passed the Mann-Kendall^70,71 test for significance of trends, fairly evenly distributed over the five regions considered and delineated in Fig. 1a. Considering the trend classification adopted by ref. ¹⁹, it is found that at 55% of the transects, the waterline change trend can be considered as stable, meaning that the absolute waterline change trend is below 0.5 m/yr, while about 28% (17%) of the sandy shorelines are advancing (retreating). PNW is the region with the most advancing beaches. If we consider only trends that have been found significant using the Mann-Kendall test, 46% of the beaches along the PNW are accreting, and 11% at rates greater than 2 m/yr. The four other regions are rather stable, with more than half of the beaches experiencing absolute significant trends lower than 0.5 m/yr and containing a limited share (up to 5%) of strongly eroding and/or accreting beaches. BCS is the only region found to have more eroding than accreting transects, with 20% of the beaches in a state of retreat and 3% with an retreat rate greater than 2 m/yr. A summary of these trends by region is provided in the Supplementary Material Materials (Table S1).

Regional patterns of seasonal variability

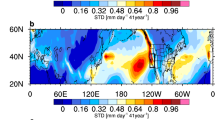
Coastal hydrodynamics exhibit distinct seasonal cycles across the NAWC, with varying magnitudes and timings, as highlighted by Fig. 2, which presents the seasonal evolution of wave power, wave direction, and MMSL along the NAWC, illustrating their latitude-dependent variability. These drivers exhibit distinct seasonal patterns across the five subregions. Superimposed on these trends, the seasonal excursion of the waterline position is displayed at each transect, allowing for a comparative assessment of shoreline response relative to its driving forces. The seasonal variability of the waterline position along the NAWC sandy beaches is calculated as its monthly mean climatology over the period 2000–2022. 99% of these seasonal cycles show a statistically significant correlation (p value < 0.05) with the overall waterline position time series, indicating that seasonal variations are a meaningful component of the total variability of waterline positions. The magnitude of these seasonal cycles varies drastically with latitude. In the PNW, beaches exhibit large seasonal variations, with the excursion-distance the waterline shifts over a season exceeding 25 m on average (median of 26 m, first and third quartile q₁ = 19.4 m and q₃ = 33.3 m, respectively). This magnitude of excursion decreases rapidly southward, dropping to a median of 17.9 m in NCA (q₁ = 8.8 m and q₃ = 27.9 m) and to just under 10 m in SCA (median of 7.3 m, q₁ = 4.0 m, and q₃ = 13.6 m), BC (median of 9.3 m, q₁ = 5.1 m, and q₃ = 16.8 m) and BCS (median of 8.7 m, q₁ = 5.9 m, and q₃ = 13.9 m). As illustrated in Fig. 2e, seasonal cycles exhibit a consistent phase from 48 to 29°N, characterized by a positive (wider beach) phase from May through November and peaking in summer, followed by a retreat (narrower beach) extending until the following May, peaking in winter. However, a noticeable shift occurs between 28°N and 27°N, in southern BC, close to BCS, where the timing of the widest (narrowest) beach shifts from summer (winter) to late winter (late summer). In BCS, the seasonal cycles are almost out of phase with those in the northern regions.

Fig. 2: Seasonal variability of waterline position and forcings along the NAWC.

a Distributions of the seasonal waterline excursion along the NAWC. Regional distributions of these excursions are shown as histograms. The median seasonal waterline excursion over each region is marked on the histogram as a dotted black line. Seasonal cycles of demeaned wave power P_wave (b), wave direction θ_wave (c), MMSL (d), and waterline position (e) as functions of the alongshore position along the NAWC. f shows the Pearson correlation coefficients between seasonal cycle of waterline position and forcings, gathered per subregion. Wave power P_wave is calculated as ${P}_{wave}=\rho g^2{H}_{s}^{2}{T}_{p}/(64\pi )$ where H_s and T_p are the monthly averaged significant wave height and peak wave period, respectively, and provided by ERA5 (ECMWF, 2020¹⁰¹). Correlation significant at a 5% (1%) significance level is marked with “*” ("**''). The background map was generated using Python’s mpl_toolkits.basemap library.

Seasonal cycles of demeaned wave power display strong and spatially homogeneous patterns along the PNW, NCA, northern SCA, and BC, with higher wave power in winter and lower values in summer. Yet, amplitudes of demeaned wave power fluctuations decrease as latitude decreases. In contrast, in southern SCA and BCS, seasonal fluctuations in wave power are weaker and lack a clear spatial uniformity. Regarding wave direction, PNW experiences westward waves in winter and northwestward waves in summer, while NCA and northern SCA receive northwest waves year-round. Southern SCA, particularly its sheltered portions, receives waves from the west in winter and the southwest in summer. BC exhibits a transition from northwest waves in winter to southwest waves in summer in its northern part, whereas its southern part is dominated by northwest waves year-round. In BCS, wave direction follows a seasonal alternation between northwest waves in winter and southwest waves in summer, with an increasing dominance of southwest waves through the year toward the southernmost extent of the region.

MMSL exhibits a pronounced seasonal cycle along the entire NAWC, although the timing of peak levels varies regionally. In the PNW and northern NCA, MMSL is highest in winter and lowest in summer. South of this region, from southern NCA to southern BCS, the seasonal signal shifts, with higher sea levels occurring in spring and lower levels in fall. The amplitude of this cycle appears to increase progressively toward the southernmost extent of the NAWC.

Waterline position generally follows the seasonal pattern of wave power, with wider beaches in summer and narrower beaches in winter across the PNW, NCA, northern SCA, and BC. However, in southern SCA, the seasonal cycle of waterline position is weaker and lacks spatial uniformity. This drop in the waterline excursion along the southern SCA matches a drop in the amplitude of seasonal fluctuations of wave power. In BCS, the seasonal pattern is distinct, with the widest beaches occurring in winter and spring, and the narrowest in summer and fall. A moderate but significant correlation is found between latitude and seasonal waterline excursion (R = 0.40, p < 0.01, all correlation values reported in this study correspond to Pearson’s correlation coefficients), indicating that higher latitudes generally experience greater seasonal variability in waterline position.

To quantify the relationship between seasonal waterline excursions and their potential drivers, Fig. 2f displays Pearson correlation coefficients between waterline position and each driver across the five subregions (refer to Fig. S2 in the Supplementary Material for the associated scatter plots). In PNW, waterline position shows moderate-to-strong correlations with wave power, wave direction, and MMSL (R = −0.78, 0.62, and  −0.66, respectively). Similar but slightly weaker correlations are observed in NCA (R = −0.75, 0.53, and  −0.42, in the same order). In SCA, wave power shows moderate correlations with waterline position (R = −0.40), while wave direction and MMSL exhibit weak correlations (−0.10 and 0.00, respectively). Along BC, both wave power and wave direction show moderate and significant correlations with waterline position (R = −0.62 and  −0.40), whereas in BCS, correlations remain weak-to-moderate, with the strongest correlation observed for MMSL (R = −0.43). All correlations are found to be significant at a 1% significance level (p − value < 0.01), except for correlations between MMSL and waterline positions in SCA and BC (p − value > 0.05).

A supplementary analysis of intercorrelations among the drivers (refer to Fig. S3 in the Supplementary Material) indicates that in the PNW and NCA, wave power, wave direction, and MMSL are moderately-to-strongly inter-correlated (PNW : 0.59 < ∣R∣ < 0.92; NCA : 0.40 < ∣R∣ < 0.68), suggesting a coherent seasonal forcing. Conversely, in SCA, BC, and BCS, the three drivers exhibit weak interdependence, reflecting a more complex and spatially variable set of forcing mechanisms, except in BC where wave power and direction are strongly correlated (R = 0.68), highlighting this seasonal switch between stronger North Pacific swells in winter and weaker South Pacific swells in summer experienced by the norther part of the region.

Contrasting regional responses to ENSO-driven waterline position variability

The percentage of variance of the cross-shore waterline position X_w explained by the sum of the trend X_trend and the seasonal cycle X_season is about 35% in average along the NAWC (refer to Methods section), leaving about two-thirds of the variability unexplained. The unexplained variance can come from various sources, but the monthly sampling of our data and all the post-processes made to eliminate noise unrelated to coastal dynamics suggest that a large share of this unexplained variance is interannual to decadal waterline variability, likely driven by climate modes. We thus investigate how waterline position anomalies, i.e., waterline position detrended and cleared from the monthly mean climatology, are shaped at the interannual to decadal scale by climate modes. Since the 1997–1998 El Niño event was one of the strongest in recent decades, we extend our dataset from 2000 to 2022 to 1997–2022 for this analysis. Due to data scarcity between 1997 and 2000, we discard ∼1000 transects along the NAWC. Further details on transect selection can be found in the Methods section.

Figure 3 shows the behavior of waterline position anomalies along the NAWC from 1997 to 2022. In panel a, we highlight a latitude-dependent pattern of interannual variability in the waterline positions, calculated as the standard deviation of the anomalies over the same period. The correlation between interannual variability and latitude is R = 0.37. Similar to the seasonal cycles presented in the previous subsection, the PNW and the northern NCA are more dynamic than the coastal regions further south. The regional-averaged waterline position anomalies, summarized in Fig. 3b–f, highlight the large variability of waterline position anomalies along the PNW and NCA. Conversely, in the SCA, BC, and BCS regions, regionally averaged anomalies are found to be very stable, except for a few erosive events followed by recovery.

Fig. 3: Waterline change anomalies along the NAWC during 1997–2022.

a Distribution of interannual waterline variability calculated as the the standard deviation of the anomalies between 1997–2022. b–f Regionally averaged waterline position anomalies along the b PNW, c NCA, d SCA, e BC, and f BCS regions. g Heatmap of Pearson correlations between regionally averaged waterline anomalies and CP, EP¹⁰⁰ and MEI³⁸ indices. h Heatmap of Pearson correlations among the climate indices. i–k Time series of CP, EP and MEI indices between 1997–2022. The three major El Niño events that occured between 1997 and 2022 are highlighted in gray on time series (b–f, i–k). Correlation significant at a 5% (1%) significance level are marked with “*” ("**''). The background map was generated using Python’s mpl_toolkits.basemap library.

Across the three southern regions, three major events are clearly visible in the time series: winter of 1997/1998, 2009/2010, and 2015/2016. As highlighted in Fig. 3i–k, representing the evolution of the CP, EP and MEI indices between 1997 and 2022, these waterline change events coincide with the three main El Niño events over the study period: the massive EP peak of 1997/1998, the CP peak of 2009/2010, and the joint EP/CP peaks of 2015/2016, all three peaking in the MEI time series. Smaller events are also visible in smaller extent, such as the minor 2002/2003 El Niño coinciding with a small drop in the waterline anomalies all along the NAWC.

While El Niño events are associated with large erosion anomalies along the PNW and NCA, their impact on driving regionally averaged anomalies to negative values is less pronounced than in regions further south. This suggests that ENSO-induced variability in these northern regions is integrated into broader, longer-term variability. This pattern is particularly evident during the 2011–2016 period, when regionally averaged waterline position anomalies in both the PNW and NCA exhibited a rising trend before experiencing a sharp decline coinciding with the 2015/2016 El Niño.

Linear regressions between climate modes and regionally averaged anomalies of waterline position reveal intriguing yet modest correlations that merit attention. Notably, waterline anomalies in the SCA, BC, and BCS regions exhibit an negative correlation with the EP index, with correlation coefficients of −0.37, −0.23, and −0.48, respectively (p − value < 0.01). In contrast, the NCA and PNW regions show no significant correlation with the EP index. Conversely, weak-to-moderate correlations emerge between waterline anomalies in the PNW, NCA, and BCS and the CP index, yielding coefficients of 0.33 and 0.28, respectively (p − value < 0.01), while SCA and BC remain largely uncorrelated or exhibit weak and non-significant correlations with this index. The MEI index, integrating both EP and CP flavors show weaker (stronger) correlations than EP (CP) along SCA, BC and BCS (R = −0.37,  −0.23,  −0.48) and reversely along the PNW and NCA (R = 0.23, 0.18).

Although the presented correlations are weak and do not necessarily imply causality, they underscore potential relationships between waterline anomalies and these climate modes. Notably, positive extremes in ENSO indices are associated with pronounced drops in waterline position anomalies, suggesting the influence of strong El Niño events on shoreline variability. To test the robustness of this observation, we analyze waterline position anomalies by categorizing them into three ENSO phases: El Niño, La Niña, and neutral conditions. Anomalies corresponding to MEI > 1 (MEI < −1) are classified as El Niño (La Niña), with the remaining data considered neutral. Using neutral phases as a reference state, we apply an signal-to-noise ratio (SNR) analysis to quantify the effect of ENSO on waterline positions. This involves comparing the distribution of waterline position anomalies during El Niño and La Niña phases against the neutral phase by computing SNR_i = ∣μ_i − μ_ref∣/σ_ref, where SNR is the SNR, i is an ENSO phase, ref is the neutral phase, and μ and σ are the median and standard deviation of the distribution of anomalies for the considered ENSO phase. To minimize the influence of longer-term variability, such as observed in waterline signals in the PNW and NCA and to homogenize transect-specific disparity in waterline position variability, waterline position anomaly time series are seasonally-sampled, scaled by their standard deviation and analyzed as changes relative to their values two seasons prior (e.g., change of anomalies relatively to winter if considering anomalies in summer) rather than considering absolute anomalies. The closest the SNR to zero, the weaker the influence of the considered ENSO phase on the waterline position anomaly changes. Figure 4 presents the distributions of these classified anomalies and the corresponding SNR scores, considering all seasons together as well as winter months only (DJF, i.e., anomaly changes from summer to winter). Results are shown for the entire NAWC and for each subregion separately. Figure S4 in the Supplementary Material shows these distributions and scores for spring, summer and fall seasons as well. A striking first observation is the difference in SNR scores between all-season and winter-only anomalies. In each subregion, both El Niño and La Niña events exhibit stronger SNR scores when considering only winter anomalies, except for La Niña along the PNW, where the score remains weak in both cases but is slightly higher for the all-season distribution. When focusing on winter anomalies, distinct regional patterns emerge: SCA, BC, and BCS display higher $SN{R}_{ni\tilde{n}o}$ values (0.65, 0.84, and 0.82, respectively) compared to the PNW and NCA (0.37 and 0.39, respectively). Similarly, SCA, BC, and BCS display higher $SN{R}_{ni\tilde{n}a}$ values (0.35, 0.35, and 0.43, respectively) compared to the PNW and NCA (0.05 and 0.07, respectively). These differences in SNR values between the northern and southern subregions underscore the greater and clearer responses of SCA, BC, and BCS to El Niño and La Niña events relatively to the PNW and NCA. This sets the stage for our examination of specific hydrodynamic responses associated with different phases of ENSO. Figure 5 illustrates the composites of these responses during the winters of 1997–2022, highlighting how the varying conditions of El Niño, neutral phases, and La Niña influence coastal behavior and Table 1 summarizes the waterline response to ENSO phases by providing quartile information on the waterline position anomaly changes per subregion of the NAWC.

Fig. 4: Signal-to-noise ratios (SNR) of waterline anomaly changes during El Niño/La Niña relatively to ENSO neutral phases (1997–2022).

Distributions of waterline anomaly change during ENSO neutral (gray), El Niño (red) and La Niña (blue) phases for (a–f) all seasons and (g–l) winters along each subregion and the whole NAWC. Waterline anomaly changes are computed at each transect by measuring the difference between the seasonally averaged waterline position anomaly of a given season and that of two seasons earlier. The SNR for El Niño and La Niña phases relatively to neutral ENSO-phases, and calculated as the differences of the median of the distribution of waterline anomaly change between El Niño (or La Niña) and neutral ENSO-phases, scaled by the standard deviation of neutral ENSO-phases (refer to Methods).

Fig. 5: Hydrodynamic and morphological responses to ENSO phases and El Niño flavors during winter (1997–2022) along the NAWC.

Composites of hydrodynamic and morphological responses to (a–c) ENSO phases and (d–f) the strongest El Niño events during winter (DJF) over 1997–2022. The figure shows spatial distributions of winter waterline position anomalies changes relatively to the summer (JJA) and wave power anomalies (scaled by their standard deviation), along with 200 hPa eddy kinetic energy (EKE) contours, proxy for storminess and storm tracks position. Waterline position anomalies are scaled by their seasonal cycle amplitude to highlight the magnitude of the anomalies relative to the seasonal cycle. The definition of ENSO phases and flavors, based on values of MEI, EP, and CP indexes¹⁰⁰, is detailed in the Methods section. The background map was generated using Python’s mpl_toolkits.basemap library.

Table 1 Regional waterline position anomaly responses to ENSO phases

Figure 5a–c illustrates the average winter (DJF) responses to El Niño, neutral, and La Niña conditions over the period 1997–2022. These responses are depicted using composites of winter-averaged wave power anomalies (scaled by their mean winter values between 1997–2022) and winter-averaged waterline position anomaly changes (scaled at each transect by the local mean waterline seasonal excursion, as shown in Fig. 2). El Niño (La Niña) winters are defined as those with a season-averaged MEI > 1 (MEI < −1). This selection identifies 1997/1998, 2009/2010, and 2015/2016 winters as El Niño winters, and 1998/1999, 1999/2000, 2007/2008, 2010/2011, 2011/2012, 2020/2021, and 2021/2022 as La Niña winters. During El Niño winters, a pronounced positive wave power anomaly extends along the entire NAWC, with values ranging from a 30–50% increase relative to mean winter conditions. This increase in wave power is accompanied by a markedly negative waterline position anomaly distribution, with scaled values ranging from −83% to −18% (first and third quartiles) across the NAWC, particularly pronounced in SCA, BC, and BCS. In neutral years, wave power anomalies are slightly negative (−8% to −10%) across the NAWC, coinciding with minimal waterline position anomaly changes (−11% to +7%) along the coastline. In contrast, La Niña winters are characterized by slightly negative wave power anomalies (−1% to −5%) along SCA, BC, and BCS, coinciding with positive waterline position changes (SCA: +1% to +40%; BC: 0% to +30%; BCS: +14% to +51%). Meanwhile, the PNW and NCA experience a mild increase in wave power (+0% to +8%), coinciding with slightly negative waterline position anomalies (PNW: −22% to +6%; NCA: −21% to +14%).

D–F further explore the nuances of ENSO-driven responses by analyzing the distinct impacts of the three El Niño winters with MEI > 1 between 1997 and 2022. These events represent different El Niño types: the 1997/1998 event, classified as an EP El Niño; the 2009/2010 event, characterized as a CP or Modoki El Niño; and the 2015/2016 event, which exhibited a mixed EP/CP signature. The EP El Niño event is associated with strong and widespread positive wave power anomalies (+48% to +93%) along the entire NAWC. This wave power increase corresponds to negative waterline position anomalies across nearly all of the NAWC (−98% to +8%), except in the PNW, where the response is more variable (−58% to +31%), with its northernmost section predominantly experiencing positive anomalies. The CP El Niño event exhibits a weaker wave response compared to the 1997/1998 EP event. At the coast, wave power anomalies are positive from NCA to BCS (+0% to +30%), but turn negative along the PNW (−1% to −11%). Scaled waterline position anomalies are almost uniformly negative across the NAWC (−101% to −10%), though slightly weaker and more variable along the PNW (−65% to +24%). The mixed El Niño event generates widespread positive wave power anomalies, particularly intense offshore of the PNW and NCA, with increases of 40–50% relative to mean winter conditions. Its waterline position anomaly response is the most spatially uniform of the three events, with nearly all locations experiencing negative changes (−101 to 0%), except for NCA (−69% to +11%), where a small central region exhibits positive anomalies.

A critical factor influencing wave power anomalies and coastal responses is the fluctuation of storm tracks, whose strength and position can be quantified using Eddy Kinetic Energy (EKE^72,73), derived from 14-day high-pass filtered winds at 200 hPa. EKE at upper levels (e.g., 200 hPa) is widely used as a proxy for storm track activity, as it quantifies the intensity of upper-level atmospheric disturbances, which are closely associated with mid-latitude cyclones and storm tracks⁷². Figure 5 superimposes contours of 200 hPa EKE, ranging from 100 to 250 m²/s², onto wave and waterline anomaly signals. Higher EKE values indicate increased storm track activity, with stronger transient eddies corresponding to more frequent and intense storms. During ENSO-neutral winters, storm tracks weaken as they approach the NAWC coastline, with EKE values decreasing from 200 m²/s² over the central North Pacific (around 35°N, 160°W) to below 175 m²/s² near the coast. The 150 m²/s² contour roughly encompasses the NAWC coastline from PNW to southern BC, peaking between 150–175 m²/s² in NCA, and declining down to 100–125 m²/s² in BCS. During La Niña winters, the central North Pacific storminess is roughly identical to neutral winters but slightly shifts north as it reaches the NAWC coastline, with the 150 m²/s² contour encompassing only the PNW and NCA. Storminess gradually decreases further south, from 125–150 m²/s² in SCA down to less than 100 m²/s² in BCS. Notably, the 150 m²/s² contour aligns with the transition between positive and negative waterline position anomaly changes along the NAWC. Southern subregions, where typical winter 200 hPa EKE values range between 100 and 150 m²/s², exhibit positive waterline anomaly changes during La Niña winters when EKE values decrease, despite little to no corresponding decrease in wave power. On the other hand, El Niño winters are marked by both an intensification and a pronounced southward shift of storm tracks, affecting both offshore regions and the NAWC coastline. At the coast, EKE peaks along BC, exceeding 200 m²/s², while the 150 m²/s² contour extends from BCS to NCA, leaving the PNW with local EKE values between 125–150 m²/s². The 1997/1998 EP El Niño is characterized by very intense storm tracks, with the 200 m²/s² EKE contour encompassing the coastline from central NCA to southern BC, peaking around 250 m²/s² at the boundary between NCA and SCA, and leaving the PNW with unusually low storminess. During the 2009/2010 CP and 2015/2016 mixed El Niño events, the storm tracks form a southward-shifted meander, allowing them to reach BC and BCS, peaking in intensity above 200 m²/s².

Figure S5 in the Supplementary Material shows the spatial distribution of the sea-level anomalies instead of scaled wave power anomalies and Figs. S6 and S7 in the Supplementary Material show the response to ENSO phases like in Fig. 5 and Fig. S5, but using a smaller threshold (MEI = ±0.5) to define ENSO phases.

Discussion

The SDW data extracted and analyzed in this study reveal numerous spatiotemporal patterns in waterline evolution along the NAWC sandy coastline. Seasonally, large fluctuations in wave power, peaking in winter and decreasing in summer, align with waterline position variability, which shows retreat in winter and advance in summer across most of the NAWC. These large-scale satellite-derived observations, consistent across the PNW, NCA, and BC, and corroborating local observations (PNW⁶, NCA⁷⁴, BC^65,66), align with general understanding of morphodynamics along wave-exposed sandy beaches: sandy beaches experiencing noticeable wave power changes are largely driven by cross-shore sediment transport mechanically resulting in beach profile and shoreline change. This relationship has been observed at multiple sites, including recently at a regional scale along the northern and central California coast²⁸. The moderate-to-strong correlations (0.62 < ∣R∣ < 0.78 along the PNW, NCA, and BC) reported in this study further support a causal link between wave and waterline variability at the seasonal scale.

In contrast to the strong seasonal signal observed in the PNW, NCA, and BC, the waterline position variability in SCA and BCS exhibits a weaker seasonal cycle and a lower correlation with wave power fluctuations, as also observed by ref. ²⁸ along the SCA coast. Even though wave and sea-level conditions remain relatively stable throughout the year (Figs. 1d, f and 2b–e), seasonal waterline change patterns in these regions differ drastically. Sandy beaches along SCA exhibit very weak and spatially heterogeneous seasonal waterline variability. This can be partially attributed to complex coastal settings, such as the presence of numerous pocket beaches, which likely “modify the incoming wave conditions, wave breaking patterns, longshore currents, and sediment transport patterns”, as noted by ref. ²⁸. Moreover, many beaches in southern SCA experience seasonal beach rotation, most likely driven by the seasonal wave direction variability, further supporting the observed lack of spatially uniform seasonal waterline cycles in the region. On the other hand, sandy beaches across BCS show a spatially consistent pattern of seasonal waterline variability. We hypothesize that this waterline retreat period, from a most advanced (accreted) state in March/April, to a most retreated (eroded) state in September/October, and overlapping with the Eastern Pacific Hurricane (EPH) season -which runs from May to November⁷⁵ might be storm-driven. During this period, many storms form in the eastern tropical Pacific, impacting the Pacific Mexican coast⁶⁷. However, there is no visible influence of the EPH season on the seasonal cycle of wave power. This could be due to the lack of consistent timing in the occurrence of these storms over the study period, leaving the influence of EPH on the regional wave climate unnoticeable with monthly wave data, which highlights the need for further analysis using refined datasets. Another hypothesis is that large seasonal sea-level variations, measured as cycles of 25 cm of change from altimetry data along BCS but likely underestimated (refer to Fig. S10 in the Supplementary Material for validation), could drive seasonal waterline variability, through passive and non-passive mechanisms, in regions where seasonal wave-power fluctuations are relatively weak. Additionally, an overlooked aspect of climate-driven waterline variability is the influence of riverine sediment supply. While the influence of riverine sediment supply on waterline variability is undoubtedly an important factor, its detailed assessment remains largely out of reach with current tools and data, especially at the seasonal scale. Solid sediment input that drives coastal morphological changes is typically linked to infrequent, localized, high-magnitude flood events with multi-year return periods^76,77.

At the interannual scale, the fact that regionally averaged waterline position anomaly signals show extreme retreat during the three major El Niño events of the study period (Fig. 3) aligns with previous observations at multiple local sites along the U.S. West Coast⁵⁶, in BC^65,78,79), and regionally along the Mexican and California coasts¹⁷. Similarly, the mild effect of La Niña in attenuating winter erosion cross the California and Mexico coastline has been observed by ref. ¹⁷. However, despite this growing body of evidence linking ENSO to coastal erosion along the NAWC, simple linear correlations between ENSO activity and regional waterline anomalies remain weak to moderate (0.23 < ∣R∣ < 0.48). We also note that accounting for ENSO diversity (EP and CP modes) slightly refines the correlation between ENSO activity and regional waterline patterns compared to the integrated MEI metric (0.07 < ∣R∣ < 0.38). Interestingly, sandy beaches along the PNW and NCA exhibit an interannual response, with large interannual variability rather than the stable anomalies seemingly punctuated by El Niño-driven erosion events observed in regions further south. These observations are consistent with regional studies conducted in north-central Oregon⁸⁰, and along the Columbia River Littoral Cell between Oregon and Washington states⁸¹. The SNR test applied to waterline anomaly changes between summer and winter highlights the influence of El Niño events within the lower-frequency variability characterizing PNW and NCA beaches. Typically, SNR are expected to be greater than 1 to be robust, meaning that the difference in median values between a reference and a studied event exceeds the standard deviation of the reference distribution. In our case, SNR scores range between 0.40 and 0.87 for El Niño and between 0.02 and 0.32 for La Niña (for the entire NAWC: 0.70 and 0.20, respectively), showing a latitude-dependent pattern with northern subregions less frankly impacted by ENSO than those further south, as well as highlighting that La Niña events are associated with less waterline variability across the NAWC than El Niño ones. This suggests that while ENSO contributes to waterline variability, its influence is contrasted along the NAWC and not always regionally-dominant, likely complicated by spatially heterogeneous geomorphic features and random event-driven coastal change.

The influence of ENSO on wave climate is largely mediated through its control on storm tracks, which dictate the frequency, intensity, and trajectory of extratropical cyclones impacting the NAWC. During El Niño winters, storms tend to track farther south and intensify, generating more frequent and energetic wave events that impact the central and southern NAWC. Elevated sea levels due to El Niño-induced steric effects and increased onshore storm surge can exacerbate coastal erosion, especially during extreme wave events. Conversely, during La Niña winters, storms are generally weaker in the southern NAWC, while the northern regions, particularly the PNW, may experience more frequent high-energy events. However, the impact of El Niño events is not uniform, as different flavors of El Niño-EP, CP, and mixed types-have distinct influences on storm tracks and associated sea-level anomalies. EP El Niños are typically associated with stronger storm tracks directed toward central California and greater wave energy along the southern NAWC, often coinciding with heightened sea levels that amplify erosion. CP El Niños tend to have a weaker influence on storm intensity but appear to shift storm tracks further south along BC, where even moderate wave events, combined with persistent sea-level anomalies, can enhance shoreline retreat. This variability in ENSO-driven wave forcing is further highlighted when comparing wave power to the MEI at the four sites displayed in Fig. 1. While ENSO’s influence on wave energy along the PNW is widely accepted⁶, our analysis reveals that the linear correlation between winter-averaged wave power and MEI at Long Beach, WA, is weak and statistically insignificant (R² = 0.29, p = 0.16; wave energy derived from ERA5 data at the Long Beach, WA, refer to Figure S8 in the Supplementary Material). High-energy winters in the PNW occur under both El Niño and La Niña conditions, limiting the predictive power of ENSO indices for wave energy in this region. In contrast, the three sites further south exhibit stronger and statistically significant correlations (R > 0.61, p < 0.01), aligning with the well-established relationship between ENSO and wave climate variability in the Northeastern Pacific. Additionally, in regions where wave power anomalies align with ENSO phases, sea-level anomalies further modulate coastal response, reinforcing erosion during El Niño and allowing for enhanced accretion during La Niña recovery phases.

In addition to ENSO, other regional climate modes, such as the Pacific Decadal Oscillation (PDO⁸²), the Pacific Meridional Mode (PMM⁸³) and the Arctic Oscillation (AO⁸⁴) influence coastal dynamics along the NAWC^80,81. These modes are not isolated from each other, and can amplify or mitigate ENSO’s impacts, adding layers of complexity to understanding coastal responses. For instance, the PDO, a 20–30 year return period climate mode reflecting SST anomalies in the northern Pacific, is suspected of modulating the frequency of ENSO events as positive (negative) PDO phases favors the appearance of El Niños (La Niñas⁸⁵). As pointed out and studied by ref. ⁸⁶, the interplay between climate modes needs further exploration to better predict and understand their combined influence on coastal environments, and similar approaches would also benefit coastal change prevision in other basin as ENSO, among other modes, interacts with climate variability worldwide. For instance, Atlantic La Niña, which is the negative phase of the Atlantic version of ENSO, is triggered by the onset of the Pacific El Niño with a few months of delay⁸⁷. Understanding how these regional climate modes interact with ENSO is crucial for predicting coastal change on interannual to multidecadal timescales. However, beyond these natural climate fluctuations, global warming is expected to further alter ENSO dynamics, potentially reshaping its influence on storm tracks, wave climate, and coastal hazards. As climate models project an intensification of ENSO variability, with more frequent and extreme El Niño and La Niña events due to enhanced ocean-atmosphere coupling^88,89, it becomes increasingly important to assess how these evolving patterns will interact with other climate modes and their cascading effects on coastal environments. For instance, a warmer mean state in the tropical Pacific could favor more EP El Niño events, while shifts in wind and thermocline feedbacks may lead to an increase in CP El Niño frequency^90,40. These projected changes highlight the need to better understand how climate variability at multiple scales will shape future coastal hazards.

A study of this scale relies heavily on satellite-derived data, which come with inherent limitations that are important to acknowledge. Over the past decades, SDW and shorelines have been increasingly used in coastal studies, with a well-established accuracy of 10–15 m at most sites. However, larger uncertainties may arise in gently sloped and/or meso-to-macrotidal environments⁹¹. Given this relatively high uncertainty compared to the magnitude of observed signals⁹², as well as the uneven time spacing between detections, we resample the time series to a monthly resolution to minimize noise. Aggregating data at monthly to seasonal scales further reduces random error, assuming it has no strong temporal dependency²⁸. Validation of our SDW product against in-situ shoreline measurements at Torrey Pines⁸ and Ensenada, BC⁶⁶ demonstrates strong agreement, with standard errors below 15 m and a well-captured, albeit slightly underestimated, seasonal cycle. Furthermore, our analysis spans ∼20 years, covering around twenty seasonal cycles and several El Niño/La Niña events. While this provides valuable insight into ENSO-driven coastal morphodynamics, an even longer time series would help confirm or refine the observed patterns and improve data-driven modeling efforts. Beyond waterline data, the ERA5 wave and wind products and AVISO sea-level data used in this study offer critical insights into regional-scale offshore conditions. However, their coarse spatial resolution (0.5° grid) and monthly sampling limit their ability to resolve fine-scale spatiotemporal variability, particularly in nearshore zones where localized wave transformation and storm surge effects are important. While these datasets are well-suited for analyzing variability at monthly to interdecadal timescales, they are less appropriate for capturing event-driven coastal dynamics at local scales.

Conclusions

This study provides new insights into the latitudinal variability of shoreline dynamics along the NAWC, leveraging 25 years of SDW data to examine seasonal to interannual shoreline fluctuations in response to wave forcing, sea-level variability, and ENSO-driven climate variability. At the seasonal scale, our results demonstrate latitude-dependent shoreline excursions, with PNW, NCA, and BC showing strong correlations with seasonal wave power variability (−0.78, −0.75, −0.62, respectively), while SCA exhibits spatially heterogeneous responses, suggesting the influence of local coastal morphology. In BCS, waterline fluctuations appear largely decoupled from wave forcing and instead moderately reflect sea-level variability (R = −0.42), emphasizing the need to consider non-wave-driven mechanisms when assessing shoreline change in this region. At the interannual scale, waterline variability follows a distinct latitudinal pattern. SCA, BC, and BCS exhibit relatively stable waterline positions except during extreme El Niño events, which trigger considerably enhanced erosion. In contrast, waterlines along the PNW and NCA experience greater interannual variability, where ENSO-driven erosion signals are embedded within broader fluctuations, making their response to climate forcing less predictable in the context of ENSO. We found that shifts in storm track intensity and position drive large-scale wave climate variability, producing a symmetrical response in SCA, BC, and BCS between El Niño and La Niña conditions, yet attenuated for La Niña phases. However, in PNW and NCA, storm track modifications introduce ambiguity, as intensified storm activity during El Niño can increase wave energy exposure despite a southward displacement of the most energetic storms. This results in a more complex, less linear relationship between ENSO and shoreline change, likely to be influenced by other climate modes operating at various timescales. Overall, our results highlight how coastal change along the NAWC is impacted by seasonal and ENSO-driven interannual climate variability, revealing spatial contrast in the response to highly seasonal wave power and to ENSO-driven wave and sea-level fluctuations, with amplitudes of waterline change associated with these scales varying accordingly to the latitude. Future research exploring the integration of local wave-sea level variability interactions into predictive models could enhance our understanding and improve forecasts of waterline evolution under changing climate conditions.

Data and methods

For the sake of this study, we generated a dataset of waterline derived from publicly available multi-spectral satellite imagery (Sentinel-2 and Landsats 5, 7, 8, and 9) following the methodology developed by ref. ⁹³. In short, it involves combining different spectral bands to produce Subtractive Coastal Water Index (SCoWI) water differentiating images, defined as

$$SCoWI=B+2\times (G-NIR)-0.5\times SWIR1-0.75\times SWIR2,$$

(2)

where B, G, NIR, SWIR1 and SWIR2 are respectively the green, blue, near infrared, short-wave infrared 1 and 2 spectral bands from multi-spectral images. As shown by ref. ⁹³, this index greatly dissociates land pixels from sea (including white-water) pixels. The method has been successfully extended to images from Landsat mission (5, 7, 8, and 9) via the cloud-platform Google Earth Engine¹⁴, enabling the calculation of SDW on images dating back to 1984. Before proceeding to the band combination, we applied bi-cubic resampling at 15 m pixel-resolution to images from the Landsat 7, 8, and 9 collections (originally at 30 m), and a 10 m for SWIR1 and SWIR2 bands form the Sentinel-2 collection (originally at 20 m). We added a filter identifying images contaminated by the presence of clouds based on the histogram of SCoWI values and discarding them from the collection of analyzed images (refer to Fig. S11 in the Supplementary Material). We then calculated for each image a threshold value of the SCoWI index discretizing land from water pixels using the refined version of Otsu’s threshold method⁹⁴ developed by ref. ⁹³, which selects the threshold as the local minimum between the wet and dry peaks in the distribution of SCoWI values, and used this threshold value to delineate the land/sea interface using a marching squares algorithm⁹⁵. Resulting waterlines were then projected over transects spaced 250 m apart and perpendicular to the coast using the high-resolution GHSSH shoreline dataset⁹⁶ as a baseline. This constituted a set of time-series over 18316 transects along the NAWC, from which we removed transects located at parts of the coast identified as non-sandy using the beach classification dataset from ref. ⁹⁷ and after conducting a visual inspection based on ESRI world imagery. About 40% of the transects were discarded at this step.

At each transect, time series of SDW positions were tide-corrected. To do so, we followed the approach developed by ref. ⁹⁸ to estimate at each transect the average intertidal beach slope, from which we derived the astronomical tide corrections using linear translation. The tide correction term ΔX_tide is therefore defined as

$$\Delta {X}_{tide}(t)=\frac{{\eta }_{tide}(t)}{tan(\beta )},$$

(3)

where η_tide(t) is the deterministic astronomical tide elevation (in meters) and tan(β) is the constant and mean intertidal beach slope estimated from the cross-shore waterline position time series using a power spectrum analysis (an histogram of the distribution of beach slopes along the NAWC is shown on Fig. S12 in the Supplementary Material). In this study, the astronomical tide data were generated using the FES2022 model⁹⁹, considering 34 harmonic constituents. Validation of FES2022 outputs (refer to Fig. S10 in the Supplementary Material) for four sites along the NAWC shows that the astronomical tide model outputs are very reliable. They are rather unbiased (∣bias∣ < 10 cm) and show very good fits (R² ≥ 0.95) with in-situ data.

Time series of tide-corrected waterline position were then corrected from eventual relative bias between the satellite missions. Data from Landsats 5, 8, and 9 and Sentinel-2 missions were systematically compared to data from Landsat 7 over their mutual operation periods, and debiased by their mean difference. Time series for which this bias was greater than 25 m were removed from the dataset. 4% of the transects were removed at this step.

Time series of cross-shore waterline position were then corrected from outliers using first the interquartile range (IQR) test, which consists in removing every data points found out of the [Q₁ − 1.5 × IQR; Q₃ + 1.5 × IQR] interval, where Q₁ (Q₃) is the first (third) quartile and IQR = Q₃ − Q₁ is the IQR (more details about outliers corrections in supplementary).

Outlier- and tide-corrected waterline data were then aggregated into monthly composites to match the temporal resolution of the sea-level anomaly and wave characteristics datasets. Missing monthly values-when there is no available estimation of the waterline position for a given month-were estimated using cubic interpolation over data contained in a sliding window of 25 months (12 months before and 12 months after the given month). If more than 50% of the months in the first half of this window are missing, the interpolation was not performed, and the missing monthly value was set to NaN (Not a Number).

A final sorting was performed to generate two distinct datasets analyzed in this study. The first dataset includes all transects with continuous data from 2000 to 2022 (9% of transects discarded at this step) and was used to derive trends and seasonal cycles of waterline change over a large number of transects. The second dataset, which includes transects with continuous data from 1997 to 2022, is more restrictive (16% of transects discarded at this step) and was used to analyze anomalies in waterline change in relation to ENSO events. Many transects along the Washington coast were discarded at this step.

We chose 2000 as the starting year for the first dataset as there are always at least two satellite missions in operation at the same time over this period, enabling us to resample at a monthly resolution the data with high confidence. We chose 1997 as the starting year for the second dataset to study coastal dynamics during the 1997/98 El Niño. We did not extend the dataset to 1984 (the first year available using Landsat 5 imagery) because there was only one major ENSO event between 1984 and 1997 (El Niño 1992), and the 16-day revisit interval of Landsat 5 would result in sparse time series, necessitating substantial interpolation to reconstruct the monthly signal.

Transects for which the estimated beach slope was greater than a maximum threshold that we set at tanβ = 0.3 were removed from the study. 7% of the transects were removed at this step. After all these operations, the number of transects covering sandy beaches of the NAWC was 7182 (6072) for the first (second) dataset, spaced by a median distance of about 275 m (285 m).

To perform this continental-scale waterline acquisition, we divided the NAWC into 987 subareas with sides of roughly 0.05° (around 5 km) on which we applied the methodology explained above. The pre-processing and band combination steps have been executed on the cloud platform Google Earth Engine (Gorelick et al.¹⁴). Then the SCoWI images have been downloaded on the CNES High Performance Computing cluster platform, from which we executed the segmentation and post-processing steps. In all, 810,897 images have been processed (822 images per subarea in average).

Monthly sampled SDW have been validated against ground truth data at Torrey Pines⁸ along profiles PF525, PF535, PF585, and PF595 (σ ~ 12 m in average, refer to Fig. S9a–d in the Supplementary Material), and at one profile (P33) at Ensenada, BC⁶⁶ against a demeaned 1 m elevation contour shoreline (σ ~ 7 m, refer to Fig. S9e in the Supplementary Material) showing good fits and giving similar results to state-of-the-art methods tested at various sites, including Torrey Pines⁹¹. Standard error has been separated between Sentinel-2 and Landsat sensors (using the individual SDW estimates, not the monthly sampled ones), and show no notable differences, highlighting the transferability of the method developed by ref. ⁹³, initially designed specifically for Sentinel-2 imagery.

From the monthly sampled time series, we derived trends and seasonal cycles of change over the period 2000–2022. First, we estimated the trend using the Theil-Sen estimator^68,69, which defines the slope of a time series as the median of the slopes of all lines passing through pairs of points in the time series considered. From the slope and the corresponding intercept, we reconstruct the time dependent trend signal

$${X}_{trend}(t)=\frac{a}{12}t+b,$$

(4)

where t is the time in months since January 2000, a is the trend (in m/yr) and b the intercept (in m). Trends a are the ones discussed in the Result section.

Seasonal cycles were estimated, for each month m ∈ {1, 2, …, 12}, as the average of the monthly sampled detrended waterline positions, noted ${\overline{{X}_{w}^{d}}}_{m}$ given by:

$${\overline{{X}_{w}^{d}}}_{m}=\frac{1}{{N}_{m}}\sum\limits_{t\in m}{X}_{wt}^{d},$$

(5)

where X_w is the waterline position time series, X_trend the linear component of waterline change derived from X_w, and ${X}_{w}^{d}={X}_{w}-{X}_{trend}$ the detrended waterline position. N_m is the number of observations in month m, and t ∈ m indicates that the sum is over all time points t that fall in month m.

The seasonal cycle signal is then reconstructed as

$${X}_{season}(t)=\{{\overline{{X}_{w}^{d}}}_{1},{\overline{{X}_{w}^{d}}}_{2},...,{\overline{{X}_{w}^{d}}}_{12},{\overline{{X}_{w}^{d}}}_{1},{\overline{{X}_{w}^{d}}}_{2},...,{\overline{{X}_{w}^{d}}}_{12}\}.$$

(6)

and the seasonal range ΔX_season at a given transect is defined as

$$\Delta {X}_{season}=max({X}_{season}(t))-min({X}_{season}(t))$$

(7)

The percentage of explained variance between the combination of the trend and seasonal cycle signals with the entire waterline signal was calculated as

$$VarExp(X,Y)=100\times (1-\frac{Var(X-Y)}{Var(X)}),$$

(8)

where X is the entire waterline signal, Y the sum of the trend and seasonal cycle signals, and Var the variance. An explained variance of 100% implies that Var(X − Y) = 0 ≡ X = Y + c, with c a constant, meaning that all the variability of X is captured by Y.

Finally, anomalies of waterline positions were defined as the residuals expressed by

$${X}_{residuals}(t)={X}_{w}(t)-[{X}_{trend}(t)+{X}_{season}(t)]$$

(9)

Climate modes analysis has been conducted based en EP and CP indices¹⁰⁰ under the form of monthly sampled time series. Winter (DJF) ENSO conditions were determined based on a seasonal resampling of the MEI, EP, and CP indices. We defined the various ENSO conditions and flavors as:

$$\left\{\begin{array}{l}El\,\,Ni\tilde{n}o\,\,:\left\{\begin{array}{l}Mixed\,\,:\,\,MEI > m {\times }{\sigma }_{MEI},\,\,CP > m\times {\sigma }_{CP}\,\,and\,\,EP > m\times {\sigma }_{EP}\quad \\ Central\,\,:\,\,MEI > m\times {\sigma }_{MEI},\,\,CP > m\times {\sigma }_{CP}\,\,and\,\,| EP| < m \times {\sigma }_{EP}\quad \\ Eastern\,\,:\,\,MEI > m\times {\sigma }_{MEI},\,\,EP > m\times {\sigma }_{EP}\,\,and\,\,| CP| < m\times {\sigma }_{CP}\quad \end{array}\right.\quad \\ La\,\,Ni\tilde{n}a\,\,:\,\,MEI < -m\times {\sigma }_{MEI}\hfill\quad \\ Neutral\,\,:\,\,| MEI| < m\times {\sigma }_{MEI}\hfill\quad \end{array}\right.$$

(10)

with MEI, the Multivariate ENSO Index, EP and CP, the Eastern and CP indices¹⁰⁰, respectively, σ_MEI, σ_EP, and σ_CP their standard deviations, and m a threshold rate set at 1. The standard deviation of these metrics is ∼1, with slight variations depending on the time series window studied.

EKE was calculated as

$$EKE=0.5({u}^{{\prime} 2}+{v}^{{\prime} 2})$$

(11)

where ${u}^{{\prime} }$ and ${v}^{{\prime} }$ denote the 14-day high-pass filtered components of the daily zonal u and meridional v winds at the 200 HPa level. u and v wind components are obtained from the ERA5 reanalysis dataset. The EKE values were then averaged monthly.