Introduction

Both afterslip and viscoelastic relaxation are widely reported after recent big earthquakes. Coseismic slip and postseismic afterslip are usually observed on the same fault plane, with evidence suggesting that these slip distributions are generally complementary to each other in space1,2,3. This spatial relationship is typically explained by variations of the fault frictional properties4, such as those described by the rate-and-state-dependent friction law5,6,7. Geodetic observations are the key dataset for afterslip studies, such as for the 1992 moment magnitude (Mw) 7.3 Landers earthquake8, the 1999 Mw 7.4 Izmit earthquake9, the 2001 Mw 7.8 Kokoxili earthquake10,11, and many more recently1,12,13,14. In these cases, afterslip was commonly observed surrounding the coseismic slip on the ruptured fault plane. Their complementary relation is thought to arise from the increased shear stress in the afterslip area surrounding the coseismic rupture15. Coseismic slip is considered to take place in velocity-weakening zones, whereas velocity-strengthening zones are more prone to afterslip16,17. Although afterslip is reported to typically occur above or below the main rupture, studies of some earthquakes, like the 2011 Mw 9.0 Tohoku18,19,20,21, 2015 Mw 8.3 Illapel22, and 2015 Mw 8.6 Nias events23,24, show that afterslip overlapped with coseismic slip to varying extents. This could suggest small-scale variations in frictional properties, with a mix of stable and unstable slip at finer scales9,25,26. When utilizing postseismic geodetic data to investigate Earth’s rheology and fault dynamics, a conventional view is that short-term deformation near the rupture zone is predominantly due to afterslip, while viscoelastic contributions are considered significant only for long-term deformation24,27. These findings come from large megathrust earthquakes with rupture depths of ~10–50 km. However, the behavior of the shallowest portions of thrust faults remains poorly constrained due to limited near-fault geodetic observations, as most of the megathrusts are located offshore. Therefore, reliable near-fault postseismic geodetic observations for megathrusts are critical for understanding the fault structure complexity and the triggering mechanism of afterslip, as well as the viscoelastic relaxation of deeper structures28,29.

Here, we report a notable case involving dense near-fault postseismic geodetic observations from the January 1, 2024, Noto Peninsula Mw 7.5 earthquake, which revealed a unique afterslip distribution in a complex fault system and heterogeneous postseismic viscoelastic relaxation. The Noto Peninsula, located on the southeastern margin of the Sea of Japan, formed through back-arc rifting related to the subduction of the Pacific Plate beneath the Eurasian Plate30 (Fig. 1). Regional studies show a high-velocity lower crust in the Toyama Trough, likely from Miocene mafic intrusions31,32. The complex tectonic settings have led to a regional complex fault system and a weakened crust33. The 2024 Mw 7.5 event, which initiated from an earthquake swarm zone, had a slow initial phase followed by relatively fast bilateral rupture along multiple faults34,35. Prior to this, the region had experienced fault opening, slow slip36 and increased seismicity37, with an Mw 6.3 event in 2022 evidenced along the sub-parallel faults in this complex fault system38.

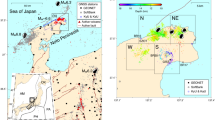
Fig. 1: Tectonic settings of the Noto Peninsula region and coseismic and postseismic deformation associated with the Mw 7.5 earthquake.
figure 1

A Tectonic settings. Volcanoes are from https://www.data.jma.go.jp/vois/data/tokyo/STOCK/souran_eng/souran.htm. B 3D coseismic deformation34. C Postseismic LOS displacements (20240106-20240716) estimated using SAR images. The inset shows the horizontal (arrows) and vertical (color-coded circles) deformation estimated using GNSS observations.

Full size image

By employing dense Global Navigation Satellite System (GNSS) and high-resolution Interferometric Synthetic Aperture Radar (InSAR) data, we precisely map the postseismic deformation over a 6-month period and investigate the driving mechanisms. Our findings reveal that large spatial scale deformation is primarily controlled by viscoelastic relaxation, while near-fault deformation is mainly driven by afterslip on sub-parallel faults, in response to changes in coseismic normal stress, rather than the widely thought shear stress. These results reflect both rheological heterogeneity and the complexity of the fault system in the region.

Results

Large-scale and localized postseismic surface deformation

We analyze the GNSS daily-solution time series by fitting the linear trend, seasonal oscillations, and postseismic deformations related to the 2011 Tohoku-Oki earthquake (Methods). This allows us to extract the postseismic deformation following the Mw 7.5 Noto event. We also process 207-time epochs of line-of-sight (LOS) preseismic (20160112-20230920) and 18-time epochs of postseismic (20240106-20240716) deformation maps using SAR images captured by the Sentinel-1 satellites. We perform similar time series fitting to SAR deformation results to extract the independent postseismic deformation of the Noto event. Our SAR-derived deformation (Fig. 1) closely matches that from GNSS time series analysis (Supplementary Fig. 2), offering a high spatial resolution (~100 m) postseismic deformation image covering nearly the entire Noto Peninsula and part of the main island.

Both the processed GNSS and InSAR deformation maps reveal broad subsidence across the northern portion of the peninsula, with an average amplitude of ~4 cm (Fig. 1), spanning an area of about 80 by 40 km. The most pronounced subsidence reaches up to 8 cm along the coastline of Suzu and Wajima City. In the Suzu area, the subsidence gradually diminishes from north to south, with a minor uplift of around 1 cm detected in Toyama Bay, aligning with the typical uplift response of the hanging wall following a thrust event. In comparison to GNSS data, InSAR observations offer higher spatial resolution insights into the near-field deformation. In the two regions characterized by the greatest coseismic uplift, significant postseismic deformation is absent. Particularly to the north of Suzu, the area has minimal postseismic deformation but extensive coseismic deformation.

The predominant horizontal motion is directed northwestward, with displacements peaking at ~6 cm near Suzu City (Fig. 1) and progressively diminishing from northwest to southeast as the distance from the epicenter increases. The horizontal displacement extends across a broad area in central Japan (Fig. 1C), indicating a response to viscoelastic relaxation processes. The horizontal motion in the southwest and northeast regions exhibits a complex rotational pattern. In the southwest region, a larger rotation angle is observed, with the horizontal motion gradually transitioning from a northwestward to a southwestward direction. Conversely, in the northeast region, the direction of horizontal motion shifts northward, though with a smaller rotation angle compared to that in the southwest. The northwest-directed horizontal movement aligns with the typical afterslip and/or viscoelastic relaxation behavior of the hanging wall following the coseismic thrust motion. However, the rotational characteristics observed in the southwest and northeast regions may suggest the presence of additional complexities in the underlying mechanisms or stress responses in these areas.

Prevalent viscoelastic relaxation and localized afterslip

We model the viscoelastic relaxation of the earthquake by constructing a model with an elastic upper layer with a 30 km thickness overlying a viscoelastic layer that has a thickness of 200 km. We use the Burgers rheology that consists of a Kelvin body in series with a Maxwell body, to account for both the transient and steady-state deformation. We use a viscoelastic layer that has a lateral extent of 800 by 800 km (Methods). Our model robustly explains a broad spectrum of deformation features, including the westward displacement and the rotational patterns. The static coseismic slip distribution (Fig. 3B) from Ma et al.34 is used in this modeling (Methods). The coseismic slip model consists of three fault planes, with most of the slip concentrated on the middle plane, while the western and eastern planes exhibit relatively minor slip.

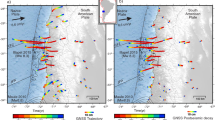
Predicted viscoelastic postseismic deformation induced by stress changes from the along-strike coseismic slip exhibits a characteristic butterfly pattern (Fig. 2A)—symmetrical uplift and subsidence on either side of the peninsula. In contrast, surface deformation in response to the along-dip coseismic slip features a subsidence zone flanked by two uplift regions, with the most pronounced subsidence occurring in the northern part of the peninsula (Fig. 2B). The combined effect of these two components reproduces the observed subsidence across the peninsula and rotational deformation on both flanks (Fig. 2C). The model predictions agree well with the wide-area deformation signals in the GNSS observations, particularly in reproducing the westward motion across central Japan and the subsidence over most areas in the northern peninsula (Fig. 2D, E). The good fits suggest that viscoelastic relaxation is the dominant mechanism driving transient surface deformation across central Japan 6 months after the earthquake. In the region close to the coseismic rupture, after subtracting the viscoelastic model predictions from GNSS data, a residual westward displacement remains in the northern peninsula and Toyama Bay area, potentially indicating the contribution from shallow afterslip (Fig. 2F). Similarly, in the InSAR observations, the large-scale subsidence pattern is also consistent with the viscoelastic model prediction, with residuals indicating localized subsidence and uplift that may be also caused by afterslip.

Fig. 2: Contribution of viscoelastic deformation in response to different motions on the fault.
figure 2

A, B viscoelastic deformation contributed from strike-slip and dip-slip components of the coseismic slip, respectively. C The sum of (A, B). D, E, F, respectively, represent observations, models, and model residuals. Arrows represent the horizontal displacements. The contour lines are the vertical displacements. The effects of a weak zone and of afterslip in controlling surface deformation have not been considered yet.

Full size image

Utilizing these residuals, we perform an afterslip inversion employing the same fault geometry as used for coseismic slip inversion34. The resolution tests show that these residual observations have a good resolution in general (Supplementary Figs. 9 and 10), especially for the middle fault plane (Fig. 3). The afterslip model results in a variance reduction of 95% (Supplementary Fig. 11). The afterslip on both the western and eastern fault planes is primarily distributed around the coseismic slip, collectively forming a complementary pattern (Fig. 3A–C). Notably, the model shows that significant afterslip occurred on both fault planes. The pronounced shallow afterslip on the western plane may include the contribution from very shallow aftershocks (Supplementary Fig. 15), whereas the substantial deep afterslip on the eastern plane is primarily constrained by the westward motion near Toyama Bay.

Fig. 3: Afterslip, coseismic slip, and static stress maps.
figure 3

A Afterslip distribution using the same fault geometry as the coseismic slip. B Coseismic slip distribution. C The 2-D plane views afterslip distribution overlaid by the coseismic slip contours. Arrows represent the rake directions, and gray dots represent aftershocks. Afterslip models and correlation with stress changes due to the Noto earthquake. D-1, D-2 The shear and normal stress changes on the middle plane are calculated using the receiver fault geometry shown in (A). E-1, E-2 The corresponding stress changes on the same plane, but using a receiver fault geometry shifted 3 km northwards (Supplementary Fig. 10).

Full size image

Extensive afterslip is also evident along the middle fault segment, displaying a complex distribution pattern. The shallow afterslip, which occurs at depths less than 10 km, is spatially separated from deep afterslip concentrated below 20 km (Fig. 3C). The afterslip gap at the central depth range (10–20 km) is characterized by scattered aftershocks. Deep afterslip is generated in regions devoid of coseismic slip, while shallow afterslip clearly overlaps with coseismic slip. In Zone I, defined as one significant coseismic slip zone, the afterslip peaks coincide with the maximum coseismic slip. In Zone II, defined as the other large coseismic slip zone, although the afterslip is distributed around the major coseismic slip area, it still shows notable spatial overlap with the coseismic slip region.

Discussion

Shallow afterslip on a hidden sub-parallel fault unclamped by coseismic slip

To further decipher the dramatic overlapping of the shallow afterslip with the coseismic slip on the middle fault segment, we analyzed the static shear stress changes caused by the coseismic slip, where shear stress is thought to either promote (positive stress change) or inhibit (negative stress change) afterslip (Fig. 3). Our calculation shows that the shallow afterslip on the middle fault segment nearly fully overlaps with the large stress drop (Fig. 3D-1). Specifically, in the significant afterslip area in Zone I, coseismic shear stress drop reaches 14 MPa. It is unlikely that the velocity-weakening regions that experienced large coseismic slip, which likely released much of the accumulated shear stress, would continue to slip months after the mainshock. Additionally, numerical simulations39 suggest that afterslip on velocity-weakening patches decelerates quickly—lasting only hours to days—under realistic rate-and-state frictional parameters. Although they show a similar exponential decay, their corresponding surface deformation should fall below the detection threshold of GNSS and InSAR observations all the time. On the other hand, the normal stress change caused by coseismic slip would unclamp (promote afterslip) or clamp (prohibit afterslip) the faults. The calculated normal stress changes show complicated overlapping patterns with shallow afterslip, with no clear correspondence between the positive stress changes and the afterslip distribution (Fig. 3D-2), warranting further investigation.

It has been shown that the stress changes caused by coseismic slip can trigger or affect the transient response of nearby faults40,41. Given the complex sub-parallel fault system identified in the seismic profiles and aftershock catalogs30, we tested the possibility of afterslip on adjacent faults for the middle fault segment. The tests were conducted in two steps. We first calculated the coseismic stress change on the receiver faults, e.g., those parallel with the coseismic ruptured fault, and then performed the afterslip inversion on these faults. We guided the test by examining better spatial complementary features between the stress changes and afterslip distributions on the receiver faults. The most promising scenario is achieved when the receiver fault is shifted northward by 3 km (Supplementary Fig. 10), located beneath the coseismic ruptured fault. The shear stress change on this shifted fault closely resembles that on the coseismic fault (Fig. 3E-1), with a significant stress reduction in the region closest to the large coseismic slip and a dramatic increase close to the edge of the large coseismic slip. The change in normal stress on this receiver fault shows a different pattern (Fig. 3E-2). The coseismic slip clamped the central portion of the receiver fault, with maximum normal stress increase of 8 MPa, while unclamping mostly takes place at the shallow part of the fault, with a peak normal stress decrease reaching 18 MPa. The unclamped regions correspond well with shallow afterslip, suggesting an unclamping triggering. Similar unclamping triggering of the transient slip has also been reported on the central creeping segment of the San Andreas Fault, where the 1983 M 6.7 Coalinga and 1986 M 5.5 Tres Pinos earthquakes produced large normal stress reduction in the transient slip area while the shear stress change is nearly zero42. Another possible mechanism attributes the overlap of afterslip with coseismic slip to the release of accumulated geometric moment rather than stress15. However, in the absence of a reliable long-term coupling model, it remains unclear whether stored strain energy can play a primary role in affecting the activation, magnitude, and velocity of the triggered slip, as suggested by laboratory experiments43,44. A detailed coupling model would help determine how much seismic moment has been released along this middle segment and how much is yet to.

Here, we argue that the shallow afterslip occurred on a hidden fault parallel to the coseismic ruptured fault is a more likely scenario for the Noto case. Further supportive evidence comes from relocated seismicity prior to and after the Noto earthquake37,45,46. This seismicity suggests that an unidentified fault beneath the coseismic rupture was activated prior to the earthquake. This fault is likely responsible for the ongoing shallow afterslip, but it is challenging to confirm if it is the same fault due to the smaller amplitude of postseismic deformation compared to coseismic deformation. Consequently, using postseismic deformation with a Bayesian approach to pinpoint the fault location is not feasible. As a result, our afterslip inversion does not yield a precise fault location. A similar stress change pattern is observed on a fault shifted 5 km northward; however, such patterns does not appear on a fault shifted 3 or 5 km southward (Supplementary Fig. 16). Given the excellent agreement between fault unclamping and afterslip on the north-shifted faults, we suggest that changes in normal stress might be more influential than shear stress on the afterslip, challenging the conventional view that shear stress is the primary driver of afterslip. However, it is not clear what the stress level is on this sub-parallel fault and its potential for a future large earthquake.

Downdip afterslip or viscoelastic relaxation of a weak zone?

The coseismic ruptured fault and the northward shifted faults all exhibit shear stress increases and normal stress decreases at the depth below the coseismic rupture, both possibly facilitate afterslip. Indeed, the afterslip models show pronounced slips in this depth range. However, due to the simplified assumption in our viscoelastic model, which approximates the lower crust and upper mantle with only one homogeneous layer, and the potentially intricate rheological structure of the lower crust in Noto, the observed deep afterslip might have trade-offs with the heterogeneous rheology response. We therefore assess the impact on the deep afterslip caused by more complex viscoelastic relaxation, using a local 3D velocity model to characterize a laterally varying viscoelastic structure.

In the Toyama Trough region, P-wave velocity tomography reveals a high-velocity body at ~20 km depth (Fig. 5H-1), associated with high Vp/Vs anomalies (Fig. 5H-2), which correspond well with anomalies in local gravity observations and seismic reflection profiles30,31. The strain rate map we derived from the GNSS horizontal velocity data prior to the 2011 Mw 9.0 Tohoku-Oki earthquake also indicates anomalies in the Toyama Trough region (Fig. 4), which resembles the previously mapped interseismic strain rate anomaly47. The derived strain rate map shows a good agreement with stress orientations inferred from historical focal mechanisms21. These evidence all suggest that the lower crust in this region exhibits relative weakness. To model this weak zone, we embedded a 10-km-thick viscoelastic layer, extending 100 km laterally and 40 km in width, into a homogeneous layer (dashed black rectangle in Fig. 5B, its top depth is 20 km, also shown in Fig. S6), and performed forward viscoelastic modeling.

Fig. 4: GNSS interseismic horizontal velocity map and the corresponding strain rate field.
figure 4

The inset map shows GNSS velocity estimated from all records before 20110311. Purple sticks indicate the azimuthal direction of SHmax21, while black arrows represent strain rate fields derived from GNSS horizontal velocity vectors.

Full size image
Fig. 5: Predicted viscoelastic deformation and afterslip models with and without a weak zone.
figure 5

A Viscoelastic deformation without a weak zone. B Viscoelastic deformation with a weak zone. C The contribution due to the presence of the weak zone, modeled as the difference between models in (A, B). Afterslip modes for the middle plane using constraints without (D) and with (E) subtracting viscoelastic predictions of the weak zone. F, G Final model residuals of GNSS observations after removing the viscoelastic model predictions and afterslip model predictions. F The results without the weak zone and G The results with the weak zone. H Velocity anomaly maps derived from the velocity structure31.

Full size image

The weak zone beneath the Toyama Trough (Fig. 6) alters the predicted viscoelastic deformations near the Toyama Bay area, up to ~1.5 cm in both horizontal and vertical deformations (Fig. 5A–C). In the coastal areas, the weak zone model reduces uplift and modifies northward motion. The changes in horizontal motion are characterized by eastward movement in the western sector and westward movement in the eastern sector, with the greatest relative displacement occurring in the Toyama region. We then subtract the viscoelastic model predictions from the observations and perform afterslip inversion. The resulting afterslip model shows a smaller deep afterslip (Fig. 5D, E), suggesting that the deep afterslip could potentially be an artifact arising from a heterogeneous viscoelastic structure. Shallow afterslip in the northern part of the peninsula also decreases as the weak zone induces stronger deformation there. The weak zone model also reduces residuals in the Toyama region (Fig. 5F, G), both for horizontal and vertical components. The reduction in model residuals emphasizes the need for this weak zone and supports the interpretation that geodetic observations reflect the complex deep rheology structure in the Noto region (Fig. 6).

Fig. 6: A schematic view of the fault system and deep structure beneath the Noto Peninsula and Toyama Trough.
figure 6

A Fault slip behaviors of the coseismic fault and the possible hidden fault, and the viscoelastic weak zone beneath the Toyama Trough. Aseismic slip area is modified from Yoshida et al.45. B A cross-section view across the fault system and deep structure.

Full size image

In short, we emphasize that high spatial resolution, reliable near-fault postseismic geodetic observations are essential for uncovering afterslip in complex fault systems and deeper viscoelastic structure, which are critical for quantifying the stress evolution and the potential for future damaging earthquakes.

Methods

GNSS data processing and modeling

We employed three-component daily coordinate solutions provided by the Nevada Geodetic Laboratory (NGL). Figure 1 shows a location map of the 211 GNSS stations selected for this study in central Japan. For each station, we fit the North-South (NS), East-West (EW), and Vertical time series using a constant term, a linear velocity, annual and semiannual oscillations, instrument and coseismic offsets, and two exponential decay components to represent the complex postseismic relaxation following the 2011 Tohoku-Oki earthquake. The potential instrument and coseismic offset terms were referenced against the database of potential steps provided by NGL. The fitting period was set from January 1, 2016, to December 31, 2023. It should be noted that the fitting process for the earthquake swarm zone was restricted to time series data collected before October 2020.

After fitting the time series, we selected stations with high signal-to-noise ratio (SNR) results, retaining only those with a data-model correlation exceeding 0.95. This high correlation threshold ensured that only robust and reliable data were included in subsequent analyses. We then performed a linear least squares inversion to forward model the deformation for the postseismic period, allowing us to correct the observations accordingly (Supplementary Fig. 1A–C). To further enhance the quality of the data, we applied a strain model-based method to reduce noise in the horizontal GNSS deformation (Supplementary Fig. 1D). In the reduction of fit from the postseismic observations, we only retained data from stations meeting the high correlation criterion. After correcting for the modeled components, the postseismic observations revealed a clear westward motion.

Sentinel-1 InSAR data processing

We used Sentinel-1 data from a single descending orbital track, acquired after the seismic event that began on January 6, 2024, to determine the postseismic deformations associated with the earthquake. The earliest available orbital track data following the earthquake enables capturing the initial postseismic deformation with maximum immediacy. This descending track data covers a period of ~6 months following the earthquake. To ensure accurate co-registration, we employed the CtSent software to align all images to a consistent spatial reference48. From the co-registered descending images, we generated 105 high SNR interferograms. To further enhance SNR, multi-looking was applied using a 20 (range) by 5 (azimuth) window, followed by the application of a spectral filter49.

The interferograms were then unwrapped, and we corrected for unwrapping errors and fading signals across all interferograms50. Corrections from the Generic Atmospheric Correction Service were also applied51. We selected the J577 GNSS station as the reference point for all InSAR observations and removed the phase history associated with this reference point from all interferograms. The fitted time series of the J577 station was converted to the LOS direction and added to all interferograms, thereby linking InSAR observations to the GNSS reference frame. Following reference point selection, a spatiotemporal filter was applied to estimate and correct tropospheric phase noise in all interferograms52. After aligning the time references to a fixed reference date of January 6, 2024, we directly converted the phase time series into displacements for subsequent analysis and afterslip inversion.

The derived InSAR LOS velocity maps in Supplementary Figs. 2 and 3 both show a good agreement with the GNSS results, and their time series results also show a high consistency.

For the following analysis, we need to estimate the linear part, the seasonal oscillation, the sudden jump, and the exponential decay components.

We applied the same data fitting procedures to preseismic Sentinel-1 images, spanning the period from January 12, 2016, to September 20, 2023. The derived LOS time series was fitted using the same methodology as for GNSS data, enabling us to model the linear trend, seasonal oscillations, sudden jumps, and exponential decay associated with the 2011 Tohoku-Oki Mw 9.0 earthquake. The correction values obtained were then applied to the postseismic period. To prevent overestimating uplift due to fluid upwelling, we restricted the fitting process to the time series data before October 2020 in the earthquake swarm zone. The original observations, the estimated correction, and the corrected observations are shown in Supplementary Fig. 4.

Viscoelastic relaxation modeling

To disentangle the contributions of viscoelastic relaxation and afterslip to postseismic deformation, we adopted a sequential approach that first constrains the viscoelastic structure using far-field GNSS observations—where afterslip effects are presumed minimal—and then removes the modeled viscoelastic deformation from the entire displacement field. The residuals are subsequently used to invert for afterslip (next section). All GNSS observations from sites located 150 km or more from the epicenter are employed to constrain a viscoelastic relaxation model. The coseismic slip model of Ma et al.34 is utilized as an input to compute the associated stress field.

To represent the rheological properties at depth in central Japan, we developed a simplified rheological structure. The model includes an elastic layer for the upper 30 km of the crust, consistent with the depth extent of relocated aftershocks34 (see Supplementary Fig. 5), which we interpret as marking the base of the seismogenic zone and the transition to a ductile layer. Below this, the lower crust and upper mantle are treated as a homogeneous 200 km-thick viscoelastic layer described by a Burgers body (Supplementary Fig. 6). The lateral extent of both the elastic and viscoelastic layers is set to 800 by 800 km. The Burger’s body consists of a Kelvin element in series with a Maxwell element. Due to the focus on observations ~6 months post-earthquake, the viscosity of the Maxwell body, which governs long-term deformation, remains poorly constrained; hence, we assigned a value of 10¹⁹ Pa·s, close to 2 × 10¹⁹ Pa·s searched in the previous study53. We performed forward simulations across a range of Kelvin body viscosity values, using only GNSS horizontal observations as constraints, as these components exhibit higher accuracy. Only GNSS stations with time series fitting correlations exceeding 0.95 are included in the viscosity inversion.

As depicted in Supplementary Figs. 7 and 8, minimizing the chi-square of the model residuals yields an optimal viscosity value of 9 × 10¹⁷ Pa·s for the Kelvin body. The corresponding surface displacements are presented in Fig. 2. Overall, the model predictions demonstrate a reasonable agreement with the GNSS data, indicating that viscoelastic relaxation predominantly governs the postseismic deformation observed ~6 months after the earthquake.

One should note that our derived viscoelastic structures here should be considered a simplified or average representation of the broader region, as it is primarily constrained by far-field observations that may still contain residual contributions from other complex postseismic processes, such as the 2011 Tohoku-Oki earthquake, despite our correction efforts. A simultaneous inversion strategy54,55 for viscoelastic relaxation and afterslip may offer a more comprehensive exploration of the model space and, in principle, yield more detailed structural geometries and better-resolved spatial heterogeneity in the estimated parameters.

Afterslip inversion and model resolution test

We used elastic dislocation theory in a homogeneous half-space to calculate surface deformation56, with a rigidity of 30 GPa and a Poisson’s ratio of 0.25. Each fault segment was divided into sub-patches, using the same fault geometry as Ma et al.34. At the top of the fault, the patch size was set to ~2 km in both the along-strike and downdip directions, varying slightly to match the total length and width of the fault segments. The size increased at a ratio of 1.1 (see Fig. 2 in the main text) to ensure consistent model resolution at different depths.

We performed a joint inversion of InSAR-derived surface motion data and GNSS data to estimate fault afterslip. The InSAR data used are shown in Supplementary Fig. 4C. For the GNSS data, we used observations after subtracting predicted viscoelastic deformations.

We applied a weighting of 10 to the horizontal GNSS observations, 3 to the vertical GNSS observations, and 1 to the InSAR-derived data. A bounded least squares method was used to estimate fault slip, with constraints on the strike-slip component to prevent left-lateral slip in the model. Laplacian spatial smoothing was applied to the slip distribution within each segment, but no spatial smoothing was imposed between segments. Our preferred model has a smoothing factor of 0.045, an empirical data inherited from Ma et al.34. The data fitting for the GNSS and InSAR data is shown in Supplementary Figs. 11 and 12 (adjusted fault geometry), respectively.

We also conducted checkerboard tests to assess the resolution of our afterslip model (Supplementary Figs. 13 and 14). The results, whether using fine or loose fault patches for the slip input, demonstrate that the areas beneath the Noto Peninsula, if constrained by the combination of InSAR and GNSS data, particularly along the middle fault segment, are well resolved, including the shallow patches. In contrast, the northern segment is less constrained due to the limited number of near-fault observations. If we only use InSAR data as constraints, the northern segment’s resolution will decrease, although the resolution of the middle plane is high.

It should be noted that we considered only the contribution of viscoelastic relaxation prior to the afterslip inversion, rather than poroelastic rebound, as previous studies have reported that the contribution of poroelastic rebound is not significant53,57. Potential poroelastic rebound may introduce additional uncertainty into our models.