Turbulent vertical heat flux under Antarctic on-shelf sea ice intensified by the Amundsen Sea Undercurrent

Abstract

The Amundsen Sea Undercurrent, off West Antarctica, transports warm Circumpolar Deep Water onto the continental shelf, driving basal melting when it reaches the ice shelves through troughs. However, vertical heat loss from the warm inflow to the cold upper ocean remains understudied. Here we use observations and numerical modeling to investigate mixing-induced vertical heat flux in a major trough, finding: (1) turbulent mixing transfers 1.7 W m⁻² of heat to the upper ocean during observational period, potentially reducing sea ice growth by 0.2 m yr⁻¹; and (2) mixing is modulated by undercurrent strength, with stronger undercurrent enhancing vertical shear across the on-shelf thermocline, promoting internal wave breaking and mixing. This flux is non-negligible in the on-shelf heat budget, particularly on annual and longer timescales. Our findings highlight the occurrence of vertical heat exchange over the Amundsen Sea shelf and indicate its potential role in modulating sea ice and ice-shelf melting.

Introduction

Against the backdrop of accelerating mass loss of West Antarctic ice shelves^1,2,3, the Amundsen Sea, experiencing rapid ice loss and grounding-line retreat^4,5,6, has received much attention in recent years. Its considerable ice loss has been associated with the ice-shelf thinning caused by basal melting^7,8,9. This basal melting is primarily controlled by the inflow of warm Circumpolar Deep Water (CDW), which crosses the Amundsen Sea shelf break and continental shelf along glacial troughs (Fig. 1a), thereby delivering heat to the ice shelves^10,11,12.

Fig. 1: Hydrography, circulation, and observational coverage in the Amundsen Sea.

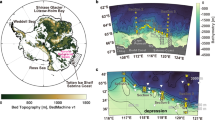
a Map of the Amundsen Sea continental shelf, highlighted in the inset Antarctica map (top left). Arrows indicate the time-mean modeled velocity at 455 m depth during the mooring observational period (2012–2014). Background colors indicate the correlation coefficient (r) between the 455-m velocity and the AU velocity (defined in Methods) at each grid-point based on monthly model output during the observational period. Black contours represent the 500-m isobath and blue contours indicate 1000- and 2000-m isobaths. White areas are regions with depths shallower than 455 m, light blue areas indicate ice shelves with names labeled, and gray areas denote grounded ice regions. b The study region marked in (a) by the blue rectangle. Arrows are the same as in (a) and background colors indicate the modeled time-mean potential temperature θ at 455 m depth during the observational period. Symbols denote observational locations used in this study: mooring (red star), conductivity-temperature-depth (CTD) stations with Lowered Acoustic Doppler Current Profiler (ADCP) velocity measurements (blue circles), and stations with additional microstructure turbulence measurements (spring green plus symbols). All CTD stations measure temperature and salinity profiles. Red rectangle indicates the region where the modeled results are used for the finescale parameterization. The yellow dashed line marks a cross-slope section that represents the main pathway of Circumpolar Deep Water inflow based on model results, as analyzed in Fig. 6. Moored observations of (c) along-trough velocity U (positive towards the shelf), (d) cross-trough velocity V, (e) the magnitude of velocity shear ∣U_z∣, and (f) potential temperature θ. U and V are derived by applying a 35° clockwise rotation, aligned with the trough axis, to the zonal and meridional velocity components. The blue dash-dotted line in (c) represents the spatially-averaged θ profile from CTD stations shown in (b) with depth-averaged standard deviation of 0.09 ^∘C. Velocities in (c) and (d) include data from both the ADCP and the current meter, whereas the velocity shear in (e) is solely from the ADCP. The salinity used to calculate θ is from the CTD station measurements.

The main conduit of such CDW inflow is the Amundsen Sea Undercurrent (AU)^12,13,14, an eastward subsurface current that forms along the shelf break due to baroclinicity associated with the Antarctic Slope Front (ASF)^15,16. The AU transports CDW and veers southward at the intersections between the shelf break and troughs¹⁷, leading to shoreward CDW inflow. In addition to the pathway shaped by shelf break-trough intersections, the cross-slope CDW transport has been shown to be sustained by vorticity input associated with localized wind-stress curl over the shelf break^18,19. An enhanced AU typically results in stronger on-shelf CDW inflow, transporting more heat and contributing to increased ice-shelf melting^12,20,21.

For short-to-medium timescales (days to years), the variability of the AU strength and the inflowing CDW transport has been linked to zonal wind anomalies near the shelf break, which affect the sea level gradients via Ekman dynamics^12,21,22,23. An eastward wind anomaly near the shelf break results in a barotropic enhancement of the AU, leading to increased on-shelf CDW inflow^23,24. The wind anomalies are significantly controlled by the Amundsen Sea Low low-pressure system^23,25, which is itself modulated by large-scale atmospheric modes through atmospheric teleconnections^{26,27,28,29,30}. Additionally, the migration of the sea ice edge and wind forcing could lead to Ekman pumping, modulating the vertical structure of on-shelf CDW and influencing the onshore CDW transport³¹.

For longer timescales (years to centuries), the buoyancy forcing—particularly surface freshwater forcing from ice shelf melting, sea ice and precipitation—influences the AU variability, with an anomalous buoyancy input to the ocean resulting in a stronger AU^32,33,34. A recent numerical study finds that the AU can be enhanced by westward wind anomalies on decadal timescales, and attributes this variability to a baroclinic response due to steepening of the ASF³⁵. A possible explanation for the ASF changes is the buoyancy difference between on-shelf and off-shelf regions increasing due to changes in Amundsen sea ice³⁶.

Most investigations on the CDW inflow onto the Amundsen Sea continental shelf have primarily focused on its horizontal transport of heat toward ice-shelf cavities, where the inflow can directly influence basal melting^20,23,37. However, across the continental shelf, this CDW inflow is extensively overlaid by cold Winter Water (WW)^10,14,24, which is formed in winter through atmospheric cooling. It is this WW that is directly involved in air-sea-ice interactions³⁸, but the vertical exchanges between the CDW inflow and the overlying WW are little understood. A similar scenario examined in the West Antarctic Peninsula shelf highlights that the mixing-induced vertical heat flux may contribute importantly to the upward transfer of heat from CDW to WW and, in so doing, drive potential sea ice melting³⁹. Although a few studies have addressed vertical processes near the ice shelves in the Amundsen Sea^40,41,42,43, these processes remain unclear over the remainder of the continental shelf, where the dynamics are likely very different due to the absence of ice shelves.

In this work, we investigate the vertical mixing dynamics over the Amundsen Sea continental shelf using observations and numerical modeling. We apply a finescale parameterization^44,45,46 to a 2-year moored Acoustic Doppler Current Profiler (ADCP) velocity dataset to quantify the diapycnal mixing rate at the interface between the CDW and WW layers and examine its physical controls. This mixing rate is then used, in combination with numerical model results, to assess the vertical heat flux. We find that, during the observational record, the mixing-induced vertical heat flux may reduce sea ice growth by up to 0.2 m per year in the most idealized condition, or roughly 10–20% of the annual mean sea ice thickness in the area (1–2 m). This heat flux is found to be governed by internal wave breaking, which is modulated by background velocity shear influenced by the AU strength, being stronger during periods of intensified AU flow. We conclude by discussing the potential implications of this mixing-driven vertical heat flux for ice-shelf melting in the Amundsen Sea.

Results

Two-layer structure of the Amundsen Sea

The vertical structure of the Amundsen Sea continental shelf is examined based on measurements collected by the Ice Sheet Stability Program (ISTAR)⁴⁷. During this program, a mooring was deployed at approximately 605 m depth in the west Pine Island Trough, near the shelf break (marked in Fig. 1b). The mooring continuously collected hydrographic and horizontal velocity data from 2012 to 2014 (see details in Methods). Numerical results suggest that the mooring is located along the pathway of the CDW inflow (Fig. 1b), as corroborated by mooring observations showing a strong bottom-intensified current (Fig. 1c, d), confirming previous findings^10,12.

Measurements from conductivity-temperature-depth (CTD) stations near the mooring (marked in Fig. 1b) exhibit a distinct upper WW layer and underlying CDW layer, with a thermocline located at 300–400 m depth (Fig. 1c). The velocity within each layer is relatively uniform vertically (Fig. 1c, d), with the lower layer consistently showing a faster along-trough current than the upper layer. The inter-layer velocity difference produces a persistent shear within the thermocline (Fig. 1e). In summer, strong velocity shear is also observed in the upper layer, occasionally extending to greater depths and merging with the persistent background shear within the thermocline. As velocity shear can induce diapycnal mixing, these observations suggest a continual source of mixing, capable of transporting heat from CDW into the WW layer. The temperature within the CDW inflow layer remains relatively stable throughout most of the observational period, except for a notable increase between April and June 2012 (Fig. 1f). This generally stable temperature supports previous findings that the variability of CDW heat transport into the west Pine Island Trough is primarily controlled by changes in volume transport, rather than changes in water mass properties¹⁴. Moreover, the correlation coefficient between daily mean velocity and temperature is only 0.1 below 400 m, indicating a weak relationship between inflow speed and CDW properties.

Vertical mixing and heat transport across the thermocline

To investigate the turbulent vertical heat flux, we calculate the turbulent dissipation rate ε within the thermocline by using the finescale parameterization method⁴⁴, and subsequently estimate the turbulent vertical heat flux Q as the product of the diapycnal diffusivity κ, calculated through the Osborn relationship⁴⁸, and the vertical temperature gradient (see Methods). The applicability of the finescale parameterization has been validated by the nearby microstructure measurements (Supplementary Fig. 1a). Mooring observations provide velocity shear at 1-hour resolution, which is used for estimating ε and is sufficient to resolve the timescales of internal waves. Due to the lack of CTD time series fully covering the thermocline, the potential temperature gradient θ_z and buoyancy frequency N are obtained from model outputs, which have been calibrated and ground-truthed with observational data (see Methods).

Constrained by the 320-m segment of velocity shear (see Methods), we could only calculate ε between 280 m and 320 m. Our results show that the estimation of ε and Q is not sensitive to this specific depth range. Fig. 2a presents the time series of the estimated ε at the depth of 300 m, which exhibits variability on timescales ranging from days to months, with differences of up to one order of magnitude. The average ε during the observational period is approximately 0.68 × 10⁻⁹ W kg⁻¹, corresponding to a diapycnal diffusivity κ of 1.5 × 10⁻⁵ m² s⁻¹, slightly higher than typical values at the global thermocline⁴⁹. This diffusivity results in an average upward heat flux Q of 1.7 W m⁻².

Fig. 2: Time series of turbulence and surface conditions in the west Pine Island Trough.

Time series of (a) estimated turbulent dissipation rate ε and (b) estimated turbulent vertical heat flux Q at 300 m depth. Black and red lines indicate the daily and monthly smoothed results. c Time series of wind speed (black line) from the European Center for Medium-Range Weather Forecasts Reanalysis Version 5 and sea ice concentration (blue line) from the NOAA/NSIDC Climate Data Record of Passive Microwave Sea Ice Concentration, Version 4, for the study region, marked in Fig. 1a.

Such vertical heat flux could be an important source of heat for maintaining WW above the freezing point, thus acting as a thermal barrier that reduces sea ice growth. As shown in Fig. 2c, the Amundsen Sea continental shelf is covered by sea ice for most of the year, restricting heat loss to the atmosphere. Although sea ice retreats during summer, surface stratification caused by sea ice melting and atmospheric heating isolates the underlying WW layer from direct interaction with the atmosphere, as shown by our model results (Supplementary Fig. 2a, b). We therefore assume that heat fluxed upward from the CDW is stored within the WW layer during summer, with minimal leaking to the atmosphere in that season. The summer observational profiles of temperature and salinity (Supplementary Fig. 1b, c) show a clear thermocline and halocline at approximately 50 m depth, further supporting this assumption. Moreover, the observed temperature profiles rise slightly with depth below 100 m, with the coldest value occurring around 50–100 m, corroborating diapycnal heat transfer from the CDW layer. Based on ISTAR summer CTD profiles in the Amundsen Sea troughs and typical winter WW temperatures from tagged seal data, we estimate the heat content increase within the 100–200 m layer (roughly between the seasonal and permanent thermoclines) since the previous winter to be 4 × 10⁷ to 7 × 10⁷ J. Heat content increments show no clear spatial trend along the AU path, likely due to the short AU travel time and other variability masking spatial difference. Assuming this warming results solely from our estimated mean upward flux of 1.7 W m⁻², the corresponding heating timescale is 270–470 days. Although longer than the heating period of 3–6 months (i.e., the period between the onset of winter convection weakening and the time of summer measurements), possibly due to underestimation of fluxes caused by unresolved events or additional turbulent processes, this estimate supports that the observed flux remains an important contributor to warming in the lower part of WW layer.

The stored heat could then be released during winter, when convective mixing associated with sea ice formation occurs, potentially reducing the annual sea ice growth by approximately 0.2 m (see Methods). Such a reduction is not minor, as the annual-mean sea ice thickness in the region is approximately 1–2 m^50,51,52,53. Notably, the 0.2 m reduction in sea ice growth represents a theoretical upper bound, as it assumes that all upward heat flux is retained and ultimately used to inhibit sea ice growth. In reality, some heat may be lost through lateral advection or intermittent loss to the atmosphere, which are not accounted for in this estimate due to the observational limitations.

Temporal variability in Q approximately aligns with that in ε (Fig. 2), as evidenced by their significant correlation coefficient (r = 0.88, p < 0.01) based on a two-sided Pearson correlation test. This alignment is due to the modest changes in the vertical gradient of potential temperature θ_z within the thermocline throughout the observational period (Supplementary Fig. 2). Both ε and Q show pronounced variability on multi-month timescales, with relatively larger values often observed during fall, winter, and early spring (March to October: 0.86 × 10⁻⁹ W kg⁻¹, 2.1 W m⁻²) and smaller values during late spring and summer (November to February: 0.5 × 10⁻⁹ W kg⁻¹, 1.3 W m⁻²). ε sometimes increases during periods with less sea ice (March 2012, 2013), usually associated with storm events (Fig. 2c). However, comparably large values are more frequently observed during periods with high sea ice concentration (Fig. 2a, c). This implies that the primary driver of vertical mixing is likely independent from surface forcing, consistent with the persistent intensification of velocity shear observed around the thermocline (Fig. 1e).

Dynamics of cross-thermocline mixing

To explore the dynamics governing the vertical mixing across the thermocline, we first apply a Fourier transform to the ε time series. The power spectrum of ε exhibits distinct peaks at semidiurnal and diurnal frequencies (Fig. 3a), indicating a critical role of internal tides in generating the turbulence. The energy of the ε spectrum is highest around the semidiurnal frequency. This prominent contribution likely arises from the close proximity of the inertial (~12.6 hours) and semidiurnal periods, which arrests the vertical propagation of semidiurnal internal tides. Such reduced vertical propagation promotes vertical shear, making internal tides more susceptible to breaking and thereby generating increased vertical mixing. Near-inertial waves (NIWs) may also contribute to the higher energy present at the semidiurnal frequency. Both upward- and downward-sloping shear bands are observed around the thermocline, oscillating near the inertial frequency (Supplementary Figs. 3 and 4). Upward-sloping bands typically appear in late summer or early fall, coinciding with reduced sea ice, and are suggestive of downward-propagating NIW energy injected into the upper ocean by wind forcing (Supplementary Fig. 3). In contrast, downward-sloping bands (Supplementary Fig. 4), occurring year-round, indicate upward-propagating waves, likely generated by intensified bottom currents impinging on the shelf-break topography^54,55. Although the propagation of diurnal internal tides is inhibited by the Coriolis frequency exceeding the diurnal frequency, these internal tides may be trapped within the thermocline, promoting breaking and mixing there⁵⁶.

Fig. 3: Spectral and coherence analysis of turbulence and inter-layer velocity difference.

Variance-preserving power spectra for (a) estimated turbulent dissipation rate ε in Fig. 2a, b the moored inter-layer along-trough velocity difference ΔU = U_bot − U_top. U_top and U_bot are the moored depth-averaged along-trough velocities for Winter Water (200–280 m) and Circumpolar Deep Water (below 400 m) layers, respectively. Vertical lines represent the inertial period, specific tidal periods, and periods of the first mode of barotropic shelf waves (15.5, 7.8, and 5.2 days, corresponding to wave numbers n = 1, 2, 3⁶¹). Wavelet analysis for (c) ε and (d) ΔU. Background color indicates the energy levels, which are normalized by standard deviations, and contours are 95% confidence levels based on an autoregressive 1 model with autoregressive coefficients α = 0.65 and 0.6. e Wavelet coherence power spectrum between ΔU and ε. Background colors indicate coherence and black contours denote the 95% confidence level against red noise. Arrows represent the relative phase relationship, with in-phase pointing right and anti-phase pointing left. The cone of influence is shaded in gray in (c–e).

To further elicit the drivers of variability in ε, which is primarily controlled by the observed velocity shear, we perform a wavelet analysis of the ε record (Fig. 3c). Consistent with ε in Fig. 2a, the wavelet analysis reveals a clear variability on multi-month timescales, with more frequent high-energy peaks observed between March and October. These peaks are apparent not only at semidiurnal and diurnal timescales, but also on intra-seasonal and intra-annual timescales. Their consistency across both short and long timescales suggests that longer-term processes may modulate the vertical mixing occurring on tidal timescales.

As shown in Fig. 1e, the vertical shear across the thermocline exhibits pronounced intra-seasonal and intra-annual variability, indicating a possible connection with changes in ε. Since the vertical shear is primarily due to the velocity difference between the WW and CDW layers, we use the inter-layer along-trough velocity difference ΔU = U_bot − U_top to represent the magnitude of vertical shear around the thermocline. U_top and U_bot are the depth-averaged along-trough velocities for WW (200–280 m) and CDW (below 400 m) layers, respectively, with these depth ranges chosen to minimize interference near the thermocline. As expected, the wavelet power spectra of ΔU and ε exhibit similar patterns with high coherence (Fig. 3c–e), highlighting the connection between the inter-layer velocity differences and the intensity of turbulence.

Figure 4a demonstrates a positive relationship between ΔU and ε, with larger ΔU magnitudes corresponding to higher ε. A significant correlation coefficient (r = 0.7, p < 0.01) between monthly-mean ε and the magnitude of ΔU restates this relationship. One possible explanation for this is that a larger ΔU implies enhanced background vertical shear, which promotes internal wave breaking^57,58,59, thereby generating turbulence and increasing vertical mixing. Notably, the power spectrum of ΔU shows that most of the energy is concentrated in low frequencies (periods  > 3 days, Fig. 3b), suggesting a dominant modulation of the background vertical shear on these timescales. However, the power spectrum of ε is more focused around semidiurnal and diurnal periods (Fig. 3a). This discrepancy indicates that the elevated background vertical shear primarily promotes mixing by facilitating internal wave breaking, rather than by directly triggering instability of the sheared background flow. These results, together with our validation with microstructure measurements, support the applicability of the finescale parameterization in this region of sheared flow, consistent with earlier research elsewhere⁶⁰.

Fig. 4: Link between turbulence and inter-layer velocity difference.

a Relationship of moored ΔU (black line) and moored U_bot (green line) with estimated turbulent dissipation rate ε. b Relationship of moored ΔU with moored U_top (red line) and moored U_bot (green line). ΔU, U_bot, and U_top have been defined in the caption of Fig. 3. For (a) and (b), the x-ranges are divided into small bins with a length of 0.01 m s⁻¹. Lines represent the bin averages and shading indicate 95% confidence intervals. To reduce noise, the data used in (a) and (b) are first averaged every 12 hours, and only bins with more than 15 samples are presented. c Time series of monthly smoothed moored ΔU (black dashed line), moored U_bot (green line), and moored U_top (red line).

This view of the background vertical shear as a key regulator of (internal wave breaking-mediated) vertical turbulent fluxes may be developed further by investigating what sets ΔU. Figure 4b, c reveal that variability in ΔU is primarily controlled by U_bot, with no significant correlation with U_top. In turn, ε has a strong relationship with the magnitude of U_bot (Fig. 4a), with the significant correlation between monthly-averaged ∣U_bot∣ and ε (r = 0.6, p < 0.01) highlighting the control of vertical mixing by the bottom-layer current.

Since the near-bottom CDW inflow results from the veering of the AU into troughs^12,13,14, we surmise that the variation in ε is most likely governed by the AU variability. As reported above, ε is generally larger in winter than in summer (Fig. 2a). This variation is consistent with the AU’s seasonality, which has been shown to be driven by the strength and location of the Amundsen Sea Low. Seasonal changes in this low-pressure system typically result in eastward (westward) wind anomalies during winter (summer), intensifying (reducing) the AU strength^23,25. It is worth noting, however, that we also observe peaks near 5.2, 7.8, and 15.5 days for ΔU (Fig. 3b). These are the characteristic periods of Antarctic barotropic shelf waves⁶¹, which are commonly generated by wind forcing perturbations at various sites around Antarctica, and then propagate rapidly around the continent with speeds up to 1000 km day⁻¹. The slight peak in the 30–60 day range (Fig. 3b) may correspond to the period of the circumpolar-coherent wavenumber zero mode⁶¹.

Conclusions and discussion

The AU transports warm CDW onto the Amundsen Sea continental shelf, where it gains access to the ice shelves along glacial troughs, leading to basal melting and influencing global sea level. The inflowing CDW over the open continental shelf may also influence the upper-ocean heat budget and sea ice processes through vertical heat fluxes into the overlying WW (Fig. 1a). However, the dynamics of these inter-layer exchanges remain little understood. We have used observations near the shelf break, along with numerical model diagnostics, to shed light onto how vertical mixing drives an on-shelf vertical heat flux.

Our observations identify that a persistent but temporally variable vertical shear exists in the thermocline between the WW and CDW layers. Applying the finescale parameterization, we find that the strength of the cross-thermocline mixing is closely correlated with this vertical shear. We show that this result is consistent with the background shear controlling mixing via its modulation of internal wave breaking. Our observations indicate an upward heat flux of 1.7 W m⁻² driven by the cross-thermocline mixing. Vertical heat fluxes of similar magnitude have been reported off the West Antarctic Peninsula^39,62.

To our knowledge, no previous direct measurements of vertical heat flux exist in our study region. Previous study⁶³ summarizes ocean-to-ice heat-flux observations from the Amundsen, Bellingshausen, and Weddell Seas and reports values ranging from 1.7 to 44 W m⁻², generally larger than our estimate. Those measurements, however, were derived either offshore or adjacent to ice-shelf fronts (i.e., areas with coastal polynyas), where hydrographic conditions differ from the open continental shelf regions examined here. The modeled net ocean surface heat flux Q_net confirms this spatial difference, showing an order of magnitude higher values in offshore and ice shelf-adjacent regions than over the open shelf (Fig. 5a, b).

Fig. 5: Modeled net surface heat flux and associated long-term variability.

Maps of modeled time-mean net surface heat flux Q_net averaged over (a) the observational period and (b) 1984–2016. Negative values denote heat loss from the ocean to the atmosphere. Contours are isobaths, identical to those in Fig. 1a. c Time series of modeled Q_net anomaly at the mooring site (red rectangle in Fig. 1b): annual means (black line) and 5-year running means (red line).

While the advection of the AU across the continental shelf occurs over monthly timescales, the associated vertical heat flux is quasi-continuous, particularly for the components traveling through the Pine Island Troughs¹⁴. Within our study area, the modeled anomaly of net surface heat flux Q_net is usually less than 5 W m⁻² on annual timescales and closer to 1 W m⁻² on inter-annual to decadal timescales (Fig. 5c). These values suggest that while the persistent, low-magnitude cross-thermocline flux is smaller than short-term (monthly to seasonal) surface flux anomalies, which can be two orders of magnitude larger (Supplementary Fig. 5), it remains a non-negligible component in the long-term (annual to decadal) upper-ocean heat budget. Neglecting its effect could introduce a bias comparable in magnitude to the interannual or decadal variability that is often the focus of broader climate studies.

By persistently transferring heat to the underlying WW, the cross-thermocline flux may affect the sea ice growth. A mean flux of 1.7 W m⁻² would, in idealized conditions, reduce annual sea-ice growth by up to 0.2 m—about 10–20% of the annual-mean sea ice thickness. During periods of complete ice cover, our model reveals Q_net near  − 10W m⁻² (Supplementary Fig. 5). Thus, episodic vertical heat fluxes that sometimes exceed 5 W m⁻² (Fig. 2b) may slow ice growth at those times. In contrast, during periods with little sea ice, the magnitude of Q_net is substantially higher (Supplementary Fig. 5) and the vertical heat flux barely influences sea ice growth or melting. Given that not all of the upward heat flux directly contributes to sea ice melting, the actual impact on sea ice thickness may be smaller than our idealized estimate. However, over the long term, the much smaller magnitude and more gradual (i.e., low-frequency) variation of Q_net still highlights the potential effects of mixing-induced vertical heat flux on the long-term variability of sea ice.

Further, we find that the velocity shear and mixing strength are significantly correlated with the velocity difference between WW and CDW layers, which is primarily controlled by the near-bottom CDW flow. Since this flow is integrated within the AU^12,13, we conclude that the on-shelf mixing across the thermocline is closely tied to the AU variability. Our work reveals a stronger vertical mixing from March to October (Fig. 2a). This variability aligns with the seasonality of the Amundsen Sea Low, which influences the AU strength through modifications to sea level gradients. Additionally, we find that some variability in bottom-layer velocity occurs on timescales consistent with barotropic shelf waves, which can influence the AU by altering sea level near the shelf break. Thus, these shelf waves appear to affect on-shelf mixing too. Taken together, this evidence suggests that the cross-thermocline mixing, and consequently the vertical heat flux, on the Amundsen Sea continental shelf are strongly affected by remote atmospheric conditions. For example, the Amundsen Sea Low is influenced by tropical events through atmospheric teleconnections. Warm conditions over the tropical Pacific Ocean characteristically induce eastward wind anomalies over the Amundsen Sea shelf break and strengthen the AU^64,65. Moreover, barotropic shelf waves can be generated by wind perturbations at any location around Antarctica, pointing to remote Antarctic winds as a further driver of changes in the vertical heat flux in the Amundsen Sea continental shelf^61,66. Notably, although the AU plays a key role in shaping the vertical structure of the CDW inflow, it is not the only driver. Barotropic and baroclinic adjustments induced by wind-driven Ekman pumping and freshwater input from sea ice or ice shelf melting may also influence shear across the thermocline.

It is important to note that the AU variability due to anomalies in sea level gradients is barotropic^22,23,24, while the modulation of internal wave breaking results from shear changes driven by baroclinic processes. Supported by model results, we propose a possible mechanism linking the barotropic and baroclinic processes at play (Fig. 6): (1) an eastward AU anomaly or a flood tide generates a shoreward barotropic flow; (2) as the flow turns onshore and climbs the continental slope, the shoaling topography causes convergence of the sub-thermocline water column, and mass conservation redistributes horizontal momentum, intensifying the on-shelf flow toward the shelf edge (Fig. 6a, b); (3) by contrast, the layer above the thermocline is only weakly affected by the topography change and largely retains its original speed; (4) this vertically differential response increases cross-thermocline shear, enhancing mixing and facilitating upward heat transport. Further, if the bottom Ekman layer approaches arrest, this may also facilitate the intensification of the CDW-layer velocity⁶⁷.

Fig. 6: Model evidence and schematic of barotropic modulation of on-shelf turbulence.

a Magnitude and (b) along-section component of the time-mean modeled velocity during the observational period, shown for the cross-slope section marked in Fig. 1b. The off-shelf, slope, and on-shelf regions are labeled, with zero distance indicating the offshore end of the section. c Schematic illustration of the vertical mixing process modulated by the variability of barotropic flow. The diagram highlights CDW inflow, topography-induced convergence, shear enhancement across the thermocline, and subsequent mixing on the shelf. WW Winter Water, CDW Circumpolar Deep Water.

Although our estimated mixing and vertical heat flux are limited by sparse observational data, restricted to a single location and two years, it is encouraging that the regional numerical model successfully captures the velocity shear peaks at the thermocline and the inter-layer velocity differences (Supplementary Fig. 6), allowing investigation of the conditions controlling cross-thermocline mixing on broader spatio-temporal scales. Modeling results suggest that the substantial inter-layer velocity differences are widespread across the continental shelf, particularly along the path of CDW inflow (Supplementary Fig. 7a, b). Consistently, a climatology of tagged-seal profiles shows that WW salinity in autumn and winter is generally lower in areas with strong inter-layer velocity differences compared to adjacent regions with weaker shear (Supplementary Fig. 7c, d). While this pattern does not unambiguously demonstrate that diapycnal heat transport causes the salinity reduction, it supports our interpretation: stronger inter-layer shear enhances vertical heat flux, which reduces brine rejection during sea-ice formation and results in fresher WW. Additionally, over the western Amundsen Sea continental shelf, velocity shear peaks are less widespread than in the eastern shelf region (Supplementary Fig. 7a, b), as the CDW inflow in the troughs of the western shelf is primarily governed by the depth of isopycnals¹⁴. Consequently, the mixing-driven vertical heat flux is likely to exert a weaker influence on sea ice in the west compared to the eastern shelf.

In addition to spatial pattern, the modeling diagnostics indicate that during our observational period, the inter-layer velocity differences are in a weak phase, corresponding to a relatively slow AU, with values potentially 2–3 times lower and covering a smaller area than in strong phases (Supplementary Figs. 6, 7a, b). Based on the relationship between mixing intensity and inter-layer velocity difference (Fig. 4a), the on-shelf mixing is enhanced during strong phases, likely facilitating greater vertical heat transport than during our observations and contributing to increased reductions in sea ice growth. Additionally, the modeled monthly variability of inter-layer velocity difference clearly demonstrates a seasonal cycle at our observational location (Supplementary Fig. 5), with larger values occurring from April to September, aligning with our observations. This consistency suggests that vertical mixing likely exhibits seasonal variability, although longer observational periods are needed to confirm this seasonal cycle conclusively.

Recent studies argue that variations in the ocean density gradient between the on-shelf and off-shelf regions of the Amundsen Sea on decadal and longer timescales can alter the ASF at the shelf break, influencing AU variability and ice-shelf melting^33,34,35,36. When the upper-ocean density increases off the shelf or decreases on the shelf, the ASF steepens, and the AU strengthens. Through this mechanism, the on-shelf mixing is likely to impact ice-shelf melting: the mixing-induced vertical heat flux warms the WW layer, predictably leading to increased sea ice melting and decreased upper-ocean density on the shelf. On decadal and longer timescales, the accumulation of reduced on-shelf density would be expected to further steepen the ASF and strengthen the AU.

Based on our estimated vertical heat flux of 1.7 W m⁻², we propose an idealized assessment of its potential contribution to AU strengthening by applying the following assumptions: (1) all heat flux is used for sea ice melting; (2) diapycnal diffusivities for temperature and salinity are equal; (3) the WW layer thickness remains constant at 300 m; and (4) the relevant horizontal length scale is 30 km, representing the typical width of the AU (Fig. 1a). Under these assumptions, and accounting for the mixing-driven salinity flux across the thermocline, we estimate a freshening of the WW layer by approximately 0.015 psu over one year. This freshening results from the reduction in sea ice growth caused by the upward heat flux, which weakens brine rejection into the upper ocean. Furthermore, using thermal wind balance, this salinity anomaly of 0.015 psu corresponds to an eastward increase in AU velocity of about 0.0084 m s⁻¹ below 300 m depth. The characteristic AU velocity is generally less than 0.1 m s⁻¹ (Fig. 1a)¹³. Our estimated AU velocity anomaly could potentially contribute to long-term AU variability, although its actual impact remains uncertain given the assumptions involved. We note, however, that this estimate is highly idealized, as it does not account for the effects of atmospheric forcing, lateral advection, or changes in the WW layer thickness, and should therefore be interpreted as a theoretical upper bound rather than a quantitative prediction of the AU response. A more comprehensive evaluation would require process-based modeling to resolve the dynamical response of the AU to this sustained thermohaline change.

The intensified AU could further enhance the mixing-mediated vertical heat flux, potentially establishing a positive feedback loop. Meanwhile, the CDW inflow might deliver more heat to the ice shelves due to the strengthened AU, likely increasing basal melting. Recent work proposes that increased ice-shelf melting in fact drives the AU and its inflow of CDW^34,68, which would then reinforce the feedback from on-shelf mixing and generate a double-positive feedback.

Applying the observed mean heat flux of 1.7 W m⁻² to the area of existing inter-layer velocity differences in the eastern Amundsen Sea continental shelf (red box in Supplementary Fig. 7a) yields a horizontally integrated cross-thermocline heat transport of  ~ 0.13 TW. This is at least an order of magnitude smaller than the onshore heat transport carried by the CDW inflow, as estimated by both our model and previous studies^10,20, indicating that only a minor fraction of the onshore heat is lost to the WW layer by AU-controlled diapycnal mixing before reaching the ice shelves. Furthermore, this vertical flux is also smaller than the horizontally integrated surface heat loss to the atmosphere within the same region. We attribute this difference to processes in ice shelf-adjacent areas, where melt-water outflow, coastal polynyas and strong upwelling markedly enhance vertical exchange. The elevated Q_net in these near-shore zones (Fig. 5a, b) supports this interpretation. Our findings highlight the importance of resolving coastal mixing in order to close the Amundsen Sea heat budget, important for forecasting the West Antarctic ice-shelf melting.

Methods

Observational data

The observations in the study region, including measurements from a mooring and stations, were collected during the Ice Sheet Stability Program (ISTAR)⁴⁷. The mooring (ISTAR1) was deployed on the eastern side of the west Pine Island Trough near the shelf break, from March 2012 to March 2014, at a depth of approximately 605 m. Current velocities were recorded by a Teledyne RD Instruments 75-kHz ADCP, positioned at 498 m, capturing hourly measurements. In addition, a Nortek Aquadopp current meter at 588 m recorded data every 10 minutes. The moored ADCP data have a vertical resolution of 16 m. The ADCP data above 100 m were often of poor quality, likely due to interference from sea ice and its movement, but this did not affect our conclusions, which focus on greater depths. Two Sea-Bird Scientific SBE37 sensors were deployed on the mooring, positioned at 501 m and 588 m. These provided CTD measurements every 5 minutes. Additionally, seven AQUAlogger 520T sensors, spaced approximately 30 m apart between 350 m and 558 m, recorded temperature at 5-minute intervals.

Station measurements were collected around the recovery of the ISTAR1 mooring (February 27 to March 3, 2014) aboard the RRS James Clark Ross. CTD profiles were taken using a Sea-Bird Scientific SBE911 system, while current velocities were measured with a Teledyne RD Instruments 300-kHz Lowered ADCP. Some of these CTD stations also included microstructure profiler (Rockland Scientific International VMP-2000) deployments to gather additional turbulence data.

In addition to the ISTAR dataset, we also utilize hydrographic data from tagged seals in the Amundsen Sea continental shelf to support our findings⁶⁹. The tagged seal profiles were post-processed in delayed mode to remove pressure, thermal-mass, spiking, and inversion errors and to correct conductivity offsets. To map the spatial-seasonal structure of the hydrographic fields, the Amundsen Sea continental shelf is divided into 0.2^∘ grid cells. For each cell, all seal CTD profiles were averaged by season. Only grid cells containing at least three profiles in a given season were retained. Although these data are spatially and temporally irregular, they provide the only in-situ hydrographic observations during the austral winter, thereby filling a critical observational gap in both space and time (Supplementary Fig. 7c, d).

Model results and calibration

The model results used in this work are identical to those in the study by Silvano et al.³⁵. That model is based on MITgcm and incorporates the ocean, sea ice, and ice shelf components, following the configuration outlined by Naughten et al.⁷⁰, with the only modification being the treatment of iceberg meltwater. This simulation covers the period from 1979 to 2019 and is forced by European Center for Medium-Range Weather Forecasts Reanalysis Version 5⁷¹.

In our study, a primary use of the model output is to provide the buoyancy frequency N required for the finescale parameterization. This is justified by the theoretical framework of the method, which assumes a slowly varying background stratification consistent with internal wave spectral models⁴⁶. Comparison with CTD station measurements shows that the model performs well below the thermocline, accurately capturing the CDW inflow and reproducing its properties. However, the model predicts slightly colder and largely saltier WW (Supplementary Fig. 1), likely due to inaccuracies in the parameterization of surface boundary layer dynamics. This model bias in salinity may lead to a reduced N, which in turn could result in an overestimation of diapycnal diffusivity and heat flux. Despite this, mooring observations indicate that the vertical temperature gradient near the base of the thermocline remains relatively constant (Supplementary Fig. 2). Observations also show that the temperature and salinity within the CDW layer are stable over time (Fig. 1f and Supplementary Fig. 2). Therefore, we assume that the properties of CDW have changed minimally. The model results support this assumption, showing a relatively stationary thermocline and CDW throughout the observation period (Supplementary Fig. 2). Given that the temperature gradients from the model agree well with observations (Supplementary Fig. 1), we use the model-derived temperature fields directly and apply a correction only to salinity. Assuming that salinity is also relatively stable within the thermocline given that the CDW inflow varies little, we apply a depth-dependent linear correction to the model salinity based on station measurements. Specifically, the correction is computed as the difference between the observed and modeled salinity profiles at stations near the mooring, and this depth-varying offset is then applied to the model salinity at the mooring site throughout the observation period.

Estimating turbulent dissipation rate

The turbulent dissipation rate ε is estimated by utilizing the finescale parameterization method based on wave-wave interaction theory⁴⁶. This method estimates ε through the observed energy density and the energy density from the Garrett-Munk (GM) internal wave model. The finescale parameterization formula is expressed as⁴⁵:

$$\varepsilon ={\varepsilon }_{0}\frac{\frac{\left\langle {{{{\bf{U}}}}}_{z}^{2}\right\rangle }{{\overline{N}}^{2}}}{\frac{\left\langle {U}_{z,{{{\rm{GM}}}}}^{2}\right\rangle }{{N}_{0}^{2}}}h({R}_{\omega })L(\frac{{f}_{{{{\rm{cor}}}}}}{\overline{N}}).$$

(1)

ε₀ is the background turbulent dissipation predicted by the GM model at latitude 30^∘ and with buoyancy frequency N₀ = 5.24 × 10⁻³ rad s⁻¹. $< {{{{\bf{U}}}}}_{z}^{2} > =1/({m}_{2}-{m}_{1})\int_{{m}_{1}}^{{m}_{2}}{{{{\bf{U}}}}}_{z}^{2}(m)dm$ indicates the shear variance integrated in the vertical wave number range (m₁, m₂), and ${U}_{z,{{{\rm{GM}}}}}^{2}$ is the corresponding value predicted by GM model. $\overline{N}$ is the segment-averaged buoyancy frequency. The function h(R_ω) accounts for the dominant wave frequency, defined as⁴⁶:

$$h({R}_{\omega })=\frac{3({R}_{\omega }+1)}{2\sqrt{2}{R}_{\omega }\sqrt{{R}_{\omega }-1}}.$$

(2)

${R}_{\omega }= \langle {{{{\bf{U}}}}}_{z}^{2} \rangle /({N}^{2} \langle {\zeta }_{z}^{2} \rangle )$ is the shear-to-strain variance ratio, where ζ is the vertical displacement of isopycnals. The function $L(\frac{{f}_{{{{\rm{cor}}}}}}{\overline{N}})$ accounts for the dependence of latitude⁷², with the form of:

$$L\left(\frac{f_{\rm{cor}}}{\overline{N}}\right)=\frac{{f}_{{{{\rm{cor}}}}}}{{f}_{{{{\rm{cor0}}}}}}\frac{cos{h}^{-1}\left(\frac{\overline{N}}{{f}_{{{{\rm{cor}}}}}}\right)}{cos{h}^{-1}\left(\frac{{N}_{0}}{{f}_{{{{\rm{cor0}}}}}}\right)},$$

(3)

where f_cor is the Coriolis parameter and f_cor0 is the value at the latitude of 30^∘.

In this study, the velocity shear profile is divided into 320-m segments. Velocity in each segment is detrended and windowed with a Hanning window before applying Fourier transformation. The Fourier-transformed velocity shear spectrum is first corrected for range averaging and finite differencing effects⁷³ and then integrated over a fixed wavelength range of (80, 130) m for a stable estimate of spectral power. For the ε estimation based on lowered ADCP velocity shear, N is obtained from the associated CTD profiles. For the ε estimation using moored ADCP velocity shear, N is taken from the calibrated model output. The value of R_ω = 6.8 is the average value calculated based on the station measurements, yielding h = 0.38. The estimated ε for both moored ADCP and lowered ADCP has been validated through microstructure measurement (Supplementary Fig. 1), confirming the reliability of the finescale parameterization method in our study. To avoid inaccurate measurements near the ocean surface, ε based on moored ADCP is only computed within the thermocline.

Diapycnal diffusivity and turbulent vertical heat flux

The diapycnal diffusivity is estimated based on the Osborn method, defined as⁴⁸:

$$\kappa =\frac{\Gamma \varepsilon }{{N}^{2}},$$

(4)

where Γ = 0.2 is the characteristic value of the dissipation ratio⁷⁴. The vertical heat flux is estimated through the diapycnal diffusivity, using:

$$Q=-{\rho }_{0}{c}_{{{{\rm{p}}}}}\kappa {\theta }_{z},$$

(5)

where ρ₀ = 1025 kg m⁻³ is the reference density, c_p = 4000 J kg⁻¹°C⁻¹ is the specific heat capacity, and θ_z is the potential temperature gradient.

Reduction in sea ice thickness growth

In our study, we assume that all mixing-induced heat flux across the thermocline is used to melt sea ice, with no direct loss to the atmosphere. The changing rate of sea ice thickness h_i is expressed as:

$$\frac{\partial {h}_{{{{\rm{i}}}}}}{\partial t}=-\frac{Q}{{L}_{{{{\rm{f}}}}}{\rho }_{{{{\rm{i}}}}}},$$

(6)

where Q is the mixing-induced upward heat flux. L_f = 2.92 × 10⁵ J kg⁻¹ and ρ_i = 922 kg m⁻³ are the latent heat of sea ice melting and the sea ice density for sea ice with salinity of 5³⁹, respectively. The reduction in sea ice thickness Δh_i over a time period Δt is then expressed as:

$$\Delta {h}_{{{{\rm{i}}}}}=-\frac{Q}{{L}_{{{{\rm{f}}}}}{\rho }_{{{{\rm{i}}}}}}\Delta t.$$

(7)

Amundsen Undercurrent definition

The definition of the AU in the model approximately follows previous studies^35,36. We locate the grid points near the 1000-m isobath between 125^∘W and 108^∘W, and average the along-slope velocity over a meridional range of three grid points on both sides of each grid point. We consider velocities below the 1028 kg m⁻³ neutral density surface down to the bottom, and define their spatial maximum as the undercurrent velocity.

Reporting summary

Further information on research design is available in the Nature Portfolio Reporting Summary linked to this article.