Introduction

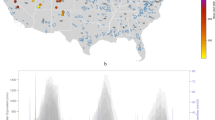
Snowmelt runoff is a key water source for approximately two billion people globally and many important agricultural regions, such as the Western United States (U.S.)1,2,3,4. In these snowmelt-dominated regions, summer water supply is predictable weeks to months in advance5,6 based on observations of the water content of snowpack (i.e., snow water equivalent, SWE) in winter and spring (Fig. 1a, b). However, networks that observe SWE for water supply prediction may not be optimized for some basins7,8, and existing networks may become less reliable with climate change and during hydrologic extremes like snow drought4,9. Accordingly, there is substantial and enduring interest in how SWE observations should evolve to increase skill in water supply predictions and to ensure resilience as the climate changes10,11,12.

Fig. 1: Snowpack can explain much of the interannual variability in summer flow volume.
figure 1

a Daily SWE measured at a snow pillow station across the 23-year period from WY 2001–2023 (lines). b Cumulative flow volume since April 1st at the stream gauge in each of the 23 years. The colors of lines in (a) and (b) correspond to the same years, where warmer colors are years with lower peak SWE and cooler colors are years with higher peak SWE (see color bar). c Conceptual graphic of fractional variance explained (R2) in summer (April–July) water supply by monthly snowpack data and other factors. The solid line is the hypothetical maximum variance (R2potential) that can be explained by snowpack data on a given date. The dashed line is the variance explained by the existing snow stations (R2stations). The difference in darker gray (ΔR2= R2potential - R2stations) is the additional predictability possible from an expansion of snowpack observations. The remaining variance (R2remaining) is unexplainable by snowpack data and is above the solid black line, where R2remaining + R2potential = 1. Note this graphic assumes a shrinking target period after 1 April (see “Methods”).

Full size image

The predictability of summer water supply increases through a water year as seasonal snowpack accumulates and melts, and as the forecast interval shortens (Fig. 1c). Given unavoidable uncertainty in future weather and attendant runoff production after the forecast date6,13,14,15,16, there is a maximum amount of variance in water supply explainable with SWE measurements alone (R2potential). To support statistical water supply forecasting in basins across the Western U.S., SWE is measured across station networks of hundreds of snow courses and snow pillows (Supplementary Fig. 1). A commonly cited limitation8,11,17 of these station data is that they do not represent average SWE at larger scales due to the high spatial variability of snow18, the sparsity of station networks, and the small sampling area (e.g., each snow pillow measures <10 m2). However, station networks were not designed for this purpose; instead, they were designed to provide an index of snow conditions for water supply forecasting16,19. Despite their spatial limitations, station SWE data strongly correlate with water supply (R2stations) in most cases, providing a robust basis for statistical forecasts5,20,21,22. Yet, for many basins and forecast dates, the predictive power of existing SWE data may not be optimized (i.e., R2stations <R2potential), and there is likely additional variance in water supply (ΔR2 = R2potential - R2stations, Fig. 1c) that could be explained with more SWE data, thereby improving forecasts.

Multiple strategies for expanded SWE monitoring could untap these improvements in water supply prediction, ranging from (1) adding measurements at one or a few strategic locations to (2) mapping everywhere in a basin to estimate average SWE (i.e., basin SWE). These present a tradeoff, as the first is spatially limited while the second implies substantially higher costs. The first strategy adds observations at locations we propose calling snow hotspots – areas with the highest available predictive information for water supply not already captured by any existing SWE measurements. While previously unnamed, prior research supports the existence of snow hotspots, as the correlation between SWE and streamflow varies spatially19,20,23,24. This is due in part to variations in runoff source area and hydrologic connectivity during snowmelt25,26,27, which depend on the complex interactions between snowpack (e.g., distribution and melt), basin characteristics, and hydrologic processes (e.g., evapotranspiration, groundwater recharge). From an observational perspective, the locations of snow hotspots are conditional – they depend not only on a basin’s hydrologic dynamics but also on the existing SWE information (i.e., from station networks). As a result, hotspots may emerge in different locations depending on the number and locations of existing snow stations in or near a basin (Supplementary Fig. 2). When no stations are available, hotspots are the single most effective monitoring locations. When a basin already has one or more stations, hotspots are the next best locations for measurements. In either case, the value and location of a snow hotspot reflects what is already known (R2stations) and what new snow information can be added. Once identified, new measurements can be strategically focused in these localized areas.

In contrast, a second strategy is spatially intensive mapping with measurements everywhere in a basin, yielding estimates of basin-averaged SWE as a measure of the total water volume potentially available upon snowmelt. Mapping the spatial distribution of SWE across mountain basins is considered the most important unsolved problem in snow hydrology7, but progress is being made with advances in remote sensing (e.g., airborne lidar surveys), modeling, data assimilation, and machine learning28,29,30,31,32,33,34. Solving the basin SWE mapping problem with remote sensing could potentially improve water supply predictions35,36, but it is unknown whether full basin SWE is necessarily the best strategy, especially in basins where station networks already exist or where adverse weather complicates routine measurements. Addressing this is important, as there is sustained interest in major initiatives that would yield spatial SWE data in near-real time, including prospective satellite missions37 and regional airborne surveying programs32. These would come with substantial costs—on the order of ~10 s to 100 s million USD37—depending on the amount of spatial snow observations collected and the number of years required to develop predictive relationships with water supply.

In this study, we assess the existing and potential predictability of water supply from SWE monitoring. We consider several scenarios for existing ground-based networks (multi-station, single station, and no stations) and then quantify and compare improvements in water supply prediction from two strategies for expanded snowpack monitoring: (1) SWE at a single hotspot versus (2) basin SWE. As a proxy for the data provided by these expanded snow monitoring strategies, we sample a daily gridded ~500 m SWE reconstruction dataset based on MODIS38. This dataset has compared well against airborne lidar30,38 and has sufficient record length to develop relationships with summer flow volume6,22. We analyze snow and streamflow data from 2001 to 2023 across 390 gaged basins in the Western U.S. where human impacts on streamflow are minimal or unimpaired runoff estimates exist (see “Methods”). As a simple metric of water supply predictability, we focus on the R2 correlation based on linear regressions between SWE (Fig. 1a) on the 1st of the month (March–June) and the total streamflow volume in summer (1 April–31 July, Fig. 1b). Although this analysis of marginal benefits (ΔR2, Fig. 1c) is retrospective, a similar approach could be applied to forecast flow using real-time monitoring in snow hotspots or basin SWE (e.g., from airborne or satellite remote sensing). We address three questions: Q1) What is the current capability of water supply prediction from existing SWE station networks? Q2) How much improvement in flow prediction is possible using different strategies to expand SWE observations for different network scenarios? Q3) When and where is there the greatest improvement in flow predictions via expanded SWE observations? We show that both strategies for expanded snow monitoring can enhance water supply predictions, but snow hotspots yield consistently greater improvements than spatially comprehensive basin-wide mapping. We replicate this result with four additional SWE datasets, more complex machine learning models16,39, and other skill metrics. These experiments support the results of our simpler correlation analysis, providing further evidence that hotspots are more effective for improving water supply prediction, even though they do not represent the total snow volume in a basin.

Results

Flow predictability across snow networks and monitoring strategies

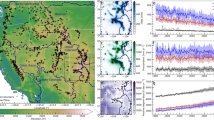
We first demonstrate the analysis concept at an example basin (Colorado River near Lake Granby) for the 1-March forecast and the single station scenario. SWE observed at a single existing station (Willow Park) has R2 = 0.61 with summer flow volume (Fig. 2a). Including a snow hotspot along with the existing station observation increases flow predictability to R2 = 0.84 (ΔR2 = 0.23), whereas including basin SWE increases R2 to only 0.69 (ΔR2 = 0.08; Fig. 2d). There are many locations in the basin where ΔR2 is higher than the ΔR2 from basin SWE (orange and red zones in Fig. 2c); hotspots correspond to the darker red areas which are spatially coherent and have some tendency to occur at higher elevations and/or locations with higher SWE (Fig. 2b). Separately we show that the locations and/or predictive value of hotspots in a given basin may persist or change depending on the network scenario (Supplementary Fig. 2).

Fig. 2: Temporal and spatial relationships between summer flow volume and strategies for expanded snowpack monitoring beyond a single station.
figure 2

Example data are from the Colorado River near Granby on 1 March. A Normalized time series of summer flow volume, SWE from a single existing station (station SWE), flow predicted from hotspot SWE and the single station SWE ( + hotspot), and flow predicted from basin SWE and the single station SWE ( + basin). B Spatial map of 1 March SWE averaged over WY 2001–2023 at ~500 m resolution, with the circle showing the existing snow station with the highest correlation to flow volume, the diamond showing the stream gauge, and the black line showing the basin boundary upstream of the gauge. C Spatial map showing improvements in flow predictability (ΔR2) if the existing SWE station was combined with new SWE monitoring at that location. Darker red zones are snow hotspots. D CDF of all pixels in panel (C), with the improvements in flow prediction shown for all pixels (black line), adding a snow hotspot (red dashed line), and adding basin average SWE (blue solid line). Here, ΔR2hotspot = 0.23 and ΔR2basin = 0.08.

Full size image

Next, we benchmark the predictability of flow volume from existing SWE stations. Across study basins (n = 390) over WY 2001–2023, most of the variability in streamflow can be predicted using existing SWE records even if only a single nearby station is available (Fig. 3a, b). For the multi-station scenario, R2 ranges from 0.67 on 1 March to 0.93 on 1 June (Fig. 3a, station(s) only boxplot) while for the single-station scenario, R2 ranges from 0.62 on 1 March to 0.82 on 1 June (Fig. 3b, station(s) only boxplot) on a median basis. For both types of network scenarios, water supply predictability from existing SWE stations increases through the snow season, as expected. This is the baseline performance against which the expanded monitoring strategies can be compared.

Fig. 3: Variance explained in flow volume by existing and expanded snowpack monitoring strategies across station network scenarios.
figure 3

Network scenarios include: a multi-station, b single-station, and c no stations. As conceptually depicted (left side), strategies for expanded snowpack monitoring beyond the existing station(s) (if any) include adding monitoring at a snow hotspot or adding basin SWE mapping. The hotspot was selected at a pixel with a 99th percentile value of ΔR2 between all pixels in and near a study basin. Basin SWE was calculated as the average of all pixels in a basin boundary. On the right side, each boxplot summarizes the fraction of variance in flow volume explained by each strategy across the study basins (n = 390). The boxes span the 25th–75th percentile and the median is shown as the bold horizontal line.

Full size image

Across all three network scenarios (multi-station, single station, and no stations), expanding snow monitoring to include a hotspot yields statistically greater improvements (two-sided Wilcoxon Rank Sum test, p < 0.005) in predicted summer flow volume than expanding to monitor basin SWE (Fig. 3, Supplementary Fig. 3). For the multi-station scenario, adding a SWE hotspot increases R2 to 0.81 in March to 0.95 in June whereas adding basin SWE monitoring raises R2 to 0.73 in March to 0.93 in June (Fig. 3a). For the single-station scenario, adding SWE monitoring at a hotspot yields R2 ranging from 0.77 in March to 0.89 in June, while basin SWE monitoring yields R2 ranging from 0.68 in March to 0.86 in June (Fig. 3b). For the no station scenario, monitoring only at a hotspot yields R2 ranging from 0.59 in March to 0.80 in June, whereas for basin SWE monitoring R2 ranges from 0.39 in March to 0.70 in June (Fig. 3c). Assuming that the multi-station plus hotspot monitoring strategy approaches the maximum predictive power from snow data (i.e., R2potential, red line in Fig. 1c), the remaining fractional variance due to future weather, runoff processes, and model error (i.e., R2remaining in Fig. 1c) ranges from 0.19 in March to 0.05 in June, on a median basis across basins.

Separately, we assess dependencies of the results on the approach used to characterize hotspots, the selected SWE dataset, the statistical approach for predicting water supply, and the skill metric. First, we compare methods for identifying hotspots, including our simple approach versus a more sophisticated approach with hybrid PCR. The two hotspot approaches yield consistent estimates of R2 for the single-station and multi-station scenarios, but higher R2 values are produced with the hybrid PCR in the no station scenario (Supplementary Fig. 4). Second, we repeat the simple linear regression analysis with four other SWE datasets gridded at 1 km or finer. This yields the same result: all SWE datasets yield higher ΔR2 when adding monitoring at a hotspot versus adding basin SWE, even though the correlation magnitudes vary between datasets (Supplementary Fig. 5). Using our selected SWE dataset with the single station scenario only, we then replace the simple statistical model with the M4 operational system that trains and applies an ensemble of six models and machine learning approaches for predicting water supply from SWE data. When using M4, again we find higher R2 from hotspot SWE versus basin SWE (Supplementary Fig. 6a). Furthermore, M4 achieves the lowest relative root mean squared error (RMSE) when informed by hotspot SWE (Supplementary Fig. 6b). This M4-RMSE experiment serves as a separate test of the predictive nature of hotspots because it uses a distinct skill metric that was not used to identify hotspot locations in a basin. Both expansion strategies yield similar maximum relative errors (Supplementary Fig. 6c), meaning that the forecast error in the worst year is similar for both strategies.

Where hotspots can improve flow prediction

Across the study domain, the hotspot strategy yields greater improvements in water supply predictability compared to the basin SWE strategy in the vast majority of basins for all three network scenarios (93% of basins for no-station, 98% for single-station, and 99% for multi-station) (Fig. 4, Supplementary Fig. 3c, f, i). Hotspot and basin SWE monitoring show similar regional patterns. For example, southern basins such as in the California Sierra Nevada have higher baseline predictability than more northern and interior basins like in the Cascades and Rocky Mountains (Fig. 4a, b). In the Sierra Nevada there are limited opportunities for improving water supply prediction from either monitoring strategy, as the existing station data are often highly effective for water supply prediction (Fig. 4c). In the more northern and interior basins, the hotspot strategy yielded greater improvements than the basin strategy, with the hotspot strategy often yielding R2 that was at least 0.05 to 0.10 higher (Fig. 4c). Opportunities for improved water predictability vary both with forecast month and network scenario, with greater opportunities earlier in the forecast period (e.g., March) and for basins with no stations (Supplementary Figs. 7–9).

Fig. 4: Maps of water supply predictability and gains on 1 April when adding a hotspot versus basin snowpack monitoring to multi-station networks.
figure 4

a The variance explained (R2) in summer water supply when predicted with SWE data combined from multiple existing stations and at a snow hotspot. b The variance explained in summer water supply when predicted with SWE data combined from multiple existing stations and basin SWE monitoring. c The difference in water supply predictability between the snow hotspot and basin SWE strategies (hotspot minus basin), where warm colors (positive values) indicate hotspots yield greater improvements, white indicates similar improvements (R2 within ±0.025), and cool colors (negative values) indicate basin SWE yields greater improvements. Basins plotted as filled black dots are cases where neither strategy improves R2 by more than 0.05, relative to the case of using existing stations only. Other months and network scenarios are shown in Supplementary Figs. 7–9.

Full size image

For a given network scenario, we can explore the spatial characteristics of locations within the study basins that yield the greatest improvements to water supply predictability; here we contrast the no station and multi-station scenarios (Fig. 5). In the no station scenario, there is an increasing but heteroscedastic relationship between SWE percentile and ΔR2 percentile, with the greatest ΔR2 found at the highest SWE percentiles (Fig. 5a). After accounting for the known information from existing stations in the multi-station scenario, the relationship becomes less coherent, though the highest improvements are still found at higher SWE percentiles (Fig. 5b). This suggests that the existing stations explain more of the low-to-middle SWE accumulation dynamics, whereas hotspots tend to fall in higher accumulation zones. For both network scenarios, these high SWE accumulation locations are not representative of basin SWE but nevertheless are optimal for water supply prediction, yet they are currently unmonitored. On a median basis, we find that the locations where local ΔR2 exceeds the ΔR2 from basin SWE monitoring range from 28 to 37% of the basin area, depending on the month. We attempted to explain the relationship between ΔR2 and physiographic factors associated with snowpack dynamics. For the analyzed SWE dataset, we were only able to find a close relationship between SWE accumulation and elevation, where the highest elevation zones in a basin were associated with greater ΔR2 (compare Fig. 5 and Supplementary Fig. 10). We also examined other terrain factors that relate to snowmelt (i.e., aspect and slope) and wind redistribution (i.e., northness, and eastness) but found that ΔR2 generally followed the prevailing distributions (Supplementary Figs. 11, 12), and therefore these terrain factors did not explain how ΔR2 varies across the basins.

Fig. 5: Relationships between SWE and potential improvements to water supply prediction when expanding measurements in different station networks.
figure 5

These 2-d histograms summarize the relative frequency of pixels from all study basins (n = 390) and forecast dates (n = 4) by percentile values for ΔR2 versus SWE for two scenarios for expanded SWE monitoring: a no existing stations, and b multiple existing stations. For each axis, percentile values are computed relative to the spatial distribution for each basin and forecast date. The histograms are normalized by basin size to avoid placing greater weight on larger basins. We define hotspots as having ΔR2 in the 99th percentile; these generally have higher SWE values relative to other locations in a basin for both network scenarios.

Full size image

Discussion

Water supply predictions in the Western U.S. have long been made with SWE records from stations that measure snowpack over a very small area at one or a few locations in or near a basin. For perspective, the 590 snow pillows and 758 snow courses analyzed here collectively measure a total area approximately the size of a football field, and are separated by long distances (median = 13 km, mean = 28 km between neighboring stations). These stations do not always represent SWE at larger scales17, as they are often located in flat, forest clearings at mid-elevations40. In spite of these commonly cited spatial and physiographic limitations7,11, our analysis (Q1) confirms that SWE stations have high information content for water prediction and explain the vast majority of variance (67–93% on a median basis) in summer water supply. This explanatory power still remains high (62–82%) even if only a single station is used (Fig. 3b). This underscores the substantial value and societal benefit of the existing snow station networks that have been long maintained and operated by government agencies. What has been less certain is how much water supply forecasts could be improved if SWE monitoring were expanded, such as to SWE hotspots or over larger spatial scales with basin SWE mapping.

This study compares potential improvements in water supply predictions from two strategies for expanded SWE monitoring in 390 basins across the Western U.S. (Q2), and assesses when and where potential improvement are greatest (Q3). On a median basis, hotspot SWE monitoring increases flow predictability by as much as ΔR2 of 11% for the multi-station scenario and ΔR2 of 14% for the single station scenario. In contrast, basin SWE monitoring offers ΔR2 on the order of 4% or less for the different station scenarios. This magnitude of improved streamflow prediction (beyond what is provided by existing stations) is consistent with expert opinions from operational water forecasters6, experimental hindcasts22, and independent model analyses23,41. Improvements beyond these levels may be difficult to achieve, given constraints imposed by sources of variability that cannot be mitigated with more snowpack information13 (e.g., future weather and runoff processes, Fig. 1c). For the scenario with no existing stations, monitoring at hotspots yields 10–20% higher R2 values than basin SWE mapping. While this study supports that basin SWE can improve water supply forecasts35 for a variety of networks, it uniquely suggests this is not the most optimal or efficient way to do so. Across network scenarios and expansion strategies, the greatest potential improvements are earlier in the forecast period (Fig. 3) and in more northern and interior locations (Fig. 4, Supplementary Figs. 7–9).

Both the hotspot and basin SWE monitoring strategies yield improved flow predictability. However, the hotspot approach consistently provides greater improvements than basin SWE, despite the fact that a hotspot covers a much smaller area. We repeated the analysis using four other gridded SWE datasets and with an ensemble of six models and machine learning approaches, all of which replicated this result (Supplementary Figs. 5, 6). Our explanation for this result and the existence of hotspots centers on the spatial variability in runoff generation rather than weather variability, as we assume future weather uncertainty is similar at hotspots versus the basin. Myriad physical processes (e.g., evapotranspiration, soil infiltration, groundwater recharge) and heterogeneous physiographic features (soil depth, vegetation, bedrock) influence what portion of the snowpack contributes most to streamflow production, and the temporal lag between snowmelt and flow at a stream gauge3,27,42,43. While basin SWE reflects the total volume of water potentially available for runoff, the fraction of that snowpack contributing to streamflow during the forecast interval varies spatially and annually. Basin SWE includes extensive areas of shallow snow (e.g., Fig. 2b) that have lower efficiency in runoff generation25,26,35,44. In contrast, snow hotspots skew toward higher elevations and areas with higher relative SWE accumulation (Fig. 5, Supplementary Fig. 10), which may be associated with higher snowmelt rates45 and enhanced subsurface and/or overland flow production27. We are unable to find any associations between snow hotspots and slope or aspect (Supplementary Figs. 11-12), which are known to be important for heterogenous melt patterns and snow redistribution. This may be due in part to the spatial resolution of the snow dataset; for instance, wind scouring and redistribution processes may be prominent at scales of 100 m or less18. A complicating factor is that a hotspot is the next best measurement location relative to the information already known (i.e., from existing stations), which make it challenging to generalize across basins with diverse monitoring network configurations, snowpack distributions, physiography, and climate. More work is needed to better understand what controls the spatial distribution of hotspots in basins (e.g., Fig. 2c; Supplementary Fig. 2).

We recognize this study has limitations that merit future attention. First, the study period (23 years) was constrained based on availability of the gridded SWE data. However, we assert that it is still possible to develop statistical relationships with this record length6,22. Second, we did not consider the use of ancillary climate or hydrologic predictors6,16,20. While commonly used in forecasting, we omitted them to isolate the forecast gains afforded by the two contrasting strategies for expanded snow monitoring. Finally, we focused on statistical forecasting techniques for operational relevance, but recognize that alternatives exist with distributed process-based models which can integrate gridded SWE data in more direct ways35. However, as in many fields in the geosciences, more complex models do not guarantee more accurate predictions.

Regardless of these limitations, our results demonstrate that sampling of snow hotspots – which typically cover only a small portion of a basin (e.g., 1% by area) – provides a more efficient pathway than basin SWE for improving water supply forecasts. In other words, the greatest gains in water prediction come from measuring snow at the right place(s), rather than measuring it everywhere. Our framework could be used by operational agencies to provide quantitative guidance for identifying optimal new measurement locations, which has not been previously possible. This also prompts questions about the best monitoring approach for optimizing water supply forecasts. One possibility is adding a new ground station in the mapped hotspots, but this creates many potential pitfalls: (1) measurement challenges in high SWE and high elevation areas; (2) constraints around site access, suitability, and ownership6,46; (3) assumptions about the stationarity of snow patterns10,47; (4) uncertainty and scale issues in identifying hotspots; (5) the need to establish and maintain long-term records (15–30 years) to support forecasting6. Thus, adding ground-based stations in hotspots may not always be feasible. An alternative option is targeted remote sensing. For instance, snow depth in hotspots could be monitored with a lidar sensor on a drone48,49 or with airborne surveys along one or two flight lines50 at a substantially lower cost than more conventional wall-to-wall basin coverage.

Finally, while there has been emphasis on acquiring new data through airborne programs or proposed satellite missions, an alternative approach is to make better use of existing snowpack datasets for water supply forecasts22,51,52. The gridded SWE dataset used here required no new expansion in snow stations or investments in remote sensing missions, but yielded better flow predictability compared to using the current stations alone (Fig. 3). This type of retrospective SWE dataset would need to be adapted for near real-time production to support operational decision making, a capability that has already been demonstrated with similar datasets34,53. More generally, new gridded SWE datasets have been developed and produced in select locations (Supplementary Fig. 1), but these are not yet widely used in water supply forecasting. Many snowpack datasets have issues with accuracy and latency, and in virtually all cases their development does not leverage historic remote sensing surveys like airborne lidar to the full extent possible. If these datasets can be improved and adapted for operational use (e.g., via machine learning or hydrologic modeling), they may help optimize snow water supply forecasting without incurring new measurement costs.

Methods

Terminology

Snow water equivalent (SWE) is the total amount of water (mm) stored as snowpack in a given location. SWE can be measured at a snow station which is either a snow pillow or a snow course in a monitoring network. We consider multiple hypothetical network scenarios, which specify the maximum number of existing snow stations assumed to be available for water supply predictions. These scenarios include no stations, single-station, and multi-station networks. For each network scenario, we test two expanded monitoring strategies which are approaches for adding new SWE measurements, specifically at snow hotspots or across a full basin. We define snow hotspots as locations within or near a basin boundary where SWE data yields the greatest increases (99th percentile) in water supply prediction relative to other locations in a basin after accounting for existing SWE data (if any). We define basin SWE as SWE averaged across all pixels within an entire drainage basin, which requires spatially complete mapping. Basin SWE is the average SWE per unit basin area and is thus proportional to the total SWE volume in a basin.

The analysis is conducted by water year (WY), each of which spans 1 October (prior calendar year) to 30 September (current calendar year) in North America. To represent water supply, we analyze seasonal flow volume, the total volume of water passing through a river gage from 1 April to 31 July. In operational settings, the forecast period may vary with basin, but we only use the April–July period here for consistency and simplicity. We define predictability as the linear fit based on in-sample correlations; out-of-sample correlations and prediction skill are assessed through tests with the M4 model (described below).

Existing snow station observations

We obtained time series of daily SWE (snow pillows) and 1st-of-the-month SWE (snow courses) from all stations from the NRCS, CDWR, and the Province of British Columbia (Supplementary Fig. 1) between WY 1980–2023. We excluded stations based on multiple criteria: stations with less than 25 years of complete and usable SWE data, stations outside of the geographic study domain (north of 54° N latitude or east of 104° W longitude), and snow pillow stations that have been burned in wildfire and replaced54,55.

We then quality-controlled and attempted to estimate missing SWE data. We first removed SWE values exceeding upper (4000 mm) or lower thresholds (0 mm). For snow pillows, we removed values that were more than three standard deviations away from the long-term mean SWE at a station for a given day of year. From the daily snow pillow data, we retained SWE on the 1st of the month from March through June to coincide with the monthly sampling frequency of the snow courses. When the 1st of the month SWE values were missing, we estimated these using a two-stage approach. For snow pillows, if peak (i.e., maximum) SWE was available in the year with a missing monthly value (e.g., 1 March SWE), we developed a linear regression between peak SWE and 1st of the month SWE for all the years when both were available. We then applied the regression to estimate the missing 1st of the month SWE value based on peak SWE. For any 1st of month SWE values that were still missing at any type of station (snow pillow or snow course), we developed and applied quantile regressions with the single neighboring station with the highest correlation to the target station. After applying these processing steps, 590 snow pillows and 758 snow courses were retained for analysis, for a total of 1348 candidate snow stations. We did not require a snow station to have data for all analysis months (e.g., we included snow courses with complete 1-April SWE data but not SWE on 1-March, 1-May, and 1-June). The final snow station dataset was then subset to the 23-year analysis period spanning WY 2001–2023.

Gridded SWE reconstructed from MODIS snow remote sensing

We obtained daily gridded SWE across the Western U.S. at a ~500 m spatial resolution over WY 2001–2023 from the ParBal-SPIReS dataset30,38,56. ParBal-SPIReS is a snowmelt energy balance reconstruction of SWE (Supplementary Fig. 1) that is based on snow depletion from daily MODIS fractional snow covered area and snow albedo retrieved with the SPIReS algorithm57, along with downscaled reanalysis data56. We emphasize that it is completely independent of the snow station data, which is necessary for the study design, a characteristic that is not true of other widely-used SWE datasets (e.g., Univ. Arizona SWE and SNODAS, see Supplementary Fig. 5). Whereas traditional SWE reconstruction methods do not produce valid estimates of SWE prior to peak SWE58, ParBal-SPIReS produces SWE estimates during the accumulation season (e.g., on 1-March) by scaling MERRA-2 reanalysis to match peak SWE38. Evaluations against airborne lidar data show high accuracy in SPIReS snow cover59 and ParBal SWE30,60, justifying its usage in this study as a proxy for airborne lidar. While SWE reconstruction data are inherently retrospective, we select this type of data because it has been effectively used to investigate and optimize snow monitoring network design for basin SWE8. Additionally, it can be combined with station data to produce near-real-time SWE estimates for operational applications34,53. Tests with two near-real-time SWE datasets (Univ. Arizona SWE and SNODAS) replicated the results of the main analysis (higher correlations with hotspots than basin or station SWE), but with smaller gains in correlations (Supplementary Fig. 5). Thus, there are readily available SWE data that could be used with the hotspot approach described here to support real-time forecasts of water supply.

While there are other readily available gridded datasets that could have served as a proxy for the expanded SWE monitoring strategies, we selected ParBal-SPIReS because it met all of our criteria: (1) independent of station SWE data, (2) daily data, (3) sufficient record length to meet operational forecasting conventions (which seek 15–30 year records6), and (4) spatial resolution of 102 m or finer to resolve mountain SWE distributions. Of the datasets considered (Supplementary Fig. 1), only two met these criteria: ParBal and the UCLA Western U.S. snow reanalysis29. We selected ParBal-SPIReS over the UCLA dataset, as it had similar or better performance (e.g., bias, RMSE, MAE) when compared to lidar-based SWE data29,60. Additionally, we found that ParBal-SPIReS SWE data had similar or improved correlations with flow, relative to four other gridded SWE datasets (Supplementary Fig. 5). Notably, the correlations were slightly higher with a version of ParBal forced with a different fractional snow cover and albedo dataset (STC-MODSCAG/MODDRFS61,62,63,64), but that SWE dataset was not used in the main analysis because the SWE data are not adjusted in the snow accumulation season (i.e., 1-March). The high correspondence between reconstructed SWE and streamflow volume aligns with other studies7,36,65, further supporting our use of ParBal-SPIReS. The trade-off was that ParBal-SPIReS had a shorter record (23 years) versus other datasets (e.g., UCLA SWE reanalysis has 37 years of data), and this was the main constraint on the length of our study period.

Basin selection and unimpaired flow volume data

We selected gauged basins that had either minimal human impacts (e.g., dams, diversions) on seasonal streamflow or that had estimates of unimpaired runoff volume. Candidate gages came from (1) USDA Natural Resources Conservation Service (NRCS) forecast points, (2) California Department of Water Resources (CDWR) forecast points, and (3) the CAMELS network66,67. For the NRCS and CDWR basins, we utilized monthly unimpaired runoff (also known as adjusted stream volume or full natural flow) where available. The CAMELS basins are long-term, reference gages from the USGS GAGES-II dataset and the Hydro-Climatic Data Network, which have low impervious area ( < 5%) upstream of the gage. We downloaded all available flow volume at these gages and extracted their basin boundaries. We filtered candidate basins based on record completeness, geography, and winter climate. We required gages to have complete records of flow volume over the study period (WY 2001–2023). To restrict our analysis to basins in the Western U.S., we only considered basins where the gage was west of 104° W longitude and south of 49° N latitude, and where the northern basin boundary was south of 50° N latitude (i.e., some gaged basins have headwaters in southern British Columbia). We also restricted our analysis to basins with a drainage area of 4000 km2 or less to only include small to moderate sized watersheds. This constraint was employed for two reasons: (1) to ensure the basin size was not too large for a single station to represent, and (2) to include only basins that might reasonably be measured with an airborne survey. Finally, to ensure only snow-influenced basins were included, we required a minimum basin-average annual snowfall fraction of 15% based on daily DayMet data and a 0 °C air temperature threshold67. These constraints left 390 basins for analysis, which spanned a range of hydroclimates, geology, land covers, and basin drainage areas (Supplementary Fig. 1). For each WY and basin, we summed the total flow volume over three target periods: April–July, May–July, and June–July (see below).

Correlation analyses of snow and flow data

Our central metric of seasonal flow volume predictability from snow data was the in-sample linear fit, as expressed with the Pearson correlation coefficient (R2, Fig. 1c). We selected R2 as a simple and objective way to assess the strength of the temporal relationship between SWE data and observed flow volume (i.e., fraction of variance explained in the annual flow data explained by the snow data). Additionally, it is a commonly used metric in other snow and water supply studies10,16,22. We tested the results using the rank-based Spearman correlation R2 and found the results were qualitatively similar to the Pearson correlation R2.

We separately calculated the variance explained (R2) in flow volume from each of three network scenarios and two strategies for expanded SWE monitoring (described below) from WY 2001–2023 at four SWE observation dates. These dates correspond to key water supply forecast dates: 1-March, 1-April, 1-May, and 1-June. The 1st of the month is when official forecasts are commonly made or updated by agencies in the western U.S20. We did not examine other forecast dates (e.g., 1-January or 1-July) for simplicity. For the 1-March and 1-April analyses, the predictand was flow volume over April–July. For 1-May and 1-June, we used a shrinking target period20: the 1-May SWE analysis predicted May-July flow volume while the 1-June SWE analysis predicted June-July flow volume.

For all basins, we tested three network scenarios: no stations, single-station, and multi-station. In the no station scenario, we neglected the existence of all snow stations across the study domain (Supplementary Fig. 1c) and proceeded to the two alternative expansion scenarios (SWE monitoring at hotspots versus basin SWE), representing the case of introducing new measurements to a basin that lacks SWE stations. The single-station scenario represents a minimal network while the multi-station scenario approximates the baseline capability of the existing network. For the single-station and multi-station scenarios, we selected the 30 snow stations closest to the centroid of each study basin (regardless of whether inside or outside the basin, following operational practice46) and used SWE at those stations as candidate predictors in a linear regression equation. We normalized each SWE and flow time series using the z-score. For the single-station scenario, we calculated an R2 value between the flow volume and the 1st of month SWE time series (n = 23 years) for each of the 30 nearest snow stations individually. We then found the single snow station with the highest R2 for each basin and forecast month. For the multi-station scenario, we used stepwise multiple linear regression to systematically add candidate stations out of the 30 nearest based on whether they significantly reduced the sum of squared errors of the regression model (if the p value < 0.05 of the F-statistic). The multi-station scenario included cases where a single station was most predictive and adding more stations did not improve the regression model. For March and April, a single station was most commonly used in the multi-station scenario, while in May and June two to four stations were typically used (Supplementary Fig. 13).

For each of the three network scenarios, we implemented the two SWE measurement expansion strategies, namely monitoring at SWE hotspots versus basin SWE. We developed multi-linear regression models that predicted flow volume based on multiple predictors: the existing station SWE (from zero, one, or multiple stations; see previous paragraph) and new SWE information (SWE at each i,j grid pixel or total basin SWE). Hence, for the hotspot analysis, we developed pixel-specific regression models between flow volume (Q) and SWE:

$$Q={\beta }_{0,M}+{\sum }_{k=1}^{{{{\rm{nSta}}}}}{\beta }_{k,M}{{{{\rm{Station}}}}}_{k,M}+{\beta }_{G,M}{{{{\rm{Grid}}}}}_{i,j,M}+{\epsilon }_{M}$$
(1)

where β0,M is the intercept, βk,M is/are the coefficient(s) for the snow station(s) used in the regression for the existing Station SWE, M is the month, βG,M is the coefficient and Gridi,j,M is SWE at the i,j pixel location of the SWE Grid, respectively, and ϵ is the residual. The number of stations (nSta) varies with network scenario: nSta=0 for the no station scenario, 1 for single-station, and N for multi-station. The grid was constrained to the rectangular area that encompassed the basin boundary, and thus included some areas just outside the basin boundary, similar to conventions for station selection46. We applied the regression at each pixel (i,j) and computed and recorded the R2. We then calculated the change in water supply predictability (ΔR2i,j) at each grid pixel as:

$$\Delta {R}_{i,j}^{2}={R}_{{{{\rm{grid}}}} \,i,j\,{{\& \; station}}}^{2}-{R}_{{{{\rm{station}}}}}^{2}$$
(2)

For each basin and forecast date, we mapped ΔR2 to identify predictive locations, and created a cumulative distribution function (CDF), with an example shown in Fig. 2d. We identified a hotspot as the 99th percentile ΔR2 correlation in the CDF.

For the basin SWE expansion strategy, we followed a similar approach but using average basin SWE rather than grid-specific SWE values. For each forecast date (e.g., 1-April) and basin, we took the average of all SWE pixels within the basin boundary from the ParBal-SPIReS gridded data for each year, applied the z-score to get a normalized time series of basin average SWE (n = 23 years), and we then used those data to develop a single regression model:

$$Q={\beta }_{0,M}+{\sum }_{k=1}^{{{{\rm{nSta}}}}}{\beta }_{k,M}{{{{\rm{Station}}}}}_{k,M}+{\beta }_{b,M}{{{{\rm{Basin}}}}}_{M}+{\epsilon }_{M}$$
(3)

where βb,M is the regression coefficient and BasinM is the average basin SWE in month M. We then calculated the potential change in water supply predictability with basin SWE as:

$$\Delta {R}_{{{{\rm{basin}}}}}^{2}={R}_{{{{\rm{basin}}}}\,\& \,{{{\rm{station}}}}\,}^{2}-{R}_{{{{\rm{station}}}}}^{2}$$
(4)

In either expansion strategy (Eq. (1) or Eq. (3)), the beta coefficients were zero when the additional predictor (grid SWE or basin average SWE) did not improve the regression, in which case ΔR2 = 0. For the no station scenario, R2station is undefined in Eqs. (2) and (4), and hence ΔR2i,j = R2grid i,j and ΔR2basin = R2basin.

For all analyses, we did not consider non-snow predictors that are often used in operational forecasts (e.g., precipitation, antecedent streamflow), so that our analysis is focused on the information content in the snowpack data. Additionally, we acknowledge that collinearity is likely between the paired predictors (e.g., station SWE and basin SWE). Given that the goal of the analysis is prediction rather than inference (e.g., the importance of each predictor), we deemed collinearity to be less critical to the predictive accuracy and did not attempt to interpret the beta coefficients.

Alternative approach for identifying snow hotspots

Our approach for selecting a snow hotspot (described above) was based on finding a pixel with high (99th percentile) improvement to R2, relative to other pixels in the basin. We separately tested a more sophisticated approach for hotspot extraction using a hybrid version of principal components regression (PCR). This entailed conducting a principal components analysis (PCA) on the gridded SWE dataset, which reduces the dimensionality and results in orthogonal (i.e., uncorrelated) principal components. We retained the first N principal components which collectively explained 95% of the variance in the original gridded SWE dataset. We then applied stepwise linear regression to predict flow, using a hybrid suite of predictors: the first N principal components along with SWE from existing stations (depending on the network scenario). We found that this approach typically utilized 1–2 of the principal components, effectively utilizing information extracted from multiple locations in a basin (whereas our main hotspot analysis introduced monitoring at a single location). Despite this difference, the two approaches yielded very similar results in terms of R2 (see Supplementary Fig. 4) in both the single station and multi-station scenarios, suggesting that much of the predictive power comes from the first one or two new measurement locations, which likely represent the dominant SWE signal. For the no station scenario, the hybrid PCR approach yielded higher R2 than our simple approach, likely because it extracted information from more than one location in the basin.

Repeat analysis with an operations-relevant water supply forecast system

We repeated the main regression analysis comparing the SWE monitoring strategies for the single-station scenario only using the multi-model machine learning metasystem (M4)16,22,39, which was recently developed for operational water supply forecasts at the NRCS. M4 includes an ensemble of six models and machine learning approaches for water supply prediction, including: standard linear regression (similar to main analysis), linear quantile regression, random forests, support vector regression, monotone artificial neural networks, and monotone composite quantile regression neural networks. All six approaches are trained and applied, with the ensemble estimate being used for evaluation with a leave-one-year out cross validation technique. For consistency, we utilized the same predictors as in the main analysis for the single-station scenario and the same predictand (summer flow volume). Given that only two predictors were used at most, we disabled the principal components regression step, but we note that in operational practice there may be dozens of candidate predictors6,22. We assessed three metrics of water supply forecast skill: (1) R2, (2) the root mean squared error (RMSE) normalized to mean summer flow (i.e., relative RMSE), and (3) the maximum relative error (i.e., the largest error found in the cross validation, expressed relative to mean summer flow). The results (Supplementary Fig. 6) show the same relative patterns as the main analysis.

Reporting summary

Further information on research design is available in the Nature Portfolio Reporting Summary linked to this article.