Interception reduction from deforestation and forest fire increases large-scale fluvial flooding risk

Abstract

Catastrophic flooding has been noted to occur with greater frequency following deforestation, but limited observations have been available to test this connection over large spatial scales. Here we used the data of mega forest fires impacting a region of 25,000 km² in Australia exhibiting rapid loss in forest canopy, where the runoff generation has been carefully observed with minimum anthropogenic influences for more than half a century. This provides a unique opportunity to assess the impact of the forest canopy loss on large-scale fluvial flooding. A state-controlled hypothesis test, with the climate and watershed states controlled to enhance robustness, shows a statistically significant increase in annual maximum flows resulting from the forest loss treatment. The reasoning for this natural experiment is that the forest loss impact on the interception potential of forest canopy, fallen leaves, and root-zone soils in wide region could have a recognizable impact on the fluvial flood.

Introduction

Four billion people depend on forested headwater catchments for fresh water¹, and more than 100 million of these live within the area of 1-in-100-year flood, in multiple countries spanning Africa, Asia and Latin America². Catastrophic fluvial flooding has been argued to be increasing in frequency along with an acceleration in global deforestation with development and population growth³. As early as the French Revolution, when deforestation became widespread in the country following the dissolution of a governing state authority, a long list of flood events ensued and were reported a decade later⁴, instigating the still unresolved debate about the role of the forest⁵ in modulating flood extremes. More recently, from the 1960s onwards, the opening of new roads across the Andes in South America resulted in vast deforestation in the upper Amazon. It was again suggested that deforestation was a likely reason for the frequent flooding in the 1970s⁶, and as deforestation continued, flood risk was noted to have further increased, with a once-in-a-20-year flood occurring every other year in the 2010s⁷. In the 1990s, when tens of thousands of square kilometres of forest were disappearing each year worldwide⁸, a statistical assessment of data from 56 developing countries in Africa, Asia and America on forest change, flood frequency (river flood events), and other confounding factors (precipitation, landscape and soil characteristics) demonstrated an increase of 4 to 28 percent in the model averaged flood frequency for a 10 percent decrease in forest area³, with questions remaining unresolved as data was limited and confounding factors many.

The conventional wisdom linking the forest and floods has been based on the analogy that the catchment operates as a sponge⁹ soaking up water during heavy rain and releasing it during dry periods^9,10,11 via groundwater recharge. According to this theory, a deforested catchment loses some capacity to soak up the rainfall, which can cause flood peaks to increase. While this may be true in cases when the deforestation is followed by additional developments such as urbanization, resulting in a net reduction in soil infiltration and percolation to groundwater, forest clearing can also be followed by agricultural development or forest regeneration, and the infiltration capacity may not be disturbed severely¹², suggesting the sponge theory alone may be insufficient for describing deforestation impacts. A more direct reason that has also been noted as influential is related to a forest evapotranspiration process⁵. After deforestation, the reduction in the evapotranspiration can increase watershed runoff rate and flood peaks, but it has again been suggested that the impact of the evapotranspiration process change on floods is only recognizable for moderate rainfall intensity and flood, but becomes relatively minor for extreme events.

The hypothesis to test in this study is that after the forest loss, the reduction of potential interception, summing up for not only all vertical layers from forest canopy to underground soil but also the spatial extent for watersheds of hundreds or thousands km², could significantly increase flood peaks. In a watershed of a few km², the potential interception of a forested watershed would already be low for extreme events, especially with previous high-intensity rainfall, and the reduction due to the forest loss could be minor. However, for a watershed larger than hundreds km², the higher spatial variability of current and previous rainfall could result in as much spatial variability of the potential interception, even for extreme events, and there could be a recognizable reduction in the potential interception, summing up for spatial extent. The reduction of the interception after the forest loss can have a recognizable impact on increasing the risk of extreme floods. Interception here includes not only the canopy interception but also the interception by the ground layers from fallen leaves and leaf mould to root-zone soils with water-retention capacity.

Addressing this hypothesis, however, is complicated by the temporal and spatial climate variability of the natural environment and anthropogenic influences (e.g., dam water regulations and water use) over time, and the lack of high-quality observations spanning large spatial extents where the flood risk is increasing due to the deforestation occurring. The frequent flooding of the 1970s in the Amazon was debated to be due to climate factors given higher annual precipitation¹³, which was supported by later arguments that it fell well within the natural variability for tropical Pacific region catchments¹⁴. The recent further intensification of flooding in the Amazon in the 2010s has again been attributed to the strengthened Walker Circulation⁷. For the flood risk increase observed in the 56 developing countries in Africa, Asia and America after deforestation, the conditions of confounding climate, hydrologic, anthropogenic and infrastructural factors have been used to deny the link as causal¹².

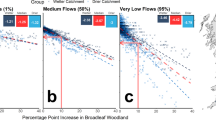
As Fig. 1a shows, if the reference and treatment groups with the treatment of the forest loss have different climate and watershed states, whether flood change is from the forest loss or other confounding climatic and watershed factors remains unclear. To test if the forest loss itself increases annual maximum flow over a large spatial area, vast forest clearance with the control of defined climate and watershed states needs to be analysed to assess the impact on the annual maximum flow (Fig. 1c). According to the state-controlled hypothesis test¹⁵, the hypothesis needs be tested separately for each specific state of confounding factors (Fig. 1c) and then gradually generalized. The paired-watershed experiment with the random assignment (Fig. 1b) for confounding factors can result in unclear and highly uncertain experiment outcomes, sometimes even including conflicting outcomes, as discussed for the deforestation impact on flood peaks⁵.

Fig. 1: State-uncontrolled and state-controlled hypothesis test¹⁵ to assess the change in the watershed process when multiple confounding processes present.

a State-uncontrolled experiment without matching for confounding factors such as climate and watershed states, b paired-watershed experiment with random assignment for the confounding factors, and c state-controlled experiment via the control of the confounding factors.

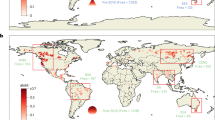
Australian disastrous mega forest fires had occurred at watersheds after over half a century of records, presenting an elaborate effort to observe larger-scale watershed processes with minimum anthropogenic influence and an almost intact forest condition. This dataset has provided a rare opportunity to disentangle forest loss impact from other confounding climate and watershed factors (Fig. 1c) in a defined regional setting. The forest fires occurred for almost 25,000 km² of forests in south-east Australia in the 2000s (Fig. 2a): the 2003 Eastern Victorian Alpine Bushfires (13,000 km²) from January to March in 2003, the Great Divides Fire (10,500 km²) from December in 2006 to March in 2007, and the Black Saturday Bushfires (4500 km²) from February to March in 2009—the fire events occurred just before the rainy season (April–November) with no major land-use change implemented post fire. Before the 2000s fire events, streamflow data for a number of large-scale catchments in this region had been meticulously maintained and observed for more than half a century, with no major forest fires reported, providing enough reference years with the fully covered ranges of the forested catchment responses from the diverse climate fluctuation states of the region. The control group with a similar climate to the treatment group of the forest fire years can be selectively retrieved from the reference group. These catchments are part of the hydrologic reference station (HRS) database maintained by Australian government agencies, representing catchments that are free of anthropogenic influences^16,17. Both the control and treatment groups are from the control of minimum anthropogenic influence (e.g., the dams, weirs, irrigation infrastructure, and land-use changes). Using the data, the treatment (the fire-induced forest loss) can be tested via the control of the climate and watershed states, as described in Fig. 1c for the state-controlled hypothesis test¹⁵.

Fig. 2: The impact of forest fires on the frequency of the annual maximum flow for the 21 catchments in south-east Australia, for which flow measurements are available for.

a The spatial extent of the bushfire impacted region⁵³ (red area, spanning a 25,000 km² area) from 2003 to 2009, and associated hydrologic reference stations⁵⁴ (blue triangle) with station ID. b The cumulative relative frequency for the reference group (green circle dots with a green line) collectively from the 21 catchments and the 9 state-controlled reference years is compared with the forest-fire impacted treatment group (orange coloured triangles) from the years 2003, 2007, and 2009. c The cumulative relative frequency from the closest (the largest green-border-line circles) and the second and third closest (the second and third largest green-border-line circles) three years to the climate state of the treatment years among the 9 state-controlled reference years (green circle dots with a green line) are compared. The cross markers are the fourth closest 2 years that are not included as the reference years, the two years being in the El Niño phase for the sea surface temperature of the central eastern tropical Pacific Ocean.

Results

The null hypothesis that can be tested using this data is that the (fire-induced) forest canopy loss itself does not change the frequency of the annual maximum flood (AMF) in large-scale watersheds. To control the climate system states, the specific years of a reference group are selectively retrieved according to the similarity to the states of the treatment group that represents the forest fire years of 2003, 2007, and 2009. The climate state of the three years of the treatment group is similar to each other without having extreme climate conditions or rainfall patterns (e.g. El Niño or La Niña anomalies as indicated by the sea surface temperatures (SSTs) of the central eastern tropical Pacific Ocean), i.e., the treatment group is within a relatively normal (neutral) state. From the 1953–2002 reference period data, nine reference years (1999, 1962, 1961, 1976, 1987, 1977, 2001, 1957, and 1953, when listed from the closest to the target climate state) are selectively retrieved as the state-controlled reference group—the group is also under the control of the watershed state of the minimum anthropogenic influence. From the 10th closest reference year, more extreme climate conditions are observed, the 10th and 11th closest years (1994 and 1997) being in the El Niño phase for SST in the central eastern tropical Pacific Ocean—El Niño being known to bring reduced rainfall to south-east Australia and as a result, the frequency of the lower AMF for the two reference years (black cross marks in Fig. 2c) are higher than the 9 years reference group (green circle dots with a green line in Fig. 2c). The state-controlled reference group shows the frequency of the AMF in the relatively normal climate and undisturbed watershed states of the treatment years but without the treatment. Details for the state-controlled reference group are provided in the method section, and the closeness of the rainfall states between treatment and reference years can be found in the supplementary information (Fig. S1).

To estimate and assess the AMF frequency, the regional frequency analysis (RFA)¹⁸ is applied. Twenty-one (21) large-scale watersheds (Fig. 2a and Table S-1 in the supplementary information) are used in the RFA, meaning that the data is also representative of larger spatial variability, although the results are interpreted as a return period (a recurrence interval) for its intuitiveness to realize the amount of change. The AMF is standardized to account for its scale variation due to different catchment properties (e.g. catchment’s size and shape). Details on the standardization and RFA are included in the method section. In all, 21 hydrologic reference stations (Fig. 2a) are available within the region with areas from 100 km² to 1200 km² that together provide a 127-year-long (from 21 stations and 9 years reference group but some stations having data from later than 1953) state-controlled reference streamflow data record (state-controlled reference group) and a 63-year-long (21 stations times 3 years) treatment streamflow data record (state-controlled treatment group).

On comparing the treatment group to the state-controlled reference group, a significant increase in the flood frequency is observed as shown in Fig. 2b. The cumulative frequency for a standardized annual maximum flood (SAMF) lower than 0.2 is found to be similar between the two groups of data as not all watersheds were affected by all three years (2003, 2007, and 2009) of the forest fires and the SAMF of the treatment group lower than 0.2 is likely from minor impact watersheds during one of the treatment years. A notable increase in frequency is detected for higher SAMF, representing more extreme flood events. Calculating the frequency exceeding the SAMF value of 0.8, the (exceedance) frequency 0.016 (corresponding to the return period of about 1-in-64 year) for the reference group (marked with green circle dots in Fig. 2c) increases to 0.127 (corresponding to the return period of about 1-in-8 year) in the treatment group (marked with orange triangle dots), implying that very rare events with the return period of 1-in-64 year under normal climate state can occur as frequently as 1-in-8 year after forest fires. When a two-sample χ² test is applied to test the null hypothesis that the treatment group is from the same population as the reference group, the test results in a p-value of 0.006 (lower than the general significance level of 0.05), implying that there exists a clear and statistically significant impact on the AMF frequency following the (fire-induced) forest loss.

Discussion

First of all, it must be noted that to show the effect of forest canopy loss on the AMF, data from only the first wet seasons after the 2003, 2007, and 2009 forest fires are used as the treatment group in the analysis reported in Fig. 2b. The forests in south-east Australia are adapted to recurring fires and have the capacity to self-regenerate^19,20 and the decrease in evaporation after fires is known to be observable only for a short period^21,22. The majority of the fire-impacted area is covered with mixed species eucalypt forests that regenerate via resprouting²³, which have fire-induced tree mortality generally <15%²⁰ and are known to more rapidly recover than other species of that area that regenerate by seedlings. One-year later after the 2009 fire (after wet winter and dry summer seasons), only a slight decrease in the evapotranspiration (3% lower than unburnt forest) was observed for a forest burnt at moderate severity, while a notable decrease (41% lower evapotranspiration) was observed for a forest burnt at high severity²⁰. After a few years, the evapotranspiration of a burnt forest can be even higher than that of an unburnt forest, with the regeneration of the forest consuming a larger amount of water, which then returns to its normal state^21,22. Therefore, in this experiment, only the first wet seasons before summer seasons are considered to ensure catchments are not dominated by a regeneration process and can represent the effect of the forest canopy loss.

In identifying the dominant hydrologic processes that can explain the change in the AMF after the (fire-induced) forest canopy loss in Fig. 2, factors can be summarized into two hydrologic components: rainfall interception and groundwater recharge (percolation to groundwater). Rainfall is intercepted by the forest canopy, fallen leaves, and root-zone soils (Fig. 3a), which then returns to the atmosphere via the evapotranspiration process, and also recharges into deeper groundwater that flows as baseflow after the cessation of rainfall. Rainfall after the interception and groundwater recharge contributes to the AMF as the quickflow process (Fig. 3a).

Fig. 3: The perceptual (a–c) and conceptual (d–f) models of the rainfall-runoff processes for the watersheds with forest, forest loss, and surface sealing.

a, c The processes of the forested watershed for the interception by the canopy, fallen leaves, and root-zone soil and the percolation to groundwater, and the quick-flow. b, d The changes of the interception processes due to the forest loss, and c, f the changes of the infiltration processes due to surface sealing.

The reduction in the rainfall interception loss and evapotranspiration after the forest loss can contribute to the increase of quickflow, as Fig. 3a and b describes. The evapotranspiration can account for up to 70–80% of annual precipitation²⁰. The canopy rainfall interception and evaporation are recognized to be a considerable net addition to the transpiration²⁴, and approximately amounts 10–30% of rainfall²⁵—a proportion of rainfall that is captured by the forest canopy and evaporates back to the atmosphere during and after the rainfall events. For heavier rainfall with larger droplets (e.g. 4–5 mm diameter), it is also splashed into smaller droplets (in size from 10 to 2500 μm) after hitting the canopy, which are subject to greater evaporation²⁶. Evaporation rates for forests can be much higher than for short vegetation, as forests have notably higher aerodynamic conductance²⁴. In addition, a proportion of rainfall is also intercepted as the root-zone soil water content (called soil moisture) that evaporates via the transpiration of the forest canopy—the native species of Australian forests are likely to use their lateral roots to reach the upper soil water content of recent rainfall during the wet season²⁷, causing a lower soil moisture condition. There are several studies concluding that the difference between minor and major flooding can be explained by the initial (root-zone) soil moisture content²⁸. The reduction of the rainfall interception by the forest canopy, fallen leaves, root-zone soil after the forest loss can have a considerable impact on the AMF change as shown in Fig. 2.

The rainfall interception and corresponding AMF depend not only on the rainfall input but also on the previous watershed wetness—this kind of input-output relation dependence on initial system states is generally called hysteresis. The drier the watershed states (the initial wetness of the canopy, fallen leaves, and root-zone soils) are, the higher the potential interception is (Fig. 3d), causing lower quickflow and corresponding AMF. Comparing Fig. 3d and e, the increase in quickflow after the forest loss can be as much as the (initial) potential interception amount. According to the scale of the watersheds, the expected value (spatially averaged) of the potential interception for extreme flood events could be different. In smaller watersheds (e.g., a few km²), the watershed states, such as the wetness of the canopy, fallen leaves, and root-zone soils, are more likely to be spatially homogeneous. The flood peak on the smaller scale can be caused by the spatially homogeneous wetter watershed states and lower potential interception. However, in larger-scale watersheds of hundreds or thousands km², the potential interception (and the rainfall intensity) can show larger spatial heterogeneity. The spatial expectation (average) of the potential interception can be higher for a larger watershed (Fig. 4) while the expectation of the rainfall becomes lower. The larger watersheds with the higher expectation of the potential interception, in addition to the lower expectation of rainfall, are more likely to have a higher deforestation impact on the AMF.

Fig. 4

The distribution and expectation of the potential interception depending on watershed scales.

The groundwater recharge to the delayed runoff pathway that accounts for the shape of the runoff (baseflow) recession after the cessation of the quickflow can be a factor that affects the AMF—the excess rainfall and quickflow can increase as much as the reduction of the percolation to groundwater. However, the AMF increase due to reduced percolation to groundwater is found to be unlikely since the treatment years of 2003, 2007, and 2009 are actually within the millennium drought from late 1996 to mid-2010²⁹. From the early 1990s, the groundwater storage had been observed to be steadily declining until early 2010, when this trend was reversed³⁰, and a similar or even higher groundwater recharge potential can be expected for the treatment years than the reference years. The increase of the AMF in Fig. 1 is unlikely to be from the groundwater recharge factor.

The forest fires not only clear the forest canopy and litter (fallen leaves) but also result in soil property change (of 1–5 cm depth from surface³¹). The surface soil layer can become hydrophobic after fire events³², and forested catchments mostly dominated by subsurface stormflow^33,34 can subsequently generate Hortonian overland flow at the hydrophobic patches³⁵ as shown in Fig. 3c and f. However, at experiment sites in south-east Australia, such deterioration of near-surface infiltration was not observable from the regeneration burn after logging operations³³. Wildfires can become more severe than the controlled fire of the site experiment, but due to its inhomogeneous spatial distribution, naturally burnt soils happen as mosaics of areas with different levels of soil property changes. For the catchments of hundreds of km² in this study, the overland flow generated at some hydrophobic patches can infiltrate near their origin because those are not laterally connected in larger areas³⁵ and contribute to the subsurface flow, as shown in Fig. 3b and e. In addition, the saturated hydraulic conductivity can become lower only for a few months after the forest fires, and after that period, it gradually increases to a state that is higher than in unburned forest areas³⁶. Instead, the interception reduction after the forest fires could significantly increase the total volume of quickflow and infiltration excess overland flow until the recovery of the forest. The soil surface loses its protection, such as fallen leaves, and with a reduced surface resistance, the larger surface runoff could flow and accumulate faster, causing greater erosion.

When forested watersheds could have recognizable potential interception capacity (Fig. 3d), the impact on the quickflow process and AMF becomes sensitive to the level of the forest loss, causing differences in the reduction of the rainfall interception. While the above rationale is consistent with the results in Fig. 2, it can be strengthened through a demonstration of an increase in sensitivity in the AMF directly as a function of the leaf area, indicating a change in the interception and evapotranspiration. The assessment reported in Fig. 2 is refined to establish the sensitivity of the AMF frequency to a change in forest cover. Instead of considering the data for all catchments, the forest-fire treatment group is divided into two sub-groups according to the change in leaf area, representing a reduction in the interception and evapotranspiration due to fewer leaves. The leaf area index (LAI), provided by NASA Earth Observations³⁷, represents a dimensionless measure of one-sided leaf area per unit ground area. The forest canopy exhibiting a unit or more decrease in LAI following the forest fires that form the treatment group is identified—a unit decrease in LAI implies a decrease of leaf coverage that equals the ground extent being studied. The marked region in Fig. 5a represents the overlap of the impacts in 2003, 2007, and 2009 (Fig. 5b–d) after each forest fire event. Minor decreases are not marked in the figures because these could have been a result of the uncertainty in the LAI retrievals, with the note that there were minor LAI decreases for most unmarked locations in Fig. 5b–d for each of the fire events. More details about the LAI analysis are presented in the method section.

Fig. 5: The frequency change of the annual maximum flow due to the two levels of decrease in leaf area.

a The extent (the transparent red-coloured areas) that has the impact of notable LAI decrease (higher than a unit decrease) at least once after the forest fires in b 2003, c 2007, and d 2009 in the forests of the target region. e SAMF frequency changes with the minor LAI change (the green circles with green lines are the state-controlled reference group and the dark green coloured dots of diamond shape are the treatment sub-group 1 for the minor LAI decrease). f SAMF frequency changes with the notable LAI decrease of the b–d (the red diamonds are the cumulative relative frequency for the treatment sub-group 2 selectively with the decreased amount of LAI higher than 1.0 for the years after the forest fires). The frequency is calculated using regional frequency analysis as Fig. 2b, and the hydrograph in Fig. 5a and f is the time series averaged for the data plotted in the cumulative distribution.

This leads to the 63-year-long forest-fire affected treatment group being divided into two sub-groups: 32 years long treatment sub-group 1 that represents less than a unit decrease in LAI, and 31 years long treatment sub-group 2 from the catchments exhibiting notable change in leaf-area as marked in Fig. 5b–d. If the AMF is sensitive to the leaf area, its frequency for treatment sub-group 1 with a minor decrease in the leaf area will be closer to the (state-controlled) reference group, while that for sub-group 2 with notable leaf area change must show more significant change. This is confirmed as illustrated in Fig. 5e and f. Although a small increase in frequency for higher SAMF is observed, the treatment sub-group 1 with minor LAI decrease has a very similar distribution to the reference group (Fig. 5e). Under the null hypothesis that the AMF frequency is not changed by the minor level of the treatment, a two sample χ² test results in a p-value of 0.83 (higher than the general significance level of 0.05), suggesting that these two samples arise from the same population—this also confirms that the state-controlled reference group can represent the treatment group without the impact of the forest clearance. The hydrograph in Fig. 5e, which is the flow time series averaged for all peak events plotted in the cumulative distribution, shows high similarity between the reference group and the treatment sub-group 1.

For the other treatment sub-group with the notable leaf area decrease, the increase in frequency of higher SAMF (Fig. 5f) is in marked contrast to the other treatment group (Fig. 5e). Under the null hypothesis that the AMF frequency is not changed by the notable level of the treatment, the p-value for the hypothesis test equals 0.00003 (lower than the general significance level of 0.05). These test results suggest that the leaf area decrease, indicative of the reduction of the potential interception due to the loss of the forest canopy, fallen leaves, and root-zone soil transpiration, has a strong correlation to the AMF change. The hydrograph in Fig. 5f shows both its peak and volume increase in the treatment sub-group 2 in comparison to the reference group. This hydrograph change also supports that the AMF increase is from the total volume increase of quickflow from the reduction of the interception and evapotranspiration as described in Fig. 3d and e, rather than the land surface change into impervious area, which causes a sharp increase in the peak but without such a recognizable increase in the total hydrograph volume.

The role of forests for the mitigation of floods has long been controversial³⁸ for centuries. The experimental framework for natural watersheds has evolved into a more sophisticated design of the paired watershed experiments during the last century. Most of the experiments have focused on smaller-scale watersheds (generally a few km²), and only a few studies have attempted larger-scale analysis, such as the recent studies for the 2019 mega forest fires³⁹ in Australia, the experiment of the forest-type in China⁴⁰ and planting extent in UK⁴¹. The studies suggested that the forest loss impact can be different according to the watershed saturation level³⁹, forest types (e.g., broadleaf and coniferous trees)⁴⁰, and planting extent⁴¹. In this study, from the 25,000 km² forest fires of 2003, 2007, and 2009 and the half-century of elaborate observations, we understood that the flood frequency change after the forest loss can be sensitive to the potential interception (by the canopy, fallen leaves, root-zone soils as described in Fig. 3) apart from the infiltration and percolation changes.

For a society vulnerable to the flood hazard increase without proper flood mitigation infrastructures and measures, the frequency change of AMF can notably affect flood risk. The concerns for the increase in flood risk are especially high given that vast deforestation is underway, with recent estimates approaching 100,000 km² per year⁸ with increasing population and development. In addition, global warming and abnormal climate states have been exacerbating extreme drought and vast forest fires globally⁴². Although the relation of the flood risk to deforestation has been repeatedly suggested in the literature, it has long been debated seriously without reaching agreement, as experimental observations, especially over large scales, were not readily available¹²—even the small-scale paired watershed experiments have shown the high variability in the results of the forest loss impact on floods¹⁵. The current question is whether the forest loss itself (due to logging or forest fires) can significantly increase the flood frequency and risk in larger-scale forested catchments, apart from the effect of land conversion to less pervious areas (e.g. urbanization and agricultural developments). Here we use data of 21 watersheds of hundreds of km² with forest fires over large spatial scales extending to 25,000 km² in the 2000s, simulating deforestation impact. The availability of half a century of meticulously maintained meteorological and hydrological observations and the lack of anthropogenic influences enable us to recognize that the forest clearance itself, due to the reduction in the interception, can significantly increase the flood risk for large-scale catchments.

Methods

Regional frequency analysis

The annual maximum flow (AMF) series using daily observations from 1953 to 2009 at 21 hydrologic reference stations (HRS) within the forest fire-impacted region (Fig. 1a) is collected, each HRS being carefully identified to be free of anthropogenic influences and land-use changes for scientific applications such as ours⁴³. The period 1953–2002 is adopted as reference representing natural climate variability (called reference years in the analysis that follows) to highlight the frequency change of the AMF for the years 2003, 2007, and 2009 corresponding to the forest fires (called treatment years). The 21 HRS collectively provide a 782-year-long AMF data series for the reference years and a 63-year AMF data series for the treatment years.

To address heterogeneity in the distribution of the AMF according to catchment properties such as size and shape, the AMF ${Q}_{i,t}$ for the year $t$ of the $i{{\rm{t}}}{{\rm{h}}}$ HRS is standardized. General methods, such as the standardization based on the first moment (mean) of the AMF, can be used if the AMF for all stations can be assumed to be from the same distribution after the standardization. However, the AMF of the 21 HRS in this study could not satisfy the assumption, and thus, the probability integral transformation is applied as the standardization method. Using the probability integral transformation (Eq. (1)), the standardized AMF (SAMF) ${Q}_{i,t}^{* }$ has a maximum value of 1.0 and follows a standard uniform distribution for all HRS. After the transformation, the SAMF is distributed between 0 and 1 uniformly for all stations of forested catchments and used to detect the change in frequency caused by the forest fires in the treatment years. The inverse cumulative distribution function ${F}_{i}^{-1}({Q}_{i,t}^{* })$ of the station $i$ can be used for the SAMF ${Q}_{i,t}^{* }$ of a group with a specific state (such as the forest fires) to see the AMF changes of the group, assuming spatial homogeneity for the SAMF distribution of the group given the state.

To avoid a subjective decision on selecting a specific distribution function, an empirical distribution function (Eq. (2)) for the AMF ${Q}_{i,{t}_{{ref}}}$ for the ${n}_{i}$ reference years at each ${i}^{{th}}$ HRS is formulated.

$${Q}_{i,t}^{* }={F}_{i}\left({Q}_{i,t}\right)$$

(1)

$${\hat{F}}_{i}({Q}_{i,t})=\frac{1}{{n}_{i}}\displaystyle {\sum }_{{t}_{{{r}}{{e}}{{f}}}=1}^{{n}_{i}}{I}_{{Q}_{i,{t}_{{{r}}{{e}}{{f}}}}\le {Q}_{i,t}}$$

(2)

where ${\hat{F}}_{i}$ is the empirical cumulative distribution function for the $i{{\rm{t}}}{{\rm{h}}}$ HRS of ${Q}_{i,t}$, ${n}_{i}$ is the number of reference years for the $i{{\rm{t}}}{{\rm{h}}}$ HRS, and ${I}_{{Q}_{i,{t}_{{{\rm{r}}}{{\rm{e}}}{{\rm{f}}}}}\le {Q}_{i,t}}$ is an indicator function which equals 1 if ${Q}_{i,{t}_{{{\rm{ref}}}}}\le {Q}_{i,t}$ or 0 otherwise. For smoothing this step function, linear interpolation is applied.

State-controlled hypothesis test

The SAMF data representing the forest fire impacted treatment years uses the same 21 HRS catchments as the reference data set. Comparing the SAMF for the treatment years directly to all of the reference years illustrates change caused not just by the forest fires but also by variations in the specific climate conditions that prevailed during the treatment years.

To reduce and control climate-driven variabilities in this hypothesis test, the state-controlled hypothesis test¹⁵ is applied. The state-controlled reference group is formed to identify a subset of reference years that bear similarity in climate conditions to those for the forest fire-impacted treatment years. The factors that influence precipitation anomalies in south-east Australia have been noted to be closely related to (i) Indian Ocean sea surface temperatures (SST), (ii) central eastern tropical Pacific Ocean SSTs, (iii) the Antarctic Oscillation, and the presence of Northwest Cloudbands and Cut-off Lows (details are available on the website of Bureau of Meteorology⁴⁴).

The Dipole Mode Index (DMI)⁴⁵ and Southern Oscillation Index (SOI)⁴⁶ are used to differentiate the Indian Ocean and the central eastern tropical Pacific Ocean SST state, and the Southern Annular Mode (SAM)⁴⁷ is used to do the same for the Antarctic Oscillation⁴⁸. With a higher chance of rainfall typically related to higher SOI and a lower DMI and SAM, the maximum of the 3-month SOI for the period of April–November over the rainy season (the last month of the three-month SOI to lie within the rainy season) is used along with the minimum of the 3-month DMI and SAM to distinguish the climate conditions prevalent. The temporal inclination of the SOI to account for its development state is additionally considered but found to exhibit low sensitivity to the selection of the state-controlled reference.

The monthly rainfall pattern is also considered to separate the effect of other factors impacting rainfall in south-east Australia (e.g., the Northwest Cloudbands interacting with the Cut-off lows⁴⁹) and associated hydrological states (e.g., soil moisture and groundwater state). The monthly rainfall data for the state of Victoria in south-east Australia is collected from the Australian Bureau of Meteorology^50,51. The maximum and average rainfall for the period of February to October are used as indices, this period being determined by excluding the months of the year with little chance of receiving high monthly rainfall in the region.

The state-controlled reference years are determined based on the similarity of the indices to those for the forest fire-impacted treatment years. After the standardisation (Eq. (3)) of each index to have the same variability, similarity is quantified by the mean square deviation (D) of the indices, the deviation representing the difference of the reference year ${t}_{{{\rm{r}}}{{\rm{e}}}{{\rm{f}}}}$ from the treatment years ${t}_{{{\rm{t}}}{{\rm{r}}}{{\rm{e}}}{{\rm{t}}}}$ (2003, 2007, and 2009) for the climate and hydrological states (Eq. (4)).

$${\delta }_{k,t}^{* }=\frac{{\delta }_{k,t}-{\bar{\delta }}_{k}}{{s}_{k}}$$

(3)

$${D}_{{t}_{{{r}}{{e}}{{f}}}}=\frac{{\sum}_{k}{\sum}_{{t}_{{{t}}{{r}}{{e}}{{t}}}}{\left({\delta }_{k,{t}_{{{r}}{{e}}{{f}}}}^{\ast }-{\delta }_{k,{t}_{{{t}}{{r}}{{e}}{{t}}}}^{\ast }\right)}^{2}}{{\sum}_{k}{\sum}_{{t}_{{{t}}{{r}}{{e}}{{t}}}}1}\propto {\sum}_{k}{\sum}_{{t}_{{{t}}{{r}}{{e}}{{t}}}}{\left({\delta }_{k,{t}_{{{r}}{{e}}{{f}}}}^{\ast }-{\delta }_{k,{t}_{{{t}}{{r}}{{e}}{{t}}}}^{\ast }\right)}^{2}$$

(4)

where ${\delta }_{k,t}$ is the $k{{\rm{t}}}{{\rm{h}}}$ index for time $t$ and ${\delta }_{k,t}^{* }$ is the index value standardized by its mean ${\bar{\delta }}_{k}$ and standard deviation ${s}_{k}$ calculated for the reference years (1953–2002). There are two measured deviations: ${D}_{{{\rm{c}}}{{\rm{l}}}{{\rm{i}}}{{\rm{m}}}{{\rm{t}}}{{\rm{e}}},{t}_{{{\rm{r}}}{{\rm{e}}}{{\rm{f}}}}}$ for the four climate indices (DMI, SAM, SOI and the inclination of SOI) and ${D}_{{{\rm{rainfall}}},{t}_{{{\rm{ref}}}}}$ for the two rainfall indices (the maximum and average monthly rainfall). The difference of the reference year ${t}_{{{\rm{r}}}{{\rm{e}}}{{\rm{f}}}}$ from the treatment years is measured by Eq. (5) with weights ${w}_{1}$ and ${w}_{2}$ that are 0.5 and 1, different weights being used to avoid our assessment being dominated by the four climate indices. Equal weights cannot readily differentiate reference years having relatively lower average rainfall with similar climate indices compared to the treatment years, e.g. the reference year 1967 has similar climate states but with at least 30% lower average monthly rainfall compared to the treatment years.

$${\tilde{D}}_{{t}_{{{r}}{{e}}{{f}}}}={D}_{{{c}}{{l}}{{i}}{{m}}{{a}}{{t}}{{e}},{t}_{{{r}}{{e}}{{f}}}}^{{w}_{1}}+{D}_{{{r}}{{a}}{{i}}{{n}},{t}_{{{r}}{{e}}{{f}}}}^{{w}_{2}}$$

(5)

The reference years are ranked according to the deviation ${\tilde{D}}_{{t}_{{{\rm{r}}}{{\rm{e}}}{{\rm{f}}}}}$ in order of closeness to the climate and rainfall conditions of the forest fire-impacted treatment years. In this study, the 9 closest years to the treatment years (1999, 1962, 1961, 1976, 1987, 1977, 2001, 1957, and 1953) are distinguished as having the maximum range of the state-controlled reference category with the 10th year (1972) having significant statistical difference (with P-value lower than significance level 0.01) from the 9 closest years for the SAMF frequency as shown in Fig. 2c. The year 1972 was in the El Niño phase based on the SST of the central eastern tropical Pacific Ocean which is known to be related to lower rainfall in south-east Australia while the conditions of the treatment and state-controlled reference years are within relatively normal states. The reliability for the classification of the paired climate was checked by the agreement between the state-controlled reference group and treatment sub-group, with the minor level of treatment as shown in Fig. 5e (dividing the treatment group according to the level of the treatment is explained below separately).

Regional frequency analysis (RFA) for the 21 HRS is used to estimate the SAMF frequency distribution for the state-controlled reference years. The RFA provides a 127-year-long data as the state-controlled reference group, which is compared in Fig. 2b in terms of its frequency distribution to the treatment group. The treatment group representing 63 years length is obtained from the 21 HRS and the three treatment years (2003, 2007, and 2009). A two-sample χ² test with 7 categories is used to test the hypothesis that the samples of the treatment group arise from the same population as the state-controlled reference group. An increase in the frequency of the higher SAMF is observed for the treatment group, with a p-value for the test equalling 0.006, lower than the general significance level of 0.05.

As the above result assumes each sample of data is independent of the other, a further refinement in the analysis was considered to enforce spatial independence across the events. The analysis was repeated by replacing the AMF in nearby catchments with the next highest flood if the flood peaks in adjacent catchments fell within 3 days of each other, the assumption here being that the same storm system would not be responsible for a flood event in adjacent catchments when events are staggered by 3 days or more. The conclusions derived earlier remained unchanged (p-values being less than 0.05), reinforcing the robustness of the arguments presented.

Change in flood frequency due to decrease in leaf area

The leaf area index (LAI) is adopted to measure the treatment level (leaf area decrease) for the region impacted by forest fire (Fig. 2a). Monthly LAI data with a resolution of 3600 × 1800 pixels over the globe is collected from NASA Earth Observations⁵² for the period of 2000–2017 and annually averaged. The LAI is the dimensionless measure of one-sided leaf area per unit ground surface area, implying the number of leaf layers as leaves spread out as a sheet. The LAI is estimated from satellite images with uncertainty, and thus, to minimize the effect of uncertainty and bias, the index values are averaged annually and used only to detect the relative change in 2003, 2007, and 2009 after the forest fires. An LAI decrease higher than a unit, implying a decrease of as much as the area of the forested region, is set as a threshold for the notable change level (Fig. 5b–d). The LAI of years preceding the forest fires can be used to detect the LAI change, but we considered the years of the highest LAI (among all years available) instead. Specific years (e.g., years preceding the forest fires) have unknown positive or negative errors, which increase uncertainty in the detection of the LAI change if it is used as a baseline. This allows us to distinguish the changes in the LAI as a result of the fires and establish the impact on the AMF if the leaf area change caused the frequency change, as compared to if there are other factors in treatment years that changed the AMF frequency instead of the leaf area reduction.

To test the effect of the leaf area change, the treatment group is divided into two sub-groups according to the level of LAI decrease. The catchments (of the 21 HRS) that belong to the areas showing an LAI decrease higher than 1.0 (Fig. 5b–d) form the treatment sub-group representing notable LAI decrease (31 years long AMF series marked as red coloured diamonds in Fig. 5f). The stations that do not belong to the areas exhibiting notable LAI decrease form the other treatment sub-group (32-years long annual maximum flow marked as dark green coloured diamonds in Fig. 5e) representing minor change. The uncertainty and resolution in the estimation of the leaf area decrease may affect the differentiation of a few catchments at the boundary of the areas in Fig. 5b–d, but does not significantly change the frequency distribution of the sub-groups formed. A two-sample χ² test with 5 categories is applied to both treatment sub-groups to test if they represent the same population as the state-controlled reference group. The p-value of the treatment sub-group with the notable LAI decrease is calculated to be 0.00003 (smaller than the general significance level of 0.05), while the p-value of the other sub-group representing minor treatment is 0.83 as described in Fig. 5e and f.

To test if the AMF change of the treatment sub-group with notable leaf area change from forest fires (Fig. 5f) is caused by leaf area reduction itself or by soil condition change that can also happen from forest fires severe enough to cause notable leaf area decrease (such as hydrophobicity discussed in the text), the difference in the hydrograph of the AMF between the reference and treatment groups is also analysed. The 10-day flow data encompassing the AMF (with a window of 3 days before and 6 days after the AMF) are collected and averaged respectively for the state-controlled reference group and both treatment sub-groups (the hydrograph in Fig. 5e and f), the same standardisation (Eq. (2)) as the AMF being applied to the flow data. If the infiltration decrease were the dominant factor for the AMF increase, the hydrograph of the treatment sub-group (with notable LAI change) would show a sharper crest and steeper recession as a result of converting sub-surface flow to surface flow without a notable change in total flow volume, as discussed in the text. However, as shown in the hydrograph of Fig. 5f, the total flow volume has notably increased for the treatment group (with notable leaf area change) in comparison to the reference group. This flow volume increase can be explained by the reduction in the forest interception by the forest canopy, fallen leaves, and root-zone soil (as described in Fig. 3) rather than the conversion of sub-surface flow to surface flow.

The test results for the AMF change of the treatment group after the fire-induced forest loss (Figs. 2 and 5) demonstrate the significance of the impact from the forest canopy loss itself on the large-scale fluvial flooding. These results agree with the discussion in the text.

Reporting summary

Further information on research design is available in the Nature Portfolio Reporting Summary linked to this article.