Introduction

Chronic kidney disease (CKD) is a prevalent benign condition affecting ~700 million people worldwide as of 20171, and it leads to progressive and irreversible damage to kidneys. The main risk factors for CKD and end-stage kidney disease (ESKD) are diabetes mellitus and hypertension, with about 75% of ESKD patients initially diagnosed with one of these conditions2. A kidney is comprised of millions of nephrons, the urine production units, each consisting of a glomerulus and various types of tubules. Kidney aging causes glomerular sclerosis, arteriosclerosis, and interstitial alterations, leading to a gradual decline in renal function3. A population-based study showed a ~25% decline in renal function from ages 36 to 754,5. Renal biopsy is an essential diagnostic tool for identifying the underlying cause and severity of CKD and can also be helpful in assessing renal prognosis. Regardless of the cause of CKD, histologic findings of glomerulosclerosis, tubular atrophy, and interstitial fibrosis are key indicators of renal function decline. Previous studies have reported the relationship of interstitial fibrosis and inflammatory cell infiltration to renal prognosis in diabetic nephropathy (DN) and nephrosclerosis, such as hypertensive nephrosclerosis (HN) and focal segmental glomerulosclerosis (FSGS)6,7,8,9. While counting glomeruli and determining global sclerosis rates in whole slide histopathology images (WSIs) of renal biopsy specimens is relatively straightforward with low intra/inter-observer variance, the accurate quantification of tubulo-interstitial injuries, such as interstitial fibrosis, is infeasible without computer assistance.

In recent years, the field of medical image analysis has experienced rapid innovation, thanks to advancements in deep learning technologies. This progress is further supported by the increased availability of computational resources and the growth of digital pathology databases. In certain diagnostic pathology tasks, deep learning models have now reached a level of performance surpassing those of human experts.10,11,12,13,14,15. In clinical practice, deep learning models offer solutions for medical image analysis, diagnosis, treatment evaluation, and prognosis prediction16,17. While deep learning-based analysis methods have been proposed for various diseases, the detection and diagnosis of malignant and benign conditions present distinct challenges due to their different visual characteristics. In the analysis of malignant diseases such as cancer, the primary goal is to identify atypical cells within normal tissues. Features of these cells can be learned from samples taken from tumor centers, and their visual distinction from normal cells makes detection relatively straightforward. On the other hand, diagnosing benign diseases like degenerative and inflammatory conditions requires more detailed analysis, including the detection of subtle morphological changes at the cellular level in normal tissues and the quantification of deviations from normal aging. Such a detailed analysis is particularly crucial in gradually progressing kidney diseases such as CKD and in pre-implantation renal biopsies18, where accurate quantification of renal injury is vital. Several deep learning-based methods have been proposed for detecting glomeruli, tubules, and vessels, as well as for classifying the conditions of glomeruli and tubules. These methods show promise for scoring and classification of renal transplant biopsy specimens19,20.

Holscher et al. introduced a deep learning-based segmentation method for quantifying renal pathological images in patients with IgA nephropathy. Their approach involved analyzing the risk of ESKD by using scores such as glomerular tuft and tubule size21. This study is an important step in demonstrating the value of objective quantification in renal disease and opens avenues for further research to explore the application of such methods to a broader spectrum of renal diseases across diverse ethnic groups, including the Japanese population. Additionally, the exploration of similar quantitative approaches in the study of benign, progressively developing kidney diseases represents an important and growing area of research.

In this study, we developed a deep learning-based segmentation method named DLRS for WSIs of renal biopsy specimens from CKD patients, aimed at quantifying tubulo-interstitial injury. DLRS consists of two deep learning models: DLRS-tissue, which classifies non-tissue areas and four major structures—glomeruli, tubules, interstitium, and arteries; and DLRS-nucleus, designed to detect nuclei in the interstitium for quantifying inflammatory cell infiltration, a recent focus in CKD progression research22. We applied DLRS to WSIs from 71 Japanese CKD patients with DN or benign nephrosclerosis (HN and FSGS), comparing the quantified scores with evaluations by nephrologists.

The results indicated that the performance of DLRS in the quantification of tubulo-interstitial injury was comparable to that of the nephrologists, demonstrating its potential for accurate renal pathology assessment and prognosis. We also demonstrated the performance of DLRS on renal prognosis in CKD using WSIs of renal biopsy specimens for 238 Japanese CKD patients from two hospitals. The findings suggest that DLRS effectively predicts renal prognosis by quantifying the severity of interstitial fibrosis and inflammatory cell infiltration. To assess the applicability of DLRS beyond DN, HN, and FSGS, we applied DLRS to biopsy specimens from 28 Japanese patients with tubulointerstitial nephritis (TIN) at one of these hospitals. We applied DLRS to 49 European-ancestry patients with nephrosclerosis from a different hospital as well, testing its effectiveness across different populations and institutions. Overall, our study highlights the potential of deep learning-based methods for precise and efficient renal pathology analysis. This has important implications for enhancing renal diagnosis and prognosis accuracy, and for developing personalized treatment strategies for CKD patients.

Methods

Ethical statements

This research was approved by the Tohoku University Hospital Institutional Review Board (Reference number: 2019-1-987) and conforms to all relevant ethical guidelines. For clinical data and renal biopsy specimens from patients at Tohoku University Hospital and JCHO Sendai Hospital, informed consent for their use in research related to kidney disease involving the respective hospitals was obtained prior to renal biopsy. Patients were informed during the consent process that they could opt out of each specific study. Details of the research plan, research period, and contact information for inquiries or opt-out requests were publicly announced on the dedicated websites of Tohoku University Hospital and JCHO Sendai Hospital, following the format specified by the Tohoku University Hospital Institutional Review Board. Data from patients who did not submit opt-out requests were used in this study. Renal pathology images and clinical information for patients at Johns Hopkins Hospital were obtained from the Johns Hopkins Renal Pathology Archive, and permission for their use was obtained through coauthors at Johns Hopkins Hospital. These images and associated information were de-identified at Johns Hopkins Hospital under the protocol approved by the Johns Hopkins Medicine Institutional Review Board (Reference number: IRB00090103) prior to analysis; no further approval from the Johns Hopkins Medicine Institutional Review Board was required.

Study population and patient selection

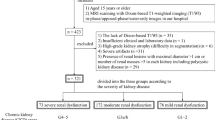
In the initial stage of this study, we analyzed 370 adult Japanese patients with biopsy-proven DN or benign nephrosclerosis (HN and FSGS) from Tohoku University Hospital (Hospital A) and JCHO Sendai Hospital (Hospital B). Among these 370 samples, 95 were from Hospital A, and the remaining 275 were from Hospital B. The progression of renal dysfunction was evaluated in terms of the therapeutic effect of immunosuppressive therapy at Hospital A from 2007 to 2019 and at Hospital B from 2015 to 2020. We randomly selected 20 samples (10 each from Hospitals A and B) to prepare training datasets for DLRS-tissue and DLRS-nucleus. We also randomly selected 10 test samples (5 each from Hospitals A and B) for testing DLRS. We excluded 132 samples from the tubulo-interstitial injury analysis for the following reasons: 70 had no follow-up visits longer than 4 months (17 from Hospital A and 53 from Hospital B), 10 had comorbidities (3 from Hospital A and 7 from Hospital B), 50 received steroid/immunosuppressive therapies (4 from Hospital A and 46 from Hospital B), and two had solitary kidneys (both from Hospital B). The remaining 71 samples from Hospital A were used for comparative evaluation with nephrologists’ diagnoses. The remaining 238 samples from both hospitals were used for prognosis analysis. This selection process is summarized in Fig. 1. Table 1 presents the clinical characteristics of these 238 samples at the time of renal biopsy. In the second stage of the study, DLRS was applied to 28 adult Japanese patients with biopsy-proven TIN from Hospital A and 49 European-ancestry patients with nephrosclerosis from Johns Hopkins Hospital (Hospital C) in order to validate its applicability to renal diseases other than DN, HN, and FSGS and in populations other than Japanese. The patients from Hospital C were selected based on appropriate diagnosis and follow-up from the Johns Hopkins Renal Pathology archive. Note that there was no overlap among the 28 Japanese TIN patients, the 49 European-ancestry patients with nephrosclerosis, and the initial group of 370 Japanese patients. Supplementary Table 1a and b present the clinical characteristics of these 28 and 49 samples at the time of renal biopsy, respectively.

Fig. 1: Flowchart of study sample selection.
figure 1

The process for selecting patients with diabetic nephropathy or benign nephrosclerosis from Hospitals A and B is outlined. Renal biopsy specimens from these patients were used for training deep learning models for DLRS-tissue and DLRS-nucleus, testing DLRS, and conducting comparative evaluation and prognosis analysis based on tubulo-interstitial injury scores derived from DLRS.

Full size image
Table 1 Baseline characteristics of 238 CKD patients at the time of biopsy
Full size table

Histological preparation of renal biopsy specimens for WSI digitization

Renal biopsy specimens were fixed using 95% ethanol at Hospital A, 15% buffered formalin at Hospital B, and 10% buffered formalin at Hospital C. For histological diagnosis, the specimens were paraffin-embedded and sectioned at 1.5 μm (Hospital A) or 1.75–2.0 μm (Hospital B), and then processed with Masson–Goldner staining. Specimens from Hospital C were processed with Masson’s trichrome staining. WSI digitization was performed using Aperio AT2 (Leica, Nussloch, Germany) with a ×40 objective at a resolution of 0.25 μm/pixel. Although the WSI files from Aperio AT2 scanner include images at lower resolutions, only images at the resolution of 0.25 μm/pixel were used for the analysis of this study.

Segmentation of WSIs with DLRS

We used DeepLabV3-ResNet23 as the deep learning model of DLRS-tissue and DLRS-nucleus and set the input image size to 512 × 512 pixels. For the segmentation of a WSI, the image was divided into overlapping image patches of 512 × 512 pixels. These patches were processed through DLRS-tissue and DLRS-nucleus, and the resulting segmentations from each patch were combined to form the complete segmentation result for the WSI. For implementing the deep learning models of DLRS-tissue and DLRS-nucleus, we used the Pytorch framework (https://pytorch.org/).

Training deep learning models of DLRS

To obtain segmentation data for WSIs of the randomly selected 20 samples, we used an in-house semantic segmentation software tool named DermAnnotation (https://github.com/KondoA9/DermAnnotation). Since it was impractical to prepare segmentation data for entire regions of WSIs due to their large size, we chose regions of 5000 × 5000 pixels from the 20 WSIs for segmentation data. We also note that 12 training samples for DLRS-nucleus in Fig. 1 are included in the randomly selected 20 samples. To minimize noise, the renal border capsule and soft tissues were excluded from the segmentation data and classified as non-tissue areas. Supplementary Table 2 presents a summary of the segmentation data counts used for training the deep learning models of DLRS-tissue and DLRS-nucleus. All segmentation data were checked and corrected by at least one board-certified nephrologist, identified as Nephrologists B and C in Supplementary Table 3.

The training of the deep learning models of DLRS-tissue and DLRS-nucleus was carried out using a weighted sum of cross-entropy and the DICE coefficient as the loss function. We optimized the model parameters iteratively under this loss function using the Adam solver24 for 25,000 steps. The learning rate for the Adam solver was set to 1.0 × 10−5, and the batch size was determined based on the capacity of our GPU resources. Each selected region was divided into patches of 512 × 512 pixels, with 10% of these patches randomly assigned as validation data. For each optimization step, we randomly selected image patches that did not overlap with the validation data patches as our training data. We applied data augmentation techniques to these selected image patches, including weak brightness changes, horizontal and vertical flips, and rotations at angles of 0°, 15°, 30°, 45°, 60°, 75°, or 90°.

Test data preparation for evaluating DLRS

We randomly selected a region measuring 2000 × 2000 pixels from the WSI of each of the ten samples. It is important to note that these ten samples were not included among the 20 samples used to prepare the training data for DLRS. Additionally, for the test data images of the DLRS-nucleus, we extracted one of the four corner regions, each measuring 1000 × 1000 pixels, from the selected 2000 × 2000 pixel regions. The segmentation data for these images were prepared using DermAnnotation. All prepared segmentation data were checked and corrected by at least one nephrologist, identified as Nephrologists B and C in Supplementary Table 3.

Selection of tissues for calculating tubulo-interstitial injury scores by DLRS

For each WSI, we excluded tissues where no glomeruli were detected by DLRS, from the calculation of tubulo-interstitial injury scores. Additionally, tissues with an area smaller than 500,000 pixels were also omitted from the score calculation. From the remaining tissues in the WSIs, the top three largest tissues were chosen for the score calculation. In cases where no tissue remained after these exclusions, the tissue with the largest area was selected for the calculation.

Calculation of distance between nearby glomerulus pairs

We initially identified renal tissues and glomeruli in each WSI using the segmentation results obtained from DLRS-tissue. We then calculated the distances between all pairs of glomeruli within each renal tissue. Subsequently, we constructed a graph where each node represented a glomerulus, and the distance between each pair of glomeruli was assigned as the weight of the edge connecting them. Using a minimum spanning tree algorithm for this graph, we identified pairs of glomeruli connected to neighboring nodes of the minimum spanning tree as nearby glomerulus pairs. The distances between these pairs were then recorded.

Selection of renal cortex and calculation of tubulo-interstitial injury scores from segmentation results

WSIs may contain various contaminated tissues, such as the renal medulla, large vessels, fat tissue, and mechanically crushed tissue, which are not relevant to the assessment of tubulo-interstitial injury. We hence limited the assessment of tubulo-interstitial injury to the renal cortex to ensure reliability. Since glomeruli are located in the renal cortex, we selected areas within a specific distance from at least one glomerulus as part of the cortex. This distance was determined by analyzing the distances between pairs of nearby glomeruli from the segmentation results of WSIs by DLRS. We adopted the 95th percentile of these distances as the criterion for selecting cortical areas. Only areas within this distance from at least one glomerulus were used for the assessment of tubulo-interstitial injury.

We calculated scores for interstitial fibrosis and inflammatory cell infiltration as indicators of tubulo-interstitial injury from the segmentation results. Interstitial fibrosis scores are calculated from the ratio of the interstitial area to the combined area of tubules and interstitium in the renal cortex selected from the above analysis. Similarly, inflammatory cell infiltration scores are calculated from the ratio of regions with interstitial nuclei to the same combined area in the selected renal cortex.

Assessment of kidney injury and glomerular count in WSIs by nephrologists

Four board-certified nephrologists (designated as Nephrologists A–D) conducted independent assessments of interstitial fibrosis and inflammatory cell infiltration in WSIs of renal biopsy specimens. Specifically, Nephrologists A–C evaluated WSIs of 71 patients from Hospital A, while Nephrologist D assessed WSIs of 49 patients from Hospital C. During the scoring process for WSIs from Hospital A, patient clinical information, such as age, was obscured to mitigate potential bias. The comprehensive professional backgrounds and training histories of these nephrologists are detailed in Supplementary Table 3. Percent global glomerulosclerosis was obtained by calculating the rate of the number of globally sclerosed glomeruli on total glomeruli count. The total count of glomeruli and the number of globally sclerosed glomeruli for each WSI were from the medical records of the respective hospitals.

Concordance and correlation analysis

We used case 2 intraclass correlation (ICC(2, 1)) analysis25 to assess the reproducibility of the nephrologists’ evaluations. To evaluate the concordance between tubulo-interstitial injury scores from DLRS and nephrologists’ evaluations, we applied case 3 intraclass correlation (ICC(3, 1)) analysis. Since the value range of tubulo-interstitial injury scores from DLRS—especially for inflammatory cell infiltration—is narrower than that from nephrologists’ evaluations, as shown in the subsequent Results section, we normalized the scores with their standard deviations to mitigate these scale differences before applying ICC(3, 1).

In simple linear regression analysis, the p-value for the slope β1 was calculated using a t-test under the null hypothesis of β1 = 0, with the t-statistic given by \(t={\hat{\beta }}_{1}/{\rm {S{E}}}_{{\beta }_{1}}\), where \({\hat{\beta }}_{1}\) is the ordinary least-squares estimator of β1, and \({\rm {S{E}}}_{{\beta }_{1}}\) is its standard error. The t-statistic follows a t-distribution with degrees of freedom n−2, where n is the sample size for simple linear regression. Since this t-statistic is analytically equivalent to the t-statistic for Pearson’s correlation coefficient r, given by \(r\sqrt{(n-1)/(1-{r}^{2})}\), the same p-values are commonly used to assess the significance of both the slope of simple linear regression and Pearson’s correlation coefficient.

Hypothesis test for the institutional difference in regression of eGFR on tubulo-interstitial injury scores

The difference in processing specimens, such as the type of fixative solution, may influence the scoring of tubulo-interstitial injury. This influence could cause differences in the simple linear regression of eGFR on each of the tubulo-interstitial injury scores. To examine this influence, we conducted hypothesis tests on the differences in intercepts and slopes of the linear regressions of eGFR on each of the interstitial fibrosis score and inflammatory cell infiltration score between Hospitals A and B.

Let yA and yB be the vectors of eGFR at the time of biopsy for samples from Hospitals A and B, respectively. We also let xA and xB be the vectors of univariate regressor for Hospitals A and B, respectively. As the regressor, each of the tubulo-interstitial injury scores is considered.

For the hypothesis test, we consider the following linear regression model:

$$\left[\begin{array}{c}{{{{\boldsymbol{y}}}}}_{A}\\ {{{{\boldsymbol{y}}}}}_{B}\end{array}\right]=\alpha {{{\boldsymbol{1}}}}+\beta \left[\begin{array}{c}{{{{\boldsymbol{x}}}}}_{A}\\ {{{{\boldsymbol{x}}}}}_{B}\end{array}\right]+{\gamma }_{1}\left[\begin{array}{c}{{{{\boldsymbol{0}}}}}_{A}\\ {{{{\boldsymbol{1}}}}}_{B}\end{array}\right]+{\gamma }_{2}\left[\begin{array}{c}{{{{\boldsymbol{0}}}}}_{A}\\ {{{{\boldsymbol{x}}}}}_{B}\end{array}\right]+{{{\boldsymbol{\varepsilon }}}},$$
(1)

where 0A is a zero vector with a size equal to the number of samples from Hospital A, and 1B is a vector of ones with a size equal to the number of samples from Hospital B. We obtain the p-value for the difference of regression intercepts by testing the null hypothesis of γ1 = 0. Similarly, we obtain the p-value for the difference of regression slopes by testing the null hypothesis of γ2 = 0.

Variable selection with the generalized cross-validation for predicting renal prognosis

We used generalized cross-validation (GCV) method26 to select the combination of regressors suitable for predicting renal prognosis. The annual eGFR decline after the biopsy was used as an indicator of renal prognosis. The annual eGFR decline was calculated as the difference between the eGFR values at follow-up visits and at the time of biopsy, divided by the period between them in years. In the selection process, the GCV value for the linear regression of annual eGFR decline was calculated for all combinations of regressors, and the regressors with the minimum GCV value were selected. The GCV value for the linear regression of y on regressor matrix X is defined as:

$$\frac{1}{n}| (I-P){{{\boldsymbol{y}}}}| /{\left[\frac{1}{n}{\mbox{trace}}(I-P)\right]}^{2},$$
(2)

where n is the number of samples, P is the projection matrix given by \(X{({X}^{{\rm {T}}}X)}^{-1}{X}^{{\rm {T}}}\), and ∣ ⋅ ∣ gives the L2 norm of a vector. Considering seven factors as regressors—eGFR at the time of biopsy, age at biopsy, sex, diagnosis of DN, interstitial fibrosis score from DLRS, inflammatory cell infiltration score from DLRS, and the deviation of eGFR from the regression line based on interstitial fibrosis and inflammatory cell infiltration scores from DLRS—we compared GCV values for all 27 = 128 possible combinations.

Use of large language models

We used ChatGPT (https://openai.com/blog/chatgpt) only for improving the readability of texts.

Reporting summary

Further information on research design is available in the Nature Portfolio Reporting Summary linked to this article.

Results

Segmentation of WSIs

We used DLRS-tissue to segment WSIs of 370 samples into non-tissue areas and four major renal tissue structures: glomeruli, tubules, interstitium, and arteries. The WSIs were prepared from specimens processed with Masson–Goldner staining, which is effective for distinguishing connective tissue components like collagen fibers (stained green) and elastic fibers (stained dark brown). Figure 2a and b illustrate an example of a local slide image and its corresponding segmentation by nephrologists, respectively, used as training data for DLRS-tissue. Figure 2c and d display an example of a local slide image and its predicted segmentation by DLRS-tissue, respectively. Figure 2e shows a predicted segmentation by DLRS-tissue for a WSI, including the local area shown in Fig. 2c and d. We used DLRS-nucleus to segment nuclei in WSIs. Segmented nuclei not in interstitium were filtered out in the downstream analysis. The interstitium predicted by DLRS-tissue was used for this filtering process. Figure 3a and b present examples of training segmentation data for DLRS-nucleus and a predicted segmentation by DLRS-nucleus, respectively.

Fig. 2: Training and predicted images for DLRS-tissue, a plot of the distribution of glomerular distance, and renal cortex selection for the assessment of tubulo-interstitial injury.
figure 2

a A local slide image from the training dataset of DLRS-tissue. b A segmentation image created by nephrologists for the local slide image in a, classifying non-tissue areas, glomeruli (in yellow), renal tubules (in purple), interstitium (in blue), and arteries (in red). c A local slide image. d A predicted segmentation result by DLRS-tissue for the local slide image in (c). e A predicted segmentation by DLRS-tissue for a whole slide image, including the local area shown in (c) and (d). f The distribution of glomerular distance (distance between nearby glomeruli), in which the red line represents the 95th percentile distance. g Renal cortex selection for the assessment of tubulo-interstitial injury. Areas within the 95th percentile glomerular distance from the nearest glomerulus (areas surrounded by circles) were selected as renal cortex (in blue).

Full size image
Fig. 3: Training and predicted images of nucleus segmentation in interstitium.
figure 3

a A training segmentation image of nuclei in the interstitium (in green) by nephrologists. b A predicted segmentation image of nuclei in the interstitium (in green) by DLRS-nucleus.

Full size image

To evaluate the accuracy of DLRS-tissue and DLRS-nucleus, we used test segmentation data from the randomly selected ten test samples (five from each of Hospitals A and B). Supplementary Fig. 1 shows the original slide images, the predicted segmentations, and the test segmentations for three of the ten test samples for DLRS-tissue. Similarly, Supplementary Fig. 2 shows the original slide images, the predicted segmentations, and the test segmentations for three of the ten test samples for DLRS-nucleus.

We assessed the performance using recall, precision, F-measure, and intersection over union (IoU) for regions segmented by DLRS-tissue and nuclei detected by DLRS-nucleus (Supplementary Table 4). For the evaluation of nuclei detection, we considered cases using manually segmented interstitium by nephrologists and that predicted by DLRS-tissue for filtering non-interstitium nuclei. The evaluation measures for nuclei detection were lower compared to those for DLRS-tissue, particularly when using interstitium predicted by DLRS-tissue (Supplementary Table 4). This is primarily because these measures rely on pixel-level concordance, and even small discrepancies in segmentation boundaries can largely affect accuracy, especially in smaller segmented regions like nuclei.

Supplementary Fig. 3a shows a plot comparing the interstitial area rates from the predicted segmentations and those from the test segmentations. The interstitial area rates were calculated as the ratio of the interstitial area to the combined area of tubules and interstitium. The rates are used for calculating interstitial fibrosis scores. Indexes above some of the points indicate the corresponding samples in Supplementary Fig. 1. Despite the misclassification of some areas in predicted segmentations, the interstitial area rates between the predicted and test segmentations show a strong correlation (r = 0.98, P = 2.43 × 10−7). Supplementary Fig. 3b shows a plot comparing the interstitial nucleus rates from the predicted segmentations and those from the test segmentations. The interstitial nucleus rates were calculated as the ratio of regions with interstitial nuclei to the combined area of tubules and interstitium. The rates in the interstitium are used for calculating inflammatory cell infiltration scores. Indexes above some points indicate the corresponding samples in Supplementary Fig. 2. As mentioned above, the accuracy of nuclei detection is lower compared to that of DLRS-tissue, and misclassifications in interstitium segmentation can further decrease the precision of nuclei detection in the interstitium. However, we observed a high correlation between the interstitial nucleus rates from the predicted and test segmentations (r = 0.97, P = 2.14 × 10−6), suggesting the effectiveness of DLRS-nucleus for the quantification of inflammatory cell infiltration.

Assessing the applicability of tubulo-interstitial injury scores

We calculated the distances between pairs of nearby glomeruli across 6703 glomeruli identified from the segmentation results of WSIs by DLRS for 370 samples, and 1590.29 μm was obtained as the 95th percentile distance between the pairs of nearby glomeruli (Fig. 2f). Based on this 95th percentile distance, we selected areas for the renal cortex as shown in Fig. 2g and calculated the interstitial fibrosis score and inflammatory cell infiltration score from these areas for each WSI.

We compared scores from DLRS with percentage-based severity scores of interstitial fibrosis and inflammatory cell infiltration assessed by three board-certified nephrologists for 71 patients from Hospital A with DN or benign nephrosclerosis (Fig. 4a, b). During the scoring process by nephrologists, clinical information such as age was masked to prevent potential bias. While high inter-observer variability was observed in cases with interstitial fibrosis severity ranging from 30% to 70%, partly due to the masking of information (Supplementary Fig. 4a and b), the reproducibility of the nephrologists’ evaluations was confirmed through ICC(2, 1) (ICC(2, 1) = 0.67, P = 2.75 × 10−27 for interstitial fibrosis; ICC(2, 1) = 0.66, P = 4.70 × 10−22 for inflammatory cell infiltration). To mitigate the variations in the nephrologists’ scores, we used their averaged scores for comparison against the scores from DLRS. We confirmed that the nephrologists’ averaged scores were negatively correlated with the estimated glomerular filtration rate (eGFR) at the time of biopsy (r = −0.51 and P = 7.03 × 10−6 for interstitial fibrosis; r =  −0.54 and P = 1.19 × 10−6 for inflammatory cell infiltration), as shown in Supplementary Fig. 5a and b.

Fig. 4: Comparison of tubulo-interstitial injury scores between nephrologists and DLRS for 71 Japanese patients with diabetic nephropathy or benign nephrosclerosis from Hospital A.
figure 4

a Scatter plot comparing interstitial fibrosis scores between nephrologists and DLRS. b Scatter plot comparing inflammatory cell infiltration scores between nephrologists and DLRS. Scores from nephrologists were averaged. The red lines represent the regression lines.

Full size image

Figure 4a and b show plots comparing the interstitial fibrosis and inflammatory cell infiltration scores from DLRS with the nephrologists’ averaged scores, respectively. Plots comparing the scores from DLRS with each nephrologist’s individual evaluations are also shown in Supplementary Figs. 6 and 7. We used ICC(3, 1) to assess the concordance between the scores from DLRS and those from nephrologists. It is important to note that nephrologists typically assign scores of 0% or close to 0% for tubulo-interstitial injury in specimens from normal kidneys, even though the actual interstitium ratio and the ratio of nuclei within the interstitium are not zero. Conversely, in the case of severely injured kidneys, while scores approaching 100% are often assigned by nephrologists, the actual interstitium and nuclei ratios in these specimens usually remain below 100%. Hence, the value range for tubulo-interstitial injury scores from DLRS—especially for inflammatory cell infiltration—is narrower than the range for scores from nephrologists as shown in the plots in Fig. 4a and b. To address these scale differences, we normalized the scores with their standard deviations before applying ICC(3, 1). Table 2a and b summarize the ICC(3, 1) results for tubulo-interstitial injury scores for each case. The scores from DLRS showed significant concordance with averaged scores from the nephrologists (ICC(3, 1) = 0.87, P = 5.70 × 10−23 for interstitial fibrosis; ICC(3, 1) = 0.81, P = 4.59 × 10−18 for inflammatory cell infiltration). The scores from DLRS were correlated with percent global glomerulosclerosis, which was obtained from medical records, as well (Supplementary Fig. 8a and b: r = 0.52, P = 3.68 × 10−6 for interstitial fibrosis; r = 0.44, P = 1.34 × 10−4 for inflammatory cell infiltration).

Table 2 Intraclass correlation (ICC) comparing tubulo-interstitial injury scores derived from DLRS with those from nephrologists
Full size table

The scores from DLRS were negatively correlated with eGFR at the time of biopsy (r = −0.59, P = 7.02 × 10−8 for interstitial fibrosis; r = −0.54, P = 1.22 × 10−6 for inflammatory cell infiltration), as shown in Fig. 5a and b. We found that the interstitial fibrosis score from DLRS showed a higher correlation with eGFR compared to the averaged scores from the nephrologists. There was also a significant correlation observed between the interstitial fibrosis and inflammatory cell infiltration scores from DLRS (r = 0.78, P = 1.56 × 10−15), as shown in Fig. 5c. To validate these findings, we analyzed 167 samples from Hospital B and found that both scores from DLRS were correlated with the percentage of global glomerulosclerosis (r = 0.55, P = 2.80 × 10−14 for interstitial fibrosis; r = 0.61, P = 1.26 × 10−18 for inflammatory cell infiltration), as shown in Supplementary Fig. 8c and d. These scores were also negatively correlated with eGFR at the time of biopsy (r = −0.59, P = 2.88 × 10−17 for interstitial fibrosis; r = −0.63, P = 3.47 × 10−20 for inflammatory cell infiltration), as shown in Fig. 6a and b.

Fig. 5: Comparison of tubulo-interstitial injury scores from DLRS and eGFR at the time of biopsy for 71 Japanese patients with diabetic nephropathy or benign nephrosclerosis from Hospital A.
figure 5

a Scatter plot comparing interstitial fibrosis scores from DLRS and eGFR at the time of biopsy. b Scatter plot comparing inflammatory cell infiltration scores from DLRS and eGFR at the time of biopsy. c Scatter plot comparing interstitial fibrosis scores and inflammatory cell infiltration scores from DLRS. The red lines represent the regression lines.

Full size image
Fig. 6: Comparison of tubulo-interstitial injury scores from DLRS and eGFR at the time of biopsy for 167 Japanese patients with diabetic nephropathy or benign nephrosclerosis from Hospital B.
figure 6

a Scatter plot comparing interstitial fibrosis scores from DLRS and eGFR at the time of biopsy. b Scatter plot comparing inflammatory cell infiltration scores from DLRS and eGFR at the time of biopsy. The red lines represent the regression lines.

Full size image

Institutional variation on eGFR prediction using tubulo-interstitial injury scores from DLRS

The primary differences in the processing of renal biopsy specimens between Hospitals A and B were the fixative solution and section thickness. Such differences may influence the scoring of tubulo-interstitial injury. To assess the influence of these differences on tubulo-interstitial injury scores to simple linear regressions of eGFR, we analyzed the variations in intercepts and slopes of simple linear regressions of eGFR based on each score between Hospitals A and B, using WSIs from 71 samples at Hospital A and 167 samples at Hospital B.

We found no significant difference in either the intercept or slope when the inflammatory cell infiltration score was used as the regressor. Conversely, a significant difference was observed in the intercept when considering the interstitial fibrosis score as the regressor (Supplementary Table 5). This was also supported by the box plots comparing injury scores between the two hospitals (Supplementary Fig. 9a and b), where the interstitial fibrosis score for Hospital A was generally higher than that for Hospital B. In contrast, there was no noticeable difference in inflammatory cell infiltration score. Although zero mean normalization of the interstitial fibrosis score for each hospital could mitigate the influence of the intercept difference, such normalization might introduce additional bias into the estimated values and limit the general applicability of these scores. Thus, in our subsequent prognosis analysis, we opted to use the interstitial fibrosis score without such normalization.

Correlation of annual eGFR decline and deviation on eGFR from expected value by tubulo-interstitial injury scores

In the plots comparing tubulo-interstitial injury scores and eGFR at the time of biopsy (Fig. 5a and b; Fig. 6a and b), some samples had higher eGFR than the regression line, while some others had lower eGFR. We hypothesized that such deviations from the regression line could be key factors in predicting renal prognosis. To test this, we used the annual eGFR decline after the biopsy as an indicator of renal prognosis and examined its correlation with the deviation in eGFR.

In our analysis, we calculated linear regressions of eGFR at the time of biopsy using each or both of the injury scores as regressors and obtained the residuals, which represent the deviation for each case. We found that the deviation in eGFR had a significant positive correlation with annual eGFR decline for both injury scores (Fig. 7a and b), and the test using the interstitial fibrosis score as the regressor resulted in a lower p-value and a higher R2 value (r = 0.25, P = 1.15 × 10−4, R2 = 0.061) compared to the test using the inflammatory cell infiltration score (r = 0.21, P = 9.80 × 10−4, R2 = 0.045). When considering a linear regression of eGFR at the time of biopsy on both scores, the deviation in eGFR from this regression showed a significant positive correlation with the annual eGFR decline, with an even lower p-value along with an even higher R2 value (r = 0.27, P = 2.22 × 10−5, R2 = 0.074), as shown in Fig. 7c.

Fig. 7: Correlation of deviation of eGFR from expected value and annual eGFR decline for 238 Japanese patients with diabetic nephropathy or benign nephrosclerosis from Hospitals A and B.
figure 7

a Scatter plot comparing the residual of eGFR regressed on interstitial fibrosis score from DLRS and the annual eGFR decline. b Scatter plot comparing the residual of eGFR regressed on inflammatory cell infiltration score from DLRS and the annual eGFR decline. c Scatter plot comparing the residual of eGFR regressed on both interstitial fibrosis score and inflammatory cell infiltration score from DLRS and the annual eGFR decline. The red lines represent the regression lines.

Full size image

Renal prognosis prediction using scores from DLRS

We assessed the impact of tubulo-interstitial injury scores on predicting renal prognosis. We again used the annual eGFR decline as the indicator of renal prognosis and conducted leave-one-out predictions using linear regression. Along with tubulo-interstitial injury scores derived from DLRS, other regressors included eGFR at the time of biopsy, age at biopsy, sex, a diagnosis of DN, and the deviation in eGFR. For the deviation in eGFR, we used the residuals of eGFR at the time of biopsy, regressed on both interstitial fibrosis and inflammatory cell infiltration scores because the deviation from the regression on both scores showed a lower p-value and a higher R2 value compared to that from the regression on either score alone.

We compared the prediction errors in scenarios with and without the inclusion of scores from DLRS in the regressors. Since both interstitial fibrosis and inflammatory cell infiltration scores were used for calculating the deviation in eGFR, this deviation was considered part of the scores from DLRS as well. For each leave-one-out prediction, we employed GCV to select the most suitable regressors for prediction. Figure 8a and b show plots comparing the predicted and actual annual eGFR declines for cases with and without the inclusion of scores from DLRS, respectively. A higher positive correlation between the predicted and actual annual eGFR declines was observed in the scenario including scores from DLRS (r = 0.33, P = 2.24 × 10−7) compared to the scenario without them (r = 0.13, P = 0.039). In the scenario including scores from DLRS, both the deviation in eGFR and the interstitial fibrosis score were consistently selected as regressors by GCV in all leave-one-out calculations (Fig. 8c), indicating their effectiveness in prediction. We also found that the absolute values of prediction errors were significantly lower in the scenario with scores from DLRS than in the scenario without them (P = 0.027), from a Wilcoxon one-tailed signed rank test (Fig. 8d).

Fig. 8: Leave-one-out prediction of annual eGFR decline with and without considering DLRS-derived scores for 238 Japanese patients with diabetic nephropathy or benign nephrosclerosis from Hospitals A and B.
figure 8

a Scatter plot comparing predicted and actual annual eGFR declines when including DLRS-derived scores (interstitial fibrosis score, inflammatory cell infiltration score, and deviation of eGFR) along with eGFR at the time of biopsy, age at biopsy, sex, and diabetic nephropathy diagnosis. The red line represents the regression line. b Scatter plot comparing predicted and actual annual eGFR declines without including DLRS-derived scores. The red line represents the regression line. c Counts of selected factors used in the prediction for cases with and without including DLRS-derived scores. d Box plot illustrating the difference in absolute prediction errors between cases with and without including DLRS-derived scores. The box represents the upper and lower quartiles, while the line within the box denotes the median. Outliers are marked as dots. The top and bottom ends of the whiskers correspond to the maximum and minimum values, excluding outliers.

Full size image

Applicability of DLRS on TIN

We applied DLRS to renal biopsy specimens from 28 Japanese TIN patients at Hospital A to assess the applicability of DLRS for quantifying injury in renal diseases other than DN, HN, and FSGS. Among these 28 TIN patients, 4 are classified as mild, 17 as moderate, and 7 as severe, based on the level of total interstitial injury from nephrologists’ diagnosis. Patients with total interstitial injury of less than 25% are classified as mild, those with 25% to less than 50% as moderate, and those with 50% or greater as severe. Note that none of the renal specimens from these 28 TIN patients were used in training the deep learning models for DLRS.

Supplementary Fig. 10a and b show a comparison of interstitial fibrosis and inflammatory cell infiltration scores between DLRS and the average scores of three board-certified nephrologists. The reproducibility of evaluations among the nephrologists was confirmed by ICC(2, 1) (ICC(2,1) = 0.73, P = 4.11 × 10−12 for interstitial fibrosis; ICC(2,1) = 0.93, P = 1.81 × 10−28 for inflammatory cell infiltration). Table 2c and d summarize the results of ICC(3, 1) analysis for tubulo-interstitial injury scores derived from DLRS and scores from the nephrologists’ evaluations. In line with the analysis of the 71 Japanese patients with DN or benign nephrosclerosis, these scores were normalized with their standard deviations before applying ICC(3, 1). The scores from DLRS showed significant concordance with averaged scores from the nephrologists (ICC(3, 1) = 0.44, P = 8.14 × 10−3 for interstitial fibrosis; ICC(3, 1) = 0.90, P = 2.21 × 10−11 for inflammatory cell infiltration).

Comparisons of these scores with each individual nephrologist’s evaluations are shown in Supplementary Figs. 11 and 12. No significant correlation was observed between the scores from DLRS and the percent of global glomerulosclerosis (Supplementary Fig. 10c and d). A significant negative correlation was found between the DLRS interstitial fibrosis score and eGFR at the time of biopsy (Supplementary Fig. 13a: r = −0.48, P = 0.0092). While there was a negative correlation between the inflammatory cell infiltration score and eGFR at the time of biopsy, this correlation was not statistically significant (Supplementary Fig. 13b).

Applicability of DLRS on European-ancestry patients with nephrosclerosis

We applied DLRS to renal biopsy specimens from 49 European-ancestry patients with nephrosclerosis at Hospital C to assess its applicability across different populations and institutions. Their tissue color phase and texture differed considerably from those of Hospitals A and B (Supplementary Fig. 14), and one of the reasons might be the difference in the staining methods. We also note that none of the renal specimens from Hospital C was used in training the deep learning models of DLRS. Supplementary Fig. 15a and b show comparisons of interstitial fibrosis and inflammatory cell infiltration scores between DLRS and a board-certified nephrologist (Nephrologist D) from Hospital C.

Table 2e and f summarize the results of ICC(3, 1) analysis for tubulo-interstitial injury scores derived from DLRS and scores from Nephrologist D’s evaluations. In line with the analysis of other datasets, these scores were normalized with their standard deviations before applying ICC(3, 1). The scores from DLRS showed significant concordance with scores from Nephrologist D (ICC(3, 1) = 0.61, P = 1.10 × 10−6 for interstitial fibrosis; ICC(3, 1) = 0.42, P = 1.19 × 10−3 for inflammatory cell infiltration). These scores were also correlated with percent global glomerulosclerosis; however, only the correlation with the inflammatory cell infiltration score from DLRS was significant (r = 0.36, P = 0.012), as shown in Supplementary Fig. 15c and d.

Both interstitial fibrosis and inflammatory cell infiltration scores from DLRS were significantly and negatively correlated with eGFR at the time of biopsy (Supplementary Fig. 16a and b: r = −0.55, P = 3.73 × 10−5 for interstitial fibrosis; r = −0.49, P = 3.04 × 10−4 for inflammatory cell infiltration). We also analyzed the correlation between the deviation in eGFR and annual eGFR decline after the biopsy in a similar manner to the 238 Japanese patients with DN or benign nephrosclerosis from Hospitals A and B (Supplementary Fig. 17). Although no significant correlation was found between eGFR deviation and annual eGFR decline, possibly due to the limited sample size, the trend observed was similar to that in the analysis of the 238 patients from Hospitals A and B.

Discussion

We have developed DLRS, a deep learning-based segmentation method for renal biopsy specimens. DLRS was applied to specimens from two institutions (Hospitals A and B), for which variations in section cutting and staining intensity reflecting differences in individual technicians’ methodologies were observed. Despite these variations, DLRS successfully segmented non-tissue areas and various renal structures, including the glomerulus, tubule, and interstitium, from specimens of both institutions, demonstrating its adaptability. While previous studies have focused on developing deep learning-based methods for accurate segmentation of the glomerulus27,28,29 and tubulo-interstitium30,31, many did not extend their research to include downstream analysis of segmentation results. In our approach, we quantified clinically relevant values from the segmentation results and evaluated their correlation with clinical phenotypes. In clinical practice, nephrologists often rely on semi-quantitative assessments, using terms like mild, moderate, severe, or percentages (e.g., 30–50%), based on subjective impressions. Although experienced nephrologists’ decisions are typically accurate, the objective scores provided by DLRS could facilitate more consistent diagnoses. Notably, for correlating with renal function (eGFR), the interstitial fibrosis score derived from DLRS demonstrated a higher correlation than the severity scores for interstitial fibrosis and inflammatory cell infiltration assessed by nephrologists (Fig. 5a and Supplementary Fig. 5a and b).

In a physiological state, the interstitium occupies only about 4.0% of the cortex volume32, increasing to 5–10% in the renal medulla. It is important to note that tissues fixed and embedded in paraffin wax can shrink by up to 33%, which may result in a higher percentage in pathological specimens. This shrinkage is more pronounced with alcohol fixation compared to 10% buffered formalin fixation33,34. The renal biopsy specimens from Hospital A were fixed with alcohol, and the interstitial fibrosis scores obtained from DLRS for these specimens were generally higher than 30%, while some nephrologist’s evaluations were under 30%. In contrast, interstitial fibrosis scores from DLRS for specimens from Hospital B, which were fixed with 10% buffered formalin, generally showed lower values than those from Hospital A (Supplementary Fig. 9a). As the DLRS-derived interstitial fibrosis scores are based on the ratio of the interstitium to the area comprising tubules and interstitium, these observations align with the variation in shrinkage between alcohol and formalin fixed tissues. Interestingly, we observed no remarkable difference in inflammatory cell infiltration scores between the two hospitals (Supplementary Fig. 9b). During fixation, tissue shrinkage can lead to traction on the interstitium by the tubules and other sparse structures, resulting in interstitial dilatation. This effect tends to be more pronounced with alcohol-based fixatives. However, regions with inflammatory cells typically have denser tissue structures compared to non-inflamed regions, which minimizes the impact of interstitial dilatation due to tissue shrinkage on the inflammatory cell infiltration scores, even in alcohol-fixed specimens.

In the dataset from 28 Japanese TIN patients at Hospital A, the correlation coefficient between scores from DLRS and nephrologists’ evaluations on inflammatory cell infiltration was exceptionally high. The importance of inflammatory cell infiltration assessment in TIN pathology suggests a strong potential for our method in TIN applications. The ratio of inflammatory cell infiltration score to interstitial fibrosis score in TIN cases was higher compared to cases of DN, HN, or FSGS, as shown in Supplementary Fig. 18. This ratio serves an important role in assessing the acute activity of TIN. Therefore, DLRS is also potentially effective at estimating both the response and the reversibility of TIN to treatment although further analyses are necessary.

We also assessed the concordance of tubulo-interstitial injury scores from DLRS with a nephrologist’s evaluations, as well as their correlation with eGFR at the time of biopsy, using the 49 European-ancestry patient datasets from Hospital C. Despite the differences in staining methods between Hospital C and Hospitals A and B, as well as the variations in patient population and institutional practices, DLRS proved its robustness by showing the significant concordance of its tubulo-interstitial injury scores with the nephrologist’s evaluation and their significant correlation with eGFR. Although these findings further confirmed the versatility of DLRS across patient demographics, the deep learning models of DLRS were trained using WSIs from specimens with Masson–Goldner staining, and hence their applicability to specimens stained with other methods, such as haematoxylin and eosin (HE) or periodic acid-Schiff (PAS), may be limited. For cases where other staining methods, such as HE and PAS are more suitable, it would be better to train deep learning models with specimens stained according to the intended purpose. An alternative approach to address staining differences involves the use of CycleGAN, which can improve robustness to staining variations35. Integrating this approach into the training process of DLRS could further enhance its robustness.

We observed a distinct correlation between the inflammatory cell infiltration score from DLRS and CKD severity, as indicated by eGFR at the time of biopsy (Fig. 5b). In response to renal injury, multiple processes are involved: secretion of cytokines and chemokines, initiation of repair mechanisms, and activation of profibrotic cells. While this regulated response aims to facilitate tissue regeneration, defective or prolonged signaling from inflammatory and fibrogenic cells can lead to fibrosis36. Conversely, the presence of anti-inflammatory cytokines in the early stages can mitigate the impact of inflammatory mediators. Therefore, a quantitative evaluation, such as the inflammatory cell infiltration score, could be vital for selecting appropriate treatments in the future.

Previous research has extensively studied interstitial fibrosis, tubular atrophy, and interstitial cell infiltration to assess pathological changes and renal outcomes in DN or benign nephrosclerosis6,7,8,9. Tubules connected to a damaged glomerulus shrink and are replaced by fibrotic interstitium, leading to reduced GFR. Such replacement also occurs in injured tubules, regardless of their associated glomerular condition. Therefore, scoring the extent of interstitial changes might be a more accurate indicator of nephron unit injury than assessing glomerular sclerosis alone. Indeed, the interstitial fibrosis score from DLRS showed a strong correlation with renal function (eGFR) at the time of biopsy, suggesting its reliability as an indicator of renal function, even without a direct assessment of glomerular sclerosis.

We furthermore found that the deviation of eGFR from its regression line based on the DLRS-derived scores correlated with the annual eGFR decline after biopsy. In essence, samples exhibiting more severe pathological changes than expected, based on eGFR, were associated with poorer prognosis. Hyperfiltration might initially compensate for decreased GFR, but it could lead to a further decline over time. Our prognosis prediction analysis also indicated that considering the diagnosis of DN, the interstitial fibrosis score, and the deviation of eGFR were effective in predicting the annual eGFR decline. DLRS is crucial in obtaining the latter two factors, and our findings confirmed that these factors significantly reduced prediction errors. Incorporating additional information like global sclerosis, family history, past medical history, and other pathological parameters might further enhance the accuracy of prognosis prediction.

While this study had certain limitations, such as being focused on specimens from a few institutions and not encompassing a comprehensive analysis of the distribution or severity spectrum of tissue injuries, our developed method, DLRS, demonstrated its effectiveness in segmenting major structures and nuclei in the renal cortex and quantifying tubulo-interstitial injury. Our findings highlight the potential of deep learning in renal pathology, and further validation of our method across various renal diseases could enhance its practical application in the diagnosis of renal pathology and the prediction of clinical outcomes.

Recent studies, including those by Salvi et al.37, Ginley et al.38, and Holscher et al.21, have explored the relationship between interstitial changes and renal outcomes through the development of deep learning-based methods. These methods have their own features, with distinct strengths and weaknesses. Since close collaboration between computer scientists and both practicing and expert renal pathologists is crucial, the influence of the expertise of each pathologist also remains a key factor in the development of deep learning-based methodologies. Hence, accumulating insights from diverse approaches, including the one proposed in this study, is essential for the advancement of highly accurate and robust methods, providing consistent and reliable evaluations of renal tissue conditions at a level appropriate for clinical practice.