Introduction

Metacognition, the process of evaluating and controlling one’s own mental functions, is a subject of extensive research in psychology1. From its early roots as a tool to understand perception and memory2,3, metacognition has matured into a productive field of research with publicised goals to understand its computational and neural basis4. Central to the field are task decisions and confidence ratings, which have served as fundamental measures for probing metacognition ever since those pioneering experiments in 18842. Participants provide a task decision and rate how confident they are that the decision is correct, with the relationship between these reports offering a lens into the underlying metacognitive process. But what of this lens? In the present study, we examine the well-established metacognitive protocol and ask how the act of reporting affects metacognition.

To use task decisions and confidence ratings, experimenters must collect them in some order. Either the task decision precedes the confidence rating (D → C), the confidence rating precedes the task decision (C → D), or they are made simultaneously (D + C). The choice of order is typically ad hoc, with the most common protocol varying from one research domain to another5. Once an order is selected, it typically remains fixed for the entire study; used in every experiment, by every participant, on every trial. Like other mature sciences, the field of metacognition seeks synthesis, and existing data plays an increasingly foundational role in new research5. This is alarming in light of the fact that report order varies in only three ways. If verified, latent effects of report order will pervade many datasets and, unless accounted for, will lead the synthesis of metacognition to invalid conclusions. Here, we undertake a thorough test of report order, with the aim of measuring its putative effects on metacognition and their underlying mechanisms.

When a task decision precedes a confidence rating, this provides extra time for metacognitive computations to take place before the participant must report confidence. It is widely accepted that post-decisional processes contribute to metacognition6,7. For instance, changes of mind during decision-making are possible because of evidence accumulation after deciding8,9. This unfolds over time, and merely providing the opportunity for evidence accumulation to take place is sufficient to change decision-making. If responses are slowed (e.g., requiring a protracted arm movement after stimulus offset), changes in mind can be observed even while the initial task decision is being completed10. There is direct evidence that report time affects metacognition, the introduction of a short lag between the task decision and confidence rating is enough to improve metacognitive accuracy11,12. Conversely, instructing participants to favour speed over careful confidence deliberation selectively affects confidence13.

The physical act of making a task decision also requires a cascade of cognitive and motor processes. These can influence the metacognitive computations that underlie confidence generation. In a series of papers, one research group investigated the role of actions for metacognitive ratings in a perceptual task, anagram task, and memory task14,15,16,17. They compared different response methods, including D → C and C → D designs, and found significant differences in metacognitive accuracy between conditions, concluding that motor processes contribute to metacognition. Wokke and colleagues18 also found evidence for motor-level influences on metacognition. In their study of verbal confidence ratings, enacting a task decision before confidence (D → C) resulted in enhanced metacognitive accuracy relative to a C → D design. This enhancement was accompanied by greater sensory-motor phase synchrony measured via electroencephalography. Causal evidence for the involvement of motor processes on metacognition was found by Fleming and colleagues19. In a perceptual task that employed a D → C design, they showed that transcranial magnetic stimulation to the premotor cortex before or after the task decision disrupted confidence ratings without affecting task accuracy.

These studies present converging evidence that metacognition is affected by report time and the motor-preparatory processes that enable task decisions. When a task decision precedes a confidence rating, a window of time is available for the brain to exploit information in the sensory buffer, improving metacognitive accuracy. The motor processes that support the task decision also feed into the metacognitive system and can increase metacognitive accuracy. Even accounting for report time and motor preparation, some other hidden mechanism may lead report order to affect metacognition. This remains unknown because past research has not examined report order while controlling for both report time and motor preparation. It is possible that in any past or future study of metacognition, employing a D → C design might enhance metacognitive accuracy compared to the same study using another order. This is alarming for the secondary analysis of metacognition because the limited diversity of report orders across the field means that even small effects of order will compound. If one order randomly coincides with some other manipulation, order effects may be spuriously associated with this manipulation. Alternatively, report order could counteract the manipulation, obscuring genuine effects.

Several issues limit our ability to infer the size of the order effect and its influence in the broader literature. (1) The few studies that manipulate report order have considered motor processes but not controlled for report time. Conversely, those that consider report time have not controlled for motor influences. (2) The majority of studies on these topics examine perceptual metacognition alone. It is unclear whether the sensory-motor network implicated in these studies is relevant in other domains such as memory. This may compromise comparisons of order, especially in light of the well-documented differences in metacognitive accuracy between task domains20,21,22,23,24. (3) Studies that examine other domains do not control for differences in task performance. It is known that task performance correlates positively with metacognitive ability25,26,27. If performance is not matched between conditions, it is difficult to conclude whether differences in metacognition arise due to report order or are a trivial by-product of differences in performance. (4) Those few studies that manipulate order consider only D → C and C → D designs. It remains unclear if the results of these studies generalise to D + C, the second-most popular protocol overall and the most common report order in memory studies5.

The evidence we have discussed indicates that the order of task decisions and confidence ratings impacts metacognitive performance and may be a pervasive source of bias in studies of metacognition. To address this, we designed a robust paradigm that examines the effect of report order on metacognition. Our design incorporated several features that make it highly relevant to past and future studies of metacognition. (1) we included the three protocols for registering task decisions and confidence ratings (D → C, D + C, and C → D). (2) we considered three factors that may influence metacognition: report order, report time, and motor preparation. (3) we examined two popular domains, probing metacognition in perception and memory tasks. (4) we controlled task performance in all conditions to eliminate performance confounds. (5) we used a within-participant protocol to minimise the influence of individual differences. Our design enabled us to determine to what extent report order affects metacognition, and critically, by manipulating report time and minimising the opportunity for motor preparation, we tested whether these manipulations are sufficient to inoculate against report order bias.

We hypothesised that when the time to enact reports is limited, the opportunity for post-decision evidence accumulation would be reduced. We predicted that this would manifest in impaired metacognitive performance in the time limited condition (hypothesis 3) and interact with report order (hypothesis 4). We also hypothesised that when participants can prepare a motor response in advance, the order of task decisions and confidence ratings would influence metacognition (hypothesis 5). We predicted that this would manifest in enhanced metacognitive performance in the D → C condition relative to the C → D condition when motor responses were fixed (hypothesis 6). We outlined 7 hypotheses that clarified to what extent these effects generalise to different report orders and task domains (Table 1). The primary outcome measure for our hypotheses was metacognitive efficiency (i.e., meta-d’/d’), a well-regarded, model-based approach to quantifying metacognitive performance26,27. We supplemented metacognitive efficiency with a hierarchical, logistic regression analysis that makes separate assumptions about the computational process that relates task accuracy and confidence28,29. Our study measures the effect of report order in popular domains of research in human confidence and metacognition. It also illuminates the role of two latent factors that may underlie why order effects have been observed in past studies: report time and motor preparation.

Table 1 Research design and hypotheses
Full size table

Methods

Participants

A total of 125 participants completed the study (nperception = 75, nmemory = 50). Following our registered sampling plan, recruitment ceased for an experiment after we achieved one of our stopping criteria (BF10 > 10 or BF10 < 0.1 for Hypothesis 5, or 80 participants). Data from 5 participants was excluded (see Sampling Plan for exclusion details). The final sample size was 120 (nperception=72, 26 female-identifying, 46 male-identifying, median age 23; nmemory = 48, 14 female-identifying, 34 male-identifying, median age 23). Participants who consented to report their gender selected from male, female, or non-binary options. Ethnicity data was not collected.

Ethics information

All participants provided written informed consent before participating in the laboratory study, which was approved by the Human Subjects Committee at RIKEN. There are no conflicts of interest to declare. Participants were compensated for their time at a rate of 6000 JPY per day.

Design

We conducted two experiments with different groups of participants. Experiment 1 probed perception and Experiment 2 examined short-term memory (see Tasks). Each experiment used a within-participant design. All participants completed 9 sessions of the experiment, comprising three report orders (see Report order) paired with three report contexts (see Report context). Participants completed three sessions per day, and we accounted for the effects of learning by counterbalancing the arrangement of sessions between participants. This was achieved using a replicated, latin square design with the three contexts nested in each report order (see Counterbalancing).

Critically, we used staircase techniques to regulate participants’ performance across conditions. These were employed in a calibration phase that preceded each session (i.e., three times per day), allowing us to control for the effects of performance and stimulus-variability on metacognition. Participants received no performance feedback, and the arrangements of report orders were counterbalanced, minimising the effects of learning.

Pilot data

We conducted two pilot studies of our experimental design (see Supplementary information). Data from the pilot studies demonstrated the feasibility of our protocol but was not used in the primary analyses (i.e., we collected new participants for Experiments 1 and 2).

Pilot study 1 illustrated how report order would be studied for perception and memory tasks when report time is unlimited and motor preparation is minimised. Pilot study 2 was conducted for the perceptual task only and demonstrated the feasibility of our paradigm for studying the effect of report order on metacognition when report time and motor preparation are manipulated.

Simulation and sensitivity analysis

We conducted a simulation and sensitivity analysis30 to test the power of our research design for effects corresponding to hypotheses 4 or 5. We simulated data for 80 participants performing our within-participant experiment. For each participant, we generated a metacognitive efficiency score in each of three report orders and two report contexts (i.e., simulating metacognitive performance in 6 blocks of trials per participant). The size of random effects, covariances, and errors were determined using statistics measured from our pilot studies. Our data generation function assumed a main effect of context (e.g., an average reduction in metacognitive efficiency of 0.2 when report time is limited vs. unlimited) and interaction between context and order (e.g., an average reduction in metacognitive efficiency of 0.2 for C → D relative to D → C when time is limited but no difference when time is unlimited).

Simulated data were fit with a linear mixed model, predicting metacognitive efficiency as a function of report order, report context, and their interaction, together with individual participant intercepts as random effects. This corresponds to the model used to test hypotheses 4 and 5.

$$ {mRatio} \sim 1+{order}* {context}+(1\left|{subjectID}\right.)$$

We performed 1000 repetitions of this experiment and examined results using both frequentist and Bayesian statistics. With an alpha value of 0.05, significant interaction effects were observed in 97% of repetitions (i.e., power = 0.97). With a Bayesian criterion of BF10 > 3, the alternative hypothesis was supported in 87.2% of repetitions, and the null hypothesis was supported in only 1.5% (i.e., a very low false negative rate).

It is possible the size of context and order effects are smaller than assumed above or even absent. To test these possibilities, we conducted a sensitivity analysis, simultaneously varying both the main effect of report context and the marginal effects of report order (i.e., the interaction). The report context effect was varied from -0.4 to 0.2 in steps of 0.2. These reflect cases where metacognitive efficiency is reduced, unchanged, or enhanced by report context. Simultaneously, we varied report order effects from -0.2 to 0 in steps of 0.02. These reflect gradually smaller and also null reductions in metacognitive efficiency as a function of report order. All other parameters of the data generation function remained unchanged.

We performed 1000 repetitions for each pairing of effects (44,000 simulated experiments total) (see Supplementary Fig. 8). With an alpha value of 0.05, report order effects of magnitude ~0.15 and higher were statistically significant more than 85% of the time (i.e., 0.85 power). Conversely, when there was null effect of report order, significant results were observed in <5% of experiments, consistent with our pre-specified alpha. Together, the results of this sensitivity analysis suggest that our research design, statistical pipeline, and 80 participants were sufficient to detect a range of effects, including cases where report order and/or report context have no influence on metacognitive efficiency.

Report order

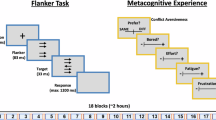
Each experiment probed three popular methods for registering a task decision and confidence rating: decision followed by confidence rating (D → C), decision simultaneous with confidence rating (D + C), and confidence rating followed by decision (C → D) (Fig. 1). All reports were made with mouse clicks, which is common in studies of metacognition. The task decision or confidence alternatives were arranged in an annulus subtending 1 degree and 9 degrees visual angle around the centre of the screen. On each report, the cursor was positioned at the centre of the annulus so response alternatives were always equidistant.

Fig. 1: Report orders and contexts.
figure 1

Three report orders determine the arrangement of task decisions and confidence ratings: (1) decision followed by confidence, (2) decision simultaneous with confidence, and (3) confidence followed by decision. Three report contexts test the influence of reaction time and motor preparation. (1) In the time limited context, participants had 2.8 seconds in total to make the task decision and confidence rating. The response annulus appeared at a new, random angle on each trial. (2) In the baseline context, participants had unlimited time to report, but the response annulus appeared at a new, random angle on each trial. (3) In the motor fixed context, participants had unlimited time to report, and the response annulus was fixed in the same position on every trial. An orange spot is added to each annulus in this figure to aid in visualising the rotation. This spot was not presented to participants.

Full size image

Report context

Each experiment examined report order in three contexts, allowing us to probe the influence of report time and motor preparation on order bias for a given task domain.

Baseline context

In this context, motor preparation is minimised, and there is unlimited time to enact each report. We removed the influence of motor preparation by presenting the response annulus at a new, randomly selected angle from 0 to 359 degrees on each trial (see Fig. 1). This eliminated the opportunity to prepare an action until the annulus appears.

Time limited context

In this context, we probed the influence of report time on metacognition for each report order. We achieved this by limiting the time available to enact both the decision and confidence rating to just 2.8 s in total. This deadline was selected on the basis of Pilot study 1, where ~75% of trials were enacted below this time. In D → C and C → D conditions, participants must make two reports within the deadline. In the D + C condition, a single report is required within the deadline. The deadline is represented to the participant as a white bar on the bottom of the screen that takes 2.8 s to reach from left to right. If the deadline is extinguished, participants were permitted to complete their report, but they were punished with a “time over” screen that paused the experiment for 6 s.

As with the baseline condition, we controlled for motor preparation by manipulating the angle of the response annulus. Contrasted against the baseline, this context allowed us to selectively examine the influence of speeding responses in the absence of motor preparatory processing.

Motor fixed context

In this context, we selectively probed the influence of motor preparation on metacognition for each report order. The response annulus was fixed, allowing the participants to prepare their response ahead of seeing the screen. Participants had unlimited time to respond.

Tasks

We conducted two experiments, involving different participants, to study the effects of report order and context. The experiments probed different domains: perception (Experiment 1) and memory (Experiment 2) (Fig. 2). We adapted tasks that are widely used in the literature. The first-order response for each task was a 2-choice discrimination between left or right (perception: left and right motion direction, memory: “old” stimulus in the left or right box). Left and right options appeared equally often in pseudo-randomised order.

Fig. 2: Task domains.
figure 2

a Experiment 1: perception task. Participants determined the net direction (left or right) of a motion coherence stimulus. Difficulty was manipulated by varying the proportion of dots that moved coherently. b Experiment 2: memory task. Participants viewed a sequence of three unique stimuli. The sequence was occluded by a mask, and the final frame appeared, containing a stimulus to the left and to the right. One was an “old” stimulus from the sequence, and the other was a “new” stimulus that had never appeared before. Participants determined whether the stimulus to the left or right was “old”. Difficulty was manipulated by varying the amount of time (signified by Δ ms) between stimuli in the sequence.

Full size image

Perception

We used a motion coherence task31 to probe metacognition in the perceptual domain (Fig. 2a). There exists a 30-year tradition of using motion coherence paradigms to study perceptual confidence and metacognition32,33,34,35. Participants are required to identify the net direction (left or right) of a stochastic dot motion stimulus while fixating on the centre of the screen. To calibrate performance, we manipulated the proportion of coherently moving dots.

Each trial started with a red fixation point subtending 0.5 degrees of visual angle. The fixation point appeared on a black background for a random interval between 500 and 1500 ms. In the next frame, 400 dots were visible in an annulus defined by invisible concentric circles of 0.5 degrees and 10 degrees (dot density 5.1 dots per square degree). Each dot was 0.12 degrees visual angle and was displaced at a speed of 24 degrees per second (13 pixels per 16.67 ms). Every three frames (50 ms at 60 Hz refresh rate), a random set of dots was chosen to be the coherently moving dots and was displaced either leftward or rightward. The number of dots in this set corresponded to the motion coherence intensity (e.g., at 10% coherence, 40 dots moved in the same direction). The remaining dots were randomly displaced within the annulus. Any dot that moved outside the annulus was replaced at a random location within the annulus. Dot motion continued for 1000 ms before it was replaced by the response screen(s).

Memory

We used a short-term memory task to probe metacognition in the memory domain (Fig. 2b). The contemporary science of metacognition was built on foundations set by meta-memory research3, and short-term memory tasks are frequently contrasted with perceptual tasks to study the domain-specificity of metacognition20,36,37. Participants viewed a rapid sequence of three abstract visual stimuli followed by a mask. They were then presented with two stimuli, a “new” foil stimulus and an “old” stimulus that appeared in the previous sequence, and had to determine which was the “old” stimulus. To calibrate performance, we manipulated the inter-stimulus interval (ISI).

Participants started each trial with a mouse click, then a navy-blue square box with sides of 6 degrees visual angle appeared at the centre of the screen for 100 ms. Next, the first stimulus appeared centred within the box for 100 ms. This was then removed, and the box remained on the screen for one ISI. This was followed by the second stimulus for 100 ms, an ISI, the third stimulus for 100 ms, and another ISI. Next, a visual mask appeared centred in the box for 800 ms. Finally, two navy-blue square boxes with sides of 6 degrees visual angle appeared to the left and right of the screen. In one box was an “old” stimulus (the target) viewed during the preceding sequence. In the other box was a “new” stimulus that was previously unseen. The stimuli remained on the screen for 2500 ms before being replaced by the response screen(s). Participants had to identify the “old” stimulus in either the left or right box, registering a left or right response.

Using techniques established in previous research20, we generated a corpus of 18000 unique visual stimuli ensuring that the participant never saw the same object twice unless it appeared as a target. Each stimulus was composed of 90 lines that emerged from the centre of the image along diagonal, vertical, and horizontal directions.

Counterbalancing

Nine sessions paired each report order with each context. On day one, participants completed trials from all three contexts using one report order. On day two, trials were completed in a new arrangement of contexts for another report order. On day three, the trials were completed for each context in another arrangement using the third and final report order. This replicated latin square design yielded 72 unique arrangements of the 9 sessions, efficiently sampling from all possible combinations of report orders and contexts.

Session structure

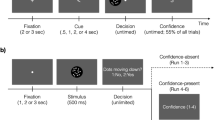
All study sessions shared the same basic structure: practice, calibration, and testing (Fig. 3).

Fig. 3: Study session design.
figure 3

Each cell represents a condition in the experiment that pairs a report order and report context. Calibration was performed in each session, allowing us to fix stimulus properties in the testing phase. Hypothesis testing included trials from the testing phase only.

Full size image

Practice

A practice phase was used to (re)-familiarise the participant with the assigned report order and context. During practice, the participant used the assigned report order (e.g., D → C) to complete trials in the assigned context (e.g., time limited). Practice trials spanned a range of difficulties from easy to hard, and performance feedback was provided.

Calibration

A calibration phase was used to identify stimulus properties that result in the participant performing at approximately 70% accuracy for the assigned report order and context. During calibration, the participant completed three staircase runs. All staircase runs shared the same psychometric parameters: a 2-down-1-up design that terminates after 10 reversals and targets a performance threshold of 70.71% accuracy. Each staircase was designed to be downward in nature, starting from an intensity value that was subjectively easy (the perception task employs a motion coherence of 80%, and the memory task employs an ISI of 600 ms). To efficiently reach the performance threshold, the initial step size was wide ( ± 35% of the current trial’s intensity) and changed to a narrow step size ( ± 15% of the current trial’s intensity) after the third reversal.

The performance threshold for each staircase run was determined by computing the geometric mean of the intensity values at the final six reversal points. After the participant completed the third staircase run, the experimenter viewed three plots representing the changes in intensity values over time, reversal points, and the final threshold intensity for each staircase run. The experimenter selected the staircase run that most precisely achieved the threshold, taking into account diagnostic features such as the distinctive “zig-zag” pattern of correct and incorrect responses that is produced at a performance threshold and uncharacteristic errors that may reflect lapses in attention. Although the selection of a threshold was subjective, this design permitted us to efficiently identify performance thresholds at multiple stages of the experiment while controlling for factors (i.e., lapses in attention) that can lead more quantitative calibration techniques to fail. In pilot testing, this design proved to be highly efficient with each staircase run terminating after an average of 32 trials with a large degree of consistency in performance threshold between runs.

Testing

A testing phase comprising 100 trials was used to assess metacognitive ability for the assigned report order and context. These trials were the only ones used to contrast metacognition between conditions. Stimulus properties were those selected by the experimenter in the calibration phase. Thus, the stimulus properties remained fixed for all trials at the participant’s 70.71% accuracy threshold.

Apparatus

The experiment was conducted using MATLAB 2019a and PsychToolbox 3.0.16. We presented the stimuli on an ASUS ROG STRIX XG258Q monitor with a 1920 × 1080 pixel resolution and 60 Hz refresh rate. The experiment was controlled by a computer running MS-Windows 11 with an Intel i7-9700 CPU. Participants performed all tasks in a dark booth with their head positioned on a head-rest located 58 cm from the monitor.

Reports were made using a standard computer mouse to select the desired task decision and confidence rating. Responding via mouse is common in many studies of metacognition, and this procedure has high ecological validity. The position of the mouse was reset to the centre of the screen following each report, ensuring alternatives were equidistant. All reports were made using the same hand. This is a common approach employed in many studies of metacognition and allowed our results to generalise to most existing and future research.

Sampling plan

We used a Bayes factor design analysis38 approach to detect our primary hypothesis 5 (Table 1). In accordance with the open-ended sequential design, we recruited additional participants until the Bayes factor provided strong evidence for the null hypothesis (BF < 0.1) or the alternative hypothesis (BF > 10). Alternatively, we would terminate data collection for each experiment when we reached 80 participants. We conducted a simulation study and sensitivity analyses that demonstrated our research design could detect a wide range of effects, including cases where report order and report context have no influence on metacognition (see Simulation and sensitivity analysis).

For our core analysis, metacognition was operationalised as metacognitive efficiency (meta-d’/d’) and computed at the participant-level using maximum likelihood estimation (MLE)27. This is a computationally efficient approach to measuring metacognition and is amenable to the analysis plan outlined below. Although the MLE data was used to determine when the sampling thresholds were achieved and to determine the outcome of each hypothesis in Table 1, we performed several supplementary analyses in our final sample to assess the robustness of our central result to alternative measures of metacognition.

Exclusion criteria

We excluded participants who used the same confidence rating on every trial in the test phase. We also excluded trials from conditions that had mean performance 2 standard deviations above or below the group mean in the testing phase. We excluded trials from the time limited context that exceeded the deadline. We also excluded trials from the untimed conditions that exceeded 5 s of total report time (equivalent to the 95% percentile of total report time in Pilot study #1). Piloting of our memory task indicated that separate thresholds exist depending on the memorisation strategy. We targeted a short threshold (inter-stimulus time of ~300 ms) corresponding to iconic memory. Data that indicated deliberate memorisation was used (inter-stimulus time of >1500 ms) resulted in the participant being excluded. Although included trials were the only data used to test our hypotheses, in supplementary analyses we tested our same models including all data.

Analysis plan

The primary outcome measure was metacognitive efficiency (meta-d’/d’), which was computed in the test phase of each condition for each participant using the maximum likelihood approach. Our general model for all tests in Table 1 was a hierarchical model with report order and report context included as fixed effects together with individual participant intercepts as random effects. Hypotheses 1 through 6 were prepared for each experiment. Pairwise comparisons were conducted between each level of the report order and context conditions to test for our a priori interest in these effects. To test hypotheses 4 and 5, we included an interaction term between report order and context into the general model outlined above (this model was used as the data generation function in our simulations and tested in the sensitivity analysis). To test hypothesis 7, we included data from both experiments as well as an interaction term between report order and experiment into the model outlined above.

We computed Bayes factors in R using the BayesFactor and bayesTestR packages39,40. Estimation was achieved using the Jeffreys-Zellner-Siow prior with a ‘wide’ scale (r = \(\sqrt{2}/2\)) for fixed effects and a ‘nuisance’ scale (r = 1) for random effects. We used these defaults because, in practice, they share properties with common frequentist tests41. To test whether BFs exceeded either evidence threshold (strong evidence of 0.1 or 10), we compared the inclusion of effects across matched models. Specifically, models that included the report order factor without report order interactions (hypothesis 1 and 6), models that included report order * report context interaction and both main effect terms (hypotheses 2 through 5), and models that included each main effect term and interactions between report order, report context, and experiment (hypothesis 7). Analysis code to compute and test these hypotheses was prepared prior to data collection and was stored on a DOI-minted, online repository (https://osf.io/wpbc8/).

After data collection, we assessed normality by visual inspection of residuals and the Shapiro-Wilk test. Homogeneity of variance was evaluated using Levene’s test. These assumptions were met for all analyses. We provide summaries of the posterior distribution for each model (mean and 95% credible intervals) in Table 2.

Table 2 Posterior parameters for all registered hypotheses
Full size table

We supplemented our Bayesian analysis with two additional analyses of metacognition in the full sample to assess the robustness of the report order effect to alternative computations of metacognition. First, we computed metacognitive efficiency at a group-level using hierarchical Bayesian estimation (Hmeta-d’)26. If the 95% highest-density interval (HDI) for the report order factor did not overlap with 0, then order contributed substantially to model fit. Second, we examined metacognitive accuracy using logistic regression to model accuracy as a function of confidence ratings. If removing the interaction between report order and confidence significantly reduced model fit, then report order contributed substantially to metacognitive ability.

Reporting summary

Further information on research design is available in the Nature Portfolio Reporting Summary linked to this article.

Results

Registered analyses

Control analysis (hypothesis 1)

Hypothesis 1 examined whether our time manipulation successfully reduced report time. For both experiments, we examined trials in the time limited and baseline contexts, and compared the total report time taken to execute the task decision and confidence rating on each trial.

In Experiment 1 (perception), total report time was faster in the time limited context (Mean = 1.48, Standard Deviation = 0.19) than the baseline context (M = 1.71, SD = 0.36, Hypothesis 1.1: BF10 = 2.49 * 1022). Likewise, in Experiment 2 (memory), we observed strong evidence for hypothesis 1. Total report time was significantly faster in the time limited context (M = 1.53, SD = 0.19) than the baseline context (M = 1.77, SD = 0.35, Hypothesis 1.2: BF10 = 2.68 * 1015). These results provide strong evidence for hypothesis 1, indicating our time manipulation was successful in both experiments.

Report order (hypothesis 2)

Hypothesis 2 examined whether report order affects metacognition independently of report time and motor preparation. This hypothesis tests for report order effects that our time and motor manipulations could not account for. For each experiment, we subset data from the baseline and time limited contexts, and computed metacognitive efficiency (meta-d’/d’) using valid trials in each test phase.

In Experiment 1, we observed strong evidence against the main effect of report order (Hypothesis 2.1a: BF10 = 0.06) with moderate evidence against the interaction between report order and context (Hypothesis 2.1b: BF10 = 0.22). In Experiment 2, we found strong evidence against the main effect of report order (Hypothesis 2.2a: BF10 = 0.09) and strong evidence against the interaction between report order and context (Hypothesis 2.2b: BF10 = 0.04). These results disconfirm hypothesis 2 and suggest effects of report order on metacognition, if present in either experiment, will be captured by our time and motor manipulations.

Report time (hypotheses 3 and 4)

Hypothesis 3 tested the effect of report time on metacognition. For each experiment, we computed metacognitive efficiency using valid, test phase trials in the baseline context (where report time was unlimited) and time limited context (where total report time was limited to just 2.8 s). In both contexts, motor preparation was controlled by changing the location of the response alternatives on each trial.

In Experiment 1, we observed strong evidence against hypothesis 3 (Hypothesis 3.1: BF10 = 0.08). Metacognitive efficiency was statistically equivalent in each context (baseline: M = 0.59, SD = 0.61; time limited M = 0.56, SD = 0.57) (Fig. 4a). In Experiment 2, we observed moderate evidence against hypothesis 3 (Hypothesis 3.2: BF10 = 0.13). Metacognitive efficiency was broadly equivalent in each context (baseline: M = 0.96, SD = 0.48; time limited M = 0.93, SD = 0.44) (Fig. 4b). These results suggest that speeding reports had no direct effect on metacognition.

Fig. 4: Report context had no direct effect on metacognition.
figure 4

In (a) perception (n = 75 participants) and b memory (n = 50 participants) tasks, metacognitive efficiency was equivalent between the time limited context (where motor preparation was controlled and total report time was limited to just 2.8 s), the baseline context (where motor preparation was controlled but reports were untimed), and the motor fixed context (where reporting actions could be prepared in advance but were untimed). M-ratio = 1 reflects theoretically optimal metacognitive efficiency. Errorbars are standard error of the mean, computed independently for each experiment.

Full size image

The lack of an overall difference in metacognition between the baseline and time limited contexts does not preclude order bias within either context. Hypothesis 4 examined each context and tested whether timing can account for report order effects. We used the same trials as hypothesis 3 and, for each experiment, examined the interaction between report order and context. Additionally, we conducted pairwise comparisons between the order conditions to directly contrast each protocol.

In Experiment 1, we observed moderate evidence against the interaction between order and context (Hypothesis 4.1: BF10 = 0.22). Metacognitive efficiency was broadly equivalent between order conditions in the time limited context (each pairwise effect BF10 = 0.14). In the baseline context, metacognitive efficiency was broadly equivalent between D + C (M = 0.50, SD = 0.67) and C → D conditions (M = 0.53, SD = 0.58; BF10 = 0.14) but was higher on average in the D → C condition (M = 0.73, SD = 0.58). However, we observed only anecdotal support for statistical differences between D → C and the other protocols (D → C vs. D + C, BF10 = 0.88; and D → C vs. C → D, BF10 = 2.29) (Fig. 5b). Overall, these results provide moderate evidence against hypothesis 4. While we observed no order bias in the time limited context, our large sample was insufficient to reliably detect the presence or absence of order bias in the baseline condition.

Fig. 5: Report order has little effect on metacognition.
figure 5

a Mean metacognitive efficiency for each report order, collapsing over experimental contexts. b Mean metacognitive efficiency for all report orders and contexts in Experiment 1 (perception, n = 75 participants) and Experiment 2 (memory, n = 50 participants). M-ratio = 1 reflects theoretically optimal metacognitive efficiency. Errorbars are standard error of the mean, computed independently for each experiment.

Full size image

In Experiment 2, we observed strong evidence against the interaction between order and context (Hypothesis 4.2: BF10 = 0.04). Metacognitive efficiency was broadly equivalent between order conditions in the time limited context (D → C vs. D + C, BF10 = 0.23; D → C vs. C → D, BF10 = 0.18; D + C vs. C → D, BF10 = 0.18). Likewise, in the baseline context there was moderate evidence against the pairwise difference between D + C (M = 0.94, SD = 0.42) and C → D conditions (M = 0.88, SD = 0.49; BF10 = 0.18). Efficiency was slightly higher on average in the D → C condition (M = 1.05, SD = 0.52) but there was anecdotal evidence against statistical differences with the other protocols (D → C vs. D + C, BF10 = 0.48; and D → C vs. C → D, BF10 = 0.59) (Fig. 5b). These findings provide moderate evidence against hypothesis 4. Report time does not account for order bias but this result is driven by insufficient evidence for order bias itself—we observed little or no statistical difference in metacognitive efficiency between each order protocol.

Motor preparation (hypotheses 5 and 6)

Hypothesis 5 examined whether motor preparation can account for order bias. For each experiment, we computed metacognitive efficiency using valid, test phase trials in the motor fixed context. Here, the location of response alternatives does not change, allowing participants to prepare report actions in advance. We contrasted this condition with the baseline context, where motor preparation was controlled. Participants had unlimited time to report.

To test hypothesis 5, we analysed the interaction between report order and context. In Experiment 1, we observed strong evidence against hypothesis 5 (Hypothesis 5.1: BF10 = 0.06) (Fig. 4a). Likewise, we observed strong evidence against hypothesis 5 in Experiment 2 (Hypothesis 5.2: BF10 = 0.06) (Fig. 4b). These findings suggest the opportunity to prepare actions in advance had no impact on report order effects.

Hypothesis 6 tested the claim that preparing a task decision before a confidence rating (i.e., D → C) improves metacognition. Data was subset to the motor fixed context only and we performed pairwise contrasts between each order condition. These conditions are standard in metacognition research, and so this is a strong test that report order affects metacognitive efficiency in common metacognition protocols.

In Experiment 1, there was strong evidence against a main effect of report order (Hypothesis 6.1a: BF10 = 0.04). We observed moderate evidence against a pairwise difference between the D → C protocol (M = 0.63, SD = 0.62) and C → D (M = 0.54, SD = 0.54; Hypothesis 6.1b: directional BF10 = 0.24, non-directional BF10 = 0.16). Likewise, we observed moderate evidence against pairwise differences between D + C (M = 0.56, SD = 0.58) and D → C (BF10 = 0.16) and C → D (BF10 = 0.16). The same pattern of results were observed in Experiment 2. We found strong evidence against a main effect of report order (Hypothesis 6.2a: BF10 = 0.05). Pairwise comparisons revealed moderate evidence against a difference between the D → C protocol (M = 1.02, SD = 0.48) and C → D (M = 0.96, SD = 0.48; Hypothesis 6.2a: directional BF10 = 0.29, non-directional BF10 = 0.20), as well as D + C (M = 0.97, SD = 0.52) compared to D → C (BF10 = 0.17) or C → D (BF10 = 0.20). These results provide moderate evidence against hypothesis 6, indicating there was little sign of order bias in these data and preparing a task decision before a confidence rating had negligible effect on metacognition (Fig. 5a).

Task domain (hypothesis 7)

Hypothesis 7 tested whether the effects of report order and context differ for perception and memory tasks. We included all valid data from test phases in both experiments and computed metacognitive efficiency for each condition.

We observed a strong effect of task domain on metacognition (BF10 = 1.78 * 107), efficiency was greater for the memory task than the perception task. However, there was strong evidence against a three-way interaction between task domain, report order, and report context (Hypothesis 7a: BF10 = 0.004). Likewise, null interaction between domain and order (Hypothesis 7b: BF10 = 0.01), and null interaction for domain and context (Hypothesis 7c: BF10 = 0.02). These results provide a strong disconfirmation of hypothesis 7. Task domain had a substantial impact on metacognitive performance, but any effects of report order or context were identical for perception and memory tasks (Fig. 5b).

Alternative metacognitive measures

To explore the robustness of our core analyses, we examined the effects of report order and context using alternative measures of metacognitive performance. First, we computed metacognitive efficiency using hierarchical Bayesian estimation26. Separate models were generated for each experiment, estimating the impact of report order and report context on the m-ratio. This analysis revealed the same pattern of results as our registered hypotheses; metacognitive efficiency was equivalent across report orders (Experiment 1: μorder = 0.014, %95HDI [–0.067, 0.084], Experiment 2: μorder = 0.032, %95HDI [–0.027, 0.094]) and report contexts (Experiment 1: μcontext = -0.007, %95HDI [–0.082, 0.073], Experiment 2: μcontext = 0.013, %95HDI [-0.042, 0.070]).

Second, we used logistic regression to model metacognitive accuracy29. For each experiment, we generated a logistic mixed model predicting trial-by-trial task accuracy from confidence ratings. Our full model included interaction terms between confidence, report order, and report context, together with random intercepts and confidence slopes42. A similar pattern of results was observed when more complex random effect structures were tested, however model convergence was not achieved when all conditions and interactions were included as random effects. We performed a series of model comparisons, progressively reducing complexity by removing factors of interest to find the most parsimonious model.

In Experiment 1, the full model was most parsimonious. Model fit was significantly reduced when removing either the interaction between confidence and report order (Χ2(6) = 19.87, p = 0.003), interaction between confidence and report context (Χ2(6) = 17.04, p = 0.009), or the three-way interaction (Χ2(4) = 10.40, p = 0.034). To explore these effects, we subset data into each context and tested the interaction between confidence and report order. In both the time limited and motor fixed contexts, the most parsimonious model excluded the interaction term (time, p = 0.211; motor, p = 0.420), indicating report order did not affect metacognitive accuracy. However, the interaction between confidence and report order was significant in the baseline context (Χ2(2) = 13.22, p = 0.001). To follow-up, we performed Tukey-adjusted pairwise contrasts between each report order pair. The only significant effect was between D → C and D + C (z = 2.36, pTukey = 0.048), suggesting the success of the full model in the perception task was driven by this difference in the baseline condition. This result indicates that confidence ratings generally predicted accuracy equally well across conditions of the perceptual task. However, in the baseline context, where participants could not prepare motor actions in advance, confidence ratings were more predictive of accuracy when given after the task decision than when given at the same time as the decision. A similar pattern of results was observed when more complex random effect structures were tested, however the pairwise comparison was not significant after correction for multiple comparisons, indicating the effect is small in magnitude.

In Experiment 2, the most parsimonious model included an interaction between confidence and report order but not report context. To follow-up, we performed Tukey-adjusted pairwise contrasts between each report order pair. A significant effect was observed between D → C and D + C (z = 3.28, pTukey = 0.003), as well as D + C and C → D (z = –2.48, pTukey = 0.035), but not D → C and C → D (z = 0.80, pTukey = 0.701), suggesting the success of the winning model in the memory task was driven by simultaneous reports. This result indicates that in the memory domain, confidence ratings were less predictive of accuracy when task decisions and confidence ratings were made simultaneously, compared with either sequential order. When more complex random effect structures were tested, we again observed an interaction between confidence and report order, but pairwise comparisons were not significant after correction for multiple comparisons, indicating these individual effects are small in magnitude.

Exploratory analyses

Successful calibration of performance for perception and memory tasks

In each condition, we used staircase procedures to calibrate task performance to the same threshold. Our pilot studies indicated that this design would tightly control performance in test trials following calibration but was this approach successful? We took trials in each test phase and examined mean accuracy as a function of report order and report context, including individual participant intercepts as random effects.

In Experiment 1, we observed strong evidence against the main effects of report order (BF10 = 0.03), report context (BF10 = 0.04), and their interaction (BF10 = 0.01). The same pattern of results was observed in Experiment 2 (order: BF10 = 0.02, context: BF10 = 0.09, and interaction: BF10 = 0.01). Together, these results indicate that our design successfully controlled performance across all experimental conditions in both perception and memory tasks.

Report order and metacognitive bias

Our research design did not manipulate metacognitive bias—differences in the overall level of confidence expressed in one condition to the next. To assess this, we took trials in each test phase and examined mean confidence as a function of report order and context, including individual participant intercepts as random effects.

In Experiment 1, we observed strong evidence against the main effect of report context (BF10 = 0.01) and interaction between order and context (BF10 = 0.003). However, we found moderate evidence for a main effect of report order (BF10 = 6.29). Pairwise comparisons revealed that mean confidence for D → C (M = 2.26, SD = 0.63) and C → D (M = 2.25, SD = 0.69) protocols were broadly equivalent (BF10 = 0.13). Confidence was lower on average for D + C (M = 2.13, SD = 0.64) but we observed anecdotal evidence favouring the null hypothesis for each pairwise difference (D + C vs. D → C: BF10 = 0.68; D + C vs. C → D: BF10 = 0.53). These results suggest that sequential report protocols yield comparable overall confidence, while evidence for a reduction in confidence under simultaneous reporting was inconclusive, even with our large sample.

In Experiment 2, we found strong evidence against all effects (order: BF10 = 0.05, context: BF10 = 0.05, and interaction: BF10 = 0.09). This result suggests that confidence was equivalent across all conditions of the memory task.

Why have past studies identified order bias?

Our registered analyses found little evidence for order bias. Why, then, has order bias been reported in the past? To answer this question, we consulted the confidence database5. It contains 5 datasets from studies that manipulate the order of task decisions and confidence ratings, including publications that motivated our registered report14,15,17,43.

The datasets comprise a variety of tasks including face-gender identification14, anagram detection15,43, and a word memory task17. There are several notable design elements that differ from our research protocol. Only D → C and C → D orders were compared, simultaneous reports were not studied. Report order was manipulated between-participants. Task performance was not calibrated. Reports were collected using a keyboard with fixed response mapping, meaning motor preparation was possible on every trial. The time available to report was either unlimited or sufficiently long (3–5 s per report) that participants were unlikely to feel time pressure.

To measure order bias in these studies, we compared metacognitive efficiency between report orders for each dataset using a Welch’s unequal variances t-test and Bayesian t-test (r = \(\sqrt{2}/2\)). Trial numbers were relatively low for the anagram task so we computed metacognitive efficiency using the HMeta-d' toolbox and only for trials with a task decision and confidence rating (the same pattern of results was observed using MLE). We observed little evidence for order bias—Bayes factors provided moderate to anecdotal support for the null hypothesis in all but one dataset (see Table 3). A large difference in metacognitive efficiency was observed between report conditions in Experiment 1 of Siedlecka and colleagues17 (BF10 = 4.691 * 109). However, this difference is explained by the engagement of distinct memory retrieval processes in each condition: the D → C protocol enabled target recognition by presenting cues (for the task decision) prior to the confidence rating, whereas the C → D protocol necessitated recall, as confidence was rated before the participant saw the retrieval cue.

Table 3 Little evidence for order bias in past studies
Full size table

To assess the overall evidence for order bias, we aggregated these datasets and compared metacognitive efficiency between report orders. This analysis revealed moderate evidence against a difference between conditions (all data: BF10 = 0.129; excluding Experiment 1 of Siedlecka and colleagues17: BF10 = 0.141). These results suggest that, in fact, past studies provide little support for the existence of order bias. Despite variations in research design, tasks, and response modality, metacognitive efficiency remains largely unaffected by the order of task decisions and confidence ratings.

However, the original studies did not use metacognitive efficiency, instead relying on logistic regression to model metacognitive accuracy. To test whether the choice of measure influences the results, we re-analysed the aggregated data using a logistic mixed model predicting trial-by-trial task accuracy from confidence ratings. The full model included an interaction between confidence and report order, as well as random intercepts and slopes. We compared it to a reduced model without the interaction. The full model provided a better fit both with all data included (Χ2(1) = 17.81, p < 0.001) and when Experiment 1 of Siedlecka and colleagues17 was excluded (Χ2(1) = 6.10, p = 0.014).

Discussion

In this study, we examined how the act of reporting affects metacognition in common experimental protocols. Our research was motivated by evidence that a crucial feature of behavioural experiments, the order of task decisions and confidence ratings, can bias metacognitive performance, possibly by influencing the timing of reports or the actions involved. In perception and memory tasks that tightly controlled participants’ accuracy, we found that manipulating the order of reports had little effect on metacognitive efficiency. This pattern held in a standard experimental context, where reports were untimed and actions could be prepared in advance, as well as in controlled contexts that restricted timing and motor preparation. Together, our 7 registered hypotheses find little evidence that report order is a practical concern when collecting or analysing metacognitive reports.

The strong results for hypotheses 1 and 2 indicate that our timing manipulation successfully limited report time, and that order bias, if present, would be captured by our context manipulations. In all conditions, we calibrated task performance to the same threshold and examined metacognition in a distinct test phase with fixed stimulus properties. This design minimised the influence of performance and stimulus variability, producing a test environment that was relatively free of task-related confounds.

Limiting report time had no direct effect on metacognitive efficiency in either experiment, disconfirming hypothesis 3. Hypothesis 4 tested whether report time can account for order bias. While the balance of evidence rejected this hypothesis, this result emerged due to a lack of evidence for order bias to begin with. Metacognitive efficiency was equivalent for all conditions in the time limited context. In the baseline context, we observed heightened metacognitive efficiency in the D → C condition for both tasks. However, this empirical difference was statistically inconclusive in our large sample, suggesting that any bias from this protocol exerts at most a small effect.

In most experimental protocols, how participants physically report does not change, meaning participants have an opportunity to prepare actions in advance. Hypothesis 5 examined whether motor preparation impacts metacognition. While participants’ reaction times benefited from motor preparation, their metacognitive efficiency was unchanged. This result disconfirms hypothesis 5 and suggests motor preparation had no direct effect on metacognitive efficiency. Hypothesis 6 examined the specific claim that preparing a task decision before a confidence rating (i.e., D → C) enhances metacognition. In both Experiment 1 and Experiment 2, metacognitive efficiency remained stable across order conditions, disconfirming hypothesis 6. This shows that in standard protocols, where reports are untimed and actions can be prepared in advance, the order of task decisions and confidence ratings has little effect on metacognitive efficiency.

Our registered analyses found little evidence for order bias. Why, then, has this effect been reported previously? To investigate, we conducted a secondary analysis of 5 datasets that have been cited as evidence that making a task decision before a confidence rating enhances metacognition. When metacognition was measured using the m-ratio, these datasets showed little evidence of order bias. Importantly, these datasets used different tasks and keyboard-based responses, suggesting that order bias cannot be attributed to these designs. Therefore, the data from past studies support our conclusion that metacognitive efficiency is unaffected by report order.

However, past studies have used a different approach to measuring metacognition: logistic regression. To test whether the choice of measure matters, we repeated our main analyses using a logistic mixed model to predict task accuracy from confidence ratings. In both experiments, the winning model included an interaction between report order and confidence, suggesting that report order influenced how well confidence predicted accuracy. A similar pattern emerged in our reanalysis of the 5 prior datasets using the same logistic regression method.

Recently, the logistic regression approach to measuring metacognition has been criticised for inflating false positive rates under certain conditions42. This critique does not apply in the present case as we followed best practices in implementing these models, finding effects of report order with complex random effects structures and tightly matched accuracy. These effects, however, were small in magnitude, context-dependent, and emerged from exploratory analyses rather than our registered hypotheses.

Logistic regression and signal detection theoretic measures like the m-ratio quantify different aspects of metacognitive performance and rest on distinct assumptions about the nature of metacognitive reports. On the one hand, the trial-level granularity of regression models may provide greater sensitivity to subtle effects of report order. On the other hand, the consistent disconfirmation of order effects across all registered hypotheses suggests these effects are practically negligible at the level of metacognitive efficiency, modelled across trials using the m-ratio. A full evaluation of these measures is outside the scope of this study, but the present results indicate that report order may provide a promising case for future studies that aim to clarify the strengths and limitations of each analytical approach. In the meantime, our results suggest that when conducting research or analysing secondary data with different report orders, spurious effects on metacognition are best avoided by using the m-ratio.

We developed a staircase procedure to control memory performance. Our protocol mimics classic staircase procedures used in perceptual psychophysics, enabling performance calibration for perception and memory using closely matched methods. We observed identical effects of report order and context in each experiment, providing a strong disconfirmation of hypothesis 7 that these factors depend on task domain. Notably, metacognitive performance was greater for memory than visual perception, approaching its theoretical optimum at a group-level25,27. This result builds on past studies that suggest both domain-general and domain-specific processes contribute to metacognition20,22,24,44,45. It shows that domain-specific differences in metacognition are present in many experiment contexts, suggesting they may be a general feature of human behaviour.

Our context manipulations revealed little impact of report timing or motor preparation on metacognitive efficiency. Do these findings challenge the idea that timing and action-related processes contribute to metacognition? We think not. Our study focussed on the practical consequences of these factors within experimental procedures commonly used in the field. The manipulations were designed to alter timing and motor preparation without disrupting standard reporting protocols.

Regarding report timing, a recent preprint by Herregods and colleagues13 investigated the effects of instructing participants to make either fast or deliberate task decisions and confidence ratings. They found little effect on average confidence, but the relation between confidence and accuracy was stronger when participants were more cautious in their confidence ratings. For motor preparation, earlier work has eliminated actions entirely using vocal responses18, or manipulated premotor cortex excitability during report epochs using transcranial magnetic stimulation19. These strong manipulations reduced metacognitive efficiency, albeit relatively weakly and only under certain conditions. To summarise, while we do not rule out the contribution of timing and motor processes on metacognition, our findings suggest these factors have little practical impact within controlled experimental paradigms. In commonly used designs, speeding responses or allowing motor preparation appears to have little effect on metacognitive efficiency once task performance is accounted for.

Limitations

When participants report metacognition, responses are typically registered using either a mouse or keyboard. We focussed on mouse reports because motor preparation can be minimised with a simple and effective method: rotating the response annulus. Equivalent control for keyboard responses (e.g., randomising response-key mappings from trial-to-trial) is burdensome for participants and unlikely to be widely adopted. Our secondary analysis examined datasets that used keyboard reports and arrived at the same conclusions as our registered analyses. Future research might systematically test other apparatus, but our findings suggest that order bias poses little practical concern when studying metacognition using either mouse or keyboard reports.

Conclusion

In conclusion, our registered report finds little evidence that the order of task decisions and confidence ratings affects metacognition. Across perception and memory tasks, and in a range of experimental contexts that accounted for report timing and motor preparation, we observed no consistent advantage for any particular report order. This suggests that metacognitive efficiency is a robust index of metacognition across many experimental contexts and researchers are unlikely to bias their results simply by adopting a reporting protocol that suits their research question. As interest grows in studying metacognition across domains and populations, the need for protocols that are both flexible and resistant to artefacts becomes increasingly important. Our findings suggest the order of task decisions and confidence ratings has little effect on metacognitive performance, and need not constrain secondary analysis or experimental design.