Introduction

While the von Neumann computing architecture1 is most likely to persist for many more years, the current demands of artificial intelligence (AI) necessitate a fundamental rethinking of how we compute, sense and communicate information2,3,4,5. The proliferation of electronic devices, edge devices, sensor-based electronics, and wearables, has led to a significant surge in raw data generation, demanding more power, real-time processing, and decision-making capabilities5,6,7. Although digital computing has revolutionized various industries and bolstered economies8, the requirements of AI computing call for a different information processing paradigm and architecture9,10. In this evolving big data landscape, the conventional von Neumann computing architecture with separated memory and processing is no longer suitable11. Computing architectures must evolve to not only enable energy efficient in-memory computations but also facilitate the deployment of robust neural networks for the execution of AI tasks12,13 that infer and learn interactively with the environment.

An emerging and innovative computing paradigm gaining momentum is physical computing or natural computing, which relies on principles rooted in physics14. In physical computing, physical variables are encoded into a dynamical system that evolves in accordance with the laws of classical or quantum mechanics15,16. This marks a departure from instruction-based information processing, where information is encoded in logical bits of either 0 or 1. In physical computing, information is represented as a continuous variable encoded either in amplitude, frequency or phase differences between signals17. In this paper, we focus mainly on physical computing based on coupled oscillators with information encoded in the phase differences between oscillators. Figure 1 illustrates the concept of physical computing using coupled oscillators.

Fig. 1: Illustration of oscillatory neural networks (ONNs) and computation involving the phase measurement between oscillators.
figure 1

ONNs are energy-based networks that minimize their energy as they evolve and stabilize towards ground minima.

Full size image

Physical computing is also closely intertwined with neuroscience, particularly in the study of biological neural networks18. The rhythmic firing (or spiking) of neurons can be described by oscillations19. Neuron oscillations have been quantified through measurements where synchronized activity of a large number neurons give rise to macroscopic oscillations that can be observed in electroencephalogram (EEG)20,21,22. Oscillations can vary in amplitude and frequency but once synchronization occurs, oscillations converge and adapt to a common frequency mode23,24. Typically neuron activity is investigated as spike change over time such as changes in neuron membrane potential with time which are commonly emulated and studied in spiking neural networks25,26,27,28. In contrast, physical computing captures the collective neural activity through oscillations or the dynamics from a single neuron to their collective29,30,31. While spiking activities provide insight into individual neurons, oscillations reveal the dynamic nature of neural activity and give insights into how spike travels across the network and interacts with other neurons32,33. Such collective dynamics allow for the extraction of spatial and temporal patterns34,35. Understanding the evolution of oscillation dynamics and propagation are key to understanding cognitive states, particularly in the context of human memory20,36,37. Furthermore, describing neurons as oscillators offers a mathematically simple yet elegant formulation for investigating the dynamics of collective neurons38. This mathematical formalism avoids the need to simulate every voltage dependence of each ionic current in a neuron and how this moves from one neuron to the next.

Oscillatory neural networks (ONNs) hold promise for realizing both physical and neuromorphic computing while enabling continuous and analog information encoding through phase modulation39. These networks benefit from the diverse collective dynamics of coupled oscillators, ranging from chaotic behavior40 to synchronization41, for encoding information, sensing and processing. The phenomenon of synchronization unveils the stability and inherent memory of the network30. Synchronization—two or more events occurring simultaneously—is a ubiquitous phenomenon in nature42,43. The beauty of synchronization can be witnessed in various domains, from sports like synchronized swimming and diving, to musical performances such as violinists in an orchestra playing perfectly in unison. Huygens was the first to observe synchronization between two coupled pendulums44. Since then, and particularly in the last century, researchers have delved into studying the computational capabilities of dynamical systems. Somehow, we are still unraveling the mystery of why Huygens pendulums swung with precision. Perhaps this essence of synchronization holds the key to our present-day computing needs. Based on their genesis, we provide a detailed review of computing with oscillators which can be identified into four main scientific branches that led to the physical computing with oscillators that we have today.

The first scientific branch is statistical physics, starting in the 1920s with contributions from Lenz and Ising45. They introduced a mathematical model describing the dynamics of magnetic spins on a lattice, establishing the groundwork for understanding how local interactions between particles can lead to global phenomena, particularly in spin systems and phase transition in magnets. Each spin represents a binary state (i.e., +1 or − 1). In ONNs, the phase of each oscillator can be thought of as analogous to the spin in the Ising model. Oscillators tend to align their phases or synchronize depending on the coupling. In-phase synchronization can be seen as aligned spins. The other connection between oscillators and Ising model is on the interactions and energy landscape. The Ising model is a mathematical framework to describe phase transitions of interacting spins and can be understood in terms of an energy landscape, where energy depends in the configurations of spins. The system tends to evolve toward spin configurations that minimize energy. Similarly, coupled oscillators interact with each other and exhibit different phase transitions (in and out of phase) as a function of coupling strength. Such interactions can also be understood in terms of an energy-like function. ONNs evolve toward configurations where the interaction energy is minimized, leading to synchronized states. In both spin and oscillatory systems, the energy landscape determines the stable states. Progressing along this branch, Metropolis and Hastings devised methods for approximating complex probability distributions46,47. Further advancements emerged on probabilistic optimization algorithms, notably by Kirkpatrick and Ackley, who developed simulated annealing, a widely applied algorithm across various domains48,49,50.

The second branch is on neural networks that eventually entwines with statistical physics. It all begins with McCullow and Pitts laying the foundation of neural networks through the mathematical neuron model and its basic operating principles51. The very first neural network architecture was the perceptron by Rosenblatt and later by Minsky and Papert to create the first computation model inspired by the human brain neural structure52,53. Hopfield introduced recurrent neural networks that can store and retrieve information also known as Hopfield neural networks (HNNs)29. Through continuous dynamics, HNNs minimize their energy as the network updates its states, serving as an inspiration to Hoppensteadt and Izhikevich for later developments of oscillatory neural networks30,38,54.

The third branch is on neuron models that closely aligns with the progress between computational neuroscience and neural networks. Taking inspiration from biological neural networks, neuronal models have evolved to capture the excitatory and inhibitory behavior of neurons to mimick their action potential role. Several neuronal models have been developed over the years, such as van der Pol55, Hodgkin and Huxley56, and FitzHugh and Nagumo57,58. These models are biologically plausible and capture the nonlinear action potential neuron behavior. Synapses also play an important role in learning and memory in neural networks. Similarly, in physical computing, coupling elements between oscillators emulate the synaptic potentiation and depression, which are mechanisms that modulate synaptic strengths such as weakly or strongly coupled oscillators. The merging of two branches, namely neuron models and engineering computing with oscillators is brought by the seminal works of Hoppensteadt et al.30 and Izhikevich38 that established the foundation for physical computing with oscillators.

The fourth branch is on engineering of computing with oscillators, with the first efforts reported to implement them for computing Boolean functions dating back to the 1960s59,60. However, oscillatory-based logic could not compete with more scalable transistor-based logic and faded away within a decade. At about the same time, Kuramoto et al.61 developed the analytical formalism to analyze the dynamics of coupled oscillators. These four branches started to merge in the late 80s that led to the rebirth of the oscillatory-based physical computing. Figure 2 presents the evolution of the research field on oscillatory neural networks covering the progress on each of the four branches. Nowadays, the design of coupled oscillatory systems is driven by the development of novel oscillator circuits which promise higher scalability compared to the classical LC-based oscillators.

Fig. 2: Timeline of the ONN computing paradigm.
figure 2

The first oscillatory-based computers were invented by von Neumann and Goto in the 1950s in parallel with the development of the perceptron by Rosenblatt52. Labeled parametron, the oscillatory circuit was used as a majority gate to solve Boolean logic, and machines with up to 9600 parametrons were used in the early 1960s. Note that this approach has been recently reconsidered using recent oscillator designs72,73. Inspired by neural networks and statistical physics, ONNs emerged in the 1990s as an analog approach to minimize some conceptual energy via gradient descent. For instance, seminal work from Hoppensteadt and Izhikevich30 proposed to implement energy-based models like Hopfield’s29 in hardware using analog coupled oscillators that naturally converge to attractors, which is useful for pattern recognition. Currently, ONN design is driven by technological progress and is applied to machine learning, image processing, and combinatorial optimization.

Full size image

In recent years, researchers have started to investigate novel materials and devices to implement oscillators and coupling elements. There are ongoing efforts on phase transition and 2D transition metal-oxide devices (TMO)62,63, spintronic devices64, microelectromechanical systems (MEMS)65, optical systems66, or CMOS accelerators67,68,69 as potentially scalable solutions70,71 for applications like digital logic72,73, classification74,75,76, computing convolutions62,77, or solving associative tasks30,39,67,78,79 and combinatorial optimization problems (COP)63,80,81,82.

This paper presents an in-depth view on the computational principles of coupled oscillatory systems used in various applications from Machine Learning (ML) to COPs covering aspects from oscillator to ONN architecture design and technology implementation. More concretely, it is divided into five parts. Starting of with “Oscillatory neuron”, we introduce some of the various implementations of oscillatory neurons. Next, “ONN computing” presents the corresponding coupling elements and the resulting dynamics that can be tailored for specific applications. “ONN architectures and demonstrators” reports on the state-of-the-art ONN architectures and demonstrators implemented in various technologies as competitive solutions for the given applications, followed by some potential challenges in “Challenges”. Finally, we discuss the possible future research directions.

Oscillatory neuron

Sustained oscillations can manifest in a wide array of dynamical systems such as mechanical, optical, electrical, biological, or chemical processes61. Despite the diverse nature of these oscillations, they are typically mathematically described as dynamical systems

$$\frac{dx}{dt}=f(x)\in {{\mathbb{R}}}^{m}$$

having a limit cycle attractor83,84, i.e., an orbit \(\gamma \subset {{\mathbb{R}}}^{m}\) with period T such that

$$\gamma (t)=\gamma (t+T)$$

For instance, van der Pol derived renowned oscillatory dynamics that correspond to an electrical harmonic oscillator with nonlinear damping55. In addition, Hodgkin-Huxley’s neuron is recognized for generating oscillations when driven by a sufficient input current56.

When computing with ONNs, the system dynamics are often reduced to frequency and phase dynamics by considering weak coupling between oscillators and the oscillation amplitude is ignored30,83. However, intrinsic parameters such as waveform shape and response to perturbations impact the collective ONN performances and can be tuned for specific applications82,85,86, just like activation functions in neural networks.

Figure 3 shows various electrical oscillator implementations used in ONNs. One of the simplest, yet promising oscillators for ONN is the Ring Oscillator (RO) which consists of a closed loop of CMOS inverters in series. ROs benefit from advanced CMOS technologies and can be integrated at a very large scale with low energy consumption and high speed (1968 oscillators demonstrated @1 GHz87), although it is still unknown whether ROs provide any computational advantages over other types of oscillators.

Another interesting CMOS oscillator is the Schmitt-based relaxation oscillator where a Schmitt trigger alternately charges and discharges a load capacitor through a resistor. This oscillator is generally bulkier than RO but exhibits interesting properties when carefully tuned, such as phase binarization which is particularly useful for solving COPs86,88.

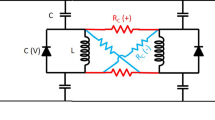
Fig. 3: Illustration of ONN computing paradigm and its circuit implementations.
figure 3

a Illustration of a frequency-based ONN. The input consists of frequency-dependent signals fed into the ONN. The latter can have oscillators locking to a common frequency and providing the computational result. Labels of locked and unlocked are shown next to the oscillators. b Schematic of a phase-based ONN. The oscillators have a uniform frequency and evolve in the phase domain, minimizing a kind of Hopfield energy. c Two coupled oscillators implemented with various technologies. Ring oscillators can be coupled by back-to-back inverters68 or using transmission gates87. Relaxation oscillators consist of a hysteresis device that charges/discharges a load capacitor, producing analog oscillations. The hysteresis component can be implemented by a Schmitt trigger86,201 or beyond-CMOS devices that have a negative differential resistance region in their I–V characteristic. A partial list of potential devices includes VO262,63,93,260, TaOx and TiOx oxide89, NbOx memristors90, PrMnO3 RRAM91, or ferroelectric transistors92.

Full size image

Moreover, beyond-CMOS devices holding hysteresis behavior such as transition metal oxide devices (TMO)62,63,89, volatile memristors90, RRAM91, and ferroelectric transistors92 are intensively studied to replace Schmitt triggers and implement more compact relaxation oscillators. A promising TMO is vanadium dioxide (VO2) which operates at room temperature and can transition from a semiconductor (insulating) to a metallic state by Joule effect93,94. When the VO2 device is biased in its negative differential resistance region, the circuit is unstable and produces sustained oscillations.

Spin-torque nano oscillators (STNO) are promising for ONNs as they operate at radio frequencies from 100 MHz to the GHz range and could be integrated at a very large scale with CMOS electronics64. An STNO consists of a magnetic tunnel junction biased by a DC current which induces a magnetization and consequently voltage oscillations across the device95. STNOs are very versatile as they react to various magnetic or electrical perturbations, enabling various types of couplings and ranges96. In addition, STNOs also possess memory in the oscillation amplitude which can be harnessed for processing time series in real-time75.

ONN computing

ONN computing is based on the synchronization of coupled oscillators, a phenomenon that naturally appears in biology, physics, or social interactions97 and was first conceptualized by Winfree in the 1960s98. To illustrate oscillator synchronization, consider a crowd of people applauding during an event. The reader probably experienced a situation where the initial state is quite chaotic but after a sufficient time, most of the participants end up applauding in synchrony. From a coupled oscillator network perspective, one can model each individual as an oscillator adjusting its frequency, i.e., increasing or reducing the clapping rate to get synchronized with the neighboring crowd99. Such a phenomenon can be captured using the following ODE which expresses the time derivative of oscillators’ phases (frequencies) ϕi generally under the presumption of weak coupling as30,83:

$$\frac{d{\phi }_{i}}{dt}={\omega }_{i}+\mathop{\sum }\limits_{j = 1}^{n}{K}_{ij}{H}_{ij}\left({\phi }_{j}-{\phi }_{i}\right)$$
(1)

with ωi being the oscillator’s free-running frequency, Kij the coupling matrix and Hij(χ) stands for the interaction between the oscillators and is neuron model dependent83. One of the most well-known models is the Kuramoto model (\({H}_{ij}(\chi )=\sin (\chi )\)), where the ODE in Eq. (1) reduces to61:

$$\frac{d{\phi }_{i}}{dt}={\omega }_{i}+\mathop{\sum }\limits_{j = 1}^{n}{K}_{ij}\sin\, ({\phi }_{j}-{\phi }_{i})$$
(2)

The sinusoidal interaction terms are responsible for the frequency adjustment and model the adaptation of individual i to other clapping agents j in our example. Despite its simple expression, the Kuramoto model produces very complex dynamics depending on the connectivity (Kij) and frequency distributions100. The model describes a large variety of rhythmic behaviors101, including ONN dynamics.

The collective dynamics of coupled oscillators such as those described in Eq. (2) can be harnessed in many different ways to perform different tasks. However, most ONN developments fall into two classes depending on the type of input/output encoding:

  • Frequency-based ONN: inputs are oscillator frequencies and outputs are the synchronization levels between oscillators.

  • Phase-based ONN: oscillators have the same frequency and input/output are encoded in-phase between oscillators.

In a frequency-based ONN (Fig. 3a), frequency-dependent input signals are injected into the ONN that reacts to the input perturbations. The computation outcome consists of groups of oscillators that lock in frequency, i.e., are synchronized. This computation scheme has been used for image processing77,78,102,103, associative memory tasks79,104, or spoken vowel classification76,105. In the latter application, input vowels are reduced to two frequencies fA and fB called “formants" injected into a 4-node ONN that assigns each input sample to a vowel by reading the synchronization state of the oscillators with inputs fA and fB. Interestingly, computing in the frequency domain can also skip the physical connections between oscillators. For that purpose, Hoppenstead and Izhikevich proposed an Oscillatory Neurocomputer106 where a time-dependent injected signal emulates all-to-all connectivity by modulating the oscillator phases, and the output consists of the averaged phases after ONN convergence. Despite the advantageous physical scaling of the proposed ONN, generating the modulation signal which includes all pairwise oscillator interactions is not straightforward107,108.

In the special case where oscillator frequencies are identical and coupling elements are symmetric (Kij = Kji), Hoppensteadt and Izhikevich30 have shown that the ONN is a gradient system that minimizes an energy function through time as:

$$\left\{\begin{array}{l}\frac{d{\phi }_{i}}{dt}=-\frac{\partial E}{\partial {\phi }_{i}}\quad \\ E=-\frac{1}{2}\mathop{\sum }\limits_{i}\mathop{\sum }\limits_{j}{K}_{ij}\cos\, ({\phi }_{i}-{\phi }_{j})\quad \end{array}\right.$$
(3)

In this regime, the inputs and outputs are encoded in-phase between oscillators whose dynamics depend on the ONN energy and phase initialization. It turns out that the ONN energy is similar to Hopfield’s energy29 and to the Ising Hamiltonian82, enabling a broad range of applications from machine learning and image processing to combinatorial optimization17.

The memory of a system described in Eq. (1) is defined as its number of stable phase states39 and is neuron model dependent. One can derive the memory of a system based on a specific neuron model by finding its phase transition function (PTF), which captures the final phase state transitions of a system composed of two oscillatory neurons given an initial phase delay and a coupling weight. More specifically, for a set of coupling weights (generally ∈ [−1, 1]) and an oscillator with initial delay of \(\Delta {\phi }_{init}\in [0,\frac{T}{2}]\), one can solve Eq. (1) and obtain the final phase differences between oscillators Δϕfinal. The weights represent the coupling strengths between oscillators. Similarly, as in Hopfield neural networks, the weights are generally in range [−1, +1] to ensure weak coupling and due to the binary nature of neuron states and calculated via the Hebbian learning rule. Weights calculated via the Hebbian learning rule generally are within [−1, +1] and shape the energy landscape to stable states corresponding to stored patterns29. In Fig. 4, we plot the phase state transitions of two coupled oscillators, representing the memory of the simplest ONN architecture. We show that depending on the coupling strength between two oscillators and initial phase delay (up to 50% of period) in one of the oscillators, the phase state transition can be obtained. The phase state transitions also represent the stored memory states of the system. Figure 4 shows the corresponding phase transition function (PTF) for the Kuramoto model simulated in software.

Fig. 4: Phase transition function of the Kuramoto model as a function of coupling strengths between two oscillators and initial delay.
figure 4

The coupling strengths represent the weights.

Full size image

Clearly, the Kuramoto model has two stable phase states (0° and 180°), i.e., it has a bistate memory. The search is still on for neuron models with a larger memory. In order to obtain the PTF at hand in hardware, one would need to know the corresponding coupling resistances. Authors in ref. 39 have developed a formalism to map weights computed by the Hebbian learning rule (software) to coupling resistances (hardware).

It is important to note that not all coupled oscillator networks can be fully understood or modeled by the described Kuramoto formalism. While the Kuramoto formalism is a very powerful, it also has its limitations, and it is applicable to only specific types of networks. Kuramoto formalism works particularly well for all-to-all and weakly coupled sinusoidal oscillators with information encoded in-phase while amplitude remains constant. Such formalism does not work well for networks with more complex topologies (i.e., sparce, hierarchical), oscillators with varying amplitude (i.e., both amplitude and phase), non-phase oscillators (i.e., chemical and biological), non-sinusoidal oscillators, time-dependent delay interactions (i.e., nonlinear coupling) and high-dimensional interactions between oscillators. For example, memory states of the coupled oscillators are influenced by the time delay in the coupling between oscillators. Delay-coupled Kuramoto oscillators extend the classic Kuramoto model by introducing time-delay interactions. This time delay introduces a greater complexity in the system and also leading to a richer variety of synchronized states and behaviors.

ONN architectures and demonstrators

From the theory of computing with coupled oscillators, researchers investigated how to build ONN demonstrators for meaningful applications, starting with Wang and Terman in 1994109 who introduced the LEGION ONN array for image segmentation, just before Hoppensteadt and Izhikevich30,54 linked the theory of coupled oscillators to energy-based Hopfield Neural Networks29 for associative memory applications. Another promising area proposes to build oscillatory Ising machines (OIM)88 to solve combinatorial optimization problems (COPs). Finally, research has recently focused on ONNs as ML accelerators such as for convolutional neural networks (CNN), or providing nonlinearity in reservoir computing. Figure 5 summarizes the three classes of problems ONN can solve.

Fig. 5: Example of problems ONN can solve.
figure 5

a Similar to HNNs, ONNs have been extensively studied for pattern recognition30,67,114,115,116. b ONN synchronization can be harnessed in various ways to solve image processing problems such as segmentation103,109,132 or edge detection71,90,92,123. c ONN phase ordering can also encode variable permutation and is useful to solve hard combinatorial optimization problems such as graph coloring81,260,261,262 or TSP163,164,165. Focusing on binary phases, one can encode COPs to ONNs and solve graph partitioning63,69,82,86 or Boolean Satisfiability problems167,168,169.

Full size image

Fully coupled oscillators for associative memory

Hopfield’s work29,110 propelled novel energy-based models of neural networks using analog phase dynamics such as phasor neural networks111 and ONNs54,80. These typically single-layered, fully connected architectures allow recurrent signal propagation with oscillating neurons capable of performing auto-associative memory tasks or pattern recognition. Although Hoppensteadt presented the first hardware solution to implement oscillatory Hopfield networks using phase-locked loops (PLLs)30, many challenges were still limiting the large-scale implementation of such networks. In 2011, the first implemented ONN with 8 analog van der Pol oscillators performing phase-based pattern recognition was reported107. Later, building fully connected ONNs with spin-torque oscillators was suggested to solve pattern recognition with frequency-based computing95.

However, oscillatory Hopfield networks raised more interest recently with novel hardware implementations. Jackson112 and Shi113 proposed to build large-scale oscillatory Hopfield networks using PLLs as neurons, and RRAM as synapses. Then, Jackson also showcased a mixed-signal PLL-free67 ONN with 100 fully connected recurrent neurons, and lately, a fully digital implementation on FPGA was proposed, allowing up to 120 fully connected neurons114. In addition, the development of novel compact and low-power devices for neuromorphic computing offered novel solutions for efficient phase-computing oscillatory Hopfield networks115,116,117.

Table 1 summarizes the various tasks, which can be solved using the auto-associative memory (AAM) capabilities of ONNs, comparing the coupled oscillators approaches to the most relevant algorithms based on artificial neural networks (ANNs). These problems include but are not limited to (multi-state) pattern recognition118,119,120, pattern classification121,122, edge detection123,124, on-chip learning125,126, and sensory processing127.

Table 1 Comparison of ANNs with ONNs for various problems
Full size table

Coupled oscillators array for image segmentation

Locally excitatory, globally inhibitory network (LEGION) was introduced in 1994 as a solution to perform image segmentation using an array topology of locally excitatory oscillators computing in-phase109,128,129,130 with an additional global inhibitory neuron. The first analog implementation was proposed in 1999131 and further improved with a neuromorphic analog image segmentation system in 2006132. Meanwhile, other works focused on adapted LEGION architectures with digital implementations133,134,135. Lately, LEGION motivated the development of phase-based and frequency-based ONNs for clustering and vision tasks102,136,137,138 using oscillators’ array topology.

Alternative architectures for AI edge applications

In the last decades, researchers also proposed alternative topologies to efficiently solve various AI tasks. For example, the star coupling topology was introduced to perform phase-based static or dynamic pattern recognition84,139. The star coupling was then derived in frequency-based computing to also perform image processing, like pattern recognition79, image segmentation103 and convolution operations77. Alternatively, convolution operations can also be solved using layered networks of oscillatory neurons62,140. The layered topology, often used in artificial neural networks shows interest to solve classification tasks using oscillatory neurons64,74,105,141,142. Dutta showcased another topology with ring architecture based on oscillatory neurons to emulate locomotion143. Finally, recently, the random and sparse topology of reservoir computing, whose neurons are typically created by time multiplexing144,145,146, combined with the high nonlinearity of coupled oscillators highlighted low-power and low-density properties to solve complex AI tasks75,147,148,149,150,151,152,153. For example, reservoir computing is also a type of complex dynamical system which transforms the input into high-dimensional representation. By time multiplexing the system can simulate the activity of multiple neurons over time allowing for reduction in hardware or computational resources. The common link between ONNs and reservoir computing is on the concepts of nonlinear and temporal dynamics for processing complex information. They are both nonlinear dynamical systems such as in ONNs, the collective dynamics and temporal sequences (past states) exhibits various nonlinear behaviors (phases) such as synchronization, multistability and chaos, whereas in reservoir computing, time multiplexing creates a sequence of states (temporal response) and helps to exploit nonlinearity to project input data into a high-dimensional space. Such systems are very attractive for processing and analyzing complex information and time-dependent data154,155. Tables 2 and 3 provide a list of notable ONN architectures and demonstrators along with their different specifications and application use cases.

Table 2 List of notable ONN architectures and demonstrators using different types of oscillator circuit, network size and coupling weights
Full size table
Table 3 Complementary list of notable ONN architectures and demonstrators (as in Table 2) with respect to weight precision, application and technology choice for implementation
Full size table

Coupled oscillator graph for combinatorial optimization

Being based on the Ising model, ONNs posses a major potential in regards to solving hard combinatorial problems, including but not limited to NP-hard problems17. Informally, a problem is NP-hard, if its runtime explodes as the problem size increases. Graph partitioning and route planning are just some of these problems156. The author in157 has shown the corresponding formulation of the Ising Hamiltonian for each NP-hard problem. Table 4 presents the (to the best of our knowledge) state-of-the-art exact and approximate algorithms for all 21 Karp’s problems. In addition, the last column of that table presents attempts at solving the corresponding problem using ONNs.

Up until now, there have been a few attempts at solving NP-hard problems using a network of coupled oscillators. Due to its simple mapping to hardware, the Max-Cut problem has arguably attracted the most attention158,159,160,161. In addition, thanks to its wide range of applicability, the traveling salesman problem has been in the spotlight as well, as the authors in refs. 162,163,164 have explored three unique ways to solve it. The last one has been applied by the authors in ref. 165. Further notable instances of applying ONNs to NP-hard problems include but are not limited to graph coloring81,158,166,167 and 3-SAT167,168,169.

Table 4 Best classical algorithms for Karp’s 21 NP-complete problems156 and attempts at solving them using ONNs
Full size table

Challenges

Training algorithms

So far, ONNs have been trained using both existing unsupervised and supervised learning rules. The most commonly applied unsupervised learning rules include Hebbian, Storkey, Diederich-Opper I and II170,171,172. In addition, equilibrium propagation (EP) presents a promising supervised alternative for energy-based models173. In particular, authors in refs. 121,174 apply it for classification tasks. Furthermore, in classification tasks of the MNIST dataset175 using the Diederich-Opper II learning rule, the best-reported results hover around 70% accuracy122. Still, this is far away from the accuracies typical for the state-of-the-art convolutional neural networks (CNNs)176,177,178. However, authors in179 have recently trained ONNs with EP to classify reduced 8x8-pixel MNIST images with 94.1% accuracy. Given its local update rule, EP constitutes a promising method for future ONN training in hardware.

While EP is a supervised alternative for energy-based systems, there are only few supervised ONN-specific learning rules. To the best of our knowledge, there have been two instances of learning rules designed for ONNs up until now. First, the authors in ref. 180 have proposed a Hebbian rule adapted to oscillators called oscillatory Hebbian rule (OHR). Furthermore, an iterative random partial update symmetric Hebbian (IRPUSH) rule has been developed by authors in ref. 181. Both proposed learning rules which expand on the classic Hebbian rule. However, there are other more powerful learning rules that have still not been redesigned for the ONNs. Hence, the development of training algorithms specific to ONNs will aid in exploring their potential advantages across various AI tasks.

Scalability

Scalability remains a significant concern in the physical design and implementation of ONNs for executing practical use cases. While each technology choice presents its own challenges, the primary limitation stems from the polynomial increase in coupling elements with the number of oscillators. As the size of the ONN network grows, implementing a fully connected network becomes challenging, primarily due to unwanted parasitics in the connections. For instance, advanced CMOS technology offers a viable platform for the design and implementation of large-scale ONNs. However, the current ONN architecture imposes certain symmetry constraints on the connectivity between oscillators to enable all-to-all coupling. Moreover, as the ONN network size increases, measuring and distinguishing the phase difference between oscillators become increasingly difficult. One potential approach being explored to scale up ONNs is to adopt a modular design, where a larger ONN is constructed from many smaller ONNs69,182.

Benchmarking and comparison

Presently, much of the literature benchmarks ONNs primarily on MNIST classification for pattern retrieval and combinatorial problems like TSP and Max-Cut121,122,163,164,183. Although some heuristics have been developed for solving combinatorial problems, such as the traveling salesman problem (TSP)157,163,164, and shared resources like the TSPLib library184 provide sample instances for benchmarking and comparison against the best-reported solutions. We firmly believe that the ONN community will find it relevant to consolidate and develop open-source benchmarks and libraries for evaluating different problems, enabling community contributions and sharing. As the community expands, setting up benchmarking contests on various problem sets will become increasingly important. These contests will aid in advancing the scientific development in ONN computing and in understanding where ONN computing can offer a competitive advantage in comparison to the classical computing.

Variety of problems that ONN can solve

Considering the ONN’s intrinsic feature as a dynamical system that exhibits rich dynamics from synchronization to non-stable states, studying a wider range of mathematical problems, that can exploit ONN dynamics, remains relevant. While intrinsically meant for pattern retrieval29,30, other problems can be investigated with ONNs such as:

  • Artificial intelligence and edge AI—various machine learning algorithms running on the edge, such as those used in human-machine interfaces, demand real-time decision-making, reinforcement learning, and incremental learning. Exploring and comprehending how ONNs can empower such algorithms, while capitalizing on their parallel processing and low-resource utilization71, could prove valuable for robotic applications and edge devices that operate with limited data for learning and decision-making.

  • Secure communication—it is observed that depending on the coupling, an oscillator can exhibit chaotic behavior185. This characteristic can be utilized in ONNs to implement random number generators and secure communication protocols186. Furthermore, ONN’s sensitivity to initial conditions and any perturbations can alter its stability, which can be intentionally exploited for secure communication.

  • Complex computation problems in engineering—ONN dynamics are described through differential equations that represent their behavior30. There is interest in further adapting these differential equations to model various physical phenomena such as fluid flow, atom interactions (like Hubbard model187), heat transfer, motion and quantum-mechanical systems (such as wave functions).

  • Complex networks—ONN’s dynamics can also be exploited for modeling large, complex networks, such as decision-making processes in economics and finance, as well as social networks. An analysis of ONN’s dynamics will allow to obtain statistical estimation and to perform data analysis to predict the behavior of time-varying data.

Perspectives

ONNs draw inspiration from oscillatory neural activity in biology and exhibit a strong connection with physics, enabling their application to various problems such as optimization45,157,158. However, there remains a significant potential for fruitful interactions between physics, machine learning, and ONNs, which could yield new insights and hardware solutions for implementing deep learning. For instance, employing the Ising formalism could enable massive parallel processing188. Ultimately, one can envision an ONN IP core coexisting alongside other accelerators and image sensors, facilitating accelerated, high-accuracy, and fast performance for specific machine learning algorithms on edge devices with limited power and computational resources. Here, we detail our vision on the perspectives of future research on computing with oscillators.

Synergy between ONN and neuroscience

The oscillatory neural dynamics observed in biological neural networks bear many similarities to ONN dynamics and offer valuable insights into learning and plasticity189. For instance, the synchronization of neural clusters and phase dynamics could provide insights into how oscillations propagate through large networks in distinct patterns, influencing memory creation and consolidation. Understanding how oscillatory propagation, such as spiral or in-plane dynamics, affects the stability of ONN networks and their memory states is crucial. Studies using electrophysiological recordings in insects and humans reveal that various conditions, including noise, non-uniformities (no two neurons are identical) and oscillation frequencies, impact short- and long-term memory formation and performance on cognitive tasks. Exploring whether insights from neuroscience can lead to new learning rules for ONNs remains a path worth investigating.

Synergy between ONN and physics

The synchronization phenomenon is extensively studied across various domains, with a substantial body of work in mathematics and physics delving into its fundamental nature97. The Kuramoto model stands out as one of the most studied models due to its simplicity and ability to exhibit rich dynamics in coupled complex networks61. From physics, the understandings of synchronization and the emergence of clusters in synchronization and chimera states can shed light not only on the stability of ONN networks but also on how factors such as noise, variability, nonidealities, and synaptic schemes (from fully to sparsely coupled) impact synchronization and cluster appearance, ultimately influencing the network’s memory and memory capacity189,190. There are numerous unexplored synergies stemming from the non-trivial physics of complex networks that could further enhance our understanding of ONN dynamics and their computing capabilities, benefiting from established rigorous mathematical formalisms.

Synergy between ONN and machine learning

Currently, classification, one of the most commonly used machine learning algorithms, is predominantly performed using convolutional neural networks (CNNs)176,177,178, which typically involve several layers and thousands to millions of neuron nodes. In addition, they are normally trained using backpropagation which makes these neural networks even more energy inefficient191. Thus far, classification using ONNs has been accomplished with a perceptron-type network and a limited number of neurons corresponding to the size of the image pixels121,183. Although the accuracy of ONNs is not yet sufficiently high for practical use (~70%)122, they demonstrate the simplicity and powerful computational capabilities of ONNs by performing classification with fewer neurons and a single fully connected layer. Recent studies have demonstrated the utility of ONNs by employing them as the first layer of CNNs, functioning as a filter layer for parallel feature extraction62,124. Furthermore, there is a potential to use ONNs for training of deep Boltzmann machines192,193. There should be additional synergies and opportunities for exploiting ONNs in machine learning that remain to be explored, and these will likely become apparent with further interdisciplinary research efforts.

Technology choice for ONN implementation

The physical implementation of ONNs remains challenging, despite numerous efforts to design them using advanced CMOS nodes, mature CMOS nodes, novel materials and devices, optically, spintronics, among others. Designing ONNs that are practical, useful, and capable of exploiting their phase dynamics necessitates a detailed analysis of the benefits and costs of each technology choice. While exploring multiple technology paths is constructive for further maturing ONN computing, envisioning ONNs as part of a larger system, where they can serve as either accelerator IP cores or be embedded in many ONN IP cores as massive parallel processors, is essential. To realize practical value from ONN computing, we believe that investing effort in CMOS-based ONN fabrication is worthy, enabling ONNs to be integrated into large system-on-chip designs. While exploring novel materials and devices represents a longer-term route to ONN implementation, valuable insights can be obtained from the silicon platform for ONN computing.

Conclusion

In this review, we explore research avenues that have shaped and marked the most promising frontiers in computing with oscillatory neural networks. Initially, considered for their associative memory as an intrinsic physical property of complex dynamical systems, the investigation of ONNs for computing has sparked significant interest in emulating quantum analogies using coupled oscillators. Recent years have witnessed the rapid growth of new techniques and fresh ideas for harnessing the rich nonlinear dynamics of ONNs.

From the perspective of diverse scientists across fields such as neuroscience, theoretical physics, computer scientists among others, there is a growing interest in solving practical, everyday intractable problems. This interest has been fueled, in part, by enthusiastic researchers like us in analog, digital and mixed-signal circuit design. They have taken a leap of faith, committing their efforts to expand the current body of knowledge within this research area to engineer such computational models. The goal is to implement complex theoretical concepts into hardware, addressing not only the energy efficiency challenge of computing but also providing alternative computing solutions for intractable problems such as NP-hard combinatorial optimization problems.

This review provides an overview of the current state of computing with ONNs. In addition, it highlights exciting methods and unresolved challenges. The use of coupled oscillators in computing holds promise as a platform to explore fundamental many-body physics, with practical implementations yet to be fully developed. What began as a curiosity-driven endeavor has evolved into an influential exploration of engineered dynamical computing systems that have the potential to unlock scientific discoveries that were previously out of reach.