Fast, slow, and metacognitive thinking in AI

Abstract

Inspired by the ”thinking fast and slow” cognitive theory of human decision making, we propose a multi-agent cognitive architecture (SOFAI) that is based on ”fast”/”slow” solvers and a metacognitive module. We then present experimental results on the behavior of an instance of this architecture for AI systems that make decisions about navigating in a constrained environment. We show that combining the two decision modalities through a separate metacognitive function allows for higher decision quality with less resource consumption compared to employing only one of the two modalities. Analyzing how the system achieves this, we also provide evidence for the emergence of several human-like behaviors, including skill learning, adaptability, and cognitive control.

Introduction

AI systems have seen great advancement in recent years in many applications that pervade our everyday life. While these successes can be accredited to improved algorithms and techniques, they are also usually tightly linked to the availability of vast datasets and computational power¹. Huge progress has been made with recent transformer-based architectures, leading to generative AI capabilities such as those manifested in large language models and image/video generation systems. However, it is generally acknowledged that AI still lacks many capabilities which would naturally be included in a notion of (human) intelligence, such as generalizability, adaptability, robustness, explainability, causal analysis, abstraction, common sense reasoning, metacognition, and ethical judgement^2,3.

To have these capabilities, humans employ a complex and seamless integration of learning and reasoning, supported by both implicit and explicit knowledge⁴. This integration is related to the so-called ”thinking fast and slow” theory of human decision making⁵, according to which both kinds of knowledge, and both intuitive/unconscious processes and deliberate ones, support creating an internal model of the world and making high-quality decisions based on it.

In this paper, we describe an AI multi-agent architecture that is inspired by this cognitive theory, with the aim of building AI systems that make high-quality decisions with limited resources through emerging behaviors that resemble some of the aforementioned human capabilities, including skill learning, cognitive control, and adaptability⁶.

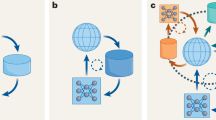
The proposed architecture, called SOFAI, for Slow and Fast AI, ingests incoming problem instances that are solved by either System 1 ("fast”) agents (also called “solvers”), that react by exploiting only past experience, or by System 2 ("slow”) agents, that are deliberately activated when there is the need to reason and/or search for solutions of higher quality beyond what is expected from the System 1 agents. Figure 1 shows a schematic description of the SOFAI architecture.

Fig. 1

The SOFAI architecture and the interplay between the various components, with a focus on Real Time metacognition.

System 1 (S1) solvers act solely by leveraging past experience (generated by them or by other solvers), thus they do not systematically reason about incoming problem instances. Just like human’s System 1, they rely on implicit knowledge (that is, training data in AI terms). On the other hand, System 2 (S2) solvers may exploit both implicit and explicit knowledge (that is, symbolic representations in AI terms) and employ multi-step systematic reasoning processes such as, for example, search, logical inference, sequential sampling, chain of thought, etc. S2 solvers typically engage in deeper reasoning that involves multiple steps, with their complexity often scaling with the size of the input problem. This explains why S2 solvers are generally computationally slower than S1 solvers, thereby motivating the use of the terms ‘fast’ and ‘slow’ to distinguish between them. However, before being able to make decisions, S1 solvers need to learn from available data, thus, they need additional offline time to do that. For example, an LLM or another ML solver has the characteristics of an S1 solver, while a symbolic planner or a search algorithm has the features of an S2 solver.

Given the need to arbitrate between these two kinds of solvers, SOFAI also includes a separate and centralized metacognitive agent. Metacognition is considered an essential component of human intelligence and refers to the ability to reflect upon one’s own thinking to efficiently use the available resources and improve decision making^7,8,9. SOFAI’s metacognitive agent assesses the quality of candidate solutions proposed by S1 solvers and then decides whether to invoke an S2 solver. In other words, the metacognitive agent does not choose between just using S1 solver and just using S2 solver, but between S1 solver and then S2 solver, or just S1 solver. Both phases are based on an analysis of resource availability, past experience with the solvers, and expected solution quality.

Besides this online arbitration function, the metacognitive agent also performs two other important offline functions: learning and reflection. Learning from past actions and their feedback is used to update the S1 solvers and the relevant models. Every time a new decision is made, all relevant information (the decision itself, its quality, its impact on the world, which solver made it, etc.) is stored in SOFAI’s models of Self, Others, and the World. Without this capability, SOFAI would be confined to its initial state, and its behavior would have no opportunity to evolve.

On the other hand, reflection employs counterfactual reasoning to simulate alternative modalities for past decisions and to possibly adjust internal parameters to promote a better behavior in the future. SOFAI utilizes S2 solvers to solve previously encountered problem instances (that may have been solved by S1 solvers or by a combination of S1 solver and S2 solver) and compares the decision quality of simulated and real past decisions: if an S2-only approach exhibits better performance, the parameters of the arbitration function will steer the metacognitive agent towards the engagement of S2 solvers. This function is necessary to allow SOFAI to adapt over time to the capabilities of the available S1 and S2 solvers.

Other approaches to the design of AI systems inspired by the dual-system theory have also been published in recent years^{10,11,12,13,14,15,16,17,18}. These approaches have attempted to integrate fast and slow thinking systems, but often done so by adopting the so-called Common Model of human cognition¹⁹, an approach in which System 1 and 2 are not clearly distinct but are components of procedural, declarative and working memory^20,21,22. In these models, the distinction between System 1 and System 2 is emergent, not explicit: fast and slow processes arise from how various cognitive components interact. For instance, ACT-R^23,24 can model fast heuristic behavior through instance-based learning and deliberative rule-based reasoning via its production system. A different model, CLARION²⁵ explicitly distinguishes implicit and explicit knowledge modules. In these cases, the dual-process distinction is embedded within rich, complex cognitive architectures, where the System 1/2 split is not always cleanly modularized but often distributed across interacting subsystems. Some approaches frame dual-process theory as a psychological interface shaping human trust in AI¹⁰, without proposing a concrete implementation; others instead provide a practical instantiation of dual-process (e.g., with reinforcement learning) but lack explicit arbitration¹¹.

Models like MRPC¹³ and EXIT¹⁵ exploit fast-reactive and slow-predictive components (e.g., reflexive vs. planning controllers or neural networks vs. tree search), their arbitration is either hard-coded or lacks adaptive self-monitoring.

In contrast, in SOFAI architecture, System 1 and System 2 are not traced back to the Common Model and are more neatly separated. Rather than distributing System 1 and System 2 across complex interacting subsystems, SOFAI implements a more explicit and modular separation between fast and slow reasoning processes providing a practical instantiation of dual-process control and introducing a learnable metacognitive mechanism that governs solver selection and adapts via reflection. This explicit, adaptive separation of reasoning modes distinguishes SOFAI as a functional architecture that both reflects and extends dual-process theory in computational agents.

To assess SOFAI’s behavior, we focus on an instance of the SOFAI architecture that is asked to generate trajectories in a grid with penalties over states, actions, and state features. SOFAI’s decisions are at the level of each move from one grid cell to another. Therefore, a trajectory made of several moves will involve several calls to SOFAI, each of which can use either an S1 solver or an S2 solver.

The experimental results compare SOFAI’s computational efficiency to that of approaches that solely use S1 or S2 solvers, showing that SOFAI is faster, with comparable or higher decision quality, meaning that it smartly uses the available solvers to minimize the resources (e.g., time) employed in the solution process.

We also examine how SOFAI can achieve this efficiency, exploring the emergence of human-like capabilities, with particular focus on three of them:

• Skill learning, the human ability to leverage experience to internalize some decision processes, that pass from System 2 to System 1. Typical examples of skills that go through this process in humans are driving or reading.

• Adaptability, the human ability to recognize one’s capabilities and limitations in order to use these capabilities optimally to make decisions. For example, visually impaired people learn to use other senses (e.g., touch) to complete tasks (e.g., reading).

• Cognitive control, the human ability to recognize when a scenario is high-risk or is subject to behavioral constraints, and to act accordingly and more carefully. For example, for humans completing a relatively simple math operation (e.g, sum of double-digit numbers) in a high-stakes context (e.g., math exam) usually requires engaging a slow solver.

Our experiments show that SOFAI performs well on all three capabilities. More precisely:

• Skill learning: Initially, SOFAI uses mostly S2 solvers, and later shifts to utilizing mostly S1 solvers when sufficient experience over moves and trajectories is collected.

• Adaptability: Given several versions of the S1 solvers, with different levels of competence, SOFAI tunes their use to make sure that solution quality is kept sufficiently high.

• Cognitive control: In a high-risk scenario, SOFAI employs solvers in a risk-averse fashion, and subsequently makes decisions that violate fewer constraints.

Results

In order to asses the performance of the system, we run different experiments. Results in Fig. 3, Tables 1 and 2 are from experiments run on a MacBook Pro (13-inch, 2017), CPU 3.5 GHz Intel Core i7, RAM 8 GB 2133 MHz LPDDR3, using Python 3.7. All experiments in the appendix were conducted on an Apple MacBook Pro equipped with an M3 chip and 16 GB of RAM, using Python version 3.11.5. In our experiments, we generated 10 scenarios at random, each of which corresponds to a grid. A scenario has 18 constrained cells chosen at random. Starting and goal states are distinct and they are chosen at random among the set of non-constrained cells. During the generation, we enforce they are at least 2 cells apart from each other in any direction. This is done to ensure that the minimum length of a trajectory is at least 2. Moreover, in each scenario used in experiments reported in this section, four actions are constrained at random.

Table 1 Average performance of S1 solver, S2 solver, and SOFAI over trajectors’ reward (that is, penalties accumulated over the moves), length, and time (in milliseconds) to generate it

Table 2 Average number of violated constraints and trajectory reward, and percentage of S2 solver use, for very low and very high risk aversion (ra = 0 and ra = 1)

Experimental setting: SOFAI for grid navigation

In this paper, we show an instance of SOFAI that aims to find a sequence of moves (that is, a trajectory) in a grid from an initial state to an unknown goal state. The grid has constraints over states and moves. When a move violates a constraint (either because there is a constraint upon the move itself or on the state where the move ends up), a penalty is imposed to the agent^26,27. For each state in the grid, there are up to eight possible moves (up, down, left, right, and the four diagonal moves, but some may not be available if the state is at the border of the grid). The grid environment is non-deterministic: a move to go to a state may actually takes us to another state, with probability 10%.

The SOFAI agents only know the current state in the grid but do not know the constraints or the position of the goal state. The aim is to generate trajectories that minimize length and computational time, and maximize the overall reward (intended as the sum of all penalties and rewards accumulated during the trajectory).

Figure 2 shows an example of a constrained grid used in our experiments. For the experiments described in this paper, we have chosen to use a penalty of −50 for each violated constraint, −4 for each move, and a reward of +10 when a trajectory reaches the goal state. We adopt an already established reward configuration from prior work, which has been shown to yield robust performance across similar tasks^28,29. The reward function design is intended to emphasize short trajectories with minimal constraint violations.

Fig. 2: Example of the constrained grid decision scenario (left part of the figure).

Black squares represent states with penalties. Penalties are also generated when the agent moves top left, bottom left, right, and bottom right (see black squares in top right grid), and when it moves to a blue or a green state (see black squares in bottom right of the figure). The red lines describe a set of trajectories generated by the agent (all with the same start point S₀ and end point S_G). The strength of the red color for each move corresponds to the number of trajectories employing such a move.

For the S1 solver, we have chosen a simple reinforcement learning agent that, at every step, chooses the move with the maximum expected reward of the trajectories starting with that move. To calculate this, the S1 solver uses the Model of Self, which includes all previous moves and their rewards. If we are in an unexplored grid state, the S1 solver chooses a move from the available ones with a uniform distribution. We developed five versions of the S1 solver, parametrized by the level of randomness of the solver’s decisions. Each version chooses a random move with probability pRand and a move that maximizes the expected reward with a probability of 1 − pRand. Thus, pRand = 1 yields a completely random S1 solver, while pRand = 0 leads to a deterministic S1 solver.

For our S2 solver, we have chosen a reasoning engine based on the so-called Multi-attribute Decision Field Theory (MDFT) model^28,30, that provides a multi-step sequential sampling method to make decisions starting from a set of possible options, their attributes, and preferences over such attributes. In MDFT, deliberation is modeled as a sequential accumulation of preferences for the available options, with attention shifting dynamically across their attributes.

For the grid environment, the options are the available moves (up to 8 in each state). For each move in each state, we consider two attributes, which represent an estimate of the quality of the move in the constrained grid and in the same grid without constraints. The preferences coincide with these estimates, that we generate by leveraging reinforcement learning machinery. In particular, they are the Q-values returned by running the Q-learning algorithm on the constrained and unconstrained grids.

The reason why we consider also a hypothetical grid without constraints is to model the best environment in terms of the trajectory’s reward and length. The preferences between the moves’ attributes model the expected quality of the moves in the two grids: in the constrained grid, the aim is to satisfy the constraints (and therefore possibly generate longer trajectories), while in the hypothetical unconstrained grid, the aim is to reach the goal without considering the constraints (and therefore possibly generating shorter trajectories that may, however, violate some constraints). MDFT allows us to achieve a compromise between these two aims, that is, to maximize constraint satisfaction (and thus maximum reward) and minimize length.

Finally, the metacognition (MC) module in SOFAI is an agent that determines which solver will make the next move (real-time MC), compares past trajectories with S2-only simulated ones to possibly update its real-time behavior (reflective MC), and stores each newly executed move in the model of Self (learning MC).

Details about the S1 solver, the MDFT model, and the way it is used to build the S2 solver, as well as the behavior of the metacognitive module, can be found in the Methods section.

Experimental results

Here we show the results from our experiment with the described instance of SOFAI.

SOFAI outperforms S1 solver or S2 solver alone

SOFAI generates trajectories in the grid, so the quality criteria that we have chosen are related to properties of a trajectory: its length, its reward (measured as the penalty accumulated from violated constraints), and the time required to generate it. In Table 1, we compare SOFAI to both S2 solver and to each of the different types of S1 solver with five values of randomness (pRand), namely {0, 0.25, 0.5, 0.75, 1.0}, over 500 generated trajectories in 10 grids. It is possible to see that SOFAI outperforms or otherwise performs comparably to the S2 solver on all criteria. Moreover, it does better than all instances of the S1 solver except for trajectory time, for which, as expected, the S1 solver is always faster. Therefore, SOFAI performs better than using the S2 solver or the S1 solver alone, in almost all of the considered criteria. It can be noticed that the S1 solver alone utilizes significantly more time at pRand = 0 than at other values. The increased time consumption at pRand = 0 is primarily due to the nature of the operations performed by S1. At higher values of pRand, the S1 solver frequently selects random actions (a lightweight operation that typically takes only a few milliseconds). In contrast, when computing the best action, the S1 solver needs to compute the max expected reward, which is more time-consuming. At pRand = 0, these max expected reward computations are executed at every step. Additionally, since trajectories tend to be longer on average at pRand = 0, the cumulative time required increases substantially compared to settings where random actions introduce more variability and avoid getting stuck in dead ends.

SOFAI adjusts to the capabilities of the S1 solver

As mentioned above, we built five different types of S1 solvers with five values of randomness (pRand), namely 0, 0.25, 0.5, 0.75, and 1.0. If pRand = 1, the S1 solver chooses its moves completely randomly, whereas if pRand = 0 it is deterministic and chooses the move with the best expected reward. This was done to evaluate whether the metacognition module could adapt to the varying quality of moves provided by each version of the S1 solver while maintaining a high standard in the final decision. What we see in Table 1 is that SOFAI—through its metacognitive module—is able to produce high quality trajectories (where quality is measured by time, reward, and length) independently of the version of S1 solver provided. As expected, the S1 solver is the fastest solver, but the quality of its trajectories can be quite poor. On the other hand, even when the S1 solver is completely random (pRand = 1), SOFAI is able to compensate for the sub-optimal moves coming from the S1 solver and produces decisions that improve on the time of the S2 solver while performing only slightly worse in terms of length and reward.

This indicates that SOFAI can adapt to the characteristics of the S1 solver we plug in, and use it less or more depending on its capabilities, in order to keep making decisions of high quality in a short time.

Skill learning in SOFAI

In Fig. 3, the x-axis shows the number of trajectories already generated, while the y-axis shows the percentage of usage of S1 (orange line) or S2 (blue line) solvers in making the individual moves in each trajectory. The five parts of the figure show the behavior of SOFAI with the five different versions of the S1 solver, from a completely random S1 solver (pRand = 1) in the far left to an S1 solver with no randomness at the far right (pRand = 0). When the S1 solver is completely random (leftmost figure), SOFAI keeps using mostly the S2 solver, and even increases its employment after about 250 trajectories. When the S1 solver includes some informed decisions (shown in the other four parts of the figure), its use increases over time and even goes above the percentage of use of the S2 solver when the randomness of the S1 solver is below 0.5. The transition time (measured by the number of generated trajectories) from predominantly using the S2 solver to mostly using the S1 solver decreases as the S1 solver becomes less randomized, reaching nearly zero when the randomness level is pRand = 0.25.

Fig. 3: Average percentage of use of the S1 and S2 solvers in SOFAI over 10 different grids, with 5 versions of the S1 solver with different levels of randomness (pRand).

The x-axis shows 500 trajectories, generated over time. When the S1 solver has access to some informed decisions, its use (invocation) increases over time and even goes above the percentage of use (invocation) of the S2 solver (when the randomness of the S1 solver parameter choice—pRand—is below 0.5).

In Fig. 3, it can be noticed that the trend of graphs gets broken at pRand = 0.0, while with values of pRand > 0, SOFAI appears to use s1 more times. This observed deviation can be attributed to the deterministic behavior of the S1 solver at lower values of pRand. Specifically, when pRand = 0.0, the S1 solver always selects the best action, eliminating any stochasticity or exploration. This rigidity can cause the S1 solver to become trapped in behavioral loops, limiting its adaptability. In such cases, SOFAI’s reflection mechanism identifies these limitations and compensates by increasing reliance on the S2 solver. This reflection encourages the use of the S2 solver when errors in the S1 solver are detected. As a result, the system activates the S1 solver less frequently at pRand = 0.0 than at slightly higher values, where some degree of exploration still allows the S1 solver to avoid repetitive failure modes.

When the S1 solver has no randomness at all (rightmost graph), the transition occurs after about 150 trajectories, with the reflecting MC impacting on the results through the reflection phases.

Cognitive control in SOFAI

Cognitive control is the psychological process that enables the employment of cognitive processes to produce more accurate results while suppressing automatic, but less reliable, responses.

In SOFAI, we introduce a risk aversion parameter (ra) to indicate the critical importance of accurately solving the problem at hand. Humans can often cognitively control their behavior to be more careful when a problem is more critical. In Table 2 we evaluate the cognitive control capabilities of SOFAI by comparing the number of violated constraints and reward of two versions of SOFAI, with risk aversion 1 and 0, respectively. It is easy to see that a high risk aversion leads SOFAI to a minimal constraint violation, while a low risk aversion generates a high level of constraint violation. This brings the MC module to choose the solver that produces fewer violations and is likely to produce more accurate results. In fact, with ra = 1 SOFAI adopts the S2 solver more frequently than with ra = 0.

Ablation analysis

The tolerance parameter (see line 2 of the MC real-time algorithm) plays a key role in balancing performance and computational efficiency by controlling when the more resource-intensive S2 solver is invoked. Specifically, the S2 solver is used only when the reward accumulated so far is non-negligibly lower than the average reward observed in the same state, thus avoiding unnecessary computational overhead. In resource-rich scenarios or when stricter performance guarantees are desired, the tolerance can be reduced—or even removed—to make the system more aggressive in consulting the S2 solver. In order to assess the contribution of this parameter, we performed an ablation study varying the value of the tolerance. As expected, lower tolerance values reduce the frequency of S2 solver activation, leading to faster computation but degraded trajectory quality. In contrast, higher tolerance values increase S2 solver usage and yield improved outcomes in terms of reward, trajectory length, and constraint violations, although at a higher computational cost. Additionally, the results demonstrate that the reflection phase consistently enhances performance across all metrics and tolerance settings, confirming its effectiveness in improving the agent’s decision-making capabilities. All the results are reported in the appendix.

Discussion

Our primary hypothesis was that SOFAI could outperform both the S1 and S2 solvers individually. This hypothesis is confirmed by the experimental results observed in the grid navigation instance while utilizing the SOFAI architecture. This indicates that integrating S1 and S2 solvers through SOFAI’s centralized metacognition module can enhance decision-making. As Table 1 indicates, on average, SOFAI leads to better performance than the S2 solver alone on all counts, and better than the S1 solver alone on two out of three key metrics. This is due to the ability of the real-time MC module to orchestrate between different solvers and decide on the best one to adopt, given the goals of saving time, avoiding constraint violations, and maximizing reward.

The experimental results also show emerging behaviors that can be observed in animal and especially human thinking: adaptability, skill learning, and cognitive control.

Indeed, human beings have the ability to leverage cognitive resources to best deal with incoming tasks. In our experiments, SOFAI shows itself to be able to do just that: when offered parterre of S1 and S2 solvers, SOFAI dynamically adapts its decision-making process to leverage the strengths of the available solvers, ensuring the best goal-driven outcomes. Once again, the metacognitive module is primarily responsible for this behavior. The capabilities of the metacognition module allow SOFAI to decide how to behave with different solvers of the same kind, such as the five different versions of the S1 solver with different degrees of randomness (see Table 1). This shows that SOFAI is able to adapt in dealing with the available solvers/resources.

Humans have the ability to learn new skills and internalize them to the point of using them almost unconsciously (a la S1 solver style). Skill learning is a fundamental aspect of psychology and refers to the process of acquiring, developing, and mastering specific abilities. In the cognitive psychology literature, there are currently various cognitive theories about how skill learning happens in humans (e.g.,³¹). Partly drawing from this literature, in SOFAI we define skill learning as the ability to go from a reasoning process such as the one typical of S2 solvers to the experience-based type of problem solving typical of S1 solvers. In our experiments, our goal was to examine whether SOFAI could learn new skills in an adaptive way. Indeed, depending on the task at hand and the types of S1 solvers at its disposal, SOFAI can transfer knowledge from the S2 solver’s decisions to the S1 solver by gradually adopting the faster S1 solver to solve the tasks that only the S2 solver was initially able to solve successfully. Figure 3 indicates that SOFAI is able to transition over time to using the S1 solver more than the S2 solver, a behavior that mirrors human skill learning.

Following the approach that sees intelligent thinking as showing flexibility and adaptability in the production of goal-oriented behavior, we believe that SOFAI displays traits of intelligence at least in the ways it is able to leverage its own resources in an effective and adaptable way. These encouraging results suggest that, as it happens for humans, leveraging different thinking modalities (endowed with different ”values” and characteristics) can produce efficient, adaptable, and resource-aware AI architectures.

Methods

Thinking fast and slow in humans

Human intelligence has been studied by focusing on at least two levels: the field of cognitive science focuses on the mind while the field of neuroscience focuses on the brain. Both approaches have been adopted in artificial intelligence (AI) research over the years and led to many cognitive architectures with interesting emerging behavior, see for example⁴. In this study, we propose an approach inspired from knowledge of the human mind, and we therefore focus on what cognitive theories tell us about how a human mind reasons and makes decisions. In particular, we focus on the ”thinking fast and slow theory”, defined by D. Kahneman in his book “Thinking, Fast and Slow”⁵. In choosing to leverage this cognitive theory, we are inspired by its versatility and adaptability, as well as the fact that AI techniques can be broadly categorized into two main classes: data-driven approaches, which align with “thinking fast,” and knowledge-based approaches, which can be considered as a form of “thinking slow”.

According to Kahneman’s theory, human decisions are supported and guided by the cooperation of two kinds of capabilities, that for the sake of simplicity are called systems: System 1 or “thinking fast,” provides tools for intuitive, imprecise, fast, and often unconscious decisions, while System 2 or “thinking slow”, handles more complex situations where logical and rational thinking is needed to reach a complex decision (depicted in Fig. 4). System 1 is guided mainly by intuition rather than deliberation. It gives fast answers to simple questions. Such answers are sometimes wrong, mainly because of unconscious bias or because they rely on heuristics or other shortcuts, and usually do not come with explanations³². However, System 1 is able to build models of the world that, although inaccurate and imprecise, can fill knowledge gaps through experience, allowing us to respond reasonably well to the many stimuli of our everyday life.

Fig. 4

A graphical representation of System 1 and System 2 characteristics.

When the problem is too complex for System 1, System 2 kicks in and solves the task at hand with access to additional computational resources, full attention, and sophisticated logical reasoning. A typical example of a problem handled by System 2 is a complex arithmetic calculation or a multi-criteria optimization problem. In order to engage System 2, humans need to be able to recognize that a problem goes beyond a threshold of cognitive difficulty and therefore identify the need to activate more systematic reasoning machinery^5,33. This recognition comes from another part of human cognition called ”meta-cognition”, which is the ability to think about our own thinking and assess our level of knowledge and skills for a specific task^34,35,36.

When a problem is recognized by metacognition as being new and/or difficult to solve, it is usually diverted to System 2³⁷. The procedures System 2 adopts become part of the experience that System 1 can later use with little effort. Thus, over time, some problems, initially solvable only by resorting to System 2 reasoning, can become manageable by System 1. This phenomenon is called ”skill learning”⁵. A typical example of skill learning is reading text in our own native language: we start by using only System 2 and then gradually we rely solely on System 1. However, this does not happen with all tasks. An example of a problem that never passes to System 1 is finding the correct solution to complex arithmetic questions. System 1 never acquires the skill to solve those. We call ”Real-Time MC” this form of metacognitive activity that allows us to choose the best decision modality (System 1 or System 2) to make a decision.

Psychologists, anthropologists, and cognitive scientists seem to agree that this cognitive flexibility generally allows us to adopt the most effective method to solve problems³⁵. Moreover, this cognitive architecture may provide us with a way to achieve value alignment: while System 1 may drive us to act instinctively, metacognition is able—often by leveraging the insights of System 2—to override this instinct and force us to act according to values and goals that are not yet embedded in our automatic reactions. Just think of the impulse of eating a large piece of cake: here our metacognition is (often) able to override System 1 to direct us to make a more rational decision, adopting System 2’s insight that eating too much sugar is not good for our health. Metacognition is also used to reflect upon past experiences³⁵. Such intervention can be done in a counterfactual mode, simulating what would have happened if we had acted in a different way, or in a learning mode, to use information about past decisions to improve future ones.

Thinking fast and slow in AI—the SOFAI architecture

SOFAI (for Slow and Fast AI) is a multi-agent AI architecture (see Fig. 1) that takes inspiration from the dual-process cognitive theory of human decision-making. The design choices for SOFAI are not intended to mimic what happens in the human brain at the neurological and physiological level, but rather to simulate the interaction of the two modalities in human decision-making. The goal is to build a general software architecture that can be instantiated to specific decision environments, that can perform better than each of the two modalities alone in terms of both decision quality and time to take the decision, and can also show some of the emergent behaviors we see in humans, such as skill learning.

SOFAI always includes agents that behave as “fast (S1) solvers”, that solve problems by relying solely on past experience, hence usually employ a data-driven approach. SOFAI may also have “slow (S2) solvers”, that solve problems by reasoning over them, hence usually employ a symbolic rule-based approach. In this architecture, S1 and S2 solvers are solving the same task, though they do it in different ways. The architecture also includes a metacognitive agent (MC) that has three distinct modalities: real-time, reflective, and learning metacognition.

All these agents are supported by models of the world (that is, the decision environment), models of possible other agents in the world, and a model of Self (that is, of the machine itself, including all past decisions, which agent made them, and their quality), all updated by the MC agent. Notice that we do not assume that S2 solvers are always better (on any performance criteria) than S1 solvers, or vice versa, analogously to the case in human reasoning³². Some tasks may be better handled by S1 solvers, especially once the system has acquired enough experience on those tasks, and others may be more effectively solved by S2 solvers. Also, different solvers may have different strengths and characteristics. For instance, some are more efficient, others are more accurate. It is the role of the MC module to decide which values to prioritize by setting the values of the parameters in its choice-matrix (Algorithm 1 below).

In the SOFAI architecture, we assume there is an essential asymmetry between S1 and S2 solvers: while S1 solvers are automatically triggered by incoming problem instances (analogously to human System 1, which is activated by default), S2 solvers are never engaged to work on a problem unless the metacognition explicitly calls them up. Incoming problem instances first trigger one or more S1 solvers. Once an S1 solver has solved the problem, the proposed solution and the associated confidence level are provided to the metacognitive agent. At this point, MC starts its operations.

Here is an explanation of how the MC module operates. If SOFAI is endowed with a S2 solver able to solve a task, real-time MC will choose between adopting the S1 solver’s solution or engaging an S2 solver. In this case, to make its decision, the MC agent assesses the current resource availability, the expected resource consumption of the S2 solver, the expected reward for a correct solution for each of the available solvers, as well as the solution and confidence evaluations coming from the S1 solver.

In order to not waste resources at the metacognitive level, the MC agent also includes two assessment phases (see Algorithm 1): the first one faster and more approximate, similar to a rapid, unconscious metacognition in humans^38,39, while the second one (to be used only if needed) is more careful and resource-costly, analogous to our conscious introspective process⁴⁰. As shown in Algorithm 1 below, both instances of MC are algorithmic in nature.

Besides the real-time activities, the MC module also operates between problem solving phases, through the reflective and the learning MC modules. Reflective MC simulates S2-only solutions for previously solved problem instances, comparing them to the actual solutions, and possibly modifying its internal parameters to make better real-time MC decisions in the future. Finally, learning MC updates the models and the S1 solvers based on the recently accumulated decision experience. While real-time MC decides which solver to use to solve a specific problem instance, reflective MC updates the real-time MC’s parameters through counterfactual reasoning, and learning MC updates solvers and models. The only part of the SOFAI architecture that is not necessarily updated over time is the S2 solvers, which do not rely on experience but rather reason about the given problem instance to find a solution.

Metacognition algorithms

Algorithm 1

MC Real-time

Input (Action a, Confidence c, State s, Partial Trajectory t)

1: trustS1 ← min(c, percNoViolation(S1))

2: if reward(t) < 0.95 ⋅ avgReward(s) or trustS1 ≤ ra then

3: $expCostS2\leftarrow \frac{expTimeS2}{remTime}$

4: if (expCostS2 > 1) then

5: return a

6: end if

7: if random > (1 − ϵ ⋅ (1 − ra)) then

8: With probability 0.5 a ← engageS2(s)

9: return a

10: end if

11: if (expRewS2(s, ra) − expRew(s, a, ra)) ≥ expCostS2 − reflection then

12: a ← engageS2(s)

13: end if

14: end if

15: return a

Algorithm 2

MC Reflection Phase

Input (Percentage p, Trajectories S)

1: end ← ∣S∣

2: start ← end$*$ (1 − p)

3: $newS\leftarrow {{\emptyset}}$

4: for all t_i ∈ S[start: end] do

5: newt_i ← allS2(t_i)

6: newS ← newS ∪ {newt_i}

7: end for

8: $scoreDiff=\mathop{\sum }_{i}^{| S| }(score(S[i])-score(newS[i]))$

9: $maxDiff=\mathop{\sum }_{i}^{| S| }| score(S[i])-score(newS[i])|$

10: $reflection=\frac{scoreDiff}{maxDiff}$

11: return reflection

We now illustrate in detail the operation of real-time metacognition (which arbitrates between S1 and S2 solvers) and of reflective metacognition.

Algorithm 1 shows the pseudo-code for real-time MC. Given an action a selected by the S1 solver, its confidence c, the current state of the grid s, and the partial trajectory already generated t, real-time MC decides whether to return the proposed action or to engage the S2 solver and return the action decided by this solver. To do that, first, in line 1, it computes the trust in the S1 solver (trustS1) as the minimum value between the solver’s confidence (c) and the percentage of moves done by the S1 solver in the past that did not violate any constraint (percNoViolation). In line 2, MC checks if it can simply return the move proposed by the S1 solver or it should consider engaging the S2 solver. This is done by checking two conditions: whether the reward accumulated by the current trajectory t is worse than the average reward up to the current state s (with a small tolerance, set to 0.95 in our experiments), and if the lever of trust in S1 solver is not higher than the risk aversion in the current decision environment. Risk aversion (ra) is a parameter within the SOFAI architecture that signifies the potential severity of decision outcomes, highlighting the importance of making accurate decisions to avoid negative consequences. If at least one of these two conditions is satisfied, MC considers the use of the S2 solver; otherwise, it just returns the S1 solver’s move (line 14). Lines 3-4-5-6 check if the system has enough time to run the S2 solver. SOFAI is assumed to start with a certain time allocation, which is consumed every time some operation is done (remTime). Line 3 computed the expected cost of the S2 solver (expCost(S2)) as the expected time to run it divided by the SOFAI remaining time. Line 4 checks if there is no time to execute the S2 solver. In this case, MC returns the S1 solver’s move. Line 7-8-9 choose between S1 and S2 solvers with a very small probability, which becomes smaller with the increase of the risk aversion level. This is done to ensure some exploration in choosing the solver to use. Line 10 is the core comparison of the pros and cons of returning the move a proposed by the S1 solver or engaging the S2 solver. On the one hand, at the left of the inequality, we have the difference between the expected reward of engaging the S2 solver in the current state and the action proposed by the S1 solver. Notice that the expected reward depends on the risk aversion, since a high value of this parameter is used to amplify the penalties of the violated constraints. If we expect the S2 solver to give a higher reward, on the other hand, we have to pay a price, which is the cost of running the S2 solver. So, it makes sense to choose the S2 solver only if this difference is higher than the expected cost. Note that the cost of running the S1 solver is not considered here, since the S1 solver has already computed a move. The variable reflection is used to convey the results of an MC reflection phase (see Algorithm 2): its value is positive when the trajectories generated during the MC reflection phase (that uses only the S2 solver) are better than those actually generated by the SOFAI system. If so, its impact in line 10 is to increase the probability that MC activates the S2 solver.

Algorithm 2 describes the steps of reflective MC, which considers a percentage (given by input parameter p) of the previously generated trajectories (in set S), identified in lines 1-2-3, recomputes them using only the S2 solver (lines 4-5-6-7), and compares the simulated S2-only trajectories with the actual trajectories generated by SOFAI. This is done in line 8 by computing the sum of the differences of the scores of each pair of trajectories (and the old one and the corresponding S2-only newly generated). The score of a trajectory is computed (not shown in the algorithm) by multiplying its reward (that is, a negative number derived by the accumulated penalties for the violated constraints) by its length. A higher score signifies a trajectory that violates fewer constraints or is shorter. Line 10 normalizes the score difference computed in line 8 by dividing it by the maximum score difference obtained by taking the sum of the absolute values (line 9) and generates the value for the ”reflection” variable, which is used in Algorithm 1.

S2 in SOFAI and MDFT

The instance of SOFAI we presented above for our experiments has only one S2 solver, which is based on the Multi-alternative Decision Field Theory (MDFT)³⁰. This theory models preferential choice as a multi-step sequential sampling process simulating a the decision maker engaging in an in depth deliberation process during which they attend to specific attributes to derive comparisons among options and update their preferences accordingly. Ultimately, the accumulation of those preferences informs the decision maker’s choice. More specifically, in MDFT, an agent is confronted with multiple options and equipped with an initial personal evaluation for them along different criteria, called attributes.

Given set of options O = {o₁, …, o_k} and set of attributes A = {A₁, …, A_J}, the subjective value of option o_i on attribute A_j is denoted by m_ij and stored in matrix M. In our grid setting, there is one M matrix for each cell of the grid, the options are the available moves, and the attributes are the estimated quality of each move with respect to maximizing constraint satisfaction and minimizing trajectory length.

Attention weights are used to express the attention allocated to each attribute at a particular time t during the deliberation. We denote them by vector W(t) where W_j(t) represents the attention to attribute j at time t. We adopt the common simplifying assumption that, at each point in time, the decision maker attends to only one attribute³⁰. Thus, W_j(t) ∈ {0, 1} and ∑_jW_j(t) = 1, ∀ t, j. In our setting, we have two attributes, so at any point in time t we will have W(t) = [1, 0], or W(t) = [0, 1], representing attention on constraint satisfaction or length minimization. The attention weights change across time according to a stationary stochastic process with probability distribution w, where w_j is the probability of attending to attribute A_j. In our setting, the attention weights model the preferences over the two attributes (maximizing constraint satisfaction and minimizing trajectory length). For example, defining w₁ = 0.55 and w₂ = 0.45 would mean that at each point in time, we will be attending to constraint satisfaction with probability 0.55 and to length minimization with probability 0.45.

In our setting, for each state reached by a trajectory, we define the weights for the MDFT instance corresponding to that state by computing the normalized difference between the length of the current trajectory and the average expected length for trajectories reaching that state. This is the first attention weight (the one referring to minimizing trajectory’s length), the other one being the complement to 1 of this weight.

Contrast matrix C is used to compute the advantage (or disadvantage) of an option with respect to the other options. In the MDFT literature^30,41,42, C is defined by contrasting the initial evaluation of one option against the average of the evaluations of the others. In our setting, we adopt this standard contrast matrix.

At any moment in time, each option is associated with a valence value. The valence for option o_i at time t, denoted v_i(t), represents its momentary advantage (or disadvantage) when compared with other options on some attribute under consideration. The valence vector for k options o₁, …, o_k at time t, denoted by column vector ${{\bf{V}}}(t)={[{v}_{1}(t),\ldots ,{v}_{k}(t)]}^{T}$, is formed by V(t) = C × M × W(t).

Preferences for each option are accumulated across the iterations of the deliberation process until a decision is made. This is done by using Feedback MatrixS, which defines how the accumulated preferences affect the preferences computed at the next iteration. This interaction depends on how similar the options are in terms of their initial evaluation expressed in M. Intuitively, the new preference of an option is affected positively and strongly by the preference it had accumulated so far, while it is inhibited by the preference of similar options. This lateral inhibition decreases as the dissimilarity between options increases.

At any moment in time, the preference of each option is calculated by P(t + 1) = S × P(t) + V(t + 1) where S × P(t) is the contribution of the past preferences and V(t + 1) is the valence computed at that iteration. Starting with P(0) = 0, preferences are then accumulated for either a fixed number of iterations (and the option with the highest preference is selected) or until the preference of an option reaches a given threshold. In our setting, we choose to use a threshold.

Ablation analysis

In Tables 3 and 4, we report all the results about the experiments. All experiments in the appendix were conducted on an Apple MacBook Pro equipped with an M3 chip and 16 GB of RAM, using Python version 3.11.5. For SOFAI, we varied the value of the tolerance reported as t2. In the table, “SOFAI REF” refers to agents that employed the reflection phase. It can be noticed that, as expected, smaller tolerance values lead to fewer S2 solver calls, resulting in lower average computation times but reduced performance in terms of trajectory length and accumulated reward. Conversely, increasing the tolerance results in more frequent use of the S2 solver, yielding better trajectories (i.e., higher rewards, shorter lengths, and fewer constraint violations) at the cost of greater computational effort. Moreover, our results show that the reflection phase itself significantly improves the overall performance of the system. When the reflection mechanism is adopted, we observe consistent improvements across all evaluation metrics, regardless of the tolerance setting. This confirms the utility of reflection in enhancing the agent’s decision-making capabilities.

Table 3 Ablation analysis, varying the value of the tolerance with 3 constrained actions

Table 4 Ablation analysis, varying the value of the tolerance with 4 constrained actions