Abstract
We report a newly discovered anomalous incident-angle of an elastically refracted P-wave, arising from a P-wave impinging on an interface between two VTI media with strong anisotropy. This anomalous incident-angle is found to be located in the post-critical incident-angle region corresponding to a refracted P-wave. Invoking Snell’s law for a refracted P-wave provides two distinctive solutions before and after the anomalous incident-angle. For an inhomogeneously refracted and elliptically polarized P-wave at the anomalous incident-angle, its rotational direction experiences an acute variation, from left-hand elliptical to right-hand elliptical polarization. The new findings provide us an enhanced understanding of acoustical-wave scattering and lead potentially to widespread and novel applications.
Similar content being viewed by others
Introduction
Concerning the interior of the Earth, it is a common understanding that the interior is composed of the regular sequences of isotropic thin layers of different properties. When the prevailing wavelength of a seismic wave is larger than the thickness of the individual layers, the sequences of thin layers behave anisotropically, whereas still transversely isotropic1,2,3,4. This macroscopically transversely isotropic medium with a vertical axis of symmetry is called a VTI medium5. In such a case, the mechanical property of a VTI medium can be described by the elastic stiffness tensor of a hexagonal crystal3,4,5,6,7. Based on these understandings, the influences of rock anisotropy on polarization, propagation and reflection/refraction of elastic waves have been studied and reported extensively7,8,9,10,11,12, e.g. the polarization direction of an elastic P-wave, which is different from propagation direction; the propagation velocity that is different from phase velocity; and the reflection/refraction coefficients, which vary with respect to the acoustic impendence and anisotropy of media.
The study on reflection of acoustic wave is very important to geophysics; for example, Nedimovic et al. analyzed the reflection signature of seismic and aseismic slip on the northern Cascadia subduction interface13 and Canales et al. discussed the seismic reflection images of a near-axis sill within the lower crust of the Juan de Fuca ridge14. Acoustic waves also bear many similarities to optical or electromagnetic waves in propagation, reflection, refraction and polarization. Grady et al. reported linear conversion and anomalous refraction for electromagnetic waves15. Genevet et al. studied the phenomena of anomalous reflection/refraction of light and its propagation with phase discontinuities16. Fa et al. predicted the existence of an anomalous incident-angle for an inhomogeneously refracted P-wave11.
In this paper, we show that there exists a physically significant anomalous incident-angle for the refracted P-wave. With this anomalous incident-angle, the incident-angle region can be classified into three sections: the pre-critical incident-angle region, the area between the critical incident-angle and the anomalous incident-angle and the post-anomalous incident-angle region. There are two distinctive phase velocity solutions before and after the anomalous incident-angle. For an inhomogeneously refracted elliptically-polarized P-wave, the anomalous incident-angle will cause an acute rotational-direction variation.
Results
Modeling
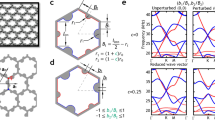
Considering a P-wave propagating in the x-z plane impinging on the interface (x-y plane) between two VTI media, the system can be described schematically as in Fig. 1.
Polarization vector and wave-front normal for incident P-wave and induced waves at the interface.
The solid-lines with arrowhead indicate the phase velocity direction and the dashed-lines with arrowhead show the polarization direction;  is a displacement and m = {0, 1, 2, 3, 4} denotes the incident P-wave, reflected P-wave, refracted P-wave, reflected SV-wave and refracted SV-wave, respectively.
is a displacement and m = {0, 1, 2, 3, 4} denotes the incident P-wave, reflected P-wave, refracted P-wave, reflected SV-wave and refracted SV-wave, respectively.
We performed calculations for two sedimentary rocks with some very well-known physical properties, as reported by geophysicists and given in Table 1 2,11,17. In this paper, we use anisotropic shale (A-shale) as the incidence medium and oil shale (O-shale) as the refraction medium. For this system, by calculation, we found that there is an anomalous incident-angle at  .
.
The elements of the elastic stiffness tensor, related to the anisotropic rock parameters, are given by Thomsen2,





For a harmonic acoustic-field, the wave displacements  can be written as
can be written as





In the equations above, θ(m) is either an incident-angle or a reflection/refraction angle and  and
and  are polarization coefficients; ϕ(m) is the phase shift for an induced wave relative to the incident P-wave and ϕ(0) is defined as 0°; R(m) is either the reflection or refraction coefficient for each induced wave and R(0) is defined as 1. For the refracted P-wave, the critical incident-angle is denoted by
are polarization coefficients; ϕ(m) is the phase shift for an induced wave relative to the incident P-wave and ϕ(0) is defined as 0°; R(m) is either the reflection or refraction coefficient for each induced wave and R(0) is defined as 1. For the refracted P-wave, the critical incident-angle is denoted by  and the anomalous incident-angle is given as
and the anomalous incident-angle is given as  .
.
For the incident-angle range of  , the reflection/refraction coefficients are real (not complex) and ϕ(m) is 0° or 180°. In the range of
, the reflection/refraction coefficients are real (not complex) and ϕ(m) is 0° or 180°. In the range of  , the reflection/refraction coefficients are complex and ϕ(m) ∈ (−180°, 180°).
, the reflection/refraction coefficients are complex and ϕ(m) ∈ (−180°, 180°).
Verification of an anomalous incident-angle
The core existence of an anomalous incident-angle for an elastically refracted P-wave can be confirmed from Snell’s law. Based on the Christoffel equation, the solutions of the phase velocity for the incident wave (P-wave or SV-wave) and the four induced waves are given by3,8

where 
 ,
, 

 ,
,  ,
,  ,
,  . Denoting the anomalous incident-angle as
. Denoting the anomalous incident-angle as  , the phase velocities of the refracted P-wave are
, the phase velocities of the refracted P-wave are  for
for  and
and  for
for  . They abide by Snell’s law such that
. They abide by Snell’s law such that  for
for  and
and  for
for  .
.
The reflection/refraction angles are calculated from the fourth-order polynomials of  11
11


where,  ,
,  ,
, 
 ,
,  ,
,  ,
,  ,
,  ,
,  and
and  . Eq. (13) can be used to calculate the refraction angles and determine the existence of the anomalous incident-angle, denoted by
. Eq. (13) can be used to calculate the refraction angles and determine the existence of the anomalous incident-angle, denoted by  .
.
As shown in Fig. 2a, the value of  is purely real for
is purely real for  ; whereas for
; whereas for  , it is purely imaginary, as shown in Fig. 2b. Figure 3a,b show that for θ(0) ∈ [0°, 90°],
, it is purely imaginary, as shown in Fig. 2b. Figure 3a,b show that for θ(0) ∈ [0°, 90°],  is real (not complex). In Fig. 3c,d, the value of
is real (not complex). In Fig. 3c,d, the value of  is real for
is real for  and purely imaginary for
and purely imaginary for  . For
. For  , both
, both  and
and  are purely imaginary. Figure 4b,c show that
are purely imaginary. Figure 4b,c show that  is equal to
is equal to  for
for  and
and  is equal to
is equal to  for
for  . The curve segment
. The curve segment  in Fig. 4b plus curve segment
in Fig. 4b plus curve segment  in Fig. 4c forms the curve in Fig. 4d, which is the same as that in Fig. 4a. Here, for
in Fig. 4c forms the curve in Fig. 4d, which is the same as that in Fig. 4a. Here, for  ,
,  is purely real and
is purely real and  is purely imaginary, so during the plotting of the relationship of
is purely imaginary, so during the plotting of the relationship of  versus θ(0), the computer takes the value of
versus θ(0), the computer takes the value of  as zero automatically.
as zero automatically.
These results show clearly that Snell’s law is satisfied only if the phase velocity solution of the refracted P-wave is switched to  from
from  at θ(0) = 62.04°. And therefore, there is an anomalous incident-angle of
at θ(0) = 62.04°. And therefore, there is an anomalous incident-angle of  . It resides in a region passing the critical incident angle
. It resides in a region passing the critical incident angle  , up to an incident angle 90°.
, up to an incident angle 90°.
Verification of elliptically-polarized rotational direction change
Verification of elliptically-polarized rotational direction change can be achieved by invoking the so called energy balance principle. The polarization coefficients for the incident wave and the four induced waves are given by11

and

where the definitions of  ,
,  and
and  refer to those of Eq. (S2) in “Supplementary material for Anomalous incident-angle and elliptical-polarization rotation of an elastically refracted P-wave”.
refer to those of Eq. (S2) in “Supplementary material for Anomalous incident-angle and elliptical-polarization rotation of an elastically refracted P-wave”.
From Eqs. (14) and (15) we can obtain the expressions of polarization coefficients for the incident P-wave and the homogenous waves induced at the interface,


For  the refracted P-wave is inhomogenous. Eqs. (14) and (15) provide two sets of solutions for the polarization coefficients (refer to Eqs. (S9) and (S10) in “Supplementary material for Anomalous incident-angle and elliptical-polarization rotation of an elastically refracted P-wave”).
the refracted P-wave is inhomogenous. Eqs. (14) and (15) provide two sets of solutions for the polarization coefficients (refer to Eqs. (S9) and (S10) in “Supplementary material for Anomalous incident-angle and elliptical-polarization rotation of an elastically refracted P-wave”).


and


An alternative confirmation of the anomalous incident-angle may be achieved by looking at the z-component of Poynting vector, which can be obtained from the reflection/refraction coefficients11. Specifically, we look at the normalized z-component,  , of the incident P-wave. We also look at the normalized real parts of z-components from the four induced waves:
, of the incident P-wave. We also look at the normalized real parts of z-components from the four induced waves:

Now, consider the polarization coefficients calculated from Eqs. (16) and (17) as those of the incident P-wave, reflected P-wave, reflected SV-wave and refracted SV-wave for θ(0) ∈ [0°, 90°] and the refracted P-wave for  . Meanwhile, Eqs.(18) and (19) provide the polarization coefficients of the refracted P-wave for
. Meanwhile, Eqs.(18) and (19) provide the polarization coefficients of the refracted P-wave for  . Then the normalized real parts of z-components of Poynting vectors are plotted dashed-lines in Fig. 5a,b. It shows clearly that, for
. Then the normalized real parts of z-components of Poynting vectors are plotted dashed-lines in Fig. 5a,b. It shows clearly that, for  , the real part of
, the real part of  is not identical to
is not identical to  . Therefore, it is a violation of the energy balance principle. However, for
. Therefore, it is a violation of the energy balance principle. However, for  , if we switch the calculation of polarization coefficients from Eqs. (18) and (19) to Eqs. (20) and (21), then the real part of
, if we switch the calculation of polarization coefficients from Eqs. (18) and (19) to Eqs. (20) and (21), then the real part of  is equal to
is equal to  , as shown by the solid-line in Fig. 5b, which abides the energy balance principle.
, as shown by the solid-line in Fig. 5b, which abides the energy balance principle.
For an inhomogenous refracted P-wave, the x-component of the polarization has a lag of 90° with respect to its z-component, which is defined as a left-rotational elliptical-polarized wave; otherwise, it is called a right-rotational elliptical-polarized wave. Figure 5 shows that a refracted P-wave is a linearly polarized wave for  , a left-rotational elliptical-polarized wave for
, a left-rotational elliptical-polarized wave for  and a right-rotational elliptical-polarized wave for
and a right-rotational elliptical-polarized wave for  . There is an elliptically-polarized rotational direction change at the anomalous incident-angle
. There is an elliptically-polarized rotational direction change at the anomalous incident-angle  .
.
Discussion
The current studies of the interface between two VTI media show that there is an anomalous incident-angle  with respect to the refracted P-wave in the area
with respect to the refracted P-wave in the area  . At such an incident-angle
. At such an incident-angle  , the phase velocity of the refracted P-wave must be switched from
, the phase velocity of the refracted P-wave must be switched from  to
to  to satisfy Snell’s law. The inhomogeneously refracted P-wave experiences a sudden change from a left-rotational to a right-rotational elliptical-polarization.
to satisfy Snell’s law. The inhomogeneously refracted P-wave experiences a sudden change from a left-rotational to a right-rotational elliptical-polarization.
It is worth noting that there is an anomalous incident-angle  for the refracted P-wave, but no such an anomalous incident-angle θ(4) for the refracted SV-wave. As an example, let’s look at the interface between S-shale and C-sandstone. In this case, there are two critical incident-angles, i.e.
for the refracted P-wave, but no such an anomalous incident-angle θ(4) for the refracted SV-wave. As an example, let’s look at the interface between S-shale and C-sandstone. In this case, there are two critical incident-angles, i.e.  and
and  . The phase velocity of P-waves in S-shale is smaller than those of P-waves and SV-waves in C-sandstone (see Fig. 6). There is an anomalous incident-angle corresponding to the refracted P-wave at
. The phase velocity of P-waves in S-shale is smaller than those of P-waves and SV-waves in C-sandstone (see Fig. 6). There is an anomalous incident-angle corresponding to the refracted P-wave at  . However, even with the second critical incident-angle
. However, even with the second critical incident-angle  and the refracted SV-wave becoming an inhomogeneous wave for
and the refracted SV-wave becoming an inhomogeneous wave for  , we have not observed the existence of an anomalous incident-angle
, we have not observed the existence of an anomalous incident-angle  corresponding to the refracted SV-wave.
corresponding to the refracted SV-wave.
Additional Information
How to cite this article: Fa, L. et al. Anomalous incident-angle and elliptical-polarization rotation of an elastically refracted P-wave. Sci. Rep. 5, 12700; doi: 10.1038/srep12700 (2015).
References
Backus, G. L. Long-wave elastic anisotropy produced by horizontal layering. J. Geophys. Res. 67, 4427–4440 (1962).
Thomsen, L. Weak elastic anisotropy. Geophysics 51, 1954–1966 (1986).
Carcione, J. M. Wave Fields in Real Media: Wave Propagation in Anisotropic, Anelastic and Porous Media (Elsevier Science Vol. 31, Pergamon, 2001).
Ĉervenŷ, V. Seismic Ray Theory (Cambridge University Press, Cambridge, U. K., 2001).
Rüger, A. Reflection Coefficients and Azimuthal AVO Analysis in Anisotropic Media (Society of Exploration Geophysicists, No. 10, USA, 2002).
Auld, B. A. Acoustic Fields and Waves in Solids (Wiley Vol. 1, New York, USA, 1972).
Rüger, A. P-wave reflection coefficients for transversely isotropic models with vertical and horizontal axis of symmetry. Geophysics 62, 713–722 (1997).
Daley, P. F. & Hron, F. Reflection and transmission coefficients for transversely isotropic media. Bull. Seismol. Soc. Amer. 67, 661–675 (1977).
Crampin, S., Stephen, R. A. & McGonigle, R. The polarization of P-waves in anisotropic media. Geophys. J. Roy. Astr. S. 68, 477–485 (1982).
Helbig, K. & Schoenberg, M. Anomalous polarization of elastic waves in transversely isotropic media. J. Acoust. Soc. Am. 81, 1235–1245 (1987).
Fa, L., Brown, R. L. & Castagna, J. P. Anomalous post-critical refraction behavior for certain transversely isotropic media. J. Acoust. Soc. Am. 120, 3479–3492 (2006).
Fa, L. et al. Polarization of plane wave propagating inside elastic hexagonal crystal solids. Sci. China: Phys. Mech. Astron. 57, 263–272 (2014).
Nedimovic, M. R., Hyndman, R. D., Ramachandran K. & Spence, G. D. Reflection signature of seismic and aseismic slip on the northern Cascadia subduction interface. Nature. 424, 416–420 (2003).
Canales, P., Nedimovic, M. R., Kent, G. M., Carbotte, S. M. & Detrick, R. S. Seismic reflection images of a near-axis sill within the lower crust at the Juan de Fuca ridge. Nature. 460, 89–93 (2009).
Grady, N. K. et al. Terahertz metamaterials for linear polarization conversion and anomalous refraction. Science. 340, 1304–1307 (2013).
Yu, N. et al. Light propagation with phase discontinuities: generalized laws of reflection and refraction. Science. 334, 333–337 (2011).
Wang, Z. Seismic anisotropy in sedimentary rocks, part 2: Laboratory data. Geophysics. 67, 1423–1440 (2002).
Acknowledgements
This work is supported by the National Natural Science Foundation of China (Grant No. 40974078) and by the Physical Sciences Division at The University of Chicago.
Author information
Authors and Affiliations
Contributions
L.F. and M.Z. initiated the project and contributed to the writing of the paper. Y.F. managed the project, Y.Z., P.D. and J.G. performed calculations, G.L. L.L. and S.T. checked calculated results. All authors co-wrote the paper.
Ethics declarations
Competing interests
The authors declare no competing financial interests.
Electronic supplementary material
Rights and permissions
This work is licensed under a Creative Commons Attribution 4.0 International License. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in the credit line; if the material is not included under the Creative Commons license, users will need to obtain permission from the license holder to reproduce the material. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/
About this article
Cite this article
Fa, L., Fa, Y., Zhang, Y. et al. Anomalous incident-angle and elliptical-polarization rotation of an elastically refracted P-wave. Sci Rep 5, 12700 (2015). https://doi.org/10.1038/srep12700
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/srep12700
This article is cited by
-
Reflection and refraction of elastic wave at VTI-TTI media interface
Frontiers of Physics (2020)
-
Acoustic Goos-Hänchen effect
Science China Physics, Mechanics & Astronomy (2017)
-
The influence of rock anisotropy on elliptical-polarization state of inhomogenously refracted P-wave
Science China Physics, Mechanics & Astronomy (2016)




 ,
,  is purely real. (b) For
is purely real. (b) For  , sin θ(2) is purely imaginary. There is an obvious abnormality provided at
, sin θ(2) is purely imaginary. There is an obvious abnormality provided at  .
.
 and
and  versus θ(0).
versus θ(0). is purely real for θ(0)
is purely real for θ(0)  is purely real for
is purely real for  and is purely imaginary for
and is purely imaginary for  . The modulus of
. The modulus of  has a maximum at θ(0) = 62.04°.
has a maximum at θ(0) = 62.04°.
 versus θ(0).
versus θ(0). stands for the phase velocity,
stands for the phase velocity,  , of the refracted P-wave for
, of the refracted P-wave for  and the phase velocity,
and the phase velocity,  , of the refracted P-wave for
, of the refracted P-wave for  .
.
 and
and  versus θ(0).
versus θ(0). stacks together with the solid-line segment
stacks together with the solid-line segment  for
for  .
.