Abstract
Controlling complex networks has become a forefront research area in network science and engineering. Recent efforts have led to theoretical frameworks of controllability to fully control a network through steering a minimum set of driver nodes. However, in realistic situations not every node is accessible or can be externally driven, raising the fundamental issue of control efficacy: if driving signals are applied to an arbitrary subset of nodes, how many other nodes can be controlled? We develop a framework to determine the control efficacy for undirected networks of arbitrary topology. Mathematically, based on non-singular transformation, we prove a theorem to determine rigorously the control efficacy of the network and to identify the nodes that can be controlled for any given driver nodes. Physically, we develop the picture of diffusion that views the control process as a signal diffused from input signals to the set of controllable nodes. The combination of mathematical theory and physical reasoning allows us not only to determine the control efficacy for model complex networks and a large number of empirical networks, but also to uncover phenomena in network control, e.g., hub nodes in general possess lower control centrality than an average node in undirected networks.
Similar content being viewed by others
Introduction
A frontier area of research in network science and engineering is controlling complex networks1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17. Nearly two decades of efforts have resulted in tremendous advances18,19,20,21,22,23 in our understanding of complex networked dynamical systems, beginning from the discoveries of the small-world24 and scale-free25 topologies in a large variety of natural, technological, and social systems. The efforts have created a knowledge foundation based on which the problem of control can be investigated. Ideally, to make controlling complex networked systems practically significant, one must consider nonlinear dynamical processes, due to the ubiquity of nonlinearity in the real world. However, to develop a general and mathematically rigorous control framework for complex networks hosting nonlinear dynamics is at present not achievable. A “stepping stone” is to consider linear dynamical processes on complex networks, an approach pioneered by Liu et al.4, who developed a framework based on Lin’s classic structural controllability theory (SCT)26. In particular, SCT answers the following question: given a complex, directed network, what is the minimal set of inputs (driver nodes) required to fully control the network in the sense that the entire network can be driven from an arbitrary initial state to an arbitrary final state in finite time? This was accomplished through a systematic methodology to find a minimum set of driver nodes to realize full control using the concept of maximum matching27,28,29. Subsequently, an exact controllability theory (ECT)10,14 was developed based on the concept of maximum multiplicity30 in linear algebra to identify the minimum set of driver nodes required to fully control the network. The ECT is applicable to a broader class of complex networks: weighted, directed or undirected, with or without any loop structure, etc. These efforts stimulated a great deal of interest in the linear controllability and observability framework of complex networks5,6,7,8,9,10,11,12,13,14,15,16,17,31,32,33, addressing problems such as linear edge dynamics5,6, energy cost of control8,16,17, the role of nodal dynamics in network controllability34,35.
In this paper, we address a fundamental and outstanding issue in controlling complex networks: control efficacy, the meaning of which can be understood and its significance can be appreciated, as follows. The SCT or ECT framework provides a solution of a minimum set of input signals to fully control any complex network. However, given an arbitrary external control signal, typically it is not possible to control the whole but only a part of the network. (The need to consider an arbitrary control signal lies in the fact that, for a network in the real world, the set of minimum input signals from the SCT or ECT framework may be physically or experimentally unrealizable.) In this regard, a related concept is control centrality36 derived from the SCT, which characterizes the ability of a single node to control a fraction of nodes in a directed network. Here we shall consider the more general situation where multiple input signals imposed on more than a single node are unable to control the entire network but but only a part of it, for broader classes of complex networks including weighted, undirected networks, with or without local loop structure. The main result is a control efficacy theorem and its proof, which provides a rigorous assessment of the role of an arbitrary set of nodes in partial control of the underlying network. In particular, for any given control inputs, our theorem gives the corresponding set of nodes in the network that are controllable. Our theorem of control efficacy can measure control centrality of a single node in terms of imposing a single external input signal on the node. The control centrality can be generally evaluated in arbitrary undirected networks with any distribution of link weights. We anticipate our finding to be practically significant for situations where the underlying network system is not fully accessible from the standpoint of delivering control signals. For example, for a social network, only a very limited set of nodes may be manipulated for control. For a neuronal network, only a small set of nodes can be perturbed externally. Our theory gives, in these realistic applications, a quantitative picture of what portion of the network may be controlled.
Results
Control efficacy of complex networks
Consider an undirected network of N nodes described by the following linear time invariant (LTI) dynamical system37,38,39:

where the vector x ≡ (x1, …, xN)T represents the state of all nodes at time t,  is an N × N coupling matrix of the network with the element aij representing the weight of a directed link from node j to node i (aij = aji for an undirected network), u(t) is the input signal of m controllers: u = (u1, …, um)T, and
is an N × N coupling matrix of the network with the element aij representing the weight of a directed link from node j to node i (aij = aji for an undirected network), u(t) is the input signal of m controllers: u = (u1, …, um)T, and  is the N × m control matrix with
is the N × m control matrix with  representing the strength of the input signal uj(t) on node i. According to the classical control theory40, the controllability of the system is determined completely and uniquely by the combined matrix
representing the strength of the input signal uj(t) on node i. According to the classical control theory40, the controllability of the system is determined completely and uniquely by the combined matrix  . For an initial state
. For an initial state  , if there exists a control input u(t) that can drive the system to the final state, say x(t1) = 0, within the finite time interval [t0, t1], we say that the state
, if there exists a control input u(t) that can drive the system to the final state, say x(t1) = 0, within the finite time interval [t0, t1], we say that the state  is a controllable state of the system and denote it as x+. The classic Kalman rank condition40 stipulates that the linear system Eq. (1) is controllable if and only if the N × Nm controllability matrix
is a controllable state of the system and denote it as x+. The classic Kalman rank condition40 stipulates that the linear system Eq. (1) is controllable if and only if the N × Nm controllability matrix  has full rank. When the system is not fully controllable or, equivalently, when the state space is not filled entirely with the controllable states x+, there can still be a controllable subspace spanned by the column vectors of the Kalman controllability matrix
has full rank. When the system is not fully controllable or, equivalently, when the state space is not filled entirely with the controllable states x+, there can still be a controllable subspace spanned by the column vectors of the Kalman controllability matrix  . The dimension of the controllable subspace is the rank of
. The dimension of the controllable subspace is the rank of  :
:  , which characterizes the control efficacy of the system.
, which characterizes the control efficacy of the system.
There are two difficulties in determining the rank of the controllability matrix: (1) the task is often computationally prohibitive for large networks, and (2) the controllability matrix is typically nearly singular due to the dramatic differences among its elements, making the numerical rank computation inaccurate or even divergent. We are thus led to develop a feasible and effective method to calculate the rank R. The starting point is a non-singular linear transformation. In particular, for an arbitrary matrix  in the system equation [Eq. (1)], there exists30 a non-singular matrix
in the system equation [Eq. (1)], there exists30 a non-singular matrix  such that
such that  or
or  with
with  , where λi(i = 1, …, l) are the distinct eigenvalues of
, where λi(i = 1, …, l) are the distinct eigenvalues of  and
and  is the Jordan block matrix of
is the Jordan block matrix of  associated with the eigenvalue λi. For an undirected network, the coupling matrix
associated with the eigenvalue λi. For an undirected network, the coupling matrix  is diagonalizable and the matrix
is diagonalizable and the matrix  reduces to the diagonal matrix with elements being all the eigenvalues41.
reduces to the diagonal matrix with elements being all the eigenvalues41.
Applying the non-singular transformations  and
and  , we can rewrite Eq. (1) in the following form:
, we can rewrite Eq. (1) in the following form:

where  is a diagonal matrix (see Method). The controllability matrix
is a diagonal matrix (see Method). The controllability matrix  for the transformed system is
for the transformed system is

We can verify that the systems Eqs (1) and (2) possess the same degree of controllability in the sense that  , i.e., the rank of the controllability matrix of the original system is equal to
, i.e., the rank of the controllability matrix of the original system is equal to  , which can be calculated reliably and accurately. For an arbitrary undirected network, we can prove that
, which can be calculated reliably and accurately. For an arbitrary undirected network, we can prove that  is determined by the corresponding element values in the transformed control input matrix
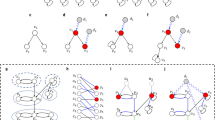
is determined by the corresponding element values in the transformed control input matrix  associated with the distinct eigenvalues (Method). A schematic illustration of our method to calculate the rank for undirected networks with self loops is presented in Fig. 1, and an explicit example is given in Supplementary Note 1. Our key analytic results are as follows.
associated with the distinct eigenvalues (Method). A schematic illustration of our method to calculate the rank for undirected networks with self loops is presented in Fig. 1, and an explicit example is given in Supplementary Note 1. Our key analytic results are as follows.
(a) The adjacency matrix  and the control input matrix
and the control input matrix  for a simple undirected network with self-loops. Each colored lattice point in
for a simple undirected network with self-loops. Each colored lattice point in  represents an element, where the colors from white to black correspond to element values from zero to one, respectively. A similar color scheme applies to the matrix
represents an element, where the colors from white to black correspond to element values from zero to one, respectively. A similar color scheme applies to the matrix  . (b) Through a nonsingular matrix transformation, the system
. (b) Through a nonsingular matrix transformation, the system  is converted into the equivalent system
is converted into the equivalent system  , where
, where  is a diagonal matrix. Distinct eigenvalues of
is a diagonal matrix. Distinct eigenvalues of  correspond to different subblocks marked with different colors. The rank of the controllability matrix for the transformed system
correspond to different subblocks marked with different colors. The rank of the controllability matrix for the transformed system  is equal to the sum of the rank values of the corresponding subblocks in the transformed control input matrix
is equal to the sum of the rank values of the corresponding subblocks in the transformed control input matrix  , which is identical to the rank of the controllability matrix of the original system
, which is identical to the rank of the controllability matrix of the original system  .
.
Single control input
When there is only a single controller (i.e., when the control input matrix  is a column vector), the task of calculating
is a column vector), the task of calculating  is reduced to counting the corresponding nonzero elements in the matrix
is reduced to counting the corresponding nonzero elements in the matrix  . Letting the element corresponding to the eigenvalue λi be
. Letting the element corresponding to the eigenvalue λi be  in
in  , we have
, we have

where

For each distinct, non-degenerate eigenvalue, the corresponding nonzero elements in  contribute equally to the value of
contribute equally to the value of  . For a degenerate eigenvalue, if there are no corresponding nonzero elements in
. For a degenerate eigenvalue, if there are no corresponding nonzero elements in  , the contribution of this eigenvalue to
, the contribution of this eigenvalue to  is zero. If the corresponding elements in
is zero. If the corresponding elements in  are nonzero, the degenerate eigenvalue contributes one to
are nonzero, the degenerate eigenvalue contributes one to  (see Method).
(see Method).
Multiple control inputs
When there are m control inputs, the matrix  has the dimension N × m. In this case, the control efficacy is determined by the sum of the rank values of the sub-block matrices composed of the corresponding rows in the transformed control input matrix
has the dimension N × m. In this case, the control efficacy is determined by the sum of the rank values of the sub-block matrices composed of the corresponding rows in the transformed control input matrix  for each distinct eigenvalue (see Method). We have
for each distinct eigenvalue (see Method). We have

Control Centrality
Given a complex network, it is often necessary to quantify the relative importance of the nodes with respect to a specific function. For this purpose, various kinds of centrality measures23 were proposed in the past, such as the degree centrality, the closeness centrality42, the betweenness centrality43, the eigenvector centrality44,45, and PageRank46. Control centrality has been defined in directed networks for quantifying the relative importance of nodes in effecting control36, i.e., if an external driver signal is applied to a node in a directed network, how many other nodes can be controlled? Our task is to extend the definition of control centrality to undirected networks and offer a control centrality measure.
Specifically, For node i in an undirected network, its control centrality is nothing but the dimension of the controllable subspace. When a single driving signal is applied to i, the corresponding control input matrix  is effectively reduced to a vector b(i) with a single non-zero element. For convenience, we set this element to be unity, let R(i) be the rank of the controllability matrix, and rewrite the system as
is effectively reduced to a vector b(i) with a single non-zero element. For convenience, we set this element to be unity, let R(i) be the rank of the controllability matrix, and rewrite the system as

where u is the strength of the input signal. The value of R(i) can be used to characterize node i’s ability to control the whole network. In Method, we provide a proof for the following inequality, which gives the upper bound of R(i):

where num(λ) is the number of the distinct eigenvalues of the matrix  . If R(i) = N, then node i alone can control the whole system. However, for R(i) = 1, node i is not able to control any other node in the networks. A value of R(i) between 1 and N gives the dimension of the controllable subspace of node i. To compare the control centrality in networks with different size, the normalized control centrality r(i) can be defined as the ratio of R(i) to the network size N. Then the average value, maximum and minimum values of r(i) are
. If R(i) = N, then node i alone can control the whole system. However, for R(i) = 1, node i is not able to control any other node in the networks. A value of R(i) between 1 and N gives the dimension of the controllable subspace of node i. To compare the control centrality in networks with different size, the normalized control centrality r(i) can be defined as the ratio of R(i) to the network size N. Then the average value, maximum and minimum values of r(i) are

For the networks with random weights, the control centrality and the normalized control centrality can be denoted by  and
and  respectively.
respectively.
We employ the criteria of control efficacy to explore undirected chains. To our surprise, complex phenomena associated with prime numbers emerge in the extremely simple regular network. Figure 2(a) shows, for an undirected chain graph of size N = 155 with identical link weights, that the values of the nodal control centrality are distributed symmetrically. For certain node (e.g., 1 or 155), the chain is fully controllable with a single input signal. For majority of the nodes, the control centrality measure is less than N. In fact, we can show analytically that the control centrality value of each node is given by (see Supplementary Note 2)

where GCD(m, n) is the greatest common divisor of the positive integers m and n. Figure 2(b) shows, the distribution of the control centrality values versus the network size N. Two clusters of periodic behavior of R(i) present as N is increased. The periodic phenomena can be verified in terms of Eq. (10).
(a) Nodal control centrality R(i) versus the node index for a one-dimensional undirected chain graph of size 155, where the squares denote the results from Eq. (4) and the blue solid circles are those from Eq. (10). (b) All the possible values of N − R(i) versus the system size N. For a fixed value of N, there are a finite number of R(i) values. (c) num(R), the number of distinct control centralities R(i) versus N. Each distinct value of num(R) is marked with a different color. It is remarkable that num(R) is related to the prime decomposition, as can be calculated from Eq. (11). For instance, the hollow circles represent that N + 1 is a prime number. (d) For the undirected chain graph with random weights, the corresponding control centralities  versus N. According to Eq. (12), there are two periodic behavior for odd and even number of nodes alternately.
versus N. According to Eq. (12), there are two periodic behavior for odd and even number of nodes alternately.
The combination of the two clusters of periodic behavior lead to the emergence of complex control centrality in undirected chains. Let num(R) be the number of the distinct control centrality values in a chain with a certain size. The dependence of num(R) on N is shown in Fig. 2(c). Analytically, num(R) can be determined from the following equation where, for fixed N, num(R) is the total number of all integer solutions of fa and fb that satisfy fa · fb = N + 1 (see Supplementary Note 2):

Thus, the solution of num(R) is related with prime numbers, accounting for the complex result of num(R) in a simple chain structure. Specifically, if N + 1 is a prime number, there is only one integer solution of Eq. (11): fa = 1 and fb = N + 1, leading to num(R) = 1 [the hollow circles in Fig. 2(c)]. When N + 1 is the square of a prime number, the integer solutions are (fa, fb) = (1, N + 1) and (fa, fb) =  , accounting for num(R) = 2, as shown by the red circles in Fig. 2(c). For num(R) > 2, the situation will become more complicated, because of the inequality of exchanging fa and fb. For example, if N + 1 is the product of two different prime number, num(R) will be 3. A typical case is N + 1 = 6, for which there are three integer solutions: (fa, fb) = (1, 6), (fa, fb) = (2, 3) and (fa, fb) = (3, 2). However, the scenario that N + 1 is cube of a prime number can result in num(R) = 3 as well. For instance, when N + 1 = 23 = 8, there are three integer solutions: (fa, fb) = (1, 8), (fa, fb) = (2, 4) and (fa, fb) = (4, 2). As a result, Fig. 2(c) exhibits rich behavior of num(R) as the length N of an undirected chain is increased.
, accounting for num(R) = 2, as shown by the red circles in Fig. 2(c). For num(R) > 2, the situation will become more complicated, because of the inequality of exchanging fa and fb. For example, if N + 1 is the product of two different prime number, num(R) will be 3. A typical case is N + 1 = 6, for which there are three integer solutions: (fa, fb) = (1, 6), (fa, fb) = (2, 3) and (fa, fb) = (3, 2). However, the scenario that N + 1 is cube of a prime number can result in num(R) = 3 as well. For instance, when N + 1 = 23 = 8, there are three integer solutions: (fa, fb) = (1, 8), (fa, fb) = (2, 4) and (fa, fb) = (4, 2). As a result, Fig. 2(c) exhibits rich behavior of num(R) as the length N of an undirected chain is increased.
For an undirected chain graph with random weights, the control centrality is simpler than that of a directed chain graph. We can as well offer theoretical results (see Supplementary Note 2). Specifically, when N = 2n + 1 is odd, we have

When N = 2n is even, we have

The results are graphically shown in Fig. 2(d), which differs from the results in Fig. 2(c) with identical weights. The fact that random weights eliminates lots of linear correlations in the network matrix accounts for the simplification of the control centrality.
For undirected regular graphs with identical weights, the eigenvalues can be calculated analytically10,47,48, so can be R(i), as listed in Table 1. We see that the control centrality of the star network is either 2 or 3, and that of the fully connected network is 2, regardless of the network size. For a ring network, almost half of the network can be controlled by a single input. The results for chain networks are relatively more complicated, for which the control centrality values are symmetrically distributed, which can be obtained from Eq. (10) (see Supplementary Note 2). In general, the control centrality  of the undirected regular graphs with random weights is simpler than that of the undirected regular graphs with identical weights, because of the elimination of linear correlation by random weights (see Table 1).
of the undirected regular graphs with random weights is simpler than that of the undirected regular graphs with identical weights, because of the elimination of linear correlation by random weights (see Table 1).
Figure 3(a) shows the control centrality versus a key structural parameter, the connecting probability, for undirected Erdös-Rényi (ER) random networks with identical link weights. We see that, regardless of the network size, in the regime of small values of the connecting probability p, the value of  increases monotonically with p, indicating that making the network more dense can on average enhance the control efficacy. However, in the extreme regime where p is close to unity (e.g., exceeding 0.99),
increases monotonically with p, indicating that making the network more dense can on average enhance the control efficacy. However, in the extreme regime where p is close to unity (e.g., exceeding 0.99),  begins to decrease toward zero due to the effect of identical link weights. The control centrality of ER random networks associated with random link weights differs significantly when the network becomes very dense. Specifically, Fig. 3(a) show that
begins to decrease toward zero due to the effect of identical link weights. The control centrality of ER random networks associated with random link weights differs significantly when the network becomes very dense. Specifically, Fig. 3(a) show that  is always one, as p approaches unity. The difference is as well attributed to the elimination of linear correlation by random weights, but such effect of random is negligible in sparse ER network.
is always one, as p approaches unity. The difference is as well attributed to the elimination of linear correlation by random weights, but such effect of random is negligible in sparse ER network.
(a) Average control centrality  versus the connecting probability p for Erdös-Rényi (ER) random networks. (b)
versus the connecting probability p for Erdös-Rényi (ER) random networks. (b)  versus half of the average degree m = 〈k〉/2 for Barabási-Albert (BA) scale-free networks. IW and RW represent identical link weights and random link weights, respectively. All the networks are undirected with symmetric coupling matrices. The data points are averaged over 50 independent network realizations. The representative network sizes are N = 300, 500 and 1000.
versus half of the average degree m = 〈k〉/2 for Barabási-Albert (BA) scale-free networks. IW and RW represent identical link weights and random link weights, respectively. All the networks are undirected with symmetric coupling matrices. The data points are averaged over 50 independent network realizations. The representative network sizes are N = 300, 500 and 1000.
Figure 3(b) shows, for Barabási-Albert (BA) scale free networks,  versus half of the average degree m = 〈k〉/2, where we see that
versus half of the average degree m = 〈k〉/2, where we see that  increases rapidly toward unity as 〈k〉 is increased, regardless of the number of new links associated with the addition of a new node into the network during its growing process. We see that, qualitatively similar to ER networks, making a scale free network more densely connected can enhance its control efficacy. We also see that because of the general sparsity of the BA network, random link weights have negligible effect on
increases rapidly toward unity as 〈k〉 is increased, regardless of the number of new links associated with the addition of a new node into the network during its growing process. We see that, qualitatively similar to ER networks, making a scale free network more densely connected can enhance its control efficacy. We also see that because of the general sparsity of the BA network, random link weights have negligible effect on  for m ≤ 2 compared to identical link weights.
for m ≤ 2 compared to identical link weights.
We characterize the control efficacy for a number of real world (empirical) networks. The results are listed in Table 2. (For the empirical networks with random weights, its corresponding control centrality are slightly higher than the origin network topology.) An issue is whether the hub nodes carry a stronger control centrality in undirected networks. We find that the average control centrality of hub nodes is generally smaller than that of the other nodes in undirected networks, which is consistent with the finding that driver nodes avoid hubs in directed networks49. To demonstrate this counterintuitive phenomenon, we divide the nodes into three groups in terms of their degrees: low, medium and high. Figure 4(a) shows, for model ER and BA networks, that the control centrality is generally higher for low-degree nodes than that for the hubs. Figure 4(b) shows the mean degree of the nodes with the maximum control centrality versus the mean degree 〈k〉 of all nodes, for each empirical network in Table 2. We see that the values of  , the degree value at which maximum control efficacy is achieved, are significantly smaller than or comparable to 〈k〉, indicating the nodes with large values of control centrality are generally not hubs. To provide further evidence for the determining role of nodal degree in the control efficacy, we randomize each empirical network by converting it into an ER random network, keeping the network size N and its diameter L unchanged. As shown in Fig. 4(c), for some networks there is no correlation between the values of
, the degree value at which maximum control efficacy is achieved, are significantly smaller than or comparable to 〈k〉, indicating the nodes with large values of control centrality are generally not hubs. To provide further evidence for the determining role of nodal degree in the control efficacy, we randomize each empirical network by converting it into an ER random network, keeping the network size N and its diameter L unchanged. As shown in Fig. 4(c), for some networks there is no correlation between the values of  for the original and randomized networks, indicating that the full randomization process has effectively eliminated any topological features of the original network that determine the control efficacy. We then apply a degree-preserving procedure4,50,51 that randomly rewires the links but keeps the degree of each node unchanged. Contrary to the case of full randomization [Fig. 4(c)], when the nodal degrees are preserved, there is little change in the value of
for the original and randomized networks, indicating that the full randomization process has effectively eliminated any topological features of the original network that determine the control efficacy. We then apply a degree-preserving procedure4,50,51 that randomly rewires the links but keeps the degree of each node unchanged. Contrary to the case of full randomization [Fig. 4(c)], when the nodal degrees are preserved, there is little change in the value of  , indicating strongly that degree is the key characteristic that determines the control efficacy.
, indicating strongly that degree is the key characteristic that determines the control efficacy.
(a) The average control centrality (bars) for the low-, medium- and high-degree nodes in ER and SA networks of size N = 500 and average degree 〈k〉 = 2, where the control centrality of hubs is generally less than that for smaller degree nodes. The results are averaged over 500 network realizations. For the ER networks, different connected components are considered separately. (b) Mean degree of the nodes with the maximum control centrality rmax as compared with the mean degree of all nodes for a number of empirical networks. It can be seen that for these real-world networks the nodes with relatively large values of the control centrality are not hub nodes, which is consistent with the results in (a). (c) For randomized empirical networks and (d) for the randomized networks but with the degrees preserved, the values of  in comparison with these from the original networks.
in comparison with these from the original networks.
Identification of controllable nodes
For an arbitrary undirected network, given a control input matrix, we can obtain the dimension of the controllable subspace by calculating the control efficacy. An issue of practical importance is how to identify the actual set of nodes that can be controllable, i.e., the set of controllable nodes for a given control input configuration. Here, we offer a general method based on network diffusion dynamics to address this issue. Specifically, note that the N × Nm controllability matrix  can be expressed iteratively as
can be expressed iteratively as

For the N × N matrix  , between any pair of nodes (e.g., i and j), there exists a path of length s:
, between any pair of nodes (e.g., i and j), there exists a path of length s:

Regarding the nonzero elements of  as sources of diffusion, the controllability matrix
as sources of diffusion, the controllability matrix  can be viewed as being formed by a diffusion process from the nodes with control matrix
can be viewed as being formed by a diffusion process from the nodes with control matrix  to all the controllable nodes in the network in (N − 1) time steps, generating the corresponding diffusion mode for each column of
to all the controllable nodes in the network in (N − 1) time steps, generating the corresponding diffusion mode for each column of  . At time step s, the matrix product
. At time step s, the matrix product  is a linear combination of the mode at the s step and the modes from all prior forward steps. The rank of
is a linear combination of the mode at the s step and the modes from all prior forward steps. The rank of  is determined by the number of the distinct modes of diffusion. In general, unless
is determined by the number of the distinct modes of diffusion. In general, unless  has a full rank, there is interdependence among its columns. Using this fact, we can prove that, for fixed
has a full rank, there is interdependence among its columns. Using this fact, we can prove that, for fixed  , the distinct diffusion modes are fully contained in the former r iteration steps (Supplementary Note 3). Consequently, we can implement the following elementary column transformation on the controllability matrix to obtain
, the distinct diffusion modes are fully contained in the former r iteration steps (Supplementary Note 3). Consequently, we can implement the following elementary column transformation on the controllability matrix to obtain

so that the controllable nodes correspond to the maximal linearly independent group of the rows. To illustrate the method explicitly, we present a concrete example, as shown in Fig. 5, where the diffusion process can be seen by noting the newly appeared diffusion mode (color marked) at each time step. We next perform the elementary column transformation on  to obtain its column canonical form that reveals the linear dependence among the rows, where the rows that are linearly independent of other rows correspond to the controllable nodes. Note that the configuration of drivers is not unique as it depends on the order with which the elementary transform is implemented. While there are many possible choices of the linearly dependent rows, the number of controllable nodes is fixed and determined solely by
to obtain its column canonical form that reveals the linear dependence among the rows, where the rows that are linearly independent of other rows correspond to the controllable nodes. Note that the configuration of drivers is not unique as it depends on the order with which the elementary transform is implemented. While there are many possible choices of the linearly dependent rows, the number of controllable nodes is fixed and determined solely by  . Our procedure of finding the driver nodes is rigorous, as guaranteed by our theory of control efficacy and the column canonical form associated with the matrix rank.
. Our procedure of finding the driver nodes is rigorous, as guaranteed by our theory of control efficacy and the column canonical form associated with the matrix rank.
Take as an example a simple undirected network with self-loops. (a) A step by step illustration of the diffusion process over the network from the driver node, where a control signal is applied at node 1. The newly appeared mode at each step is marked with different colors. At step 7, the iteration column vector  can be expressed as a linear combination of the former modes, so the corresponding value of the control efficacy is 6. (b) For the controllability matrix
can be expressed as a linear combination of the former modes, so the corresponding value of the control efficacy is 6. (b) For the controllability matrix  , its column canonical form generated by the elementary column transformation. For a fixed value of the control efficacy measure r, the column canonical form can be performed only for r iterations of the column vector. (c) There is a one-to-one correspondence between the controllable nodes and the rows that are linearly dependent upon others in the column canonical form. In the specific case shown, there are four distinct configurations of the controllable nodes (marked in blue). Nevertheless, the number of controllable nodes is fixed and solely determined by
, its column canonical form generated by the elementary column transformation. For a fixed value of the control efficacy measure r, the column canonical form can be performed only for r iterations of the column vector. (c) There is a one-to-one correspondence between the controllable nodes and the rows that are linearly dependent upon others in the column canonical form. In the specific case shown, there are four distinct configurations of the controllable nodes (marked in blue). Nevertheless, the number of controllable nodes is fixed and solely determined by  .
.
Discussion
For complex networks in the real world, from the standpoint of control not every node is externally accessible. Often, control signals can be applied to a limited set of nodes or just a few nodes. If the network structure is known, theoretically it is possible to determine a specific set of nodes to apply the control signals, e.g., through identification of maximum matching in SCT. However, the set of control nodes so determined may not overlap with the set of externally accessible nodes. Under these circumstances it is not possible to control the whole network. Nonetheless, there are situations where full control of the entire network is not necessary. A fundamental question is then, if control is applied to a few nodes or even a single node, what fraction of the network can be controlled? That is, for a complex network of arbitrary structure, what is the control efficacy or, equivalently, the dimension of the controllable subspace of the underlying network?
The issue of control efficacy (or control centrality if control is applied at a single node) was addressed in a previous work36 but for directed networks. The contribution of the present paper is a rigorous framework based on the theory of exact controllability10,14 to determine, for undirected complex networks of arbitrary structure (regular, random, or scale-free, weighted or unweighted, with or without self loops, etc.), their control efficacy. From the mathematical control theory, the control efficacy is given by the rank of the Kalman controllability matrix, the determination of which is computationally prohibitive for large networks. Utilizing the non-singular similarity transformation, we discovered a mathematical theorem that enables us to convert rank calculation into a counting problem in terms of the block matrices associated with the distinct eigenvalues of the network coupling matrix. The framework allows us to determine, rigorously, the control efficacy of not only model complex networks, but also a large number of real world networks. Physically, we developed the picture of diffusion, i.e., to view the control process as a signal originated from the driver node and diffused through the controllable subnetwork. The powerful combination of rigorous mathematical theorem and physical reasoning leads to the discovery of striking phenomena in controlling complex networks. For example, more densely connected networks in general have stronger control efficacy, regardless of their topology, and nodal degree is key to control efficacy. However, hub nodes in general have low values of control centrality as compared with majority of the nodes in the network.
From the perspective of fundamental science, our framework of control efficacy represents an important step forward in understanding, quantitatively, the controllability of complex networks at the detailed level of individual nodes. (Extension of our control efficacy framework to analyzing the efficacy of observability of complex networks is straightforward - see Supplementary Note 5). Practically, our theory provides a method and algorithms that can be used to identify efficiently the nodes that possess the strongest possible control centrality. This can have significant applications. For example, given a social network, our framework allows the nodes with the largest control efficacy, i.e., the nodes that can control the largest possible fraction of the network, to be identified. Similarly, for a complex infrastructure network, we can determine a small set of critical nodes to obtain maximum possible control of the network to achieve the highest possible energy efficiency.
Despite our initial success as reported in the present paper, many outstanding issues remain. For example, in real world networks the estimated link weights are not exactly known, which will lead to errors in determining the control efficacy. A mathematical uncertainty or error analysis is needed, but at the present a rigorous treatment seems difficult. Also, our framework of control efficacy relies on complete knowledge of the network structure. What if there is missing information about nodes, links and/or their weights? - at the present we do not have a theory to deal with this practically important issue. Last but not least, our entire theory is based on hypothesizing the underlying complex network as a linear and time invariant dynamical systems. Although much effort has been dedicated to controlling complex networks with nonlinear dynamics52,53,54, a general approach for measuring control efficacy remains to be an outstanding problem55. The main challenge stems from the fact that the control efficacy is determined by both network structure and dynamics, in contrast to the network governed by linear dynamics. Much further effort is called for in the extremely rapidly developing field of controlling complex networks.
Methods
For an undirected network with arbitrary link weights [Eq. (1)], the matrix  is symmetric and so is diagonalizable: there exists an orthogonal matrix
is symmetric and so is diagonalizable: there exists an orthogonal matrix  and a diagonal matrix
and a diagonal matrix  such that
such that  with
with  , where λi’s (i = 1, …, l) are the distinct eigenvalues of
, where λi’s (i = 1, …, l) are the distinct eigenvalues of  and
and  is the diagonal block matrix of
is the diagonal block matrix of  associated with λi. The size of
associated with λi. The size of  is given by the multiplicity of λi. We write
is given by the multiplicity of λi. We write

For a linear dynamical system, its controllability is invariant under any non-singular transform. The control efficacy of the original system can then be determined by calculating the rank of the transformed Kalman matrix  [Eq. (3)].
[Eq. (3)].
Single control input
When the system is subject to a single control input, the control matrix  and the transformed control matrix
and the transformed control matrix  is an N × 1 column vector. If
is an N × 1 column vector. If  has zero element, the corresponding row in the the transformed Kalman matrix
has zero element, the corresponding row in the the transformed Kalman matrix  is zero. For the nonzero elements in
is zero. For the nonzero elements in  , the corresponding eigenvalues can be of two types.
, the corresponding eigenvalues can be of two types.
(i) Case I: Distinct eigenvalues. An illustrative example for this case is shown in Fig. 1(a), where the values of q1, q2 and q3 are assumed to be nonzero, corresponding to the eigenvalues λ1, λ2 and λ3, respectively. The corresponding row of (q1, q2, q3) in  is a Vandermonde matrix, whose rows are linearly independent. In this case, the rank of the controllability matrix is nothing but the number of the nonzero elements corresponding to distinct eigenvalues of
is a Vandermonde matrix, whose rows are linearly independent. In this case, the rank of the controllability matrix is nothing but the number of the nonzero elements corresponding to distinct eigenvalues of  .
.
(ii) Case II: Degenerate eigenvalues. When there is eigenvalue multiplicity, the rows of  are linearly dependent upon each other. An example of the controllability matrix is
are linearly dependent upon each other. An example of the controllability matrix is

where the rows of q4 and q6 are linearly dependent. If the linearly dependent rows in  have nonzero elements, they together contribute one to the rank of the controllability matrix.
have nonzero elements, they together contribute one to the rank of the controllability matrix.
For a single control input, the calculation of the rank of  is thus equivalent to counting the corresponding nonzero elements in
is thus equivalent to counting the corresponding nonzero elements in  . We have
. We have

Since the control matrix  has a single column, the control centrality of the input node is given by
has a single column, the control centrality of the input node is given by

where the num(λ) is the number of the distinct eigenvalues of  .
.
Multiple control inputs
With multiple control input signals, the transformed control matrix  has the dimensional N × m. To illustrate our method of rank calculation explicitly, we consider the first two columns in
has the dimensional N × m. To illustrate our method of rank calculation explicitly, we consider the first two columns in  . The matrices
. The matrices  and
and  can be written as
can be written as

Adjusting the order of the original column vectors appropriately, we can convert the transformed Kalman matrix  into a form in which two single controller inputs are applied sequentially, i.e.,
into a form in which two single controller inputs are applied sequentially, i.e.,

For the case where the control matrix  has distinct eigenvalues, if certain rows of the transformed control matrix
has distinct eigenvalues, if certain rows of the transformed control matrix  contain nonzero elements, the corresponding rows of the transformed Kalman matrix
contain nonzero elements, the corresponding rows of the transformed Kalman matrix  must be linearly independent of each other. The matrix
must be linearly independent of each other. The matrix  can be organized into a block matrix form, where each block corresponds to one distinct eigenvalue and its dimension is the multiplicity of the eigenvalue. The rank of such a matrix is the sum of the rank values of the sub-block matrices. In particular, letting the algebraic multiplicity of the eigenvalue λ1 be l1, we have
can be organized into a block matrix form, where each block corresponds to one distinct eigenvalue and its dimension is the multiplicity of the eigenvalue. The rank of such a matrix is the sum of the rank values of the sub-block matrices. In particular, letting the algebraic multiplicity of the eigenvalue λ1 be l1, we have

In general, for multiple control inputs, the control efficacy  is the sum of the rank values of the sub-block matrices:
is the sum of the rank values of the sub-block matrices:

Additional Information
How to cite this article: Gao, X.-D. et al. Control efficacy of complex networks. Sci. Rep. 6, 28037; doi: 10.1038/srep28037 (2016).
References
Lombardi, A. & Hörnquist, M. Controllability analysis of networks. Phys. Rev. E 75, 056110 (2007).
Liu, B., Chu, T., Wang, L. & Xie, G. Controllability of a leader-follower dynamic network with switching topology. IEEE Trans. Automat. Contr. 53, 1009–1013 (2008).
Rahmani, A., Ji, M., Mesbahi, M. & Egerstedt, M. Controllability of multi-agent systems from a graph-theoretic perspective. SIAM J . Contr. Optim . 48, 162–186 (2009).
Liu, Y.-Y., Slotine, J.-J. & Barabási, A.-L. Controllability of complex networks. Nature (London) 473, 167–173 (2011).
Wang, W.-X., Ni, X., Lai, Y.-C. & Grebogi, C. Optimizing controllability of complex networks by minimum structural perturbations. Phys. Rev. E 85, 026115 (2012).
Nepusz, T. & Vicsek, T. Controlling edge dynamics in complex networks. Nat. Phys. 8, 568–573 (2012).
Nacher, J. C. & Akutsu, T. Dominating scale-free networks with variable scaling exponent: heterogeneous networks are not difficult to control. New J. Phys. 14, 073005 (2012).
Yan, G., Ren, J., Lai, Y.-C., Lai, C.-H. & Li, B. Controlling complex networks: How much energy is needed? Phys. Rev. Lett. 108, 218703 (2012).
Liu, Y.-Y., Slotine, J.-J. & Barabási, A.-L. Observability of complex systems. Proc. Natl. Acad. Sci. (USA) 110, 2460–2465 (2013).
Yuan, Z.-Z., Zhao, C., Di, Z.-R., Wang, W.-X. & Lai, Y.-C. Exact controllability of complex networks. Nature Commun. 4, 2447 (2013).
Menichetti, G., Dall’Asta, L. & Bianconi, G. Network controllability is determined by the density of low in-degree and out-degree nodes. Phys. Rev. Lett. 113, 078701 (2014).
Ruths, J. & Ruths, D. Control profiles of complex networks. Science 343, 1373–1376 (2014).
Wuchty, S. Controllability in protein interaction networks. Proc. Natl. Acad. Sci. (USA) 111, 7156–7160 (2014).
Yuan, Z.-Z., Zhao, C., Wang, W.-X., Di, Z.-R. & Lai, Y.-C. Exact controllability of multiplex networks. New J. Phys. 16, 103036 (2014).
Whalen, A. J., Brennan, S. N., Sauer, T. D. & Schiff, S. J. Observability and controllability of nonlinear networks: The role of symmetry. Phys. Rev. X 5, 011005 (2015).
Yan, G. et al. Spectrum of controlling and observing complex networks. Nature Phys. 11, 779–786 (2015).
Chen, Y.-Z., Wang, L.-Z., Wang, W.-X. & Lai, Y.-C. The paradox of controlling complex networks: control inputs versus energy requirement. arXiv:1509.03196v1 (2015).
Strogatz, S. H. Exploring complex networks. Nature (London) 410, 268–276 (2001).
Albert, R. & Barabási, A.-L. Statistical mechanics of complex networks. Rev. Mod. Phys 74, 47–97 (2002).
Mendes, J. F. F., Dorogovtsev, S. N. & Ioffe, A. F. Evolution of Networks: From Biological Nets to the Internet and the WWW. (Oxford University Press, Oxford UK, 2003) first edn.
Pastor-Satorras, R. & Vespignani, A. Evoloution and Structure of the Internet: A Statistical Physics Approach (Cambridge University Press, Cambridge UK, 2004) first edn.
Barrat, A., Barthélemy, M. & Vespignani, A. Dynamical Processes on Complex Networks (Cambridge University Press, Cambridge UK, 2008) first edn.
Newman, M. E. J. Networks: An Introduction (Oxford University Press, Oxford, 2010) first edn.
Watts, D. J. & Strogatz, S. H. Collective dynamics of small-worldnetworks. Nature 393, 440–442 (1998).
Barabási, A.-L. & Albert, R. Emergence of scaling in random networks. Science 286, 509–512 (1999).
Lin, C.-T. Structural controllability. IEEE Trans. Automat. Contr. 19, 201–208 (1974).
Hopcroft, J. E. & Karp, R. M. An n5/2 algorithm for maximum matchings in bipartite graphs. SIAM J. Comput. 2, 225–231 (1973).
Zhou, H. & Ou-Yang, Z.-C. Maximum matching on random graphs. arXiv preprint cond-mat/0309348 (2003).
Zdeborová, L. & Mézard, M. The number of matchings in random graphs. J. Stat. Mech. 2006, P05003 (2006).
Horn, R. A. & Johnson, C. R. Matrix analysis (Cambridge university press, 1985).
Jia, T. et al. Emergence of bimodality in controlling complex networks. Nature Commun . 4 (2013).
Jia, T. & Barabási, A.-L. Control capacity and a random sampling method in exploring controllability of complex networks. Sci. Rep. 3 (2013).
Gao, J., Liu, Y.-Y., D’Souza, R. M. & Barabási, A.-L. Target control of complex networks. Nature Commun. 5 (2014).
Zhao, C., Wang, W.-X., Liu, Y.-Y. & Slotine, J.-J. Intrinsic dynamics induce global symmetry in network controllability. Sci. Rep. 5 (2015).
Cowan, N. J., Chastain, E. J., Vilhena, D. A., Freudenberg, J. S. & Bergstrom, C. T. Nodal dynamics, not degree distributions, determine the structural controllability of complex networks. PLoS One 7, e38398 (2012).
Liu, Y.-Y., Slotine, J.-J. & Barabási, A. L. Control centrality and hierarchical structure in complex networks. PLoS One 7, e44459 (2012).
Slotine, J.-J. E. & Li, W. Applied Nonlinear Control, vol. 199 (Prentice-Hall Englewood Cliffs, NJ, 1991).
Luenberger, D. G. Introduction to Dynamical Systems: Theory, Models, and Applications (John Wiley & Sons, Inc, New Jersey, 1999) first edn.
Kailath, T. Linear systems, vol. 1 (Prentice-Hall Englewood Cliffs, NJ, 1980).
Kalman, R. E. Mathematical description of linear dynamical systems. J. Soc. Indus. Appl. Math. Ser. A 1, 152–192 (1963).
Strang, G. Linear Algebra and Its Applications (Academic Press, 1976).
Sabidussi, G. The centrality index of a graph. Psychometrika 31, 581–603 (1966).
Freeman, L. C. A set of measures of centrality based on betweenness. Sociometry 40, 35–41 (1977).
Bonacich, P. Power and centrality: A family of measures. Ame. J. Socio. 92, 1170–1182 (1987).
Bonacich, P. & Lloyd, P. Eigenvector-like measures of centrality for asymmetric relations. Soc. Net. 23, 191–201 (2001).
Brin, S. & Page, L. Reprint of: The anatomy of a large-scale hypertextual web search engine. Comp. Net. 56, 3825–3833 (2012).
van Mieghem, P. Graph Spectra for Complex Networks (Cambridge University Press, 2010).
Parlangeli, G. & Notarstefano, G. On the reachability and observability of path and cycle graphs. IEEE Trans. Autom. Contr. 57, 743–748 (2012).
Liu, Y.-Y., Slotine, J.-J. & Barabási, A.-L. Controllability of complex networks. Nature 473, 167–173 (2011).
Maslov, S. & Sneppen, K. Specificity and stability in topology of protein networks. Science 296, 910–913 (2002).
Milo, R. et al. Network motifs: simple building blocks of complex networks. Science 298, 824–827 (2002).
Cornelius, S. P., Kath, W. L. & Motter, A. E. Realistic control of network dynamics. Nature Commun 4, 1942 (2013).
Well, D. K., Kath, W. L. & Motter, A. E. Control of Stochastic and Induced Switching in Biophysical Networks. Phys. Rev. X 5, 031036 (2015).
Wang, L.-Z., Su, R.-Q., Huang, Z.-G., Wang, X., Wang, W.-X., Grebogi, C. & Lai, Y.-C. A geometrical approach to control and controllability of nonlinear dynamical networks. Nature Commun. 7, 11323 (2016).
Lai, Y.-C. Controlling complex, nonlinear dynamical networks. Nat. Sci. Rev. 1, 339–341 (2014).
Newman, M. E. Finding community structure in networks using the eigenvectors of matrices. Phys. Rev. E 74, 036104 (2006).
Lusseau, D. et al. The bottlenose dolphin community of doubtful sound features a large proportion of long-lasting associations. Behav. Ecol. Sociobio. 54, 396–405 (2003).
Girvan, M. & Newman, M. E. Community structure in social and biological networks. Proc. Nat. Acad. Sci. (USA) 99, 7821–7826 (2002).
Zachary, W. W. An information flow model for conflict and fission in small groups. J. Anthrop. Res. 452–473 (1977).
Knuth, D. E., Knuth, D. E. & Knuth, D. E. The Stanford GraphBase: A Platform for Combinatorial Computing, vol. 37 (Addison-Wesley Reading, 1993).
Ripeanu, M., Foster, I. & Iamnitchi, A. Mapping the gnutella network: Properties of large-scale peer-to-peer systems and implications for system design. arXiv preprint cs/0209028 (2002).
Newman, M. E. The structure of scientific collaboration networks. Proc. Nat. Acad. Sci. (USA) 98, 404–409 (2001).
Guimera, R., Danon, L., Diaz-Guilera, A., Giralt, F. & Arenas, A. Self-similar community structure in a network of human interactions. Phys. Rev. E 68, 065103 (2003).
Gleiser, P. M. & Danon, L. Community structure in jazz. Adv. Complex Sys . 6, 565–573 (2003).
http://vlado.fmf.uni-lj.si/pub/networks/pajek/data/gphs.htm.
Acknowledgements
W.-X.W. was supported by CNNSF under Grant No. 61573064, and No. 61074116 the Fundamental Research Funds for the Central Universities and Beijing Nova Programme, China. Y.-C.L. was supported by ARO under Grant W911NF-14-1-0504.
Author information
Authors and Affiliations
Contributions
W.-X.W. designed research. X.-D.G. and W.-X.W. performed research; all analyzed data; W.-X.W. and Y.-C.L. wrote the paper.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing financial interests.
Supplementary information
Rights and permissions
This work is licensed under a Creative Commons Attribution 4.0 International License. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in the credit line; if the material is not included under the Creative Commons license, users will need to obtain permission from the license holder to reproduce the material. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/
About this article
Cite this article
Gao, XD., Wang, WX. & Lai, YC. Control efficacy of complex networks. Sci Rep 6, 28037 (2016). https://doi.org/10.1038/srep28037
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/srep28037
This article is cited by
-
Energy scaling of targeted optimal control of complex networks
Nature Communications (2017)