Introduction

New information on morph frequency in the peppered moth Biston betularia has recently become available, and some earlier conclusions about this example of evolution have been challenged. The nature of the criticisms is discussed by Grant (1999) and Cook (2000). One feature which has always received comparatively little attention is the status of the intermediate melanic morphs. The darkest melanic, known as carbonaria, is a uniform black colour except for two small white marks at the base of the fore wings. Forms which are intermediate in colour between this and the typical phenotype are known as insularia. At least five alleles are involved altogether, each dominant to paler alleles in the series. These phenotypes are illustrated by Kettlewell (1973), Lees & Creed (1977) and Bishop & Cook (1980). The different insularia alleles segregate in progeny of crosses, but often cannot be separated into discrete categories in collections of wild insects (Steward, 1977). It is therefore not always clear whether more than one phenotype is present in a sample, or which phenotype is intended in the scoring used by different observers. In the past, insularia has been up to about 40% in South Wales and Gloucestershire, where it was sometimes at a higher frequency than carbonaria, but never rose above 15% elsewhere (Kettlewell, 1973).

Where carbonaria was at high frequency, insularia was usually rare, so that when describing the recent dramatic drop in frequency of carbonaria in industrial areas it has been appropriate to leave the intermediate phenotypes out of the discussion (e.g. Clarke et al., 1994; Grant et al., 1996; Cook et al., 1999). In this paper some more recent data on insularia are presented, and the patterns of change in insularia frequency are discussed.

Results

Data

When Kettlewell (1973) reviewed the data on insularia he had available a small amount of evidence from the time of increase in melanics in the 19th and early 20th centuries and from 1950 to 1970, when frequencies across the country were more or less unchanging. He concluded that three patterns were evident, which had different geographical distributions. In the Severn Valley region of western England and South Wales, insularia was at 15–40% and carbonaria at a lower frequency. In the south of England insularia and carbonaria were both at low frequencies, while in the highly industrialized parts of England carbonaria was at a high and insularia at a low frequency. In the 1950–70 period insularia sometimes appeared to change in frequency. At Kettlewell’s home site in Oxfordshire the frequency of typical dropped roughly from 50% to 40% whereas insularia increased from 15% to 25% and carbonaria remained more or less constant. At Newbury, Berkshire, insularia also increased at the expense of typical while at Minstead, Hampshire, a small increase in insularia coincided with a corresponding decline in carbonaria.

As carbonaria dropped in frequency in the latter part of the 20th century, insularia often increased. At Caldy, on the Wirral peninsula, the frequency of carbonaria changed from over 90% in the 1960s to less than 10% by the end of the century (Clarke et al., 1994; Grant et al., 1996). At the same time the frequency of insularia rose from about 1% to about 3.5% (Mani & Majerus, 1993; Grant et al., 1996). Although this change is small it is significant (Table 1b). An equally spectacular change in carbonaria frequency occurred in Manchester. It has not been as well recorded and different sites have been used in different surveys, spread over the area of the conurbation. Nevertheless, pooling results listed separately in Bishop et al. (1978) and Cook et al. (1999) provides figures which appear to show a similar increase in the insularia morph (Table 1a). Mani & Majerus (1993) give data for sites in Cambridge, Cambridgeshire, Northwood, Middlesex, and Egham, Surrey, where the insularia frequency rose from 5% or less in the mid 1960s to about 15% by 1990, while carbonaria declined from about 80% to about 35%. Data for Nottingham and York are shown in Table 1a. For Nottingham insularia appears unchanged at about 6% from 1993 to 1999, while carbonaria declined from 59% to 19%. At York the insularia frequency was between 5% and 10% in 1990–2000, while carbonaria has declined from 60% to 30%. At a site in Kent insularia rose in frequency from about 7.5% in 1971 to more than 30% by 1994, while carbonaria dropped from over 75% to between 20% and 30% (West, 1994). Where change is evident the general pattern is for insularia to be constant or to increase in frequency, while the darker melanic morph carbonaria has experienced a decline.

Table 1 Data relating to insularia frequency.
Full size table

If fitness of insularia were intermediate between that of the other two morphs it should increase in frequency when carbonaria was common, because it is relatively advantageous, but decline as the most favoured morph, typica, becomes the most common. During the original period of increase in melanics insularia presumably rose in frequency and then declined in localities where carbonaria was the most favoured form. Mani (1980) has shown that these patterns may be simulated in a theoretical model based on ecological data, and that patterns in specific locations can be effectively reproduced (Mani & Majerus, 1993). His model runs for a period of 150 generations, and includes changing selection imposed by sight-hunting predators, estimates of selection arising from developmental or metabolic differences, and migration. Under the circumstances it is not transparently clear which components contribute to the relative change in frequency of the intermediate melanic phenotypes. It is therefore of interest to consider the expected deterministic change when the additional ecological considerations are ignored. The dynamics of multiallelic systems have been examined in the past (Owen, 1954; Kimura, 1956; Mandel, 1959; Li, 1967), but to investigate stable equilibria rather than the consequences of directional selection.

Analysis

Two considerations arise when we examine probable patterns of change in insularia frequency. The first results from the dominance relations of the alleles. If insularia is present in a population largely composed of carbonaria it is recessive to the alternative allele and only homozygotes are distinguishable. In one composed mostly of typicals it is dominant and heterozygotes are distinguishable. As typica replaces carbonaria the visibility of insularia alleles changes. If the gene frequencies of carbonaria, insularia and typica are p, q and r (p + q + r=1) the system is as follows, (See the Table 2 below)

Table 2
Full size table

The effect of the change in dominance of the alternative alleles is most easily seen if we assume a population containing the three morphs, in which, for the sake of the demonstration, the insularia allele remains unchanged at frequency q. Frequency of typica, r, may vary from zero to 1 − q, the remainder being carbonaria alleles at frequency p=1 − q − r. The insularia phenotype frequency is B=q2 + 2qr. The slope of B on r is 2q, and B=q when r=½(1 − q). Suppose earlier events have reduced r to a low frequency, and it is now increasing under selection. When it is low the insularia phenotype frequency will be less than the allele frequency, but it will become greater than q when r > ½(1 − q). Systematic change in prevalence of the insularia phenotype will occur, for which we might be tempted to suggest a selective basis, whereas the effect is due to nothing but the genetic background against which the allele is apparent.

The second consideration is that under selection insularia allele frequency is affected by the change in relative frequency of the other two alleles. The simplest demonstration of the basic dynamics of the situation can be made by imagining a haploid system with three genetically controlled colour types. This hypothetical model is introduced to avoid the effect of segregation of alleles into genotypes, although, of course, it has no biological relevance to Lepidoptera. As before, carbonaria, insularia and typica are assumed to have allele frequencies p, q and r, so that (See the Table 3 below)

Table 3
Full size table

Fitnesses are assumed to be related to appearance, that of i lying between c and t. When typicals have highest fitness s is positive. The mean fitness is w¯=1 − s(p − r) + kq. Change in frequency of the insularia allele over one generation is,

It is evident that when the darker melanics are very common, so that p is larger than r, Δq is positive and q increases. When typicals are very common, so that r exceeds p and q is small, Δq is negative and q decreases. When Δq=0,

This equation describes a straight line from q=1, p=0 to q=0, p=½(s − k)/s. At q=0 the frequency p is zero when k=s (insularia has the same fitness as typica), and 1 when k=−s (insularia has the same fitness as carbonaria). When k lies between these limits the trajectory for insularia has a maximum. When k=0, so that insularia is exactly intermediate in fitness between the other morphs, p=0.5 at q=0. The maximum is then independent of s. Where a given trajectory crosses this line depends on frequencies at the beginning of a period of selection. The equation for Δq shows that if two populations had the same initial frequency q, and were subject to the same selection, the frequency in the next generation is determined by their respective values of p − r. This quantity can have a wide range of values subject only to the restriction that p + r=1 − q, and will in turn determine the change in subsequent generations.

In the simplest possible case of directional selection, therefore, a genotype with intermediate phenotype and fitness shows an initial rise and subsequent fall in frequency in whichever direction the change occurs. The rate of change depends on strength of selection and frequency, but the path followed and the peak frequency are strongly dependent on initial frequencies of the three genotypes.

To illustrate the true diploid case we will assume that fitness differences are related to visual appearance and k=0. We then have (See the Table 4 below)

Table 4
Full size table

The mean fitness is w¯=1 − s[p(2 − p) − r2]. The changes in carbonaria and insularia frequencies are

The expression for Δq changes in sign as r moves from being very rare to very common, while that for Δp does not. The carbonaria and insularia morphs change in frequency in opposite directions at one extreme and in the same direction at the other, whether melanics are favoured or disfavoured. The maximum at which Δq=0 occurs at

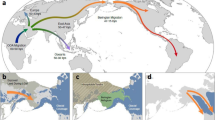
This is a curve running from p=0, q=1, to p=0.5, q=0. If k is introduced to modify the fitness of insularia, and allowed to vary between s and −s, the curve changes in position in a similar way to that for the haploid model. Figure 1 shows possible frequencies of q plotted on p. On the diagonal border r=0, whereas r is greater than 0 in the body of the diagram, moving towards 1 at p=0, q=0. The curve running from p=0, q=1, to p=0.5, q=0, defines Δq=0. Representative trajectories are illustrated for four populations starting from the same frequency q but with different frequencies p and r.

Fig. 1
figure 1

Relation of frequency of the insularia allele (q) to that of the carbonaria allele (p) in populations which also include the typical allele (frequency of typical = 1 − p − q). Fitnesses of carbonaria, insularia and typica are 1 − s, 1 and 1 + s. Solid line: Δq=0. Pecked lines: trajectories for populations moving towards p=0, q=0, starting from the same value of q but different values of p and r. With this model the paths of the trajectories do not depend on s.

Full size image

If there were two insularia alleles with fitnesses related directly to appearance in the way described, then both would show the rise and fall in frequency, with the less extreme form changing in frequency after the more extreme one. For the haploid case, suppose the four types have frequencies p, q, r and u, with fitnesses 1 − 2s, 1 − s, 1 and 1 + s. Changes in the two insularia types are described by

For the darker morph, change is positive or negative depending on the frequency of carbonaria, on the one hand, and of pale insularia and typica on the other. For the paler morph the change depends on the ratio of carbonaria and dark insularia to typica.

Discussion

Of the 12 examples of changing frequency considered here, the insularia phenotype increased in frequency in nine and was more or less stable in three. The recorded change from Manchester (Table 1) illustrates the changing detectability of the insularia alleles. The allele frequency declines from 0.12 to 0.03, while the phenotype frequency increases from 1.5%, when most of the rest were carbonaria to 5.2% when most others are typica. In all other cases discussed the relation of allele to phenotype frequency is positive, significantly so when more than one or two records are available. Phenotype frequency therefore correctly indicates the direction of change, although not necessarily the precise amount.

Like Manchester, the Nottingham site is moving in the expected final direction of loss of all nontypical alleles; the range of values is beyond the theoretical Δq maximum and both insularia and carbonaria are declining (Table 1). When examining change in carbonaria frequency Grant et al. (1998) compared this site with one at Chesterfield, Derbyshire. Experience from field surveys shows that patches of similar frequencies are large, except where there are marked clines, and this site was acceptably close. In Kettlewell’s (1973) list no insularia were recorded there in 1952–56 (99.5% carbonaria, total=170) and 0.9% in 1967–8 (96.6% carbonaria, total=293, allele frequency of insularia, 0.026). The insularia frequency therefore appears to have risen to its peak between then and the commencement of the sequence in Table 1.

In two cases discussed by Kettlewell which start in the 1950s the carbonaria frequency was stable over the period, while an increase in insularia was compensated for by a decline in typical. The data from Hampshire in Table 1 look more or less unchanging. Mani & Majerus (1993) illustrate data from this county in which the carbonaria frequencies are consistent with these; they do not show the insularia. In the rest, carbonaria declined, sometimes to a very great extent. In none of these examples has insularia been separated into subcategories, but it is possible that sometimes more than one insularia allele is involved. Brakefield & Liebert (2000) provide evidence from the Netherlands of different insularia phenotypes showing different changes during a decline of carbonaria frequency.

Examination of the dynamics of a system of three or more alleles with directional selection shows that the observed changes in insularia are usually consistent with a fitness lying between that of carbonaria and typica. This, in turn, is consistent with the assumption that fitness is directly dependent on visual appearance, although of course that assumption is not essential. The actual path followed at any given site is affected by numerous factors, such as changes in selection over time, migration from sites with different frequencies and regional differences in characteristic vegetation or kind of resting sites available. It is therefore not appropriate to attempt further analysis of the fitness relationships.

An additional and interesting complication is that the frequency achieved after a period of time may be strongly influenced by initial frequency. The order in which the different melanic phenotypes first entered an area could have a marked effect of frequencies 50−100 generations later, even in localities where similar selection operated. A difference in frequency at the time of the main Kettlewell surveys may therefore reflect initial conditions as well as, or instead of ecological differences. Equally, differences in response over the last three decades may reflect differences in frequencies at the beginning of the present decline in melanism, as well as local selective conditions. Consideration of the fate of insularia adds another dimension to the study of this example of extremely rapid genetic change in response to changing natural conditions.