Thermalization of a two-dimensional photonic gas in a ‘white wall’ photon box

Abstract

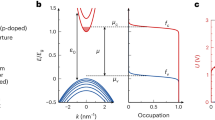
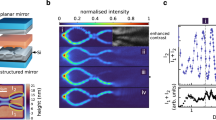
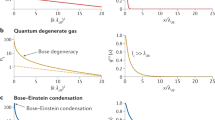
Bose–Einstein condensation¹, the macroscopic accumulation of bosonic particles in the energetic ground state below a critical temperature, has been demonstrated in several physical systems^{2,3,4,5,6,7,8}. The perhaps best known example of a bosonic gas, blackbody radiation⁹, however exhibits no Bose–Einstein condensation at low temperatures¹⁰. Instead of collectively occupying the lowest energy mode, the photons disappear in the cavity walls when the temperature is lowered—corresponding to a vanishing chemical potential. Here we report on evidence for a thermalized two-dimensional photon gas with a freely adjustable chemical potential. Our experiment is based on a dye-filled optical microresonator, acting as a ‘white wall’ box for photons. Thermalization is achieved in a photon-number-conserving way by photon scattering off the dye molecules, and the cavity mirrors provide both an effective photon mass and a confining potential—key prerequisites for the Bose–Einstein condensation of photons. As a striking example of the unusual system properties, we demonstrate a yet unobserved light concentration effect into the centre of the confining potential, an effect with prospects for increasing the efficiency of diffuse solar light collection¹¹.