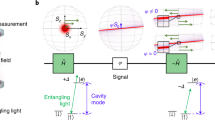
Abstract
Phase-insensitive optical amplification of an unknown quantum state is known to be a fundamentally noisy operation that inevitably adds noise to the amplified state1,2,3,4,5. However, this fundamental noise penalty in amplification can be circumvented by resorting to a probabilistic scheme as recently proposed and demonstrated in refs 6, 7, 8. These amplifiers are based on highly non-classical resources in a complex interferometer. Here we demonstrate a probabilistic quantum amplifier beating the fundamental quantum limit using a thermal-noise source and a photon-number-subtraction scheme9. The experiment shows, surprisingly, that the addition of incoherent noise leads to a noiselessly amplified output state with a phase uncertainty below the uncertainty of the state before amplification. This amplifier might become a valuable quantum tool in future quantum metrological schemes and quantum communication protocols.
This is a preview of subscription content, access via your institution
Access options
Subscribe to this journal
Receive 12 print issues and online access
$259.00 per year
only $21.58 per issue
Buy this article
- Purchase on SpringerLink
- Instant access to the full article PDF.
USD 39.95
Prices may be subject to local taxes which are calculated during checkout




Similar content being viewed by others
References
Louisell, W. H. et al. Quantum fluctuations and noise in parametric processes. I. Phys. Rev. 124, 1646–1654 (1961).
Haus, H. A. & Mullen, J. A. Quantum noise in linear amplifiers. Phys. Rev. 128, 2407–2413 (1962).
Caves, C. M. Quantum limits on the noise in linear amplifiers. Phys. Rev. D 26, 1817–1839 (1982).
Ou, Z. Y., Pereira, S. F. & Kimble, H. J. Quantum noise reduction in optical amplification. Phys. Rev. Lett. 70, 3239–3242 (1993).
Josse, V. et al. Universal optical amplification without nonlinearity. Phys. Rev. Lett. 96, 163602 (2006).
Ralph, T. C. & Lund, A. B. in Quantum Communication Measurement and Computing Proc. 9th Int. Conf. (ed. Lvovsky, A.) 155–160 (AIP, 2009).
Xiang, G. Y., Ralph, T. C., Lund, A. P., Walk, N. & Pryde, G. J. Heralded noiseless linear amplification and distillation of entanglement. Nature Photon. 4, 316–319 (2010).
Ferreyrol, F. et al. Implementation of a nondeterministic optical noiseless amplifier. Phys. Rev. Lett. 104, 123603 (2010).
Marek, P. & Filip, R. Coherent-state phase concentration by quantum probabilistic amplification. Phys. Rev. A 81, 022302 (2010).
Dirac, P. A. M. The quantum theory of the emission and absorption of radiation. Proc. R. Soc. Lond. A 114, 243–265 (1927).
Shapiro, J. H., Shepard, S. R. & Wong, N. C. Ultimate quantum limits on phase measurement. Phys. Rev. Lett. 62, 2377–2380 (1989).
Fiurášek, J. Engineering quantum operations on travelling light beams by multiple photon addition and subtraction. Phys. Rev. A 80, 053822 (2009).
Menzies, D. & Croke, S. Noiseless linear amplification via weak measurements. Preprint at http://arxiv.org/abs/0903.4181v1 (2009).
Ourjoumtsev, A., Tualle-Brouri, R., Laurat, J. & Grangier, P. Generating optical Schrödinger kittens for quantum information processing. Science 312, 83–86 (2006).
Neergaard-Nielsen, J. S., Melholt Nielsen, B., Hettich, C., Mølmer, K. & Polzik, E. S. Generation of a superposition of odd photon number states for quantum information networks. Phys. Rev. Lett. 97, 083604 (2006).
Takahashi, H. et al. Generation of large-amplitude coherent-state superposition via ancilla-assisted photon subtraction. Phys. Rev. Lett. 101, 233605 (2008).
Wiseman, H. & Kilip, R. B. Adaptive single-shot phase measurements: The full quantum theory. Phys. Rev. A 57, 2169–2185 (1998).
Armen, M. A. et al. Adaptive homodyne measurement of optical phase. Phys. Rev. Lett. 89, 133602 (2002).
Lvovsky, A. I. Iterative maximum-likelihood reconstruction in quantum homodyne tomography. J. Opt. B: Quantum Semiclass. Opt. 6, 556–559 (2004).
Hradil, Z. Quantum-state estimation. Phys. Rev. A 6, R1561–R1564 (1997).
Wittmann, C. et al. Demonstration of near-optimal discrimination of optical coherent states. Phys. Rev. Lett. 101, 210501 (2008).
Banaszek, K. et al. Direct measurement of the Wigner function by photon counting. Phys. Rev. A 60, 674–677 (1999).
Wittmann, C. et al. Demonstration of coherent state discrimination using a displacement controlled photon number resolving detector. Phys. Rev. Lett. 104, 100505 (2010).
Holevo, A. S. Covariant measurements and imprimitivity systems. Lect. Notes Math. 1055, 153–172 (1982).
Acknowledgements
This work was supported by the EU project COMPAS, the BIOP Graduate school, the Lundbeck foundation and the DFG project LE 408/19-1. R.F. and P.M. acknowledge support from projects No. MSM 6198959213 and No. LC06007 of the Czech Ministry of Education, the Grant 202/08/0224 of GA CR and the Alexander von Humboldt Foundation. P.M. acknowledges support from the Grant P205/10/P319 of GA CR.
Author information
Authors and Affiliations
Contributions
M.A.U., C.R.M. and C.W. carried out the experimental work, P.M. and R.F. did the theoretical calculations and all authors discussed the results. U.L.A., M.A.U. and C.R.M. wrote the manuscript and Ch.M., G.L. and U.L.A. coordinated the project.
Corresponding authors
Ethics declarations
Competing interests
The authors declare no competing financial interests.
Supplementary information
Supplementary Information
Supplementary Information (PDF 302 kb)
Rights and permissions
About this article
Cite this article
Usuga, M., Müller, C., Wittmann, C. et al. Noise-powered probabilistic concentration of phase information. Nature Phys 6, 767–771 (2010). https://doi.org/10.1038/nphys1743
Received:
Accepted:
Published:
Issue date:
DOI: https://doi.org/10.1038/nphys1743
This article is cited by
-
A high-gain and high-fidelity coherent state comparison amplifier
Communications Physics (2018)
-
Work and information from thermal states after subtraction of energy quanta
Scientific Reports (2017)
-
Surpassing the no-cloning limit with a heralded hybrid linear amplifier for coherent states
Nature Communications (2016)
-
Two-dimensional distributed-phase-reference protocol for quantum key distribution
Scientific Reports (2016)
-
Performance Improvement of Two-way Quantum Key Distribution by Using a Heralded Noiseless Amplifier
International Journal of Theoretical Physics (2016)