Skip to main content

Thank you for visiting nature.com. You are using a browser version with limited support for CSS. To obtain the best experience, we recommend you use a more up to date browser (or turn off compatibility mode in Internet Explorer). In the meantime, to ensure continued support, we are displaying the site without styles and JavaScript.

  • Letter
  • Published:

Twisting of light around rotating black holes

Nature Physics volume 7, pages 195–197 (2011)Cite this article

Abstract

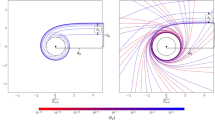
Kerr black holes are among the most intriguing predictions of Einstein’s general relativity theory1,2. These rotating massive astrophysical objects drag and intermix their surrounding space and time, deflecting and phase-modifying light emitted near them. We have found that this leads to a new relativistic effect that imprints orbital angular momentum on such light. Numerical experiments, based on the integration of the null geodesic equations of light from orbiting point-like sources in the Kerr black hole equatorial plane to an asymptotic observer3, indeed identify the phase change and wavefront warping and predict the associated light-beam orbital angular momentum spectra4. Setting up the best existing telescopes properly, it should be possible to detect and measure this twisted light, thus allowing a direct observational demonstration of the existence of rotating black holes. As non-rotating objects are more an exception than a rule in the Universe, our findings are of fundamental importance.

This is a preview of subscription content, access via your institution

Access options

Buy this article

  • Purchase on SpringerLink
  • Instant access to the full article PDF.

USD 39.95

Prices may be subject to local taxes which are calculated during checkout

Figure 1: Total phase variation of light generated in a region of size 100RS×100RS in the equatorial xy plane of a quasi-extremal rotating black hole (a=0.99) as seen by an asymptotic observer.
Figure 2: Phase variation of photons as measured by an asymptotic observer.

Similar content being viewed by others

References

  1. Chandrasekhar, S. The Mathematical Theory of Black Holes (Oxford Univ. Press, 1992).

    MATH  Google Scholar 

  2. Bozza, V. Gravitational lensing by black holes. Gen. Rel. Grav. 42, 2269–2300 (2010).

    Article  ADS  MathSciNet  Google Scholar 

  3. Ćadež, A. & Calvani, M. Relativistic emission lines from accretion disks around black holes. Mon. Not. R. Astron. Soc. 363, 177–182 (2005).

    Article  ADS  Google Scholar 

  4. Torner, L., Torres, J. & Carrasco, S. Digital spiral imaging. Opt. Express 13, 873–881 (2005).

    Article  ADS  Google Scholar 

  5. Dehnen, H. Gravitational Faraday-effect. Int. J. Theor. Phys. 7, 467–474 (1973).

    Article  Google Scholar 

  6. Molina-Terriza, G., Torres, J. P. & Torner, L. Twisted photons. Nature Phys. 3, 305–310 (2007).

    Article  ADS  Google Scholar 

  7. Beckwith, K. & Done, C. Extreme gravitational lensing near rotating black holes. Mon. Not. R. Astron. Soc. 359, 1217–1228 (2005).

    Article  ADS  Google Scholar 

  8. Carini, P., Long-Long, F., Miao, L. & Ruffini, R. Phase evolution of the photon in Kerr spacetime. Phys. Rev. D 46, 5407–5413 (1992).

    Article  ADS  MathSciNet  Google Scholar 

  9. Long-Long, F. & Wo-Lung, L. Gravitomagnetism and the Berry phase of photon in a rotating gravitational field. Int. J. Mod. Phys. D 10, 961–969 (2001).

    Article  ADS  MathSciNet  Google Scholar 

  10. Marucci, L., Manzo, C. & Paparo, D. Optical spin-to-orbital angular momentum conversion in inhomogeneous anisotropic media. Phys. Rev. Lett. 96, 163905 (2006).

    Article  ADS  Google Scholar 

  11. Grier, D. G. A revolution in optical manipulation. Nature 424, 810–816 (2003).

    Article  ADS  Google Scholar 

  12. Gibson, G. et al. Free-space information transfer using light beams carrying orbital angular momentum. Opt. Express 12, 5448–5456 (2004).

    Article  ADS  Google Scholar 

  13. Thidé, B. et al. Utilization of photon orbital angular momentum in the low-frequency radio domain. Phys. Rev. Lett. 99, 087701 (2007).

    Article  ADS  Google Scholar 

  14. Harwit, M. Photon orbital angular momentum in astrophysics. Astrophys. J. 597, 1266–1270 (2003).

    Article  ADS  Google Scholar 

  15. Elias, N. M. II Photon orbital angular momentum in astronomy. Astron. Astrophys. 492, 883–922 (2008).

    Article  ADS  Google Scholar 

  16. Tamburini, F., Anzolin, G., Bianchini, A. & Barbieri, C. Overcoming the Rayleigh criterion limit with optical vortices. Phys. Rev. Lett. 97, 163903 (2006).

    Article  ADS  Google Scholar 

  17. Serabyn, E., Mawet, D. & Burruss, R. An image of an exoplanet separated by two diffraction beamwidths from a star. Nature 464, 1018–1020 (2010).

    Article  ADS  Google Scholar 

  18. Anzolin, G., Tamburini, F., Bianchini, A., Umbriaco, G. & Barbieri, C. Optical vortices with star light. Astron. Astrophys. 488, 1159–1165 (2008).

    Article  ADS  Google Scholar 

  19. Berestetskii, V. B., Lifshitz, E. M. & Pitaevskii, L. P. Quantum Electrodynamics 2nd edn,Vol. 4 (Butterworth-Heinemann, 1982).

    Google Scholar 

  20. Mair, A., Vaziri, A., Weihs, G. & Zeilinger, A. Entanglement of the orbital angular momentum states of photons. Nature 412, 313–316 (2001).

    Article  ADS  Google Scholar 

  21. Leach, J., Padgett, M. J., Barnett, S. M., Franke-Arnold, S. & Courtial, J. Measuring the orbital angular momentum of a single photon. Phys. Rev. Lett. 88, 257901 (2002).

    Article  ADS  Google Scholar 

  22. Tamburini, F. & Vicino, D. Photon wave function: A covariant formulation and equivalence with QED. Phys. Rev. A 78, 052116 (2008).

    Article  ADS  Google Scholar 

  23. Falcke, H., Melia, F. & Agol, E. Viewing the shadow of the black hole at the Galactic Center. Astrophys. J. 528, L13–L16 (2000).

    Article  ADS  Google Scholar 

  24. Genzel, R. et al. Near-infrared flares from accreting gas around the supermassive black hole at the Galactic Centre. Nature 425, 934–937 (2003).

    Article  ADS  Google Scholar 

  25. Aschenbach, B., Grosso, N., Porquet, D. & Predehl, P. X-ray flares reveal mass and angular momentum of the Galactic Center black hole. Astron. Astrophys. 417, 71–78 (2004).

    Article  ADS  Google Scholar 

  26. Broderick, A. E., Fish, V. L., Doeleman, S. S. & Loeb, A. Estimating the parameters of Sagittarius A*’s accretion flow via millimeter VLBI. Astrophys. J. 697, 45–54 (2009).

    Article  ADS  Google Scholar 

  27. Tamburini, F., Sponselli, A., Thidé, B. & Mendonça, J. T. Photon orbital angular momentum and mass in a plasma vortex. Europhys. Lett. 90, 45001 (2010).

    Article  ADS  Google Scholar 

  28. Darwin, C. The gravity field of a particle. Proc. R. Soc. Lond. 249, 180–194 (1959).

    Article  ADS  MathSciNet  Google Scholar 

  29. Su, F. S. & Mallett, R. L. The effect of the Kerr metric on the plane of polarization of an electromagnetic wave. Astrophys. J. 238, 1111–1125 (1980).

    Article  ADS  Google Scholar 

  30. Mendonça, J. T. & Thidé, B. Neutrino orbital angular momentum in a plasma vortex. Europhys. Lett. 84, 41001 (2008).

    Article  ADS  Google Scholar 

Download references

Acknowledgements

The authors thank J. P. Torres, M. Calvani, A. Čadež and M. Berry for helpful comments and suggestions. F.T. gratefully acknowledges the financial support from the CARIPARO Foundation within the 2006 Program of Excellence and the kind hospitality of Uppsala University/Swedish Institute of Space Physics and ICFO during the writing of the manuscript. B.T. gratefully acknowledges financial support from the Swedish Research Council (VR) and the hospitality of the Nordic Institute for Theoretical Physics (NORDITA), the University of Padova, and the Institute for Quantum Optics and Quantum Information, Austrian Academy of Sciences, Vienna, where parts of this work were carried out.

Author information

Authors and Affiliations

  1. Department of Astronomy, University of Padova, vicolo dell’Osservatorio 3, IT-35122 Padova, Italy

    Fabrizio Tamburini

  2. Swedish Institute of Space Physics, Box 537, Ångström Laboratory, SE-75121 Uppsala, Sweden

    Bo Thidé

  3. QsciTech and Department of Physics and Astronomy, Macquarie University, 2109 New South Wales, Australia

    Gabriel Molina-Terriza

  4. ICFO, Parc Mediterrani de la Tecnologia, Av. del Canal Olı´mpic s/n, ES-08860 Castelldefels (Barcelona), Spain

    Gabriele Anzolin

Authors
  1. Fabrizio Tamburini
    View author publications

    Search author on:PubMed Google Scholar

  2. Bo Thidé
    View author publications

    Search author on:PubMed Google Scholar

  3. Gabriel Molina-Terriza
    View author publications

    Search author on:PubMed Google Scholar

  4. Gabriele Anzolin
    View author publications

    Search author on:PubMed Google Scholar

Contributions

F.T., B.T. and G.M-T. developed the model. F.T. carried out the numerical simulations. G.A. calculated and plotted the OAM spectra. F.T. and B.T. wrote the manuscript. All authors discussed and commented on the manuscript.

Corresponding author

Correspondence to Bo Thidé.

Ethics declarations

Competing interests

The authors declare no competing financial interests.

Supplementary information

Supplementary Information

Supplementary Information (PDF 712 kb)

Rights and permissions

Reprints and permissions

About this article

Cite this article

Tamburini, F., Thidé, B., Molina-Terriza, G. et al. Twisting of light around rotating black holes. Nature Phys 7, 195–197 (2011). https://doi.org/10.1038/nphys1907

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue date:

  • DOI: https://doi.org/10.1038/nphys1907

This article is cited by

Search

Advanced search

Quick links

Nature Briefing

Sign up for the Nature Briefing newsletter — what matters in science, free to your inbox daily.

Get the most important science stories of the day, free in your inbox. Sign up for Nature Briefing