Skip to main content

Thank you for visiting nature.com. You are using a browser version with limited support for CSS. To obtain the best experience, we recommend you use a more up to date browser (or turn off compatibility mode in Internet Explorer). In the meantime, to ensure continued support, we are displaying the site without styles and JavaScript.

  • Letter
  • Published:

Experimental investigation of the entanglement-assisted entropic uncertainty principle

Nature Physics volume 7, pages 752–756 (2011)Cite this article

Abstract

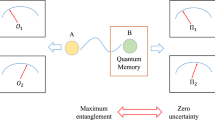
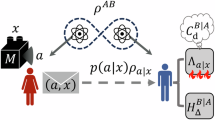
The uncertainty principle, which bounds the uncertainties involved in obtaining precise outcomes for two complementary variables defining a quantum particle, is a crucial aspect in quantum mechanics. Recently, the uncertainty principle in terms of entropy has been extended to the case involving quantum entanglement1. With previously obtained quantum information for the particle of interest, the outcomes of both non-commuting observables can be predicted precisely, which greatly generalizes the uncertainty relation. Here, we experimentally investigated the entanglement-assisted entropic uncertainty principle for an entirely optical set-up. The uncertainty is shown to be near zero in the presence of quasi-maximal entanglement. The new uncertainty relation is further used to witness entanglement. The verified entropic uncertainty relation provides an intriguing perspective in that it implies the uncertainty principle is not only observable-dependent but is also observer-dependent2.

This is a preview of subscription content, access via your institution

Access options

Buy this article

  • Purchase on SpringerLink
  • Instant access to the full article PDF.

USD 39.95

Prices may be subject to local taxes which are calculated during checkout

Figure 1: Experimental setup.
Figure 2: Experimental results for the conditional entropies with the input state ρ1.
Figure 3: Experimental results for the entanglement witness using the input state of ρ1.
Figure 4: Experimental results for the density matrix χ of the spin-echo based quantum memory and the entropies as a function of the angle θ.

Similar content being viewed by others

References

  1. Berta, M., Christandl, M., Colbeck, R., Renes, J. M. & Renner, R. The uncertainty principle in the presence of quantum memory. Nature Phys. 6, 659–662 (2010).

    Article  ADS  Google Scholar 

  2. Winter, A. Coping with uncertainty. Nature Phys. 6, 640–641 (2010).

    Article  ADS  Google Scholar 

  3. Heisenberg, W. Über den anschaulichen Inhalt der quantentheoretischen Kinematik und Mechanik. Z. Phys. 43, 172–198 (1927).

    Article  ADS  Google Scholar 

  4. Robertson, H. P. The uncertainty principle. Phys. Rev. 34, 163–164 (1929).

    Article  ADS  Google Scholar 

  5. Biłynicki-Birula, I. & Mycielski, J. Uncertainty relations for information entropy in wave mechanics. Commun. Math. Phys. 44, 129–132 (1975).

    Article  ADS  MathSciNet  Google Scholar 

  6. Deutsch, D. Uncertainty in quantum measurements. Phys. Rev. Lett. 50, 631–633 (1983).

    Article  ADS  MathSciNet  Google Scholar 

  7. Kraus, K. Complementary observables and uncertainty relations. Phys. Rev. D 35, 3070–3075 (1987).

    Article  ADS  MathSciNet  Google Scholar 

  8. Maassen, H. & Uffink, J. B. M. Generalized entropic uncertainty relations. Phys. Rev. Lett. 60, 1103–1106 (1988).

    Article  ADS  MathSciNet  Google Scholar 

  9. Einstein, A., Podolsky, B. & Rosen, N. Can quantum mechanical description of physical reality be considered complete? Phys. Rev. 47, 777–780 (1935).

    Article  ADS  Google Scholar 

  10. Popper, K. R. Zur Kritik der Ungenauigkeitsrelationen. Naturwissenschaften 22, 807–808 (1934).

    Article  ADS  Google Scholar 

  11. Kim, Y. H. & Shih, Y. Experimental realization of Popper’s experiment: Violation of the uncertainty principle? Found. Phys. 29, 1849–1861 (1999).

    Article  Google Scholar 

  12. Reid, M. D. & Drummond, P. D. Quantum correlations of phase in nondegenerate parametric oscillation. Phys. Rev. Lett. 60, 2731–2733 (1988).

    Article  ADS  Google Scholar 

  13. Reid, M. D. Demonstration of the Einstein–Podolsky–Rosen paradox using nondegenerate parametric amplification. Phys. Rev. A 40, 913–923 (1989).

    Article  ADS  Google Scholar 

  14. Ou, Z. Y., Pereira, S. F., Kimble, H. J. & Peng, K. C. Realization of the Einstein–Podolsky–Rosen paradox for continuous-variables. Phys. Rev. Lett. 68, 3663–3666 (1992).

    Article  ADS  Google Scholar 

  15. Hofmann, H. F. & Takeuchi, S. Violation of local uncertainty relations as a signature of entanglement. Phys. Rev. A. 68, 032103 (2003).

    Article  ADS  MathSciNet  Google Scholar 

  16. Howell, J. C., Bennink, R. S., Bentley, S. J. & Boyd, R. W. Realization of the Einstein–Podolsky–Rosen paradox using momentum- and position-entangled photons from spontaneous parametric down conversion. Phys. Rev. Lett. 92, 210403 (2004).

    Article  ADS  Google Scholar 

  17. Bowen, W. P., Schnabel, R., Lam, P. K. & Ralph, T. C. Experimental investigation of criteria for continuous variable entanglement. Phys. Rev. Lett. 90, 043601 (2003).

    Article  ADS  Google Scholar 

  18. Renes, J. M. & Boileau, J. C. Conjectured strong complementary information tradeoff. Phys. Rev. Lett. 103, 020402 (2009).

    Article  ADS  Google Scholar 

  19. Devetak, I. & Winter, A. Distillation of secret key and entanglement from quantum states. Proc. R. Soc. A 461, 207–235 (2005).

    Article  ADS  MathSciNet  Google Scholar 

  20. Fano, R. Transimission of Information: A Statistical Theory of Communications (Cambridge, Mass., M.I.T. Press, 1961).

    Google Scholar 

  21. Kwiat, P. G., Waks, E., White, A. G., Appelbaum, I. & Eberhard, P. H. Ultrabright source of polarization-entangled photons. Phys. Rev. A 60, R773–R776 (1999).

    Article  ADS  Google Scholar 

  22. Xu, J-S., Li, C-F. & Guo, G-C. Generation of a high-visibility four-photon entangled state and realization of a four-party quantum communication complexity scenario. Phys. Rev. A 74, 052311 (2006).

    Article  ADS  Google Scholar 

  23. Aiello, A., Puentes, G., Voigt, D. & Woerdman, J. P. Maximally entangled mixed-state generation via local operations. Phys. Rev. A 75, 062118 (2007).

    Article  ADS  MathSciNet  Google Scholar 

  24. James, D. F. V., Kwiat, P. G., Munro, W. J. & White, A. G. Measurement of qubits. Phys. Rev. A 64, 052312 (2001).

    Article  ADS  Google Scholar 

  25. Wootters, W. K. Entanglement of formation of an arbitrary state of two qubits. Phys. Rev. Lett. 80, 2245–2248 (1998).

    Article  ADS  Google Scholar 

  26. Prevedel, R., Hamel, D. R., Colbeck, R., Fisher, K. & Resch, K. J. Experimental investigation of the uncertainty principle in the presence of quantum memory. Nature Phys.doi:10.1038/nphys2048 (2011).

  27. Chuang, I. L. & Nielsen, M. A. Prescription for experimental determination of the dynamics of a quantum black box. J. Mod. Opt. 44, 2455–2467 (1997).

    Article  ADS  Google Scholar 

  28. O’Brien, J. L. et al. Quantum process tomography of a controlled-NOT gate. Phys. Rev. Lett. 93, 080502 (2004).

    Article  ADS  Google Scholar 

  29. Altepeter, J. B., Jeffrey, E. R. & Kwiat, P. G. in Advances in Atomic, Molecular and Optical Physics Vol. 52 (eds Berman, P. & Lin, C.) 107–161 (Elsevier, 2005).

    Google Scholar 

Download references

Acknowledgements

This work was supported by the National Basic Research Program of China (Grants No. 2011CB921200), National Natural Science Foundation of China (Grant Nos 11004185, 60921091, 10874162), and the China Postdoctoral Science Foundation (Grant No. 20100470836). The CQT is funded by the Singapore MoE and the NRF as part of the Research Centres of Excellence programme.

Author information

Author notes

  1. Chuan-Feng Li and Jin-Shi Xu: These authors contributed equally to this work

Authors and Affiliations

  1. Key Laboratory of Quantum Information, University of Science and Technology of China, CAS, Hefei, 230026, China

    Chuan-Feng Li, Jin-Shi Xu, Xiao-Ye Xu & Guang-Can Guo

  2. Center for Quantum Technologies, National University of Singapore, 2 Science Drive 3, 117542, Singapore

    Ke Li

Authors
  1. Chuan-Feng Li
    View author publications

    Search author on:PubMed Google Scholar

  2. Jin-Shi Xu
    View author publications

    Search author on:PubMed Google Scholar

  3. Xiao-Ye Xu
    View author publications

    Search author on:PubMed Google Scholar

  4. Ke Li
    View author publications

    Search author on:PubMed Google Scholar

  5. Guang-Can Guo
    View author publications

    Search author on:PubMed Google Scholar

Contributions

C-F.L. and J-S.X. designed the experiment. C-F.L. supervised the project. J-S.X. and X-Y.X. performed the experiment. J-S.X. analysed the theoretical prediction and experimental data. K.L. and G-C.G. contributed to the theoretical analysis. X-Y.X. drew the sketch of the experimental setup. J-S.X. wrote the paper. All authors commented on the manuscript.

Corresponding author

Correspondence to Chuan-Feng Li.

Ethics declarations

Competing interests

The authors declare no competing financial interests.

Supplementary information

Supplementary Information

Supplementary Information (PDF 291 kb)

Rights and permissions

Reprints and permissions

About this article

Cite this article

Li, CF., Xu, JS., Xu, XY. et al. Experimental investigation of the entanglement-assisted entropic uncertainty principle. Nature Phys 7, 752–756 (2011). https://doi.org/10.1038/nphys2047

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue date:

  • DOI: https://doi.org/10.1038/nphys2047

This article is cited by

Search

Advanced search

Quick links

Nature Briefing

Sign up for the Nature Briefing newsletter — what matters in science, free to your inbox daily.

Get the most important science stories of the day, free in your inbox. Sign up for Nature Briefing