Skip to main content

Thank you for visiting nature.com. You are using a browser version with limited support for CSS. To obtain the best experience, we recommend you use a more up to date browser (or turn off compatibility mode in Internet Explorer). In the meantime, to ensure continued support, we are displaying the site without styles and JavaScript.

  • Letter
  • Published:

Universal spin dynamics in two-dimensional Fermi gases

Nature Physics volume 9, pages 405–409 (2013)Cite this article

Subjects

A Corrigendum to this article was published on 31 January 2014

This article has been updated

Abstract

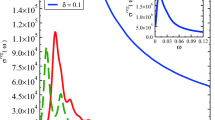
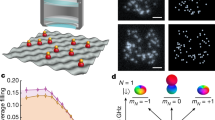
Harnessing spins as information carriers has emerged as an elegant extension to the transport of electrical charges1. The coherence of such spin transport in spintronic circuits is determined by the lifetime of spin excitations and by spin diffusion. Fermionic quantum gases allow the study of spin transport from first principles because interactions can be precisely tailored and the dynamics is on directly observable timescales2,3,4,5,6,7,8,9,10,11,12. In particular, at unitarity, spin transport is dictated by diffusion and the spin diffusivity is expected to reach a universal, quantum-limited value on the order of the reduced Planck constant ħ divided by the mass m. Here, we study a two-dimensional Fermi gas after a quench into a metastable, transversely polarized state. Using the spin-echo technique13, for strong interactions, we measure the lowest transverse spin diffusion constant14,15 so far 6.3 (8) × 10-3 ħ/m. For weak interactions, we observe a collective transverse spin-wave mode that exhibits mode softening when approaching the strongly interacting regime.

This is a preview of subscription content, access via your institution

Access options

Buy this article

  • Purchase on SpringerLink
  • Instant access to the full article PDF.

USD 39.95

Prices may be subject to local taxes which are calculated during checkout

Figure 1: Quench of a 2D Fermi gas in which all atoms were initially prepared in the |↓〉 state.
Figure 2: Spin-echo signals in the strongly interacting regime.
Figure 3: Observation of spin waves for the non-interacting gas ().
Figure 4: Spin waves in the collisionless regime as a function of interaction strength.

Similar content being viewed by others

Change history

  • 04 June 2013

    In the version of this Letter originally published online, in the third main paragraph, the formula for the maximum elastic scattering cross section between atoms should have read σ∼λdBD−1. In the previous paragraph, penultimate sentence, the terms 'parallel to M' and 'orthogonal to M' should not have been included. In the section 'Interactions in two dimensions', the first equation should have included square brackets, as here: f(q) = 4π/[ln(1/q2a2D2)+iπ]. These corrections have been made in the HTML and PDF versions of the Letter.

  • 23 December 2013

    In the version of this Letter originally published, the stated value for the difference in the gyromagnetic ratio for the |↑> and |↓> state, δγ, was missing a factor of 2π. Consequently, the diffusion constants were overestimated by a factor of (2π)2. In particular, the value at ln(kFa2D) = 0 stated in the text should be 6.3(8) × 10-3ħ/m instead of 0.25(3)ħ/m. Other quantities, such as the magnetic field gradient, which was independently calibrated, are not affected. All other statements and observations in the published version are correct and remain unaffected. These errors have now been corrected in the online versions of the Letter.

References

  1. Awschalom, D. D., Loss, D. & Samarth, N. (eds) Semiconductor Spintronics and Quantum Computation (NanoScience and Technology, Springer, 2007).

  2. Gensemer, S. D. & Jin, D. S. Transition from collisionless to hydrodynamic behavior in an ultracold Fermi gas. Phys. Rev. Lett. 87, 173201 (2001).

    Article  ADS  Google Scholar 

  3. Du, X., Luo, L., Clancy, B. & Thomas, J. E. Observation of anomalous spin segregation in a trapped Fermi gas. Phys. Rev. Lett. 101, 150401 (2008).

    Article  ADS  Google Scholar 

  4. Du, X., Zhang, Y., Petricka, J. & Thomas, J. E. Controlling spin current in a trapped Fermi gas. Phys. Rev. Lett. 103, 010401 (2009).

    Article  ADS  Google Scholar 

  5. Sommer, A., Ku, M., Roati, G. & Zwierlein, M. W. Universal spin transport in a strongly interacting Fermi gas. Nature 472, 201–204 (2011).

    Article  ADS  Google Scholar 

  6. Sommer, A., Ku, M. & Zwierlein, M. W. Spin transport in polaronic and superfluid Fermi gases. New J. Phys. 13, 055009 (2011).

    Article  ADS  Google Scholar 

  7. Bruun, G. M. Spin diffusion in Fermi gases. New J. Phys. 13, 035005 (2011).

    Article  ADS  Google Scholar 

  8. Wulin, D., Guo, H., Chien, C-C. & Levin, K. Spin transport in cold Fermi gases: A pseudogap interpretation of spin diffusion experiments at unitarity. Phys. Rev. A 83, 061601 (2011).

    Article  ADS  Google Scholar 

  9. Ebling, U., Eckardt, A. & Lewenstein, M. Spin segregation via dynamcially induced long-range interactions in a system of ultracold fermions. Phys. Rev. A 84, 063607 (2011).

    Article  ADS  Google Scholar 

  10. Bruun, G. M. Shear viscosity and spin-diffusion coefficient of a 2D Fermi gas. Phys. Rev. A 85, 013636 (2012).

    Article  ADS  Google Scholar 

  11. Enss, T., Küppersbusch, C. & Fritz, L. Shear viscosity and spin diffusion in a 2D Fermi gas. Phys. Rev. A 86, 013617 (2012).

    Article  ADS  Google Scholar 

  12. Enss, T. & Haussmann, R. Quantum mechanical limitations to spin diffusion in the unitary Fermi gas. Phys. Rev. Lett. 109, 195303 (2012).

    Article  ADS  Google Scholar 

  13. Hahn, E. L. Spin echoes. Phys. Rev. 80, 580–594 (1950).

    Article  ADS  Google Scholar 

  14. Leggett, A. J. & Rice, M. J. Spin echoes in liquid 3H and mixtures: A predicted new effect. Phys. Rev. Lett. 20, 586–589 (1968).

    Article  ADS  Google Scholar 

  15. Leggett, A. J. Spin diffusion and spin echoes in liquid 3H at low temperature. J. Phys. C 3, 448 (1970).

    Article  ADS  Google Scholar 

  16. Weber, C. P. et al. Observation of spin Coulomb drag in a 2D electron gas. Nature 437, 1330–1333 (2005).

    Article  ADS  Google Scholar 

  17. Dobbs, E. R. Helium Three (Oxford Univ. Press, 2000).

    Google Scholar 

  18. Corruccini, L. R., Osheroff, D. D., Lee, D. M. & Richardson, R. C. Spin diffusion in liquid 3He: The effect of Leggett and Rice. Phys. Rev. Lett. 27, 650–653 (1971).

    Article  ADS  Google Scholar 

  19. Mullin, W. J. & Jeon, J. W. Spin diffusion in dilute, polarized 3He–4He solutions. J. Low Temp. Phys. 88, 433–482 (1992).

    Article  ADS  Google Scholar 

  20. Martiyanov, K., Makhalov, V. & Turlapov, A. Observation of a 2D Fermi gas of atoms. Phys. Rev. Lett. 105, 030404 (2010).

    Article  ADS  Google Scholar 

  21. Fröhlich, B. et al. Radiofrequency spectroscopy of a strongly interacting 2D Fermi gas. Phys. Rev. Lett. 106, 105301 (2011).

    Article  ADS  Google Scholar 

  22. Conduit, G. J. & Altman, E. Dynamical instability of a spin spiral in an interacting Fermi gas as a probe of the Stoner transition. Phys. Rev. A 82, 043603 (2010).

    Article  ADS  Google Scholar 

  23. Lhuillier, C & Laloë, F Transport properties in a spin polarized gas, II. J. Phys. France 43, 225–241 (1982).

    Article  Google Scholar 

  24. Silin, V. Oscillations of a Fermi-liquid in a magnetic field. Sov. Phys. JETP 6, 945–950 (1958).

    ADS  MathSciNet  MATH  Google Scholar 

  25. Lévy, L. P. & Ruckenstein, A. E. Collective spin oscillations in spin-polarized gases: Spin-polarized hydrogen. Phys. Rev. Lett. 52, 1512–1515 (1984).

    Article  ADS  Google Scholar 

  26. Bloom, P. Two-dimensional Fermi gas. Phys. Rev. B 12, 125 (1975).

    Article  ADS  Google Scholar 

  27. Fröhlich, B. et al. Two-dimensional Fermi liquid with attractive interactions. Phys. Rev. Lett. 109, 130403 (2012).

    Article  ADS  Google Scholar 

  28. Vichi, L. & Stringari, S. Collective oscillations of an interacting trapped Fermi gas. Phys. Rev. A 60, 4734 (1999).

    Article  ADS  Google Scholar 

  29. Fuchs, J. N., Gangardt, D. M. & Laloë, F. Internal state conversion in ultracold gases. Phys. Rev. Lett. 88, 230404 (2002).

    Article  ADS  Google Scholar 

  30. Feld, M., Fröhlich, B., Vogt, E., Koschorreck, M. & Köhl, M. Observation of a pairing pseudogap in a 2D Fermi gas. Nature 480, 75–78 (2011).

    Article  ADS  Google Scholar 

  31. Petrov, D. & Shlyapnikov, G. Interatomic collisions in a tightly confined Bose gas. Phys. Rev. A 64, 012706 (2001).

    Article  ADS  Google Scholar 

  32. Bertaina, G. & Giorgini, S. BCS–BEC crossover in a 2D Fermi gas. Phys. Rev. Lett. 106, 110403 (2011).

    Article  ADS  Google Scholar 

Download references

Acknowledgements

We thank E. Altman, G. Conduit, E. Demler, U. Ebling, A. Eckardt, C. Kollath, M. Lewenstein, A. Recati and W. Zwerger for discussions and B. Fröhlich and M. Feld for contributions to the experimental apparatus. The work has been supported by EPSRC (EP/J01494X/1, EP/K003615/1), the Leverhulme Trust (M. Koschorreck), the Royal Society, the Wolfson Foundation, and the Alexander-von-Humboldt Professorship.

Author information

Authors and Affiliations

  1. Cavendish Laboratory, University of Cambridge, JJ Thomson Avenue, Cambridge CB3 0HE, UK

    Marco Koschorreck, Daniel Pertot, Enrico Vogt & Michael Köhl

  2. Physikalisches Institut, University of Bonn, Wegelerstrasse 8, 53115 Bonn, Germany

    Michael Köhl

Authors
  1. Marco Koschorreck
    View author publications

    Search author on:PubMed Google Scholar

  2. Daniel Pertot
    View author publications

    Search author on:PubMed Google Scholar

  3. Enrico Vogt
    View author publications

    Search author on:PubMed Google Scholar

  4. Michael Köhl
    View author publications

    Search author on:PubMed Google Scholar

Contributions

The measurements were conceived by M. Koschorreck and M. Köhl, data were taken by M. Koschorreck, D.P., and E.V., data analysis and writing of the manuscript was performed by M. Koschorreck and M. Köhl.

Corresponding authors

Correspondence to Marco Koschorreck or Michael Köhl.

Ethics declarations

Competing interests

The authors declare no competing financial interests.

Rights and permissions

Reprints and permissions

About this article

Cite this article

Koschorreck, M., Pertot, D., Vogt, E. et al. Universal spin dynamics in two-dimensional Fermi gases. Nature Phys 9, 405–409 (2013). https://doi.org/10.1038/nphys2637

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue date:

  • DOI: https://doi.org/10.1038/nphys2637

This article is cited by

Search

Advanced search

Quick links

Nature Briefing

Sign up for the Nature Briefing newsletter — what matters in science, free to your inbox daily.

Get the most important science stories of the day, free in your inbox. Sign up for Nature Briefing