Skip to main content

Thank you for visiting nature.com. You are using a browser version with limited support for CSS. To obtain the best experience, we recommend you use a more up to date browser (or turn off compatibility mode in Internet Explorer). In the meantime, to ensure continued support, we are displaying the site without styles and JavaScript.

  • Letter
  • Published:

Topological excitations and the dynamic structure factor of spin liquids on the kagome lattice

Nature Physics volume 10, pages 289–293 (2014)Cite this article

Subjects

An Erratum to this article was published on 03 May 2016

This article has been updated

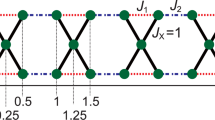
Abstract

Recent neutron scattering experiments on the spin-1/2 kagome lattice antiferromagnet ZnCu3(OH)6Cl2 (Herbertsmithite) provide the first evidence of fractionalized excitations in a quantum spin liquid state in two spatial dimensions1. In contrast to existing theoretical models of both gapped and gapless spin liquids2,3,4,5,6,7,8, which give rise to sharp dispersing features in the dynamic structure factor9,10, the measured dynamic structure factor reveals an excitation continuum that is remarkably flat as a function of frequency. Here we show that many experimentally observed features can be explained by the presence of topological vison excitations in a Z2 spin liquid11. These visons form flat bands on the kagome lattice, and thus act as a momentum sink for spin-carrying excitations that are probed by neutron scattering. We compute the dynamic structure factor for two different Z2 spin liquids2 and find that our results for one of them are in qualitative agreement with the neutron scattering experiments above a very low energy cutoff, below which the structure factor is probably dominated by impurities.

This is a preview of subscription content, access via your institution

Access options

Buy this article

  • Purchase on SpringerLink
  • Instant access to the full article PDF.

USD 39.95

Prices may be subject to local taxes which are calculated during checkout

Figure 1: Density plots of the the dynamic spin-structure factor S(k, ω) for the Q1 = Q2 spin liquid state.
Figure 2: Feynman diagrams for the spinon self energy and spin susceptibility for the theory in equation (2).
Figure 3: Qualitative comparison between experimental measurements1 and our theoretical results for the dynamic structure factor S(k, ω).

Similar content being viewed by others

Change history

  • 22 April 2016

    In the version of this Letter originally published square root symbols were mistakenly included in the x-axis tick labels in Figure 3a-d. This has now been corrected in the online versions of the Letter.

References

  1. Han, T-H. et al. Fractionalized excitations in the spin-liquid state of a kagome-lattice antiferromagnet. Nature 492, 406–410 (2012).

    Article  ADS  Google Scholar 

  2. Sachdev, S. Kagome- and triangular-lattice Heisenberg antiferromagnets: Ordering from quantum fluctuations and quantum-disordered ground states with unconfined bosonic spinons. Phys. Rev. B 45, 12377 (1992).

    Article  ADS  Google Scholar 

  3. Wang, F. & Vishwanath, A. Spin-liquid states on the triangular and Kagome lattices: A projective-symmetry-group analysis of Schwinger boson states. Phys. Rev. B 74, 174423 (2006).

    Article  ADS  Google Scholar 

  4. Lu, Y-M., Ran, Y. & Lee, P. A. Z2 spin liquids in the S =1/2 Heisenberg model on the kagome lattice: A projective symmetry-group study of Schwinger fermion mean-field states. Phys. Rev. B 83, 224413 (2011).

    Article  ADS  Google Scholar 

  5. Iqbal, Y., Becca, F. & Poilblanc, D. Projected wave function study of Z2 spin liquids on the kagome lattice for the spin-1/2 quantum Heisenberg antiferromagnet. Phys. Rev. B 84, 020407 (2011).

    Article  ADS  Google Scholar 

  6. Tay, T. & Motrunich, O. I. Variational study of J1−J2 Heisenberg model on kagome lattice using projected Schwinger-boson wave functions. Phys. Rev. B 84, 020404(R) (2011).

    Article  ADS  Google Scholar 

  7. Tay, T. & Motrunich, O. I. Sign structures for short-range RVB states on small kagome clusters. Phys. Rev. B 84, 193102 (2011).

    Article  ADS  Google Scholar 

  8. Hao, Z. & Tchernyshyov, O. Spin-1/2 Heisenberg antiferromagnet on the kagome lattice: Z2 spin liquid with fermionic spinons. Phys. Rev. B 87, 214404 (2013).

    Article  ADS  Google Scholar 

  9. Messio, L., Cepas, O. & Lhullier, C. Schwinger-boson approach to the kagome antiferromagnet with Dzyaloshinskii–Moriya interactions: Phase diagram and dynamical structure factors. Phys. Rev. B 81, 064428 (2010).

    Article  ADS  Google Scholar 

  10. Dodds, T., Bhattacharjee, S. & Kim, Y. B. Quantum spin liquids in the absence of spin-rotation symmetry: Application to Herbertsmithite. Phys. Rev. B 88, 224413 (2013).

    Article  ADS  Google Scholar 

  11. Senthil, T. & Fisher, M. P. A. Z2 gauge theory of electron fractionalization in strongly correlated systems. Phys. Rev. B 62, 7850–7881 (2000).

    Article  ADS  Google Scholar 

  12. Shores, M. P., Nytko, E. A., Bartlett, B. M. & Nocera, D. G. A structurally perfect s=1/2 kagome antiferromagnet. J. Am. Chem. Soc. 127, 13462–13463 (2005).

    Article  Google Scholar 

  13. De Vries, M. A. et al. Scale-free antiferromagnetic fluctuations in the s=1/2 kagome antiferromagnet herbertsmithite. Phys. Rev. Lett. 103, 237201 (2009).

    Article  ADS  Google Scholar 

  14. Helton, J. S. et al. Spin dynamics of the spin−1/2 kagome lattice antiferromagnet ZnCu3(OH)6Cl2 . Phys. Rev. Lett. 98, 107204 (2007).

    Article  ADS  Google Scholar 

  15. Read, N. & Chakraborty, B. Statistics of the excitations of the resonating-valence-bond state. Phys. Rev. B 40, 7133–7140 (1989).

    Article  ADS  Google Scholar 

  16. Kivelson, S. Statistics of holons in the quantum hard-core dimer gas. Phys. Rev. B 39, 259–264 (1989).

    Article  ADS  Google Scholar 

  17. Read, N. & Sachdev, S. Large-N expansion for frustrated quantum antiferromagnets. Phys. Rev. Lett. 66, 1773–1776 (1991).

    Article  ADS  Google Scholar 

  18. Wen, X-G. Mean-field theory of spin-liquid states with finite energy gap and topological orders. Phys. Rev. B 44, 2664–2672 (1991).

    Article  ADS  Google Scholar 

  19. Nikolic, P. & Senthil, T. Physics of low-energy singlet states of the kagome lattice quantum Heisenberg antiferromagnet. Phys. Rev. B 68, 214415 (2003).

    Article  ADS  Google Scholar 

  20. Huh, Y., Punk, M. & Sachdev, S. Vison states and confinement transitions of Z2 spin liquids on the kagome lattice. Phys. Rev. B 84, 094419 (2011).

    Article  ADS  Google Scholar 

  21. Yan, S., Huse, D. A. & White, S. R. Spin-liquid ground state of the s=1/2 kagome Heisenberg antiferromagnet. Science 332, 1173–1176 (2011).

    Article  ADS  Google Scholar 

  22. Jiang, H. C., Wang, Z. & Balents, L. Identifying topological order by entanglement entropy. Nature Phys. 8, 902–905 (2012).

    Article  ADS  Google Scholar 

  23. Depenbrock, S., McCulloch, I. P. & Schollwöck, U. Nature of the spin-liquid ground state of the s=1/2 Heisenberg model on the kagome lattice. Phys. Rev. Lett. 109, 067201 (2012).

    Article  ADS  Google Scholar 

  24. Wegner, F. Duality in generalized Ising models and phase transitions without local order parameters. J. Math. Phys. 12, 2259–2272 (1971).

    Article  ADS  MathSciNet  Google Scholar 

  25. Bert, F. et al. Low temperature magnetization of the S =1/2 kagome antiferromagnet ZnCu3(OH)6Cl2 . Phys. Rev. B 76, 132411 (2007).

    Article  ADS  Google Scholar 

  26. Nilsen, G. J., de Vries, M. A., Stewart, J. R., Harrison, A. & Ronnow, H. M. Low-energy spin dynamics of the s=1/2 kagome system herbertsmithite. J. Phys. Condens. Matter 25, 106001 (2013).

    Article  ADS  Google Scholar 

  27. Huh, Y., Fritz, L. & Sachdev, S. Quantum criticality of the kagome antiferromagnet with Dzyaloshinskii–Moriya interactions. Phys. Rev. B 81, 144432 (2010).

    Article  ADS  Google Scholar 

  28. Laeuchli, A. M. & Lhuillier, C. Dynamical correlations of the kagome s=1/2 Heisenberg quantum antiferromagnet. Preprint available at http://arxiv.org/0901.1065

Download references

Acknowledgements

We acknowledge illuminating discussions with M. Babadi, S. Gopalakrishnan, M. Lawler, J. D. Sau and especially Y. S. Lee. Furthermore, we thank T-H. Han and Y. S. Lee for providing the neutron scattering data shown in Fig. 3. This research was supported by the US NSF under Grant DMR-1103860 and by the John Templeton Foundation. This research was also supported in part by the Perimeter Institute for Theoretical Physics; research at the Perimeter Institute is supported by the Government of Canada through Industry Canada and by the Province of Ontario through the Ministry of Research and Innovation. M.P. is supported by the Erwin Schrödinger Fellowship J 3077-N16 of the Austrian Science Fund (FWF). The computations were performed in part on the Odyssey cluster supported by the FAS Science Division Research Computing Group at Harvard University.

Author information

Authors and Affiliations

  1. Department of Physics, Harvard University, Cambridge, Massachussetts 02138, USA

    Matthias Punk, Debanjan Chowdhury & Subir Sachdev

  2. Institute for Theoretical Physics, University of Innsbruck, 6020 Innsbruck, Austria

    Matthias Punk

Authors
  1. Matthias Punk
    View author publications

    Search author on:PubMed Google Scholar

  2. Debanjan Chowdhury
    View author publications

    Search author on:PubMed Google Scholar

  3. Subir Sachdev
    View author publications

    Search author on:PubMed Google Scholar

Contributions

M.P. performed the numerical computations. M.P., D.C. and S.S. contributed to the theoretical research described in the paper and the writing of the manuscript.

Corresponding author

Correspondence to Subir Sachdev.

Ethics declarations

Competing interests

The authors declare no competing financial interests.

Supplementary information

Supplementary Information

Supplementary Information (PDF 828 kb)

Rights and permissions

Reprints and permissions

About this article

Cite this article

Punk, M., Chowdhury, D. & Sachdev, S. Topological excitations and the dynamic structure factor of spin liquids on the kagome lattice. Nature Phys 10, 289–293 (2014). https://doi.org/10.1038/nphys2887

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue date:

  • DOI: https://doi.org/10.1038/nphys2887

This article is cited by

Search

Advanced search

Quick links

Nature Briefing

Sign up for the Nature Briefing newsletter — what matters in science, free to your inbox daily.

Get the most important science stories of the day, free in your inbox. Sign up for Nature Briefing