Skip to main content

Thank you for visiting nature.com. You are using a browser version with limited support for CSS. To obtain the best experience, we recommend you use a more up to date browser (or turn off compatibility mode in Internet Explorer). In the meantime, to ensure continued support, we are displaying the site without styles and JavaScript.

  • Letter
  • Published:

Correlation-induced inhomogeneity in circular quantum dots

Nature Physics volume 2, pages 336–340 (2006)Cite this article

Abstract

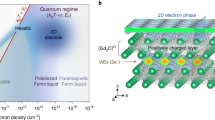
Properties of the ‘electron gas’—in which conduction electrons interact by means of Coulomb forces but ionic potentials are neglected—change dramatically depending on the balance between kinetic energy and Coulomb repulsion. The limits are well understood1. For very weak interactions (high density), the system behaves as a Fermi liquid, with delocalized electrons. In contrast, in the strongly interacting limit (low density), the electrons localize and order into a Wigner crystal phase. The physics at intermediate densities, however, remains a subject of fundamental research2,3,4,5,6,7,8. Here, we study the intermediate-density electron gas confined to a circular disc, where the degree of confinement can be tuned to control the density. Using accurate quantum Monte Carlo techniques9, we show that the electron–electron correlation induced by an increase of the interaction first smoothly causes rings, and then angular modulation, without any signature of a sharp transition in this density range. This suggests that inhomogeneities in a confined system, which exist even without interactions, are significantly enhanced by correlations.

This is a preview of subscription content, access via your institution

Access options

Buy this article

  • Purchase on SpringerLink
  • Instant access to the full article PDF.

USD 39.95

Prices may be subject to local taxes which are calculated during checkout

Figure 1: Electron density, n(r), for the ground state of an N=20 circular quantum dot (L=0, S=0).
Figure 2: Pair density of the circular quantum dot with an up-electron fixed on the outer ring.
Figure 3: Ground-state energy.

Similar content being viewed by others

References

  1. Giuliani, G. & Vignale, G. Quantum Theory of the Electron Liquid (Cambridge Univ. Press, Cambridge, 2005).

    Book  Google Scholar 

  2. Tanatar, B. & Ceperley, D. M. Ground state of the two-dimensional electron gas. Phys. Rev. B 39, 5005–5016 (1989).

    Article  ADS  Google Scholar 

  3. Attaccalite, C., Moroni, S., Gori-Giorgi, P. & Bachelet, G. B. Correlation energy and spin polarization in the 2D electron gas. Phys. Rev. Lett. 88, 256601 (2002).

    Article  ADS  Google Scholar 

  4. Attaccalite, C., Moroni, S., Gori-Giorgi, P. & Bachelet, G. B. Phys. Rev. Lett. 91, 109902(E) (2003).

    Article  ADS  Google Scholar 

  5. Abrahams, E., Kravchenko, S. V. & Sarachik, M. P. Metallic behavior and related phenomena in two dimensions. Rev. Mod. Phys. 73, 251–266 (2001).

    Article  ADS  Google Scholar 

  6. Chakravarty, S., Kivelson, S., Nayak, C. & Voelker, K. Wigner glass, spin liquids, and the metal insulator transition. Phil. Mag. B 79, 859–868 (1999).

    Article  ADS  Google Scholar 

  7. Jamei, R., Kivelson, S. & Spivak, B. Universal aspects of Coulomb-frustrated phase separation. Phys. Rev. Lett. 94, 56805 (2005).

    Article  ADS  Google Scholar 

  8. Waintal, X. On the quantum melting of the two-dimensional Wigner crystal. Phys. Rev. B 73, 75417 (2006).

    Article  ADS  Google Scholar 

  9. Foulkes, W. M. C., Mitas, L., Needs, R. J. & Rajagopal, G. Quantum Monte Carlo simulations of solids. Rev. Mod. Phys. 73, 33–83 (2001).

    Article  ADS  Google Scholar 

  10. Kouwenhoven, L. P., Austing, D. G. & Tarucha, S. Few-electron quantum dots. Rep. Prog. Phys. 64, 701–736 (2001).

    Article  ADS  Google Scholar 

  11. Reuter, D. et al. Coulomb-interaction-induced incomplete shell filling in the hole system of InAs quantum dots. Phys. Rev. Lett. 94, 26808 (2005).

    Article  ADS  Google Scholar 

  12. Reimann, S. M. & Manninen, M. Electronic structure of quantum dots. Rev. Mod. Phys. 74, 1283–1342 (2002).

    Article  ADS  Google Scholar 

  13. Reusch, B. & Grabert, H. Unrestricted Hartree-Fock for quantum dots. Phys. Rev. B 68, 45309 (2003).

    Article  ADS  Google Scholar 

  14. Yannouleas, C. & Landman, U. Unified description of floppy and rigid rotating Wigner molecules formed in quantum dots. Phys. Rev. B 69, 113306 (2004).

    Article  ADS  Google Scholar 

  15. Reimann, S. M., Koskinen, M. & Manninen, M. Formation of Wigner molecules in small quantum dots. Phys. Rev. B 62, 8108–8113 (2000).

    Article  ADS  Google Scholar 

  16. Rontani, M., Cavazzoni, C., Bellucci, D. & Goldoni, G. Full configuration interaction approach to the few-electron problem in artificial atoms.. J. Chem. Phys. 124, 124102 (2006).

    Article  ADS  Google Scholar 

  17. Egger, R., Häusler, W., Mak, C. H. & Grabert, H. Crossover from Fermi liquid to Wigner molecule behavior in quantum dots. Phys. Rev. Lett. 82, 3320–3323 (1999).

    Article  ADS  Google Scholar 

  18. Egger, R., Häusler, W., Mak, C. H. & Grabert, H. Phys. Rev. Lett. 83, 462(E) (1999).

    Article  ADS  Google Scholar 

  19. Filinov, A. V., Bonitz, M. & Lezovik, Yu. E. Wigner crystallization in mesoscopic 2D electron systems. Phys. Rev. Lett. 86, 3851–3854 (2001).

    Article  ADS  Google Scholar 

  20. Pederiva, F., Umrigar, C. J. & Lipparini, E. Diffusion Monte Carlo study of circular quantum dots. Phys. Rev. B 62, 8120–8125 (2000).

    Article  ADS  Google Scholar 

  21. Pederiva, F., Umrigar, C. J. & Lipparini, E. Phys. Rev. B 68, 89901(E) (2003).

    Article  ADS  Google Scholar 

  22. Güçlü, A. D. & Umrigar, C. J. Maximum-density droplet to lower-density droplet transition in quantum dots. Phys. Rev. B 72, 45309 (2005).

    Article  ADS  Google Scholar 

  23. Ghosal, A., Umrigar, C. J., Jiang, H., Ullmo, D. & Baranger, H. U. Interaction effects in the mesoscopic regime: A quantum Monte Carlo study of irregular quantum dots. Phys. Rev. B 71, 241306(R) (2005).

    Article  ADS  Google Scholar 

  24. Bedanov, V. M. & Peeters, F. M. Ordering and phase transitions of charged particles in a classical finite two-dimensional system. Phys. Rev. B 49, 2667–2676 (1994).

    Article  ADS  Google Scholar 

  25. Koulakov, A. A. & Shklovskii, B. I. Charging spectrum and configurations of a Wigner crystal island. Phys. Rev. B 57, 2352–2367 (1998).

    Article  ADS  Google Scholar 

  26. Umrigar, C. J., Wilson, K. G. & Wilkins, J. W. Optimized trial wave functions for quantum Monte Carlo calculations. Phys. Rev. Lett. 60, 1719–1722 (1988).

    Article  ADS  Google Scholar 

  27. Umrigar, C. J. in Quantum Monte Carlo Methods in Physics and Chemistry (eds Nightingale, M. P. & Umrigar, C. J.) 129–160 (Kluwer, Dordrecht, 1999).

    Book  Google Scholar 

  28. Umrigar, C. J., Nightingale, M. P. & Runge, K. J. A diffusion Monte Carlo algorithm with very small time-step errors. J. Chem. Phys. 99, 2865–2890 (1993).

    Article  ADS  Google Scholar 

  29. Liu, K. S., Kalos, M. H. & Chester, G. V. Quantum hard spheres in a channel. Phys. Rev. A 10, 303–308 (1974).

    Article  ADS  Google Scholar 

Download references

Acknowledgements

This work was supported in part by the NSF (grants DMR-0506953 and DMR-0205328). A.G. was supported in part by the funds from the David Saxon chair at UCLA.

Author information

Author notes

  1. Amit Ghosal

    Present address: Physics Department, University of California, Los Angeles, California, 90095-1547, USA

Authors and Affiliations

  1. Department of Physics, Duke University, Durham, North Carolina 27708-0305, USA

    Amit Ghosal, Denis Ullmo & Harold U. Baranger

  2. Theory Center and Laboratory of Atomic and Solid State Physics, Cornell University, Ithaca, New York 14853, USA

    A. D. Güçlü & C. J. Umrigar

  3. CNRS; Univ. Paris-Sud, LPTMS UMR 8626, 91405 Orsay Cedex, France

    Denis Ullmo

Authors
  1. Amit Ghosal
    View author publications

    Search author on:PubMed Google Scholar

  2. A. D. Güçlü
    View author publications

    Search author on:PubMed Google Scholar

  3. C. J. Umrigar
    View author publications

    Search author on:PubMed Google Scholar

  4. Denis Ullmo
    View author publications

    Search author on:PubMed Google Scholar

  5. Harold U. Baranger
    View author publications

    Search author on:PubMed Google Scholar

Corresponding authors

Correspondence to Amit Ghosal or Harold U. Baranger.

Ethics declarations

Competing interests

The authors declare no competing financial interests.

Supplementary information

Supplementary Information

Supplementary Material (PDF 106 kb)

Rights and permissions

Reprints and permissions

About this article

Cite this article

Ghosal, A., Güçlü, A., Umrigar, C. et al. Correlation-induced inhomogeneity in circular quantum dots. Nature Phys 2, 336–340 (2006). https://doi.org/10.1038/nphys293

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue date:

  • DOI: https://doi.org/10.1038/nphys293

This article is cited by

Search

Advanced search

Quick links

Nature Briefing

Sign up for the Nature Briefing newsletter — what matters in science, free to your inbox daily.

Get the most important science stories of the day, free in your inbox. Sign up for Nature Briefing