Skip to main content

Thank you for visiting nature.com. You are using a browser version with limited support for CSS. To obtain the best experience, we recommend you use a more up to date browser (or turn off compatibility mode in Internet Explorer). In the meantime, to ensure continued support, we are displaying the site without styles and JavaScript.

  • Letter
  • Published:

Symmetry-protected topological photonic crystal in three dimensions

Nature Physics volume 12, pages 337–340 (2016)Cite this article

Subjects

Abstract

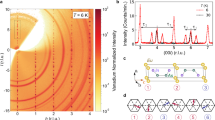
Topology of electron wavefunctions was first introduced to characterize the quantum Hall states in two dimensions discovered in 1980 (ref. 1). Over the past decade, it has been recognized that symmetry plays a crucial role in the classification of topological phases, leading to the broad notion of symmetry-protected topological phases2. As a primary example, topological insulators3,4 are distinguished from normal insulators in the presence of time-reversal symmetry (). 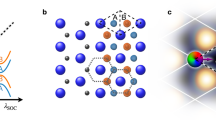A three-dimensional (3D) topological insulator3,4,5,6 exhibits an odd number of protected surface Dirac cones, a unique property that cannot be realized in any 2D systems. Importantly, the existence of topological insulators requires Kramers’ degeneracy in spin–orbit coupled electronic materials; this forbids any direct analogue in boson systems7. In this report, we discover a 3D topological photonic crystal phase hosting a single surface Dirac cone, which is protected by a crystal symmetry8,9,10—the nonsymmorphic glide reflection11,12,13 rather than . Such a gapless surface state is fully robust against random disorder of any type14,15. This bosonic topological band structure is achieved by applying alternating magnetization to gap out the 3D ‘generalized Dirac points’ discovered in the bulk of our crystal. The Z2 bulk invariant is characterized through the evolution of Wannier centres16. Our proposal—readily realizable using ferrimagnetic materials at microwave frequencies17,18—expands the scope of 3D topological materials from fermions to bosons.

This is a preview of subscription content, access via your institution

Access options

Buy this article

  • Purchase on SpringerLink
  • Instant access to the full article PDF.

USD 39.95

Prices may be subject to local taxes which are calculated during checkout

Figure 1: BP I photonic crystal.
Figure 2: The (001) surface states after breaking .
Figure 3: Hybrid Wannier centres in the surface BZ indicating bulk topologies and the connections of the surface states.

Similar content being viewed by others

References

  1. Thouless, D. J., Kohmoto, M., Nightingale, M. P. & den Nijs, M. Quantized Hall conductance in a two-dimensional periodic potential. Phys. Rev. Lett. 49, 405–408 (1982).

    Article  ADS  Google Scholar 

  2. Chiu, C.-K., Teo, J. C. Y., Schnyder, A. P & Ryu, S. Classification of topological quantum matter with symmetries. Preprint at http://arXiv.org/abs/1505.03535 (2015).

  3. Hasan, M. & Kane, C. Colloquium: Topological insulators. Rev. Mod. Phys. 82, 3045–3067 (2010).

    Article  ADS  Google Scholar 

  4. Qi, X.-L. & Zhang, S.-C. Topological insulators and superconductors. Rev. Mod. Phys. 83, 1057–1110 (2011).

    Article  ADS  Google Scholar 

  5. Zhang, H. et al. Topological insulators in Bi2Se3, Bi2Te3 and Sb2Te3 with a single Dirac cone on the surface. Nature Phys. 5, 438–442 (2009).

    Article  ADS  Google Scholar 

  6. Moore, J. E. The birth of topological insulators. Nature 464, 194–198 (2010).

    Article  ADS  Google Scholar 

  7. Lu, L., Joannopoulos, J. D. & Soljačić, M. Topological photonics. Nature Photon. 8, 821–829 (2014).

    Article  ADS  Google Scholar 

  8. Fu, L. Topological crystalline insulators. Phys. Rev. Lett. 106, 106802 (2011).

    Article  ADS  Google Scholar 

  9. Hsieh, T. H. et al. Topological crystalline insulators in the SnTe material class. Nature Commun. 3, 982 (2012).

    Article  ADS  Google Scholar 

  10. Ando, Y. & Fu, L. Topological crystalline insulators and topological superconductors: From concepts to materials. Annu. Rev. Condens. Matter Phys. 6, 361–381 (2015).

    Article  ADS  Google Scholar 

  11. Liu, C.-X., Zhang, R.-X. & VanLeeuwen, B. K. Topological nonsymmorphic crystalline insulators. Phys. Rev. B 90, 085304 (2014).

    Article  ADS  Google Scholar 

  12. Fang, C. & Fu, L. New classes of three-dimensional topological crystalline insulators: Nonsymmorphic and magnetic. Phys. Rev. B 91, 161105 (2015).

    Article  ADS  Google Scholar 

  13. Shiozaki, K., Sato, M. & Gomi, K. Z 2 topology in nonsymmorphic crystalline insulators: Möbius twist in surface states. Phys. Rev. B 91, 155120 (2015).

    Article  ADS  Google Scholar 

  14. Fu, L. & Kane, C. L. Topology, delocalization via average symmetry and the symplectic Anderson transition. Phys. Rev. Lett. 109, 246605 (2012).

    Article  ADS  Google Scholar 

  15. Fulga, I. C., van Heck, B., Edge, J. M. & Akhmerov, A. R. Statistical topological insulators. Phys. Rev. B 89, 155424 (2014).

    Article  ADS  Google Scholar 

  16. Taherinejad, M., Garrity, K. F. & Vanderbilt, D. Wannier center sheets in topological insulators. Phys. Rev. B 89, 115102 (2014).

    Article  ADS  Google Scholar 

  17. Wang, Z., Chong, Y., Joannopoulos, J. D. & Soljačić, M. Observation of unidirectional backscattering-immune topological electromagnetic states. Nature 461, 772–775 (2009).

    Article  ADS  Google Scholar 

  18. Skirlo, S. A., Lu, L., Igarashi, Y., Joannopoulos, J. & Soljacic, M. Experimental observation of large chern numbers in photonic crystals. Preprint at http://arXiv.org/abs/1504.04399 (2015).

  19. Varjas, D., de Juan, F. & Lu, Y.-M. Bulk invariants and topological response in insulators and superconductors with nonsymmorphic symmetries. Phys. Rev. B 92, 195116 (2015).

    Article  ADS  Google Scholar 

  20. Meiboom, S., Sammon, M. & Berreman, D. W. Lattice symmetry of the cholesteric blue phases. Phys. Rev. A 28, 3553–3560 (1983).

    Article  ADS  Google Scholar 

  21. Young, S. M. et al. Dirac semimetal in three dimensions. Phys. Rev. Lett. 108, 140405 (2012).

    Article  ADS  Google Scholar 

  22. Liu, Z. K. et al. Discovery of a three-dimensional topological Dirac semimetal, Na3Bi. Science 343, 864–867 (2014).

    Article  ADS  Google Scholar 

  23. Wang, Z., Weng, H., Wu, Q., Dai, X. & Fang, Z. Three-dimensional Dirac semimetal and quantum transport in Cd3As2 . Phys. Rev. B 88, 125427 (2013).

    Article  ADS  Google Scholar 

  24. Lu, L., Fu, L., Joannopoulos, J. D. & Soljačić, M. Weyl points and line nodes in gyroid photonic crystals. Nature Photon. 7, 294–299 (2013).

    Article  ADS  Google Scholar 

  25. Lu, L. et al. Experimental observation of Weyl points. Science 349, 622–624 (2015).

    Article  ADS  MathSciNet  Google Scholar 

  26. Mock, A., Lu, L. & O’Brien, J. Space group theory and Fourier space analysis of two-dimensional photonic crystal waveguides. Phys. Rev. B 81, 155115 (2010).

    Article  ADS  Google Scholar 

  27. Lu, L. et al. Three-dimensional photonic crystals by large-area membrane stacking. Opt. Lett. 37, 4726–4728 (2012).

    Article  ADS  Google Scholar 

  28. Parameswaran, S. A., Turner, A. M., Arovas, D. P. & Vishwanath, A. Topological order and absence of band insulators at integer filling in non-symmorphic crystals. Nature Phys. 9, 299–303 (2013).

    Article  ADS  Google Scholar 

  29. Roy, R. Space group symmetries and low lying excitations of many-body systems at integer fillings. Preprint at http://arXiv.org/abs/1212.2944 (2012).

  30. Young, S. M. & Kane, C. L. Dirac semimetals in two dimensions. Phys. Rev. Lett. 115, 126803 (2015).

    Article  ADS  Google Scholar 

  31. Watanabe, H., Po, H. C., Vishwanath, A. & Zaletel, M. Filling constraints for spin–orbit coupled insulators in symmorphic and nonsymmorphic crystals. Proc. Natl Acad. Sci. USA 112, 14551–14556 (2015).

    Article  ADS  Google Scholar 

  32. Haldane, F. D. M. & Raghu, S. Possible realization of directional optical waveguides in photonic crystals with broken time-reversal symmetry. Phys. Rev. Lett. 100, 013904 (2008).

    Article  ADS  Google Scholar 

  33. Yu, R., Qi, X. L., Bernevig, A., Fang, Z. & Dai, X. Equivalent expression of Z2 topological invariant for band insulators using the non-abelian Berry connection. Phys. Rev. B 84, 075119 (2011).

    Article  ADS  Google Scholar 

  34. Alexandradinata, A., Dai, X. & Bernevig, B. A. Wilson-loop characterization of inversion-symmetric topological insulators. Phys. Rev. B 89, 155114 (2014).

    Article  ADS  Google Scholar 

  35. Ludwig, A. W. W., Fisher, M. P. A., Shankar, R. & Grinstein, G. Integer quantum Hall transition: An alternative approach and exact results. Phys. Rev. B 50, 7526–7552 (1994).

    Article  ADS  Google Scholar 

  36. Bardarson, J. H., Tworzydło, J., Brouwer, P. W. & Beenakker, C. W. J. One-parameter scaling at the Dirac point in graphene. Phys. Rev. Lett. 99, 106801 (2007).

    Article  ADS  Google Scholar 

  37. Khanikaev, A. B. et al. Photonic topological insulators. Nature Mater. 12, 233–239 (2013).

    Article  ADS  Google Scholar 

  38. Chen, W.-J. et al. Experimental realization of photonic topological insulator in a uniaxial metacrystal waveguide. Nature Commun. 5, 5782 (2014).

    Article  ADS  Google Scholar 

  39. Wu, L.-H. & Hu, X. Scheme for achieving a topological photonic crystal by using dielectric material. Phys. Rev. Lett. 114, 223901 (2015).

    Article  ADS  Google Scholar 

  40. Fang, K., Yu, Z. & Fan, S. Realizing effective magnetic field for photons by controlling the phase of dynamic modulation. Nature Photon. 6, 782–787 (2012).

    Article  ADS  Google Scholar 

  41. Rechtsman, M. C. et al. Photonic Floquet topological insulators. Nature 496, 196–200 (2013).

    Article  ADS  Google Scholar 

  42. Wang, P., Lu, L. & Bertoldi, K. Topological phononic crystals with one-way elastic edge waves. Phys. Rev. Lett. 115, 104302 (2015).

    Article  ADS  Google Scholar 

  43. Liu, C.-X. Antiferromagnetic crystalline topological insulators. Preprint at http://arXiv.org/abs/1304.6455 (2013).

  44. Alexandradinata, A., Fang, C., Gilbert, M. J. & Bernevig, B. A. Spin–orbit-free topological insulators without time-reversal symmetry. Phys. Rev. Lett. 113, 116403 (2014).

    Article  ADS  Google Scholar 

  45. Wang, Z., Alexandradinata, A., Cava, R. J. & Bernevig, B. A. (in review, 2015).

Download references

Acknowledgements

We thank T. H. Hsieh, A. Alexandradinata, B. Andrei Bernevig, S. Skirlo, A. Men, J. Liu and F. Wang for discussions. S.G.J. and J.D.J. were supported in part by the US ARO. through the ISN, under Contract No. W911NF-13-D-0001. C.F. and L.F. were supported by the DOE Office of Basic Energy Sciences, Division of Materials Sciences and Engineering under Award No. DE-SC0010526. L.L. was supported in part by the MRSEC Program of the NSF under Award No. DMR-1419807. M.S. and L.L. (analysis and reading of the manuscript) were supported in part by the MIT S3TEC EFRC of DOE under Grant No. DE-SC0001299.

Author information

Author notes

  1. Chen Fang

    Present address: Present address: Beijing National Laboratory for Condensed Matter Physics, and Institute of Physics, Chinese Academy of Sciences, Beijing 100190, China.,

  2. Ling Lu and Chen Fang: These authors contributed equally to this work.

Authors and Affiliations

  1. Department of Physics, Massachusetts Institute of Technology, Cambridge, Massachusetts 02139, USA

    Ling Lu, Chen Fang, Liang Fu, John D. Joannopoulos & Marin Soljačić

  2. Department of Mathematics, Massachusetts Institute of Technology, Cambridge, Massachusetts 02139, USA

    Steven G. Johnson

Authors
  1. Ling Lu
    View author publications

    Search author on:PubMed Google Scholar

  2. Chen Fang
    View author publications

    Search author on:PubMed Google Scholar

  3. Liang Fu
    View author publications

    Search author on:PubMed Google Scholar

  4. Steven G. Johnson
    View author publications

    Search author on:PubMed Google Scholar

  5. John D. Joannopoulos
    View author publications

    Search author on:PubMed Google Scholar

  6. Marin Soljačić
    View author publications

    Search author on:PubMed Google Scholar

Contributions

L.L. proposed the BP I structure and performed the calculations with the help of S.G.J. and C.F.; C.F. and L.F. conceived and analysed the band topology; all authors contributed to the discussion of the results and preparation of the manuscript.

Corresponding authors

Correspondence to Ling Lu or Liang Fu.

Ethics declarations

Competing interests

The authors declare no competing financial interests.

Supplementary information

Supplementary information

Supplementary information (PDF 611 kb)

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Lu, L., Fang, C., Fu, L. et al. Symmetry-protected topological photonic crystal in three dimensions. Nature Phys 12, 337–340 (2016). https://doi.org/10.1038/nphys3611

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue date:

  • DOI: https://doi.org/10.1038/nphys3611

This article is cited by

Search

Advanced search

Quick links

Nature Briefing

Sign up for the Nature Briefing newsletter — what matters in science, free to your inbox daily.

Get the most important science stories of the day, free in your inbox. Sign up for Nature Briefing