Skip to main content

Thank you for visiting nature.com. You are using a browser version with limited support for CSS. To obtain the best experience, we recommend you use a more up to date browser (or turn off compatibility mode in Internet Explorer). In the meantime, to ensure continued support, we are displaying the site without styles and JavaScript.

  • Letter
  • Published:

Engineered swift equilibration of a Brownian particle

Nature Physics volume 12, pages 843–846 (2016)Cite this article

Subjects

Abstract

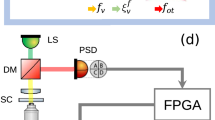
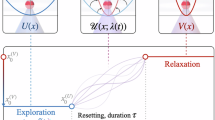
A fundamental and intrinsic property of any device or natural system is its relaxation time τrelax, which is the time it takes to return to equilibrium after the sudden change of a control parameter1. Reducing τrelax is frequently necessary, and is often obtained by a complex feedback process. To overcome the limitations of such an approach, alternative methods based on suitable driving protocols have been recently demonstrated2,3, for isolated quantum and classical systems4,5,6,7,8,9. Their extension to open systems in contact with a thermostat is a stumbling block for applications. Here, we design a protocol, named Engineered Swift Equilibration (ESE), that shortcuts time-consuming relaxations, and we apply it to a Brownian particle trapped in an optical potential whose properties can be controlled in time. We implement the process experimentally, showing that it allows the system to reach equilibrium 100 times faster than the natural equilibration rate. We also estimate the increase of the dissipated energy needed to get such a time reduction. The method paves the way for applications in micro- and nano-devices, where the reduction of operation time represents as substantial a challenge as miniaturization10.

This is a preview of subscription content, access via your institution

Access options

Buy this article

  • Purchase on SpringerLink
  • Instant access to the full article PDF.

USD 39.95

Prices may be subject to local taxes which are calculated during checkout

Figure 1: Sketch of the process.
Figure 2: Dynamics of the system along the STEP and ESE protocol.
Figure 3: Energetics of the ESE protocol.

Similar content being viewed by others

References

  1. Boltzmann, L. Lectures on Gas Theory (Univ. California Press, 1964).

    Book  Google Scholar 

  2. Torrontegui, E. et al. Shortcuts to adiabaticity. Adv. At. Mol. Opt. Phys. 62, 117–169 (2013).

    Article  ADS  Google Scholar 

  3. Deffner, S., Jarzynski, C. & del Campo, A. Classical and quantum shortcuts to adiabaticity for scale-invariant driving. Phys. Rev. X 4, 021013 (2014).

    Google Scholar 

  4. Couvert, A., Kawalec, T., Reinaudi, G. & Guéry-Odelin, D. Optimal transport of ultracold atoms in the non-adiabatic regime. Europhys. Lett. 83, 13001 (2008).

    Article  ADS  Google Scholar 

  5. Schaff, J.-F., Song, X.-L., Vignolo, P. & Labeyrie, G. Fast optimal transition between two equilibrium states. Phys. Rev. A 82, 033430 (2010).

    Article  ADS  Google Scholar 

  6. Schaff, J.-F., Song, X.-L., Capuzzi, P., Vignolo, P. & Labeyrie, G. Shortcut to adiabaticity for an interacting Bose–Einstein condensate. Europhys. Lett. 93, 23001 (2011).

    Article  ADS  Google Scholar 

  7. Bason, M. G. et al. High-fidelity quantum driving. Nature Phys. 8, 147–152 (2012).

    Article  ADS  Google Scholar 

  8. Bowler, R. et al. Coherent diabatic ion transport and separation in a multizone trap array. Phys. Rev. Lett. 109, 080502 (2012).

    Article  ADS  Google Scholar 

  9. Walther, A. et al. Controlling fast transport of cold trapped ions. Phys. Rev. Lett. 109, 080501 (2012).

    Article  ADS  Google Scholar 

  10. Peercy, P. S. The drive to miniaturization. Nature 406, 1023–1026 (2000).

    Article  Google Scholar 

  11. Maxwell, J. C. On the dynamical theory of gases. Phil. Trans. R. Soc. Lond. 157, 49–88 (1867).

    Article  ADS  Google Scholar 

  12. Chen, X. et al. Fast optimal frictionless atom cooling in harmonic traps: shortcut to adiabaticity. Phys. Rev. Lett. 104, 063002 (2010).

    Article  ADS  Google Scholar 

  13. Guéry-Odelin, D., Muga, J., Ruiz-Montero, M. & Trizac, E. Nonequilibrium solutions of the Boltzmann equation under the action of an external force. Phys. Rev. Lett. 112, 180602 (2014).

    Article  ADS  Google Scholar 

  14. Papoular, D. & Stringari, S. Shortcut to adiabaticity for an anisotropic gas containing quantum defects. Phys. Rev. Lett. 115, 025302 (2015).

    Article  ADS  Google Scholar 

  15. Tseng, S.-Y. & Chen, X. Engineering of fast mode conversion in multimode waveguides. Opt. Lett. 37, 5118–5120 (2012).

    Article  ADS  Google Scholar 

  16. Tseng, S.-Y. Robust coupled-waveguide devices using shortcuts to adiabaticity. Opt. Lett. 39, 6600–6603 (2014).

    Article  ADS  Google Scholar 

  17. Ho, C.-P. & Tseng, S.-Y. Optimization of adiabaticity in coupled-waveguide devices using shortcuts to adiabaticity. Opt. Lett. 40, 4831–4834 (2015).

    Article  ADS  Google Scholar 

  18. Stefanatos, D. Design of a photonic lattice using shortcuts to adiabaticity. Phys. Rev. A 90, 023811 (2014).

    Article  ADS  Google Scholar 

  19. Kaka, S. et al. Mutual phase-locking of microwave spin torque nano-oscillators. Nature 437, 389–392 (2005).

    Article  ADS  Google Scholar 

  20. Martínez, I. A. et al. Brownian Carnot engine. Nature Phys. 12, 67–70 (2016).

    Article  ADS  Google Scholar 

  21. Collin, D. et al. Verification of the Crooks fluctuation theorem and recovery of RNA folding free energies. Nature 437, 231–234 (2005).

    Article  ADS  Google Scholar 

  22. Cui, Y.-Y., Chen, X. & Muga, J. G. Transient particle energies in shortcuts to adiabatic expansions of harmonic traps. J. Phys. Chem. A http://dx.doi.org/10.1021/acs.jpca.5b06090 (2015).

  23. Schmiedl, T. & Seifert, U. Optimal finite-time processes in stochastic thermodynamics. Phys. Rev. Lett. 98, 108301 (2007).

    Article  ADS  Google Scholar 

  24. Schmiedl, T. & Seifert, U. Efficiency at maximum power: an analytically solvable model for stochastic heat engines. Europhys. Lett. 81, 20003 (2008).

    Article  ADS  MathSciNet  Google Scholar 

  25. Aurell, E., Gawedzki, K., Mejia-Monasterio, C., Mohayaee, R. & Muratore-Ginanneschi, P. Refined second law of thermodynamics for fast random processes. J. Stat. Phys. 147, 487–505 (2012).

    Article  ADS  MathSciNet  Google Scholar 

  26. Acconcia, T. V., Bonança, M. V. S. & Deffner, S. Shortcuts to adiabaticity from linear response theory. Phys. Rev. E 92, 042148 (2015).

    Article  ADS  MathSciNet  Google Scholar 

  27. Zheng, Y., Campbell, S., De Chiara, G. & Poletti, D. Cost of transitionless driving and work output. Preprint at http://arXiv.org/abs/1509.01882 (2016).

  28. Neuman, K. C. & Block, S. M. Optical trapping. Rev. Sci. Instrum. 75, 2787–2809 (2004).

    Article  ADS  Google Scholar 

  29. Sekimoto, K. Stochastic Energetics Vol. 799 (Springer, 2010).

    Book  Google Scholar 

  30. Barrat, J.-L. & Hansen, J.-P. Basic Concepts for Simple and Complex Liquids (Cambridge Univ. Press, 2003).

    Book  Google Scholar 

  31. Risken, H. The Fokker-Planck Equation (Springer, 1984).

    Book  Google Scholar 

  32. Sivak, D. A. & Crooks, G. E. Thermodynamic metrics and optimal paths. Phys. Rev. Lett. 108, 190602 (2012).

    Article  ADS  Google Scholar 

  33. Bonança, M. & Deffner, S. Optimal driving of isothermal processes close to equilibrium. J. Chem. Phys. 140, 244119 (2014).

    Article  ADS  Google Scholar 

Download references

Acknowledgements

We would like to thank B. Derrida for useful discussions. I.A.M., A.P. and S.C. acknowledge financial support from the European Research Council Grant OUTEFLUCOP.

Author information

Authors and Affiliations

  1. Laboratoire de Physique, CNRS UMR5672 Université de Lyon, École Normale Supérieure, 46 Allée d’Italie, 69364 Lyon, France

    Ignacio A. Martínez, Artyom Petrosyan & Sergio Ciliberto

  2. Laboratoire Collisions Agrégats Réactivité, CNRS UMR5589, Université de Toulouse, 31062 Toulouse, France

    David Guéry-Odelin

  3. LPTMS, CNRS, Univ. Paris-Sud, Université Paris-Saclay, 91405 Orsay, France

    Emmanuel Trizac

Authors
  1. Ignacio A. Martínez
    View author publications

    Search author on:PubMed Google Scholar

  2. Artyom Petrosyan
    View author publications

    Search author on:PubMed Google Scholar

  3. David Guéry-Odelin
    View author publications

    Search author on:PubMed Google Scholar

  4. Emmanuel Trizac
    View author publications

    Search author on:PubMed Google Scholar

  5. Sergio Ciliberto
    View author publications

    Search author on:PubMed Google Scholar

Contributions

All authors contributed substantially to this work.

Corresponding author

Correspondence to Sergio Ciliberto.

Ethics declarations

Competing interests

The authors declare no competing financial interests.

Supplementary information

Supplementary information

Supplementary information (PDF 3035 kb)

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Martínez, I., Petrosyan, A., Guéry-Odelin, D. et al. Engineered swift equilibration of a Brownian particle. Nature Phys 12, 843–846 (2016). https://doi.org/10.1038/nphys3758

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue date:

  • DOI: https://doi.org/10.1038/nphys3758

This article is cited by

Search

Advanced search

Quick links

Nature Briefing

Sign up for the Nature Briefing newsletter — what matters in science, free to your inbox daily.

Get the most important science stories of the day, free in your inbox. Sign up for Nature Briefing