Skip to main content

Thank you for visiting nature.com. You are using a browser version with limited support for CSS. To obtain the best experience, we recommend you use a more up to date browser (or turn off compatibility mode in Internet Explorer). In the meantime, to ensure continued support, we are displaying the site without styles and JavaScript.

  • Letter
  • Published:

Superconducting qubit–oscillator circuit beyond the ultrastrong-coupling regime

Nature Physics volume 13, pages 44–47 (2017)Cite this article

Subjects

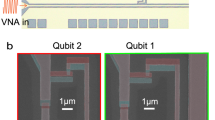
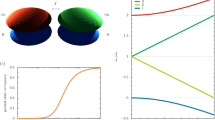
Abstract

The interaction between an atom and the electromagnetic field inside a cavity1,2,3,4,5,6 has played a crucial role in developing our understanding of light–matter interaction, and is central to various quantum technologies, including lasers and many quantum computing architectures. Superconducting qubits7,8 have allowed the realization of strong9,10 and ultrastrong11,12,13 coupling between artificial atoms and cavities. If the coupling strength g becomes as large as the atomic and cavity frequencies (Δ and ωo, respectively), the energy eigenstates including the ground state are predicted to be highly entangled14. There has been an ongoing debate15,16,17 over whether it is fundamentally possible to realize this regime in realistic physical systems. By inductively coupling a flux qubit and an LC oscillator via Josephson junctions, we have realized circuits with g/ωo ranging from 0.72 to 1.34 and g/Δ ≫ 1. Using spectroscopy measurements, we have observed unconventional transition spectra that are characteristic of this new regime. Our results provide a basis for ground-state-based entangled pair generation and open a new direction of research on strongly correlated light–matter states in circuit quantum electrodynamics.

This is a preview of subscription content, access via your institution

Access options

Buy this article

  • Purchase on SpringerLink
  • Instant access to the full article PDF.

USD 39.95

Prices may be subject to local taxes which are calculated during checkout

Figure 1: Superconducting qubit–oscillator circuit.
Figure 2: Transmission spectra for circuits I and II.
Figure 3: Selection rules and transmission spectrum around the symmetry point.

Similar content being viewed by others

References

  1. Wineland, D. J. & Itano, W. M. Spectroscopy of a single Mg+ ion. Phys. Lett. A 82, 75–78 (1981).

    Article  ADS  Google Scholar 

  2. Haroche, S. & Raimond, J. M. Cavity quantum electrodynamics. Sci. Am. 268, 54–60 (1993).

    Article  Google Scholar 

  3. Brune, M. et al. Quantum Rabi oscillation: a direct test of field quantization in a cavity. Phys. Rev. Lett. 76, 1800–1803 (1996).

    Article  ADS  Google Scholar 

  4. Raimond, J. M., Brune, M. & Haroche, S. Manipulating quantum entanglement with atoms and photons in a cavity. Rev. Mod. Phys. 73, 565–582 (2001).

    Article  ADS  MathSciNet  Google Scholar 

  5. Mabuchi, H. & Doherty, A. C. Cavity quantum electrodynamics: coherence in context. Science 298, 1372–1377 (2002).

    Article  ADS  Google Scholar 

  6. Walls, D. F. & Milburn, G. J. Quantum Optics (Springer Science & Business Media, 2007).

    MATH  Google Scholar 

  7. Nakamura, Y., Pashkin, Yu. A. & Tsai, J. S. Coherent control of macroscopic quantum states in a single-Cooper-pair box. Nature 398, 786–788 (1999).

    Article  ADS  Google Scholar 

  8. Clarke, J. & Wilhelm, F. K. Superconducting quantum bits. Nature 453, 1031–1042 (2008).

    Article  ADS  Google Scholar 

  9. Chiorescu, I. et al. Coherent dynamics of a flux qubit coupled to a harmonic oscillator. Nature 431, 159–162 (2004).

    Article  ADS  Google Scholar 

  10. Wallraff, A. et al. Strong coupling of a single photon to a superconducting qubit using circuit quantum electrodynamics. Nature 431, 162–167 (2004).

    Article  ADS  Google Scholar 

  11. Devoret, M., Girvin, S. & Schoelkopf, R. Circuit-QED: how strong can the coupling between a Josephson junction atom and a transmission line resonator be? Ann. Phys. 16, 767–769 (2007).

    Article  Google Scholar 

  12. Niemczyk, T. et al. Circuit quantum electrodynamics in the ultrastrong-coupling regime. Nat. Phys. 6, 772–776 (2010).

    Article  Google Scholar 

  13. Forn-Diaz, P. et al. Observation of the Bloch-Siegert shift in a qubit-oscillator system in the ultrastrong coupling regime. Phys. Rev. Lett. 105, 237001 (2010).

    Article  ADS  Google Scholar 

  14. Hepp, K. & Lieb, E. H. On the superradiant phase transition for molecules in a quantized radiation field: the Dicke Maser model. Ann. Phys. 76, 360–404 (1973).

    Article  ADS  MathSciNet  Google Scholar 

  15. Rza̧żewski, K., Wódkiewicz, K. & Żakowicz, W. Phase transitions, two-level atoms, and the A2 term. Phys. Rev. Lett. 35, 432–434 (1975).

    Article  ADS  Google Scholar 

  16. Nataf, P. & Ciuti, C. No-go theorem for superradiant quantum phase transitions in cavity QED and counter-example in circuit QED. Nat. Commun. 1, 72 (2010).

    Article  ADS  Google Scholar 

  17. Viehmann, O., von Delft, J. & Marquardt, F. Superradiant phase transitions and the standard description of circuit QED. Phys. Rev. Lett. 107, 113602 (2011).

    Article  ADS  Google Scholar 

  18. Mooij, J. E. et al. Josephson persistent-current qubit. Science 285, 1036–1039 (1999).

    Article  Google Scholar 

  19. Rabi, I. I. Space quantization in a gyrating magnetic field. Phys. Rev. 51, 652–654 (1937).

    Article  ADS  Google Scholar 

  20. Shimoda, K., Wang, T. C. & Townes, C. H. Further aspects of maser theory. Phys. Rev. 102, 1308–1321 (1956).

    Article  ADS  Google Scholar 

  21. Jaynes, E. T. & Cummings, F. W. Comparison of quantum and semiclassical radiation theories with application to the beam maser. Proc. IEEE 51, 89–109 (1963).

    Article  Google Scholar 

  22. Braak, D. Integrability of the Rabi model. Phys. Rev. Lett. 107, 100401 (2011).

    Article  ADS  Google Scholar 

  23. Bourassa, J. et al. Ultrastrong coupling regime of cavity QED with phase-biased flux qubits. Phys. Rev. A 80, 032109 (2009).

    Article  ADS  Google Scholar 

  24. Casanova, J., Romero, G., Lizuain, I., Garca-Ripoll, J. J. & Solano, E. Deep strong coupling regime of the Jaynes-Cummings model. Phys. Rev. Lett. 105, 263603 (2010).

    Article  ADS  Google Scholar 

  25. Ashhab, S. & Nori, F. Qubit-oscillator systems in the ultrastrong-coupling regime and their potential for preparing nonclassical states. Phys. Rev. A 81, 042311 (2010).

    Article  ADS  Google Scholar 

  26. Lamb, W. E. & Retherford, R. C. Fine structure of the hydrogen atom by a microwave method. Phys. Rev. 72, 241–243 (1947).

    Article  ADS  Google Scholar 

  27. Forn-Díaz, P. et al. Ultrastrong coupling of a single artificial atom to an electromagnetic continuum in the nonperturbative regime. Nat. Phys. http://dx.doi.org/10.1038/nphys3905 (2016).

  28. Hopfield, J. J. Theory of the contribution of excitons to the complex dielectric constant of crystals. Phys. Rev. 112, 1555–1567 (1958).

    Article  ADS  Google Scholar 

Download references

Acknowledgements

We thank K. Nemoto, M. Hirokawa, K. Inomata, J. W. Munro, Y. Matsuzaki, M. Bamba and N. Mizuochi for stimulating discussions. The authors are grateful to M. Fujiwara, K. Wakui, A. Hoshi, M. Takeoka and M. Sasaki for their continued support through all the stages of this research. We thank J. Komuro, S. Inoue and E. Sasaki for assistance with experimental set-up. We also thank S. Weinreb for his support by providing excellent cryoamplifiers, and N. Matsuura and Y. Kato for their cordial support in the startup phase of this research. This work was supported in part by the Scientific Research (S) Grant No.25220601 by the Japanese Society for the Promotion of Science (JSPS).

Author information

Author notes

  1. Fumiki Yoshihara and Tomoko Fuse: These authors contributed equally to this work.

Authors and Affiliations

  1. National Institute of Information and Communications Technology, 4-2-1, Nukui-Kitamachi, Koganei, Tokyo 184-8795, Japan

    Fumiki Yoshihara, Tomoko Fuse & Kouichi Semba

  2. Qatar Environment and Energy Research Institute, Hamad Bin Khalifa University, Qatar Foundation, PO Box 5825, Doha, Qatar

    Sahel Ashhab

  3. NTT Basic Research Laboratories, NTT Corporation, 3-1 Morinosato-Wakamiya, Atsugi, Kanagawa 243-0198, Japan

    Kosuke Kakuyanagi & Shiro Saito

Authors
  1. Fumiki Yoshihara
    View author publications

    Search author on:PubMed Google Scholar

  2. Tomoko Fuse
    View author publications

    Search author on:PubMed Google Scholar

  3. Sahel Ashhab
    View author publications

    Search author on:PubMed Google Scholar

  4. Kosuke Kakuyanagi
    View author publications

    Search author on:PubMed Google Scholar

  5. Shiro Saito
    View author publications

    Search author on:PubMed Google Scholar

  6. Kouichi Semba
    View author publications

    Search author on:PubMed Google Scholar

Contributions

All authors contributed extensively to the work presented in this paper. F.Y., T.F. and K.S. carried out measurements and data analysis on the coupled flux qubit–LC-oscillator system. F.Y. and T.F. designed and F.Y., T.F. and K.K. fabricated the flux qubit and associated devices. T.F., F.Y., K.K., S.S. and K.S. designed and developed the measurement system. S.A. provided theoretical support and analysis. F.Y., T.F., S.A. and K.S. wrote the manuscript, with feedback from all authors. K.S. designed and supervised the project.

Corresponding authors

Correspondence to Fumiki Yoshihara, Tomoko Fuse, Sahel Ashhab or Kouichi Semba.

Ethics declarations

Competing interests

The authors declare no competing financial interests.

Supplementary information

Supplementary information

Supplementary information (PDF 1688 kb)

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Yoshihara, F., Fuse, T., Ashhab, S. et al. Superconducting qubit–oscillator circuit beyond the ultrastrong-coupling regime. Nature Phys 13, 44–47 (2017). https://doi.org/10.1038/nphys3906

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue date:

  • DOI: https://doi.org/10.1038/nphys3906

This article is cited by

Search

Advanced search

Quick links

Nature Briefing

Sign up for the Nature Briefing newsletter — what matters in science, free to your inbox daily.

Get the most important science stories of the day, free in your inbox. Sign up for Nature Briefing