Skip to main content

Thank you for visiting nature.com. You are using a browser version with limited support for CSS. To obtain the best experience, we recommend you use a more up to date browser (or turn off compatibility mode in Internet Explorer). In the meantime, to ensure continued support, we are displaying the site without styles and JavaScript.

  • Letter
  • Published:

Algebraic charge liquids

Nature Physics volume 4, pages 28–31 (2008)Cite this article

Abstract

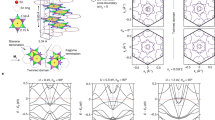
High-temperature superconductivity emerges in the copper oxide compounds on changing the electron density of an insulator in which the electron spins are antiferromagnetically ordered. A key characteristic of the superconductor1 is that electrons can be extracted from it at zero energy only if their momenta take one of four specific values (the ‘nodal points’). A central enigma has been the evolution of those zero-energy electrons in the metallic state between the antiferromagnet and the superconductor, and recent experiments yield apparently contradictory results. The oscillation of the resistance in this metal as a function of magnetic field2,3 indicates that the zero-energy electrons carry momenta that lie on elliptical ‘Fermi pockets’, whereas ejection of electrons by high-intensity light indicates that the zero-energy electrons have momenta only along arc-like regions4,5, or ‘Fermi arcs’. We present a theory of new states of matter, which we call ‘algebraic charge liquids’, and which arise naturally between the antiferromagnet and the superconductor, and reconcile these observations. Our theory also explains a puzzling dependence of the density of superconducting electrons on the total electron density, and makes a number of unique predictions for future experiments.

This is a preview of subscription content, access via your institution

Access options

Buy this article

  • Purchase on SpringerLink
  • Instant access to the full article PDF.

USD 39.95

Prices may be subject to local taxes which are calculated during checkout

Figure 1: Schematic phase diagram at small x.
Figure 2: Square-lattice Brillouin zone containing the ‘diamond’ Brillouin zone (dashed line).

Similar content being viewed by others

References

  1. Damascelli, A., Hussain, Z. & Shen, Z.-X. Angle-resolved photoemission studies of the cuprate superconductors. Rev. Mod. Phys. 75, 473–541 (2003).

    Article  ADS  Google Scholar 

  2. Doiron-Leyraud, N. et al. Quantum oscillations and the Fermi surface in an underdoped high-Tc superconductor. Nature 447, 565–568 (2007).

    Article  ADS  Google Scholar 

  3. Yelland, E. A. et al. Quantum oscillations in the underdoped cuprate YBa2Cu4O8. Preprint at <http://front.math.ucdavis.edu/0707.0057> (2007).

  4. Norman, M. R. et al. Destruction of the Fermi surface underdoped high-Tc superconductors. Nature 392, 157–160 (1998).

    Article  ADS  Google Scholar 

  5. Kanigel, A. et al. Evolution of the pseudogap from Fermi arcs to the nodal liquid. Nature Phys. 2, 447–451 (2006).

    Article  ADS  Google Scholar 

  6. Anderson, P. W. The resonating valence bond state in La2CuO4 and superconductivity. Science 235, 1196–1198 (1987).

    Article  ADS  Google Scholar 

  7. Lee, P. A., Nagaosa, N. & Wen, X.-G. Doping a Mott insulator: Physics of high-temperature superconductivity. Rev. Mod. Phys. 78, 17–86 (2006).

    Article  ADS  Google Scholar 

  8. Kivelson, S. A. et al. How to detect fluctuating stripes in the high-temperature superconductors. Rev. Mod. Phys. 75, 1201–1241 (2003).

    Article  ADS  Google Scholar 

  9. Senthil, T. et al. Deconfined quantum critical points. Science 303, 1490–1494 (2004).

    Article  ADS  Google Scholar 

  10. Kohsaka, Y. et al. An intrinsic bond-centered electronic glass with unidirectional domains in underdoped cuprates. Science 315, 1380–1385 (2007).

    Article  ADS  Google Scholar 

  11. Rantner, W. & Wen, X.-G. Electron spectral function and algebraic spin liquid for the normal state of underdoped high Tc superconductors. Phys. Rev. Lett. 86, 3871–3874 (2001).

    Article  ADS  Google Scholar 

  12. Hermele, M. et al. Stability of U(1) spin liquids in two dimensions. Phys. Rev. B 70, 214437 (2004).

    Article  ADS  Google Scholar 

  13. Hermele, M., Senthil, T. & Fisher, M. P. A. Algebraic spin liquid as the mother of many competing orders. Phys. Rev. B 72, 104404 (2005).

    Article  ADS  Google Scholar 

  14. Altshuler, B. L., Ioffe, L. B. & Millis, A. J. Low-energy properties of fermions with singular interactions. Phys. Rev. B 50, 14048–14064 (1994).

    Article  ADS  Google Scholar 

  15. Kaul, R. K. et al. Hole dynamics in an antiferromagnet across a deconfined quantum critical point. Phys. Rev. B 75, 235122 (2007).

    Article  ADS  Google Scholar 

  16. Lee, P. A. Gauge field, Aharonov-Bohm flux, and high-Tc superconductivity. Phys. Rev. Lett. 63, 680–683 (1989).

    Article  ADS  Google Scholar 

  17. Kim, Y. B., Lee, P. A. & Wen, X.-G. Quantum Boltzmann equation of composite fermions interacting with a gauge field. Phys. Rev. B 52, 17275–17292 (1995).

    Article  ADS  Google Scholar 

  18. Flambaum, V. V., Kuchiev, M. Yu. & Sushkov, O. P. Hole–hole superconducting pairing in the t–J model induced by long-range spin-wave exchange. Physica C 227, 267–278 (1994).

    Article  ADS  Google Scholar 

  19. Belinicher, V. I. et al. Hole–hole superconducting pairing in the t–J model induced by spin-wave exchange. Phys. Rev. B 51, 6076–6084 (1995).

    Article  ADS  Google Scholar 

  20. Vafek, O., Tesanovic, Z. & Franz, M. Relativity restored: Dirac anisotropy in QED3 . Phys. Rev. Lett. 89, 157003 (2002).

    Article  ADS  Google Scholar 

  21. Chubukov, A. V., Sachdev, S. & Ye, J. Theory of two-dimensional quantum Heisenberg antiferromagnets with a nearly critical ground state. Phys. Rev. B 49, 11919–11961 (1994).

    Article  ADS  Google Scholar 

  22. Bonn, D. A. et al. Surface impedance studies of YBCO. Czech. J. Phys. 46, 3195–3202 (1996).

    Article  Google Scholar 

  23. Boyce, B. R., Skinta, J. & Lemberger, T. Effect of the pseudogap on the temperature dependence of the magnetic penetration depth in YBCO films. Physica C 341–348, 561 (2000).

    Article  ADS  Google Scholar 

  24. Le Tacon, M. et al. Two energy scales and two quasiparticle dynamics in the superconducting state of underdoped cuprates. Nature Phys. 2, 537–543 (2006).

    Article  ADS  Google Scholar 

  25. Lee, P. A. & Wen, X.-G. Unusual superconducting state of underdoped cuprates. Phys. Rev. Lett. 78, 4111–4114 (1997).

    Article  ADS  Google Scholar 

  26. Nave, C. P., Ivanov, D. A. & Lee, P. A. Variational Monte Carlo study of the current carried by a quasiparticle. Phys. Rev. B 73, 104502 (2006).

    Article  ADS  Google Scholar 

  27. Hetel, I., Lemberger, T. R. & Randeria, M. Quantum critical behaviour in the superfluid density of strongly underdoped ultrathin copper oxide films. Nature Phys. 3, 700–702 (2007).

  28. Anderson, P. W. et al. The physics behind high-temperature superconducting cuprates: The plain vanilla version of RVB. J. Phys. Condens. Matter 16, R755 (2004).

    Article  Google Scholar 

  29. Shraiman, B. I. & Siggia, E. D. Mobile vacancies in a quantum Heisenberg antiferromagnet. Phys. Rev. Lett. 61, 467 (1988).

    Article  ADS  MathSciNet  Google Scholar 

Download references

Acknowledgements

We thank E. Hudson, A. Lanzara, P. Lee, M. Randeria, L. Taillefer, Z. Wang, Z.-Y. Weng and X. Zhou for many useful discussions. This research was supported by the NSF grants DMR-0537077 (S.S. and R.K.K.), DMR-0132874 (R.K.K.), DMR-0541988 (R.K.K.), the NSERC (Y.B.K.), the CIFAR (Y.B.K.) and The Research Corporation (T.S.).

Author information

Authors and Affiliations

  1. Department of Physics, Harvard University, Cambridge, Massachusetts 02138, USA

    Ribhu K. Kaul & Subir Sachdev

  2. Department of Physics, University of Toronto, Toronto, Ontario M5S 1A7, Canada

    Yong Baek Kim

  3. Department of Physics, Massachusetts Institute of Technology, Cambridge, Massachusetts 02139, USA

    T. Senthil

Authors
  1. Ribhu K. Kaul
    View author publications

    Search author on:PubMed Google Scholar

  2. Yong Baek Kim
    View author publications

    Search author on:PubMed Google Scholar

  3. Subir Sachdev
    View author publications

    Search author on:PubMed Google Scholar

  4. T. Senthil
    View author publications

    Search author on:PubMed Google Scholar

Corresponding author

Correspondence to T. Senthil.

Rights and permissions

Reprints and permissions

About this article

Cite this article

Kaul, R., Kim, Y., Sachdev, S. et al. Algebraic charge liquids. Nature Phys 4, 28–31 (2008). https://doi.org/10.1038/nphys790

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue date:

  • DOI: https://doi.org/10.1038/nphys790

This article is cited by

Search

Advanced search

Quick links

Nature Briefing

Sign up for the Nature Briefing newsletter — what matters in science, free to your inbox daily.

Get the most important science stories of the day, free in your inbox. Sign up for Nature Briefing