Abstract
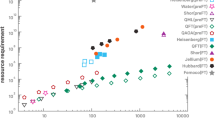
Today, ion traps are among the most promising physical systems for constructing a quantum device harnessing the computing power inherent in the laws of quantum physics1,2. For the implementation of arbitrary operations, a quantum computer requires a universal set of quantum logic gates. As in classical models of computation, quantum error correction techniques3,4 enable rectification of small imperfections in gate operations, thus enabling perfect computation in the presence of noise. For fault-tolerant computation5, it is believed that error thresholds ranging between 10−4 and 10−2 will be required—depending on the noise model and the computational overhead for realizing the quantum gates6,7,8—but so far all experimental implementations have fallen short of these requirements. Here, we report on a Mølmer–Sørensen-type gate operation9,10 entangling ions with a fidelity of 99.3(1)%. The gate is carried out on a pair of qubits encoded in two trapped calcium ions using an amplitude-modulated laser beam interacting with both ions at the same time. A robust gate operation, mapping separable states onto maximally entangled states is achieved by adiabatically switching the laser–ion coupling on and off. We analyse the performance of a single gate and concatenations of up to 21 gate operations.
This is a preview of subscription content, access via your institution
Access options
Subscribe to this journal
Receive 12 print issues and online access
$259.00 per year
only $21.58 per issue
Buy this article
- Purchase on SpringerLink
- Instant access to the full article PDF.
USD 39.95
Prices may be subject to local taxes which are calculated during checkout




Similar content being viewed by others
References
Nielsen, M. A. & Chuang, I. L. Quantum Computation and Quantum Information (Cambridge Univ. Press, Cambridge, 2000).
Cirac, J. I. & Zoller, P. Quantum computations with cold trapped ions. Phys. Rev. Lett. 74, 4091–4094 (1995).
Shor, P. W. Scheme for reducing decoherence in quantum computer memory. Phys. Rev. A 52, R2493–R2496 (1995).
Steane, A. M. Error correcting codes in quantum theory. Phys. Rev. Lett. 77, 793–797 (1996).
Shor, P. W. 37th Symposium on Foundations of Computing 56–65 (IEEE Computer Society Press, Washington DC, 1996).
Knill, E. Quantum computing with realistically noisy devices. Nature 434, 39–44 (2005).
Raussendorf, R. & Harrington, J. Fault-tolerant quantum computation with high threshold in two dimensions. Phys. Rev. Lett. 98, 190504 (2007).
Reichardt, B. W. Improved ancilla preparation scheme increases fault-tolerant threshold. Preprint at <http://arxiv.org/abs/quant-ph/0406025v1> (2004).
Sørensen, A. & Mølmer, K. Quantum computation with ions in thermal motion. Phys. Rev. Lett. 82, 1971–1974 (1999).
Sørensen, A. & Mølmer, K. Entanglement and quantum computation with ions in thermal motion. Phys. Rev. A 62, 022311 (2000).
Sackett, C. A. et al. Experimental entanglement of four particles. Nature 404, 256–259 (2000).
Schmidt-Kaler, F. et al. Realization of the Cirac–Zoller controlled-NOT quantum gate. Nature 422, 408–411 (2003).
Leibfried, D. et al. Experimental demonstration of a robust, high-fidelity geometric two ion-qubit phase gate. Nature 422, 412–415 (2003).
Haljan, P. C. et al. Entanglement of trapped-ion clock states. Phys. Rev. A 72, 062316 (2005).
Home, J. P. et al. Deterministic entanglement and tomography of ion spin qubits. New J. Phys. 8, 188 (2006).
Riebe, M. et al. Process tomography of ion trap quantum gates. Phys. Rev. Lett. 97, 220407 (2006).
Milburn, G. J., Schneider, S. & James, D. F. V. Ion trap quantum computing with warm ions. Fortschr. Phys. 48, 801–810 (2000).
Solano, E., de Matos Filho, R. L. & Zagury, N. Deterministic Bell states and measurement of the motional state of two trapped ions. Phys. Rev. A 59, R2539–R2543 (1999).
Ozeri, R. et al. Errors in trapped-ion quantum gates due to spontaneous photon scattering. Phys. Rev. A 75, 042329 (2007).
Roos, C. F. Ion trap quantum gates with amplitude-modulated laser beams. New J. Phys. 10, 013002 (2008).
Benhelm, J. et al. Measurement of the hyperfine structure of the S1/2–D5/2 transition in 43Ca+. Phys. Rev. A 75, 032506 (2007).
Roos, C. F., Chwalla, M., Kim, K., Riebe, M. & Blatt, R. ‘Designer atoms’ for quantum metrology. Nature 443, 316–319 (2006).
Mølmer, K. & Sørensen, A. Multiparticle entanglement of hot trapped ions. Phys. Rev. Lett. 82, 1835–1838 (1999).
Leibfried, D. et al. Creation of a six-atom ‘Schrödinger cat’ state. Nature 438, 639–642 (2005).
Chiaverini, J. et al. Realization of quantum error correction. Nature 432, 602–605 (2004).
Reichle, R. et al. Experimental purification of two-atom entanglement. Nature 443, 838–841 (2006).
Vandersypen, L. M. K. & Chuang, I. L. NMR techniques for quantum control and computation. Rev. Mod. Phys. 76, 1037–1069 (2004).
Häffner, H. et al. Precision measurement and compensation of optical Stark shifts for an ion-trap quantum processor. Phys. Rev. Lett. 90, 143602 (2003).
Leibfried, D., Knill, E., Ospelkaus, C. & Wineland, D. J. Transport quantum logic gates for trapped ions. Phys. Rev. A 76, 032324 (2007).
Acknowledgements
We gratefully acknowledge the support of the European network SCALA and the Disruptive Technology Office and the Institut für Quanteninformation GmbH. We thank R. Gerritsma and F. Zähringer for help with the experiments.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
About this article
Cite this article
Benhelm, J., Kirchmair, G., Roos, C. et al. Towards fault-tolerant quantum computing with trapped ions. Nature Phys 4, 463–466 (2008). https://doi.org/10.1038/nphys961
Received:
Accepted:
Published:
Issue date:
DOI: https://doi.org/10.1038/nphys961
This article is cited by
-
Entangling gates for trapped-ion quantum computation and quantum simulation
Journal of the Korean Physical Society (2023)
-
Limits on atomic qubit control from laser noise
npj Quantum Information (2022)
-
Quantum computation using action variables
Quantum Information Processing (2022)
-
Highlighting photonics: looking into the next decade
eLight (2021)
-
Realisation of high-fidelity nonadiabatic CZ gates with superconducting qubits
npj Quantum Information (2019)