Background and research questions

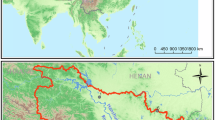
By 7500 BCE, sedentary agriculture had emerged in the middle reaches of the Yangtze River Plain, including the Dongting Lake and Jianghan Plains (Fig. 1). Prehistoric populations continuously inhabited this region for millennia, making it one of the most significant cradles of Chinese civilization. It is among the earliest regions in the world to domesticate rice and is also considered one of the key areas contributing to the development of prehistoric urbanization in China.

Fig. 1
figure 1

Map of Jianghan-Dongtinghu Plain and burial site locations.

Full size image

Current research on the prehistoric social complexity of this region has primarily focused on its contributions to the formation of Chinese civilization, with particular emphasis on cultural traditions, settlement patterns, the origins of urbanization, subsistence strategies, craft specialization, regional interactions, population movements, and trade. However, these studies have rarely provided systematic quantitative analyses of inequality and its underlying causes. A diachronic comparative study of inequality in this region would not only offer deeper insights into the long-term processes of local social complexity and their driving forces but also contribute valuable knowledge to the general understanding of inequality.

Archaeologists often observe social inequality in ancient societies by examining burial goods1,2, house sizes3,4, and artifacts found in houses or storage pits5,6,7 and so on. Extensive studies have explored the relationship between inequality and various factors, including population size8,9,10, social network and dominance11,12,13, resource acquisition and monopolization14,15, warfare16,17, technology18,19,20, human adaptation to climate21 and culture/ideology22 so on.

In this study, we analyzed burial data from the middle Yangtze River Plain, covering a prehistoric span of approximately 5,000 years, to provide a comprehensive examination of burial wealth inequality. Based on this analysis, the paper explores the relationship between wealth inequality and variables such as population size, hydraulic works, social wealth, ritual and political-military powers, and wealth stratification. The aim is to systematically elucidate the nature of wealth inequality in prehistoric societies of the Middle Yangtze Plain. Additionally, the study compares archaeological data from the middle and lower Yangtze regions and incorporates historical records to propose a model for the emergence of prehistoric states in China. This model suggests that the effective centralization of ritual and political-military powers by ruling elites was a critical factor in the emergence of the early state.

Data

Burial data were selected from 16 archaeological sites situated in the middle reaches of the Yangtze River, specifically within the Jianghan Plain and Dongting Lake Plain (Fig. 1). These sites were chosen based on the substantial size of their burial samples, with each site contributing a minimum of 10 burials across all phases included in the analysis (Table 1). The dataset comprises a total of 1941 individuals, spanning several significant prehistoric periods: the Pengtoushan Period (7100–5700 BCE), Daxi Period (4500–3200 BCE), Youziling Period (3900–3400 BCE), Qujialing Period (3400–2500 BCE), Shijiahe Period (2500–2200 BCE), and Xiaojiawuji Period (2200–1900 BCE). For the purposes of this study, these burials were systematically classified into 39 distinct prehistoric societies, according to the chronological framework associated with each sample.

Table 1 Sites and burial sample size
Full size table

Methods

The Gini coefficient, a widely recognized metric for assessing income or wealth inequality in economics, ranges between 0 and 1, where 0 denotes perfect equality and 1 signifies absolute inequality. In this study, we utilized objects found in prehistoric burials as a proxy for individual wealth, applying the Gini coefficient to quantitatively assess the wealth inequality.

To quantify burial wealth, we derived values based on Feinman’s framework for assessing the production stages of artifacts23, in conjunction with Peterson et al.’s estimates of artifact production costs6. Since these studies do not account for the labor costs associated with constructing burials, we introduced a labor cost coefficient. This coefficient was estimated based on the characteristics of Neolithic tools and the actual labor involved in burial construction. We hypothesized that an adult could dig and bury ~1.5 m3 of earth per day. Consequently, a burial pit of 3 m3 would require about two days of labor, a time investment comparable to that needed for crafting a medium-sized pottery vessel (with estimates derived from Dr. Tao Li’s experimental pottery-making data at Wuhan University). This approach allows us to incorporate both the labor required for burial construction and the cost of burial goods into a unified calculation, enabling us to calculate the Gini coefficient accordingly. It is important to emphasize that the calculated values of burial goods and labor input are approximations rather than exact representations of the true value of prehistoric artifacts and labor. However, we argue that this approximation is methodologically sound, particularly given the large sample size, which mitigates potential errors in estimation and preserves the overall trend of the data.

To ensure robust estimations and minimize the impact from skewed distribution of wealth estimation, we employed the bootstrap method to calculate the Gini coefficient for each society. Specifically, we performed 1000 random samplings of burial wealth values from each period, maintaining the original sample size in each iteration. We then calculated the Gini coefficient for each resampled dataset and determined the median of these 1000 coefficients as the representative value of wealth inequality for that society. Finally, we calculated the margin of error for this coefficient at a 90% confidence level.

While the Gini coefficient is effective as a single value measure for normalizing and comparing wealth inequality across societies, it does not intuitively convey the internal wealth structure within each society. To address this issue, we drew on Thomas Piketty’s structural differentiation of income distribution in Capital in the Twenty-First Century, which divides labor income into three tiers: the top 10%, the middle 40%, and the bottom 50%24. Similarly, we categorized the burial wealth of a society into three comparable tiers to examine historical changes in the structure of social wealth in “ Overall trend of wealth inequality”.

In “Wealth inequality and population”, when we extended our analysis by examining the contribution of population size to the level of inequality, we used the number of individuals interred in burials across various societies as a proxy for population size, to assess its relationship with wealth inequality as expressed by the Gini coefficient. Although the number of individuals in burials does not precisely reflect the actual population of ancient societies, it is a reasonable proxy for observing correlations with the Gini coefficient.

In “Wealth inequality and stratification”, we explored the relationship between wealth inequality and wealth stratification. It is crucial to distinguish between these two aspects of social wealth differentiation. The degree of wealth inequality in burials, as quantified by the Gini coefficient, reflects the concentration of wealth within a society, particularly the extent to which wealth is concentrated among a small group of elites. On the other hand, wealth stratification pertains to the distribution density of individual wealth within burials, which often exhibits a multi-peaked numerical distribution. To analyze wealth stratification, we first normalized the burial wealth values for each society using min-max scaling, adjusting the minimum and maximum values to a range between 0 and 1. Subsequently, we plotted the kernel density estimation (KDE) curves for these normalized burial wealth values (with bandwidth computed using Scott’s Rule: \(h=0.9\cdot A \cdot n^{-1/5}\) where n is the number of point and A is min(std(X),IQR/1.349), and IQR is the interquartile range of X). As shown in Fig. 2, the KDE curves reveal that burial wealth distributions are predominantly skewed, with several societies exhibiting a multi-peaked pattern. While in most societies, a few values of burial wealth extend to the far right, obscuring the full number of peaks in the array, we need a more reasonable way to identify the lower density values on the right side as separate peaks. We then employed a peak-splitting method to define wealth stratification. This method involves detecting the local maxima (peaks) in the multi-peaked data and identifying the valleys between adjacent peaks as division points. These division points then split the original array into multiple subarrays, each representing a mathematically meaningful tier (Table 2). The bandwidth algorithm used in peak extraction remains consistent with Scott’s Rule. It is important to emphasize that the stratification of wealth based on mathematical logic is intended solely to facilitate the quantitative observation of the relationship between social wealth inequality (as measured by the Gini coefficient) and the number of wealth tiers. Furthermore, the division of wealth stratum within a society inherently involves some degree of subjectivity. Given that this study does not focus on evaluating the validity of various stratifying approaches, we stratified the wealth data based solely on the observable patterns in the burial wealth distribution, without delving into differences in the of specific societies.

Fig. 2: Ridge plot of normalized burial wealth values across societies.
figure 2

The ridge plot is based on min-max normalized burial wealth values, which range from 0 to 1. Consequently, the kernel density estimation (KDE) curves are truncated to ensure their maximum and minimum values are 1 and 0, respectively. For the periods, YZL Youziling, QJL Qujialing, SJH Shijiahe, XJWJ Xiaojiawuji, PTS Pengtoushan, TJG Tangjiagang, DX Daxi.

Full size image
Table 2 Burial wealth stratification of societies
Full size table

In “Wealth inequality and power”, in order to investigate the relationship between wealth inequality and power, we categorized two main forms of power associated with burials: political-military power and ritual power. These categories are distinguished on the basis of the artifacts present in the burials. Specifically, we used the presence of political-military symbols, such as stone battle axes25,26, and ritual symbols, including white earthenware vessels27, jade huang28, and jade statuettes29, to distinguish between the two types of power. Individuals buried with these artifacts are assumed to have held the corresponding form of power. We delineated societies with power burials versus those without, societies with political-military power burials versus those without, and societies with ritual power burials versus those without. Because of the skewed distribution of Gini coefficients in some of these categories, we computed the median Gini coefficients and their margins of error at the 80%, 90%, and 99% confidence levels (see Fig. 3 and Table 3). Due to the skewed distribution of Gini coefficient, we conducted 1000 random samplings of the Gini coefficient for each type of society, preserving the original sample size in each iteration. For each resampled dataset, we used the median of these 1000 coefficients as the representative measure of wealth inequality for that type of society. Finally, we determined the margin of error for this coefficient across various confidence levels.

Fig. 3: Wealth inequality of power-related societies.
figure 3

A Gini comparison between societies with and without power burials; B Gini comparison between societies with and without political-military power burials; C Gini comparison between societies with and without ritual power burials.

Full size image
Table 3 Gini Coefficient and error ranges in power-related societies
Full size table

In the same section, due to the skewed distribution of wealth ratio, we conducted 1000 random samplings of the ratios for each type of society, preserving the original sample size in each iteration. For each resampled dataset, we used the median of these 1000 ratios as the representative measure of wealth ratio for that type of society. At last, we determined the margin of error for this ratio across various confidence levels.

Results

Overall trend of wealth inequality

The temporal pattern of wealth inequality, as captured by the Gini coefficient, is clearly illustrated in the LOESS regression results presented in Fig. 4 (α = 0.8, r² = 0.12, n = 39). The distribution of Gini coefficients indicates that during the period from 7000 to 4500 BCE, there is minimal variation in burial wealth inequality across different societies. However, following 4500 BCE, a more pronounced divergence in burial wealth inequality emerges, particularly between 3000 and 2000 BCE. During this latter period, the Gini coefficients reveal significant disparities among societies, with some exceeding 0.4 while others fall below this threshold.

Fig. 4: Trends in Gini coefficients over time.
figure 4

Quadratic localized polynomial LOESS regression results, α = 0.8, r2 = 0.12, n = 39, the gray range is 90% CL. The chronological medians serve as reference points for each period. Here, the time variable is not utilized as an explanatory factor but is intended to facilitate the observation of the trajectory of wealth inequality over a 5000-year span.

Full size image

Moreover, the data demonstrate a decreasing trend in Gini coefficients from 4000 to 3000 BCE, followed by an increasing trend from 3000 to 2000 BCE. The LOESS regression results underscore these non-linear trends in Gini coefficient variation across different stages, suggesting localized changes that likely reflect the dynamic evolution of socio-economic structures over time (Fig. 4).

As shown in the area stacked plot in Fig. 5, the periods with the highest wealth shares for the top 10% of the population are Daxi II and Xiaojiawuji, with wealth shares of 46.4% and 53.3%, respectively. In other periods (excluding Daxi Phase I), the wealth share of the top 10% ranges from about 20% to 30%. Conversely, the wealth share of the middle 40% fluctuates between 33.1% and 52.8%, exceeding that of the top 10% in most periods. The bottom 50% consistently has the lowest wealth share, ranging from 10.2% to 33.1%. Notably, both the wealth shares of the middle 40% and bottom 50% show similar trends over time and are negatively correlated with the wealth share of the top 10%.

Fig. 5: Trends in the structure of social wealth over time.
figure 5

Note: The percentage of wealth for each period represents the average share of wealth across different sites within that specific period.

Full size image

The wealth share of the top 10% exhibits a slight upward trend, while the shares held by the middle 40% and the bottom 50% show a corresponding decline. Analysis indicates that the reduction in the wealth share of the middle 40% contributes slightly more to the increasing wealth concentration of the top 10% than the decline in the share held by the bottom 50% (see Table 4). This suggests that the middle 40% may be more adversely impacted by the growing wealth of the top 10%. However, this difference is not statistically significant (Fisher’s z test, p = 0.577, n = 15).

Table 4 Correlation matrix of wealth share among the groups
Full size table

Wealth inequality and population

The linear regression analysis of the Gini coefficient in relation to population size reveals a significant positive correlation (p < 0.001), with an \({r}^{2}\) value of 47% (Fig. 6A). This result indicates that population size is a significant factor influencing wealth inequality, accounting for 47% of the variation in the Gini coefficient.

Fig. 6: Relation between inequality, population and total wealth.
figure 6

A Linear relationship between wealth inequality and population size (log10) with 90% confidence interval; B Linear relationship between total wealth (log10) and population size (log10) with 90% confidence interval. Total wealth and population size are transformed by applying log10 to the total wealth and the number of individuals in each society’s burial sample, respectively.

Full size image

Additionally, we investigated the relationship between population size and total burial wealth. By calculating the total amount of burial wealth for each society and examining its correlation with population size, we found a significant positive correlation (Fig. 6B). When total burial wealth is used as a proxy for overall social wealth and the number of individuals in burials as a proxy for population size, the analysis reveals that agricultural societies in the prehistoric middle Yangtze plain, social total wealth is significantly positively correlated with population size, with population size explaining 57% of the variation. This finding underscores that population size was a major determinant of total social wealth in prehistoric societies of the Middle Yangtze River plain.

Wealth inequality and stratification

To assess the relationship between wealth inequality and wealth stratification, we calculated Kendall’s rank correlation coefficient between Gini coefficients and wealth tiers of each society, given that wealth stratification is an ordinal variable. The analysis yielded a Kendall’s Tau-a of 0.2537, a Tau-b of 0.2887, and a p-value of 0.0182 (n = 39). Because some societies share the same number of wealth strata, Kendall’s Tau-b, which adjusts for ties, offers a more accurate measure. The Tau-b value of 0.2887 indicates a moderate positive correlation between wealth inequality and wealth stratification. The significant p-value (p < 0.05) suggests that this correlation is unlikely to be the result of random sampling error. Therefore, we can conclude that there is a statistically significant, albeit moderate, positive correlation between the degree of wealth inequality and wealth stratification.

Wealth inequality and power

When comparing societies with power-related burials to those without, we found that at the 90% and 99% confidence levels, the margins of error for the Gini coefficients of societies with power symbols often exceed the median Gini coefficients of their counterparts. At the 80% confidence level, the margins of error for societies with power symbols also exceed those of their counterparts, although the converse is not the case (Fig. 3A). This pattern suggests that societies with power-related burials may have greater wealth inequality, although this could also be due to smaller sample sizes. Comparisons between other pairs of societies show no statistically significant differences in Gini coefficients at any confidence level. However, we observed that societies with burials containing political-military or ritual power symbols have larger margins of error, indicating greater variation in wealth inequality within these societies (Fig. 3B, C). This suggests that while power may contribute to wealth inequality, its impact is not substantial, and the influence of categorical power on wealth inequality is limited to certain societies.

Over a long period of time, both at individual sites and regionally, the continuity of power symbols in burials is uneven, with relatively long intervals between their appearances. For example, the two forms of power may have been absent at the Chengtoushan site during certain periods. Similar pattern also can be seen from other sites. This leads us to hypothesize that the continuity of political-military and ritual power traditions in the Middle Yangtze Plain was weak. Moreover, prehistoric burials in this region often show that political-military and ritual powers existed independently, with only a few instances of both types of power appearing to the same individual. For example, both types of power are found in burial M5 of the Youziling period at the Fangyingtai site30 and in burial W8 and W37 of the Xiaojiawuiji period at the Zaolingang site31. The ratio of burials with centralized power to all power-related burials is 1:19, indicating that the concentration of both powers in a single individual was rare and lacked temporal continuity.

In terms of the ratio of excavated power object burials to median social wealth (see Table 5), burials associated with ritual power exhibit a significantly higher wealth-to-median ratio compared to those associated with political-military power at the 90% confidence level (Fig. 7). This suggests that holders of ritual power were more capable of amassing wealth. Additionally, the broader error range in the ratio indicates a greater disparity in wealth among different ritual power holders.

Fig. 7
figure 7

Wealth ratio of power-related individuals.

Full size image
Fig. 8
figure 8

Comparison of wealth Inequality between hydraulic societies and non-hydraulic societies.

Full size image

Wealth inequality and hydraulic works

Over the past few decades, archaeologists have identified a series of prehistoric sites featuring public works such as walls, ditches, and dams in the Jianghan Plain and Dongting Lake Plain. Utilizing remote sensing technology, Liu et al. analyzed these structures in the middle reaches of the Yangtze River, concluding that their primary functions were flood control and irrigation32. This discovery provides new evidence for the role of prehistoric hydraulic engineering in these regions, as well as its contribution to social complexity. Consequently, we categorized the societies in question into those with hydraulic engineering works and those without, comparing the inequality of burial wealth between them.

Table 5 Ratio of wealth in power-associated burials to the median burial wealth
Full size table

Bullet plots of the Gini coefficients for burial wealth in the two categories of societies reveal that neither the Gini coefficients nor their margins of error exceed the mean Gini coefficients of the other type of society at the 80%, 90%, and 99% confidence levels (Table 6 and Fig. 8). The degree of burial wealth inequality in societies with hydraulic engineering work is significantly higher than in those without. These findings correspond to the differentiation in Gini coefficients among different societies during the period from 4500 to 2000 BCE, as depicted in Fig. 4. Therefore, we can say with at least 99% confidence that a statistically significant difference exists in the degree of social wealth inequality between societies with and without hydraulic engineering works. This implies that the advent of hydraulic projects probably has contributed to social wealth inequality in the prehistoric Middle Yangtze River Plain.

Table 6 Error ranges of Gini Coefficients of societies with and without hydraulic works
Full size table
Fig. 9: Wealth ratio of powers in hydraulic and non-hydraulic societies.
figure 9

Due to the skewed distribution of wealth ratio, we conducted 1000 random samplings of the wealth ratio of power for each category, preserving the original sample size in each iteration. For each resampled dataset, we used the median of these 1000 ratios as the representative measure of wealth ratio for that category. Finally, we determined the margin of error for this ratio across different confidence levels. A Comparison of wealth ratio of political-military power burials in two types of society; B comparison of wealth ratio of ritual power burials in two types of society; C comparison of wealth ratio of two types of power burial in hydraulic society; D comparison of wealth ration of two types of power burial in non-hydraulic society.

Full size image

Given the significant relationship between hydraulic projects and the Gini coefficient, a deeper exploration of this connection is warranted. The most influential and controversial theoretical framework linking hydraulic engineering works and social complexity is the “hydraulic civilization” hypothesis proposed by Wittfogel33. This hypothesis centers on the nature and impact of large-scale irrigation tasks, positing that the construction and management of irrigation systems require extensive collaborative labor, which in turn necessitates organizational changes such as discipline and leadership. In this context, farmers must adopt collaborative mechanisms and submit to top-down leadership to ensure their survival. Wittfogel further postulated that the socio-political organization of “hydraulic civilizations” led to the concentration of power and the emergence of despotic states, a concept he termed “Oriental Despotism.” The implications of this hypothesis are far-reaching, particularly in understanding the role of irrigated agriculture in the process of social complexity.

Archaeologists have generally tested this hypothesis through two key assumptions: first, that large-scale irrigation systems must precede the emergence of centralized states, and second, that irrigation requires central leadership for coordination34. While some scholars argued that centralized states in regions like Mesopotamia and Mesoamerica developed prior to large-scale irrigation activities35, others reached similar conclusions in their studies of early state formation in Mesopotamia and Mesoamerica36,37. Conversely, scholars like Sanders et al. argued that hydraulic agriculture was a crucial factor in the development of early states in Mesoamerica and the Central Andes38,39. Rowe observed that early large cities in Peru emerged before the development of extensive irrigation projects, suggesting that urban growth, rather than irrigation, was the driving force behind social complexity in this region40. This debate continues to shape our understanding of the relationship between hydraulic engineering and social complexity.

In examining the archaeological materials in the Dongting Lake Plain, we found that the relationship between hydraulic projects and the emergence of political and ritual power is complex and non-linear. For example, at the Chengtoushan site, enclosed ditches for irrigation appeared during the Tangjiagang period, well before the emergence of ritual and political-military power as indicated by burial goods41. Conversely, at the Tangjiagang site, ritual power symbols in burial such as white pottery appeared earlier than the hydraulic works27. In the Jianghan Plain, hydraulic works were present during the early Qujialing period at the Shijiahe site, yet burial objects symbolizing power did not appear until much later32,42. This lack of a uniform antecedent relationship between hydraulic works and the emergence of power suggests that the connection between the two may be more complex.

Our analysis of wealth distribution among individuals in power within their societies further illustrates the complexity of this relationship. For those with political-military power, the ratio of burial wealth in hydraulic societies is moderately higher than that of their counterparts in non-hydraulic societies (Table 7 and Fig. 9A). Similarly, for those with ritual power, the wealth ratio in hydraulic societies is significantly higher than in non-hydraulic societies (Table 7 and Fig. 9B). This suggests that hydraulic projects may have provided a mechanism for individuals in both political-military and ritual power to accumulate greater wealth.

Table 7 Error ranges of wealth ratio of powers in societies with and without hydraulic works
Full size table

Moreover, within hydraulic societies, the wealth ratio associated with ritual power tends to be moderately higher than that associated with political-military power (Table 7 and Fig. 9C). In contrast, within non-hydraulic societies, the wealth ratio shows no significant difference between ritual and political-military power (Table 7 and Fig. 9D). This indicates that holders of ritual power in hydraulic societies might have had a greater capacity to amass wealth compared to those with political-military power. However, as previously noted, there is no direct causal link between the construction of hydraulic works and the emergence of such powers. Instead, it is more plausible that the construction of these works contributed, to some extent, to the wealth accumulation of those in power.

If hydraulic projects are indeed a driving force behind the increased inequality of social wealth, as expressed through the Gini coefficient, and if those in power within hydraulic societies are able to acquire more wealth, it becomes worthwhile to compare the stratification of social wealth between societies with and without hydraulic works evidence. Since the variable of societies and wealth strata are ordinal there are ties on strata among societies, we employed Wilcoxon rank-sum test to investigate the differences in wealth stratification. The analysis yields a W = 217.5, p = 0.3766, indicating there is no statistically significant difference between the hydraulic and non-hydraulic societies.

Multivariate interpretation of the wealth inequality (Gini Coefficient)

We have quantified the relationship between burial wealth inequality and variables such as population size, power, hydraulic works, and wealth stratification. However, it is essential to remain cautious about the robustness of the results derived from this analysis. To test the robustness of our findings within a multivariate context, we conducted multiple linear regressions. The variables considered in these regressions include the presence or absence of hydraulic works (coded as 0 or 1), population size (logarithm of the number of individuals buried), total wealth (logarithm of total burial wealth across societies), political-military power burial density, ritual power burial density, and the presence or absence of political-military and ritual power (both coded as 1 or 0).

Before proceeding with the regression analysis, we examined the multicollinearity between these variables using the Pearson product-moment correlation coefficient. The results, presented in Fig. 10, reveal a correlation coefficient of 0.76 between population size and total wealth, indicating a potential issue with multicollinearity, which could affect the stability of the multiple regression results. So, we excluded total wealth temporarily from the multiple regression analysis and treated the entire dataset as pooled cross-sectional data. The multiple regression analysis (Table 8) demonstrates that wealth inequality is positively and robustly correlated with both population size (log10) and the presence of hydraulic works. These findings align with the patterns observed in our earlier analysis. Additionally, the presence of ritual power is significantly positively correlated with the Gini coefficient, indicating that social wealth inequality tends to be higher in societies where ritual power is present.

Fig. 10: Pearson product-moment correlation coefficients between variables.
figure 10

Var1 = Population Size(log10), Var2 = Wealth(log10), Var3 = Density of Political-Military Power Burials, Var4 = Density of Ritual Power Burials, Var5 = Presence/Absence of Hydraulic Works (1,0), Var6 = Presence/Absence of Ritual Power (1,0), Var7 = Presence/Absence of Political-Military Power (1,0).

Full size image
Table 8 Multiple regression analysis (ordinary least square regression)
Full size table

Meanwhile, the strong positive correlation between total wealth and population cannot be overlooked due to its potential impact on the Gini coefficient. To address the potential multicollinearity between population size and total wealth, which could affect the stability of the multiple regression results, we conducted a ridge regression with ten-fold cross-validation. This approach allowed us to simultaneously assess the contributions of total wealth and population size to wealth inequality while enhancing model stability. The ridge regression model effectively mitigates the impact of multicollinearity by introducing the regularization parameter Lambda, resulting in relatively stable and reasonable coefficient estimates. The results (Tables 9, 10 and Fig. 11) of the ridge regression indicate that the R² is 0.5878, meaning the model explains approximately 58.78% of the variance in the Gini coefficient. This suggests that the independent variables have a strong explanatory power over the dependent variable. The adjusted R² is 0.4948, which is lower than the original R², likely due to adjustments for model complexity. Despite this, the adjusted R² value still indicates that the model retains significant explanatory power after accounting for the number of variables included.

Table 9 Results of ridge regression analysis
Full size table
Table 10 Ridge regression diagnostic table
Full size table
Fig. 11
figure 11

Ridge trace plot and ten-fold cross-validation plot.

Full size image

The ridge regression results reveal that the positive effects of population size (log10), total wealth (log10), and hydraulic project on the dependent variable are significant, with these factors contributing meaningfully to the explanation of wealth inequality. The standardized coefficients of the ridge regression indicate that, among these variables, population size has the strongest influence on wealth inequality, followed by presence of hydraulic works. Total wealth has a smaller effect on wealth inequality than these two variables. Additionally, the presence of ritual power positively influences social wealth inequality, though to a lesser extent. On the other hand, the burial densities of political-military and ritual power exert significant negative impacts on wealth inequality, suggesting that the more dispersed these forms of power are, the smaller their effect on social wealth inequality. Conversely, when these forms of power are more centralized, their contribution to wealth inequality is greater.

Discussion and conclusion

Chronological burial wealth inequality in the middle Yangtze River Plain, as indicated by prehistoric Gini coefficients, fluctuated between 4500 and 2000 BCE, with some societies experiencing significant increases as revealed in Fig. 4. This trend is largely linked to hydraulic project construction, leading to wealth concentration and possible population increase. Ridge analysis shows that population size has the strongest impact on wealth inequality, followed by hydraulic projects, with total wealth having a smaller effect. Ritual power (Table 9) also contributes to inequality but is the weakest factor. Conversely, the dispersed distribution of political-military and ritual power correlates with lower wealth inequality, while centralization amplifies it.

Among these variables, it is particularly important to focus on the impact of hydraulic projects on social complexity, including wealth inequality. In light of the early emergence of hydraulic projects, with roots tracing back to the Pengtoushan period at the Bashidang site, and in consideration of our statistical findings (Table 10), we put forth the proposition that hydraulic engineering may have been one of the earliest, if not the initial, triggers of inequality in the prehistoric Middle Yangtze River Plain. The construction of such projects likely stabilized agricultural production, facilitating steady population growth. It’s socio-political and economic impacts also give rise to a series of complex transformations, including the reconfiguration of irrigation rights, the redistribution of water resources, varied effects on different types of land and crops, shifts in the valuation of land in relation to labor, and indirect influences on craft production and trade networks. These cascading effects could in turn lead to greater inequality43,44,45.

The “hydraulic civilization” hypothesis and the concept of “Oriental despotism” both assume that irrigation necessitated central leadership and emergence of states33. However, the relationship between hydraulic projects and the differentiation of ritual and political-military powers over time may not have been consistent across sites in the middle reaches of the Yangtze River Plain. Additionally, the centuries that separate the emergence of power structures and the construction of hydraulic projects complicate the establishment of a causal link between the two. But it is highly possible that the construction of hydraulic works facilitates those in ritual and political-military powers to accumulate wealth, particularly for those in ritual power (Fig. 9).

In the prehistoric Middle Yangtze Plain, the presence of both political-military and ritual power objects in same burials is uncommon, suggesting that these two types of power were likely separate in most cases. Even if a concentration of these powers occurred occasionally, it was likely practiced intermittently over time and did not form a widely accepted tradition or social consensus across the entire region. In terms of wealth accumulation, those in power tend to have greater economic resources than the general population in general, with wealth being more prominent among ritual power holders than among those holding political-military power in hydraulic societies, indicating a stronger influence of ritual power in hydraulic societies (Fig. 9).

The “Zuo Zhuan” states that “the major events of the state lie in rituals and warfare,” reflecting the importance of ritual and political-military power in maintaining state power46. These two forms of power are also crucial for studying the origins of the state. The available archaeological evidence from the middle reaches of the Yangtze River Plain does not indicate a systematic concentration of the two forms of power that led to state formation and maintenance suggested by the record of Zuo Zhuan, much less the establishment of a bureaucratic system as defined by Max Weber47. If the absence of evidence is not due to gaps in archaeological work, it is reasonable to assume that the lack of a centralized power system based on “ritual and warfare” is at least one reason why large state societies did not emerge in the prehistoric middle Yangtze River Plain. This development suggests that the construction of hydraulic projects in the region, characterized by dikes, ditches, and dams, likely corresponded to a mechanism of social cooperation driven by practical considerations, rather than a top-down leadership model. The hypotheses of a “hydraulic civilization” and “Oriental despotism” attempt to correlate the scale of hydraulic projects with centralized leadership, aligning with the general principle that large-scale irrigation projects were constructed by large-scale regimes. However, archaeological evidence indicates that prehistoric hydraulic projects in the middle reaches of the Yangtze River were the result of continuous construction by prehistoric populations over hundreds or even thousands of years48. The large-scale hydraulic projects formed by the accumulation of cultural layers are consistent with the understanding that the middle reaches of the Yangtze River Plain temporarily lacked centralized prehistoric power and professional bureaucracies. Additionally, the region was densely populated with rivers and lakes, providing abundant water resources, so that the demand for hydraulic construction could be met through community coordination. Even today, hydraulic projects at the village level are typically built through negotiation and cooperation among villagers49. While inter-regional or inter-site differences in hydraulic patterns, such as those in the Jianghan Plain and Dongtinghu Plain, cannot be ruled out, the construction of prehistoric hydraulic projects in the middle reaches of the Yangtze River Plain likely resulted from a mechanism of negotiation and cooperation among communities. Under this cooperative mechanism, coordinators with limited power likely emerged within or among different communities, rather than through the centralized leadership model advocated by Wittfogel. These coordinators probably came from capable individuals or elders who already possessed a degree of prestige within or among communities, and their power bases were not exclusively tied to the hydraulic projects described by Wittfogel. The multiplicity of power bases complicates the reasons for the emergence of power, necessitating an examination of the process of power emergence, strengthening, and centralization from its origins.

Another case with clear evidence of large-scale hydraulic projects is the Liangzhu site in the lower Yangtze River Plain50,51. The supreme ruler of the Liangzhu societies during the middle and late Liangzhu combined political-military and ritual power, potentially generating a complex bureaucracy52. In terms of social organization and the scale of hydraulic projects, the Liangzhu societies seems consistent with Wittfogel’s “hydraulic civilization” hypothesis. However, from a broader spatial and temporal perspective, the political-military power represented by the stone battleaxe and the ritual power represented by other ritual objects (e.g., the huang, the trident-shaped objects, the crown-shaped objects, the scepter, the round plaque, the jade bi and cong) in the Ningshao-Taihu Plain can be traced back to the Majiabang Period, much earlier than Liangzhu. For instance, burials like M51 at the Qitoushan site53, M219 at the Shendun site54, and M58 at the Majiabang site contain evidence of these two power objects55. The presence of these power symbols in the same burial dates back at least to the Songze period, as seen in M16 from the Nanhebang site56. More importantly, the density of these two power symbols in burials in the lower Yangtze River plains is significantly higher than in the middle Yangtze River plains, and their continuity appears to be stronger (Fig. 12, Table 11). This long period of continuous and proficient power practice likely accumulated social organizational experience and a widely accepted social consensus, contributing to the emergence of the state-like Liangzhu society. The large-scale hydraulic projects may have been the result of a highly developed centralized power mechanism. The simultaneous presence of political-military and ritual power objects in the burials of the highest power holders later also became a convention at Taosi and Erlitou, which are also considered early state-like societies. The comparison of prehistoric power traditions in the Middle and Lower Yangtze regions tend to support an alternative model of state formation, where the centralization of political-military and ritual power by elites was crucial. The concentration of ritual and political-military powers, as evidenced by historical accounts like “the major events of the state lie in rituals and warfare,” was a key factor in early state development.

Fig. 12: Bullet graphs of power burial density in the Middle and Lower Yangtze Plains.
figure 12

The bars represent the mean of densities, lines represent the 99% confidence intervals. The burial samples from the Lower Yangtze River Plain, encompassing Qitoushan, Shendun, Xingang, Majiabang, Nanhebang, Songze, Liangzhu, Bishan, and Xindili, comprise 1152 individuals. Disturbed or looted burials have been excluded. Each society’s sample consists of more than 10 individuals or burials.

Full size image
Table 11 Density of power related burials in the Middle and Lower Yangtze Plains
Full size table

In conclusion, the Gini coefficients from 7000 to 2000 BCE in the middle Yangtze River Plain reveal non-linear trajectories and significant variation in wealth inequality, with hydraulic projects as one of the earliest, if not the initial, triggers of inequality. These projects boosted agricultural productivity, population growth and total social wealth, leading to increased inequality. Population size had the greatest impact on inequality, followed by hydraulic projects, with total social wealth having a smaller influence. Ritual power also contributed to inequality. Archaeological evidence indicates that hydraulic projects often preceded power symbols, with no consistent temporal relationship between hydraulic project development and power consolidation, challenging the “Hydraulic Civilization” and “Oriental Despotism” hypotheses. Prehistoric ritual and political-military power developed independently in the middle Yangtze Plain, suggesting that hydraulic projects were possibly products of negotiation and cooperation, rather than top-down centralized leadership.