Research on flood resistance performance of traditional corridor woven arch bridges

Abstract

Corridor woven arch bridges hold significant cultural value but are often threatened by flood. This study employs computational fluid dynamics (CFD) to quantify the effects of water level and flow velocity on force of the bridge. Overturning and sliding risks are evaluated, and the effectiveness of removing the weather-boards and adding weight to the bridge is assessed. The results show that rising water levels greatly increase the bridge’s drag force. Higher flow velocity leads to negative lift growth, which is positively correlated with water level. When water level exceeds the deck, overturning risk arises, and removing the weather-boards is recommended. Corridor bridges are more prone to sliding failure. Both measures are recommended when the water level exceeds the deck, while adding weight to the bridge is sufficient at lower water levels. This study provides a scientific basis for flood resistance assessment and preventive protection of corridor woven arch bridges.

Introduction

Traditional corridor woven arch bridges are a traditional form of bridge in the Fujian and Zhejiang provinces of China. The main arches employ interwoven timber structures to achieve a larger span, and the corridor on the bridge deck serves to protect the underlying bridge structure and increase the vertical load, to enhance structural stability¹. In 2009, the “Traditional Construction Techniques of Chinese Timber Arch Bridges” was included in UNESCO’s “List of Intangible Cultural Heritage in Need of Urgent Safeguarding.” By 2024, it had been transferred to the “Representative List of the Intangible Cultural Heritage of Humanity.” Due to their unique engineering value and historical cultural connotation, traditional corridor woven arch bridges have attracted the attention of numerous experts and scholars. Researchers have conducted relevant studies focusing on the construction technology², development history³, folk culture⁴, and form and structure^5,6 of traditional corridor woven arch bridges.

Most traditional corridor woven arch bridges in China have a history of over a hundred years⁷, and they frequently suffer damages due to material degradation, human factors, and natural disasters. The scientific evaluation of factors affecting the structural performance of traditional corridor woven arch bridges, as well as the proposal of viable preventive and restorative methods, have become an important area of research. Researchers have investigated the structural performance of the bridge through experimental and numerical simulation methods. For instance, the influence of frog-leg strut on the structural performance and failure modes of the timber arches under both symmetrical and asymmetrical loads has been analyzed⁸. Studies have also examined the mechanical behavior of traditional corridor woven arch bridge structures and the contributions of various components in structural stress^9,10, proposing structural safety evaluation methods applicable to traditional corridor woven arch bridges^11,12. To assess the material degradation, researchers used non-destructive testing technology to detect the load-bearing timber columns of traditional corridor woven arch bridges and classified their safety levels¹³. In addition, researchers have proposed various preventive and restoration methods for traditional corridor woven arch bridges, considering various influencing factors. These include a component repair technique that does not require disassembly of the main arch structure¹⁴, CFRP reinforcement for corridor woven arch bridge components¹⁵, and an adaptive restoration design combining structural disassembly, component reinforcement, and structural reintegration¹⁶.

In addition to these extensive researches on traditional corridor woven arch bridges, there remains a lack of studies on disaster prevention. Hydraulic factors are the primary cause of bridge failure. In various regions, nearly half of all bridge failure incidents are attributed to hydraulic causes, most of which occur during flood events¹⁷. The Fujian and Zhejiang provinces experience frequent rainy seasons with heavy rainfall, especially during typhoon seasons, resulting in significant flood impacts and frequent damage incidents to traditional timber corridor woven arch bridges. In 2016, several traditional timber corridor woven arch bridges, such as Wenxing Bridge, Xuezha Bridge, and Longjin Bridge, were destroyed by the flood caused by Typhoon Meranti¹⁸. In 2024, the corridor of Huanxiu Bridge was destroyed by the flood caused by continuous rainfall (Fig. 1). Most of these bridges are major historical and cultural sites protected at the national level, underscoring the importance of flood resistance research for traditional corridor woven arch bridges conservation. Currently, some scholars have employed computational fluid dynamics (CFD) simulations to investigate the flood response of the first system, the second system, and weather-boards in traditional corridor woven arch bridges¹⁸. However, the research on the flood response of the entire traditional corridor woven arch bridges and the effectiveness of flood resistance measures is still lacking. Against the backdrop of significant global climate change, the increasing frequency of extreme rainfall events has further intensified the risk of flood disasters¹⁹, posing growing threats to the safety of traditional corridor woven arch bridges.

Fig. 1: Huanxiu Bridge before and after the flood.

a Before, b After.

This study investigates the load distribution and failure risks of traditional corridor woven arch bridges under various flood conditions, and evaluates the effectiveness of commonly used flood resistance measures. The remainder of the paper is organized as follows. The “Method” section includes the determination of a typical model for corridor woven arch bridges, the CFD computational domain and setup, the selection of governing equations and turbulence model, the validation of the simulation method, and the configuration of simulation conditions. The “Results” section presents the numerical results of the flood force distribution of the corridor woven arch bridge and its key components under various flood conditions. It includes the calculation of overturning and sliding risks of the entire bridge, as well as the evaluation of the effectiveness of two flood resistance measures—removing the weather-boards and adding weight to the bridge. Based on the calculation, appropriate flood resistance measures are recommended for different failure model. Discusses section the implications of the findings, highlights the limitations of the study, and suggests directions for future research. The results of this research can provide a scientific basis for the flood resistance performance assessment and preservation of traditional corridor woven arch bridges.

Methods

Model overview

Based on several existing examples of corridor woven arch bridges, this study develops a typical model of a traditional corridor arch bridge, which consists of two main components: the bridge body and the corridor (Fig. 2a). The detailed structural layout of the bridge is illustrated in Fig. 2b, c. The main arch of the bridge body serves as the primary load-bearing component, consisting of a first system and a second system The bridge structure includes two sets of X-shaped struts, positioned above and below, to improve its lateral stability. The upper X-shaped strut is connected to the crossbeam of the first system, while the lower X-shaped strut connects to the lower crossbeam of the second system. The distal ends of both X-shaped struts are attached to the commander-pillars. Additionally, frog-leg struts are attached to the lower crossbeam of the second system to reduce the span of the bridge deck beam. The corridor is structured in a four-column, nine-purlin, and three-bay configuration⁶.

Fig. 2: Traditional corridor woven arch bridge.

a Corridor woven arch bridge model, b Front view of bridge structure, c Bottom view of bridge structure.

Computational domain and computational setup

A computational domain model is constructed by Rhino, leveraging the symmetry of the bridge geometry and flood basins, enabling simulation of only half of the bridge structure. The dimensions of the computational domain are depicted in Fig. 3.

Fig. 3: Computational domain calculation model.

a Model with weather-boards, b Model without weather-boards.

The model is partitioned in SpaceClaim and then imported into Fluent Meshing for mesh generation, with mesh sizes ranging from 50 mm to 1000 mm. A mesh expansion ratio of 1.2 is applied throughout the domain to ensure simulation accuracy. The meshing schemes of the model with weather-boards contains 642,965 cells, while the model without weather-boards contains 592,508 cells. Transient simulations are performed in Fluent, with a pressure-inlet boundary for flow entry, a pressure-outlet for the exit, and no-slip wall conditions for the bridge, riverbed, and sidewalls. The computational domain’s top and symmetry planes are set as symmetry boundary conditions, with gravitational acceleration at 9.81 m/s². The PISO (Pressure-Implicit with Splitting of Operators) algorithm manages pressure-velocity coupling²⁰.

With air and water present, the VOF (Volume of Fluid) multiphase model simulates free surface flows. Here, α_q denotes the air volume fraction in the computational domain, while 1-α_q denotes the volume fraction of water. Regions with α_q = 1 or α_q = 0 represent domains occupied by air or water, respectively, while values of 0 < α_q < 1 indicate mixed domains of air and water, and α_q = 0.5 captures the air-water interface, which is the free surface. The constants used in Fluent are presented in Table 1.

Table 1 Property constants of air and water phases

Governing equations

Based on the Fluent platform, the Navier-Stokes equations are employed as the governing equations, which consist of velocity and pressure formulation of the incompressible fluid. Navier-Stokes equations are shown as follows:

$$\frac{{\partial }_{{{\rho }}}}{\partial {{t}}}+\frac{\partial ({{\rho }}{{{U}}}_{{{i}}})}{\partial {{{\chi }}}_{{{i}}}}=0$$

(1)

$$\frac{\partial {{\rho }}{{U}}_{{i}}}{\partial {t}}+\frac{\partial {{\rho }}{{U}}_{{i}}{{U}}_{{j}}}{\partial {{x}}_{{j}}}=-\frac{\partial {{p}}}{\partial {{x}}_{{i}}}+\frac{\partial }{\partial {x}_{j}}\left[\left({{\mu }}+{{{\mu }}}_{{{T}}}\right)\left(\frac{\partial {{{U}}}_{i}}{\partial {x}_{j}}+\frac{\partial {{{U}}}_{j}}{\partial {x}_{i}}\right)\right]$$

(2)

Where ρ is the fluid density, t is the time, U_i is the ith component of velocity, x_i is the Cartesian coordinates, p is the dynamic pressure, μ is the viscosity, μ_T is the eddy viscosity, calculated by turbulence model as detailed in “Turbulence model”.

Turbulence model

The study employed the standard k-epsilon turbulence model, which is widely used and reasonably accurate²¹. Research by Saghravani and Azhari²² demonstrated that the standard k-epsilon model can effectively predict the flow field and forces around circular piers arranged in a linear arrangement, which shares certain similarities with the arrangement of arch components in traditional corridor woven arch bridges. Moreover, considering the complex structure of traditional corridor woven arch bridges, the standard k-epsilon model provides a suitable balance between computational accuracy and efficiency. The two-equation model for incompressible fluid is as follows:

$$\frac{\partial ({{\rho }}{{k}})}{\partial {{t}}}+\frac{\partial ({{\rho }}{{k}}{{{U}}}_{{{i}}})}{\partial {{{x}}}_{{{i}}}}=\frac{\partial }{\partial {{{x}}}_{{{j}}}}\left[\left({{\mu }}+\frac{{{{\mu }}}_{{{T}}}}{{{{\sigma }}}_{{{k}}}}\right)\frac{\partial {{k}}}{\partial {{{x}}}_{{{j}}}}\right]+{{{G}}}_{{{k}}}-{{\rho }}{{\varepsilon }}$$

(3)

$$\frac{\partial ({{\rho }}{{\varepsilon }})}{\partial {{t}}}+\frac{\partial ({{\rho }}{{\varepsilon }}{{{U}}}_{{{i}}})}{\partial {{{x}}}_{{{i}}}}=\frac{\partial }{\partial {{{x}}}_{{{j}}}}\left[\left({{\mu }}+\frac{{{{\mu }}}_{{{T}}}}{{{\sigma }}_{{{\varepsilon }}}}\right)\frac{\partial {{\varepsilon }}}{\partial {{{x}}}_{{{j}}}}\right]+{{{C}}}_{1{{\varepsilon }}}{{{G}}}_{{{k}}}\frac{{{\varepsilon }}}{{{k}}}-{{{C}}}_{2{{\varepsilon }}}{{\rho }}\frac{{{{\varepsilon }}}^{2}}{{{k}}}$$

(4)

$${{{G}}}_{{{k}}}={{{\mu }}}_{{{T}}}\frac{\partial {{{U}}}_{{{i}}}}{\partial {{{x}}}_{{{j}}}}\left(\frac{\partial {{{U}}}_{{{j}}}}{\partial {{{x}}}_{{{i}}}}\,+\frac{\partial {{{U}}}_{{{i}}}}{\partial {{{x}}}_{{{j}}}}\right)$$

(5)

$${{{\mu }}}_{{{T}}}={{\rho }}{{{C}}}_{{{\mu }}}\frac{{{{k}}}^{2}}{{{\varepsilon }}}$$

(6)

where G_k is the generation of turbulent kinetic energy due to mean velocity gradients, C_1ε, C_2ε, and C_μ are empirical constants; σ_k and σ_ε are the Prandtl numbers corresponding to turbulent kinetic energy and its dissipation rate, respectively, with their values listed in Table 2.

Table 2 parameters related to the standard k-epsilon model

Validation of the simulation method

Since no flume experiments have been conducted specifically on the flood resistance performance of traditional corridor woven arch bridges. To verify the effectiveness of the numerical simulation method employed in this study, drag force experiments on cylindrical pile groups are selected as the validation case, considering the geometric characteristics of the linear arrangement of components in traditional corridor woven arch bridges. Four groups of pile with different parameter combinations are selected for numerical simulation. The variables include the diameter, D, of the cylinder piles, the spacing between them, and the total number of cylindrical piles. Detailed information is provided in Table 3, where each pile group consists of m columns and n rows, giving a total of m × n piles. The spacing is determined based on the pile diameter. The drag forces obtained from the simulations are extracted and compared with the experimental results, as illustrated in Fig. 4. The differences between the simulated and experimental drag forces range from 0.053 N to 0.122 N, which correspond to relative errors of 7.00% to 13.54%. The simulation results showed good agreement with the flume test results, indicating that the numerical simulation method adopted in this study is reliable and can be used to analyze the flood response of traditional corridor woven arch bridges.

Table 3 Experimental cylindrical pile group parameters

Fig. 4

Comparison between numerical simulation results and experimental results.

Simulation conditions

To evaluate the flood response of the bridge structure under varying water levels, three flood levels are set: H = 4 m, 6 m, and 8 m. Specifically, the 4 m water level corresponds to a situation where the water surface is slightly above the arch foot, and only a small number of structural components are either partially or fully submerged. At 6 m, more components are either partially or fully submerged, although the water does not yet reach the lower edge of the weather-boards of the corridor. The 8 m level represents a more severe flood condition where the water reaches the bridge deck. These three water levels were chosen to simulate and analyze the bridge’s response under different flood intensities (Fig. 5). Two flood flow velocities, V = 4 m/s and 6 m/s are established based on previous research to evaluate the influence of flow velocity on the bridge’s flood response¹⁸ and to estimate the failure risk of bridge. To examine the effectiveness of removing the weather-boards in enhancing flood resistance performance, simulations are conducted with and without the weather-boards under identical conditions. The conditions and their identifiers are summarized in Table 4.

Fig. 5

Relative position of the water level to the bridge.

Table 4 Scenarios investigated in this study

Results

Influence of water level on the force response of bridge

Simulations were done under conditions H4V4-FYB, H6V4-FYB, and H8V4-FYB to assess the impact of water level on the flood response of the traditional corridor woven arch bridges. Figure 6 illustrates the pressure contour maps and overall force of the traditional corridor woven arch bridge following flood stabilization. As water levels increase, the pressure on the bridge structure also increases significantly, particularly on the lower sections. The weather-boards shield the structure from direct water impact and subsequent flow, resulting in lower pressure on components near the upstream side.

Fig. 6

Pressure contour maps of the traditional corridor woven arch bridge under different water level conditions.

A comparison of the pressure distribution on the upstream and downstream faces of the bridge under the three conditions in Fig. 7 indicates that when water levels increase, the water-blocking area of the weather-boards expands, hence increasing the pressure on the structure. This then increases the drag force acting on the bridge, thereby increasing the failure risks during flood conditions. To further understand this effect, the drag force (F_D) and lift force (F_L) on the bridge structure were obtained once the flood stabilized (Fig. 8). The results indicate that increasing water levels amplify the forces acting on the bridge, particularly affecting the drag force (F_D) more significantly. At water levels of 6 m and 8 m, F_D is approximately 5.2 and 17.3 times greater than at 4 m, while F_L increases by about 1.7 and 7.1 times, respectively.

Fig. 7

Pressure contour maps of the upstream and downstream faces of the traditional corridor woven arch bridge under different water level conditions.

Fig. 8

Overall force of the traditional corridor woven arch bridge under different water level conditions.

Influence of water level on the force response of key components

To evaluate the impact of water levels and component location on force distribution, the F_D and F_L of individual components were recorded after flood stabilization under each condition.

The slanted beams of the first system and lower slanted beams of the second system are numbered sequentially in the flow direction, with the slanted beams of the first system labeled S-F1 ~ S-F9 and the lower slanted beams of the second system labeled LS-S1 ~ LS-S8. Figure 9a, b illustrates the forces acting on the components under each condition. Due to the influence of the weather-boards, the flow velocity distribution around the first system components is complex, and reverse flow is observed in the sheltered area of the weather-boards (Fig. 10). Furthermore, certain components on the downstream side exhibit higher pressure than those on the upstream side (Fig. 11), leading to negative F_D values. This phenomenon becomes more pronounced at higher water levels (H6V4-FYB and H8V4-FYB), with similar effects observed in the slanted beams of the second system. The F_D of the slanted beams of the first system exhibits an initial drop and then an increase in the direction of water flow, and the lower the water level, the smaller the component’s label number corresponding to the minimum value of F_D. Under all conditions, F_L values for both the first system and second system components gradually increase along the flow direction, with a significant rise in F_L values due to greater immersion depths at higher water levels.

Fig. 9: Forces on the key components of traditional corridor woven arch bridge.

a Forces on the slanted beam of the first system, b Forces on the lower slanted beam of the first system.

Fig. 10

Y-direction velocity contour maps at H = 3.9 m in the horizontal plane.

Fig. 11

Pressure contour maps at H = 3.9 m in the horizontal plane.

The forces acting on the upstream and downstream weather-boards (FYB-Y and FYB-B) are listed in Table 5. As the water level rises from 4 m to 8 m, the water-blocking area of the upstream weather-boards expands, increasing water pressure. The inclined angle of the weather-boards causes force components in the y and z directions, with F_D and F_L on the upstream weather-boards increasing positively along the y-axis and negatively along the z-axis as water levels rise. Upon the water flow bypassing of the downstream weather-boards, significant pressure acts on its downstream face, leading to a negative value for the downstream weather-boards F_D, which intensifies in the negative y direction as the water level increases. Simultaneously, there is a minor negative increase in the downstream weather-boards F_L along the z-axis.

Table 5 Force of the weather-boards

Influence of flow velocity on the force response of bridge

The impact of flow velocity on bridge forces was assessed by comparing conditions H4V4-FYB, H6V4-FYB, and H8V4-FYB with H4V6-FYB, H6V6-FYB, and H8V6-FYB. Figure 12 presents the pressure contour maps on the upstream face under six conditions, while Fig. 13 illustrates the overall forces acting on the bridge following flood stabilization. The line graph illustrates that the force increases multiple times as flow velocity increases at varying water levels. When flow velocity increases from 4 m/s to 6 m/s, the kinetic energy of the water rises, directly elevating impact forces on the bridge, as indicated by the pressure contour maps. The bridge’s F_D increases by a factor of 1.4 to 1.8 with increased flow velocity. At higher flow velocities, the weather-boards additionally amplify the negative F_L on the bridge, with these effects becoming more substantial at higher water levels.

Fig. 12

Comparison of pressure contour maps on the upstream face of the traditional corridor woven arch bridge under different flow velocity conditions.

Fig. 13

Overall force of traditional corridor woven arch bridge with different flow velocity conditions.

Influence of flow velocity on the force response of key components

The horizontal beams of the first system are numbered sequentially from H-F1 to H-F9, following the direction of water flow. Figure 14a illustrates the forces on the first system components. Under H = 4 m and H = 6 m conditions, the horizontal beams of the first system are minimally affected by flood forces and thus are not discussed further. However, increased flow velocity improves kinetic energy, increasing F_D for S-F1 while exerting minimal impact on F_D for the other slanted beams of the first system. When comparing the two H = 8 m conditions, the overall pressure on the slanted beams of the first system decreases at higher flow velocities (Fig. 15), causing a reduction in F_L on the component sections. The horizontal beams of the first system, located near the water surface, display force variations closely related to flow patterns (Fig. 14b).

Fig. 14: Forces on the key components of the first system.

a Forces on the slanted beam of the first system, b Forces on the horizontal beam of the first system.

Fig. 15

Pressure contour maps on the horizontal plane under conditions with H = 8 m.

The flow patterns around the weather-boards change with velocity (Fig. 16), where blue indicates the water surface). At a lower velocity (V = 4 m/s), the water flows smoothly along the weather-boards surface, resulting in minimal disturbance and maintaining stable flow. At V = 6 m/s, the increased kinetic energy generates a stronger pressure gradient, causing water separation at the weather-board edge. This separation leads the water surface to bypass the lower components of the bridge deck, resulting in a reduction in F_D on the horizontal beams of the first system.

Fig. 16

Comparison of flow patterns under different flow velocity conditions.

The upper slanted beams of the second system and horizontal slanted beams of the second system are numbered sequentially in the flow direction, with the upper slanted beams of the second system labeled US-S1 ~ US-S9 and the horizontal slanted beams of the second system labeled H-S1 ~ H-S8. The forces acting on the second system components are illustrated in Fig. 17. Changes in water levels and flow velocity alter the flow patterns, thereby impacting the forces acting on slanted beams of the second system differently. Most of the lower slanted beams of the second system exhibit a reduction in negative F_D due to these changes. Higher flow velocities reduce the immersion depth of the upper slanted beams of the second system (Fig. 16), resulting in decreased pressure on these elements (Fig. 18). This reduction in pressure subsequently reduces both F_D and F_L. The effect of increased flow velocity on F_L for the lower inclined and horizontal beams of the second system follows a similar trend to that of the first system.

Fig. 17: Forces on the key components of the second system.

a Forces on the lower slanted beam of the second system, b Forces on the upper slanted beam of the second system, c Forces on the horizontal beam of the second system.

Fig. 18

Pressure contour maps of the upper slanted beams of the second system.

Table 6 illustrates the variations in forces acting on the weather-boards as flow velocity increases. As velocity increases, the F_D of the weather-boards increases in magnitude as a positive value, while the F_L also increases in magnitude but as a negative value. As the water level increases, the water-blocking area expands, resulting in more significant changes in force due to increased flow velocity. Moreover, the upstream weather-boards are more sensitive to velocity changes compared to the downstream weather-boards. The weather-board’s sheltering effect leads to lower F_D on the commander-pillar near the upstream side, while flow velocity exerts a minimal impact on forces, with a peak increase of 165.9 N as velocity increases from 4 m/s to 6 m/s.

Table 6 Force variation of the weather-boards after increasing the flow velocity

Failure risk and flood force

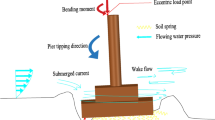
Since the connection between the corridor woven arch bridge and the abutments cannot withstand tensile forces, the bridge may experience sliding or overturning failure under substantial flood forces. Therefore, the failure risk of the bridge is assessed by quantifying the sliding risk and overturning risk, and the effectiveness of flood resistance measures is evaluated accordingly. Flood resistance measures can be classified into two categories based on the failure mechanisms of the bridge: reducing the drag force and adding weight to the bridge (increasing the self-weight G or force in the direction of gravity).

As illustrated in Fig. 19, an analysis of the forces acting on the bridge components reveals that the axis l_G, passing through the center of gravity of the bridge, divides it into two halves. Components on the right side generally bear more F_L in the positive direction along the y-axis than those on the left side. In contrast, the distribution of F_D is more complex, and its magnitude is greater, posing a higher risk of overall structural failure for the bridge. To simplify the calculation while maintaining a safety margin, F_L on the bridge is approximated as a concentrated force acting at the center of gravity. F_D is distributed within 40 segments along the bridge height, with the force acting on each segment recorded for calculation.

Fig. 19

Force diagram of the traditional corridor woven arch bridge.

Figure 20 illustrates the distribution of F_D at various water levels, whereas Fig. 21 illustrates the distribution at various flow velocities. The F_D is transformed into a line load l_FD, where the area under the bar chart in Figs. 20 and 21 represents the F_D. The flow velocity has a minimal effect on F_D distribution patterns. In all conditions, the maximum F_D value of the traditional corridor woven arch bridge is observed near the corresponding water level height.

Fig. 20: F_D distribution of the traditional corridor woven arch bridge under different water level conditions.

a H4V4-FYB, b H6V4-FYB, c H8V4-FYB, d Comparison of three conditions at V = 4 m/s.

Fig. 21: F_D distribution of the traditional corridor woven arch bridge under different flow velocity conditions.

a Comparison of two conditions at H = 4 m, b Comparison of two conditions at H = 6 m, c Comparison of two conditions at H = 8 m, d Comparison of three conditions at V = 6 m/s.

Overturning risk

Converting the gravity of the corridor to a uniform load q_corridor = 1.5 kN/m²¹⁴, and the timber components of the bridge are made of China fir (Cunninghamia lanceolata (Lamb.) Hook.)¹² with a density ρ = 380 kg/m³²³. The self-weight G of the bridge is calculated to be 195.13 kN using Eq. (7). The anti-overturning moment M_G is determined by Eq. (8), while the overturning moment M_overturn is calculated using Eq. (9). Define the anti-overturning stability factor of the corridor bridge, K_overturn, through Eq. (10), and the corridor bridge is at risk of overturning failure when K_overturn < 1.

$$G={q}_{{\rm{corridor}}}S+{\rho }{Vg}$$

(7)

$${{M}}_{{G}}={Gl}$$

(8)

$${M}_{\text{overturn}}={M}_{\text{D}}+{M}_{\text{L}}=\mathop{\sum}\limits_{i=1}^{40}{F}_{\text{D}i}{l}_{\text{D}i}+{F}_{\text{L}}l$$

(9)

$${K}_{{\rm{overturn}}}=\frac{{M}_{G}}{{M}_{\text{overturn}}}$$

(10)

where S is the deck area in m²; V is the volume of the bridge components calculated by Rhino software in m³; g is the gravitational acceleration, set at 9.8 m/s²; l is the lever arm of G and F_L to point O in m; M_D and M_L are the moments generated by the F_D and F_L in kN m; F_Di is the F_D on i segment of the bridge in kN; l_Di is the lever arm of F_Di to point O in m.

The calculated overturning moments and the K_overturn for six conditions are illustrated in Fig. 22. The two conditions with an 8 m water level exhibit the overturning moment greater than the anti-overturning moment, indicating a risk of overturning. All other conditions satisfy the requirement of K_overturn ≥ 1. Although increased water levels and flow velocities lead to increased F_D, higher flow velocity reduces F_L to a certain degree. In contrast, higher water levels increase F_L and lengthen the lever arm of F_D. As a result, overturning moments are more sensitive to increases in water level, with this sensitivity positively correlated with the bridge’s water-blocking area. The increase in overturning moment from 6 m to 8 m water levels is substantially higher compared to the increase from 4 m to 6 m.

Fig. 22

Overturning moment of the traditional corridor woven arch bridge under six conditions.

To quantify the improvement in the anti-overturning performance of the corridor woven arch bridge by removing the weather-boards, the K_overturn for models with and without the weather-boards were evaluated under identical conditions (Fig. 23). The results indicate that removing the weather-boards can improve flood resistance performance by decreasing F_D in high water level conditions. However, the negative F_L generated by the impact on the weather-boards also decreases, resulting in a slight increase in the overturning moment under certain conditions. Despite a decrease in K_overturn, the values remain above 1, causing minimal impacts on structural safety.

Fig. 23

Anti-overturning stability factors for each condition.

To further analyze the effect of removing the weather-boards on the overturning moment, models both with and without the weather-boards were calculated for conditions at risk of overturning (Fig. 24). The calculation results indicate that removing the weather-boards significantly decreases the overturning moments caused by F_D by over 50% under both conditions. Additionally, removing the weather-boards allows floodwater to flow directly onto the bridge deck, thus increasing the force in the direction of gravity of the bridge to a certain degree (Fig. 25), further reducing the overturning moment by 68.59% and 92.66% under the two conditions, respectively.

Fig. 24

Comparison of overturning moments for traditional corridor woven arch bridge with and without weather-boards.

Fig. 25

Flow pattern of the traditional corridor woven arch bridge without weather-boards under two conditions at H = 8 m.

Adding weight to the bridge is typically achieved by placing heavy objects on the deck. However, excessive loading on one side of the arch or at the mid-span could adversely impact the bridge structure and even cause irreversible damage^8,18. Therefore, a uniform weight distribution across the bridge deck is adopted. The initial uniform load is 0.5 kN/m², increasing by 0.5 kN/m² at each level until the K_overturn exceeds 1. Table 7 illustrates the overturning moment and K_overturn for H8V4-FYB and H8V6-FYB with added weight. When the uniform load on the bridge deck reaches 4.5 kN/m², the K_overturn satisfies the required threshold.

Table 7 Anti-overturning stability factors of the corridor woven arch bridge with adding weight to the bridge

Although adding weight to the bridge is an effective and feasible flood resistance measure, the structural safety of the bridge must be considered in practice, excessive loading should be avoided. According to the calculated overturning risks and the effectiveness of the two flood resistance measures, the bridge shows a higher risk of overturning when the water level exceeds the bridge deck. Under such conditions, removing the weather-boards is recommended to enhance the anti-overturning performance of the bridge.

Sliding risk

When the frictional resistance between the corridor woven arch bridge and the abutments is smaller than the drag force, sliding of the bridge may occur. According to GB 50003-2011 (Code for Design of Masonry Structures)²⁴, the friction coefficient between the bridge and the abutment system is taken as µ_f = 0.5. Under flood conditions, the frictional resistance F_f of the bridge is calculated as follows:

$${{F}}_{{{f}}}={\mu }_{{{f}}}\left(G-{F}_{{{L}}}\right)$$

(11)

To prevent sliding failure of the corridor woven arch bridge, its frictional resistance must exceed the maximum drag force. The anti-sliding stability factor of the bridge, K_sliding, is defined by Eq. (12). When K_sliding < 1, the bridge is considered at risk of sliding failure.

$${K}_{{\rm{sliding}}}=\frac{{F}_{{\rm{f}}}}{{F}_{{\rm{D}}}}$$

(12)

Under the six conditions, the frictional force and the K_sliding of the corridor woven arch bridge are illustrated in Fig. 26. The bridge is at risk of sliding under conditions H8V4-FYB, H6V6-FYB, and H8V6-FYB. Under both flow velocities, F_D increases as the water level rises. At a flow velocity of V = 4 m/s, the rise in water level causes F_L to increase in the positive direction along the y-axis, resulting in a decrease in frictional force. At V = 6 m/s, the rise in water level causes F_L to increase in the negative direction along the y-axis, leading to an increase in frictional force. Therefore, as the water level increases, the decrease in the K_sliding is more significant under the condition with V = 4 m/s

Fig. 26

Friction force and anti-sliding stability factor of the corridor woven arch bridge under six conditions.

To quantify the improvement in anti-sliding performance of the corridor woven arch bridge by removing the weather-boards, the K_sliding of models with and without the weather-boards under the same conditions were compared (Fig. 27). The results show that under conditions where the water level exceeds the bridge deck (H = 8 m), removing the weather-boards not only reduces the drag force on the bridge but also increases the lift force along the negative direction of y-axis. Therefore, this method can enhance the anti-sliding performance of the corridor woven arch bridge under high water level conditions to some extent. However, removing the weather-boards does not satisfy the anti-sliding performance requirement under the H8V4, H6V6, and H8V6 flood conditions, as the corresponding K_sliding remain below 1.

Fig. 27

Anti-sliding stability factors for each condition.

To evaluate the effect of adding weight to the bridge on sliding resistance, the K_sliding of the models both with and without the weather-boards were calculated under H8V4, H6V6, and H8V6 flood conditions (Fig. 28). When the water level exceeds the bridge deck (H = 8 m), adding weight to the bridge provides only slightly enhances the anti-sliding performance of the model with weather-boards. Even with a uniform load of 5.0 kN/m², the bridge remains at risk of sliding failure. Under the H8V4 and H8V6 flood conditions, the model without weather-boards meets the sliding performance requirement when the uniform load reaches 2.0 kN/m² and 4.0 kN/m², respectively. Therefore, when the water level exceeds the bridge deck, both flood resistance measures—removing the weather-boards and adding weight to the bridge—should be implemented simultaneously. At this point, the heavy objects should be fastened to prevent uneven loading due to displacement. When the water level is lower than the bridge deck, adding weight to the bridge can be prioritized.

Fig. 28

Anti-sliding stability factors of the corridor woven arch bridge with adding weight to the bridge.

Discussion

To investigate the flood resistance performance of traditional corridor woven arch bridges, computational fluid dynamics (CFD) simulations were used to examine the effects of water levels and flow velocities on the forces acting on both the entire bridge and its key structural components. Additionally, this study evaluated the effectiveness of two flood resistance measures in enhancing the performance of traditional corridor woven arch bridges.

Key findings of this study include

The overall structural response of the traditional corridor woven arch bridge is jointly influenced by water level and flow velocity. F_D increases with both factors, with water level having a more pronounced effect and dominating the distribution pattern of F_D. F_L decreases as flow velocity increases, and the magnitude of this reduction is positively correlated with water level.

The upstream weather-boards are the primary water-blocking components of the bridge and play a dominant role in the F_D of corridor woven arch bridges. As flow velocity increases, the weather-boards experience higher F_D and lower F_L. At higher water levels, the water-blocking area of the weather-boards increases, and the force variation caused by increased velocity becomes more significant. Components located near the weather-boards generally experience greater F_D, while those closer to the downstream face experience greater F_L. The loading response of components near the deck is mainly affected by flood flow patterns. For other components, as both flow velocity and water level increase, a significant rise in F_D is observed only in the upstream-side components. In contrast, rising water levels generally increase their F_L, while increasing flow velocity tends to reduce it.

Corridor woven arch bridges are more prone to sliding failure under flood conditions, and the overturning risk becomes significant when the water level exceeds the deck. It is recommended that, under high water level conditions, both removing the weather-boards and adding weight to the bridge be adopted simultaneously to prevent sliding and overturning failures. When the water level is below the bridge deck, adding weight to the bridge should be prioritized to counteract sliding failure.

However, this study focuses on the overall failure mechanisms of corridor woven arch bridges under flood conditions and does not investigate component-level failure behavior. Future research will aim to explore the flood resistance performance of such bridges across multiple scales and component levels. The effects of floating debris impact and the coupling effect of flood and wind will also be considered, with the goal of developing a generalized method for evaluating the flood resistance of corridor woven arch bridges.

Overall, this study can inform flood management strategies for corridor woven arch bridges. The recommendations for applying flood resistance measures help improve flood response efficiency, support rational resource allocation, and facilitate long-term bridge maintenance. In addition, this study offers a theoretical and technical foundation for further research on the flood resistance performance and flood resistance measures of corridor woven arch bridges and similar historic structures, contributing to the sustainable preservation and management of cultural heritage.