Introduction

India’s rich cultural legacy includes a wide variety of unique painting styles, each with its own symbolic and esthetic attributes. Among them, Gond, Kalamkari, Pichwai, Madhubani, Mandla, and Warli are six prominent types. Kalamkari paintings are distinguished by their intricate and vibrant designs, whereas Gond art, which comes from the Gond tribal community, is distinguished by its vivid and detailed representations of nature and mythology. Pichwai paintings, which are frequently connected to religious themes, showcase intricate and embellished designs primarily depicting narratives from Lord Krishna’s life. Madhubani art, originating from the Mithila region, is characterized by its precise geometric patterns and mythical motifs. Mandala art, showcases recurrent circular patterns, whereas Warli paintings, produced by the Warli paintings crafted by Warli tribes, utilize basic, monochrome figures to narrate tales of everyday existence and customs.

The rich diversity and unique characteristics of these Indian painting styles pose significant challenges for effective retrieval from vast digital archives and online galleries, so the effective retrieval of images from these databases has become increasingly paramount. For this reason, CBIR systems have become increasingly effective, using visual content to find images in large datasets1,2. On the other hand, the intricate patterns and distinctive forms present in artistic works can pose a challenge for traditional CBIR techniques3. This is especially true with Indian paintings, which cover a wide range of historical contexts and stylistics4,5.

There are numerous image retrieval techniques, each with benefits and limitations of their own. Textual annotations, tags, and descriptions are used in metadata-based retrieval to index and search for images6. Although this strategy can be effective, it is frequently constrained by the subjective and labor-intensive nature of producing comprehensive and high-quality metadata. Another approach, known as keyword-based retrieval, is using specific keywords to search for images.7, but it also significantly depends on how relevant and accurate the related keywords are.

Another approach for image retrieval is CBIR systems, which do not rely on metadata; instead, they work by examining the visual content of images. A conventional CBIR system is built to locate and retrieve images from an extensive database by utilizing a query image. This method initiates with an input consisting of a query image and database images. Then, a feature extraction algorithm is applied to seek standardized visual representations of all database images for the purpose of comparison with the query image. Conventional techniques for feature extraction include Speeded-Up Robust Features (SURF) and Scale-Invariant Feature Transform (SIFT), which find and describe local features in images8,9,10. Currently, Convolutional Neural Networks (CNNs) are used to extract high-level features from images11. Commonly pre-trained CNN models like VGG, Inception, and ResNet12 are used to capture features of images that are represented as vectors in a high-dimensional space. Deep learning techniques create embeddings from the last layers of a CNN, whereas traditional approaches produce key points and descriptors for every image.

The next step is to measure the level of similarity between the query image and the database images. The effectiveness of image retrieval systems depends on the proper choice of similarity metrics and image representation techniques. The best-ranked images from the database are retrieved after being ranked according to how similar they are to the query image using these similarity metrics. The semantic gap—a difference between low-level image representations and human-level semantics—remains a challenge to the task, even though numerous novel strategies based on handcrafted features or deep features have been investigated and documented in the literature.

Several fields have seen the successful application of CBIR, including medical imaging13,14, facial recognition15,16,17, and trademark image retrieval18. CBIR systems in medical imaging aid in the diagnosis of diseases by obtaining images with comparable pathological features. In facial recognition, CBIR is used for individual identification by comparing facial features. For trademark image retrieval, CBIR facilitates identifying visually similar trademarks, hence assisting in the prevention of infringement. These applications demonstrate the adaptability and efficiency of CBIR systems in managing various image datasets and retrieval tasks.

The difficulties presented by the sheer amount and variety of Indian paintings19, which include works in the Madhubani, Kalamkari, Gond, Pichwai, and Warli styles, make a CBIR system necessary. The fine visual elements of these paintings are typically beyond the reach of traditional text-based retrieval techniques. A CBIR system can precisely classify and retrieve paintings based on visual content, offering a more effective search experience by utilizing advanced feature extraction and machine learning techniques. It also helps to preserve these important cultural art forms digitally, making them easier to access for scholars, researchers, and art followers. A CBIR system for Indian paintings is necessary to connect ancient expressions with contemporary digital capabilities, allowing for the preservation, study, and appreciation of the rich tapestry of Indian art. A CBIR system for Indian art has been proposed in this study.

The following are the authors’ major contributions to this work:

  1. 1.

    A dataset comprising annotated images of six distinct Indian art forms—Gond, Kalamkari, Pichwai, Madhubani, Mandla, and Warli has been created.

  2. 2.

    Several pre-trained deep learning models, including VGG16, EfficientNetB0, ResNet50, InceptionV3, and MobileNetV2, were evaluated for the task of image retrieval.

  3. 3.

    Based on the evaluation, the two best-performing models, EfficientNetB0 and ResNet50, were selected, and a fusion approach was adopted by concatenating the features extracted from these two models.

  4. 4.

    Recursive Feature Elimination (RFE) was applied for dimensionality reduction of the extracted features, improving the efficiency of the CBIR system.

  5. 5.

    Various distance metrics, such as Hamming, Minkowski, Cosine Similarity, Jaccard, Euclidean, and Manhattan, were explored to compute the similarity scores between the query image and the database images.

  6. 6.

    The performance of the CBIR system was measured using standard metrics, including mean average precision, recall, and F1-score, to assess its effectiveness in retrieving relevant Indian paintings from the diverse dataset.

Feature extraction is a crucial step in image processing for the retrieval of relevant images. It is broadly classified into two main categories: Handcrafted methods and automatic learning-based methods of feature extraction. Several techniques for CBIR using handcrafted features have been proposed. Mehmood et al.8 used triangle histograms’ weighted average and SIFT feature vectors, employing k-means clustering and the Hellinger kernel function with Support Vector Machine (SVM) for classification. Another method8 incorporated global features, and Gray Level Co-occurrence Matrix (GLCM) features using the meta-heuristic algorithms on the Corel dataset. Saritha et al.20 combined texture features, edge directions, color histogram, and edge histogram with CNN for signature matching. Ashraf et al.9 developed a CBIR system based on the YCbCr color space, Canny edge histogram, and discrete wavelet transform. Y-luminance, Cr, and Cb matrices are merged with edge features to create a final RGB image, using the Manhattan distance for image comparison. Sharif et al.10 presented fused Binary Robust Invariant Scalable Key points and SIFT feature descriptors for the retrieval of images, achieving a mean average precision of 39.1. Sampathila et al.13 developed a CBIR technique for Magnetic Resonance Imaging images using texture, shape, and color features based on GLCM features. To assess the similarity between the images, the K-Nearest Neighbor (kNN) algorithm is employed, achieving 95.5% average accuracy. The authors in ref. 21 introduced a cloud-based method for CBIR using exact Euclidean Local Sensitivity Hashing and a secure block identifier protocol for image retrieval. The study in ref. 22 proposed a CBIR approach using local binary patterns and GLCM descriptors to extract image structural information. Further, for the reduction of features Particle swarm optimization algorithm was used. Three classifiers—decision tree, SVM, and kNN—were trained, with SVM achieving the best precision at 85%. Salih et al.23 developed a hybrid CBIR technique with a bi-layer search system. The first layer uses the SURF descriptor to eliminate dissimilar images, narrowing the search range. The second layer retrieves the most relevant images related to the query image. This dynamic approach achieved a precision of 86.06% for the top 10 and 80.72% for the top 20 images.

Several techniques for CBIR using automatic learning-based methods have also been developed. Ahmad et al.24 proposed A CBIR system, which preprocesses images using Gaussian filtering and Hessian detector, extracts features like skewness and kurtosis, uses an Artificial Neural Network for interpolation to store results in a database, and retrieves similar images by feeding query features to a similarity measurement function. Tan et al.25 proposed a modified version of the VGG16 model to extract visual features, achieving 61% accuracy. Varshney et al.26 present an interactive CBIR system that uses InceptionV3 and InceptionResNetV2 models for feature extraction from traditional Indian textiles, achieving 0.92 average precision. Tena et al.27 developed a retrieval system using a modified CNN model to extract features from traditional woven fabrics. Wan et al.28 proposed a method based on wavelet transform and dual propagation neural network for retrieving images from distinct art styles, achieving an accuracy of 91%. Ghrabat et al.29 retrieved images using Gaussian filtering for preprocessing, extracted texture and color features including GLCM and novel statistical and intensity-based color features, clustered the features using k-means, optimized the features with a modified genetic algorithm, and classified them using SVM-based CNN. Filip et al.11 retrieved images using a modified CNN model on Oxford buildings and Holiday datasets. Another image retrieval framework was proposed by Liu et al.30 by combining the CNN model with SVM. Rajkumar and Sudhamani31 presented a residual network-based CBIR system. The system was evaluated on a dataset of 50,000 images belonging to 250 classes. Wang et al.32 developed a CBIR system based on neural network to obtain advanced image features. A hybrid CBIR system was introduced by Sikandar et al.12 combining deep learning and machine learning. Transfer learning models such as ResNet50 and VGG16 were used to extract image features, and KNN with Euclidean distance to calculate image similarity.

The rest of the paper is structured as follows: The proposed methodology adopted for this research is shown in the section “Methods.” Results and discussions of this study are presented in the section “Results and discussions.”

Methods

In this study, we utilized the Traditional Indian Art Painting Art Dataset (TIAPD) to evaluate our proposed methodology, which comprises a diverse collection of traditional Indian art images. Our methodology includes automatic learning-based feature extraction techniques, with a CNN model employed for the retrieval of images. Various similarity measures and performance metrics are then used for the evaluation to ensure validation of the proposed methodology.

Dataset description

The images of the TIAPD used in this study were collected from Pinterest33, a popular social networking site with strong visual content. Different images from various art forms like Gond, Pichwai, Madhubani, Mandala, Warli, and Kalamkari are included in the dataset as shown in Fig. 1. Each art form is represented by images that are visually distinct and characterize the respective art form. Identifying and classifying images according to their art form is one of the main purposes of the dataset, which is meant to be used for image retrieval applications. The dataset is distinctive because it contains a wide variety of art forms and a substantial number of images, which makes it an excellent resource for developers and scholars studying computer vision and image processing. The dataset contains 600 images, with 100 images belonging to each category.

Fig. 1: Sample images from the TIAPD dataset.
figure 1

a Gond painting, b Pichwai painting, c Madhubani Painting, d Mandala Painting, e Warli Painting, and e Kalamkari painting.

Full size image

Furthermore, for the validation of the results of the proposed methods, simulations are also conducted on various conventional datasets, in addition to the TIAPD dataset. These datasets include:

  1. 1.

    Wang-A: This dataset has been widely used for image retrieval and classification tasks34. It comprises 1000 images that belong to 10 different categories.

  2. 2.

    OT Scene: This dataset comprises 2688 images of outdoor locations divided into 8 different categories35.

  3. 3.

    Wang 10k: There are 10,000 images in this database distributed into 100 classes36.

  4. 4.

    Caltech 256: This dataset has been commonly used for object recognition and image classification37. It comprises 30,607 images categorized into 257 object categories.

  5. 5.

    Corel-1K: This dataset comprises 1000 images of 10 distinct classes. This database has been commonly employed in image retrieval tasks38.

By conducting trials on these standardized datasets, the study ensures that the proposed techniques are not only efficient for the TIAPD dataset but also have good generalizability to other types of image data.

Proposed methodology

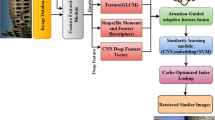
The main modules of the research methodology are reading of images, resizing of images, extraction of features, reduction of features, and retrieval of images from the TIAPD. The flow chart of the methodology is shown in Fig. 2. In this methodology, initially TIAPD dataset is used as input. Each image of this dataset is resized to 224 × 224 pixels to ensure uniformity of all images. After resizing, feature extraction is performed using two CNN models: ResNet50V2 and EfficientNetB0. These pre-trained networks are selected for their ability to capture both high-level and low-level features from images. Both these features are important for the retrieval of images in an accurate way because they contain information about important characteristics of images. High-level features include information about the shape of objects, patterns, etc., while low-level features contain information about colors, edges, and textures of the image.

Fig. 2
figure 2

Block diagram of proposed methodology

Full size image

ResNet50V239, as shown in Fig. 3, is a version of the Residual Networks (ResNet) architecture that helps mitigate the vanishing gradient problem and allows the network to learn complex features effectively. On the other hand, EfficientNetB040, as shown in Fig. 4, uses a compound scaling method, leading to high efficiency with fewer parameters.

Fig. 3
figure 3

Architecture of ResNet50V2

Full size image
Fig. 4
figure 4

Architecture of EfficientNetB0

Full size image

After the extraction of features from both models, all these features are concatenated to improve the robustness of the feature set, which provides a more detailed understanding of the images. The fusion of both these models is important to extract all features of the image for performing the image retrieval process in an efficient way. After the concatenation of features, the RFE technique is applied to all features for the reduction of feature space and computational complexity of the algorithm. This RFE technique reduces the feature space by preserving the most significant features.

This similar process, which includes resizing of the image, extraction of features using both pre-trained models, concatenations of features, and reduction of features using RFE, is applied to the query image also. Features extracted from all database images and query images are important to check the similarity measurement between them. To accomplish the task of similarity measurement, different distance metrics like Euclidean, Cosine Similarity, Manhattan, Minkowski, Hamming, and Jaccard are used, and distances computed by different distance methods are sorted in ascending order to get the most relevant images at the top. The retrieved images are ranked based on their similarity to the query image. In the end, the efficacy of the system is assessed using different evaluation metrics like mean average precision, recall, and F1-score. Algorithm 1 presents the pseudo-code of the proposed methodology.

Algorithm 1

Content-Based Image Retrieval of traditional Indian paintings

Input:

  • Database of images: D = {I1, I2,…. IN}

  • Query Image Q

Output:

  • Top k most similar images to the query Q

1. Initialize pre-trained models:

  • Load EfficientNetB0 and ResNet50V2 models without the final classification layers

2. Read and Resize Image:

  • Define a function read_and_resize_image (image_path) to:

    • Read the image from image_path

    • Resize the image to 224 × 224 pixels

    • Return the resized image

3. Extract features:

  • Define a function extract_features (resized image, model) to:

    • Pass the resized image through the model.

    • Extract features from the intermediate layers.

    • Return the feature vector.

4. Extract and concatenate features for Database images:

  • Initialize an empty list to store features for all database images.

  • For each Ii in D:

    • Read and resize Ii using read_and_resize_image.

    • Extract features \({f}_{i}^{{M}_{1}}\) from EfficientNetB0 and \({f}_{i}^{{M}_{2}}\) from ResNet50V2 using extract_features

    • Concatenate the features:         

$${f}_{i}=[{f}_{i}^{{M}_{1}\,}{{\rm{||}}f}_{i}^{{M}_{2}}]$$

    • Store \({f}_{i}\) in the list.

5. Extract and Concatenate features for query image

  • Read and resize Q using read_and_resize_image

  • Extract features \({f}_{Q}^{{M}_{1}}\) and \({f}_{Q}^{{M}_{2}}\).

  • Concatenate the features:          

$${f}_{Q}=[{f}_{Q}^{{M}_{1}\,}{{\rm{||}}f}_{Q}^{{M}_{2}}]$$

6. Dimensionality reduction using RFE

  • Define a function apply_rfe(features,estimator) to:

    • Apply Recursive Feature Elimination (RFE)

    • Select the optimal subset of features

    • Return the reduced feature set.

 • Apply RFE to both \({f}_{Q}\) and \({f}_{i}\)

7. Compute distance scores

  • Initialize an empty list for distance scores.

  • For each \({f}_{i}^{{Reduced}}\) in the database:

    • Compute the Euclidean distance between \({f}_{i}^{{Reduced}}\) and \({f}_{Q}^{{Reduced}}\) .           

$$d=\,\sqrt{\mathop{\sum }\limits_{j=1}^{n}{({f}_{Q,j}^{{Reduced}}-{f}_{i,j}^{{Reduced}})}^{2}}$$

    • Store d in the list.

8. Rank Database Images Based on Distance Scores:

  • Sort the database images in ascending order of distance scores.

9. Output the Top k most Similar Images:

  • Retrieve and display the top k images with the lowest distance scores.

Distance metrics

The distance metrics are used to find the most relevant images related to the query image. To find the similarity between the images, the features of both the query image and the database images are represented as feature vectors. Different distance metrics used to compute distances using feature vectors for image retrieval are given below:

  1. a.

    Euclidean Distance: It computes the straight-line distance between two feature vectors. It can be calculated using Eq. (1).

    $$d\left(q,{x}_{i}\right)=\sqrt{\mathop{\sum }\limits_{j=1}^{n}{({q}_{j}-{x}_{{ij}})}^{2}}$$
    (1)

    Here, \(d\left(q,{x}_{i}\right)\) represents the distance computed between query image and the dataset retrieved image, n represents the number of features in feature vectors, q is the feature vector of the query image, which is represented by [q1, q2, q3, …., qn] and \({x}_{{ij}}\) is the feature vector of the retrieved images. Here, xi, which is the feature vector of the ith retrieved images, is represented as [xi1, xi2, xi3, …., xin]

  2. b.

    Cosine Similarity: The formula used to compute cosine similarity is given by Eq. (2). It is used to measure the cosine of the angle between two image feature vectors.

    $${\rm{cosine}}\; {\rm{similarity}}\left(q,{x}_{i}\right)=\frac{q.{x}_{i}}{{||q||\,||}{x}_{i}{||}}$$
    (2)
  3. c.

    Manhattan Distance: The formula used to measure the Manhattan distance metric is given by Eq. (3). It calculates the dissimilarity between two feature vectors by summing the absolute differences of their coordinates.

    $$d\left(q,{x}_{i}\right)=\mathop{\sum }\limits_{j=1}^{n}\left|{q}_{j}-{x}_{{ij}}\right|$$
    (3)
  4. d.

    Minkowski Distance: This similarity measure is a generalization of Euclidean and Manhattan distance. The formula of Manhattan distance is shown by Eq. (4).

    $$d\left(q,{x}_{i}\right)={\left(\mathop{\sum }\limits_{j=1}^{n}{\left|{q}_{j}-{x}_{{ij}}\right|}^{p}\right)}^{\frac{1}{p}}$$
    (4)

    where p defines the order of the distance metric.

  5. e.

    Hamming Distance: This distance is applicable for feature vectors that are binary in nature and is given by Eq. (5). To calculate the similarity between two feature vectors, it determines the bit positions where the two binary strings differ.

    $$d\left(q,{x}_{i}\right)=\mathop{\sum }\limits_{j=1}^{n}({q}_{j}\ne {x}_{{ij}})$$
    (5)
  6. f.

    Jaccard Similarity: It measures the similarity of two sets by taking the ratio of their intersection with their union. It is given by Eq. (6).

$${Jaccard\; similarity}\left(q,{x}_{i}\right)=\frac{\left|Q\cap {X}_{i}\right|}{\left|Q\cup {X}_{i}\right|}$$
(6)

where Q and Xi are the sets of indices where q and xi have non-zero values.

Evaluation of performance metrics

To check the efficacy of the proposed CBIR system, precision, recall, and F1-score fundamental metrics are used. Precision represents the accuracy of the system by computing the relevancy of images against retrieved images for the query image. The formula used to calculate precision is represented by Eq. (7). Recall represents the robustness of the system by identifying all the relevant images of the dataset. The formula used to evaluate recall is shown by Eq. (8). The F1-score is a measure of a model’s accuracy, which provides a balance between the precision and recall. The formula used to compute the F1-score is given by Eq. (9). To compute these metrics, the model is applied to the query image to get the relevant images from the dataset. After visualizing the results, the number of relevant images are checked, and then performance metrics are evaluated based on the quantitative analysis of images.

$${{Precision}\,({Pre}})=\frac{{{Number\; of\; relevant\; images\; retrieved}}\,}{{{Total\; number\; of\; images\; reterieved}}}$$
(7)
$${{Recall}\,({Rec}})=\frac{{{Number\; of\; relevant\; images\; retrieved}}\,}{{{Total\; number\; of\; relevant\; images\; in\; the\; dataset}}}$$
(8)
$$F1\,{{Score}}(F1)=\,\frac{2* {{Pre}}* {{Rec}}}{{{Pre}}+{{Rec}}}$$
(9)

In the proposed work, precision, recall, and F1-score are computed for each query image. So, to show the effectiveness of the entire system, average of both these metrices has been taken for each category of the TIAPD dataset. Where Eq. (10), Eq. (11), and Eq. (12) representing the average precision, average recall, and average F1-score, respectively.

$${{Average\; Precision}}\,\left({{APre}}\right)=\,\frac{1}{C}\mathop{\sum }\limits_{n=1}^{C}{{Pre}}(n)$$
(10)

Here, C represents the number of query images for each category.

$${{Average\; Recall}}\,({{ARec}})=\frac{1}{C}\mathop{\sum }\limits_{n=1}^{C}{{Rec}}(n)$$
(11)
$${{Average}}\,F1\,{{Score}}({{AF}}1)=\frac{1}{C}\mathop{\sum }\limits_{n=1}^{C}F1(n)$$
(12)

To represent the precision, recall, and F1-score of the proposed CBIR system, mean average precision, mean average recall, and mean average F1-score are computed for the complete dataset as represented by Eq. (13), Eq. (14), and Eq. (15), respectively.

$${{Mean\; Average\; Precision}}\,\left({{mAPre}}\right)=\,\frac{1}{N}\mathop{\sum }\limits_{n=1}^{N}{{APre}}(n)$$
(13)
$${{Mean\; Average\; Precision}}\,\left({{mARec}}\right)=\,\frac{1}{N}\mathop{\sum }\limits_{n=1}^{N}{{ARec}}(n)$$
(14)
$${{Mean\; Average}}\,F1\,{{Score}}\left({\rm{mAF}}1\right)=\,\frac{1}{N}\mathop{\sum }\limits_{n=1}^{N}{{AF}}1(n)$$
(15)

Here, N represents the number of categories of the TIAPD dataset.

Results and discussions

This section presents the results of the proposed image retrieval system using the TIAPD dataset. First, the selection of the best models that will be further used for the concatenation of features is addressed. Then, the impact of feature concatenation on average precision, recall, and F1-score is explored. Further, the results of the proposed fused model with RFE and without RFE are investigated. Finally, the selection of the best similarity measure, followed by the visual analysis of the sample images retrieved using the proposed system, is discussed.

Analysis based on different models

In this research work, various transfer learning models, specifically VGG16, ResNet50V2, InceptionV3, MobileNetV2, and EfficientNetB0, were used to extract features for the image retrieval task. We have taken 100 random images from all categories of the TIAPD dataset for simulation purposes. So, the total number of images used for simulation is 600. For the computation of average precision, recall, and F1-score, we retrieved the top 20 images for each image of all categories. For initial experiments, we have used Euclidean distance to measure the similarity between the images.

Sample retrieval results obtained using the VGG16 model are shown in Fig. 5. As shown in this figure, the query image has been taken from the Madhubani category. The top 20 images matching the query image were displayed. From the retrieval results, it was analyzed that out of 20, 15 images belong to the Madhubani category, so precision came out to be 15/20 = 0.75 and recall came out to be 15/100 = 0.15. Similarly, we computed precision and recall for each image of each category of TIAPD. The mean average precision, mean average recall, and mean average F1-score for all the pre-trained models are shown in Table 1.

Fig. 5
figure 5

Sample image retrieval result obtained using VGG16 for Madhubani query image

Full size image
Table 1 Computation of mean average precision, mean average recall, and mean average F1-score for various pre-trained models
Full size table

After that, we selected the top two performing models among the 5 pre-trained models evaluated on the TIAPD dataset. From Table 1, it can be observed that ResNet50V2 and EfficientNetB0 performed best by obtaining 88.13% and 86.93% mean average precision, 17.63% and 17.39% mean average recall, and 29.38% and 28.98% mean average F1-score. Therefore, based on their superior performance, these two models were selected further for feature concatenation to further improve the performance of the image retrieval system.

Concatenation of features from Resnet50V2 and EfficientNetB0

After the selection of two top-performing pre-trained models, feature concatenation has been done. Figure 6 shows the number of features obtained from both models. After feature extraction, 1028 and 2048 features were obtained from EffcientNetB0 and ResNet50V2, respectively. Feature concatenation has been done to combine the limitations and strengths of different models, enhancing the performance of the image retrieval system and making the system more robust by combining the different aspects of an image. After feature concatenation, a total of 3076 features were obtained as shown in Fig. 6.

Fig. 6
figure 6

Concatenation of features extracted from EfficientNetB0 and ResNet50V2

Full size image

Using these concatenated features, the proposed image retrieval system was evaluated using evaluation metrics, average precision, average recall, and average F1-score. All metrics were computed for each category in the TIAPD dataset, and the results obtained for each category are shown in Table 2. It has been observed that, the mean average precision, mean average recall, and mean average F1-score obtained after feature concatenation are 83.44%,17.02%, and 28.26%, respectively.

Table 2 Computation of average precision, average recall, and average F1-score after features concatenation
Full size table

RFE for dimensionality reduction

After the concatenation of features, the next step involved applying RFE for dimension reduction. RFE is an iterative feature selection algorithm that aims to identify the most important features from a dataset by recursively removing the least significant ones. A Support Vector Regressor (SVR) with a linear kernel was employed as a proxy model on the entire set of features for evaluating their importance. The flow chart of RFE is shown in Fig. 7.

Fig. 7
figure 7

Flow chart of RFE

Full size image

The importance of each image is evaluated based on the model’s weights “w,” which is derived by minimizing the loss function \({\mathcal{L}}(X,y,w)\) as represented by Eq. (16).

$$w={{argmin}}{\mathcal{L}}(X,y,w)$$
(16)

where X shows the dataset, y is the target vector, and w denotes the model’s weights. The importance of each feature j is measured as \(\left|{{w}}{{j}}\right|\). The features with the lowest importance scores are removed, and the SVR model is retrained on the remaining features. This process continues until the optimal subset of features is obtained, as described in Eq. (17):

$${X}_{{{new}}}=\frac{X}{{{Features\; with\; minimum}}\left|{{w}}{{j}}\right|\,}$$
(17)

RFE correctly identifies the features that contribute most to the retrieval of images. Firstly, RFE helps to reduce the number of features by simplifying subsequent processing steps and improving computational efficiency. Secondly, RFE aids in removing noise and redundant information from the feature vectors.

RFE identifies and retains the most informative components, thereby enhancing the performance of the image retrieval system. After applying RFE to the concatenated feature vectors, the reduced-dimensional representations were used to compute mean average precision, mean average recall, and mean average F1-score. All metrics were computed for each category in the TIAPD dataset, and the results obtained for each category are shown in Table 3. From the results obtained after applying RFE, the mean average precision, recall, and F1-score increased to 91.52%, 18.30%, and 30.50% respectively.

Table 3 Computation of average precision, average recall, and average F1-score after dimensionality reduction
Full size table

Analysis based on different distance metrics

Further analysis and interpretation of these results provide valuable insights into optimizing the image retrieval system, emphasizing the importance of selecting appropriate distance metrics to enhance the accuracy and efficiency of retrieval processes in complex image datasets like TIAPD. In this phase of the study, we applied various distance metrics to measure similarity and evaluate the retrieval effectiveness using the TIAPD dataset.

After that, average precision, average recall, and average F1-score were computed for each distance metric to assess their performance in retrieving relevant images from the dataset, as shown in Table 4, Table 5, and Table 6, respectively. The results show that Euclidean Distance consistently outperformed other distance metrics for all metrics across different classes of traditional Indian art forms. The mean average precision, recall, and F1-score obtained using Euclidean distance metrics are 91.52%, 18.30%, and 30.50%, respectively.

Table 4 Comparison between various distance metrics based on average precision in percentage for the proposed model
Full size table
Table 5 Comparison between various distance metrics on the basis of average recall in percentage for the proposed model
Full size table
Table 6 Comparison between various distance metrics on the basis of average F1-score in percentage for the proposed model
Full size table

Analysis based on top N retrieved images for different query images

In this phase of the study, two sample images were selected for each of the traditional Indian art forms—Warli, Mandala, and Kalamkari—to evaluate the image retrieval system using Euclidean Distance exclusively. For the visual analysis, we have taken two different sample images from three different categories namely, Warli, Mandala, and Kalamkari as shown in Fig. 8. From results shown in Fig. 8a, it has been observed that when the first Warli sample query image is taken then from top 20 images, 19 images belong the same category as the query image. Therefore, the precision becomes 19/20 = 0.95. Since there are a total of 100 images in the Warli category, so recall for this query image comes out to be 19/100 = 0.19. Similarly, for the second query image of the Warli category as shown in Fig. 8b, out of 20 images, 17 images belong to this category, so the precision for these query images comes out to be 17/20 = 0.85, and the recall is 17/100 = 0.17.

Fig. 8
figure 8

Retrieval results for different sample query images using the proposed model

Full size image

The efficacy of the system has also been checked by retrieving the top 10 images, top 20 images and top 30 images across various art forms. Results of different performance metrics for all art forms are shown in Table 7. It has been observed that mAPre for the top 10 images is more, and mARec is less when compared with performance metrics computed by taking the top 20 and top 30 images. While retrieving the top 30 images, it has been observed that there is a slight decrease in precision from the top 20 images, which shows the robustness and effectiveness of the system.

Table 7 Performance of the proposed model for different top N retrieved images
Full size table

The average of all mAPre, the average of all mARec, and the average of all mAF1 computed using different numbers of retrieved images come out to be 91.64%, 18.17%, and 29.55%, respectively, which shows the effectiveness of the system.

Comparison with other proposed datasets

After retrieving images by checking the similarity measure on our Indian painting dataset, we implemented our proposed system on several other standard datasets to further evaluate its performance. These datasets included Wang-A, OT Scene, Wang 10k, Caltech 256, and Corel-1K. For each dataset, we calculated the mean average precision, mean average recall, and mean average F1-score to assess the effectiveness of our approach, as shown in Table 8. Implementing our proposed system on these diverse datasets allowed us to validate its robustness and generalizability, demonstrating its capability to handle different types of images and categories effectively. This broader evaluation provided valuable insights into the strengths and potential areas for improvement in our image retrieval system, confirming its versatility and reliability across various image retrieval tasks.

Table 8 Performance of the proposed model on other standard datasets
Full size table

In this research, a CBIR system to retrieve images from the Indian painting database has been proposed. First, a dataset of traditional Indian art paintings focusing on six distinct art forms, namely, Gond, Pichwai, Kalamkari, Warli, Madhubani, and Mandala, is created. For feature extraction, different pre-trained models were tried first, out of those the top two best-performing models, namely ResNet50V2 and EffiientNetB0 are selected. Then, the hybrid approach was adopted to make the final feature set by concatenating the features extracted from both models. For the reduction of the feature set obtained after feature concatenation, RFE is applied to keep only essential information. This also leads to better computational efficiency and performance of the proposed system. Different similarities, namely, Minkowski, Hamming, Euclidean, Manhattan, Jaccard, and cosine similarity, are used to measure the similarity between the retrieved images and the query image. The effectiveness of the system is also checked by retrieving a different number of top images. Our results showed that Euclidean Distance provided the highest mean average precision, mean average recall, and mean average F1-score of 91.64%, 18.17%, and 29.55% on the TIAPD dataset. Our model was evaluated not only on the TIAPD dataset, but also on other standard datasets available including Wang-A, OT Scene, Wang 10k, Caltech 256, and Corel-1K. For future work, other deep learning architectures can be explored for more effective retrieval of images. Also, we can expand the dataset including more traditional art forms and a greater number of images to check the robustness of the proposed model. Additionally, multi-modal approaches combining text and image-based retrieval could be implemented to improve the system’s versatility.