Abstract
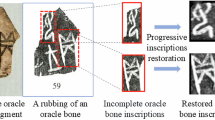
Rubbing images of oracle bones are crucial for studying ancient Chinese culture, but their quality often hinders character recognition and analysis. Current super-resolution approaches face notable limitations when applied to oracle bone rubbing images, particularly in preserving the integrity of genuine character structures, and often introduce character distortions and visual artifacts. To address this issue, we propose an unsupervised super-resolution method for oracle bone rubbing images, named OBISR. The model is based on a generative adversarial network and introduces a two-stage reconstruction generator built upon Transformer architecture, along with a more stable generator variant obtained via the Exponential Moving Average (EMA) mechanism. Meanwhile, an artifact loss function is employed to suppress artifacts and distortions in character regions, and a set of local discriminators is designed to enhance detail perception. Experiments show OBISR outperforms existing methods across quantitative metrics and visual evaluations, offering superior enhancement for oracle bone rubbing images.
Similar content being viewed by others
Introduction
Oracle bone inscriptions, as the earliest known mature writing system in China, provide irreplaceable primary evidence for studying the history, culture, and script evolution of the Shang and Zhou dynasties1. These inscriptions have largely been preserved in the form of ink rubbings, which constitute the main corpus for contemporary research. However, due to the considerable age of these artefacts, rubbing images often suffer from significant degradation, such as ink bleeding, surface damage, and character blurring, which severely limits their usability in digital archiving, intelligent recognition, and in-depth scholarly analysis. Enhancing their clarity is therefore crucial for restoring structural details and stylistic features, improving recognition accuracy, and advancing the digital preservation and intelligent study of oracle bone inscriptions.
Manual restoration methods, such as hand-tracing, depend heavily on the subjective judgment of experts, are time-consuming, and often struggle to balance fidelity with stylistic consistency. In recent years, super-resolution (SR) techniques, which aim to reconstruct high-resolution (HR) images from low-resolution (LR) inputs, have demonstrated substantial potential in domains such as remote sensing2,3,4, medical imaging5,6,7, and cultural heritage conservation8,9,10. Yet, in practice, these oracle bone rubbing images often contain substantial noise, which can cause models to learn noise patterns rather than meaningful features. Moreover, oracle bone datasets typically contain only LR images, with no paired HR counterparts, which restricts the applicability of conventional supervised SR approaches11,12,13,14,15.
To overcome the paired-data limitation, research on real-world SR for unpaired data can be broadly divided into two categories: unpaired SR based on degradation modelling and complex-degradation SR using only HR data. The first category leverages independently collected HR and LR images to explicitly model the degradation process. Inspired by unpaired image-to-image translation methods such as CycleGAN16, early works used adversarial learning with cycle consistency to bridge the domain gap. Building on this, SCGAN17 introduced a semi-cyclic architecture with a dedicated degradation network to generate pseudo-LR images, thereby improving reconstruction consistency18,19,20,21. Wang et al.22 further developed a method leveraging a compact proxy space for unpaired image matching in SR. Other approaches23,24,25 trained stand-alone degradation models to synthesize realistic LR data for supervised training in the absence of genuine HR-LR pairs. The second category bypasses the need for LR data entirely by synthesizing degraded images directly from HR inputs using handcrafted or statistically defined degradation pipelines9,26,27,28,29. For example, HiFaceGAN26 employs a multi-stage adaptive SR architecture for perceptual enhancement; Real-ESRGAN27 uses a tailored degradation pipeline with GAN training for realistic artifacts; MM-RealSR28 introduces interactive modulation for controllable restoration; WFEN29 applies wavelet-based frequency fusion to reduce distortion; ConvSRGAN9 cascades enhanced residual modules to capture multi-scale textures. While these approaches offer valuable strategies for handling unpaired data and complex degradations, they remain suboptimal for oracle bone rubbings, particularly in suppressing noise and preserving the fine-grained texture of ancient characters. They also often introduce artifacts or structural distortions in character regions, thereby degrading recognition and analytical performance. These limitations motivate the development of domain-specific solutions.
To address the aforementioned challenges, we propose a super-resolution method specifically designed for oracle bone friction images, called OBISR, which effectively tackles the practical limitation of lacking paired HR and LR samples in image reconstruction methods. We introduce a two-stage reconstruction generator DTG based on the Transformer architecture30, and further develop an enhanced variant DTGEMA to improve the stability of the generation process by incorporating the EMA technique. To more accurately restore the finer structural details of oracle bone inscriptions, a custom local discriminator is devised, specifically tailored to the varying sizes and textural characteristics of rubbing images. In addition, an artifact loss function is introduced31 to measure the discrepancy between the outputs of DTG and DTGEMA and the input LR images. Comparison with state-of-the-art super-resolution methods demonstrates that our OBISR achieves significantly superior performance in oracle bone image restoration. It not only outperforms existing approaches on quantitative evaluation metrics including PSNR, SSIM32 and LPIPS33, while also delivering clearer and more structurally accurate visual results.
The main contributions of this work are as follows:
-
We propose OBISR, a super-resolution approach specifically designed for oracle bone rubbings, which effectively circumvents the need for paired training data while preserving intricate inscription features.
-
A two-stage Transformer-based generator is introduced, along with an enhanced variant developed using the EMA technique. Additionally, a custom local discriminator is designed to more accurately capture the structural and textural variations of rubbing images.
-
An artifact-aware loss function is further introduced, which suppresses character artifacts and distortions by comparing the outputs of the two generators with HR reference images.
-
Extensive experiments demonstrate that OBISR significantly outperforms existing state-of-the-art methods in oracle bone image restoration, achieving superior performance in both quantitative evaluation metrics and visual quality.
Methods
Model architecture
Inspired by the SCGAN17 framework, we propose a novel super-resolution model for oracle bone rubbing images, named OBISR. As illustrated in Fig. 1, the model adopts a dual half-cycle architecture, where two LR degradation generators (GHL and GSL), two super-resolution reconstruction generators (DTG and DTGEMA), and four discriminators (DP1, DP2, DP3, DP4) are jointly integrated into a multi-branch adversarial optimization framework.
In the first half-cycle, OBISR takes a HR oracle bone rubbing image IHR as the input to the degradation generator GHL. By incorporating a random noise vector z, GHL simulates real-world degradation patterns and generates a 4 × downsampled LR image ISL. This degraded image ISL is then fed into both reconstruction generators DTG and DTGEMA, resulting in two reconstructed HR images ISS and ISSEMA, respectively. To suppress artifacts and distortions around character regions, a hallucination-aware loss \({{\mathcal{L}}}_{{\rm{M}}}\) is computed based on the differences among IHR, ISS, and ISSEMA.
In the second half-cycle, a real LR oracle bone image ILR is input into the DTG generator, producing a reconstructed HR image ISR. This image is subsequently passed through the degradation generator GSL to yield a synthetic LR image ISSL.
These two half-cycle reconstruction sub-networks are connected via the DTG reconstruction generator, which helps mitigate the adverse effects caused by the domain gap between synthetic LR rubbing images and real LR rubbing images.
Low-resolution degradation generator
Both our degradation generators GHL and GSL adopt the same LR generator architecture. As shown in Fig. 2, the generator consists of an encoder-decoder structure. The encoder begins with a spectral normalization34 (SN) layer, followed by a 3 × 3 convolutional layer, a global average pooling35 (GAP) layer and six residual blocks. These residual blocks are responsible for extracting meaningful and representative features from the HR input. The decoder also includes six residual blocks. After the 2nd and 4th residual blocks, pixel unshuffling operations are applied to increase the spatial resolution of the feature maps by a factor of 2. Finally, the output is activated by either a ReLU36 or Tanh function, resulting in a degraded LR oracle bone rubbing image.
This design enables the generator to simulate realistic degradation patterns observed in ancient oracle bone images.
Super-resolution reconstruction generator
As shown in Fig. 3, the proposed reconstruction generator is specifically designed for the oracle rubbing image super-resolution task. It consists of two modules: the DTG and the DTGEMA. These two generator modules share the same architecture as the super-resolution reconstruction generator. The main difference lies in the application of the EMA strategy to the DTGEMA generator’s parameters, resulting in more consistent and stable performance.
EMA assigns greater weight to recent observations in order to smooth time-series data, effectively reducing short-term fluctuations and highlighting long-term trends. During training, the parameters of the DTG generator are dynamically updated using EMA to obtain a smoothed version, denoted as DTGEMA. Specifically, EMA performs an exponentially weighted average over the parameter trajectory of the generator, which significantly suppresses noise and parameter oscillations, thereby improving training stability. The update rule of EMA is defined as:
Compared to the DTG generator, DTGEMA demonstrates greater robustness in reducing the occurrence of random artifacts and improving image fidelity. Since DTGEMA is a smoothed variant of DTG’s parameters, it shares the same loss function. The outputs of both generators are fed into the artifact map module Mrefine31 to compute the artifact loss \({{\mathcal{L}}}_{{\rm{M}}}\), which further alleviates the loss of fine details during optimization. In the inference phase, both generators are executed separately, producing two distinct outputs. This dual-generator inference strategy allows for a comprehensive evaluation of each generator’s performance.
To effectively extract both global structures and local textures, the input ILR is first upsampled to 128 × 128. Then, a Laplacian decomposition module is applied to perform frequency separation, resulting in a low-frequency component ILR_LF of size 64 × 64 and a high-frequency component ILR_HF of size 128 × 128. As a near-lossless transformation, the Laplacian decomposition preserves structural integrity during this process. Specifically, the low-frequency component captures global contours and stroke layouts, while the high-frequency component retains fine textures and edges. This separation allows the network to process complementary information in a targeted manner. As shown in Fig. 4, both components clearly preserve their respective characteristics, which are later fused to produce structurally coherent and detail-rich reconstructions.
Subsequently, the low-frequency component is processed by a structure enhancement block to enhance the global representation and produce an initial super-resolved image \({I}_{{\text{SR}}^{* }}\). Then, the high-frequency component ILR_HF and \({I}_{{\text{SR}}^{* }}\) are jointly fed into a recurrent detail supplement, which progressively injects high-frequency details in a recursive manner.
Finally, a convolutional fusion module combines and refines the dual-path features to generate the final HR output ISR. By leveraging frequency separation and dual-branch design, this generator effectively enhances both structural restoration and detail fidelity, achieving high-quality super-resolution reconstruction for oracle bone rubbing images.
Discriminator
We design a discriminator architecture based on PatchGAN37, which judges the authenticity of local regions within the image instead of evaluating the entire image globally. Specifically, the discriminator divides the input image into multiple N × N receptive field patches and outputs the real/fake probability of each patch, enabling more precise perception of artifacts and local details. To accommodate different resolution inputs, as shown in Fig. 5, we design different network depths for 64 × 64 and 16 × 16 images, respectively.
For 64 × 64 input images, the discriminator consists of five feature extraction modules and one output layer: The first layer is a convolutional layer with a stride of 2, followed by a LeakyReLU activation function; The second to fourth layers adopt a structure of convolution → Batch Normalization → LeakyReLU, with the number of channels set to 128, 256 and 512, respectively; The fifth layer maintains 512 channels and uses a stride-1 convolution to preserve spatial resolution; The output layer uses a 4 × 4 convolutional kernel to produce a one-channel discrimination map, and a Sigmoid function is applied to obtain the realness probability of each local region.
For 16 × 16 input images, the network is relatively shallower and contains four feature extraction modules and one output layer: The first four layers share the same structure as in the 64 × 64 case, with the number of channels set to 64, 128, 256, and 512, respectively; The final layer uses a 2 × 2 convolutional kernel to output the discrimination map, followed by a Sigmoid function to get the probability values.
In implementation, we use 4 × 4 convolutional kernels as basic building blocks, apply stride-2 convolutions for spatial downsampling, and use stride-1 in the last two layers to maintain receptive field precision. LeakyReLU is used as the activation function, and Batch Normalization is adopted in all layers except the first.
The entire discriminator generates a “discrimination map” composed of outputs from multiple receptive field areas, thereby enhancing its ability to recognize local structures and artifacts in the image and improving both discrimination performance and stability.
G HL generator loss
This module takes HR images and a random noise vector Z as input, aiming to generate LR oracle rubbing images with realistic degradation characteristics. To approximate the degradation found in real LR oracle rubbing images, we combine adversarial loss38 and pixel loss to formulate the loss function for the GHL degradation generator. The loss is defined as:
where α and β are the weighting coefficients. The adversarial loss38\({{\mathcal{L}}}_{adv}^{{D}_{P1}}\) is defined as:
where the discriminator DP1 is trained to classify the real LR rubbing image ILR as 1 and the synthesized LR image ISL as 0. Although the training data is unpaired, the proposed dual half-cycle architecture constructs pseudo-paired paths, thereby establishing an internally consistent learning framework. The pixel loss \({{\mathcal{L}}}_{pix}^{{I}_{SL}}\) is defined as the ℓ1 distance between the synthesized LR image ISL and the downsampled version of its corresponding input IHR, where average pooling is used to match the resolution of ISL. This design ensures internal consistency, as both ISL and its optimization target are derived from the same HR image.
D T G generator loss
To distinguish between GAN-generated pseudo-textures and real image details, we introduce the artifact mapping Mrefine31 to compute artifact loss, which helps regulate and stabilize the training process. The method seeks to learn an artifact probability map \(M\in {{\mathbb{P}}}^{H\times W\times 1}\), indicating the likelihood of each pixel ISR(i, j) being an artifact.
First, we compute the residual between the real HR image IHR and the generated image ISS from the DTG generator to extract high-frequency components:
Then, the local variance of the residual R is used to obtain the preliminary artifact map M:
where var denotes the variance operator and n is the local window size. To prevent misclassification of local pixels, we further compute a stabilization coefficient σ from the residual R:
where a = 5. Residual maps R1 and R2 are then generated from the outputs of the DTG and DTGEMA generators respectively:
Finally, the preliminary artifact map M is refined using both residuals R1 and R2 to enable more accurate localization of artifact-prone regions. This refinement does not assume that the EMA-based generator consistently produces fewer artifacts. Instead, it employs a pixel-wise comparison: penalization is applied only when ∣R1(i, j)∣ ≥ ∣R2(i, j)∣, suggesting that ISS(generated by DTG) yields a higher reconstruction error at that location. When ∣R1(i, j)∣ < ∣R2(i, j)∣, it implies that ISS is already close to the target value at that pixel, and therefore no additional penalty is applied. This selective strategy helps suppress artifacts while preserving high-frequency details.
As shown in Fig. 6, the last two columns visualize the mask of ∣R1∣ < ∣R2∣ and the refined artifact map Mrefine, where well-preserved textures and sharp edges are effectively excluded from penalization.
The DTG generator is shared across the forward and backward cycle processes to reconstruct HR images from LR rubbings. In the forward cycle, adversarial loss and cycle-consistency loss are used; in the backward cycle, adversarial loss and pixel loss are adopted. The total loss for the DTG generator is defined as:
where θ and γ are the corresponding weights, and the expressions of \({{\mathcal{L}}}_{DTG}^{{I}_{SS}}\) and \({{\mathcal{L}}}_{DTG}^{{I}_{SR}}\) are defined as follows:
Here, the adversarial losses38\({{\mathcal{L}}}_{adv}^{{D}_{P3}}\) and \({{\mathcal{L}}}_{adv}^{{D}_{P4}}\) are defined as:
The cycle-consistency loss \({{\mathcal{L}}}_{cyc}^{{I}_{SS}}\)16 ensures the generator can preserve semantic information and accurately restore character details. The pixel loss \({{\mathcal{L}}}_{pix}^{{I}_{SR}}\) is computed between the recovered SR image ISR and the upsampled version of its corresponding input ILR, where upsampling is performed via bicubic interpolation. Although the training data is unpaired, both ISR and the optimization target originate from the same LR image, ensuring consistency within the LR → HR reconstruction path.
The artifact loss \({{\mathcal{L}}}_{{\rm{M}}}\) is derived from the artifact map Mrefine31, which is expressed as:
D T G EMA generator loss
The EMA technique performs temporal smoothing on the parameters of the DTG generator to produce a more stable generator, DTGEMA. Compared with the DTG generator, the DTGEMA generator is more robust in suppressing stochastic artifacts, thereby improving the quality of generated images.
Since DTGEMA is optimized from DTG via parameter smoothing, it adopts the same loss function as the DTG generator. The output images from the generator are passed into the artifact mapping Mrefine31 to compute artifact loss, which further reduces the loss of real details during optimization. For a detailed description of the loss design for the DTG generator, please refer to Section 3.4.2 of this paper.
G SL generator loss
By learning DTG, the rubbing image ISR degraded into a LR rubbing image ISSL. The loss function of GSL is defined as:
The adversarial loss38\({{\mathcal{L}}}_{adv}^{{D}_{P2}}\) is defined as:
where the discriminator DP2 is trained to predict 1 for the real LR rubbing image ILR and 0 for the synthesized LR rubbing image ISSL.
The cycle-consistency loss16\({{\mathcal{L}}}_{{I}_{SSL}}^{cyc}\) is an ℓ1 loss function that penalizes the difference between the degraded image ISSL and the real LR image ILR.
Results
Experimental settings
Our model is implemented based on PyTorch39 version 1.11.0, using Python 3.7 and an NVIDIA L40S GPU. The optimizer is Adam40 with parameters β1 = 0.9 and β2 = 0.999. The initial learning rate is set to 1 × 10−4 and decays to 1 × 10−5 every 10 epochs via a cosine annealing schedule. The batch size is set to 64.
The training and testing data used in our study are respectively sourced from two oracle bone image datasets: the OBC306 dataset41, released by Yinque Wenyuan, and the OBI41957 dataset, provided by the research team of the Key Laboratory of Oracle Bone Inscriptions Information Processing, Ministry of Education, Henan Province, China.
For training, we randomly select 3000 clean images from the OBI41957 dataset as HR reference images, and 3000 low-noise images from the OBC306 dataset as LR inputs.
To comprehensively assess model generalization, we construct three representative test sets:
-
OBI_BI (with noise): 100 clear images are randomly selected from the OBI41957 dataset, and LR images are generated via bicubic downsampling.
-
OBI_AR (without noise): 1000 hand-drawn oracle character images are selected from OBI41957, and LR images are produced through black-white inversion followed by region-based interpolation.
-
OBITrue (with real degradation): 1440 real oracle bone rubbing images are randomly sampled from the OBC306 dataset and used as low-resolution images with authentic degradation characteristics.
We employ both pixel-level and perceptual-level metrics to evaluate the quality of generated results. Specifically, we use PSNR, SSIM32, and VIF as fidelity-oriented metrics. Additionally, to approximate human visual perception, we incorporate two deep-feature-based perceptual similarity metrics: LPIPS33 and DISTS.
Based on these five metrics, we construct a normalized radar chart and additionally propose a “radar area” metric as an intuitive indicator for the overall performance of each method. This metric reflects both the balance and effectiveness of the model across multiple dimensions, facilitating a holistic comparison among different approaches. Since LPIPS and DISTS are inverse metrics, we apply a transformation of 1 − normalized value during normalization to ensure that all metrics are mapped to the [0, 1] range, and follow the principle that higher values indicate better performance. Finally, the area of the pentagonal radar chart is calculated using the vector cross product method.
To evaluate the perceptual quality of super-resolved images on the OBITrue dataset, which lacks paired high-resolution ground truth, we conducted a Mean Opinion Score (MOS) evaluation. Given the poor suitability of general no-reference quality metrics (e.g., NIQE, BRISQUE) for assessing the visual characteristics of ancient script imagery, we performed a blind subjective assessment involving 16 participants comprising domain experts and graduate students specializing in oracle bone epigraphy. All participants possessed specialized knowledge in this field. They were asked to rate the visual outputs of different methods based on three key criteria: image clarity, structural consistency, and semantic interpretability. Ratings were collected using a five-point Likert scale (1 = Very Poor, 5 = Excellent). The final MOS for each method was obtained by averaging scores across all participants and test samples.
Comparative study
To comprehensively evaluate the performance of the proposed OBISR model, we conduct comparative experiments against several representative state-of-the-art methods, including Bicubic interpolation, CycleGAN16, LRGAN23, HiFaceGAN26, MM-RealSR28, SCGAN17, WFEN29 and NeXtSRGAN14. For a fair comparison, we retrain all comparative methods rigorously to ensure their optimal performance on the target datasets.
Table 1 presents a quantitative comparison between our proposed OBISR model and various state-of-the-art methods on the OBI_BI and OBI_AR datasets, while Fig. 7 presents a comprehensive performance comparison of different methods on these two datasets using radar charts.On both OBI_BI and OBI_AR datasets, OBISR-DTGEMA achieved the largest radar chart area, demonstrating its superior comprehensive performance in structural reconstruction, detail restoration, and perceptual quality. Particularly on the OBI_AR dataset, OBISR-DTGEMA attained a radar area of 2.1888, outperforming OBISR-DTG across all metrics. Furthermore, it demonstrated significant advantages in key metrics such as VIF and PSNR over mainstream methods including NeXtSRGAN14 and WFEN29. These results demonstrate that our method exhibits enhanced generalization capability and robustness in the oracle bone rubbing super-resolution task.
Figure 8 shows the qualitative visual results of different methods on the OBI_BI dataset. It can be observed that methods such as Bicubic, CycleGAN16, LRGAN23, HiFaceGAN26, and WFEN29 exhibit significant defects in reconstructing stroke continuity and structural outlines. LRGAN23, MM-RealSR28, and SCGAN17 produce varying degrees of character distortion and even introduce non-existent noise. NeXtSRGAN14 is capable of generating generally clear character structures; however, it still exhibits certain shortcomings in stroke-level details, such as subtle gaps or unnatural protrusions, which compromise the overall structural fidelity. In contrast, the images generated by the DTG generator in our proposed OBISR method exhibit superior structural consistency and detail preservation, resulting in visual outputs that more closely resemble the ground truth high-resolution images.
Figure 9 further presents the qualitative results on the OBI_AR and OBITrue datasets. Since the OBITrue dataset consists of real-world LR oracle rubbings and is an unpaired dataset, the corresponding ground truth images are not provided. We observe that both Bicubic and HiFaceGAN26 generate overly smooth and blurry results. CycleGAN16 suffers from stroke disconnection on OBI_AR and severe character deformation on OBITrue. Moreover, LRGAN23 introduce varying levels of noise and character artifacts. MM-RealSR28 tends to produce unnatural character structures, and its outputs on the OBI_AR dataset exhibit partially clear but largely blurred image results. Both SCGAN17 and NeXtSRGAN14 demonstrate substantial character shape distortion across both datasets. On the OBI_AR dataset, WFEN29 produces visually competitive results. However, evaluations on the OBITrue dataset indicate that its generated images exhibit slight blurring and white noise artifacts, which negatively affect the overall visual perception. In contrast, the proposed OBISR model demonstrates more stable reconstruction performance across both datasets, achieving superior overall quality in terms of image clarity, stroke continuity, and structural integrity.
To further validate visual quality, Table 2 reports the Mean Opinion Scores (MOS) on the OBITrue dataset. It achieves superior mean MOS scores of 4.53 and 4.36 using the DTG and DTGEMA generators, exceeding those of other methods. This experimental evidence verifies that OBISR successfully enhances image sharpness and maintains the inscriptions’ structural and semantic integrity, demonstrating high effectiveness and robustness for reconstructing real-world rubbing images.
Beyond comparative experiments, a series of ablation studies are conducted to further analyze the contribution of individual components in the proposed OBISR model, as described in the following subsections.
Impact of PatchD discriminator count on OBISR performance
To ensure the validity and isolation of each proposed module, this section and the subsequent ablation studies follow a unified experimental principle. The primary objective is to evaluate the individual and joint contributions of the key architectural components, including the DTG generator. To maintain consistency and ensure a fair comparison, all experimental variants are evaluated using a unified DTG generator, with the DTG module either activated or deactivated according to the specific configuration. When the DTG generator is disabled, the generator from SCGAN is employed to produce the inference results. The DTGEMA generator is excluded from this analysis to avoid introducing confounding variables, since its performance has already been validated in the comparative study.
As clearly shown in Table 3, our proposed OBISR model, configured with four PatchD discriminators (DP1, DP2, DP3 and DP4), achieves the top performance in PSNR, SSIM, and VIF. Compared to any other variant, OBISR demonstrates global superiority, attaining comprehensive advantages in all three dimensions. This validates the strong synergy and generalization ability of our designed PatchD discriminator architecture.
Although certain variants come close to optimal performance in individual metrics, they generally fail to maintain consistent superiority across all metrics. In contrast, OBISR achieves top scores in all three metrics, indicating stable and overall optimal performance. This further corroborates the significant benefits of employing four PatchD discriminators in restoring image structures and details.
It is worth noting that, from the perspective of sub-module combinations, using individual PatchD discriminators or partial combinations may yield some improvements. However, their overall performance still lags behind that of OBISR. This suggests that localized improvements are insufficient for achieving comprehensive performance gains, and only the full integration of all four discriminators can fully unleash the model’s potential.
In summary, OBISR demonstrates outstanding performance in terms of image quality, structural consistency and visual fidelity, making it the optimal solution among all configurations.
Effect of discriminator depth on reconstruction performance
The use of 16 × 16 and 64 × 64 resolutions is based on the classical 4 × super-resolution setting, which aligns well with the characteristics of oracle bone rubbings, where character regions are generally small and localized. Accordingly, the discriminator depth in our framework is determined based on the spatial characteristics of the input resolution.
For 64 × 64 images, employing a deeper discriminator with six convolutional layers enables the network to capture finer local details and high-frequency artifacts more effectively. Increasing the depth beyond this point, however, would cause the feature maps to shrink below 1 × 1, making it infeasible to retain spatially localized discriminative capability.
For 16 × 16 images, further increasing depth beyond four would cause the feature maps to shrink excessively, leading to unstable training or ineffective convolution operations. To strike a balance between discriminative capacity and architectural feasibility, we thus adopt a six-layer PatchD discriminator for 64 × 64 inputs and a five-layer version for 16 × 16 inputs.
To evaluate the impact of discriminator depth on image quality, we conduct ablation studies across multiple depth configurations. As shown in Table 4, increasing the number of convolutional layers consistently improves PSNR, SSIM, and VIF scores across both the OBI_BI and OBI_AR datasets. These results validate the effectiveness of our resolution-aware depth design in enhancing reconstruction performance.
Comparison of upsampling and downsampling strategies in the reconstruction generator
To systematically evaluate the individual contributions of each component in our model, we conduct ablation studies by progressively removing specific modules and analyzing their impact. Given the significant role of the PatchD discriminators in enhancing discriminative capability, which may obscure the effects of other design factors, we choose to base our analysis on the simplified version OBISR-K, where PatchD discriminators are not included. This allows us to focus on the impact of different upsampling and downsampling strategies on reconstruction performance.
Specifically, we design three structural variants based on OBISR-K by adopting different combinations of bicubic and bilinear interpolation for upsampling and downsampling, resulting in four configurations in total. We then conduct quantitative evaluations on two datasets: OBI_BI and OBI_AR. The results are presented in Table 5.
Experimental results show that, on the OBI_BI dataset, the OBISR-K variant using bilinear for both upsampling and downsampling achieves the best performance in terms of PSNR, SSIM and VIF, indicating that OBISR-K is more effective in enhancing reconstruction quality under complex degradation with noise. On the OBI_AR dataset, OBISR-K also leads in PSNR (17.5109) and VIF (0.2421), demonstrating consistent and stable superiority.
In summary, although bicubic interpolation may retain structural information more effectively in certain scenarios, bilinear exhibits better overall reconstruction accuracy and visual fidelity, especially in severely degraded images affected by noise.
Performance comparison of structural module designs
Table 6 presents a comprehensive ablation study evaluating the individual and joint contributions of four core modules: EMA, \({{\mathcal{L}}}_{{\rm{M}}}\), DTG, and PatchD. Results on the OBI_BI dataset demonstrate that each module provides distinct improvements to image reconstruction quality. Specifically, EMA alone leads to consistent performance gains, while the artifact loss proves effective even in the absence of EMA, highlighting its independent ability to suppress visual artifacts. The DTG module enhances the recovery of structural details, and PatchD contributes positively when used individually.
Furthermore, combining these modules yields stronger performance than using them in isolation. In particular, PatchD demonstrates more significant improvements when paired with DTG, suggesting a strong synergy between structural guidance and local discrimination. The full OBISR model, which integrates all four components, achieves the best overall results on both OBI_BI and OBI_AR datasets. These findings confirm not only the effectiveness of each individual module but also the complementarity among them in improving visual fidelity and structural consistency.
Discussion
In this work, we propose OBISR, a generative adversarial network designed for super-resolution reconstruction of oracle rubbing images. Without relying on paired low- and high-resolution data, OBISR enhances structural and detail recovery through a Transformer-based two-stage generator DTG and its improved variant DTGEMA. By incorporating the artifact loss \({{\mathcal{L}}}_{{\rm{M}}}\) and the PatchD discriminator, our model effectively suppresses artifacts and character distortions. Experimental results demonstrate that OBISR outperforms existing methods in both quantitative metrics and qualitative visual assessments, showcasing its superior performance in oracle rubbing image super-resolution tasks. Future research could further optimize the model architecture to enhance its adaptability to real-world degradation patterns, thereby better supporting the digital preservation and scholarly study of oracle bone inscriptions.
Data availability
Data is available at https://github.com/Qisisi/OBISR.git. Code are available from the corresponding author upon reasonable request.
References
Gao, J. & Liang, X. Distinguishing oracle variants based on the isomorphism and symmetry invariances of oracle-bone inscriptions. IEEE Access 8, 152258–152275 (2020).
Wang, C. & Sun, W. Semantic guided large scale factor remote sensing image super-resolution with generative diffusion prior. ISPRS J. Photogramm. Remote Sens. 220, 125–138 (2025).
Xiao, H., Chen, X., Luo, L. & Lin, C. A dual-path feature reuse multi-scale network for remote sensing image super-resolution. J. Supercomputing 81, 17 (2024).
Zhang, K. et al. Csct: Channel-spatial coherent transformer for remote sensing image super-resolution. IEEE Trans. Geosci. Remote Sens. 63, 1–14 (2025).
Ma, J., Jian, G. & Chen, J. Diffusion model-based mri super-resolution synthesis. Int. J. Imaging Syst. Technol. 35, e70021 (2025).
Wei, J., Yang, G., Wei, W., Liu, A. & Chen, X. Multi-contrast mri arbitrary-scale super-resolution via dynamic implicit network. IEEE Transactions on Circuits and Systems for Video Technology 1–1 (2025).
Hu, J., Qin, Y., Wang, H. & Han, J. Ms2cam: Multi-scale self-cross-attention mechanism-based mri super-resolution. Displays 88, 103033 (2025).
Cao, J., Jia, Y., Yan, M. & Tian, X. Superresolution reconstruction method for ancient murals based on the stable enhanced generative adversarial network. EURASIP J. Image Video Process. 2021, 1–23 (2021).
Hu, Q. et al. Convsrgan: super-resolution inpainting of traditional chinese paintings. Herit. Sci. 12, 176 (2024).
Xiao, C., Chen, Y., Sun, C., You, L. & Li, R. Am-esrgan: Super-resolution reconstruction of ancient murals based on attention mechanism and multi-level residual network. Electronics13 (2024).
Ledig, C. et al. Photo-realistic single image super-resolution using a generative adversarial network. In 2017 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), 105–114 (2017).
Wang, X. et al. Esrgan: Enhanced super-resolution generative adversarial networks. In Leal-Taixé, L. & Roth, S. (eds.) Computer Vision – ECCV 2018 Workshops, 63–79 (Springer International Publishing, Cham, 2019).
Li, L., Zhang, Y., Yuan, L. & Gao, X. Sanet: Face super-resolution based on self-similarity prior and attention integration. Pattern Recognit. 157, 110854 (2025).
Park, S.-W., Jung, S.-H. & Sim, C.-B. Nextsrgan: enhancing super-resolution gan with convnext discriminator for superior realism. Vis. Computer 41, 7141–7167 (2025).
Li, F. et al. Srconvnet: A transformer-style convnet for lightweight image super-resolution. Int. J. Computer Vis. 133, 173–189 (2025).
Zhu, J.-Y., Park, T., Isola, P. & Efros, A. A. Unpaired image-to-image translation using cycle-consistent adversarial networks. In 2017 IEEE International Conference on Computer Vision (ICCV), 2242–2251 (2017).
Hou, H. et al. Semi-cycled generative adversarial networks for real-world face super-resolution. IEEE Trans. Image Process. 32, 1184–1199 (2023).
Wu, C. & Jing, Y. Unsupervised super resolution using dual contrastive learning. Neurocomputing 630, 129649 (2025).
Wang, W., Zhang, H., Yuan, Z. & Wang, C. Unsupervised real-world super-resolution: A domain adaptation perspective. In 2021 IEEE/CVF International Conference on Computer Vision (ICCV), 4298–4307 (2021).
Maeda, S. Unpaired image super-resolution using pseudo-supervision. In 2020 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), 288–297 (2020).
Chen, S. et al. Unsupervised image super-resolution with an indirect supervised path. In 2020 IEEE/CVF Conference on Computer Vision and Pattern Recognition Workshops (CVPRW), 1924–1933 (2020).
Wang, L., Li, J., Wang, Y., Hu, Q. & Guo, Y. Learning coupled dictionaries from unpaired data for image super-resolution. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), 25712–25721 (2024).
Bulat, A., Yang, J. & Tzimiropoulos, G. To learn image super-resolution, use a gan to learn how to do image degradation first. In Ferrari, V., Hebert, M., Sminchisescu, C. & Weiss, Y. (eds.) Computer Vision – ECCV 2018, 187–202 (Springer International Publishing, Cham, 2018).
Lugmayr, A., Danelljan, M. & Timofte, R. Unsupervised learning for real-world super-resolution. In 2019 IEEE/CVF International Conference on Computer Vision Workshop (ICCVW), 3408–3416 (2019).
Lee, S., Ahn, S. & Yoon, K. Learning multiple probabilistic degradation generators for unsupervised real world image super resolution. In Karlinsky, L., Michaeli, T. & Nishino, K. (eds.) Computer Vision – ECCV 2022 Workshops, 88–100 (Springer Nature Switzerland, Cham, 2023).
Yang, L. et al. Hifacegan: Face renovation via collaborative suppression and replenishment. In Proceedings of the 28th ACM International Conference on Multimedia, MM ’20, 1551-1560 https://doi.org/10.1145/3394171.3413965 (Association for Computing Machinery, New York, NY, USA, 2020).
Wang, X., Xie, L., Dong, C. & Shan, Y. Real-esrgan: Training real-world blind super-resolution with pure synthetic data. In 2021 IEEE/CVF International Conference on Computer Vision Workshops (ICCVW), 1905–1914 (2021).
Mou, C. et al. Metric learning based interactive modulation for real-world super-resolution. In Avidan, S., Brostow, G., Cissé, M., Farinella, G. M. & Hassner, T. (eds.) Computer Vision – ECCV 2022, 723–740 (Springer Nature Switzerland, Cham, 2022).
Li, W. et al. Efficient face super-resolution via wavelet-based feature enhancement network. In Proceedings of the 32nd ACM International Conference on Multimedia, MM ’24, 4515-4523 https://doi.org/10.1145/3664647.3681088 (Association for Computing Machinery, New York, NY, USA, 2024).
Li, Y. et al. Swin-unit: Transformer-based gan for high-resolution unpaired image translation. In Proceedings of the 31st ACM International Conference on Multimedia, MM ’23, 4657-4665 https://doi.org/10.1145/3581783.3612518. (Association for Computing Machinery, New York, NY, USA, 2023).
Liang, J., Zeng, H. & Zhang, L. Details or artifacts: A locally discriminative learning approach to realistic image super-resolution. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), 5657–5666 (2022).
Wang, Z., Bovik, A., Sheikh, H. & Simoncelli, E. Image quality assessment: from error visibility to structural similarity. IEEE Trans. Image Process. 13, 600–612 (2004).
Zhang, R., Isola, P., Efros, A. A., Shechtman, E. & Wang, O. The unreasonable effectiveness of deep features as a perceptual metric. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR) (2018).
Miyato, T., Kataoka, T., Koyama, M. & Yoshida, Y. Spectral normalization for generative adversarial networks. In International Conference on Learning Representations https://openreview.net/forum?id=B1QRgziT- (2018).
Lin, M., Chen, Q. & Yan, S. Network in network https://arxiv.org/abs/1312.4400 (2014).
Glorot, X., Bordes, A. & Bengio, Y. Deep sparse rectifier neural networks. J. Mach. Learn. Res. 15, 315–323 (2011).
Isola, P., Zhu, J.-Y., Zhou, T. & Efros, A. A. Image-to-image translation with conditional adversarial networks. In 2017 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), 5967–5976 (2017).
Goodfellow, I. J. et al. Generative adversarial nets. In Proceedings of the 28th International Conference on Neural Information Processing Systems - Volume 2, NIPS’14, 2672-2680 (MIT Press, Cambridge, MA, USA, 2014).
Paszke, A. et al. Pytorch: An imperative style, high-performance deep learning library https://arxiv.org/abs/1912.01703 (2019).
Kingma, D. P. & Ba, J. Adam: A method for stochastic optimization https://arxiv.org/abs/1412.6980 (2017).
Huang, S., Wang, H., Liu, Y., Shi, X. & Jin, L. Obc306: A large-scale oracle bone character recognition dataset. In 2019 International Conference on Document Analysis and Recognition (ICDAR), 681–688 (2019).
Acknowledgements
This work was supported by the Key Research Project of Higher Education Institutions in Henan Province (Grant No. 24A520018) and the National Natural Science Foundation of China (Grant No. 62072160).
Author information
Authors and Affiliations
Contributions
S.W. conceived the research idea, designed the overall methodology, and co-wrote the main manuscript text. Q.Y. developed the OBISR framework, performed the experiments, and co-wrote the main manuscript text. Y.W. collected and preprocessed the digital dataset of oracle bone rubbings. D.L. conducted data analysis. X.L. contributed to result interpretation. S.W., Q.Y., and Y.W. revised the manuscript critically for important intellectual content. All authors reviewed and approved the final manuscript.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution-NonCommercial-NoDerivatives 4.0 International License, which permits any non-commercial use, sharing, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if you modified the licensed material. You do not have permission under this licence to share adapted material derived from this article or parts of it. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by-nc-nd/4.0/.
About this article
Cite this article
Wang, S., Yu, Q., Wang, Y. et al. Unsupervised GAN-based model for super-resolution of oracle bone rubbing images. npj Herit. Sci. 13, 584 (2025). https://doi.org/10.1038/s40494-025-02154-3
Received:
Accepted:
Published:
Version of record:
DOI: https://doi.org/10.1038/s40494-025-02154-3