Intelligent prediction of residual strength in blended hydrogen–natural gas pipelines with crack-in-dent defects

Abstract

Accurately predicting the residual strength of blended hydrogen natural gas pipelines containing a crack-in-dent defect is critical for ensuring their safe and stable operation. Machine learning methods offer an effective approach for predicting residual strength. However, the application of machine learning models to the prediction of residual strength in blended hydrogen natural gas pipelines is often challenged by limited sample sizes and the difficulty of interpreting feature interactions. To address these challenges, a model integrating a tabular foundation model with interpretability analysis techniques was proposed. This model not only achieves highly accurate residual strength prediction under limited data conditions but also facilitates interpretability analysis of feature interactions. Comparative experimental results indicate that the model outperforms baseline models in predictive accuracy, achieving an R² of 0.9961. The model also demonstrates outstanding predictive stability, with the majority of absolute errors falling within 0.15 MPa and the maximum absolute error reaching only 0.2858 MPa. In addition, the interpretability analysis method facilitates the interpretability analysis of both individual features and their interactions, thereby improving model transparency. This methodological framework holds significant potential for supporting safety assessments and intelligent decision-making in the operation of blended hydrogen natural gas pipelines.

Introduction

As a crucial clean energy carrier, hydrogen plays an essential role in mitigating greenhouse gas emissions and accelerating the global transition toward a low-carbon energy system^1,2,3,4. Pipeline transportation is widely regarded as one of the most efficient methods for hydrogen delivery^5,6,7; however, dedicated hydrogen pipelines still encounter substantial challenges related to cost and operational efficiency. To mitigate this challenge, blending hydrogen with natural gas at variable ratios and utilizing existing natural gas pipeline infrastructure for transport is widely regarded as one of the most practical and cost-effective delivery strategies currently available⁸. This approach can substantially reduce the costs associated with hydrogen transportation⁹. Consequently, the integration of hydrogen into natural gas pipeline systems is increasingly recognized as a promising technological pathway with broad application prospects¹⁰.

However, the transportation of blended hydrogen natural gas through pipelines continues to face multiple challenges in practical applications, with safety concerns gaining increased attention in recent years. On one hand, pipelines transporting blended hydrogen natural gas are subjected to complex loading conditions during service and are simultaneously affected by environmental factors such as corrosion, which can lead to structural defects such as dents and cracks¹¹. Furthermore, under pipeline transportation conditions, hydrogen readily diffuses into the steel matrix, inducing hydrogen embrittlement that significantly compromises the mechanical properties and structural reliability of the pipeline¹². Moreover, previous studies have demonstrated that hydrogen atoms tend to accumulate at corrosion defect sites, increasing the pipeline’s susceptibility to hydrogen embrittlement under specific environmental and loading conditions, thereby further undermining its mechanical properties and operational safety^13,14. Residual strength refers to the maximum internal pressure a pipeline can withstand in its current condition and serves as a key indicator for assessing its remaining service life and structural integrity. Hence, accurate assessment of the residual strength of blended hydrogen natural gas pipelines containing crack defects is essential to ensure their safe and reliable operation.

In recent years, the prediction of residual strength in blended hydrogen natural gas pipelines with crack defects has attracted growing research interest, and numerous studies have been undertaken to address this challenge. Ghaednia et al. conducted experimental investigations on four full-scale pipeline specimens containing dent and crack defects, and their results demonstrated that crack depth has a significant impact on the residual strength of the pipeline. Based on these findings, they further developed a finite element model to predict the residual strength of defective pipelines¹⁵. Qin et al. employed the extended finite element method (XFEM) to evaluate the structural integrity of pipelines with crack-in-dent defects. Their findings revealed that the synergistic effects of dents, cracks, and hydrogen-induced degradation (HID) can significantly reduce the residual strength of the pipeline, with crack depth identified as the most critical factor influencing the failure pressure¹¹. Okodi et al. developed a finite element model (FEM) containing a rectangular dent with an embedded longitudinal crack, and used it to perform predictive analysis of residual strength. The results indicated that both the crack depth and its location within the dent are critical parameters for evaluating the impact of crack-in-dent defects on pipeline performance¹⁶. Although full-scale burst testing and finite element simulation are recognized as two of the most effective approaches for evaluating pipeline residual strength, each presents notable limitations. Full-scale experiments are labor-intensive, require substantial infrastructure, and involve considerable costs. In contrast, finite element methods necessitate the specification of complex parameters under varying service conditions and place significant demands on computational resources as well as technical expertise. In recent years, machine learning (ML) methods have been widely employed in the evaluation of residual strength in oil and gas pipelines, owing to their efficiency and strong predictive capabilities^17,18,19,20. Some researchers have also begun to explore the application of ML methods in assessing the residual strength of blended hydrogen natural gas pipelines. Li et al. proposed a hybrid prediction model, FEM-FC-BP, for estimating the residual strength of blended hydrogen natural gas pipelines. This model innovatively incorporates the feature crossing (FC) technique to overcome the limitation of low feature dimensionality. The resulting hybrid model exhibits high predictive accuracy²¹. Xie et al. developed a residual strength prediction model for blended hydrogen natural gas X80 pipelines under internal corrosion conditions by integrating finite element analysis with a genetic algorithm-optimized backpropagation neural network²². Qin et al. developed a Whale Optimization Algorithm (WOA)-optimized XGBoost model to predict the residual strength of blended hydrogen natural gas pipelines containing crack-in-dent defects. In addition, eXplainable Artificial Intelligence (XAI) was employed to interpret the key features influencing residual strength¹⁰.

XAI refers to a set of techniques that make the decision-making process of machine learning models transparent and understandable to humans. In the field of machine learning research, XAI plays a critical role by enhancing trust, improving model reliability, and facilitating knowledge discovery beyond pure prediction accuracy²³. Among these approaches, SHapley Additive exPlanations (SHAP) has been widely applied in the prediction of pipeline residual strength^10,24,25, as it provides intuitive insights into the relative importance of input features. However, SHAP is limited in its ability to capture and interpret the interactions between features. To address this limitation, the Shapley interaction quantification (SHAPIQ) method has been proposed as a powerful tool for explaining how feature interactions influence model predictions. However, to the best of our knowledge, this method has not yet been explored in the context of pipeline residual strength prediction.

Machine learning models for predicting the residual strength of corroded pipelines typically rely on large volumes of experimental data to ensure high predictive accuracy. However, experimental studies on blended hydrogen natural gas pipelines remain limited due to high costs and substantial safety risks, leading to a scarcity of available data²¹. The limited sample size significantly degrades model performance, underscoring the necessity for strategies that improve prediction accuracy under constrained data conditions. In addition, although previous studies have employed the SHAP method to interpret key factors influencing the residual strength of blended hydrogen natural gas pipelines¹⁰, they have primarily focused on the importance of individual features. The complex interactions among features and their collective impact on residual strength remain largely unexplored.

Given the problems existing in the above research, this work investigates the prediction of residual strength in blended hydrogen natural gas pipelines with crack-in-dent defects under small-sample conditions. A predictive framework based on TabPFN-SHAPIQ is developed. The TabPFN model is first trained to achieve high predictive performance, followed by an interpretability analysis using the SHAPIQ method, with a particular focus on the effects of feature interactions on model outputs. Compared with the model proposed by Qin et al.¹⁰, the present framework not only achieves improved predictive accuracy but also enables interpretability analysis of feature interactions, thereby providing deeper insights into the factors influencing residual strength. This framework is intended to provide valuable insights and theoretical support for the accurate assessment of residual strength under data-scarce scenarios.

Results and discussion

Model performance analysis

This section compares the predictive performance of the TabPFN model against four baseline models to demonstrate its superior capability. All models were trained on 105 samples and evaluated on an independent test set consisting of 27 previously unseen samples. The performance metrics are presented in Table 1, as well as in Figs. 1e and 2e. Among all models, XGBoost achieved the best performance on the training set; however, TabPFN outperformed all other models on the test set, achieving the highest predictive accuracy with an R² of 0.9961. Compared with the WOA-XGBoost model reported by Qin et al.¹⁰, which achieved an R² of 0.986 on the same dataset, our TabPFN model demonstrates an improved predictive accuracy, highlighting the effectiveness of the proposed approach in capturing the residual strength behavior of pipelines. This superior performance underscores that TabPFN is the most effective model for accurately predicting the residual strength of blended hydrogen natural gas pipelines containing crack-in-dent defects. The superior performance of TabPFN compared to other baseline models may be attributed to its powerful pre-trained architecture, which enables high prediction accuracy even under small-sample conditions through fine-tuning^26,27. This approach has proven to be highly effective for enhancing model performance. Future research may investigate transfer learning to adapt high-performing models from other domains for residual strength prediction of pipelines, thereby enhancing prediction accuracy and ensuring safe, stable pipeline operation. The LightGBM and XGBoost models also demonstrated strong predictive performance, achieving R² values of 0.9859 and 0.9810, respectively. In contrast, the RF model achieved a comparatively low R² of 0.9047, indicating lower accuracy in predicting residual strength.

Fig. 1: Performance metrics of the models on the training set.

Scatter plots of the models on the training set: a TabPFN, b LightGBM, c XGBoost, d RF. e Performance metrics of the four models on the training set.

Fig. 2: Performance metrics of the models on the test set.

Scatter plots of the models on the test set: a TabPFN, b LightGBM, c XGBoost, d RF. e Performance metrics of the four models on the test set.

Table 1 Evaluation metrics of different models

As shown in Figs. 1 and 2, scatter plots were used to visualize the model’s predictive performance on the training and test sets, providing a clear assessment of its accuracy. It depicts the relationship between predicted and true values, with the diagonal line indicating perfect prediction where predicted values equal true values. The closer the data points cluster around this diagonal, the higher the prediction accuracy of the model. The scatter plots reveal that the data points of the TabPFN model are densely distributed near the diagonal line, reflecting a close correspondence between predicted and true values and further highlighting the model’s high predictive accuracy. In contrast, the data points for the LightGBM, XGBoost, and RF models are more dispersed, particularly in the RF model, where many points deviate substantially from the diagonal, reflecting lower prediction accuracy. Overall, both the evaluation metrics and scatter plots demonstrate that TabPFN achieves high predictive accuracy for the residual strength of blended hydrogen natural gas pipelines containing crack-in-dent defects, validating it as a reliable tool for pipeline residual strength prediction. Although not the top performers, XGBoost and LightGBM still show strong performance on this dataset, indicating their potential for further investigation in future studies.

Model stability analysis

Prediction stability is another key performance metric, as it reflects the model’s ability to avoid large prediction errors at specific data points^28,29. Table 2 presents the standard deviation of errors (SDE) for the TabPFN model and three baseline models on the test set. It can be observed that TabPFN not only achieves the highest prediction accuracy but also demonstrates the greatest prediction stability. Figure 3 illustrates the fitting performance of the four models on the test set using a line-and-point plot. Consistent with the scatter plot analysis, the TabPFN model’s predicted values closely match the true values, with no evident high-error points, demonstrating a clear advantage over the other three baseline models.

Fig. 3: The degree of data point fitting on the test set.

Goodness of fit between the true values and model predictions on the test set: a TabPFN, b LightGBM, c XGBoost, d RF.

Table 2 SDE of the models on the test dataset

Figure 4 presents the error statistical analysis of the models. In Fig. 4a, the red lines indicate an absolute error boundary of ±0.30 MPa. It can be seen that many error points of the three baseline models exceed this range. The violin plot of error distribution in Fig. 4b further confirms this observation. Based on the above analysis, TabPFN exhibits greater prediction stability than the LightGBM, XGBoost, and RF models. As shown in Fig. 4c, the error histogram of TabPFN demonstrates that most absolute errors fall within 0.15 MPa, with a maximum error of only 0.2858 MPa, further confirming the model’s strong overall predictive performance.

Fig. 4: Error distribution of the models on the test set.

a Error distribution scatter plot, b Error distribution violin plot, c Error distribution histogram.

Based on the above analysis, it can be concluded that the TabPFN model is capable of accurately predicting the residual strength of blended hydrogen natural gas pipelines containing crack-in-dent defects without the need for large amounts of experimental or simulation data.

Interpretability analysis

To establish the relationship between pipeline-related input features and the residual strength, and to enhance the transparency and interpretability of the machine learning model, Qin et al. integrated the developed WOA-XGBoost model with the SHAP method for interpretability analysis¹⁰. However, the previous study considered only the effects of individual features on the model output, neglecting the complex interactions among features. To overcome this limitation, this study employed the SHAPIQ method to interpret the best-performing TabPFN model, thereby providing a more comprehensive understanding of how both individual features and their interactions influence the model’s predictions.

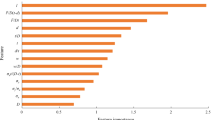
Figure 5 presents a global interpretability analysis of the TabPFN model based on the SHAPIQ method, highlighting the influence of both individual features and their interactions on the model output. The vertical axis displays all features ranked by their relative importance to the model’s predictions, while the horizontal axis shows the average contribution of each feature to the output. The results indicate that Lc, H₂, t, d, and the interaction feature Lc×Dc are the top five most influential predictors, with Lc and H₂ being the two most dominant individual features. Notably, the interaction feature Lc×Dc exhibits a higher importance score than individual features, Dc and D. This critical finding, which is difficult to capture using traditional SHAP methods, underscores the importance of modeling complex feature interactions when interpreting machine learning models.

Fig. 5: Global explanation of the TabPFN model using the SHAPIQ method.

Workflow of global interpretability using SHAPIQ.

Figure 6 provides a detailed case study of model interpretability from a local perspective by analyzing four representative samples from the test set. The feature information of the samples is presented in Table 3. This visualization intuitively illustrates the decision rationale and feature influence mechanisms underlying the model’s predictions of residual strength. In Fig. 6, color denotes the direction of each feature’s impact: red features indicate a positive contribution, where higher feature values lead to higher residual strength, while blue features signify a negative contribution. The length of each colored bar represents the magnitude of influence: longer bars indicate greater impact on the predicted residual strength. Notably, the sum of all feature contributions plus the base value (the average predicted value across the test dataset, 13.97) equals the final prediction for each sample.

Fig. 6: Local explanation of the TabPFN model using the SHAPIQ method.

Four samples from the test set were selected for local interpretability analysis, comparing explanations with and without consideration of feature interactions. Red edges indicate positive contribution, and blue edges indicate negative contribution.

Table 3 Parameters of samples used in this study

Unlike traditional SHAP, which considers only the marginal contributions of individual features under the assumption of feature independence, SHAPIQ integrates feature interaction terms into both computation and visualization. This enables a more comprehensive interpretability framework that not only quantifies the marginal impact of each feature but also reveals the synergistic effects of feature combinations on model outputs. Such insights provide a deeper and more nuanced understanding of the model’s prediction process.

Figure 7 presents the feature interaction network graphs for the four selected test samples, with node and edge colors consistent with the previous visualizations. In each graph, the size of the circular nodes represents the importance of individual features to the model output: larger circles indicate greater influence on the predicted residual strength. The connecting edges between features illustrate the strength of their interactions in affecting the model output. Thicker and more opaque lines denote stronger feature interactions.

Fig. 7: Visualization of the feature interaction network based on SHAPIQ analysis.

Feature interaction network diagrams for four samples generated by SHAPIQ interpretability analysis: a Sample 1, b Sample 2, c Sample 3, d Sample 4.

To further illustrate the contributions of features and their interactions to the model predictions, UpSet plots were constructed for each sample based on the above analysis, as shown in Fig. 8. In these plots, the upper bar chart shows the most influential combinations of features, while the lower matrix indicates the specific features involved in each combination. This visualization approach provides valuable insights into the model’s decision-making mechanism at the individual sample level, emphasizing the varied effects of both individual features and their interactions on prediction outcomes.

Fig. 8: UpSet plot of feature interactions generated by SHAPIQ.

UpSet plots clearly illustrating the contributing factors for four samples: a Sample 1, b Sample 2, c Sample 3, d Sample 4.

In conjunction with Table 2 and Figs. 7 and 8, it can be observed that the samples primarily differ in wall thickness, crack length, and hydrogen blending ratio, which provides the basis for analyzing the interactions among defect severity, hydrogen embrittlement, and structural parameter. In Sample 1, a significant positive main effect is identified between crack depth and wall thickness, indicating that shallow cracks combined with thicker walls enhance structural integrity and thereby increase the predicted residual strength. A comparison with other samples reveals that wall thickness plays a distinct protective role, buffering the negative effects of hydrogen blending ratio and crack length. Overall, the contribution of wall thickness to residual strength remains consistently positive, with its effect more pronounced in thicker pipelines, which aligns with the engineering principle that increasing wall thickness enhances load-bearing capacity. In contrast, crack length emerges as the dominant negative driver, with its impact intensifying progressively as cracks extend from short (Sample 2) to long (Samples 3-4), given that crack length directly influences crack initiation and propagation under pressure loading. Furthermore, hydrogen blending not only introduces a negative main effect but also amplifies the adverse interaction with crack length. In particular, Samples 3 and 4 demonstrate that even a modest addition of 5% hydrogen markedly exacerbates the detrimental effect of crack length, highlighting the synergistic risk of hydrogen embrittlement and cracking. These findings suggest that, in hydrogen-blended transmission systems, prioritizing an increase in pipeline wall thickness can help offset crack-related risks, while stringent monitoring of crack length thresholds is critical to maintaining residual strength above a safe critical level.

In summary, the proposed TabPFN-SHAPIQ model exhibits several notable advantages. Firstly, it achieves superior predictive accuracy compared to baseline models, with most absolute errors controlled within 0.15 MPa, demonstrating both accuracy and stability. Secondly, by integrating SHAPIQ, the model provides valuable insights into feature interactions, identifying Lc, H₂, t, d, and Lc×Dc as the most influential factors, while also enabling localized interpretability for individual predictions.

Despite these strengths, this study mainly considers pairwise feature interactions. Higher-order interactions involving multiple features, which may further enrich the interpretability of machine learning models, remain unexplored. Future research should therefore focus on extending the analysis to capture such complex interactions, thereby enhancing the explanatory power and applicability of predictive models in pipeline integrity assessment.

Methods

TabPFN

TabPFN, proposed by Hollmann in a 2025 publication in Nature, is a machine learning algorithm specifically designed for tabular data under small-sample conditions²⁷. It leverages a Transformer model pre-trained on a large corpus of synthetic data to make predictions directly on new small-sample datasets at test time, without requiring gradient-based optimization or model fine-tuning. Compared with traditional machine learning algorithms, TabPFN requires neither data preprocessing nor hyperparameter tuning, while achieving high predictive accuracy even under small-sample conditions. Further technical details can be found in the original work by Hollmann²⁷. In this study, the TabPFN framework was implemented using the TabPFN package developed by Prior Lab^30,31,32.

Baseline models

LightGBM is a lightweight gradient boosting algorithm introduced by Microsoft in 2017³³. It employs a histogram-based decision tree learning approach, which enables efficient handling of large-scale feature sets and datasets. Another notable feature of LightGBM is its leaf-wise tree growth strategy. Unlike traditional level-wise growth, LightGBM grows trees leaf-wise by always splitting the leaf with the highest loss reduction. This strategy allows the use of histogram-based algorithms to efficiently identify optimal split points within leaf nodes, thereby significantly improving both training speed and accuracy. Further details can be found in the study conducted by Zhang³⁴. In this study, the LightGBM model was implemented using the lightgbm package.

XGBoost is an efficient and scalable machine learning algorithm developed by Chen and Guestrin³⁵. It improves predictive accuracy by iteratively training decision trees and progressively adjusting the contribution of each tree. In XGBoost, the objective function consists of two components: a loss function and a regularization term, as shown in Eq.(1)²⁸.

$${\mathcal{L}}\left(\phi \right)=\mathop{\sum }\limits_{i=1}^{n}l\left({y}_{i},{\hat{y}}_{i}\right)+\mathop{\sum }\limits_{k=1}^{K}\Omega \left({f}_{k}\right)$$

(1)

where ${\mathcal{L}}(\phi )$ is overall objective function; ${\sum }_{j=1}^{n}l({y}_{i},{\hat{y}}_{i})$ is loss function; ${y}_{i}$ is true value; ${\hat{y}}_{i}$ is predicted value; $\Omega ({f}_{k})$ is regularization term; ${f}_{k}$ is the model corresponding to the k-th decision tree. The final prediction is obtained by summing the outputs of all individual trees, as shown in Eq.(2). In this study, the XGBoost model was implemented using the xgboost package.

$${\hat{y}}_{i}=\mathop{\sum }\limits_{k=1}^{K}{f}_{k}\left({x}_{i}\right)$$

(2)

Random Forest (RF) is an ensemble learning method based on the Bagging strategy and composed of multiple decision trees. It consists of an ensemble of decision trees, each generating a prediction based on the input features. The final output is obtained by aggregating the predictions of all trees through averaging, as shown in Eq.(3)³⁶.

$$f\left(x\right)=\frac{1}{N}\mathop{\sum }\limits_{n=1}^{N}{f}_{N}\left(x\right)$$

(3)

where $f(x)$ is the prediction result of the RF regression model; ${f}_{N}(x)$ is the prediction made by the N-th individual decision tree. In this study, the RF model was implemented using the scikit-learn package.

SHAPIQ

SHAP analysis is theoretically well-founded and highly interpretable, and has been widely applied in recent years^37,38. However, traditional SHAP analysis methods face limitations in capturing and interpreting feature interactions. To address this issue, the SHAPIQ method was employed to conduct interpretability analysis considering feature interactions. Similar to SHAP, SHAPIQ also employs a game-theoretic approach to compute the Shapley values of the model, enhancing the traditional Shapley value approach by decomposing feature contributions into individual effects and higher-order interactions³⁹. In this study, SHAPIQ is applied to quantify the impact of each input feature on the predicted residual strength, while simultaneously capturing the interactions among features, thereby providing a comprehensive understanding of both individual and combined feature effects within the predictive model. Further algorithmic details of SHAPIQ can be found in the work of Muschalik³⁹. In this study, SHAP values were computed based on the trained model and the corresponding training dataset. All SHAP value computations were performed using the shapiq package.

Numerical database

In this study, the machine learning models were developed using a dataset constructed by Qin et al. based on finite element simulations, which contains 132 samples of X80 pipeline residual strength¹⁰. The input features include pipeline outer diameter (D), wall thickness (t), dent depth (d), crack length (Lc), crack depth (Dc), and hydrogen blending ratio (H₂). The model output is the pipeline residual strength (P). Figure 9 illustrates the distributions of each input feature and pipeline residual strength using histograms, along with their correlations depicted in a correlation heatmap. As shown in Fig. 9, the input features display wide distribution ranges; however, the sample counts within certain intervals remain relatively low. Such data sparsity can cause underfitting in machine learning models, consequently diminishing prediction accuracy. Moreover, all input features exhibit correlations with the pipeline residual strength and were therefore retained for subsequent model training.

Fig. 9: Data distribution and correlation of features.

Distribution plots of each feature in the dataset: a pipeline outer diameter, b wall thickness, c dent depth, d crack length, e crack depth, f hydrogen blending ratio, g pipeline residual strength. h Pearson correlation heatmap of all variables.

Research framework

Figure 10 illustrates the overall framework of this study. First, a limited-size dataset of residual strength for blended hydrogen natural gas pipelines was collected from the literature. In the second step, two modeling strategies were applied to the original dataset: (1) The first strategy directly split the raw data into 80% training and 20% test set, followed by training the TabPFN model without any preprocessing; (2) The second strategy first applied normalization to the raw data, then split it into 80% training and 20% test set, and finally trained the LightGBM, XGBoost, and RF models. In the second strategy, Bayesian optimization combined with 5-fold cross-validation was employed to tune the model hyperparameters, whereas the TabPFN model was deliberately applied without hyperparameter tuning, as it is a prior-data fitted network pre-trained on a large number of synthetic tasks, embedding inductive biases that enable direct application without task-specific optimization^31,32. All experiments were conducted in Python using the Google Colab platform. In the third step, the predictive performance and stability of the TabPFN and baseline models were systematically evaluated. In the fourth step, the SHAPIQ method was applied to perform interpretability analysis and investigate the effects of individual features and their interactions on the predictions of the TabPFN model.

Fig. 10: General workflow of our work.

This study mainly comprises four parts: (1) Collection of residual strength data, (2) Construction of machine learning models, (3) Evaluation of model performance, and (4) Interpretability analysis of the model.

Based on the above procedures, a TabPFN-SHAPIQ predictive model was ultimately developed to estimate the residual strength of blended hydrogen natural gas pipelines containing crack-in-dent defects.

Four evaluation metrics, coefficient of determination (R²), Mean Squared Error (MSE), Mean Absolute Error (MAE), and Mean Absolute Percentage Error (MAPE), are used as the evaluation metrics for all predictive models employed in this study. The formulas for these metrics are presented below^40,41:

$${R}^{2}=1-\frac{{\sum }_{i=1}^{n}{\left({y}_{i}-{p}_{i}\right)}^{2}}{{\sum }_{i=1}^{n}{\left({y}_{i}-\bar{y}\right)}^{2}}$$

(4)

$${\rm{MSE}}=\frac{1}{n}\sum {({y}_{i}-{p}_{i})}^{2}$$

(5)

$${\rm{MAE}}=\frac{1}{n}\mathop{\sum }\limits_{i=1}^{n}\left|{y}_{i}-{p}_{i}\right|$$

(6)

$${\rm{MAPE}}=\frac{1}{n}\mathop{\sum }\limits_{i=1}^{n}\left|\frac{{p}_{i}-{y}_{i}}{{y}_{i}}\right|\times 100 \%$$

(7)

where $i$ is each sample; $n$ represents the total number of samples; ${y}_{i}$ is the true value, ${p}_{i}$ is the predicted value and $\bar{y}$ denotes the mean value of the samples.