Experimental demonstration of quantum finite automaton

Abstract

In quantum information science, a major task is to find the quantum models that can outperform their classical counterparts. Automaton is a fundamental computing model that has wide applications in many fields. It has been shown that the quantum version of automaton can solve certain problem using a much smaller state space compared to the classical automaton. Here we report an experimental demonstration of an optical quantum automaton, which is used to solve the promise problems of determining whether the length of an input string can be divided by a prime number P with no remainder or with a remainder of R. Our quantum automaton can solve such problem using a state space with only three orthonormal states, whereas the classical automaton needs no less than P states. Our results demonstrate the quantum benefits of a quantum automaton over its classical counterpart and paves the way for implementing quantum automaton for more complicated and practical applications.

Introduction

Quantum information science is a research field focused on enhancing problem-solving efficiency by utilizing quantum effects. The most prominent example is quantum computer—by changing the basic elements of a computer from bits and logic gates to quantum bits and quantum logic gates, quantum computer can achieve an exponential speedup in solving certain problems, including factoring¹ and simulation of complex systems.^2,3,4 Extensive efforts have been made to build such computing machine and small-scale quantum computers have already been constructed in different physical systems.^{5,6,7,8,9,10,11} A series of quantum algorithms have been demonstrated on these prototype machines to show the quantum benefits in tackling particular problems.^{12,13,14,15,16}

Computer is not the only device whose capability can be boosted by introducing quantum elements. Finite automaton (FA) is another good example. As one of the most fundamental models in computer science, FA can be used to model problems in many fields, including mathematics, artificial intelligence, games or linguistics.^17,18 The concept of quantum finite automaton (QFA) was invented as the quantum version of FA by Kondacs and Watrous¹⁹ and also by Moore and Crutchfield.²⁰ It has been theoretically predicted that QFA can solve certain problems more efficiently than its classical counterpart.^21,22 However, to the best of our knowledge, no experiment has been performed to prove the quantum benefits of QFA yet.

In this letter, we have built a proof-of-principle optical QFA that can solve some certain problems more space-efficiently than a classical FA. In our experiment, we have proven that a QFA composed with a three-dimensional quantum state suffice to solve a promise problem whereas a classical FA needs much larger state space to solve the same problem.

The paper is structured as follows. We will first introduce some background knowledge about FA and QFA. Then we will explain how to use a QFA to solve a certain promise problem. At last, we will present our experimental demonstration of an optical QFA solving a promise problem.

Results

A deterministic finite automaton (DFA) is a finite-state machine that accepts or rejects input strings of symbols. Here deterministic refers to the fact that a DFA only produces a unique computation for each input string. We only consider the case of DFAs as it has been proven that DFAs have equivalent computing power to non-deterministic finite automata.^17,23,24

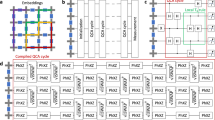
As shown in Fig. 1a, a typical DFA is illustrated with a state diagram. In this example automaton, there are two states S₀ and S₁, which are denoted graphically by circles. The automaton takes a finite sequence of 0 s and 1 s as input. For each state, there is a transition arrow leading out to a next state for both 0 and 1. Upon reading a symbol, a DFA jumps deterministically from one state to another by following the transition arrow. For example, if the automaton is currently in state S₀ and the current input symbol is 1, then it deterministically jumps to state S₁. A DFA has a start state (denoted graphically by an arrow coming in from nowhere) where computations begin, and a set of accepted states (denoted graphically by a double circle). If the automaton ends at an accepted state after reading the last symbol of the input string, this string of symbols is regarded as being accepted by the DFA; otherwise, it is regarded as being rejected by the DFA. DFAs are often used to solve (recognize) decision problems, which are defined as computational problems where the answer for every instance is either Yes or No. For example, determining whether a binary number is even or not is a typical decision problem, which can be solved by the DFA shown in Fig. 1a.

Fig. 1

State diagrams of deterministic finite automata (DFAs) and quantum finite automata (QFAs). a The state diagram of a typical DFA. S₀ and S₁ are the two possible states of the DFA, where S₀ is both the start state and the accepted state. For each state, there is a transition arrow leading out to a next state for both 0 and 1. Upon reading a symbol (0 or 1), the DFA will jump deterministically from one state to another following the transition arrow. The current DFA accepts only binary numbers that are multiples of 2. b The state diagram of a general QFA. Inside the QFA is an m-dimensional quantum state, with |ψ₀〉 as the start state and |0〉, |1〉, ..., |m−2〉, |m−1〉 being its m orthonormal basis states, where some of these basis states are designated as accepted states. The input string σ₁σ₂⋯σ_n−1σ_n determines how the quantum state will evolve. Every time a symbol σ_i is read in, a corresponding unitary operator $U_{\sigma _i}$ is applied on the quantum state. After reading the last symbol of the string, the final quantum state would be measured and thus projected to one of the m basis states. The input string would then be accepted or rejected by the QFA according to whether or not the quantum state is projected to one of the accepted states. c A DFA for solving a promise problem. This DFA can be used to determine whether the length of an input string is an integer multiple of a prime number P or not. d A QFA for solving the same promise problem. Inside the DFA is a three-dimensional quantum state, with |0〉, |1〉, and |2〉 being its 3 orthonormal basis states, where |0〉 is both the start state and the only accepted state. The quantum state will go through n copies of unitary operator U, where n is the length of the input string

QFA, the quantum version of DFA, is realized by changing the basic elements of DFA to the quantum components. As shown in Fig. 1b, inside a QFA sits a quantum state |ψ〉 with m orthonormal basis states |0〉, |1〉, ..., |m − 2〉, |m − 1〉. One or several of the m basis states are designated as accepted states. Before the computation starts, the QFA rests at a starting state |ψ₀〉. The computation of a QFA with an input string σ₁σ₂...σ_n−1σ_n (σ_i is the ith symbol of the string) works as follows: The QFA reads in the string from left to right, symbol by symbol. Upon reading a symbol σ_i, a corresponding unitary operator $U_{\sigma _i}$ is applied on the state. After reading the last symbol of the string, the final state of the QFA would be $|\psi _n\rangle = U_{\sigma _n}U_{\sigma _{n - 1}} \cdots U_{\sigma _2}U_{\sigma _1}|\psi _0\rangle$. A projective measurement in the basis of |0〉, |1〉, ..., |m − 2〉, |m − 1〉 is then applied on |ψ_n〉 and the state would be projected to one of the m basis states. If the state is projected to an accepted state, the string is regarded as being accepted by the QFA; otherwise the string is rejected.

To show the quantum benefits of QFA over DFA, we now consider a particular problem. Assuming the length of an input string is guaranteed to be either k * P or k * P + R, where P is a prime number, R is a positive integer less than P, and k is an arbitrary integer no less than 0. The task is to determine whether the length of the string can be divided by P with no remainder or with a remainder of R. Such task is a promise problem,²⁵ which is a generalization of decision problem, where the input is promised to belong to a particular subset of all possible inputs. Let us show how to solve this problem with a DFA first. As shown in Fig. 1c, there are P states in the diagram and S₀ is both the start and only accepted state in the DFA. Here symbols with different alphabets are treated the same way as the concrete alphabets of symbols do not affect the length of the string. Therefore, the labels besides the transition arrows are omitted here. The P states and the transition arrows form a circle in the diagram, which means the DFA will change back to its original state after k * P moves. As a result, if the length of the string is k * P, the DFA, which starts at S₀, will also end at S₀, signifying the acceptance of the input string; if the length is k * P + R, the DFA will end at S_R and the input string would be rejected. Although the DFA can only end at either of the two states S₀ or S_R here, its state space cannot be squeezed. It has been proven that, to solve this problem, one needs a DFA with no less than P states.²²

We now explain how to solve this problem with a QFA, using a quantum state space with just three orthonormal basis states. As shown in Fig. 1d, inside the QFA is a 3-dimensional quantum state, namely a qutrit, with three orthonormal basis states |0〉, |1〉, and |2〉. The start state of the QFA is set as |0〉. Just as the DFA, symbols with different alphabets are treated the same way here as well. Upon reading in a symbol, no matter what the symbol is, the same unitary U would be applied to the quantum state. As a result, after reading in the last symbol of the input string, the final quantum state would be either U^k*P|0〉 or U^{k*P + R}|0〉. By properly choosing unitary operator U, these two states can be orthogonal to each other. We will set the unitary operator $U = U_{\mathrm{e}}^\dagger U_{\mathrm{c}}U_{\mathrm{e}}$, where both of U_e and U_c are three-dimensional unitary operators. U_c is defined as

$$U_{\mathrm{c}} = \left( {\begin{array}{*{20}{c}} 1 & 0 & 0 \\ 0 & {{\mathrm{cos}}\frac{{2\pi Q}}{P}} & { - {\mathrm{sin}}\frac{{2\pi Q}}{P}} \\ 0 & {{\mathrm{sin}}\frac{{2\pi Q}}{P}} & {{\mathrm{cos}}\frac{{2\pi Q}}{P}} \end{array}} \right),$$

(1)

in which Q is a positive integer less than P. Here Q is properly chosen to ensure that the inequality ${\mathrm{cos}}\left( {\frac{{2\pi Q}}{P}R} \right) < 0$ holds. For given P and R, if $\frac{P}{4} \le R \le \frac{{3P}}{4}$, Q is set to be 1; if $R \;<\; \frac{P}{4}$, Q is set to be $\left\lceil {\frac{P}{{4R}}} \right\rceil$; if $R \;>\; \frac{{3P}}{4}$, Q is set to be $\left\lfloor {\frac{P}{R}\left( {j + \frac{1}{4}} \right)} \right\rfloor + 1$, where j is an integer such that $\frac{1}{4} \;<\; j\frac{{P - R}}{R} - \left\lfloor {j\frac{{P - R}}{R}} \right\rfloor < \frac{2}{3}$.²² It can be verified that

$$U_c^{k \ast P} = \left( {\begin{array}{*{20}{c}} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \end{array}} \right)$$

(2)

and

$$U_c^{k^\ast P + R} = \left( {\begin{array}{*{20}{c}} 1 & 0 & 0 \\ 0 & t & { - \sqrt {1 - t^2} } \\ 0 & {\sqrt {1 - t^2} } & t \end{array}} \right),$$

(3)

where $t = {\mathrm{cos}}\left( {\frac{{2\pi Q}}{P}R} \right)$. U_e is defined as

$$U_e = \left( {\begin{array}{*{20}{c}} {\sqrt {\frac{{ - t}}{{1 - t}}} } & {\sqrt {\frac{1}{{1 - t}}} } & 0 \\ {\sqrt {\frac{1}{{1 - t}}} } & { - \sqrt {\frac{{ - t}}{{1 - t}}} } & 0 \\ 0 & 0 & 1 \end{array}} \right)$$

(4)

and $U_{\mathrm{e}}^2\,=\,I$. It can converts |0〉 to $\left( {\sqrt {\frac{{ - t}}{{1 - t}}} ,\sqrt {\frac{1}{{1 - t}}} ,0} \right)^T$ and also convert $\left( {\sqrt {\frac{{ - t}}{{1 - t}}} ,\sqrt {\frac{1}{{1 - t}}} ,0} \right)^T$ back to |0〉. Putting them together, one gets U^k*P|0〉 = |0〉 and $U^{k \ast P + R}|0\rangle = \sqrt { - t} |1\rangle + \sqrt {1 + t} |2\rangle$ which are derived from the following calculations

$$\begin{array}{*{20}{l}} {} \hfill & {U_{\mathrm{e}}^\dagger U_{\mathrm{c}}^{k \ast P}U_{\mathrm{e}}|0\rangle = U_{\mathrm{e}}^\dagger U_{\mathrm{e}}|0\rangle = |0\rangle ,} \hfill \\ {} \hfill & {U_{\mathrm{e}}^\dagger U_{\mathrm{c}}^{k \ast P + R}U_{\mathrm{e}}|0\rangle } \hfill \\ = \hfill & {\left( {\begin{array}{*{20}{c}} {\sqrt {\frac{{ - t}}{{1 - t}}} } & {\sqrt {\frac{1}{{1 - t}}} } & 0 \\ {\sqrt {\frac{1}{{1 - t}}} } & { - \sqrt {\frac{{ - t}}{{1 - t}}} } & 0 \\ 0 & 0 & 1 \end{array}} \right)\left( {\begin{array}{*{20}{c}} 1 & 0 & 0 \\ 0 & t & { - \sqrt {1 - t^2} } \\ 0 & {\sqrt {1 - t^2} } & t \end{array}} \right)} \hfill \\ {} \hfill & {\left( {\begin{array}{*{20}{c}} {\sqrt {\frac{{ - t}}{{1 - t}}} } & {\sqrt {\frac{1}{{1 - t}}} } & 0 \\ {\sqrt {\frac{1}{{1 - t}}} } & { - \sqrt {\frac{{ - t}}{{1 - t}}} } & 0 \\ 0 & 0 & 1 \end{array}} \right)\left( {\begin{array}{*{20}{c}} 1 \\ 0 \\ 0 \end{array}} \right) = \left( {\begin{array}{*{20}{c}} 0 \\ {\sqrt { - t} } \\ {\sqrt {1 + t} } \end{array}} \right).} \hfill \end{array}$$

(5)

As |0〉 is the only accepted state, after the projective measurement on the final state, the QFA will accept the input string when its length is k * P and reject the string when its length is k * P + R.

We now present our experimental demonstration of a QFA in linear optics. As shown in Fig. 2, a UV pulse laser with a central wavelength of 390 nm, produced by second harmonic generation using Mira-HP (repetition rate of 76 MHz and central wavelength of 780 nm), is focused onto a barium borate (BBO) crystal cut for type-II spontaneous parametric down-conversion (SPDC) to generate a two-photon state. By detecting a horizontally-polarized single photon at detector D3, a vertically-polarized single photon on path a (|V_a〉) is obtained as the starting state of our QFA. We define |0〉 = |V_a〉, |1〉 = |H_b〉 and |2〉 = |V_b〉, where H_b (V_b) denotes the photon in horizontal (vertical) polarization on path b. The photon now encodes a qutrit and the starting state of the QFA is |0〉. To run the computation of the QFA, one needs to implement n copies of U on the qutrit, where n is the length of the input string. As U_c is simpler for experimental implementation, we will thus realize Uⁿ by cascading U_e, $U_{\mathrm{c}}^n$ and $U_{\mathrm{e}}^\dagger$. The qutrit photon first passes through the unitary U_e, which is realized by the half-waveplate HWP1 and the beam-displacer BD1, and the state is converted to $\sqrt {\frac{{ - t}}{{1 - t}}} |0\rangle + \sqrt {\frac{1}{{1 - t}}} |1\rangle$. The photon then goes through a sequence of HWPs on path b. Every two consecutive HWPs (HWP2 and HWP3 for example) realize a U_c which rotates the polarization state on path b by an angle of $\frac{{2\pi Q}}{P}$ and leaves the polarization on path a unchanged. There are n copies of U_c along the path, where n = k * P or k * P + R. After passing through $U_{\mathrm{c}}^n$, the qutrit state would become $\sqrt {\frac{{ - t}}{{1 - t}}} |0\rangle + \sqrt {\frac{1}{{1 - t}}} |1\rangle$ if n = k * P or $\sqrt {\frac{{ - t}}{{1 - t}}} |0\rangle - \sqrt {\frac{{t^2}}{{1 - t}}} |1\rangle + \sqrt {1 + t} |2\rangle$ if n = k * P + R. The qutrit photon further gets through HWP4 on path a (used to change V_a to H_a), HWP5 on path b (used to swap H_b and V_b) and BD2. These three optical devices together implement a unitary M which maps V_a to H_b, H_b to V_b, and V_b to H_c. After passing through M, the photon state can still be written as $\sqrt {\frac{{ - t}}{{1 - t}}} |0\rangle + \sqrt {\frac{1}{{1 - t}}} |1\rangle$ or $\sqrt {\frac{{ - t}}{{1 - t}}} |0\rangle - \sqrt {\frac{{t^2}}{{1 - t}}} |1\rangle + \sqrt {1 + t} |2\rangle$ if we redefine the basis states of the qutrit as |0〉 = |H_b〉, |1〉 = |V_b〉 and |2〉 = |H_c〉. At last, the qutrit photon passes through the unitary $U_{\mathrm{e}}^\dagger$, which is realized by HWP6, and the state is thus converted |0〉 = |H_b〉 or $\sqrt { - t} |1\rangle + \sqrt {1 + t} |2\rangle = \sqrt { - t} |V_{\mathrm{b}}\rangle + \sqrt {1 + t} |H_{\mathrm{c}}\rangle$. The qutrit photon is then measured in the |0/1/2〉 basis and the string is accepted if the photon is detected at D0 or rejected if the photon is detected at D1 or D2.

Fig. 2

Experimental setup of an optical quantum finite automaton (QFA). The experimental setup is used to implement a QFA for determining whether the length of the string n is k * P or k * P + R, where P is a prime number, R is a positive integer less than P and k is an arbitrary integer no less than 0. With (P, R) setting as (3, 1), (3, 2), (5, 1), or (5, 2), four different QFAs are built accordingly. A photon pair with central wavelength at 780 nm is generated by pumping a type-II beta barium borate (BBO) crystal with a UV laser. By detecting a photon at detector 3, a heralded single photon, working as a qutrit in the QFA, is created and led into the optical circuit. The photon qutrit, encoded in both the polarization and the path degree of freedom, passes through the unitary operators U_e, $U_{\mathrm{c}}^n$, M and $U_{\mathrm{e}}^\dagger$ in turn. U_e is realized by a half-waveplate (HWP1) and a beam displacer (BD1). HWP2 and HWP3 together realize a U_c. $U_{\mathrm{c}}^n$ is realized by cascading n copies of such U_c. M, composed of HWP4 (at 45°), HWP5 (at 45°) and BD2, maps V_a to H_b, H_b to V_b and V_b to H_c, where H and V denote horizontal and vertical polarizations and a, b, and c denote the paths of the photon. By redefining the basis states, the qutrit, written in the form of the expansion of the basis states, would remain unchanged after passing through M. $U_{\mathrm{e}}^\dagger$ is realized by a single half-waveplate (HWP6). The qutrit is at last measured and projected to the basis states

To assess the performance of our experiment, we have configured our setup to realize 4 different QFAs. The first (second) QFA is used to determine whether the length of the string is 3k or 3k + 1 (3k + 2). The third (fourth) QFA is used to determine whether the length of the string is 5k or 5k + 1 (5k + 2). As shown in Fig. 3a, b, for the first (second) QFA, the qutrit is projected to |0〉 with an average probability of 98.452 ± 0.073% (98.516 ± 0.087%) if the length of the string is 0, 3 or 6 (0 or 3); If the length of the string is 1, 4, or 7 (2 or 5), the qutrit is projected to |1〉 or |2〉 with an average probability 99.562 ± 0.037% (99.634 ± 0.041%). Similarly, as shown in Fig. 3c, d, for the third (fourth) QFA, the qutrit is projected to |0〉 with an average probability of 98.697 ± 0.080% (98.711 ± 0.079%) if the length of the string is 0 or 5 (0 or 5); If the length of the string is 1 or 6 (2 or 7), the qutrit is projected to |1〉 or |2〉 with an average probability of 99.461 ± 0.052% (99.443 ± 0.052%). The experimental results are all in good agreement with the theoretical predictions.

Fig. 3

Experimental results for four different quantum finite automata (QFAs). 0, 1, and 2 on the x axis denote photon detections on D0, D1, and D2, respectively. a The results of QFA for determining whether the length of the input string is 3k or 3k + 1. The QFA can distinguish between the two sets {0, 3, 6} and {1, 4, 7} with an average success rate of 99.007 ± 0.041%. b The results of QFA for determining whether the length of the input string is 3k or 3k + 2. The QFA can distinguish between the two sets {0, 3} and {2, 5} with an average success rate of 99.075 ± 0.048%. c The results of QFA for determining whether the length of the input string is 5k or 5k + 1. The QFA can distinguish between the two sets {0, 5} and {1, 6} with an average success rate of 99.079 ± 0.048%. d The results of QFA for determining whether the length of the input string is 5k or 5k + 2. The QFA can distinguish between the two sets {0, 5} and {2, 7} with an average success rate of 99.077 ± 0.047%.The error bars (SD) are calculated according to Poissonian counting statistics

Our experimental setup can be used to distinguish much longer input strings by using more waveplates. As optical waveplates have very high transmission rate (>99.5%), in principle we can use more than 1000 waveplates to implement the QFA, which can handle input strings longer than 500 characters. The main reasons prevent us from doing so are the high cost of a thousand waveplates and the limited size of the optical bench.

Discussion

Here we highlight the key differences between DFA and QFA. By definition, in both DFA and QFA, the state transition will happen n times, where n is the length of the input string. As a result, there is no difference between DFA and QFA in time complexity. The key difference between DFA and QFA is in space complexity. For a DFA, the state inside is a classical system, which means all of its possible states are always orthogonal to each other. As a result, to distinguish between strings with the length of k * P and k * P + R, the classical system inside the DFA must have a state space with at least P orthonormal states.^22,26 In contrast, for a QFA, the state inside is a quantum system, which means it can be in a superposition state and its possible states do not need to be orthogonal to each other. By utilizing this feature, the QFA with a state space of just three orthonormal states can be used to solve the same promise problem. Our proof-of-principle optical experiment have demonstrated this quantum advantage of QFA in space efficiency. By using a photonic quantum system with just three orthonormal states, our QFA solves a promise problem which would needs a DFA with at least P orthonormal states.

Compared with DFA, Turing machine (classical computer) is a more general computing model equipped with memory. However, a Turing machine cannot solve the promise problem more space efficiently than a DFA. It would also need a state space with no less than P orthonormal states to solve the same problem. To simulate a QFA solving the promise problem with a classical computer, the computer would needs an even larger state space (much larger than the state space with P orthonormal states) to track the change of the amplitudes of the quantum state in the QFA.

In summary, we have experimentally constructed a proof-of-principle optical QFA, which can solve a particular promise problem—determining whether the length of an input string can be divided by a prime number P with no remainder or with a remainder of R—with much higher space efficiency than its classical counterpart. To solve this problem, a classical DFA needs a state space with at least P states, whereas a QFA only needs a quantum state space with three orthonormal states. The size of quantum state space for solving such problem is constant and does not depend on the value of P. Our results have clearly proven this quantum benefit of QFAs. However, in this work, the QFAs are just used to solve a special promise problem with unary alphabets. There are more interesting decision and promise problems using binary alphabets to be solved by QFAs.^22,27 Our experiments pave the way for further research on using QFAs to tackle such problems.

Methods

Experimental settings

As shown in Fig. 2, the setup are configured to realized four different QFAs to determine whether the length of an input string can be divided by P with no remainder or with a remainder of R, where (P, R) are set to be (3, 1), (3, 2), (5, 1), or (5, 2). To realize these four QFAs, the half-waveplates are reconfigured to realize different U_e, U_c, and $U_{\mathrm{e}}^\dagger$. For the case of (P, R) = (3, 1) ((3, 2), (5, 1), (5, 2)), HWP1, HWP3, and HWP6 are set at 60° (60°, 72°, 36°), 27.37° (27.37°, 24.02°, 24.02°), and 60° (60°, 72°, 36°), respectively. For all the four cases, HWP2, HWP4, and HWP5 are always set at 0°, 45° and 45°, respectively.