Introduction

Entanglement plays a pivotal role in several quantum technologies in the field of quantum communication and information. For these applications miniaturized plug and play photonic sources are desired. Additionally, the chosen quantum emitter has to be compatible with the quantum hardware such that the light source can drive the latter. For example, efficient distribution and sharing of entanglement between different nodes is important for the realization of quantum communication networking infrastructure. In many proposals, the nodes of such a network would consist of atomic or atom-like systems1. The optical transitions of those systems typically exhibit narrow bandwidths in the range from 10 to 100 MHz. An efficient interface between different nodes, therefore, requires sources of entangled states with the optical bandwidths in the same order.

Often, one generates entangled states with non-linear processes such as spontaneous parametric downconversion (SPDC) in second-order non-linear materials2,3,4,5 or spontaneous four-wave mixing in materials exhibiting third-order non-linearities6. To realize the entangled states, one superimposes the outputs of two independent processes which are highly indistinguishable. The two typical configurations are using two nonlinear crystals whose optical axes are perpendicular2 or a crystal with an interferometric setup3,4. One drawback of such sources is that the bandwidth is magnitudes wider and not compatible with atomic systems without further effort. In our case, we use a whispering gallery mode resonator (WGMR) as a source for generating polarization entanglement. Such sources typically have a bandwidth of a few tens of MHz and can interact with narrowband systems without additional filters.

WGMRs are made of highly transparent dielectric materials. When light propagates in such a resonator, it is confined near the rim due to the total internal reflection. There are several interesting advantages to achieving SPDC in WGMRs7. Firstly, WGMRs have a high Q-factor (Q > 107) and small mode volume (<106λ3, where λ is the optical wavelength inside the resonator), which can increase the efficiency of SPDC. The high Q factor ensures a narrow bandwidth for the whole transparency region of the material. Moreover, the spectrum of WGMRs can be widely tuned by various techniques8,9,10,11. Additionally, it is possible to fine-tune the bandwidth via the distance of the coupling prisms relative to the WGMR8. It has been shown that with these properties one can efficiently tune the generated parametric photons from the same WGMR to narrowband transitions of rubidium and cesium9. Those features make WGMRs a potentially promising source of quantum states of light for developing quantum networks. However, one key aspect of this source is missing: polarization entanglement has not been demonstrated in WGMRs.

In this work, we demonstrate for the first time two-photon polarization entanglement from a WGMR in an interferometric scheme. In this scheme, we leverage the directional degeneracy of the whispering gallery modes. By coupling the pump laser into the equivalent clockwise (CW) and counterclockwise (CCW) modes, we generate the parametric signal and idler photon pairs that populate counterpropagating but otherwise identical, whispering gallery modes. These photon pairs can be used to yield polarization entanglement. This is achieved by rotating the polarization of the cw-propagating beams and combining the two signal beams as well as the two idler beams on polarizing beamsplitters. We show that by adjusting the relative phase between the combined parametric beams, we can access various polarization-entangled Bell states. These states can be characterized by the Clauser–Horne–Shimony–Holt’s (CHSH) S-parameter12. The quantum states, for which this parameter takes the values S > 2, incorporate two-partite superpositions exhibiting tighter correlations than classical systems can have. For the maximally entangled states, this parameter takes the value \(S=2\sqrt{2}\). The classical boundary S ≤ 2 is known as the CHSH inequality12. We demonstrate a violation of this inequality by more than six standard deviations, attesting to the quantum nature of the producing polarization states. Apart from the direct measurement of the CHSH S-parameter, it is possible to extract it from the visibility of the observed interference fringe. We compare these two S-values for the generated state and find them consistent.

Results

Experimental setup

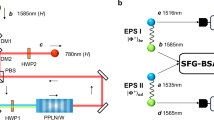
In the following, we explain the experimental setup as shown in Fig. 1a. The WGMR is made of a z-cut 5% MgO-doped LiNbO3 wafer. The shape of the WGMR is the same as reported in paper13, with the resonator radius R ≈ 0.7 mm and rim radius r ≈ 0.14 mm. We couple a 532 nm continuous-wave laser into the WGMR from the CW and CCW directions. The non-polarizing beamsplitter is used to detect the reflected pump spectrum. The x-cut LiNbO3 prism is used to couple the pump light into the WGMR while minimizing the parametric photon loss due to the parasitic out-coupling14. The diamond prism is used to couple the signals and idlers out of the WGMR. Note that because of the wavelength difference, the pump loss due to evanescent coupling through this prism is strongly suppressed when the signal and idler out-coupling are optimized. See Supplementary Note 1 for details. In this way, using two separate prisms to couple the three involved light fields allows us to selectively optimize the coupling rates. The optic elements located on the right side of the WGMR are used to create polarization-entangled states and examine their quality. The WGMR is coarsely temperature-stabilized using a Peltier element and a temperature controller. In addition, we implement a fast temperature control technique by shining a blue light on top of the WGMR15.

Fig. 1: Sketches of the experimental arrangement.
figure 1

a Is the experimental setup. EOM electro-optic modulator, FG function generator, HWP half-wave plate, PBS polarizing beamsplitter, BS non-polarizing beamsplitter, PID proportional-integral-derivative controller, LN x-cut LiNbO3 prism, D diamond prism, DM dichroic mirror, Piezo piezoelectric transducer, Pol polarizer, D1(2) detector. b and c Illustrate the interferometric arrangement for the CCW and CW propagation of the involved beams, respectively. The side views of the electric field distributions are presented for the resonator mode numbers d L = m, q = 1, e ∣L−m∣ = 1, q = 1, and f L = m, q = 2. The top view of the electric field distribution for a resonator in g equals to m = 20.

Full size image

The eigenfunction of electromagnetic modes of this resonator can be parameterized with three numbers L, m, and q13. The first two numbers represent the photon’s orbital momentum and its z-projection, respectively, while the radial mode number q is equal to the number of the optical field anti-nodes encountered in the radial direction (Fig. 1d–f). Note that the eigenvalues of different modes can be equal, which is always the case for the counter-propagating modes, (L, m, q) and (L, −m, q). The type-I non-critical phase matching is achieved by controlling the temperature of the resonator, which fulfills the photon energy conservation between the pump (p), signal (s), and idler (i) modes: ωp = ωs + ωi16. The phase matching between a combination of three modes can be symbolically written as (Lp, mp, qp) = (Ls, ms, qs) + (Li, mi, qi). The selection rules associated with this phase matching are discussed in ref. 17. The fundamental property of the whispering gallery mode phase matching leveraged in our approach is that if (Lp, mp, qp) = (Ls, ms, qs) + (Li, mi, qi) is achieved, then (Lp, −mp, qp) = (Ls, −ms, qs) + (Li, −mi, qi) is granted for the same set of mode frequencies. Furthermore, the CW and CCW modes differ only in the sign of their m number and have identical spatial profiles for both the internal and evanescent fields. As a result, the parametric photons emitted in the CW and CCW directions are, in principle, indistinguishable, and the interferometric generation of the polarization-entangled states is enabled. Any deviations from this can be attributed to technical imperfections in the setup.

Since the most efficient SPDC conversion is achieved for the fundamental modes, when all Lj = mj and qj = 1, we adjust the set point temperature (T = 90.21 °C) to achieve this type of phase matching. The central signal wavelength is measured at 950 nm, while the central idler wavelength is calculated to be at 1210 nm due to energy conservation. The Q factor of the pump mode is 1.31 × 107 with a bandwidth of 38.7 MHz. The properties of the generated photons are characterized by measuring the cross-correlation and auto-correlation functions in both propagating directions (see Fig. 2). The bandwidths of the signal and idler which are calculated from the time constants shown in Fig. 2a and b are 5.31 and 7.23 MHz, corresponding to Q factors close to 5.95 × 107 and 3.43 × 107, respectively18. The pair detection rates normalized to the pump power are 7.29 × 106 s−1 mW−1 in the CW and 1.37 × 107 s−1 mW−1 in the CCW direction. These rates relate to the in-coupled pump and are corrected for the detection efficiency. The reason why the pair detection rates in the CW are lower than in the CCW direction is that the corresponding free-space beams are handled separately (see Fig. 1a). The alignment imperfections, as well as losses of the individual optics component, lead to the difference in observed single-detector counting and coincidence rates. In our setup, the losses in the CW path are larger than those in the CCW path. The heralding efficiency of the signal and idler in the CW(CCW) direction are 0.9%(1.0%) and 0.8%(1.3%), respectively. The heralding efficiencies can be improved by eliminating the experimental imperfections mentioned above. In Table 1, we collect recent polarization entanglement sources in different systems19,20,21,22,23,24. Compared to these works, our source is the brightest source with the narrowest bandwidth, with pump powers at least two orders of magnitude lower than the others. These parameters are important for efficient atom-photon interaction and scalability. We also characterize the effective number of modes presented in the CW and CCW beams by investigating the signal-signal autocorrelation function. When measuring the signal-signal autocorrelation of a perfectly single-mode SPDC process, one expects a peak value of exactly 2, arriving from the expected thermal photon number statistics25. The measured peak values for the CW and CCW beams are 1.90 ± 0.20 and 1.80 ± 0.11, respectively, which show that the states are close to single mode. A single-mode source here means a single resonator mode and a single Schmidt frequency mode26. Note that while under the continuous-wave pumping, the source is expected to produce frequency entanglement, which can, in principle, be observed in a measurement having another spectro-temporal resolution, the implemented measurement renders the state unentangled by having a high temporal resolution for precisely measuring the photon detection time, due to the time-frequency relationship for light. See Supplementary Note 2 for details.

Fig. 2: Conventional characterization of the CW and CCW PDC processes.
figure 2

a and b Represent the cross-correlation functions of the signals and idlers generated from the CW and CCW directions. The leading and trailing time constants τs,i31 are calculated by exponential fitting. c and d Show the auto-correlation functions of the signals generated from the CW and CCW directions. The red lines are the theoretical prediction of the peak value for a perfectly single-mode quantum state.

Full size image
Table 1 List of common narrowband polarization-entangled photon sources
Full size table

Experimental results with two-photon interference

Figure 1b and c illustrate the working principle of how to generate bidirectionally pumped polarization-entanglement from a WGMR. Since we use type-I phase matching and the phase of the generated two-photon state is equal to that of the pump light27, the state with a low pump power at the out-coupling prism (D) can be expressed in terms of the pump frequency ωp, the pump propagation time from the laser to the WGMR tp, and the polarization of the signal and idler as \({{\rm{e}}}^{{\rm{i}}{\omega }_{{\rm{p}}}{t}_{{\rm{p}}}}{\left\vert {\rm{H}}\right\rangle }_{{\rm{s}}}{\left\vert {\rm{H}}\right\rangle }_{{\rm{i}}}\). For the CCW beam, after propagating, the state at the PBSs can be expressed as

$$\left\vert {\Phi }_{{\rm{CCW}}}\right\rangle \propto {{\rm{e}}}^{{\rm{i}}({\omega }_{{\rm{p}}}{t}_{{\rm{CCW}},{\rm{p}}}+{\omega }_{{\rm{s}}}{t}_{{\rm{CCW}},{\rm{s}}}+{\omega }_{{\rm{i}}}{t}_{{\rm{CCW}},{\rm{i}}})}{\left\vert {\rm{H}}\right\rangle }_{{\rm{s}}}{\left\vert {\rm{H}}\right\rangle }_{{\rm{i}}}$$
(1)

where ωs and ωi are the central frequencies of the signal and idler, and tCCW,s and tCCW,i are the propagation time of the signal and idler from the out-coupling prism to the PBSs.

For the CW beam, the state has a π/2 polarization rotation. The state at the PBSs is

$$\left\vert {\Phi }_{{\rm{CW}}}\right\rangle \propto {{\rm{e}}}^{{\rm{i}}({\omega }_{{\rm{p}}}{t}_{{\rm{CW}},{\rm{p}}}+{\omega }_{{\rm{s}}}{t}_{{\rm{CW}},{\rm{s}}}+{\omega }_{{\rm{i}}}{t}_{{\rm{CW}},{\rm{i}}})}{\left\vert {\rm{V}}\right\rangle }_{{\rm{s}}}{\left\vert {\rm{V}}\right\rangle }_{{\rm{i}}}$$
(2)

Since we perform coincidence measurements, photons from different pairs do not have a correlation and only contribute to the noise. We can represent the state as

$$\left\vert \Phi \right\rangle =\frac{1}{\sqrt{2}}(\left\vert {\rm{HH}}\right\rangle +{{\rm{e}}}^{{\rm{i}}\varphi }\left\vert {\rm{VV}}\right\rangle )$$
(3)
$$\varphi ={\omega }_{{\rm{p}}}\Delta {t}_{{\rm{p}}}+{\omega }_{{\rm{s}}}\Delta {t}_{{\rm{s}}}+{\omega }_{{\rm{i}}}\Delta {t}_{{\rm{i}}}$$
(4)

where Δt = tCW−tCCW and the overall phase is dropped. Note that by moving one of the HWPs from the CW to CCW channels we could produce other types of entangled states, such as \(\left\vert \Psi \right\rangle =(\left\vert {\rm{HV}}\right\rangle +{{\rm{e}}}^{{\rm{i}}\varphi }\left\vert {\rm{VH}}\right\rangle )/\sqrt{2}\).

Our setup is a nonlinear optical interferometer operating at three different wavelengths. A control over the phase φ can be implemented in any part of this interferometer. We choose to do it with a piezo-actuated mirror in the CW signal channel thereby affecting the Δts in Eq. (4). Besides being actively controlled, the phase φ can drift due to variations in the optical path lengths that need to be stabilized for the duration of the experiment. Furthermore, even for the stable optical path lengths, there is a variation Δφ around the fixed value φ arising from the pump, signal and idler frequency fluctuations around their central values:

$$\Delta \varphi =\Delta {\omega }_{{\rm{p}}}\Delta {t}_{{\rm{p}}}+\Delta {\omega }_{{\rm{s}}}\Delta {t}_{{\rm{s}}}+\Delta {\omega }_{{\rm{i}}}\Delta {t}_{{\rm{i}}}$$
(5)

Here the pump laser linewidth Δωp is very small and may be safely neglected. However, the signal and idler resonance widths defining its spectral widths Δωs and Δωi are not insignificant. This means that the difference of the interferometer arm lengths Ls(i),CW, Ls(i),CCW need to be smaller than the coherent lengths of the signal and idler to provide a good overlap of the interfering biphoton wavepackets: ∣Ls,CCW−Ls,CW∣ ≪ cΔωs, ∣Li,CCW−Li,CW∣ ≪ cΔωi. This would be very difficult to achieve with a free-space SPDC, which is characterized by very broad phase matching and, hence, large signal and idler spectral widths. But with our WGMRs, whose signal and idler linewidth are given above, it is sufficient to balance the interferometer on lengths that are longer than a few meters. Since the length of each interferometer arm is less than 1 m, this condition is always satisfied in our setup.

Changing the relative phase φ by applying a voltage to the piezo in the experiment, we can freely change from one Bell state \(\left\vert {\Phi }^{-}\right\rangle =(\left\vert {\rm{HH}}\right\rangle -\left\vert {\rm{VV}}\right\rangle )/\sqrt{2}\) to another \(\left\vert {\Phi }^{+}\right\rangle =(\left\vert {\rm{HH}}\right\rangle +\left\vert {\rm{VV}}\right\rangle )/\sqrt{2}\). This is shown in Fig. 3. When measured on a diagonal/anti-diagonal polarization basis, the coincidence counts for the state \(\left\vert {\Phi }^{+}\right\rangle\) is expected to reach a maximum while that of the state \(\left\vert {\Phi }^{-}\right\rangle\) is expected to reach a minimum. Using the latter setting, we characterized the passive stability of our interferometric setup by tracking the coincidence counts. We found it to be stable on a scale of several minutes, which is sufficient for the following measurements. Details of this can be found in the “Methods” section.

Fig. 3: Two-photon interference fringe as a function of the piezo displacement.
figure 3

By changing the displacement of the piezo, the phase φ can be changed from 0 to 2π and the generated state can be changed from ∣Φ+〉 to ∣Φ−〉.

Full size image

We further demonstrated the non-local two-photon interference by changing the polarization projections. The entangled state we used in the following measurements is \(\left\vert {\Phi }^{-}\right\rangle\). The data shown in Fig. 4 are measured with the polarizer in the signal arm set to project the polarization onto the directions θs = 0°/90°/45°/135° (further denoted as the H/V/D/A basis) while changing the projection angle θi the polarizer in the idler arm. From Eq. (3) it is easy to find that the normalized coincidence counts ρ should fit the prediction

$$\rho =A{\cos }^{2}({\theta }_{{\rm{i}}}+{\theta }_{{\rm{s}}})+B$$
(6)

Ideally, the amplitude term A should be the same in all four bases and the offset term B should be 0. However, due to the experimental imperfection described above, the amplitude A would not be the same and the offset B is not 0. We fit the data with Eq. (6), resulting in a visibility of 95%/89%/89%/86% on an H/V/D/A basis, respectively. These results exceed the classical limit of 71%3 thus verifying the generation of Bell states. In Fig. 4b, c we further illustrate the single counting rates for the signal and idler detectors recorded during the coincidence counting. By showing that these rates are nearly constant, we emphasize that the observed pattern is the result of a true two-photon quantum interference effect and not a statistical product of two single counting rates. The reason why the maximum value of the coincidences in the H base is higher than that of the other bases is the difference in the loss in the CW and CCW directions, which has been discussed above.

Fig. 4: Count rate measurements in terms of rotating the polarization in the idler beam path.
figure 4

a Represents the coincidence counts in the four different polarizations H/V/D/A selected in the signal arm. b and c Are the idler and signal count rates in the four different polarization bases. The error bars represent the standard error of the mean.

Full size image

To highlight the nonlocal character of the observed two-photon interference, we rotate both polarizers at the same time in the same and opposite directions. The results shown in Fig. 5 fit the prediction in Eq. (6).

Fig. 5: The coincidence counts which are measured when rotating both polarizers at the same time.
figure 5

The gray line is the theoretical prediction of the coincidence counts of θi−θs = 0°. The error bars represent the standard error of the mean.

Full size image

The nonlocal nature of observed two-photon interference allows us to test Bell-type inequalities. We calculated the S value of the CHSH inequality12 in two ways, arriving at consistent results. On the one hand, we measured the coincidence counts in four polarization combinations, and extracted the S value from the measurements2. The results show S = 2.45 ± 0.07, which violates the CHSH inequality S ≤ 2 by more than 6 sigmas (Fig. 6). Additionally, we calculated the S value from the visibilities of the four sinusoidal curves in Fig. 4a3,5. The result yields a value of S = 2.54 ± 0.06, which violates the CHSH inequality by more than eight sigmas. These are below the theoretical limit due to technical reasons, such as the detector’s dark counts, the residual drift of the phase shown in Eq. (3) during the measurement, and the imperfections of the polarizers. Nonetheless both our measurements demonstrate the quantum nature of our source with a significant margin.

Fig. 6: The S values extracted from 15 repetitions of the CHSH measurements were done within 3 days.
figure 6

The errors are calculated assuming that the main uncertainties come from the photon counting statistics and that the statistics are Poissonian.

Full size image

Discussion

In conclusion, we have demonstrated the creation of polarization-entangled photons from a WGMR. The fact that the visibilities extracted from the measured coincidence fringes are >85%, while the single count rates remain unchanged, providing us a genuine sign of the generation of the high-quality entanglement. The S value of the CHSH inequality is S = 2.45 ± 0.07, confirming that the generated quantum states are polarization-entangled.

The polarization-entangled photon pairs from the WGMRs can potentially be used for entanglement swapping, in order to distribute entanglement over long distances between the “material” qubits, such as atoms or ions. By design, the signals can meet the frequency and bandwidth requirements of atomic systems for efficient atom-photon interactions, while the wavelength of the idlers is located in the telecom band favorable for long-distance transmission. As a result, long-distance quantum information processing can be realized28. Besides, with the same configuration as shown in Fig. 1, it is possible to generate higher-order states, such as 4-photon GHZ states, which makes this type of source interesting for various advanced quantum information applications and protocols. Apart from that, by choosing the coupling regime, one can switch between a high photon count rate and long coherence time, making this type of source compatible with applications in two extreme regions. Finally, as the required pump power is low (only a few hundreds nanowatt is needed in this experiment), our source can be enabling for applications with limited power budgets such as space satellite projects29,30.

Methods

Stability of the setup

We measured the free-running phase drift of our setup to determine how long we could measure without actively stabilizing the interferometer. The result is shown in Fig. 7. We found that the drift is slow enough, and we do not need to stabilize the interferometers actively if we finish a single measurement in <5 min.

Fig. 7: The phase stability is measured by setting both polarizers to 45° and recording the coincidence counts.
figure 7

In the last few minutes we modulated the piezo to know the maximum and minimum coincidence counts, so we can estimate the speed of the phase drift in our setup.

Full size image

Coincidence contrasts

For the measurements in the D/A basis shown in Fig. 4, we first rotate both polarizers to 45°/135° and apply a voltage on the piezo to minimize the coincidence counts. Since we do not actively stabilize the interferometers, this step is necessary to ensure the state we measured is \(\left\vert {\Phi }^{-}\right\rangle\). During the measurements, the voltage applied to the piezo remains unchanged. After that, we record the coincidence counts of different polarizer settings for 30 s each and then rotate the polarizer in the idler arm by 30°. This step is repeated until the idler polarizer is rotated to 225°/315°. Then, we minimize the coincidence counts again to compensate for the phase drifts of our setup. After that, we continue to step through the remaining polarizer settings until the polarizer is rotated to 375°/465°. This procedure is repeated 10 times in total to gather sufficient statistics for an error estimation.

For the measurements in the H/V basis, the polarizer in the signal arm is rotated to 0°/90° and the polarizer in the idler arm is set to 0°. The coincidence counts are recorded for 30 s and repeated 10 times. After that, we rotate the polarizer in the idler arm in step of 30° and record the coincidence counts until it is rotated to 330°.

For the measurements θi−θs = 0°/θi + θs = 270° shown in Fig. 5, the steps are similar to that of in the D/A basis, but this time we rotate both polarizers simultaneously in the same/opposite direction. Since the oscillation frequency is twice as fast as the frequency in Fig. 4, we rotate the polarizers by 22. 5° instead to catch the feature.

S value

For the measurements of the S value, we first rotate both polarizers to 45° and minimize the coincidence counts with the piezo. After that, we rotate the polarizer in the idler arm to 67. 5°/112.5°/157.5°/202.5° in sequence and record the coincidence counts for 30 s. We choose these four angles because the greatest violation of the CHSH inequality occurs under these measurements12. Then, we rotate the polarizer in the signal arm to 90° and the polarizer in the idler arm to 202.5°/157.5°/112. 5°/67. 5° in sequence and record the coincidence counts. After that, we rotate both polarizer to 135° and minimize the coincidence counts again. Later, we rotate the polarizer in the idler arm to 157. 5°/202.5°/247.5°/292.5° in sequence and record the coincidence counts. Then, we rotate the polarizer in the signal arm to 180° and the polarizer in the idler arm to 292.5°/247.5°/202.5°/157.5° in sequence and record the coincidence counts. The measurements are repeated 15 times for the error estimation.