Crosstalk-resilient quantum MIMO for scalable quantum communications

Abstract

We address the challenge of crosstalk in quantum multiplexing–an obstacle to scaling throughput in quantum communication networks. Crosstalk arises when physically coupled quantum modes interfere, degrading signal fidelity. We propose a mitigation strategy based on encoding discrete-variable (DV) quantum information into continuous-variable (CV) bosonic modes using Gottesman-Kitaev-Preskill (GKP) codes. By analyzing the effect of mode-mixing interference, we show that under specific noise strength conditions, the interaction can be absorbed into a gauge subsystem that leaves the logical content intact. We provide rigorous conditions for perfect transmission in the ideal case, derive the structure of the output codes and prove the existence of a gauge-fixing decoder enabling recovery of the logical information. Numerical simulations under displacement Gaussian noise illustrate the fidelity behavior and rate-fidelity tradeoff. Our results establish a coding-theoretic foundation for crosstalk-resilient multiplexing in quantum networks.

Introduction

The vision of a scalable quantum internet¹ depends critically on the ability to establish high-fidelity end-to-end entanglement across large, distributed quantum networks^2,3. Achieving this goal requires both increasing the throughput of quantum links and maintaining the fidelity of transmitted quantum states⁴. Multiplexing—the simultaneous use of multiple channels over a shared resource—has emerged as a key strategy for boosting quantum communication rates^5,6. Meanwhile, diversity techniques^7,8—the use of redundant or parallel transmissions to improve reliability—offer a path toward robust state transfer under noise^7,9,10. These approaches are foundational for advanced quantum communication paradigms, including Quantum Multiple-Input Multiple-Output (MIMO) systems^7,8, which leverage multiple spatial modes to enhance data rates and robustness. However, the increased complexity of such systems makes them inherently more susceptible to crosstalk. Both multiplexing and diversity are fundamentally challenged by the problem of crosstalk: interference between quantum modes caused by physical coupling, such as mode mixing in photonic hardware^4,11,12. Crosstalk can degrade the fidelity of quantum transmission and limit the effectiveness of network-level parallelism.

In quantum information science, DV and CV systems offer complementary strengths. DV systems, such as qubits, are naturally suited to logical operations and are standard in many communication protocols. However, they are highly susceptible to noise and crosstalk, especially in multiplexed settings. On the other hand, CV systems–particularly bosonic modes–offer a rich structure for encoding and robust error correction but often lack native digital logic. The interplay between these paradigms opens new possibilities: by encoding DV quantum information into CV modes via GKP codes, one can combine the discrete control and processing advantages of DV systems with the error resilience and resource efficiency of CV encodings. In this work, we propose to mitigate crosstalk in multiplexed quantum networks by encoding DV quantum states into CV bosonic modes using Gottesman-Kitael-Preskill (GKP) codes¹³. GKP states are a powerful family of bosonic quantum error-correcting codes that embed DV logical information into structured grids in phase space¹⁴. They have found broad application in quantum technologies, ranging from fault-tolerant quantum computing^15,16,17,18 and metrology¹⁹ to recent advances in quantum communication²⁰. In particular, GKP codes are promising candidates for photonic quantum networks, including all-optical quantum repeater schemes²¹. These platforms inherently rely on CV hardware (e.g., squeezed light, beamsplitters, homodyne detection), making GKP encodings naturally compatible with physical-layer implementations.

Prior work on quantum MIMO communication has demonstrated the potential of spatial-mode diversity and multiplexing to boost quantum channel capacities^7,8,9,10. However, such schemes often suffer from inter-mode crosstalk, which limits scalability. In parallel, GKP codes have shown promise in enhancing fault tolerance and error correction in continuous-variable systems^14,15,17, but their potential in structured quantum communication–especially in MIMO settings–remains underexplored. Our work aims to bridge these directions by employing GKP encodings as a method for mitigating crosstalk in multiplexed quantum channels. In this paper, we investigate whether encoding DV states into GKP modes enables crosstalk-resilient multiplexing—under specific, quantifiable conditions on the crosstalk strength. We show that when the crosstalk strength lies at specific values, and the GKP stabilizers are appropriately scaled, the interference caused by mode coupling can be absorbed into a gauge subsystem. As a result, the logical information is preserved and can be recovered deterministically. We analyze this effect rigorously, characterizing the structure of the output state, the code conditions for perfect transmission, and the emergent gauge symmetry. Furthermore, we show how this structure can be exploited through gauge-fixing procedures, enabling reliable logical recovery. Our work establishes a foundation for crosstalk-aware encoding in quantum networks based on CV hardware and opens up new directions in entanglement distribution through structured code design, thereby contributing to the development of robust Quantum MIMO communications.

In this work, we develop a theoretical framework for preserving DV quantum information encoded in CV bosonic modes using GKP codes in the presence of crosstalk from induced mode mixing. We introduce the GKP code formalism, establish notation, and formulate the interference model, identifying the mechanism by which crosstalk manifests as displacements in phase space. Our main results provide exact conditions under which these displacements can be incorporated into the stabilizer structure of the code, enabling perfect logical transmission. We derive lattice-matching criteria and prove that certain rational crosstalk strength values permit crosstalk-mitigated multiplexing. We further characterize the output state, decomposing it into logical and gauge subsystems, and analyze the structure and role of gauge entanglement. A gauge-fixing method and a decoder based on modular arithmetic and Clifford operations are proposed. Numerical simulations under Gaussian noise quantify the fidelity trade-offs as a function of code dimension. These results establish design principles for structured GKP codes suitable for scalable, interference-resilient quantum networking.

Results

In DV quantum information processing, crosstalk between spatial or spectral modes can be a major source of noise, if left untreated. When two modes undergo a mode mixing, information encoded in one mode will generally affect the other, leading to undesired logical errors. In this section, we show how such coupling–modeled as a passive linear interaction–can be made harmless by encoding the DV information into GKP code states. This allows us to multiplex quantum information in a crosstalk-robust manner. We refer the reader to Methods for clear overview of the tools used in this section.

Crosstalk-mitigated multiplexing via GKP encodings

We aim to determine conditions under which logical information in both GKP-encoded modes is preserved after the crosstalk transformation ${\hat{U}}_{\eta }$. Ideally, we require:

$$D(\eta ){\hat{U}}_{\eta }\left\vert {\lambda }_{A}\right\rangle \left\vert {\lambda }_{B}\right\rangle =\left\vert {\lambda }_{A}\right\rangle \left\vert {\lambda }_{B}\right\rangle$$

(1)

with D(η) would be a decoder depending on a priori knowledge of the average behavior of the stochastic η, or more generally, that the output remains within the original GKP code spaces up to correctable displacements. The main question is: for which pairs of lattices (f_A, g_A) and (f_B, g_B) is the logical subspace preserved under the mode-mixing crosstalk transformation ${\hat{U}}_{\eta }$? Equivalently, we ask: under what conditions does the joint stabilizer group transform into an equivalent stabilizer group (modulo correctable errors), such that the logical content in both modes is unaffected by crosstalk?

More precisely, let each mode’s GKP code be defined by stabilizer lattices ${\Lambda }_{A}={{\rm{Span}}}_{{\mathbb{Z}}}\{{{\boldsymbol{f}}}_{A},{{\boldsymbol{g}}}_{A}\}$ and ${\Lambda }_{B}={{\rm{Span}}}_{{\mathbb{Z}}}\{{{\boldsymbol{f}}}_{B},{{\boldsymbol{g}}}_{B}\}$. After undergoing crosstalk, these are mapped to new lattices ${\tilde{\Lambda }}_{A}$, ${\tilde{\Lambda }}_{B}$ with basis vectors $({\tilde{{\boldsymbol{f}}}}_{A},{\tilde{{\boldsymbol{g}}}}_{A})$ and $({\tilde{{\boldsymbol{f}}}}_{B},{\tilde{{\boldsymbol{g}}}}_{B})$, respectively. Logical preservation (up to correctable displacement) requires that the original stabilizer lattice be contained in the transformed one:

$${\Lambda }_{A}\subseteq {\tilde{\Lambda }}_{A},\quad {\Lambda }_{B}\subseteq {\tilde{\Lambda }}_{B},$$

and that any displacement incurred by the transformation lies within the correctable region—e.g., the Voronoi cell¹⁴–of the respective new lattices. Under these conditions, the logical subspace is preserved and can be recovered by standard GKP error correction and appropriate decoding.

The mode mixing crosstalk

In order to understand the effect of crosstalk on stabilizers of each mode, we should understand how generic displacement operators transform under this mode mixing model. The reason is that stabilizers of GKP codes are given in terms of displacement operators (see “Methods”). Under beamsplitter evolution, the product of displacements, each acting on its corresponding mode, transforms as:

$${\hat{U}}_{\eta }{T}_{1}(\alpha ){T}_{2}(\beta ){\hat{U}}_{\eta }^{\dagger }={T}_{1}\left(\sqrt{\eta }\alpha +\sqrt{1-\eta }\beta \right){T}_{2}\left(\sqrt{\eta }\beta -\sqrt{1-\eta }\alpha \right).$$

(2)

This reveals that displacements applied to one mode result in induced displacements on the other, as expected from a crosstalk mechanism. As a matter of fact, our goal is to find a way to absorb these induced displacements into the stabilizers of a code, such that the logical information remains unchanged. For instance, suppose we wish to transmit logical states encoded in mode 1 and mode 2, undergoing crosstalk, while both modes are initialized in a GKP codewords. In order to prevent the induced displacement from corrupting both modes, we aim to ensure that this displacement falls within the code’s stabilizer lattice.

Observation

If the second mode is initialized in a GKP code with stabilizers ${{\mathcal{S}}}_{2}=\langle {T}_{2}({{\bf{u}}}_{2}),{T}_{2}({{\bf{v}}}_{2})\rangle$, then any displacement of the form T₂(γ) with γ ∈ Λ₂ (the stabilizer lattice) acts trivially on the code space.

Now suppose we apply a displacement T₁(α) to mode 1. From equation (2), we notice that to ensure the induced displacement on mode 2 does not affect the output we require that:

$$\sqrt{1-\eta }\,\alpha =\sqrt{\eta }\beta \Rightarrow \quad \alpha =\frac{\sqrt{\eta }}{\sqrt{1-\eta }}{\boldsymbol{\beta }},\quad {\boldsymbol{\beta }}\in {\Lambda }_{2}.$$

(3)

The key point is that β was arbitrary in Λ₂, so if we define β to be one of the lattice vectors of the GKP code of mode 2 (u₂, v₂) then:

$${\tilde{{\bf{u}}}}_{1}=\sqrt{\frac{\eta }{1-\eta }}\,{{\bf{u}}}_{2},\quad {\tilde{{\bf{v}}}}_{1}=\sqrt{\frac{\eta }{1-\eta }}\,{{\bf{v}}}_{2}$$

(4)

then ${\tilde{{\bf{u}}}}_{1},{\tilde{{\bf{v}}}}_{1}$ generate a new lattice in mode 1, and any displacement in the group:

$$\Lambda ({\tilde{{\bf{u}}}}_{1},{\tilde{{\bf{v}}}}_{1}):= \{{T}_{1}(s{\tilde{{\bf{u}}}}_{1}+t{\tilde{{\bf{v}}}}_{1})\,| \,s,t\in {\mathbb{Z}}\}$$

(5)

can be realized through the beamsplitter interaction from mode 2.

Subsequently, investigate the effect of this transmofrmation of the symplectic form of the generators ${\tilde{{\bf{u}}}}_{1},{\tilde{{\bf{v}}}}_{1}$, assuming ω(u₂, v₂) = 2πd₂. Then:

$$\omega ({\tilde{{\bf{u}}}}_{1},{\tilde{{\bf{v}}}}_{1})=\left(\frac{\eta }{1-\eta }\right)\omega ({{\bf{u}}}_{2},{{\bf{v}}}_{2})=\frac{\eta }{1-\eta }\cdot 2\pi {d}_{2}.$$

In order to define a GKP code on mode 1 with stabilizer area ω = 2πd₁, the new lattice vectors ${\tilde{{\bf{u}}}}_{1},{\tilde{{\bf{v}}}}_{1}$ must satisfy:

$$\omega ({\tilde{{\bf{u}}}}_{1},{\tilde{{\bf{v}}}}_{1})=\frac{2\pi q}{p{d}_{1}},\quad {\rm{for}}\,{\rm{some}}\,p,q\in {\mathbb{Z}}.$$

Combining the expressions yields:

$$\frac{\eta }{1-\eta }\cdot 2\pi {d}_{2}=\frac{2\pi q}{p{d}_{1}}\quad \Rightarrow \quad \eta =\frac{q}{q+p{d}_{1}{d}_{2}}$$

(6)

This provides a discrete set of values for η where perfect GKP logical transmission is possible. We summarize this result below.

Theorem 1

(Perfect Transmission Under Crosstalk) Let two GKP codes ${{\mathcal{C}}}_{{S}_{1},{d}_{1}},{{\mathcal{C}}}_{{S}_{2},{d}_{2}}$ with stabilizer areas 2πd₁ and 2πd₂ be encoded in two bosonic modes undergoing crosstalk ${\hat{U}}_{\eta }$. Then there exists a choice of stabilizers for both codes such that the logical information is perfectly preserved if and only if:

$$\eta =\frac{q}{q+p{d}_{1}{d}_{2}},\quad q,p\in {\mathbb{Z}}.$$

The above implies a matching condition between the stabilizer lattices. In particular, if S₁ and S₂ are generator matrices for the two lattices, then they must be related by:

$${S}_{2}=\left(\begin{array}{cc}\sqrt{\frac{{p}_{2}{q}_{1}}{{p}_{1}{q}_{2}}}&0\\ 0&\sqrt{\frac{{q}_{1}{p}_{2}}{{p}_{2}{q}_{1}}}\end{array}\right){S}_{1},$$

under the constraint q = q₁q₂, p = p₁p₂. This guarantees that each logical mode’s stabilizers are compatible with the crosstalk pattern imposed by mode mixing. One may ask whether adapting the lattices to satisfy the matching condition sacrifices GKP code quality. Importantly, the total lattice area is preserved in the symplectic sense. However, individual codes may require rescaling — effectively increasing the physical extent of their stabilizer generators — to satisfy the rational compatibility constraint:

$$\omega (\tilde{{\boldsymbol{u}}},\tilde{{\boldsymbol{v}}})=\frac{2\pi q}{pd},\quad \,\text{with}\,\,d\in {\mathbb{Z}}.$$

To understand this constraint, we remind that displacement operators satisfy the canonical commutation relation:

$$\hat{T}({\boldsymbol{u}})\hat{T}({\boldsymbol{v}})={e}^{-i\omega ({\boldsymbol{u}},{\boldsymbol{v}})}\hat{T}({\boldsymbol{v}})\hat{T}({\boldsymbol{u}})$$

where ω(u, v) = u_qv_p − u_pv_q is the symplectic form. In a GKP code encoding a qudit of dimension d, the logical operators are chosen as ${\hat{X}}_{d}=\hat{T}({\boldsymbol{u}}/d),{\hat{Z}}_{d}=\hat{T}({\boldsymbol{v}}/d),$ and must obey the Weyl commutation relation:

$${\hat{Z}}_{d}{\hat{X}}_{d}={e}^{2\pi i/d}{\hat{X}}_{d}{\hat{Z}}_{d}$$

From the displacement algebra, we also have:

$${\hat{Z}}_{d}{\hat{X}}_{d}={e}^{i\omega ({\boldsymbol{u}},{\boldsymbol{v}})/{d}^{2}}{\hat{X}}_{d}{\hat{Z}}_{d}$$

For the two expressions to match, the symplectic area must satisfy:

$$\omega ({\boldsymbol{u}},{\boldsymbol{v}})=2\pi d$$

More generally, for a transformed lattice generated by $\tilde{{\boldsymbol{u}}},\tilde{{\boldsymbol{v}}}$, with logical operators ${\hat{X}}^{{\prime} }=\hat{T}(\tilde{{\boldsymbol{u}}}/d),{\hat{Z}}^{{\prime} }=\hat{T}(\tilde{{\boldsymbol{v}}}/d)$, one finds:

$${\hat{Z}}^{{\prime} }{\hat{X}}^{{\prime} }={e}^{i\omega (\tilde{{\boldsymbol{u}}},\tilde{{\boldsymbol{v}}})/{d}^{2}}{\hat{X}}^{{\prime} }{\hat{Z}}^{{\prime} }$$

To preserve the structure of the qudit Weyl algebra, this phase must again be a root of unity:

$$\frac{\omega (\tilde{{\boldsymbol{u}}},\tilde{{\boldsymbol{v}}})}{{d}^{2}}=\frac{2\pi q}{p}\quad \Rightarrow \quad \omega (\tilde{{\boldsymbol{u}}},\tilde{{\boldsymbol{v}}})=\frac{2\pi q}{pd},\quad p,q\in {\mathbb{Z}}$$

This condition ensures that the logical operators generate a finite-dimensional unitary representation of the Weyl algebra^22,23,24.

Output state structure

In what follows, we would like to understand the structure of the output states and their dependence on the crosstalk parameter in order to design a decoder that is able to retrieve meaningfully the encoded logical information. Accordingly, we analyze the output state resulting from sending two GKP codewords $\left\vert {\mu }_{1}\right\rangle \otimes \left\vert {\mu }_{2}\right\rangle$ where η is an appropriate rational number for the corresponding code dimensions as highlighted by equation (6). We characterize the structure of the output code, derive explicit expressions for the resulting quantum state, and interpret the emergence of a gauge subsystem both algebraically and operationally. Finally, we provide a decoding strategy to retrieve the logical information in the output states.

Code dimension after crosstalk coupling

Although Theorem 1 establishes when logical information is preserved under crosstalk by identifying suitable transmissivity values η, the following lemma refines this by characterizing the structure of the resulting output codes under these values. Specifically, it shows how the logical codes are embedded in higher-dimensional GKP spaces, quantifying the effective enlargement factor n = q + pd₁d₂.

Lemma 1

(Output Code Dimensions) Let the input GKP codes be ${{\mathcal{C}}}_{{S}_{1},{d}_{1}}$ and ${{\mathcal{C}}}_{{S}_{2},{d}_{2}}$. Then after crosstalk with η satisfying equation (6), the output state lies in the code basis:

$${{\mathcal{C}}}_{{S}_{3},n{d}_{1}}\otimes {{\mathcal{C}}}_{{S}_{4},n{d}_{2}},\quad \,{\text{with}}\,\,n=q+p{d}_{1}{d}_{2}.$$

(7)

and S₃, S₄ being the symplectic areas of the output codes.

Proof

Let the input GKP codes ${{\mathcal{C}}}_{{S}_{1},{d}_{1}}$ and ${{\mathcal{C}}}_{{S}_{2},{d}_{2}}$ be defined by stabilizer lattices with lattice vectors (u₁, v₁) and (u₂, v₂), satisfying:

$$\omega ({{\bf{u}}}_{1},{{\bf{v}}}_{1})=2\pi {d}_{1},\quad \omega ({{\bf{u}}}_{2},{{\bf{v}}}_{2})=2\pi {d}_{2}$$

(8)

These define the logical area of each code. Under the action of the crosstalk, displacement operators transform accrodign to equation (2). To preserve the GKP code structure under this transformation, the stabilizer displacements of one mode must map into stabilizer displacements of the other. A sufficient condition is equation (4) which shows that transformed stabilizers from mode 2 cancel displacements in mode 1, where $(\tilde{{\boldsymbol{u}}},\tilde{{\boldsymbol{v}}})$ denote the transformed stabilizer generators of mode 1 matching the condition in equation (3). The mode remains in a valid GKP code space only if the stabilizer lattice ${\Lambda }_{1}^{{\prime} }={{\rm{Span}}}_{{\mathbb{Z}}}\{\tilde{{\boldsymbol{u}}},\tilde{{\boldsymbol{v}}}\}$ contains a sublattice (u₁, v₁) such that:

$${\tilde{{\boldsymbol{u}}}}_{1}=\frac{{r}_{1}}{{d}_{1}}{{\boldsymbol{u}}}_{1}+{t}_{1}{{\boldsymbol{v}}}_{1},\quad {\tilde{{\boldsymbol{v}}}}_{1}=\frac{{r}_{2}}{{d}_{1}}{{\boldsymbol{v}}}_{1}+{t}_{2}{{\boldsymbol{u}}}_{1}$$

(9)

for integers r₁, r₂, t₁, t₂. That is, the logical shifts must lie in the 2D plane spanned by the transformed stabilizers. From equation (9), we note that, if we choose $\alpha ={p}_{1}{d}_{1}{\tilde{{\bf{u}}}}_{1}={q}_{1}{{\bf{u}}}_{1}$ and $\alpha ={p}_{2}{d}_{1}{\tilde{{\bf{v}}}}_{1}={q}_{2}{{\bf{v}}}_{1}$, and commuting the stabilizers accordign to equation (2), this results in the following relations:

$${u}_{3}=\frac{{q}_{1}{u}_{1}}{\sqrt{\eta }},\quad {u}_{4}=\frac{{q}_{2}{u}_{2}}{\sqrt{\eta }}$$

(10)

Together this yields that the area of the symplectic area S₃ of the output state is:

$${\omega }_{out,1}=\frac{q\omega ({{\bf{u}}}_{1},{{\bf{v}}}_{1})}{\eta }=2\pi n{d}_{1}$$

(11)

Applying the same logic to mode 2, we note that the output codes must have symplectic areas:

$${\omega }_{{\rm{out}},1}=2\pi n{d}_{1},\quad {\omega }_{{\rm{out}},2}=2\pi n{d}_{2},$$

(12)

corresponding to GKP codes ${{\mathcal{C}}}_{{S}_{3},n{d}_{1}}$ and ${{\mathcal{C}}}_{{S}_{4},n{d}_{2}}$. This completes the proof. □

The change of GKP lattices between the input and output following lattice matching conditions and equation (10) is schematized in Fig. 1.

Fig. 1

The effect of the crosstalk on the lattice area of the GKP codes in the (q₁, p₁) and (q₂, p₂) planes for GKP codes of dimensions d₁ = d₂ = 2 and crosstalk average $\eta =\frac{1}{3}$.

General output state derivation

Since we discovered that the output GKP codes live in a larger space scaled by the factor n = q + pd₁d₂, which results from the rational structure of the crosstalk parameter η, we have to investigate the structure of the output states in a proper basis.

Theorem 2

(General Output State) Let ${\alpha }_{1},{\alpha }_{2}\in {\mathbb{Z}}$ satisfy the Bézout identities:

$${\alpha }_{1}q+{\beta }_{1}p{d}_{1}{d}_{2}=1,\quad {\alpha }_{2}q+{\beta }_{2}p{d}_{1}{d}_{2}=1.$$

Then the output of the mode mixing U_η applied to the input state $\left\vert {\mu }_{1}\right\rangle \otimes \left\vert {\mu }_{2}\right\rangle$ is:

$$\left\vert {\mu }_{1},{\mu }_{2}\right\rangle =\frac{1}{\sqrt{n}}\mathop{\sum }\limits_{j=0}^{n-1}\left\vert {\mu }_{1}{\alpha }_{1}n+jp{d}_{1}{d}_{2}\right\rangle \otimes \left\vert {\mu }_{2}{\alpha }_{2}n+jq{d}_{2}\right\rangle ,$$

where the output states belong to ${{\mathcal{C}}}_{n{d}_{1}}\otimes {{\mathcal{C}}}_{n{d}_{2}}$.

Proof

We begin with input GKP codewords $\left\vert {\mu }_{1}\right\rangle \in {{\mathcal{C}}}_{{d}_{1}}$, $\left\vert {\mu }_{2}\right\rangle \in {{\mathcal{C}}}_{{d}_{2}}$, which can be formally written as superpositions over lattice displacements:

$$\left\vert {\mu }_{i}\right\rangle =\sum _{{s}_{i}\in {\mathbb{Z}}}{T}_{i}({s}_{i}{{\bf{u}}}_{i}+{\mu }_{i}{{\bf{u}}}_{i}/{d}_{i})\left\vert 0\right\rangle .$$

The logical operator ${\hat{X}}_{i}$ corresponds to a displacement T_i(u_i/d_i). Applying U_η to the tensor product of these two codewords yields:

$$\begin{array}{lll}\left\vert {\mu }_{1},{\mu }_{2}\right\rangle &=&{U}_{\eta }\left(\left\vert {\mu }_{1}\right\rangle \otimes \left\vert {\mu }_{2}\right\rangle \right)\\ &=&\mathop{\sum}\limits _{{s}_{1},{s}_{2}}{U}_{\eta }\left({T}_{1}({s}_{1}{{\bf{u}}}_{1}+{\mu }_{1}{{\bf{u}}}_{1}/{d}_{1})\right.\\&&\left.\otimes {T}_{2}({s}_{2}{{\bf{u}}}_{2}+{\mu }_{2}{{\bf{u}}}_{2}/{d}_{2})\right)\vert 0\rangle \vert 0\rangle.\end{array}$$

(13)

Using the transformation law under the beamsplitter:

$${U}_{\eta }{T}_{1}(\alpha ){T}_{2}(\beta ){U}_{\eta }^{\dagger }={T}_{1}(\sqrt{\eta }\alpha +\sqrt{1-\eta }\beta )\cdot {T}_{2}(\sqrt{\eta }\beta -\sqrt{1-\eta }\alpha ),$$

each term becomes:

$${T}_{1}({\lambda }_{1}({s}_{1},{s}_{2}))\cdot {T}_{2}({\lambda }_{2}({s}_{1},{s}_{2}))\left\vert 0,0\right\rangle ,$$

where the displacement vectors are:

$$\begin{array}{rcl}{\lambda }_{1}&=&\sqrt{\eta }({s}_{1}{{\bf{u}}}_{1}+{\mu }_{1}{{\bf{u}}}_{1}/{d}_{1})+\sqrt{1-\eta }({s}_{2}{{\bf{u}}}_{2}+{\mu }_{2}{{\bf{u}}}_{2}/{d}_{2}),\\ {\lambda }_{2}&=&\sqrt{\eta }({s}_{2}{{\bf{u}}}_{2}+{\mu }_{2}{{\bf{u}}}_{2}/{d}_{2})-\sqrt{1-\eta }({s}_{1}{{\bf{u}}}_{1}+{\mu }_{1}{{\bf{u}}}_{1}/{d}_{1}).\end{array}$$

and $\left\vert 0,0\right\rangle ={U}_{\eta }\left\vert 0\right\rangle \left\vert 0\right\rangle$. Simplifying the displacement vectors, we noted previously that the stabilizer lattice vector of the outputs are

$${{\rm{u}}}_{3}=\frac{{q}_{1}{{\rm{u}}}_{1}}{\eta }\quad {{\rm{u}}}_{4}=\frac{{q}_{2}{{\rm{u}}}_{2}}{\eta }$$

(14)

and that:

$$\sqrt{1-\eta }{{\bf{u}}}_{2}==\frac{1-\eta }{\eta }\frac{{q}_{1}}{{d}_{1}{p}_{1}}{{\bf{u}}}_{1}$$

(15)

we arrive at:

$${\lambda }_{1}={q}_{1}{\mu }_{1}\frac{{{\bf{u}}}_{3}}{nd1}+{p}_{2}{d}_{1}{\mu }_{2}\frac{{{\bf{u}}}_{3}}{nd1}$$

(16)

$${\lambda }_{2}={q}_{2}{\mu }_{2}\frac{{{\bf{u}}}_{4}}{nd2}-{p}_{1}{d}_{2}{\mu }_{1}\frac{{{\bf{u}}}_{4}}{nd2}$$

(17)

with the same relations and with the use of the fact that the output GKP states are considered mod n and mod n, we obtain the output vacuum state in terms of the basis vectors $\left\vert {\mu }_{3}\right\rangle$ and $\left\vert {\mu }_{4}\right\rangle$ as:

$$\left\vert 0,0\right\rangle =\mathop{\sum }\limits_{j=0}^{n-1}\left\vert jp{d}_{1}{d}_{2}\right\rangle \left\vert j{d}_{2}q\right\rangle$$

(18)

Applying the necessary translations with vectors in equation (17), we obtain:

$$\left\vert {\mu }_{1},{\mu }_{2}\right\rangle =\mathop{\sum }\limits_{j=0}^{n-1}\left\vert {q}_{1}{\mu }_{1}+{p}_{2}{d}_{1}{\mu }_{2}+jp{d}_{1}{d}_{2}\right\rangle \left\vert {q}_{2}{\mu }_{2}-{p}_{1}{d}_{2}{\mu }_{1}+j{d}_{2}q\right\rangle$$

(19)

considering the states now are left mod d₁ and mod d₂ respectively, and using the Diophantine equations:

$${\alpha }_{i}q+{\beta }_{i}p{d}_{1}{d}_{2}=1,$$

so that ${\mu }_{i}{\alpha }_{i}n\equiv {\mu }_{i}\,{\mathrm{mod}}\,\,{d}_{i}$ We get:

$$\left\vert {\mu }_{1},{\mu }_{2}\right\rangle =\frac{1}{\sqrt{n}}\mathop{\sum }\limits_{j=0}^{n-1}\left\vert {\mu }_{1}{\alpha }_{1}n+jp{d}_{1}{d}_{2}\right\rangle \otimes \left\vert {\mu }_{2}{\alpha }_{2}n+jq{d}_{2}\right\rangle ,$$

which proves the theorem.

This specific structure ensures that the logical information (μ₁, μ₂) is encoded into distinct cosets in the enlarged lattices. It also ensures that the index j sweeps over the gauge orbit corresponding to a subgroup of the full lattice that does not alter the logical labels. □

We note that the enlargement of the stabilizer lattices introduces a gauge degree of freedom that increases the size of the decoding space. While the logical subspace remains of dimension d₁ × d₂, the physical lattice now supports n gauge cosets, which can increase decoding complexity. In particular, minimum distance decoding must resolve among n degenerate candidates, potentially raising the complexity from ${\mathcal{O}}(d)$ to ${\mathcal{O}}(n\cdot d)$ in the worst case. This overhead is mitigated if gauge fixing is applied prior to logical decoding, as will be discussed subsequentely.

Corollary 1

(Symmetric Case) In the symmetric setting where d₁ = d₂ = d, q₁ = q₂ = 1, p₁ = p₂ = 1, and α₁ = α₂ = 1, the output simplifies to:

$$\left\vert {\mu }_{1},{\mu }_{2}\right\rangle =\frac{1}{\sqrt{n}}\mathop{\sum }\limits_{j=0}^{n-1}\left\vert {\mu }_{1}n+j{d}^{2}\right\rangle \otimes \left\vert {\mu }_{2}n+jd\right\rangle .$$

Proof

We consider the general output state from the previous theorem:

$$\left\vert {\mu }_{1},{\mu }_{2}\right\rangle =\frac{1}{\sqrt{n}}\mathop{\sum }\limits_{j=0}^{n-1}\left\vert {\mu }_{1}{\alpha }_{1}n+j{p}_{2}{d}_{1}{d}_{2}\right\rangle \otimes \left\vert {\mu }_{2}{\alpha }_{2}n+j{q}_{1}{d}_{2}\right\rangle ,$$

and impose the symmetric assumptions:

$${d}_{1}={d}_{2}=d,\quad {q}_{1}={q}_{2}=1,\quad {p}_{1}={p}_{2}=1,\quad {\alpha }_{1}={\alpha }_{2}=1.$$

Under these conditions, we substitute:

$${p}_{2}{d}_{1}{d}_{2}={d}^{2},\quad {q}_{1}{d}_{2}=d,\quad {\alpha }_{1}n={\alpha }_{2}n=n.$$

Then the expression becomes:

$$\left\vert {\mu }_{1},{\mu }_{2}\right\rangle =\frac{1}{\sqrt{n}}\mathop{\sum }\limits_{j=0}^{n-1}\left\vert {\mu }_{1}n+j{d}^{2}\right\rangle \otimes \left\vert {\mu }_{2}n+jd\right\rangle .$$

This is a superposition over n values, with step size d in both modes, and offsets determined by μ₁, μ₂, each scaled by n, consistent with embedding the logical indices into ${{\mathcal{C}}}_{nd}\otimes {{\mathcal{C}}}_{nd}$. Thus, the output state lies in ${{\mathcal{C}}}_{nd}\otimes {{\mathcal{C}}}_{nd}$ and has the simplified form claimed. □

Gauge degrees of freedom and symmetry

In order to retrieve the logical information encoded in the GKP codes, we would like to understand the possibility of decoupling the logical degrees of freedom from the gauge degrees of freedom, to be able to retrieve the logical information witout any gauge coupling.

Theorem 3

(Gauge Subsystem Structure) The output state $\left\vert {\mu }_{1},{\mu }_{2}\right\rangle$ admits a factorization of the form:

$$\left\vert {\mu }_{1},{\mu }_{2}\right\rangle ={\left\vert {\mu }_{1},{\mu }_{2}\right\rangle }_{L}\otimes {\left\vert {\Phi }_{n}\right\rangle }_{G},$$

where:

${\left\vert {\mu }_{1},{\mu }_{2}\right\rangle }_{L}$ encodes the logical state in ${{\mathcal{H}}}_{{d}_{1}}\otimes {{\mathcal{H}}}_{{d}_{2}}$,

$\left\vert {\Phi }_{n}\right\rangle =\frac{1}{\sqrt{n}}\mathop{\sum }\nolimits_{j = 0}^{n-1}\left\vert j\right\rangle \otimes \left\vert j\right\rangle$ is a maximally entangled state in the gauge subsystem ${{\mathcal{H}}}_{n}\otimes {{\mathcal{H}}}_{n}$,

The decomposition holds: ${{\mathcal{C}}}_{n{d}_{1}}\otimes {{\mathcal{C}}}_{n{d}_{2}}\cong {{\mathcal{H}}}_{{d}_{1}}\otimes {{\mathcal{H}}}_{n}\otimes {{\mathcal{H}}}_{{d}_{2}}\otimes {{\mathcal{H}}}_{n}$.

Proof

We start with the general form of the output state derived in the previous theorem:

$$\left\vert {\mu }_{1},{\mu }_{2}\right\rangle =\frac{1}{\sqrt{n}}\mathop{\sum }\limits_{j=0}^{n-1}\left\vert {\mu }_{1}{\alpha }_{1}n+j{p}_{2}{d}_{1}{d}_{2}\right\rangle \otimes \left\vert {\mu }_{2}{\alpha }_{2}n+j{q}_{1}{d}_{2}\right\rangle ,$$

with all terms in the Hilbert space ${{\mathcal{C}}}_{n{d}_{1}}\otimes {{\mathcal{C}}}_{n{d}_{2}}$, which has total dimension nd₁ × nd₂.

We aim to show that this state admits a decomposition into a logical component and a gauge-entangled component. To do so, we define a bijective relabeling of the basis of ${{\mathcal{C}}}_{n{d}_{i}}\cong {{\mathcal{H}}}_{{d}_{i}}\otimes {{\mathcal{H}}}_{n}$ via the map:

$${\mu }_{i}{\alpha }_{i}n+j{r}_{i}\!\!\longmapsto {\left\vert {\mu }_{i}\right\rangle }_{L}\otimes {\left\vert j\right\rangle }_{G},$$

where r₁ = p₂d₁d₂, r₂ = q₁d₂, and $j\in {{\mathbb{Z}}}_{n}$. This map is well-defined because the terms μ_iα_in span a sublattice of spacing n, and the shifts jr_i span cosets within that lattice, labeling the gauge degree of freedom.

We now define a new basis for the enlarged code space:

$$\left\vert {\mu }_{i}n+j{r}_{i}\right\rangle \equiv {\left\vert {\mu }_{i}\right\rangle }_{L}\otimes {\left\vert j\right\rangle }_{G},$$

so that the full state becomes:

$$\left\vert {\mu }_{1},{\mu }_{2}\right\rangle =\frac{1}{\sqrt{n}}\mathop{\sum }\limits_{j=0}^{n-1}{\left\vert {\mu }_{1}\right\rangle }_{L}\otimes {\left\vert j\right\rangle }_{G}\otimes {\left\vert {\mu }_{2}\right\rangle }_{L}\otimes {\left\vert j\right\rangle }_{G}.$$

Regrouping:

$$\left\vert {\mu }_{1},{\mu }_{2}\right\rangle =\left({\left\vert {\mu }_{1}\right\rangle }_{L}\otimes {\left\vert {\mu }_{2}\right\rangle }_{L}\right)\otimes \left(\frac{1}{\sqrt{n}}\mathop{\sum }\limits_{j=0}^{n-1}\left\vert j\right\rangle \otimes \left\vert j\right\rangle \right).$$

We identify the first tensor factor as the logical state ${\left\vert {\mu }_{1},{\mu }_{2}\right\rangle }_{L}\in {{\mathcal{H}}}_{{d}_{1}}\otimes {{\mathcal{H}}}_{{d}_{2}}$, and the second factor as a maximally entangled Bell-like state $\left\vert {\Phi }_{n}\right\rangle \in {{\mathcal{H}}}_{n}\otimes {{\mathcal{H}}}_{n}$, defined by:

$$\left\vert {\Phi }_{n}\right\rangle =\frac{1}{\sqrt{n}}\mathop{\sum }\limits_{j=0}^{n-1}\left\vert j\right\rangle \otimes \left\vert j\right\rangle .$$

Therefore, the state admits a decomposition:

$$\left\vert {\mu }_{1},{\mu }_{2}\right\rangle ={\left\vert {\mu }_{1},{\mu }_{2}\right\rangle }_{L}\otimes {\left\vert {\Phi }_{n}\right\rangle }_{G},$$

and the total space decomposes as:

$${{\mathcal{C}}}_{n{d}_{1}}\otimes {{\mathcal{C}}}_{n{d}_{2}}\cong {{\mathcal{H}}}_{{d}_{1}}\otimes {{\mathcal{H}}}_{n}\otimes {{\mathcal{H}}}_{{d}_{2}}\otimes {{\mathcal{H}}}_{n}.$$

□

Lemma 2

(Symmetry Origin of Gauge Subsystem) The gauge subsystem arises from the residual symmetry induced by the mode mixing on the stabilizer structure. Define the input stabilizer lattices Λ₁, Λ₂ and let Λ_logical ⊂ Λ₁ ⊕ Λ₂ denote the sublattice that preserves logical equivalence. Then:

$$G=({\Lambda }_{1}\oplus {\Lambda }_{2})/{\Lambda }_{{{logical}}}$$

is a finite Abelian group of order n acting on the gauge index j. This symmetry results in maximal entanglement between the gauge subsystems.

Proof

Let ${\Lambda }_{1},{\Lambda }_{2}\subset {{\mathbb{R}}}^{2}$ be the input stabilizer lattices of the two GKP codes ${{\mathcal{C}}}_{{d}_{1}}$ and ${{\mathcal{C}}}_{{d}_{2}}$. These lattices are generated by primitive vectors (u₁, v₁), (u₂, v₂) satisfying symplectic conditions:

$$\omega ({{\bf{u}}}_{1},{{\bf{v}}}_{1})=2\pi {d}_{1},\quad \omega ({{\bf{u}}}_{2},{{\bf{v}}}_{2})=2\pi {d}_{2}.$$

The stabilizer group of the joint system is Λ₁ ⊕ Λ₂, i.e., the product lattice of displacements acting on both modes.

When the two modes interact through a crosstalk U_η, the phase-space coordinates transform linearly:

$$({\xi }_{1},{\xi }_{2})\,\mapsto \left(\sqrt{\eta }{\xi }_{1}+\sqrt{1-\eta }{\xi }_{2},\,\sqrt{\eta }{\xi }_{2}-\sqrt{1-\eta }{\xi }_{1}\right).$$

This transformation mixes the lattices Λ₁, Λ₂ into a coupled sublattice in ${{\mathbb{R}}}^{4}$, generating new displacement operators acting nontrivially across both modes. However, not all elements of Λ₁ ⊕ Λ₂ map to distinct logical states in the output code. There exists a sublattice Λ_logical ⊂ Λ₁ ⊕ Λ₂ consisting of those displacement combinations that ct trivially on the logical space, i.e., leave logical states invariant up to stabilizer equivalence, and that commute with the logical operators of the output code ${{\mathcal{C}}}_{n{d}_{1}}\otimes {{\mathcal{C}}}_{n{d}_{2}}$. Hence, the quotient group

$$G=({\Lambda }_{1}\oplus {\Lambda }_{2})/{\Lambda }_{{\rm{logical}}}$$

classifies the inequivalent cosets of logical actions modulo stabilizer redundancy. By construction, G is a finite Abelian group. Its order is given by:

$$| G| =\frac{{\rm{Vol}}({\Lambda }_{{\rm{logical}}})}{{\rm{Vol}}({\Lambda }_{1}\oplus {\Lambda }_{2})}=n,$$

since the logical lattice scales by a factor of n due to the mode mixing-induced enlargement of the stabilizer unit cell (as previously shown in the output code dimension lemma). This finite group G acts transitively on the label j that indexes the gauge orbit in the output state:

$$\left| {\mu }_{1},{\mu }_{2}\right\rangle =\frac{1}{\sqrt{n}}\mathop{\sum }\limits_{j=0}^{n-1}\left| {\mu }_{1}^{(j)}\right\rangle \otimes \left| {\mu }_{2}^{(j)}\right\rangle .$$

Thus, the existence of the gauge subsystem arises from this residual symmetry: different elements of the quotient G correspond to gauge-equivalent configurations of logical information that are indistinguishable by any logical observable. The entanglement of the gauge subsystems reflects the nontrivial correlation between these symmetry orbits across both modes. □

Gauge fixing and logical recovery

Having the output state depending on the gauge degrees of freedom, does not allow for perfect recovery of the logical information unless the gauge is fixed and then is collapsed to one of its orbits. In what follows we provide an existence argument of such gauge fixing decoder.

Theorem 4

(Gauge Fixing Procedure) Let $\vert {\psi }_{{\mu }_{1},{\mu }_{2}}\rangle$ be the output state as above. Then there exists a unitary U_gauge-fix acting on ${{\mathcal{C}}}_{n{d}_{1}}\otimes {{\mathcal{C}}}_{n{d}_{2}}$ such that:

$${U}_{{\rm{gauge}}\text{-}{\rm{fix}}}\left\vert {\psi }_{{\mu }_{1},{\mu }_{2}}\right\rangle =\left\vert {\mu }_{1}\right\rangle \otimes \left\vert {\mu }_{2}\right\rangle \otimes {\left\vert 0\right\rangle }_{G},$$

where $\left\vert {\mu }_{1}\right\rangle ,\left\vert {\mu }_{2}\right\rangle$ are logical states in ${{\mathcal{C}}}_{{d}_{1}},{{\mathcal{C}}}_{{d}_{2}}$, and ${\left\vert 0\right\rangle }_{G}$ is a fixed state in the gauge register. The unitary U_gauge-fix is constructible from modular arithmetic operations and GKP logical Clifford gates (e.g., modular multiplication, modular subtraction, controlled shift).

Proof

We begin with the output state of the form derived earlier:

$$\left\vert {\psi }_{{\mu }_{1},{\mu }_{2}}\right\rangle =\frac{1}{\sqrt{n}}\mathop{\sum }\limits_{j=0}^{n-1}\left\vert {\mu }_{1}{\alpha }_{1}n+j{r}_{1}\right\rangle \otimes \left\vert {\mu }_{2}{\alpha }_{2}n+j{r}_{2}\right\rangle ,$$

where r₁ = p₂d₁d₂, r₂ = q₁d₂, and ${\alpha }_{i}\in {\mathbb{Z}}$ satisfy the Bézout identities. This state lies in the Hilbert space ${{\mathcal{C}}}_{n{d}_{1}}\otimes {{\mathcal{C}}}_{n{d}_{2}}$, which we know decomposes as:

$${{\mathcal{C}}}_{n{d}_{1}}\otimes {{\mathcal{C}}}_{n{d}_{2}}\cong {{\mathcal{H}}}_{{d}_{1}}\otimes {{\mathcal{H}}}_{n}\otimes {{\mathcal{H}}}_{{d}_{2}}\otimes {{\mathcal{H}}}_{n}.$$

We aim to apply a unitary transformation U_gauge-fix that maps the entangled gauge part into a separable form and re-expresses the state as:

$$\left\vert {\mu }_{1}\right\rangle \otimes \left\vert {\mu }_{2}\right\rangle \otimes {\left\vert 0\right\rangle }_{G}.$$

To construct this unitary, observe that the terms μ₁α₁n + jr₁ index states of the form:

$${\left\vert {\mu }_{1}\right\rangle }_{L}\otimes {\left\vert j\right\rangle }_{G},$$

under the identification:

$${\left\vert {\mu }_{1}\right\rangle }_{L}=\left\vert {\mu }_{1}{\alpha }_{1}n\,\,{\mathrm{mod}}\,\,n{d}_{1}\right\rangle ,\quad {\left\vert j\right\rangle }_{G}=\left\vert j{r}_{1}\,\,{\mathrm{mod}}\,\,n{d}_{1}\right\rangle .$$

Hence, the full state is:

$$\left\vert {\psi }_{{\mu }_{1},{\mu }_{2}}\right\rangle ={\left\vert {\mu }_{1}\right\rangle }_{L}\otimes {\left\vert {\mu }_{2}\right\rangle }_{L}\otimes \left(\frac{1}{\sqrt{n}}\mathop{\sum }\limits_{j=0}^{n-1}{\left\vert j\right\rangle }_{G}\otimes {\left\vert j\right\rangle }_{G}\right).$$

Define the unitary U_gauge-fix as follows:

Apply modular inverse multiplication: $j\,\mapsto {r}_{i}^{-1}j\,{\mathrm{mod}}\,\,n$, to bring gauge indices into canonical form 0, 1, …, n − 1,

Use a controlled modular subtraction to align both gauge indices,

Shift the gauge register into a basis where $\left\vert j\right\rangle \otimes \left\vert j\right\rangle \mapsto \left\vert 0\right\rangle \otimes \left\vert j\right\rangle$,

Then discard (or reinitialize) the second register.

All these operations can be constructed from GKP logical Clifford unitaries:

Modular multiplication and inverses can be implemented via shift and scaling gates,

Controlled modular subtraction is a Clifford operation on GKP codes,

Basis change from entangled to separable form is equivalent to a Bell-to-product basis transformation.

After applying U_gauge-fix, we obtain:

$${U}_{{\rm{gauge}}\text{-}{\rm{fix}}}\left\vert {\psi }_{{\mu }_{1},{\mu }_{2}}\right\rangle =\left\vert {\mu }_{1}\right\rangle \otimes \left\vert {\mu }_{2}\right\rangle \otimes {\left\vert 0\right\rangle }_{G},$$

with ${\left\vert 0\right\rangle }_{G}$ a fixed state (e.g., the zero state in the canonical basis of ${{\mathcal{H}}}_{n}$). □

Operational construction of the decoder

A summary of an operational construction of the decoder, for gauge fixing the output state to recover the logical state, is highlighted in Fig. 2, and is given as follows:

Fig. 2: The gauge fixing decoder.

A logical Controlled-X gate is applied to the ancillary mode, followed by measurement in the logical Z basis. The gauge parameter is estimated mod-n and a logical inverse gate map is applied to the target mode to retrieve the logical state without gauge coupling.

Ancilla Preparation: Initialize two ancillary GKP modes, each with Hilbert space dimension nd₁ and nd₂, respectively, in the logical vacuum state $\left\vert 0\right\rangle$.

Entangling Coupling: Apply modular controlled-X (CX) gates from each output mode to its respective ancilla. These gates act as ${\mathsf{\text{CX}}}:\left\vert x\right\rangle \left\vert 0\right\rangle \mapsto \left\vert x\right\rangle \left\vert x\right\rangle \,\mathrm{mod}\,\,n{d}_{i}$, entangling the mode and ancilla. The shared gauge index j is thus encoded redundantly in both ancillas.

Measurement: Measure the ancillas in the computational basis, yielding outcomes:

$$x={\mu }_{1}{\alpha }_{1}n+j{r}_{1},\quad y={\mu }_{2}{\alpha }_{2}n+j{r}_{2}$$

modulo nd₁ and nd₂, respectively. These results reveal the value of the gauge index $j\,{\mathrm{mod}}\,\,n$ via modular inversion:

$$j=x\cdot {r}_{1}^{-1}\,{\mathrm{mod}}\,\,n=y\cdot {r}_{2}^{-1}\,{\mathrm{mod}}\,\,n$$

since gcd(r₁, n) = gcd(r₂, n) = 1 by construction, hence this is a physical unitary gate.

Feedback Correction: Apply modular displacement gates (logical $\bar{X}$ or $\bar{Z}$) to the output modes, conditioned on the measured value of j. These correct for the gauge entanglement, mapping:

$$\left\vert {\mu }_{1}{\alpha }_{1}n+j{r}_{1}\right\rangle \,\mapsto\, \left\vert {\mu }_{1}{\alpha }_{1}n\right\rangle ,\quad \left\vert {\mu }_{2}{\alpha }_{2}n+j{r}_{2}\right\rangle \,\mapsto\, \left\vert {\mu }_{2}{\alpha }_{2}n\right\rangle$$

This is equivalent to applying a modular shift $-j{r}_{i}\,\mathrm{mod}\,\,n{d}_{i}$, which is a GKP logical Clifford operation.

Gauge Reset: After correction, the ancillas are disentangled from the logical system. They can be reinitialized to $\left\vert 0\right\rangle$, discarded, or traced out. The logical state is now in canonical form.

This sequence constitutes an operational realization of the unitary gauge-fixing map U_gauge-fix, acting unitarily and reversibly on the joint system, up to classical feedforward corrections based on the gauge index j. It is worth-noting that the above gauge-fixing protocol assumes that the receiver knows the gauge dimension n, which depends on the rational structure of the average mode-mixing strength η, but no information on the stochastic crosstalk behavior. In scenarios without channel state information (CSI), this value is unknown, and modular inversion or correction cannot be deterministically applied. Therefore, this decoding method is valid in the with-CSI regime. Extending gauge correction to the no-CSI setting would require adaptive or statistical decoding strategies beyond the scope of this paper.

Discussion

In what follows, we illustrate the practical implications of the multiplexing structure and rational transmissivity conditions by computing fidelity upper bounds for finite-energy GKP states under cross-talk and Gaussian noise. We consider a scenario where two independent GKP encoded EPR pairs prepared in parallel: one between parties A and A’, and the other between B and B’. Each half-pair, A’ and B’, is transmitted through a shared channel with passive crosstalk with parameter $\eta =\frac{q}{q+p{d}^{2}}$. The other halves, A and B, are held locally. The scenario is illustrated in Fig. 3

Fig. 3: The scheme considered for the simulation.

We consider transmitted GKP encoded EPR shares $\left\vert {\mu }_{1}\right\rangle$ and $\left\vert {\mu }_{2}\right\rangle$ affected by crosstalk modeled by a beam splitter of transmitivity η. The two modes then are affected by displacement gaussian noise. Upon reception, an ideal disjoint decoding scheme as described in the text, tracing out the gauge degrees of freedom, is applied.

The joint state before transmission is:

$$\left\vert \Psi \right\rangle =\frac{1}{2}\mathop{\sum }\limits_{\mu ,\nu =0}^{1}{\left\vert \mu \right\rangle }_{A}\otimes {\left\vert \mu \right\rangle }_{{A}^{{\prime} }}\otimes {\left\vert \nu \right\rangle }_{B}\otimes {\left\vert \nu \right\rangle }_{{B}^{{\prime} }}.$$

After encoding and crosstalk interaction, the transmitted shares transform as:

$$\left\vert \mu ,\nu \right\rangle =\frac{1}{\sqrt{n}}\mathop{\sum }\limits_{j=0}^{n-1}{\left\vert n\mu +j{r}_{1}\right\rangle }_{{A}^{{\prime} }}\otimes {\left\vert n\nu +j{r}_{2}\right\rangle }_{{B}^{{\prime} }},$$

where r₁ = p₂d₁d₂, r₂ = q₁d₂, and α₁ = α₂ = 1. For example, with d₁ = d₂ = 2, $\eta =\frac{1}{5}$, n = 5, the output becomes:

$${\left\vert \Psi \right\rangle }_{{\rm{after}}}=\frac{1}{2\sqrt{5}}\mathop{\sum }\limits_{\mu ,\nu =0}^{1}\mathop{\sum }\limits_{j=0}^{4}{\left\vert \mu \right\rangle }_{A}\otimes {\left\vert \nu \right\rangle }_{B}\otimes {\left\vert 5\mu +4j\right\rangle }_{{A}^{{\prime} }}\otimes {\left\vert 5\nu +2j\right\rangle }_{{B}^{{\prime} }}.$$

We assume a standard GKP error model where noise acts via random phase-space displacements drawn from an isotropic Gaussian distribution. A single-mode displacement noise channel with variance σ² is modeled as:

$$\rho \to \int\,P(\alpha )D(\alpha )\rho {D}^{\dagger }(\alpha )d\alpha$$

(20)

with the Gaussian distribution for the displacement channel given by:

$$P(\alpha )=\frac{1}{\sqrt{2\pi {\sigma }^{2}}}{e}^{-\frac{{\alpha }^{2}}{2{\sigma }^{2}}}$$

(21)

This model captures thermal or stochastic noise affecting position and momentum symmetrically, and is appropriate for modeling finite-energy GKP states under Gaussian channels.

Assuming exact rational transmissivity (i.e., perfect lattice matching), the decoding fidelity for a single GKP mode under Gaussian noise is the probability that the displacement remains within the Voronoi cell of the nearest lattice point. For square GKP lattices, this leads to:

$${F}_{{\rm{single}}}(\sigma ,d)={\rm{erf}}{\left(\sqrt{\frac{\pi }{2d{\sigma }^{2}}}\right)}^{2}.$$

For a two-mode product GKP code ${{\mathcal{C}}}_{{d}_{1}}\otimes {{\mathcal{C}}}_{{d}_{2}}$, the joint fidelity is simply the square of the individual success probabilities:

$${F}_{{\rm{ideal}}}(\sigma ;{d}_{1},{d}_{2})={\left[{\rm{erf}}\left(\sqrt{\frac{\pi }{2{d}_{1}{\sigma }^{2}}}\right)\cdot {\rm{erf}}\left(\sqrt{\frac{\pi }{2{d}_{2}{\sigma }^{2}}}\right)\right]}^{2}.$$

This expression assumes ideal (infinite-energy) GKP decoding in the absence of lattice mismatches.

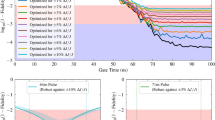
In Fig. 4, the fidelity landscape as function of η and noise Level σ is given. We compute an upper bound on the entanglement fidelity F_e(η, σ²) of the GKP code under Gaussian noise and cross-talk, where rational transmissivity points of the form $\eta =\frac{q}{q+p{d}_{1}{d}_{2}}$ are expected to support exact code embedding. The effective fidelity is bounded by:

$${F}_{e}(\eta ,{\sigma }^{2})\le \mathop{\max }\limits_{{\eta }_{i}}\exp \left(-\frac{\delta {(\eta ,{\eta }_{i})}^{2}}{2{\sigma }^{2}}\right){F}_{{\rm{ideal}}}(\sigma ),$$

where δ(η, η_i) = η − η_i∣L is the geometric mismatch between the actual η and rational alignment points η_i, scaled by a lattice parameter L. The color plot is produced across a grid of η and σ, with bright bands indicating regions of high-fidelity transmission centered around rational η-values, with exponential decay in the neighberhood of each peak. In comparison to non-encoded EPR pairs in Fig. 5, we notice that bosonic encoding of EPR pairs via GKP codes improve drastically the fidelity of entanglement multiplexing in the presence of mode mixing crosstalk (XX coupling between polarization encoded EPR’s), especially when the mixing is maximal around η = 0.5.

Fig. 4: Upper bound on the entangleemnt fidelity for GKP-encoded EPR pairs transmission over mode mixing crosstalk with transmissivity η and dipslacement Gaussian noise of variance σ.

The plot assumes square GKP codes and dimensions d₁ = d₂ = 2 and σ_c = 0.4.

Fig. 5: Entanglement fidelity of two polarization encoded EPR pairs under crosstalk and depolarizing noise.

The tranmitted shares of the EPR pairs interact via a coherent XX coupling with strength controlled by parameter η.

Figure 6, a simulation of the trade-off between code dimension and fidelity was carried. We fix a rational alignment $\eta =\frac{q}{q+p{d}^{2}}$ with d = d₁ = d₂, and explore the decay in entanglement fidelity F_e as d increases. The fidelity decays with increasing code dimension due to reduced spacing between lattice points and increased sensitivity to noise. Each curve corresponds to a fixed noise level σ, and rational transmissivity points η(d) are annotated for interpretation. Polynomial fits highlight smooth decay behavior, illustrating the trade-off between code rate (larger d) and achievable fidelity.

Fig. 6

The rate-fidelity tradeoff.

These simulations confirm the analytical expectations that high-fidelity code transmission occurs near rational values of η, consistent with the gauge-based embedding theory. The numeric exploration also shows how fidelity decreases with code size due to practical effects of Gaussian noise, emphasizing the role of rational η tuning and finite squeezing in real devices. We note that for both simulations, the ideal decoder from the previous section was considered, which is not optimal in the presence of displacement gaussian noise.

To summarize, we have presented a framework for mitigating crosstalk in multiplexed quantum communication systems using GKP encoding. By embedding DV quantum information into CV modes, we identified precise lattice-matching conditions under which logical information can be preserved despite mode-mixing interactions. A key result is the identification of rational transmissivity values that allow the joint stabilizer structure to be preserved, enabling crosstalk-immune communication. Our work establishes a foundation for crosstalk-aware encoding in quantum networks based on CV hardware and opens up new directions in entanglement distribution through structured code design. Importantly, the principles and techniques developed here for crosstalk-resilient multiplexing are directly applicable to the development of robust Quantum MIMO communication systems, which are critical for future high-capacity quantum networks. Additionally, we proposed an explicit decoder that leverages the symplectic structure of the output state, decomposes it into logical and gauge components, and applies a modular arithmetic-based recovery procedure. While this decoder is effective in idealized conditions, it is suboptimal in the presence of Gaussian displacement noise and stochasticity of the crosstalk.

Future work will investigate optimized decoding strategies that account for physical noise models, including error rates and channel-specific distortions, particularly within the context of Quantum MIMO channels. In particular, we aim to adapt the decoder to scenarios with no CSI, where the average mode mixing η is unknown. Such robust decoding would enable practical implementation of GKP-based crosstalk mitigation in dynamic network environments and pave the way for truly scalable Quantum MIMO communications. We also plan to explore the direct application of these crosstalk mitigation strategies in full Quantum MIMO architectures, including the optimization of encoding and decoding schemes for multiple spatial modes.

Specifically, the proposed framework for crosstalk-resilient GKP encoding and decoding has potential applications in advanced quantum communication systems. In multicarrier CVQKD scenarios, such as those described in refs. ^25,26, the use of multiple bosonic modes with orthogonal or partially overlapping spectral-temporal support introduces natural cross-mode interactions. Our method could be used to protect quantum information across such multi-carrier structures, improving the stability and scalability of secret key generation. Furthermore, in the context of the quantum internet, where quantum information must traverse large-scale networks with imperfect isolation between channels, our approach may support modular quantum repeaters or MIMO-like quantum transceivers that manage interference while maintaining high logical fidelity. These directions motivate future work on integrating our decoder into practical error correction and channel estimation pipelines.

Moreover, our proposed scheme marks an important step toward realizing scalable and resilient quantum repeater networks, a foundational requirement for the quantum internet. By mitigating both loss-induced degradation and inter-mode crosstalk, our framework ensures that high-fidelity logical information can be transmitted even in dense multiplexed settings. This resilience is particularly crucial for enabling parallel entanglement distribution across large-scale networks⁷, where uncontrolled interference would otherwise be a major bottleneck. In this sense, our results not only establish a coding-theoretic foundation for robust Quantum MIMO but also directly contribute to the design of modular, fault-tolerant quantum repeaters. Looking ahead, extending this framework to fully all-photonic repeater architectures based on GKP codes could provide a powerful path to long-distance, hardware-efficient quantum communication. Such advances would consolidate the role of GKP encodings as a unifying bridge between discrete-variable protocols and continuous-variable hardware, further accelerating progress toward a practical quantum internet^27,28.

Methods

Here we give an overview of the main techniques used to establish our results.

GKP States and logical encoding

Here, we introduce our notations and the GKP states. For a bosonic mode with creation and annihilation operators $\hat{a}$ and ${\hat{a}}^{\dagger }$ satisfying $[\hat{a},{\hat{a}}^{\dagger }]=1$, the quadrature operators are

$$\hat{q}=\frac{\hat{a}+{\hat{a}}^{\dagger }}{\sqrt{2}},\quad \hat{p}=\frac{-i(\hat{a}-{\hat{a}}^{\dagger })}{\sqrt{2}}$$

The translation operator in the phase space is defined as

$$\hat{T}({\boldsymbol{u}})\equiv \exp [i({u}_{p}\hat{q}-{u}_{q}\hat{p})],$$

where ${\boldsymbol{u}}=({u}_{q},{u}_{p})\in {{\mathbb{R}}}^{2}$ is the displacement vector. Notice that $\hat{T}({\boldsymbol{u}})=\hat{D}(({u}_{q}+i{u}_{p})/\sqrt{2})$, where $\hat{D}(\alpha )=\exp (\alpha {\hat{a}}^{\dagger }-{\alpha }^{* }\hat{a})$ is the usual displacement operator. The commutation relation is

$$\hat{T}({\boldsymbol{u}})\hat{T}({\boldsymbol{v}})={e}^{-i\omega ({\boldsymbol{u}},{\boldsymbol{v}})}\hat{T}({\boldsymbol{v}})\hat{T}({\boldsymbol{u}}),$$

where the phase $\omega ({\boldsymbol{u}},{\boldsymbol{v}})={u}_{q}{v}_{p}-{u}_{p}{v}_{q}=\det \left(\begin{array}{rc}{u}_{q}&{u}_{p}\\ {v}_{q}&{v}_{p}\end{array}\right)$ is the oriented area of the parallelogram spanned by vectors u and v.

GKP states are defined as states that are invariant under certain phase space displacements. Given two displacement operators ${\hat{S}}_{X}=\hat{T}({\boldsymbol{u}})$ and ${\hat{S}}_{Z}=\hat{T}({\boldsymbol{v}})$, the states that are invariant under the stabilizers ${\hat{S}}_{X}$ and ${\hat{S}}_{Z}$ form a d-dimensional GKP code space^14,29:

$${\mathcal{C}}({\boldsymbol{u}},{\boldsymbol{v}})\equiv \left\{\left\vert \psi \right\rangle \,:\,{\hat{S}}_{X}\left\vert \psi \right\rangle ={\hat{S}}_{Z}\left\vert \psi \right\rangle =\left\vert \psi \right\rangle \right\}$$

if the area ω(u, v) = 2πd and d is an integer. We can equivalently denote a GKP code as ${{\mathcal{C}}}_{d,{\bf{S}}}$ where S is the normalized basis matrix for the GKP lattice defined as

$$\sqrt{2\pi d}\,{\bf{S}}=\left(\begin{array}{cc}{u}_{q}&{u}_{p}\\ {v}_{q}&{v}_{p}\end{array}\right)\equiv ({\boldsymbol{u}},{\boldsymbol{v}}).$$

It is easy to see that S is a 2 × 2 symplectic matrix since $\det ({\bf{S}})=1$, i.e., The condition of having det(S) = 1 is sufficient in this case, because by construction S preserves the lattice area. Throughout the paper, we will interchangeably use the notation ${\mathcal{C}}({\boldsymbol{u}},{\boldsymbol{v}})$ or ${{\mathcal{C}}}_{d,{\bf{S}}}$ to represent a GKP code based on convenience.

The logical operators for a GKP code ${\mathcal{C}}({\boldsymbol{u}},{\boldsymbol{v}})$ are $\hat{X}=\hat{T}({\boldsymbol{u}}/d)$ and $\hat{Z}=\hat{T}({\boldsymbol{v}}/d)$, satisfying $\hat{X}\hat{Z}={e}^{2\pi i/d}\hat{Z}\hat{X}$. We choose the eigenstates $\left\vert \mu \right\rangle ,\mu =0,\ldots ,d-1$ of $\hat{Z}$ as the basis states of the GKP code ${\mathcal{C}}({\boldsymbol{u}},{\boldsymbol{v}})$, where

$$\hat{Z}\left\vert \mu \right\rangle ={e}^{2\pi i\mu /d}\left\vert \mu \right\rangle ,\quad \hat{X}\left\vert \mu \right\rangle =\left\vert \mu +1\,{\mathrm{mod}}\,\,d\right\rangle .$$

Without loss of generality, we consider square lattice GKP codes. Any other lattice with the same phase space area is equivalent via a rotation, offering no inherent advantage. For a square lattice GKP code ${{\mathcal{C}}}_{d,{\bf{S}}}$ where ${\bf{S}}={{\mathbb{I}}}_{2}$ is the 2 × 2 identity matrix, the basis states in the position space are

$$\left\vert \mu \right\rangle =\sum _{k\in {\mathbb{Z}}}\left\vert \hat{q}=\sqrt{2\pi d}(k+\mu /d)\right\rangle ,\quad \mu =0,\ldots ,d-1.$$

The logical operators for a square lattice GKP code ${{\mathcal{C}}}_{d,{\bf{S}}}$ are

$$\hat{X}=\exp \left(i\sqrt{2\pi /d}\hat{p}\right),\quad \hat{Z}=\exp \left(i\sqrt{2\pi /d}\hat{q}\right).$$

Finally, when d = 1, the GKP state $\left\vert \mu =0\right\rangle$ is called a qunaught state since it does not carry any quantum information.

We now consider two GKP-encoded modes, labeled A and B, each carrying logical information via lattices defined by vectors (f_A, g_A) and (f_B, g_B) respectively. The logical operators for each mode are:

$${\hat{X}}_{i}=T\left(\frac{{{\boldsymbol{f}}}_{i}}{{d}_{i}}\right),\quad {\hat{Z}}_{i}=T\left(\frac{{{\boldsymbol{g}}}_{i}}{{d}_{i}}\right),\quad i\in \{A,B\}.$$

These operators generate the logical Pauli group for an embedded d_i-dimensional DV system within each CV bosonic mode. The eigenstates of ${\hat{Z}}_{i}$ serve as the computational basis ${\{{\left\vert \mu \right\rangle }_{i}\}}_{\mu = 0}^{{d}_{i}-1}$, which are localized along a one-dimensional lattice in phase space. The logical operator ${\hat{X}}_{i}$ acts as a shift between these basis states, while ${\hat{Z}}_{i}$ applies a phase. Together, ${\hat{X}}_{i}$ and ${\hat{Z}}_{i}$ satisfy the Weyl commutation relation:

$${\hat{Z}}_{i}{\hat{X}}_{i}={e}^{2\pi i/{d}_{i}}{\hat{X}}_{i}{\hat{Z}}_{i},$$

mirroring the algebra of qudit Pauli operators. In this way, the GKP code enables encoding of DV logical states (such as qubits or qudits) into structured CV states.

Transmission model

We model the crosstalk arising from mode mixing interfecrence by a beam splitter ${\hat{U}}_{\eta }$, jointly transforming the modes, while η relflecting the strength of mode mixing is considered to be stochastic. The beam splitter model, schematized in Fig. 7, acts as a linear symplectic transformation:

Fig. 7

Crosstalk between two GKP-encoded modes via mode mixing beam splitter interaction.

$${\hat{U}}_{\eta }\left\vert {q}_{A}\right\rangle \left\vert {q}_{B}\right\rangle =\left\vert \sqrt{\eta }{q}_{A}+\sqrt{1-\eta }{q}_{B}\right\rangle \otimes \left\vert \sqrt{\eta }{q}_{B}-\sqrt{1-\eta }{q}_{A}\right\rangle$$

(22)

where η is modeled by a log-normal distribution, characterized by the probability density function:

$${f}_{\eta }(\eta )=\frac{1}{\eta {\sigma }_{c}\sqrt{2\pi }}\exp \left(-\frac{{({\rm{In}}\, \eta -\mu )}^{2}}{2{\sigma }_{c}^{2}}\right)$$

(23)

with μ being the mean of $\cos \eta$, and σ_c is its standard deviation reflecting the strength of fading. This operation introduces undesired correlation between the two modes A and B reflected in the displacement, which potentially disrupts independent logical recovery. The effect of this crosstalk mixing on the lattice vectors is highlighted in Fig. 8.

Fig. 8

The effect of the crosstalk on the lattice vectors of the GKP codes in the (q₁, q₂) and (p₁, p₂) planes for GKP codes of dimensions d₁ = d₂ = 2 and crosstalk average $\eta =\frac{1}{3}$.