Quantum computing for corrosion simulation: workflow and resource analysis

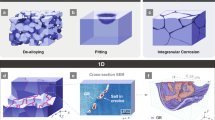
Abstract

Corrosion is a pervasive issue that impacts the structural integrity and performance of materials across various industries, imposing a significant economic impact globally. In fields like aerospace and defense, developing corrosion-resistant materials is critical, but progress is often hindered by the complexities of material-environment interactions. While computational methods have advanced in designing corrosion inhibitors and corrosion-resistant materials, they fall short in understanding the fundamental corrosion mechanisms due to the highly correlated nature of the systems involved. This paper explores the potential of leveraging quantum computing to accelerate the design of corrosion inhibitors and corrosion-resistant materials, with a particular focus on magnesium and niobium alloys. We investigate the quantum computing resources required for high-fidelity electronic ground-state energy estimation (GSEE), which will be used in our hybrid classical-quantum workflow. Representative computational models for magnesium and niobium alloys show that 2292 to 38598 logical qubits and (1.04 to 1962) × 10¹³ T-gates are required for simulating the ground-state energy of these systems under the first quantization encoding using plane waves basis.

Introduction

Corrosion is a natural process that degrades materials through chemical or electrochemical reactions with their environment, impacting both the structural integrity and performance of engineering materials¹. It imposes a significant economic burden, with global costs exceeding $2.5 trillion annually². In aerospace and defense, corrosion-resistant materials reduce maintenance costs and enhance sustainability³. The development of corrosion-resistant materials relies on a combination of experimental and computational methods. Computational models can aid in the designing of corrosion inhibitors and the development of corrosion-resistant materials,^4,5 with experiments validating these materials⁶. However, no single mathematical framework currently exists that can fully capture the complexity of the physical and chemical processes driving corrosion^7,8. As a result, different computational models need to be investigated for various corrosion applications. This work introduces a complete workflow from first principles for simulating corrosion processes. The novel quantum-classical hybrid approach unifies previously unrelated classical and quantum algorithms. We present computational models for aqueous corrosion in magnesium and magnesium-aluminum alloy surfaces, which may be extendable to other metallic systems; and for high-temperature oxidation in niobium alloys, which are critical for extreme environments but highly susceptible to degradation. Our models for magnesium corrosion are based on nudged elastic band modeling, while our niobium algorithm involves a coupled-cluster approximation to map the problem to a classical Ising model. In both cases, ground-state energy estimation is a key computational bottleneck.

Traditional modeling techniques, like finite element analysis (FEA), are poorly suited to corrosion due to the highly localized, non-uniform environments in which it occurs⁹. Corrosion processes often span multiple length and time scales and can evolve over time, transitioning from localized pitting to more catastrophic modes such as stress corrosion cracking or corrosion fatigue⁸. Factors such as material properties, corrosive environments, and component assembly further complicate these interactions^10,11. The lack of an integrated framework that combines chemistry, microstructure, and mechanical behavior into a single model necessitates significant simplifying assumptions¹².

At the atomic scale, the chemical reactions driving corrosion are governed by the electronic structure of materials, which can be described by the time-independent Schrödinger equation. Accurate solutions to the Schrödinger equation are crucial for predicting properties such as corrosion rates but are computationally prohibitive due to the superpolynomial scaling of the wavefunction size with the number of orbitals (N) and electrons (N_e)¹³. Many of these processes involve highly correlated electronic states,⁸ making exact diagonalization infeasible when N and N_e exceed 25¹⁴. For example, Fig. 1 shows a magnesium alloy model that incorporates 1000 water molecules and eight atomic layers, highlighting the scale and complexity of these systems. Simulating such a model with high accuracy is far beyond the capabilities of classical methods.

Fig. 1: 1000 water model of Mg grain boundary with Mg-Al secondary phase.

The golden spheres represent Mg atoms, red oxygen, white hydrogen, and light blue aluminum.

Quantum computers offer a promising path forward, as they are uniquely suited for simulating strongly correlated chemical systems^15,16. Recent advances in quantum algorithms for simulating chemical models,^17,18 along with new quantum software libraries,¹⁹ make quantum computing increasingly practical. While quantum computers are not expected to completely negate high-performance computer costs, it will potentially enable high-fidelity computations on larger atomistic models and more accurate simulation of corrosion processes that are highly correlated. We conduct a comprehensive resource assessment for quantum modeling of aqueous and high-temperature corrosion processes, marking the first application of the pyLIQTR computational tool to a real-world materials science problem. Our work develops and implements a hybrid quantum-classical workflow that incorporates Ground-State Energy Estimation (GSEE) and details the required logical-level quantum hardware resources for high-fidelity simulations of magnesium and niobium alloy corrosion. In particular, we cost utility-scale instances and establish the feasibility of quantum-enhanced approaches in materials degradation studies by estimating the total number of logical qubits and T gates necessary to implement the quantum phase estimation subroutine. An overview of these resources is provided in Table 1.

Table 1 Summary of logical resource estimate on a single shot of qubitized QPE for selected computational models, not including initial state preparation procedure

Results

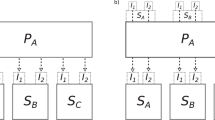
We develop a hybrid classical-quantum workflow to investigate the corrosion mechanisms at the atomic scale in two classes of alloys, under aqueous and high-temperature environments. These workflows are expressed using the Quantum Benchmarking Graph (QBG) formalism. QBG is a technique intended to graphically and systematically decompose an application instance into foundational subroutines and core enabling computations. A QBG is realized as an attributed, directed acyclic graph (DAG). In these graphs, both nodes and edges have attributes that convey computational capabilities, requirements, performance measures, data requirements, and additional metadata. The QBG framework serves as a critical component for assessing the resources required for a given application, by composing the resource usage of the algorithms/modules upon which the application relies. We have developed a detailed QBG framework with cost modeling for both application instances, depicted in Figs. 2, 3 and 4.

Fig. 2: Magnesium QBG: the directed acyclic graph decomposes the magnesium workflow into individual computational subroutines along with its required inputs and actions.

To compute the HER rate, we first need to determine the reaction pathways, generate the model slabs and compute the activation energies. Each node is then broken down further to visualize the workflow.

Fig. 3

Visualization of a simulation cell of a Nb alloy, Nb₉₇Hf₃Ti₂₂Zr₆O, with interstitial oxygen.

Fig. 4

Quantum benchmark workflow for the niobium-rich refractory alloys.

In this section we present the workflows for both application instances: specifically, we study interface between water and magnesium (or magnesium-rich alloys), as well as the diffusivity of oxygen at high temperatures in niobium-rich alloys. Magnesium-rich sacrificial coatings disrupt the electro-chemical processes that driving corrosion in aqueous environments, offering a promising avenue for effective corrosion mitigation and potential replacements for chromate-based coatings in aerospace aluminum alloys²⁰. In contrast, Niobium alloys, with their high-temperature resistance, have great potential in the development of more efficient jet engines ^21,22.

For both workflows, a major component is estimating the resources required for the quantum phase estimation (QPE) subroutine for GSEE. Resource estimations for QPE in the provided examples were calculated using the pyLIQTR software package²³. A summary of the resource estimates found is provided in Table 1.

Magnesium and Mg-rich alloys

Here we give an overview of the full classical-quantum workflow, a more detailed exposition is provided in the Supplementary Materials. In aqueous environment, the corrosion of Mg or Mg alloy is dominated by the highly-exothermic hydrogen evolution reaction (HER), which constitutes the cathodic part of the electrochemical corrosion reaction. HER is further complicated by the highly-reactive, and short-lived corrosion intermediates formed during cathodic polarization, presenting a significant challenge in both computational and experimental investigations of the reaction mechanism. While experimental methods like mass loss, electrochemical characterization, and in situ monitoring of hydrogen gas evolution can provide corrosion rate measurements, these techniques are time-consuming, resource-intensive, and they do not offer detailed insights into the atomic-scale mechanisms of HER. As such, developing new materials that effectively mitigate corrosion in aqueous environments requires a deeper mechanistic understanding, and computational approaches, though challenging, are critical.

Workflow

This workflow is designed to develop a comprehensive understanding of HER. The workflow is depicted schematically in the quantum benchmark graph (QBG) shown in Fig. 2, with dependencies of subroutines marked by arrows. A theoretical model for HER was proposed by Williams et al.²⁴, based on the Volmer-Tafel reaction mechanisms, which decomposes HER into three simpler steps:

$${\text{Mg}}+{{\text{2H}}}_{2}{\text{O}}\to {\text{Mg}}({\text{OH}}_{{\rm{a}}{\rm{d}}{\rm{s}}})({{\text{H}}}_{{\rm{a}}{\rm{d}}{\rm{s}}})+{{\text{H}}}_{2}{\text{O}}$$

(1)

$${\text{Mg}}({\text{OH}}_{{\rm{a}}{\rm{d}}{\rm{s}}})({{\text{H}}}_{{\rm{a}}{\rm{d}}{\rm{s}}})+{{\text{H}}}_{2}{\text{O}}\to {\text{Mg}}{({\text{OH}}_{{\rm{a}}{\rm{d}}{\rm{s}}})}_{2}{({{\text{H}}}_{{\rm{a}}{\rm{d}}{\rm{s}}})}_{2}$$

(2)

$${\text{Mg}}{({\text{OH}}_{{\rm{a}}{\rm{d}}{\rm{s}}})}_{2}{({{\text{H}}}_{{\rm{a}}{\rm{d}}{\rm{s}}})}_{2}\to {\text{Mg}}{({\text{OH}}_{{\rm{a}}{\rm{d}}{\rm{s}}})}_{2}+{{\text{H}}}_{{2}}({\text{g}})$$

(3)

where (ads) designates a species adsorbed on the surface and (g) designates a gaseous species.

The first stage of the computational workflow identifies the relevant reaction pathways associated with the reactions in Eqs. (1) to (2), using the nudged elastic band (NEB) method, a state-of-the-art approach for transition-state searches²⁵. NEB constructs a series of intermediate atomic configurations ("images") that represent intermediate configurations during the reaction. The resulting path is relaxed to the minimum energy path (MEP) between optimized reactant and product states, or roaming path, depending on the model for the reaction²⁶. NEB simultaneously optimizes the geometries of all intermediate images, either serially or in parallel, but this process is computationally demanding due to the repeated ground-state energy calculations required.

In the second stage of the workflow, rate constants for reaction pathways are calculated using the Arrhenius equation:

$$k=A\exp \left(-\frac{{E}_{a}}{RT}\right)$$

(4)

where A is the Arrhenius factor, R the gas constant, and T the temperature. Here, E_a represents the energy difference between an initial state and a transition state. Accurate determination of E_a, often requiring a precision threshold of 10⁻³ Hartree, is crucial due to its exponential effect on k. If the MEP from NEB using DFT is sufficiently accurate, or if the discrepancy between DFT and high-fidelity methods is negligible, high-fidelity solvers can focus solely on refining E_a for the reactant and transition state. However, the size of these models renders high-fidelity classical solvers intractable. At this stage, quantum computers, specifically through quantum phase estimation, can be strategically integrated to efficiently calculate E_a. While quantum computers could be used throughout the entire process, doing so might needlessly consume quantum resources, so strategically integrating quantum processing ensures improved efficiency and resource usage, as shown in the QBG in Fig. 2.

In this workflow, the practitioner (corrosion scientist or engineer) specifies the magnesium-rich alloy and solvent, the quantum chemist constructs the computational model (defining supercell size, slab geometry, accuracy thresholds, suitable basis sets, and performing transition state searches), and the quantum computing scientist uses these parameters–along with tools like PEST in pyLIQTR–to generate the electronic Hamiltonian for quantum algorithm execution²³.

By uncovering the most energy-efficient pathway for the HER on magnesium-alloy surfaces–using methods like comparing Gibbs free energies at various transition states or ab-initio molecular dynamics to directly track atomic movement, alongside analyses of chemical properties such as band structures and charge transfer–we gain insight into the reaction mechanism, and in this work, ground-state energies along the reaction coordinate are computed on a quantum computer.

To estimate the resource requirements for the quantum subroutines in our computational workflow on the magnesium–water interface, we selected three models of magnesium, labelled “Mg Dimer,” “Mg Monolayer,” and “Mg Cluster,” as well as the magnesium–aluminum alloy Mg₁₇Al₁₂, which is a secondary phase prevalent in alloys such as the AZ91 alloy. These four systems span a range of increasing size and electronic complexity, which in turn escalates their computational demands. The final resource estimates for these three models and the alloy are summarized in Table 1. To reduce space–time volume in the quantum algorithms, we formulated the problem in first quantization.

Niobium-rich alloys

Niobium-rich refractory alloys are ideal candidates for aerospace, defense, and aviation applications due to their ductility, high melting point, and superior strength-to-weight ratios compared to Ni-based superalloys^21,22. Poor oxidation resistance in niobium necessitates identifying alloying elements that improve oxidation behavior, a challenge amplified by the vast search space of possible multi-component alloys, motivating the need for computational approaches that allows for efficient screening²⁷. While modeling oxygen diffusivity within niobium alloys provides insight into their oxidation resistance, the computational cost dramatically increases with the addition of more alloying elements.

Modeling oxygen diffusion using kinetic Monte Carlo (KMC) methods can help to identify promising alloys. While previous studies of binary Nb alloys have had some success using cluster expansion methods,²⁸ the larger design space of multicomponent Nb-rich alloys, incorporating elements like Ti, Ta, Zr, W, and Hf, adds complexity to the search for optimal compositions.

Workflow

In order to evaluate chemical formulas for different niobium-rich alloys, a set of alloying elements is selected. In general, the alloy’s chemical formula is of the form ${Nb}_{(1-{\sum }_{i}{x}_{i})}{A}_{{x}_{1}}{B}_{{x}_{2}}\ldots {Z}_{{x}_{n}}$ where A through Z denote the n alloying elements. This work focuses on compositions containing three or four alloying elements. The computational resource requirements grow with the size of the supercell, which must be large enough to accurately capture the proportions of each alloying element. Consequently, four-element alloys demand more computation than those with three elements (ternary), or simpler binary systems.

Once a set of alloying elements is selected, numerous alloy structures with varying amounts of each element are randomly generated and relaxed using density functional theory (DFT). These structures include an oxygen atom positioned at octahedral sites within the lattice, as well as transition state geometries between octahedral sites, obtained using the climbing-image nudged elastic band (CI-NEB) method²⁵. For each geometry, the electronic ground state energy is computed with as high accuracy as possible, serving as training data for cluster expansions (CEs). Fitting conventional CEs to multi-component alloys is difficult, however recently developed techniques provide embedded CEs (eCEs) that can reproduce the energetics of quinary alloys using around 500 data points²⁹. The objective is to compute high-fidelity energy estimates for points for two separate cluster expansions: one for oxygen at octahedral sites and another for transition state geometries.

To determine the oxygen diffusivity D(T) at high temperatures (≥1600 °C (1873.15 K)), one can simulate the movement of oxygen between interstitial sites in an atomic lattice. Using kinetic Monte Carlo (KMC) methods, oxygen atoms are propagated between these sites with probabilities proportional to the rate constants that govern each site-to-site jump. Determining this rate constant involves computing the energy barriers by solving the Hamiltonian DFT or other first-principles methods³⁰. Given the size of the search space, cluster expansions are incorporated into this workflow to obtain energy barriers²⁸. Specifically, for a given choice of alloying elements, cluster models are trained on energies obtained from random configurations of the alloying atoms in various proportions. Once trained, the cluster model allows for the estimation of energy barriers of alloy models that sweep over many stoichiometries beyond those considered in the training dataset. This approach not only allows for an efficient computation of the energy barriers, but the cluster model can also provide entire phase diagrams³¹.

At a high level, for a given set of alloying elements the objective is to estimate the energy barriers associated with oxygen transitioning from one octahedral interstitial site to another with high accuracy. During these transitions, the oxygen atom will pass through a transition state. For pure niobium, the transition state is an interstitial site with tetrahedral symmetry, and thus are amenable to classical computational methods. When considering disordered niobium alloys, the transition states are no longer retain perfect tetrahedral symmetry and require a transition state search algorithm to determine the geometry of the transition state, we consider the application of CI-NEB.

The classical preprocessing in this workflow begins by generating a set of supercells, as shown in Fig. 3, where alloying elements are embedded into a Niobium lattice for various ratios. Next, oxygen atoms are randomly placed at octahedral interstitial sites, and the entire supercell is relaxed. In addition, another set of transition-state geometries is produced by running a transition-state search algorithm. Both the octahedral and transition-state geometries are stored in a database²⁸. Special quasi-random structures are designed to statistically mimic the random distribution of atoms or elements in an alloy or compound while using a finite, periodic unit cell, making them computationally manageable³².

We focus on modeling how oxygen diffuses in multi-component, Nb-rich alloys by using cluster expansions–a technique that approximates how different atomic arrangements affect the energy of an oxygen atom in the lattice²⁹. First, we generate various alloy structures with different atomic configurations and compute their energies using high-accuracy electronic structure methods. These data points are then used to train the cluster expansions so that they can predict the solution energy of oxygen in either its usual (octahedral) site or a neighboring (tetrahedral) site that represents the transition state for migration.

Once the cluster expansions are fitted, we extract the energy barriers for oxygen hopping between adjacent octahedral sites by comparing these predicted energies. Finally, a KMC simulation uses those barriers to stochastically move oxygen atoms through the alloy and track the resulting diffusion over time. The KMC calculations yield estimates of the overall diffusivity of oxygen as a function of temperature. By identifying alloy compositions with lower diffusivities, we can highlight candidates that are likely to be more resistant to high-temperature oxidation, although other factors also play a role in selecting the best alloy.

The inputs to this computational workflow are a set of alloying elements {A, B, C, … } and specified ranges for their fractional stoichiometries. For example, when considering alloys of the form Nb_1−(x+y+z) A_x B_y C_z, we focus on niobium-rich compositions by restricting (x, y, z) to [0, a] × [0, b] × [0, c], where a, b, c ≪ 1. The number of alloying elements and these composition ranges then determine the required size of the computational supercell, ensuring that there are enough atoms to accurately represent each element’s proportion.

The primary output of this computational workflow is the oxygen diffusivity at various temperatures for different alloy compositions. If a cluster expansion is also trained on the alloy’s formation energy, an additional phase diagram can be constructed to assess the alloy’s stability and thermodynamics across the composition range (x, y, z). Because oxygen diffusivity D(T) at elevated temperatures T directly influences the rate of oxidation in niobium alloys, it is the key quantity of interest. Ideally, a protective oxide film forms—akin to the behavior in aluminum alloys—to prevent further oxidation³³. Table 1 presents the quantum resource estimates for four Nb-rich alloys that were selected using this computational workflow process.

Discussion

CPC remains a significant challenge across various industries, resulting in enormous economic costs and impacts. Developing computational models to explain and/or predict corrosion typically focuses on empirical modeling using data from laboratory experiments, field tests or in-service findings. However, the application of physics-based techniques to model and understand fundamental corrosion mechanisms, including first principles approaches, has increased within the past decade as researchers have gained access to high performance computers and commercial software.

Despite having access to supercomputers and highly-optimized classical codes, researchers are still limited in the sizes of physical models they can study. For the majority of first principles codes, a few hundred atoms is considered a large, computationally-demanding model: running an ab initio calculation of a few thousand atoms is practically impossible without approximations (e.g., DFT), significant processing power and time³⁰. Furthermore, the DFT approximations that are typically used to reduce computational costs are known to give inaccurate results for highly-correlated states. This makes it challenging to develop atomistic models of corrosion that have both sufficient scale to mimic realistic systems and high fidelity to produce accurate, reliable predictions.

This paper presents computational workflows associated with developing advanced corrosion-resistant materials and anti-corrosion coatings, focusing on magnesium-rich sacrificial coatings, corrosion resistant magnesium alloys, and niobium-rich refractory alloys. We assess the potential of quantum computing and its applicability to the described workflows. This assessment focuses on obtaining accurate ground state energy estimations for each computational model.

For the quantum algorithmic framework used in the present study, resource estimates indicate that the smallest model related to magnesium alloy design would require over 2300 qubits, with the associated T-gate count for the QPE circuit being on the order of 10¹³. The largest computational model studied in this paper would require approximately 40,000 qubits and a T-gate count on the order of 10¹⁶. For computational models associated with the Nb-rich refractory alloys use case, the approximate number of qubits needed ranges from roughly 6000 to 10,000, and the T-gate count for the targeted QPE algorithm ranges from ~ 10¹³ to ~ 10¹⁵. We believe these estimates are far from optimal, and that several research directions that could significantly reduce these resources while maintaining utility. For example, combining techniques like BLISS³⁴ or tensor factorizations with the first quantized representation could further reduce the Hamiltonian 1-norm. Indeed, recent studies have shown dramatic decreases in resource estimates through simple, but clever, modifications³⁵. We hope that this work will spark more research into similar optimisations.

Further research into refining these algorithms is especially important when considering that the reported resource estimates are for a single instance of QPE. This is separate consideration from the total quantum resources required to perform ground state energy estimation to high accuracy - which could potentially require many repetitions of this subroutine. The actual number of QPE shots needed depends on the overlap between the initial state generated by an ansatz and the true ground state (see Supplementary Materials for a more detailed discussion of this).

In summary, this work evaluates the quantum computing resources needed to address realistic, industrial-scale problems with high utility. While state-of-the-art machine learning interatomic potentials enable efficient, near-DFT molecular dynamics at scale, we use the quantum computer to compute a small number of high-fidelity electronic energies at configurations where DFT errors consequential. By quantifying the resource requirements to study corrosion reaction mechanisms, this paper lays the groundwork for understanding the potential impact of quantum computing in the development of advanced corrosion-resistant materials.

Methods

This section describes the methodology for constructing classical-quantum hybrid workflows using the QBG framework and the methods used to estimate resources presented in the main paper. QBG decomposes each workflow into individual nodes where each node represents a specific computational kernel along with its required inputs and actions. The key nodes are presented in Table 2 with their inputs, outputs and runtime complexity.

Table 2 Computational Kernels for the computational workflows described in the designing of corrosion-resistant magnesium alloys in aqueous environment and corrosion resistant niobium alloys in temperature

Magnesium

Various surface and alloy environments were selected to facilitate scalable benchmark tests based on system size and to focus on chemically relevant species for corrosion studies in industrial applications. Magnesium slabs were selected as baselines due to the breadth of experimental³⁶ and computational work,^37,38 as well as their widespread industrial relevance^39,40. We concentrate on three configurations of uniform magnesium as well as an alloyed magnesium-aluminum slab to assess the quantum computation capabilities for modeling surface chemistry.

We explore an hcp Mg(0001) slab interacting with water at its surface in three different sizes to examine resource estimation. The smallest system is a 4 × 4 × 4 slab with one adsorbed water molecule (70 atoms), comparable to DFT and CASSCF studies³⁷. The mid-sized system, 6 × 6 × 5, includes a water monolayer of 26 molecules (257 atoms), reflecting larger DFT analyses⁴¹. Lastly, a 6 × 6 × 6 slab with 99 water molecules and 36 adsorbed hydroxyl groups (586 atoms) aligns with AIMD-level simulations⁴².

For alloy modeling, we focus on AZ91 and EV31A, both recognized for their corrosion resistance. These alloys have a pure hcp Mg(0001) α-phase and a dominant β-phase consisting of cubic Mg₁₇Al₁₂ in AZ91, and Mg₁₂RE₂ or Mg₃RE in EV31A, where RE is a rare-earth metal such as neodymium or gadolinium. Given these alloys’ complexities, it is essential to model surface interactions both at the β-phase alone and at boundary layers between primary and secondary phases.

The first proposed approach for capturing this complex environment is shown in Fig. 5. Primary and secondary phase structures for AZ91 were obtained from the Materials Project Materials Explorer⁴³. The hcp Mg(0001) α-phase was extended to a 12 × 6 × 12 rectangular supercell (lattice constants a = 31.7 Å, b = 18.3 Å, c = 42.6 Å and angles θ = φ = ξ = 90^∘) to align with the secondary Mg₁₇Al₁₂ cubic structure. A large slab was chosen to capture various boundary-layer sizes, including subsurface secondary phases and extended periodic regions dominated by the second phase. All magnesium slab supercells include a vacuum layer for consistency in surface interaction studies. Supercell structures were built using the Schrödinger Materials Science Suite version 2024-2⁴⁴.

Fig. 5: Schematic of approach for generating supercells of composite structures in magnesium alloys.

Beginning with two independent primary and secondary phase structures, a guess-geometry is established by embedding Mg₁₇Al₁₂ within the primary structure and define a cubic periodic boundary that still maintains hcp magnesium. Secondary phase aluminum is in gold, secondary phase magnesium is in pink, and primary phase magnesium is in blue.

Modeling corrosion environments typically begins with selecting surface geometries that accurately reflect the chemical phenomena yet remain computationally tractable. This process often starts with DFT, a method known for its computational efficiency by establishing a one-to-one mapping between the electronic density and the external potential in the electronic Hamiltonian⁴⁵. DFT is used to locate optimum points on the nuclear potential energy surface, revealing stable geometries and transition states. In corrosion chemistry, such optimizations commonly employ periodic boundary conditions to mimic lattice periodicity and capture surface interactions with corrosive or protective agents. Consequently, DFT provides an initial exploration of the model space and generates structures that inform higher-fidelity simulations.

In our studies of corrosion chemistry in Mg, we often care not only about the minima along the nuclear potential energy surface but also saddle points. These saddle points represent paths of least resistance during reactions, providing critical insight into reaction kinetics, and can be directly used in larger length-scale simulations^8,26. To complete transition state searches on surfaces, NEB methods interpolate images along a reaction coordinate from an initial reactant and product pair that are then iteratively optimized in search of potential transition states. NEB simulations leverage periodic DFT during this process, and scans are often performed at increasing k-point grid selections to systematically verify the convergence of geometries.

Niobium

Since we are interested in the diffusion of oxygen, we can leverage cluster expansions to fit the solution energy E_sol, as outlined in ref. ²⁸. For niobium alloyed with Zr, Ta, and W, E_sol, is computed as

$$\begin{array}{rcl}{{\text{E}}}_{{\rm{s}}{\rm{o}}{\rm{l}}} & = & {\text{E}}({\text{Nb}}_{1-(x+y+z)}{{\text{Zr}}}_{x}{{\text{Ta}}}_{y}{{\text{W}}}_{z}{\text{O}})\\ & & -{\text{E}}({\text{Nb}}_{1-(x+y+z)}{{\text{Zr}}}_{x}{{\text{Ta}}}_{y}{{\text{W}}}_{z})-\frac{1}{2}{\text{E}}({{\text{O}}}_{2}).\end{array}$$

(5)

Let ${E}_{sol}^{Oct}$ and ${E}_{sol}^{Tetra}$ represent the solution energies computed for oxygen at fixed locations within the alloy matrix. These locations correspond, respectively, to “octahedral” reactant/product geometries and “tetrahedral” transition-state geometries obtained via CI-NEB calculations. For each type of geometry, we introduce a cluster expansion,

$${F}^{Oct}:{\boldsymbol{\Omega }}\to {\mathbb{R}}\,and\,{F}^{Tetra}:{\boldsymbol{\Omega }}\to {\mathbb{R}},$$

(6)

which share the general form

$$F({\boldsymbol{\sigma }})={J}_{0}+\mathop{\sum }\limits_{\alpha }{m}_{\alpha }\,{J}_{\alpha }\,{\Theta }_{\alpha }({\boldsymbol{\sigma }}).$$

(7)

Here, α indexes all symmetrically distinct clusters of lattice sites; we denote by m_α the multiplicity of cluster set α per unit cell, and by J_α the effective cluster interaction (ECI) coefficients, which are obtained by fitting this expansion to computed energies. The functions Θ_α(σ) take the form

$${\Theta }_{\alpha }({\boldsymbol{\sigma }})=\frac{1}{{N}_{\alpha }}\mathop{\sum }\limits_{\beta \subset \alpha }\mathop{\prod }\limits_{i=1}^{N}{\phi }_{{\beta }_{i}}({\sigma }_{i}),$$

(8)

where N_α is the number of sub-clusters β ⊂ α, and σ_i are “spin” variables indicating which atom occupies site i. The basis functions ${\phi }_{{\beta }_{i}}({\sigma }_{i})$ can be, for instance, simple indicator functions (one-hot encoding) or alternative forms such as polynomial or trigonometric functions.

The configuration vector σ corresponds to possible choices for various elements at each position in the alloy. The configuration vector for a lattice of M sites is an element of a space of configurations σ ∈ Ω₁ × Ω₂ × ⋯ Ω_M = Ω, for example a 4 site lattice could be described by Ω = {0, 1, 2, 3}⁴ and σ = (0, 1, 0, 3) where 0 is Nb, 1 is Zr, 2 is Ta, and 3 is W. For the training data, we collect energies computed at the full-configuration interaction (FCI) level for ${E}_{sol}^{Oct}$ and ${E}_{sol}^{Tetra}$ corresponding to configurations (σ). This training is then used to find an optimal set of ECI coefficients ${\boldsymbol{J}}=({J}_{0},{J}_{{\alpha }_{1}},\ldots )$ which requires us to solve the following least squares problem.

Let Π(σ) be the vector of functions ${\Theta }_{{\alpha }_{i}}({\boldsymbol{\sigma }})$ for i = 1, …, d

$${\boldsymbol{\Pi }}({\boldsymbol{\sigma }})=({\Theta }_{0}({\boldsymbol{\sigma }})\equiv 1,{\Theta }_{{\alpha }_{1}}({\boldsymbol{\sigma }}),{\Theta }_{{\alpha }_{2}}({\boldsymbol{\sigma }}),\ldots )\in {{\mathbb{R}}}^{d}.$$

(9)

We can then compute the cluster expansion with a dot product

$$F({\boldsymbol{\sigma }})={\boldsymbol{\Pi }}({\boldsymbol{\sigma }})\cdot {\boldsymbol{J}}.$$

(10)

We then construct the matrix Π that contains the values for the vector Π(σ_j) for each training configuration σ_j for j = 1, …, m

$${\boldsymbol{\Pi }}={({\boldsymbol{\Pi }}({{\boldsymbol{\sigma }}}_{1}),{\boldsymbol{\Pi }}({{\boldsymbol{\sigma }}}_{2}),\ldots ,{\boldsymbol{\Pi }}({{\boldsymbol{\sigma }}}_{m}))}^{T}\in {{\mathbb{R}}}^{m\times d}$$

(11)

Let E = (E₁, …E_m) be the FCI-level energies associated with the m training structures, then the least squares problem is posed as

$${{\boldsymbol{J}}}^{* }=\mathop{\mathrm{argmin}}\limits_{{\boldsymbol{J}}}\parallel {\boldsymbol{\Pi }}{\boldsymbol{J}}-{\boldsymbol{E}}{\parallel }_{2}^{2}+\rho ({\boldsymbol{J}}).$$

(12)

where ρ is a regularization term for which there are few different choices.

Evaluating the quality of the fit typically involves computing cross-validation (CV) and related quantities. The canonical choice is the leave-one-out CV which is given by

$$CV=\sqrt{\frac{1}{n}\mathop{\sum }\limits_{i=1}^{n}{({E}_{i}-{\widehat{E}}_{i})}^{2}}$$

(13)

where E_i are the FCI-level energies computed for structure i and ${\widehat{E}}_{i}$ is the predicted energy from a cluster expansion trained on other (n − 1) structures²⁸. A good score for leave-one-out cross-validation is below 5 meV/atom.

Once sufficiently accurate cluster expansions are computed, we can estimate the energy barrier between octahedral sites i and j, denoted by E_i→j, as in ref. ²⁸

$${E}_{i\to j}={F}^{{\text{Tetra}}}({{\boldsymbol{\sigma }}}_{i\to j})-{F}^{{\text{Oct}}}({\boldsymbol{\sigma }}).$$

(14)

These energy barriers are then fed into KMC simulations of oxygen on a random walk through the alloy’s sublattice of “octahedral” sites. As outlined in ref. ²⁸, for each time step, we generate two random numbers r₁, r₂ ~ Unif(0, 1), which determines the transition path and the moving time of the simulation. If a system in state i, then the transition rate between i and another site j in the transition path P = (i₁, i₂, …, i_n−1, j)

$${k}_{i\to j}={\nu }_{0}\exp (-{E}_{i\to j}/{k}_{B}T)$$

(15)

where T is temperature, k_B is the Boltzmann constant, and ν₀ is the attempt frequency, defined as

$${\nu }_{0}\approx \left(\mathop{\prod }\limits_{i=1}^{3N-4}\frac{{\nu }_{i}^{\mathrm{IS}}}{{\nu }_{i}^{\mathrm{TS}}}\right){\nu }_{3N-3}^{{\rm{I}}{\rm{S}}}.$$

(16)

In the interest of computational efficiency, we adopt the strategy outlined in ref. ²⁸ setting ν₀ to be the value for pure Nb and true octahedral and tetrahedral initial (IS) and transition state (TS).

The total transition rate k_tot is the sum of all k_i→j for all possible moving paths (i₁, i₂, …, i_n−1, j). If

$$\mathop{\sum }\limits_{{P}_{n-1}}{k}_{i\to j}\le {r}_{1}{k}_{{\text{tot}}}\le \mathop{\sum }\limits_{{P}_{n}}{k}_{i\to j}$$

(17)

where P_n−1 = (i₁, i₂, …, i_n−1) and P_n = (i₁, i₂, …, i_n = j^*), then j^* is selected for i_n in the path P. The system moves to the next state with moving time calculated according to the time step equation $\delta t=(1/{k}_{tot})\mathrm{ln}(1/{r}_{2})$. This random process is repeated in order to estimate the diffusivity at various temperatures T given by the formula

$$D(T)=\frac{1}{{n}_{s}}\mathop{\sum }\limits_{m=1}^{{n}_{s}}\frac{\parallel {\boldsymbol{x}}({t}_{m})-{\boldsymbol{x}}({t}_{m-1}){\parallel }_{2}^{2}}{6\delta t}$$

(18)

where n_s is the number of sampled trajectories, x(t_m) is the position of an oxygen atom at time t_m and x(t_m) = x(t_m−1 + δt). The KMC calculation assumes that $\delta t\gg {\nu }_{0}^{-1}$ that kinetic jump times of oxygen are large enough to include all local jump correlations and n_s should also be large enough to obtain a statistically meaningful diffusion coefficient²⁸. Alloy compositions with low diffusivities are selected as this is an indication of their oxidation resistance, however, this is not the only factor to consider. Therefore, this computational workflow helps narrow down the search for a desirable alloy formula.

Hamiltonian generation

A central challenge in electronic-structure calculations is choosing a finite basis set to discretize the Hamiltonian. Under the Born–Oppenheimer approximation, wavefunction “cusps” appear at nuclear coordinates, often suggesting local Gaussian orbitals for molecular systems. However, for large periodic systems, plane-wave (PW) bases are typically more suitable. Here, we adopt a first-quantized PW basis following ref. ⁴⁶, defining plane waves on a cubic reciprocal lattice:

$$\begin{array}{rcl}{k}_{p} & = & \frac{2\pi p}{{\Omega }^{1/3}},\,\,p\in G,\\ G & = & {\left[-\frac{{N}^{1/3}-1}{2},\frac{{N}^{1/3}-1}{2}\right]}^{3}\subset {{\rm{{\mathbb{Z}}}}}^{3},\end{array}$$

(19)

where N is the total number of basis functions or grid points, and Ω is the volume of the simulation cell⁴⁷. One advantage of the plane wave basis is that it enables quantum algorithms with lower asymptotic gate complexity compared to those using Gaussian orbitals. Unless stated otherwise, we use a valence-only Hamiltonian in which core electrons are treated by pseudopotentials. We then verify convergence with respect to vacuum spacing and the plane-wave kinetic-energy cutoff E_c. In first quantization, the Born–Oppenheimer Hamiltonian is represented as:

$${H}_{BO}=T+U+V+\frac{1}{2}\mathop{\sum }\limits_{\ell \ne \kappa =1}^{L}\frac{{\zeta }_{\ell }{\zeta }_{\kappa }}{\parallel {R}_{\ell }-{R}_{\kappa }\parallel },$$

(20)

where r_i represent the positions of electrons whereas R_ℓ represent the positions of nuclei, ζ_ℓ are the atomic numbers of nuclei; the kinetic (T), nuclear potential (U), and electron–electron interaction (V) terms are defined as:

$$T=\mathop{\sum }\limits_{i=1}^{\eta }\mathop{\sum }\limits_{p\in G}\frac{{\parallel {k}_{p}\parallel }^{2}}{2}| p\rangle {\langle p| }_{i},$$

(21)

$$U=-\frac{4\pi }{\Omega }\mathop{\sum }\limits_{\ell =1}^{L}\mathop{\sum }\limits_{i=1}^{\eta }\mathop{\sum }\limits_{\begin{array}{l}p,q\in G\\ p\ne q\end{array}}\left({\zeta }_{\ell }\frac{{e}^{i{k}_{q-p}\cdot {R}_{\ell }}}{\parallel {k}_{p-q}{\parallel }^{2}}\right)| p\rangle {\langle q| }_{i},$$

(22)

$$V=\frac{2\pi }{\Omega }\mathop{\sum }\limits_{i\ne j=1}^{\eta }\mathop{\sum }\limits_{p,q\in G}\mathop{\sum }\limits_{\begin{array}{c}\nu \in {G}_{0}\\ (p+\nu )\in G\\ (q-\nu )\in G\end{array}}\frac{1}{{\parallel {k}_{\nu }\parallel }^{2}}| p+\nu \rangle {\langle p| }_{i}\,| q-\nu \rangle {\langle q| }_{j},$$

(23)

with ${G}_{0}={[-{N}^{1/3},{N}^{1/3}]}^{3}\subset {{\mathbb{Z}}}^{3}\backslash \{(0,0,0)\}$ being the set of valid frequency differences. The wavefunction is stored in a computational basis that encodes configurations of η electrons among N basis functions, i.e., $| {\varphi }_{1}{\varphi }_{2}\cdots {\varphi }_{\eta }\rangle$, where each φ_j denotes the index of an occupied basis function.

The discretization error in this PW approach is asymptotically equivalent to Galerkin discretizations using other single-particle bases (including Gaussian orbitals)⁴⁸. Moreover, the first quantization framework offers a much more space-efficient (algorithmically) representation compared to the second quantization formalism. This is particularly critical for our calculations, as we require a large number of plane waves to accurately capture the system’s electronic structure. However, we also consider the second quantization framework. In Supplementary Materials, we discuss the Hamiltonian formulation and the implementation of the quantum algorithm within this framework, following the approach of¹⁷.

Vacuum space and wavefunction cutoff convergence

Another key consideration is ensuring wavefunction convergence with respect to the vacuum space allocated for simulating surface environments. In surface chemistry, periodicity is typically restricted to the xy-plane, so the z-dimension must be chosen carefully to prevent surface molecules from interacting with the metal slab’s periodic image in the next cell. However, increasing the cell size also increases the required k-point sampling, adding to the overall computational expense.

Vacuum-space convergence is assessed by examining electrostatic potentials, charge densities, and energies as the z-axis length is varied (see Fig. 6). We investigated vacuum layers between 12.7 Å and 32.4 Å. While the energetic analysis considered the entire range, representative cases of 12.7 Å, 17.7 Å, 25.4 Å, and 32.4 Å are shown for electrostatic potential and charge density. From these data, a 25.4 Å vacuum ensures that surface species do not artificially interact with their periodic images, aligning with previous recommendations²⁴. Notably, this is about twice the original z-axis dimension of the 64-atom magnesium lattice. However, more extensive vacuum layers may be required for systems featuring additional adsorbed species or realistic environment modeling.

Fig. 6: Determination of vacuum-space limits.

a Average electrostatic potential and charge density profiles along the z-axis. b Energetic convergence showing percent energy change. Insets in (a) highlight the potential and charge density attributed to a water dimer at the surface interface.

With the cell size determined, the next step is to set the wavefunction cutoff for chemically accurate simulations. Furthermore, physically, the high-frequency PW modes are used to reconstruct rapid wavefunction oscillations near atomic nuclei (the so-called “nuclear cusp”). Fortunately, these oscillations are generally tied to (often) irrelevant core electrons. Classical calculations mitigate this by using so-called pseudopotentials (PPs) to represent core electrons as a classical potential and reduce computational complexity. Since plane-wave calculations are widely used for classical electronic structure (DFT, etc.), we can often adopt a validated cutoff energy. In the context of ultrasoft pseudopotentials, we can define a low- and high-resolution bases as having kinetic cutoffs of E_c = 30 Ry and E_c = 60 Ry respectively. This maps to a real-space lattice constant via the equation ${a}_{0}=\gamma \sqrt{2{\pi }^{2}/{E}_{c}} \sim \gamma {\lambda }_{cut}$, where we assume atomic units, i.e., a₀ measured in Bohr radii and E_c in Hartree (1 Ry = 2 Ha), and λ_cut is the wavelength corresponding to the highest-energy plane-wave mode and γ is a scaling factor. Setting the scaling factor to γ = 1.0 will place grid points at the highest PW wavelength, while γ = 0.5 will apply these every half-wavelength. An ideal value would depend on pseudopotential details, though likely this would be closer to γ = 0.5.

We have determined the necessary wavefunction cutoffs and vacuum layer convergences to reduce computational costs with minimal energetic penalties for our specific application instances. Wavefunction convergence criteria were tested for Vanderbilt ultrasoft (USPPs), Goedecker-Teter-Hutter (GTH),⁴⁹ and Hartwigsen-Goedecker-Hutter (HGH)⁵⁰ pseudopotentials. Systematic evaluation of these pseudopotentials across different convergence criteria informs decisions during the resource estimation stage. See the Supplementary Materials for more details. These modeling choices uniquely fix the discretized H and thus the LCU weights {w_ℓ} used in Sec. E.

Quantum subroutines

In this work, we employ the qubitized quantum phase estimation (QPE) algorithm, as described in ref. ⁴⁶, to extract spectral information, specifically the ground state energies, for chemical systems of interest. Qubitized QPE encodes information about the Hamiltonian using a Szegedy walk via the technique of qubitization. The encoding procedure is as follows.

First, we express the electronic structure Hamiltonian as a linear combination of unitaries (LCU), i.e.,

$$H=\mathop{\sum }\limits_{\ell =0}^{L-1}{w}_{\ell }{H}_{\ell }{H}_{\ell }^{2}={\bf{1}}$$

(24)

where ${w}_{\ell }\in {{\mathbb{R}}}_{0}^{+}$ and H_ℓ are self-inverse operators on n qubits. In particular, H is the Hamiltonian that arises from performing Galerkin discretization of the Hamiltonian under the plane-wave basis functions as described in Methods C. Next, we encode the Hamiltonian spectra in a Szegedy quantum walk W defined as

$$W=R\cdot SELECT,R=2| {\mathcal{L}}\rangle \langle {\mathcal{L}}| \otimes {\bf{1}}-{\bf{1}}.$$

(25)

where $| {\mathcal{L}}\rangle$ is a state that can be prepared by the “preparation oracle”, referred to as PREPARE, and SELECT is the “Hamiltonian selection oracle”. PREPARE is defined as

$$PREPARE\equiv \mathop{\sum }\limits_{\ell =0}^{L-1}\sqrt{\frac{{w}_{\ell }}{\lambda }}| \ell \rangle \langle 0| ,$$

(26)

$$PREPARE{| 0\rangle }^{\otimes \log L}\mapsto \mathop{\sum }\limits_{\ell =0}^{L-1}\sqrt{\frac{{w}_{\ell }}{\lambda }}| \ell \rangle \equiv | {\mathcal{L}}\rangle$$

(27)

with λ (1-norm) defined as $\lambda ={\sum }_{\ell =0}^{L-1}{w}_{\ell }$, and SELECT is defined as

$$SELECT\equiv \mathop{\sum }\limits_{\ell =0}^{L}| \ell \rangle \langle \ell | \otimes {H}_{\ell },$$

(28)

$$SELECT| \ell \rangle | \psi \rangle \mapsto | \ell \rangle {H}_{\ell }| \psi \rangle .$$

(29)

Note that R and SELECT are both reflection operators, ensuring that W takes the form of a Szegedy walk. In particular, W exhibits a block-diagonal structure with each block corresponding to a two-dimensional subspace spanned by $\{| 0\rangle | {\phi }_{k}\rangle ,| {\psi }^{\perp }\rangle \}$, where $| {\phi }_{k}\rangle$ is an eigenstate of H with eigenvalue E_k, and $| {\psi }^{\perp }\rangle$ is a state that is orthogonal to $| 0\rangle | {\phi }_{k}\rangle$. Furthermore, within the subspace $\{| 0\rangle | {\phi }_{k}\rangle ,| {\psi }^{\perp }\rangle \}$, W acts as follows:

$$W| 0\rangle | {\Phi }_{k}\rangle =\cos ({\theta }_{k})| 0\rangle | {\Phi }_{k}\rangle -\sin ({\theta }_{k})| {\psi }^{\perp }\rangle ,$$

(30)

$$W| {\psi }^{\perp }\rangle =\cos ({\theta }_{k})| {\psi }^{\perp }\rangle +\sin ({\theta }_{k})| 0\rangle | {\Phi }_{k}\rangle .$$

(31)

where $\cos ({\theta }_{k})={E}_{k}/\lambda$. The qubitization procedure exploits this structure to encode spectral information in the phase of W, enabling the use of QPE on W to efficiently extract eigenvalues of H. The λ parameter has a significant impact on the computational cost of the algorithm and is therefore an important parameter in the resource estimation. Hence, we report this value for each of the instances considered in this paper as shown in Supplementary Materials. The overall algorithm can be implemented with a quantum circuit as shown in Fig. 7. Note that this particular implementation of the QPE circuit differs from the standard approach, where one typically applies a controlled operation on each of the ${W}^{{2}^{k}}$ operators. In this implementation, instead of leaving the ancilla qubit in the $| 0\rangle$ state unchanged, we apply an inverse unitary. This adjustment effectively doubles the effectiveness of the phase estimation procedure. It can be achieved by simply removing the controls from the ${W}^{{2}^{k}}$ operators and inserting controlled reflection operators R into the circuit, as shown in Fig. 7. We discuss the implementation of each component in the first quantization framework in more detail in the Supplementary Materials. We also discuss the implementation of this algorithm in the second quantization framework, following the Linear-T encoding by Babbush et al.¹⁷. The code for our implementation is available in ref ²³.

Fig. 7: Quantum circuit illustration of quantum phase estimation algorithm based on qubitization.

This algorithm queries powers of the qubitized walk operator W instead of the standard time evolution oracle. The eigenphases ϕ_k of W have a simple functional relation with the eigenenergies E_k of H. Specifically, ${\phi }_{k}\approx \arccos ({E}_{k}/\lambda )$, where λ is a normalization factor in the block encoding procedure of H and can be taken as the 1-norm of H. This relationship allows us to extract the eigenenergies using phase estimation.

A major factor in the computational expense of using QPE for ground-state energy estimation lies in choosing the initial state for the algorithm. The success probability of QPE depends on how well this initial state overlaps with the true ground state. In particular, the likelihood of successfully projecting onto the ground state scales inverse polynomially with the overlap between the initial state and the true ground state.

In much of the quantum computing for quantum chemistry literature, the initial state is determined by the Hartree-Fock (HF) state–a single Slater determinant used as the starting point for QPE. Although HF works well for smaller chemical systems, there are concerns about its ability to achieve adequate overlap with the true ground state in larger systems. Since initial state preparation is beyond the purview of this work, we defer this discussion to Supplementary Materials.

Tools and methodology

The pyLIQTR workflow consists of specifying a Hamiltonian, selecting a block encoding, and building the circuit for the desired algorithm based on those choices. One feature of the pyLIQTR circuits is their hierarchical nature, where the top-level circuit is the entire qubitized algorithm which can then be decomposed in stages all the way down to one and two qubit gates. This structure allows for more efficient resource estimation, since repeated elements can be analyzed once with the result cached and used again later.

The circuits for our application instances were generated as follows. First, the Hamiltonian coefficients for the PW basis output by PEST were fed into the pyLIQTR circuit generation framework. Then the pyLIQTR implementation of the first quantization of the electronic structure block encoding presented in ref. ⁴⁶ was chosen. Next, the qubitized phase estimation circuit was generated for an error target of 0.001. Finally, this circuit was passed into the pyLIQTR resource estimation protocol.

The pyLIQTR resource estimation protocol is built atop Qualtran’s T-complexity methods⁵¹ and can be used to determine the Clifford+T cost of any circuit generated with pyLIQTR. For a given circuit, the resources reported by pyLIQTR include logical qubits, T gates, and Clifford gates. The gate counts include the additional T and Clifford gates from rotation synthesis, which are estimated using a heuristic model that depends on the user specified rotation gate precision. The resource costs of the quantum circuit are determined, in part, by the desired precision and accuracy of the final output. During the circuit design stage, a number of precision bounds are chosen to ensure that the quantum output attains a specified additive error ε in energy. For the resources reported in this work, a gate precision of 10⁻¹⁰ was used, well below the ~ 10⁻⁶ typically sufficient for ε = 10⁻³ (chemical accuracy). Therefore, our resource estimate values will be higher than actually needed.