Metastable photo-induced superconductivity far above T_c

Abstract

Inspired by the striking discovery of metastable superconductivity in K₃C₆₀ at 100K, far above T_c = 20 K, we discuss possible mechanisms for long-lived, photo-induced superconductivity. Starting from a model of optically-driven Raman phonons coupled to inter-band electronic transitions, we develop a microscopic mechanism for photo-controlling the pairing interaction. Leveraging this mechanism, we first investigate long-lived superconductivity arising from the thermodynamic metastable trapping of the driven phonon. We then propose an alternative route, where the superconducting gap created by an optical drive leads to a dynamical bottleneck in the equilibration of quasi-particles. We conclude by discussing the implications of both scenarios for experiments that can be used to discriminate between them. Our work provides falsifiable explanations for the nanosecond-scale photo-induced superconductivity found in K₃C₆₀, while simultaneously offering a theoretical basis for exploring metastable superconductivity in other quantum materials.

Introduction

Breakthroughs in the structural control of matter using intense, infrared (IR) light have enabled the exploration of quantum order outside of the confines of thermal equilibrium^1,2. From photo-induced ferroelectricity in SrTiO₃^3,4 to laser-driven charge density wave ordering in LaTe₃^5,6 to optically-stabilized ferromagnetism in YTiO₃⁷ to transient, light-induced superconductivity in layered cuprates^8,9,10, a striking array of experiments have traced a path towards the photo-control of complex, quantum materials, a focal project for modern condensed matter. Among the most captivating puzzles in this field is the metastable superconductivity uncovered in K₃C₆₀, far above T_c = 20 K^11,12,13,14. In the K₃C₆₀ experiments, signatures of photo-induced superconductivity at T = 100 K were observed to persist over 10 nanoseconds after driving, 1000 times longer than any microscopic time-scale in the experiment. The staggering longevity of this response can be further appreciated when contrasted with the lifetime of the transient superconductivity observed in, e.g., driven cuprates^9,10, where optical superconducting signatures dissipate within the picosecond scale ring-down time of the resonantly driven apical oxygen phonon. Conceptualizing the K₃C₆₀ experiments thus poses a double-headed challenge: it demands both a microscopic mechanism for photo-induced superconductivity—a topic that has invited intense theoretical attention^{15,16,17,18,19,20,21,22,23,24,25,26,27,28,29,30,31,32,33,34,35}—and an explanation for its metastability.

Galvanized by the experiments performed in K₃C₆₀, we take on both questions. Within an experimentally motivated minimal model, we first describe a microscopic mechanism for non-equilibrium superconductivity arising from the photo-displacement of a local Raman phonon coupled to the inter-band transition between two narrow electronic bands. We then lay out two distinct paradigms for non-equilibrium superconductivity that persist long after driving and provide emergent life times for the superconducting state. We first compute the adiabatic free energy landscape of our model as a function of the induced structural distortion, uncovering thermodynamically metastable superconductivity far above T_c. We then advance a dynamical route to long-lived superconductivity—we call this quasi-particle trapping. We argue that photo-inducing a large superconducting gap during driving can lead to bottlenecks in the equilibration of quasi-particles; the slow equilibration of quasi-particles then enables the formation of a non-thermal superconducting gap. We find that both pictures may provide inroads toward conceptualizing metastable photo-induced superconductivity in K₃C₆₀ and other molecular superconductors.

Results

Model for photo-control pairing

Inspired by aspects relevant to superconductivity in alkali-doped fullerides—strong, local electron-phonon coupling and narrow bands—we begin with a minimal model that couples dispersionless optical Raman phonons to the local inter-orbital transition between two electronic states. The electrons are allowed to weakly tunnel across sites on a three-dimensional lattice. Specifically, our Hamiltonian H is given by

$$H={H}_{0}+{H}_{{\rm{int}}}+{H}_{{\rm{K}}},$$

(1)

where ${H}_{0}=-\frac{\Delta E}{2}{\sum }_{i,\sigma }({c}_{i,\sigma }^{\dagger }{c}_{i,\sigma }-{d}_{i,\sigma }^{\dagger }{d}_{i,\sigma })+{\sum }_{i}\frac{{P}_{i}^{2}}{2M}+\frac{M{\omega }^{2}}{2}{Q}_{i}^{2}$, the electron-phonon interaction is ${H}_{{\rm{int}}}=g{\sum }_{i,\sigma }{Q}_{i}({c}_{i,\sigma }^{\dagger }{d}_{i,\sigma }+{d}_{i,\sigma }^{\dagger }{c}_{i,\sigma })$, and the (weak) nearest neighbor hopping Hamiltonian is ${H}_{{\rm{K}}}=-t{\sum }_{\langle i,j\rangle ,\sigma }({c}_{i,\sigma }^{\dagger }{c}_{j,\sigma }+{d}_{i,\sigma }^{\dagger }{d}_{j,\sigma }+h.c.)$. Here ${c}_{i,\sigma }^{\dagger }({d}_{i,\sigma }^{\dagger })$ creates a c (d)-electron with spin σ ∈ {↑, ↓} at site i; P_i and Q_i are the momentum and position coordinates for a phonon of frequency ω and mass M at site i; ΔE is the splitting between levels c and d; g is the electron-phonon coupling. We concern ourselves with a system in which the c-band is partially filled at equilibrium.

We consider what happens when the mean local Raman coordinate $\left\langle Q\right\rangle$ is homogeneously distorted by driving the system with intense, off-resonant laser light. For orientation, in the experiments performed on K₃C₆₀¹³, the solid is driven at 41 THz, whereas relevant, strongly coupled Raman phonons are found below 22 THz. Furthermore, as they are inversion symmetric, Raman modes are driven by the laser non-linearly through the Hamiltonian, H_R ∝ E²(t)Q, where E(t) is the electric field of the laser light^36,37. Non-linear, off-resonant driving rectifies the average position of the Raman mode during driving, displacing $\left\langle Q\right\rangle$ and hybridizing the upper and lower bands. To build intuition for this hybridization, we examine the limit of $g\langle Q\rangle\, \ll \,\Delta E$. Shifting $\left\langle Q\right\rangle$ facilitates virtual, inter-orbital transitions between occupied c and unoccupied d levels. A pair of c electrons at the same site can energetically benefit from this virtual tunneling and form a local, singlet pair. As the tunneling is enhanced by increasing $\left\langle Q\right\rangle$, shifting $\left\langle Q\right\rangle$ photo-enhances local pair formation. We rigorize this intuition by deriving in the “Methods”, for instantaneous $\left\langle Q\right\rangle$, an attractive Hubbard Hamiltonian for effective lower-band f electrons:

$${H}_{{\rm{eff}}}=\sum _{k,\sigma }{\xi }_{k}{f}_{k,\sigma }^{\dagger }{f}_{k,\sigma }-\frac{U}{N}\sum _{\begin{array}{c}k,{k}^{{\prime} }\\ | {\xi }_{k}| ,| {\xi }_{k}^{{\prime} }| < \omega \end{array}}{f}_{k,\uparrow }^{\dagger }{f}_{-k,\downarrow }^{\dagger }{f}_{{k}^{{\prime} },\uparrow }{f}_{-{k}^{{\prime} },\downarrow },$$

(2)

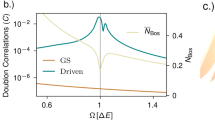
where ξ_k = ϵ_k − μ and ϵ_k is the free electron energy dispersion. For a fixed value of $\left\langle Q\right\rangle$, we find that the induced attraction is given by (Fig. 1):

$$U={U}_{0}+\frac{{g}^{2}}{M{\omega }^{2}}\frac{4{g}^{2}{\left\langle Q\right\rangle }^{2}}{\Delta {E}_{{\rm{eff}}}^{2}},$$

(3)

where $\Delta {E}_{{\rm{eff}}}=\sqrt{\Delta {E}^{2}+4{g}^{2}{\left\langle Q\right\rangle }^{2}}$ and U₀ is the net attractive interaction arising from extrinsic pairing mechanisms that give rise to equilibrium superconductivity for the undistorted material. Photo-distorting the strongly coupled Raman mode thus allows us to dynamically enhance the pairing strength. We note here, that while a static distortion within the model of equation (1) always enhances attraction mediated by inter-band coupled phonons, it may reduce attraction mediated by intra-band coupled phonons not included in this model. We analyze such an extended model in the “Methods” section, where we discuss under which conditions equation (3) is valid.

Photo-induced metastability

We first investigate the feasibility of the conventional picture of a long-lived superconducting state accessed by optically driving the material into a hidden, thermodynamically metastable phase² within the scope of our microscopic mechanism. To do so, we examine the free energy of the combined electron-Raman phonon system as a function of $\left\langle Q\right\rangle$ (hereafter Q), which captures the free energetic trade-off between the benefit of a displacively induced distortion Q—leading to enhanced U and a stronger superconductor—and the elastic cost of the distortion. We ascertain under what conditions the free energy has a non-trivial local minimum—thereby a thermodynamically metastable state—which can be accessed via (sufficiently strong) optical driving. After driving the phonon coordinate into such a metastable trap, a return to equilibrium proceeds through slow thermal nucleation.

Fig. 1: Photo-control of superconductivity.

Schematic plot of the attractive pairing strength between electrons as a function of the photo-induced structural distortion: Inducing local structural distortions (e.g., distorting the on-ball Hg(3) mode in K₃C₆₀) via laser driving provides a route towards controlling superconductivity in molecular solids with light.

Within a mean-field analysis, developed in the “Methods”, we uncover two types of metastability and, for parameters relevant to K₃C₆₀, provide a phase diagram delimiting their boundaries provided in Fig. 2b) as a function of the effective density of states at the Fermi energy ν(0) and the band-splitting ΔE for a particular distorted phonon with electron-phonon coupling g and frequency ω. The first type, metastability I (Fig. 2a) corresponds to a scenario in which the undistorted state is always the equilibrium state and a metastable state with finite distortion and stronger superconductivity exists between 0 < T < T_B. Above T_B, the free energy monotonically increases with Q, and the metastable state becomes untrapped, as shown by the gray landscape in Fig. 2a. Metastability II, occurs when at, low-temperatures, a distorted state is energetically favorable (see Fig. 2c). Here, equilibrium superconductivity exists until a critical temperature T_c where a first order phase transition occurs and the superconductivity-inducing distortion is no longer free energetically favorable. In metastability II, optically switchable superconductivity is possible for T_c < T < T_B. A prominent, equilibrium, experimental signature accompanying metastability II is the presence of a distortion-driven, first-order superconducting phase-transition.

Fig. 2: Thermodynamically metastable superconductivity.

Metastability diagram (b) for metastable superconductivity at fixed electron-phonon coupling $\frac{g{\ell }_{0}}{\omega }=0.6$ and (second order) T_c = 20 K as a function of the level splitting ΔE and density of states at the Fermi level ν(0). Distinct regimes of metastability are presented: metastable I (green) and metastable II (blue), with DFT parameters for K₃C₆₀ indicated. Schematic free energy landscape for metastable I (a), depicted across three temperatures—T = 0 (light red), T > T_c (dark red), T > T_B (gray). (Inset) Comparison between the gap in the metastable state, Δ_MS, and the gap in equilibrium Δ(T). c Free energy landscapes at T ≪ T_c corresponding to metastable I (left) and metastable II (right) as a function of Δ and Q, in units of ω and ${\ell }_{0}=\frac{1}{\sqrt{m\omega }}$. In metastable I, The undistorted state is the global free energy minimum: in metastable II, the state with a larger gap due to distortion is the ground state.

In “Methods”, we detail the mapping between our model and K₃C₆₀, with an eye towards capturing details around the Fermi Energy, E_F. We associate our lower, c band with the lower-lying t_1u bands crossing the Fermi energy in K₃C₆₀ and the driven phonon mode to strongly coupled, inter-orbital, on-ball Jahn-Teller Hg phonons. In particular, we identify the 22 THz Hg(3) phonon as the phonon whose free energy is most susceptible to hosting a metastable state due to its combination of high-frequency and strong electron-phonon coupling. We note that while the effective parameters translated from DFT (top left, Fig. 2b) lie outside the metastability region, even equilibrium superconductivity in K₃C₆₀ cannot be accounted for by using the DFT band-structure. Instead, strong electronic correlations—arising from the proximity of K₃C₆₀ in equilibrium to the Mott insulator phase—can significantly quench the electronic kinetic energy and reshape the band structure, engendering thermodynamic metastability^38,39. A distinct signature for metastability is the presence of Jahn-Teller static distortion. For the Hg(3) phonon, such a distortion is at the pico-meter scale, which, while small, is detectable by ultra-fast, time-resolved diffraction experiments in sufficiently clean systems.

Quasi-particle trapping

In the absence of a metastable trap (e.g., as occurs in the normal region in Fig. 2b), metastable superconductivity can still arise from the slow equilibration of Bogolyubov quasi-particles, a mechanism we name quasi-particle trapping. We begin by considering an undistorted superconductor above T_c. We then imagine displacing Q to a large Q^*, inducing a large pairing attraction U*, where it is held long enough to quasi-equilibrate to a BCS superconducting state with a sizeable gap Δ(Q^*, T) and low quasi-particle density n*.

After the drive shuts off, given the lack of a metastable trap, the phonon coordinate relaxes from Q* to Q = 0, relaxing the pairing strength from U* to U₀. This relaxation occurs over the ring-down time τ_r of the perturbed Raman mode, the timescale for the driven excitations to damp out. In the K₃C₆₀ experiments τ_r ~ 10 ps¹³. While this is short compared to the lifetime of the metastable superconductor, it is far slower than the inverse gap. Thus while a careful consideration of diabatically excited pairs is necessary if the interaction was quenched from U* to U₀⁴⁰, as the relaxation proceeds adiabatically from the perspective of the superconductor, such effects are negligible. As Q is relaxed back to 0 and U relaxes back to U₀, in order for the electrons to equilibrate, quasi-particles need to be generated out of the condensate via phonon-induced pair-breaking processes (Fig. 3).

Fig. 3: Quasi-particle trapping.

Schematic of the “quasi-particle” trapping mechanism for long-lived superconductivity. Starting from the metallic phase, displacively driving the phonon coordinate Q from 0 to Q* and holding it there photo-induces a superconductor with a gap Δ* with a quasi-particle density n^*, which is smaller than the thermal quasi-particle density in the metal. After driving for τ_dr, the drive is switched off, and the phonon relaxes to Q = 0. However, due to suppressed pair-breaking rates ${\tau }_{g}^{-1}$, the quasi-particle density equilibrates slowly, enabling a non-thermal state with gap Δ. (Inset) The dynamics of the photo-induced superconducting gap, persist out-of-equilibrium for τ_MS, until an eventual avalanche collapse.

We argue that this process is slow. A large superconducting gap can make scattering processes, which conserve quasi-particle numbers dramatically faster than those that alter the quasi-particle number^41,42—While number-conserving quasi-particle scattering involves phonons at arbitrarily low energies, quasi-particle generation, for example, requires the absorption of thermally-populated phonons above 2Δ. In the presence of a large gap, the drastic separation of time-scales between the short number-conserving quasi-particle scattering time and much longer quasi-particle generation and recombination time-scales implies that while the electronic temperature is fixed to the phonon bath temperature due to fast number conserving scattering, the non-equilibrium quasi-particle density evolves slowly.

Drawing from such considerations, we describe the evolution of the superconducting state after the relaxation of the displaced phonon using an effective, sparse encoding of the quasi-particle spectrum and distribution in terms of two slow variables: the superconducting gap Δ(t) and a Bogolyubov chemical potential, λ(t), respectively. Here, λ(t) is used to constrain the instantaneous quasi-particle density to a non-thermal value. The joint dynamics of Δ(t) and λ(t), after the relaxation of the displaced phonon, can be modeled by solving self-consistent equations for the instantaneous Bogolyubov chemical potential and superconducting gap coupled with an equation for the quasi-particle population dynamics—for details, see the “Methods” section.

The instantaneous superconducting gap Δ(t) is given by a modified BCS equation with Debye cutoff ω:

$$\frac{1}{\nu (0){U}_{0}}=\mathop{\int}\nolimits_{0}^{\omega }d\xi \frac{1}{\sqrt{{\xi }^{2}+\Delta {(t)}^{2}}}\tanh \left(\frac{\sqrt{{\xi }^{2}+\Delta {(t)}^{2}}+\lambda }{2T}\right),$$

(4)

which involves a non-equilibrium quasi-particle distribution parameterized by λ: $n(\omega )={(\exp \left(\beta (\omega +\lambda (t))\right)+1)}^{-1}$. Removing thermal quasi-particles (corresponding to λ > 0) by opening up a large gap during driving enables superconductivity above the equilibrium T_c, by enabling a greater number of near-degenerate electrons to resonantly participate in pairing. Note that this concept also lies at the core of other mechanisms to enhance superconductivity, such as quasi-particle extraction⁴³ and the Eliashberg Effect⁴⁴, the latter developed to conceptualize the enhancement of T_c in microwave-driven superconductors^45,46. We underscore that for large λ (small n), Eq. (4) reduces to the BCS equation at T = 0, a perfect extraction of thermal quasi-particles. Therefore, Δ → Δ(U₀, T = 0) as n → 0.

Alongside Eq. (4), a constraint for the instantaneous quasi-particle density n(t), allows us to fix λ(t):

$$n(t)=4\nu (0)\mathop{\int}\nolimits_{0}^{\omega }d\xi \frac{1}{\exp \left(\beta \left(\sqrt{{\xi }^{2}+\Delta {(t)}^{2}}+\lambda (t)\right)\right)+1}.$$

(5)

Finally, we derive the net dynamics of the quasi-particle density, balancing quasi-particle generation and quasi-particle recombination due to phonon scattering:

$$\frac{dn}{dt}=\frac{\pi }{2\hslash }\mathop{\int}\nolimits_{2\Delta (t)}^{W}d\Omega \,{\alpha }^{2}(\Omega )F(\Omega )\Gamma (\Omega ),$$

(6)

where the phonon-frequency dependent net quasi-particle generation rate, Γ(Ω), given by

$$\Gamma (\Omega )={\Omega }^{\frac{1}{2}}{\left(\Omega -2\Delta \right)}^{-\frac{1}{2}}{\rm{csch}}\left(\frac{\Omega }{2T}\right)\times {\rm{sech}} \left(\frac{\Delta +\lambda }{2T}\right){\rm{sech}} \left(\frac{\Omega -\Delta +\lambda }{2T}\right)\sinh \left(\frac{\lambda }{T}\right),$$

(7)

is weighted by the Eliashberg function, α²(Ω)F(Ω), the electron-phonon coupling weighted phonon density of states; where the minimum phonon frequency to break/form Cooper pairs is given by 2Δ(t), and the maximum phonon frequency is set by the electronic bandwidth W, the largest electronic energy transfer possible for dissipative, resonant electron-phonon scattering. As expected, λ > 0—a dearth of quasi-particles compared to equilibrium—implies a net generation of quasi-particles, as is required for equilibration.

A brief comment on the initial conditions of our post-relaxation dynamics is in order. First, note that we operate under the following ordering of time-scales: $\frac{1}{\Delta (0)}\,\ll \,{\tau }_{{\rm{eq}}}$, where ${\tau }_{{\rm{eq}}}^{-1}=\frac{dn}{dt}{| }_{t = 0}$. This implies that during the relaxation of the phonon, the quasi-particle density is frozen, therefore n(0) = n*, the quasi-equilibrium, quasi-particle density attained upon driving. However, as U has relaxed to the equilibrium attraction U₀, the initial gap Δ(0) is given by the solution of Eq (4), with U₀ and λ(n^*). $\Delta (0) \sim {\mathcal{O}}(\Delta (T=0))$ is typically much smaller than Δ*.

In a solid with an unstructured phonon continuum, the transient gap will generically collapse rapidly as quasi-particle generation decreases the gap, increasing the quasi-particle generation rate and leading to an “avalanche” feedback loop. K₃C₆₀ and other molecular solid superconductors, however, possess a crucial structural motif in their phonon spectra: A continuum of low-frequency inter-molecular modes (e.g., acoustic, librational modes) and relatively sharp, high-frequency, local intra-molecular vibrational modes, separated by a sizeable phonon gap. If after the driven phonon relaxes, 2Δ(0) lies inside the phonon gap, the avalanche collapse of the gap is prevented, and the gap decreases instead very slowly due to quasi-particle generation from thermally suppressed high-frequency intra-molecular modes. This slow evolution of the gap persists until it reaches the upper bound of the inter-molecular continuum ${\Omega }_{\max }$, after which the gap avalanche collapses.

Remarkably, this optimistic scenario is viable in K₃C₆₀. While the precise nature of electron-phonon coupling in the material is intensely debated³⁶, an incontrovertible aspect of the phonon spectrum is the existence of a large phonon gap between inter- and intra-molecular modes: Neutron scattering experiments⁴⁷ find a precipitous drop in the phonon density of states starting at 6 meV, persisting to 28 meV. Moreover, an estimate of the Eliashberg function computed from an inversion of reflectance data^47,48 implies that α²(Ω)F(Ω) is negligible in the vicinity of 10–33 meV. On the other hand, experimentally measured values of 2Δ(T = 0 K)—the largest initial 2Δ(0), achievable via “perfect quasi-particle extraction”—is believed to lie within this gap^49,50. Furthermore, a conservative estimate of the gap extracted from optical conductivity in the photo-induced metastable state is consistent with $2\Delta \sim 14\,{\rm{meV}}\, > \,{\Omega }_{\max } \sim 6-10\,{\rm{meV}}$¹¹.

If 2Δ(0) lies in the phonon gap, a steady build-up of quasi-particles occurs at a roughly fixed rate, ${\tau }_{{\rm{g}}}^{-1}$, set by the molecular vibrational modes above 2Δ, until the avalanche density n_av—the quasi-particle density corresponding to a transient gap of ${\Omega }_{\max }/2$—is reached. Thus, an approximate lifetime of the superconducting state is given by τ_MS ≈ n_avτ_eq, where for a set of sharp, vibrational modes Ω_ν ≫ T, Δ(0), τ_eq is:

$${\tau }_{{\rm{eq}}}^{-1}=\sum _{\nu }{g}_{\nu }^{2}\,{\nu }_{{\rm{SC}}}\left({\Omega }_{\nu }-\Delta (0)\right)\exp \left(-\frac{{\Omega }_{\nu }}{T}\right),$$

(8)

with g_ν, the electron-phonon coupling for mode ν, and ν_SC, the superconducting density of states. As discussed in detail in “Methods”, choosing realistic, albeit optimistic, ab initio estimates of parameters that model the simultaneous suppression of charge fluctuations and electronic bandwidth due to strong repulsive interactions^36,38,39, alongside weak Hg(1) coupling⁵¹ in K₃C₆₀, allows us to estimate a metastable lifetime of nearly 20 ns at 100 K. Furthermore, as shown in Fig. 4, depleting the quasi-particle density during driving to a value below but at the order of the threshold density n_av is sufficient to reach the 10 ns scale lifetime observed in the experiment.

Fig. 4: Metastable lifetime & avalanche threshold.

The superconducting excitation gap 2Δ (orange) and the corresponding lifetime of the quasi-particle trapped state τ_MS (navy) as a function of the density of quasi-particles n ≡ n(0) after driving. Reducing the quasi-particle density below a threshold n_av avoids the rapid, avalanche collapse of the gap. Experimentally plausible parameters for K₃C₆₀ reproduce the nanosecond scale lifetime observed in experiments for sufficiently strong driving.

Discussion

In our work we first present a microscopic mechanism for inducing non-equilibrium superconductivity by photo-distorting inter-band Jahn-Teller modes. We subsequently offer two alternate paradigms for metastability: first, a conventional picture of optically switching into a hidden thermodynamically metastable state, and second, a dynamical paradigm for metastable superconductivity resulting from the slow thermalization of quasi-particles. In our quantitative considerations, we find while both mechanisms are not beyond physical plausibility, quasi-particle trapping can yield the staggering experimentally observed lifetime within assumptions that are supported by optimistic ab initio estimates from the literature.

Before continuing further, we situate our work within the broader context of contemporary theory work^{15,16,17,18,19,20,21,22,23,24,25,26,27,28,29,30,31,32,33,34,35} addressing questions that arise from the recent experiments on the optical control of superconductivity^8,9,11,13. In our ultra-fast review, we focus on the literature concerning K₃C₆₀. While certainly fascinating in their own right, photo-control of superconductivity in LSSCO^8,19—where competing charge density order is melted by an ultrafast pulse—and underdoped YBCO^9,24,25,26—where the theoretical work has primarily focused on the non-linear dynamics of Josephson plasmons in the pre-formed pair regime—are not clearly relevant to K₃C₆₀ where, despite recent experiments hinting otherwise⁵², pairing is not believed to occur at the temperatures (from 100–300 K) in which photo-control is observed. We also acknowledge but do not discuss in detail, works that seek to leverage Floquet engineering techniques^20,27,30, which have been experimentally demonstrated in ultracold atoms, to optically induce (transient) pair correlations at elevated temperatures.

With regard to photoinduced superconductivity in K₃C₆₀, as mentioned in the Introduction, theorists have focused on the microscopics of how laser driving can possibly give rise to pairing far above T_c, primary, although not exclusively^17,21,31, focusing on phononic pairing mechanisms. A crucial problem that was identified early on is that linear driving of the paradigmatic linear electron-phonon, as encoded in the Holstein model, could not explain the photo-induced enhancement of pairing¹⁶. Subsequent studies examined two workarounds, finding enhanced pairing by either resonantly driving non-linearly coupled IR vibrational modes^15,35,53 or parametrically driving linearly coupled Raman modes^16,18,29. While these studies were schematically successful in reproducing gross features of the K₃C₆₀, although not without their discontents^22,34, the microscopics they prescribe are hard to reconcile with the material facts of K₃C₆₀ where the possibly resonant IR modes are insufficiently coupled to electrons³⁶ and where the relevant drive frequency is far above the parametric resonance condition for strongly coupled Raman modes. The microscopics we articulate in this work deal with off-resonantly driven but strongly coupled Raman modes, both features that have not been examined within the literature, both features that are highly relevant to the microscopics of K₃C₆₀. Crucially, we show that photo-controlling a linearly coupled inter-band electron phonon coupling by off-resonant driving is a physical mechanism for the putative pairing enhancement observed in K₃C₆₀. As noted before, our considerations of the mechanisms for nanosecond scale metastability, an aspect uncovered in relatively recent experiments¹³, is an entirely novel consideration. Subsequent work⁴⁰ has examined the short-term post-driving dynamics of the superconducting state within a similar physical context to “quasi-particle” trapping but has focused largely on picosecond scale coherent dynamics, making no claims about the nanosecond scale metastability.

The two metastable pictures presented in our manuscript can be distinguished by performing Rothwarf-Taylor-style quasi-particle injection experiments in the metastable state⁴¹. Here, one would expect that the quasi-particle trapped state should be significantly more susceptible to gap collapse than the thermodynamically metastable superconductor upon injection of quasi-particles: For the latter, once a density of n_av quasi-particles is reached, avalanche collapse is inevitable. Another key distinguishing feature between the two pictures is the size of the metastable gap. Whereas in the quasi-particle trapping scenario, the metastable gap is bounded by the zero temperature gap, a thermodynamically metastable state typically has a much larger superconducting gap than in equilibrium (see Fig. 2a inset as an example). Accurate experimental extraction of the non-equilibrium superconducting gap may also be used to discriminate between quasi-particle trapping and thermodynamic metastability mechanisms.

In addition, systematically examining the metastable lifetime under pressure could offer an additional test for the quasi-particle trapping mechanism. Qualitatively, one should expect that as the pressure is increased, the metastable lifetime of the quasi-particle trapped state should go down. Applying pressure in alkali-doped fullerides in the metallic phase is believed to increase the bandwidth as applied pressure moves the system away from the Mott transition³⁹. Increasing the bandwidth shifts density of states away from the Fermi energy towards the tails. Thus, it increases the quasi-particle generation rate, while the decreased ν(0) lowers the zero-temperature gap. Furthermore, an increasing in pressure typically corresponds to an increase in the Debye frequency of acoustice modes, ${\Omega }_{\max }$, lowering n_av, possibly to 0, if 2Δ(0) becomes smaller than ${\Omega }_{\max }$. While this prediction is consistent with previous experiments which uncovered that applied pressure destroys photo-induced superconductivity in K₃C₆₀(ref. ¹²), these experiments neither observed nor interrogated the lifetime of the effect.

This work opens up several directions for future investigation. Given the central role that strong repulsive interactions play, subsequent work should rigorously examine the interplay between strong Mott repulsion and Jahn-Teller pairing in the driven setting, seeking to resolve if the cooperation between the two that is implicated in equilibrium^36,38 extends to the photo-induced case.

Future work addressing metastable superconductivity without invoking a thermodynamically hidden metastable state should also aim to resolve the (drastic) asymmetry between the longevity of the state and the time it takes to prepare it. In the quasi-particle trapping scenario articulated above, we claimed by postulate that, through laser-driving, a quasi-equilibrium state with a large gap Δ* and significantly reduced quasi-particle density n* could be realized. Naively, thermalizing towards a state with a large induced attractive interaction would require significant quasi-particle recombination, which, like quasi-particle generation, is very slow compared to number-conserving scattering for superconductors with a large gap. A first-order concern may be that given that recombination is slow, preparing a metastable quasi-particle trapped superconductor necessitates driving for long times.

Such anxieties can be partially addressed. The asymmetry between the preparation time and lifetime of the state, in this case, could arise from a distinct asymmetry between quasi-particle recombination and quasi-particle generation rates: While the latter involves phonon emission, the former involves absorption. Thus, while generation is bottlenecked by a lack of thermal photons, recombination is slow because of a lack of thermally populated quasi-particles⁴¹. Notice, however, that when preparing the quasi-particle trapped state, one starts with an excess of quasi-particles, implying that recombination is fast at the beginning of driving (within a minimal quasi-particle kinetics model, the optimal ratio between lifetime and preparation time at T = 100 K is 30, consistent with the longest drive durations reported in the experiment¹³).

Beyond quasi-particle kinetics, one may speculate that for shorter drive durations, the dynamical instabilities implicated in the formation of the superconducting gap play a crucial role. Indeed, theoretical analysis of instantaneous quenches of the Feschbach-mediated pairing interaction in ultra-cold fermions suggests that the gap formation dynamics are governed by the near-integrable dynamics of the superconductor, not quasi-particle kinetics⁵⁴. In particular, in the cold atoms setting, for a rapid quench from a free Fermi gas to a superconductor with a large gap Δ^*, the order parameter grows exponentially with rate γ ~ Δ* to $\Delta \sim {\mathcal{O}}({\Delta }^{* })$, followed by damped solitonic oscillations for T ≪ Δ^*. Naively extrapolating these results to the regime where the drive duration Δ*τ_dr ≫ 1 implies that a gap on the order of Δ* should form over a time scale shorter than τ_dr. Such considerations inspire future investigations of the precise interplay between dynamical instabilities and quasi-particle kinetics in solid-state superconductors at finite temperatures, studies which should illuminate how the non-equilibrium superconducting state can be robustly formed from metal at incredibly short times—empirically, as short as 1.5 ps.

Finally, we advertise that recent experiments¹⁴ uncover not only a resonant enhancement of photo-induced superconductivity for driving between 11 and 15 THz—enabling superconductivity at significantly lower intensities—but also, tantalizingly, non-equilibrium superconductivity at room temperature. While these experiments do not interrogate metastability explicitly, they reveal that signatures of superconductivity do not vary over at least 50 ps. Intriguingly, the lifetime of a quasi-particle trapped state at room temperature—using the same parameters used to attain a lifetime of 20 ns at 100 K—is 0.4ns, far exceeding this experimental lower bound. On the microscopic side, the resonant features around 11 THz are suggestive of photo-induced superconductivity arising from the resonant driving—vis-a-vis, displacive excitation—of the 22 THz Hg(3) phonon. The non-equilibrium dynamics of a driven phonon coupled to inter-band transitions were recently considered, albeit in a different experimental context, by some of the authors⁵⁵, showing the enticing opportunity of resonantly enhanced transient superconductivity. Interrogating whether such effects are indeed metastable demands understanding the competition between resonantly enhanced superconductivity and amplified electronic dissipation, a daunting challenge to grapple with in future investigations.

Methods

$\left\langle Q\right\rangle$-dependent superconductivity

In this section, using a local electron-phonon coupling model, we derive a $\left\langle Q\right\rangle$ dependent BCS-type s-wave pairing interaction by performing a judiciously chosen rotation and a disentangling Schrieffer-Wolff transformation. We begin by diagonalizing the solely electronic part of the Hamiltonian of Eq. (1) in momentum space:

$$H=\mathop{\sum}\limits_{k}{\xi }_{k}\left({c}_{k}^{\dagger }{c}_{k}+{d}_{k}^{\dagger }{d}_{k}\right)-\frac{\Delta E}{2}\mathop{\sum}\limits_{k}\left({c}_{k}^{\dagger }{c}_{k}-{d}_{k}^{\dagger }{d}_{k}\right)+g\mathop{\sum}\limits_{i}{Q}_{i}\left({c}_{i}^{\dagger }{d}_{i}+{d}_{i}^{\dagger }{c}_{i}\right)+\mathop{\sum}\limits_{i}\frac{{P}_{i}^{2}}{2M}+\left(\frac{M{\omega }^{2}{Q}_{i}^{2}}{2}\right).$$

(9)

Here, again for ease of readability, ${c}_{i,\sigma }^{\dagger }({d}_{i,\sigma }^{\dagger })$ creates a c (d)-electron with spin σ ∈ {↑, ↓} at site i; P_i and Q_i are the momentum and position coordinates for dispersionless phonons of frequency ω and mass M at site i; ΔE is the splitting between levels c and d; g is the local electron-phonon coupling. We concern ourselves with a system in which the c-band is partially filled at equilibrium.

In the presence of a fixed distortion $\left\langle Q\right\rangle$, we re-write ${Q}_{i}=\left\langle Q\right\rangle +\tilde{{Q}_{i}}$, where $\tilde{{Q}_{i}}$ are the fluctuations of the phonon coordinate. Our aim is to diagonalize the (non-interacting) electronic Hamiltonian as a function of the structural distortion $\left\langle Q\right\rangle$, thereby accounting for the crucial, non-perturbative enhancement of level-hybridization between the c and d levels arising from increasing $\left\langle Q\right\rangle$. To carry this out, we perform the following rotation:

$$\left(\begin{array}{c}{f}_{k}\\ {g}_{k}\end{array}\right)=\left(\begin{array}{cc}\cos (\theta )&\sin (\theta )\\ -\sin (\theta )&\cos (\theta )\end{array}\right)\left(\begin{array}{c}{c}_{k}\\ {d}_{k}\end{array}\right),$$

(10)

where θ is given by $\tan (2\theta )=\frac{2g\left\langle Q\right\rangle }{\Delta E}$. Upon rotating to f and g electrons, our Hamiltonian becomes:

$$H=\sum _{k}{\xi }_{k}\left({f}_{k}^{\dagger }{f}_{k}+{g}_{k}^{\dagger }{g}_{k}\right)-\frac{\Delta {E}_{{\rm{eff}}}}{2}\sum _{k}\left({f}_{k}^{\dagger }{f}_{k}-{g}_{k}^{\dagger }{g}_{k}\right)+2g\sum _{q}{\tilde{Q}}_{q}\left(\cos (\theta ){S}_{q}^{x}+\sin (\theta ){S}_{q}^{z}\right)+\sum _{i}\left(\frac{{P}_{i}^{2}}{2M}+\frac{M{\omega }^{2}{Q}_{i}^{2}}{2}\right),$$

(11)

where ${S}_{q}^{z}=\frac{1}{2}\left({f}_{k+q}^{\dagger }{f}_{k}-{g}_{k+q}^{\dagger }{g}_{k}\right)$, ${S}_{q}^{x}=\frac{1}{2}\left({f}_{k+q}^{\dagger }{g}_{k}+{g}_{k+q}^{\dagger }{f}_{k}\right)$, and $\Delta {E}_{{\rm{eff}}}=\sqrt{\Delta {E}^{2}+{(2g\left\langle Q\right\rangle )}^{2}}$. For ΔE_eff ≫ ω, we can restrict our attention to the effective lower f-band and write our effective Hamiltonian as:

$$\begin{array}{ll}{H}_{{\rm{eff}}}=\mathop{\sum}\limits_{k}{\xi }_{k}{f}_{k}^{\dagger }{f}_{k}+g\sin (\theta )\mathop{\sum}\limits_{q}{Q}_{-q}{f}_{k+q}^{\dagger }{f}_{k}\\ \qquad\qquad+\mathop{\sum}\limits _{i}\left(\frac{{P}_{i}^{2}}{2M}+\frac{M{\omega }^{2}{Q}_{i}^{2}}{2}\right),\end{array}$$

(12)

We can now decouple the electronic and phonon degrees of freedom to the lowest order in g by using the following Schrieffer-Wolff unitary:

$$U={e}^{i\mathop{\sum}\limits_{q}\left({\alpha }_{q}{P}_{q}+{\beta }_{q}{Q}_{-q}\right){f}_{k+q}^{\dagger }{f}_{k}},$$

(13)

where α_q, β_q satisfy:

$${\beta }_{q}=M{\alpha }_{q}\left({\xi }_{k+q}-{\xi }_{k}\right),$$

(14)

$${\alpha }_{q}=-\frac{g\sin (\theta )}{M\left({\omega }^{2}-{({\xi }_{k+q}-{\xi }_{k})}^{2}\right)}.$$

(15)

Upon decoupling electrons and phonons, we are left with an interacting electronic Hamiltonian with:

$${H}_{{\rm{int}}}=-\sum _{k,{k}^{{\prime} },q}\frac{{g}^{2}{\sin }^{2}(\theta )}{2M\left({\omega }^{2}-{({\xi }_{k+q}-{\xi }_{k})}^{2}\right)}{c}_{k+q,{\sigma }^{{\prime} }}^{\dagger }{c}_{{k}^{{\prime} }-q,\sigma }^{\dagger }{c}_{{k}^{{\prime} },\sigma }{c}_{k,{\sigma }^{{\prime} }}.$$

(16)

Similar to how retardation is captured in BCS theory, we approximate H_int above with an instantaneous interaction with $\left\langle Q\right\rangle$ dependent interacting $U=\frac{{g}^{2}{\sin }^{2}\left(\right.\theta (\left\langle Q\right\rangle )}{2M{\omega }^{2}}$ and an energy cut-off at ω. All told, this yields our desired attractive interaction Eq. (3):

$$\delta U(\left\langle Q\right\rangle )=\frac{{g}^{2}}{M{\omega }^{2}}\frac{4{g}^{2}{\left\langle Q\right\rangle }^{2}}{\Delta {E}_{{\rm{eff}}}^{2}},$$

(17)

Extended model including intra-band phonons

Within a two-electronic band model, there are two types of Raman modes that can linearly couple to the electrons locally. These modes are (a) Eg modes, which couple to the pseudospin of the two bands, ${S}_{x,i}=\frac{{c}_{i}^{\dagger }{d}_{i}+{d}_{i}^{\dagger }{c}_{i}}{2}$ and ${S}_{z,i}=\frac{{c}_{i}^{\dagger }{c}_{i}-{d}_{i}^{\dagger }{d}_{i}}{2}$ and have two polarizations, and (b) Ag modes, that couple to the total density $n={c}_{i}^{\dagger }{c}_{i}+{d}_{i}^{\dagger }{d}_{i}$. Within the two band model these are all the possibilities for Raman modes, and the resulting Hamiltonian is given by the extended model:

$$H={H}_{{\rm{el}}}+{H}_{{\rm{el-ph}}}+{H}_{{\rm{ph}}},$$

(18)

$${H}_{{\rm{el}}}=\sum _{k}{\xi }_{k}\left({c}_{k}^{\dagger }{c}_{k}+{d}_{k}^{\dagger }{d}_{k}\right)-\frac{\Delta E}{2}\sum _{k}\left({c}_{k}^{\dagger }{c}_{k}-{d}_{k}^{\dagger }{d}_{k}\right),$$

(19)

$${H}_{{\rm{el-ph}}}={g}_{{\rm{x}}}\mathop{\sum}\limits_{i}{Q}_{x,i}\left({c}_{i}^{\dagger }{d}_{i}+{d}_{i}^{\dagger }{c}_{i}\right)+{g}_{{\rm{z}}}\mathop{\sum}\limits_{i}{Q}_{z,i}\left({c}_{i}^{\dagger }{c}_{i}-{d}_{i}^{\dagger }{d}_{i}\right)+{g}_{{\rm{Ag}}}\mathop{\sum}\limits_{i}{Q}_{Ag,i}\left({c}_{i}^{\dagger }{c}_{i}+{d}_{i}^{\dagger }{d}_{i}\right),$$

(20)

$${H}_{{\rm{ph}}}=\sum _{i}\left(\frac{{P}_{x,i}^{2}}{2M}+\frac{M{\omega }_{{\rm{x}}}^{2}{Q}_{x,i}^{2}}{2}+\frac{{P}_{z,i}^{2}}{2M}+\frac{M{\omega }_{{\rm{z}}}^{2}{Q}_{z,i}^{2}}{2}+\frac{{P}_{Ag,i}^{2}}{2M}+\frac{M{\omega }_{{\rm{Ag}}}^{2}{Q}_{Ag,i}^{2}}{2}\right),$$

(21)

where {Q_x,i, Q_z,i, Q_Ag,i} correspond to phonon coordinates of the inter-band Eg mode, intra-band Eg mode, and Ag mode, respectively, at position i, with {g_x, g_z, g_Ag} the corresponding electron–phonon couplings and {ω_x, ω_z, ω_Ag} the corresponding phonon frequencies. Using this extended Hamiltonian, the phonon-induced attraction in equilibrium between electrons in the occupied lower band c_i is given by an effective attractive Hubbard U, ${U}_{{\rm{ph,0}}}=\frac{{g}_{{\rm{Ag}}}^{2}}{M{\omega }_{{\rm{Ag}}}^{2}}+\frac{{g}_{{\rm{z}}}^{2}}{M{\omega }_{z}^{2}}$. Note that in the undistorted case, only intra-band phonon modes contribute such as Q_Ag and Q_z. Next, we consider a general distortion of all three Raman modes : ${Q}_{{\rm{z}}}\to {\tilde{Q}}_{{\rm{z}}}+\left\langle {Q}_{{\rm{z}}}\right\rangle$, ${Q}_{{\rm{x}}}\to {\tilde{Q}}_{{\rm{x}}}+\left\langle {Q}_{{\rm{x}}}\right\rangle$ and ${Q}_{{\rm{Ag}}}\to {\tilde{Q}}_{{\rm{Ag}}}+\langle {Q}_{{\rm{Ag}}}\rangle$. Re-diagonalizing the bands in the presence of these distortions and projecting to the lowest energy band as is done in the previous section, we find that the photo-induced attraction is given by:

$${U}_{{\rm{ph,dist}}}=\frac{{g}_{{\rm{Ag}}}^{2}}{M{\omega }_{{\rm{Ag}}}^{2}}+\frac{{g}_{{\rm{z}}}^{2}}{M{\omega }_{z}^{2}}+\frac{4{g}_{{\rm{x}}}^{2}{\left\langle {Q}_{{\rm{x}}}\right\rangle }^{2}}{\sqrt{{\left(\Delta E+2{g}_{{\rm{z}}}\left\langle {Q}_{{\rm{z}}}\right\rangle \right)}^{2}+4{g}_{{\rm{x}}}^{2}{\left\langle {Q}_{{\rm{x}}}\right\rangle }^{2}}}\left(\frac{{g}_{{\rm{x}}}^{2}}{M{\omega }_{{\rm{x}}}^{2}}-\frac{{g}_{{\rm{z}}}^{2}}{M{\omega }_{{\rm{z}}}^{2}}\right)$$

(22)

From this expression, we see that the contribution from the Ag modes remains unchanged while the contribution from the inter-band mode Q_z, is depleted in favor of an added contribution from the inter-band Q_x mode. The extra attraction is given by,

$$\delta U=\frac{4{g}_{{\rm{x}}}^{2}{\left\langle {Q}_{{\rm{x}}}\right\rangle }^{2}}{\sqrt{{\left(\Delta E+2{g}_{{\rm{z}}}\left\langle {Q}_{{\rm{z}}}\right\rangle \right)}^{2}+4{g}_{{\rm{x}}}^{2}{\left\langle {Q}_{{\rm{x}}}\right\rangle }^{2}}}\left(\frac{{g}_{{\rm{x}}}^{2}}{M{\omega }_{{\rm{x}}}^{2}}-\frac{{g}_{{\rm{z}}}^{2}}{M{\omega }_{{\rm{z}}}^{2}}\right),$$

(23)

whose sign explicitly depends on the difference $\frac{{g}_{{\rm{x}}}^{2}}{M{\omega }_{{\rm{x}}}^{2}}-\frac{{g}_{{\rm{z}}}^{2}}{M{\omega }_{{\rm{z}}}^{2}}$. The enhancement presented in this manuscript is recovered in the case that $\frac{{g}_{{\rm{x}}}^{2}}{M{\omega }_{{\rm{x}}}^{2}} > > \frac{{g}_{{\rm{z}}}^{2}}{M{\omega }_{{\rm{z}}}^{2}}$.

The fact that different polarizations of the same phonon mode can have very different electron-phonon coupling is supported by experimental data. Indeed, the peak structure observed in Raman studies of the Hg modes in K₃C₆₀⁵⁶ has been interpreted as arising from different polarizations having different electron-phonon coupling^36,56. Moreover, the 5-fold degeneracy of the molecular modes is broken when the C₆₀ molecules form an FCC lattice, leading to non-negligible shifts in the phonon frequencies, thereby changing the effective phonon-mediated interaction, $\frac{{g}_{i}^{2}}{M{\omega }_{i}^{2}}$. While a detailed ab initio characterization of the polarization dependence of the electron-phonon coupling is still lacking, for photo-induced superconductivity to arise within our model, a large inter-band coupling is required to occur. Since the goal of this article is to describe the physics arising from the inter-band coupling alone, a detailed characterization of the multi-band multi-phonon model presented here is left for future work.

Mean-field metastability

We now explore the simplest quasi-equilibrium picture for long-lived, light-induced superconductivity: optically driving the material into a hidden, thermodynamically metastable phase². We study the driven, dissipative dynamics of the mean phonon coordinate Q in an adiabatic free-energy landscape that weights the free-energy benefit of inducing a displacive shift Q—leading to enhanced U and a stronger superconductor—and the elastic cost of such a distortion. We work within a finite-temperature BCS ansatz for the electrons. Note that while this at first may be seem ill suited to describe superconductivity for putatively non-BCS superconductor K₃C₆₀, following the suggestion proffered by Capone et al.³⁸, such an approach is both tractable and sensible for considering the superconductivity of the reduced quasi-particle weight, free-fermion like quasi-particles. Accordingly, when considering K₃C₆₀ specifically, we keep in mind the quasi-particle spectrum obtained from DMFT.

Using a finite-temperature BCS ansatz for the electrons, we model the evolution of Q as:

$$\left({\partial }_{t}^{2}+\gamma {\partial }_{t}+\frac{1}{M}\frac{\partial {{\mathcal{F}}}_{{\rm{SC}}}}{\partial Q}+{\omega }^{2}\right)Q=z{E}^{2}(t)+\eta (t),$$

(24)

where zE²(t) is the effective displacive acceleration arising from laser driving; where η(t) is fluctuation-dissipation obeying white noise $\langle \eta (t)\eta ({t}^{{\prime} })\rangle =2\frac{\gamma }{M}T\delta (t-{t}^{{\prime} })$; and where the BCS superconducting free-energy density ${{\mathcal{F}}}_{SC}$ is given by:

$${{\mathcal{F}}}_{{\rm{SC}}}=\frac{{\Delta }^{2}}{U}-2\nu (0)\mathop{\int}\nolimits_{0}^{\omega }d\xi \left(\sqrt{{\xi }^{2}+{\Delta }^{2}}-\xi \right)-4\nu (0)T\mathop{\int}\nolimits_{0}^{\omega }d\xi \ln \left(1+{e}^{-\beta \sqrt{{\xi }^{2}+{\Delta }^{2}}}\right).$$

(25)

Here ν(0) is the effective density of states per spin per site at the Fermi-level, and Δ(Q) is obtained by solving the BCS self-consistency equation for U(Q).

We start with a system without a shift (Q = 0), in the normal state, at finite temperature T > T_c. We assume that the drive is sufficiently strong to traverse any free-energy barrier between the global free-energy minimum at Q = 0 and the putative, superconducting metastable state at Q_MS ≠ 0. After driving the phonon coordinate into such a metastable trap, a return to equilibrium through macroscopic nucleation due to thermal fluctuations is, canonically, slow. Our goal is thus to ascertain when the free energy landscape has a non-trivial local minimum. A sufficient (and from numerical observations, necessary) condition for the free energy landscape to host a metastable state is that T = 0 energy landscape should have a non-trivial local minimum. For U₀ = 0, a metastable state exists if:

$${Q}_{{\rm{c}}}^{2}=\frac{\Delta E\,\omega }{\sqrt{2}{g}^{2}}\Delta ({Q}_{c}),$$

(26)

has two positive solutions Q_B and Q_MS, corresponding to a local maximum and minimum in the energy landscape, respectively. Metastability persists until T_B where the free energy landscape no longer has non-trivial critical points, and the metastable state becomes untrapped, as shown by the gray landscapes in Fig. 2a.

We reiterate the distinction between the two types of metastability that we find. The first type, metastability I, corresponds to the scenario in which E(Q_MS) > E(0), where $E(Q)=\frac{1}{2}M{\omega }^{2}{Q}^{2}-{\omega }^{2}\nu (0)\coth \left(\frac{1}{\nu (0)U(Q)}\right)$. In this scenario, the distortionless, normal state is always the equilibrium state, and metastability occurs between 0 < T < T_B. The alternate scenario, metastability II, occurs when at T = 0 a distorted ground state is energetically favorable. Equilibrium superconductivity exists until a critical temperature T_c where a first order phase transition occurs and the superconductivity-inducing distortion is no longer free energetically favorable. In metastability II, optically switched superconductivity is possible for T_c < T < T_B. In passing, we note that while our approach near the local maximum is within BCS, the precise position of the local minima, thereby the quantitative boundary between metastability I & II, may require treatment beyond BCS to capture the effects of strong fluctuations.

Superconductivity with fixed quasi-particle number

In this section, we provide a derivation of the steady state equations Eqs. (4) & (5) within the BCS mean field approximation. We note that similar considerations were asserted previously by Parmenter⁴³ in the case of quasi-particle extraction. We begin by reiterating that (number-conserving) scattering between quasi-particles and thermally occupied acoustic phonons is much faster than the number of non-conserving scattering events needed to generate quasi-particles. While the latter is emphasized throughout our work as what enables a long-lived non-equilibrium gap, the former suggests that the effective temperature that governs the quasi-particle distribution should coincide with the temperature of the phonon bath—we do not invoke a two-temperature model. Thus, to find our steady state quasi-particle distribution, it suffices to solve for the gap Δ and Bogolyubov chemical potential λ self-consistently while minimizing an effective thermal free energy at temperature T. Concretely, our quasi-particle number constrained, Δ-dependent free energy can be expressed as:

$$\begin{array}{ll}F(\Delta )=\,{\rm{Tr}}\,\{\rho H(\Delta )\}+T\,{\rm{Tr}}\,\{\rho \log \rho \}+z\left(\,{\rm{Tr}}\,\{\rho \}-1\right)\\ \qquad\qquad+\,\lambda \left(\,{\rm{Tr}}\,\left\{\rho \mathop{\sum}\limits_{k,\sigma }{\gamma }_{k,\sigma }^{\dagger }(\Delta ){\gamma }_{k,\sigma }(\Delta )\right\}-n\right),\end{array}$$

(27)

where the first two terms correspond to the usual BCS decoupled free energy at a given temperature and superconducting gap Δ, the fixed quasi-particle constraint is enforced by minimizing with respect to a Lagrange multiplier λ, and the final term enforces that the density matrix has trace 1, by minimizing with respect to z. The operators γ_k,σ(Δ) (${\gamma }_{k,\sigma }^{\dagger }(\Delta )$) correspond to the Bogolyubov quasi-particle annihilation (creation) operators defined by canonical Bogolyubov rotations parametrized by Δ: ${\gamma }_{k,\uparrow }={u}_{k}{c}_{k,\uparrow }-{v}_{k}{c}_{k,\downarrow }^{\dagger }$ and ${\gamma }_{-k,\downarrow }^{\dagger }={u}_{k}^{* }{c}_{-k,\downarrow }^{\dagger }-{v}_{k}^{* }{c}_{k,\uparrow }$, where $| {u}_{k}{| }^{2}=\frac{1}{2}\left(1+\frac{{\xi }_{k}}{\sqrt{{\xi }_{k}^{2}+{\Delta }^{2}}}\right)$ and ∣v_k∣² + ∣u_k∣² = 1. We note now that the operator portion of the quasi-particle number constraint can be subsumed into the Hamiltonian, which within BCS mean-field, is diagonal in γ_k,σ(Δ). Thus, one readily interprets the Lagrange multiplier as a chemical potential for the Bogolyubov quasi-particles.

For completeness, by factorizing our density matrix into different momentum k-dependent and psuedo-spin σ-dependent contributions,

$$\rho ={\Pi }_{k,\sigma }{\rho }_{k,\sigma },\qquad \,\text{with}\,\qquad \,\text{Tr}\,\{{\rho }_{k,\sigma }\}=1.$$

(28)

The ρ_k,σ’s are found by minimizing F:

$$\begin{array}{ll}\frac{\partial F}{\partial {\rho }_{k,\sigma }}={E}_{k}\langle {\gamma }_{k,\sigma }^{\dagger }{\gamma }_{k,\sigma }\rangle +T\log ({\rho }_{k,\sigma })+T+\lambda \langle {\gamma }_{k,\sigma }^{\dagger }{\gamma }_{k,\sigma }\rangle +z=0,\\\qquad \Rightarrow \rho =\frac{{e}^{-\beta {\sum }_{k,\sigma }\left({E}_{k}+\lambda \right){\gamma }_{k,\sigma }^{\dagger }{\gamma }_{k,\sigma }}}{{Z}_{k}},\end{array}$$

(29)

where λ and Δ are determined self-consistently as:

$$n=\mathop{\sum}\limits_{k,\sigma }\langle {\gamma }_{k,\sigma }^{\dagger }{\gamma }_{k,\sigma }\rangle =\mathop{\sum}\limits_{k,\sigma }\frac{1}{\exp \left(\beta (\sqrt{{\xi }_{k}^{2}+{\Delta }^{2}}+\lambda )\right)+1}$$

(30)

$$\begin{array}{l}\Delta =\frac{U}{N}\mathop{\sum}\limits_{\begin{array}{c}k\\ | {\xi }_{k}| \,< \,\omega \end{array}}\langle {c}_{-k,\downarrow }{c}_{k,\uparrow }\rangle =\frac{U}{N}\mathop{\sum}\limits_{\begin{array}{c}k\\ | {\xi }_{k}|\, <\, \omega \end{array}}{u}_{k}^{* }{v}_{k}(1-2\langle {\gamma }_{k,\uparrow }^{\dagger }{\gamma }_{k,\uparrow }\rangle )\\\quad=\frac{U}{N}\mathop{\sum}\limits_{\begin{array}{c}k\\ | {\xi }_{k}|\, < \,\omega \end{array}}\frac{\Delta }{2\sqrt{{\xi }_{k}^{2}+{\Delta }^{2}}}\tanh \left(\beta \left(\sqrt{{\xi }_{k}^{2}+{\Delta }^{2}}+\lambda \right)\right)\end{array}$$

(31)

Relaxation time-scales: pair-breaking and quasi-particle recombination

In this section, we derive a set of characteristic time scales relevant to the equilibration of Bogolyubov quasi-particles coupled to a thermal bath of phonons, supporting Eqs. (6)–(8) in the main text. We note that the bath we consider contains weakly coupled, low-frequency lattice/intermolecular modes up to a cutoff ${\Omega }_{\max }$ and sharp, high-frequency optical modes Ω_ν. The details of the former are not particularly relevant as they set the precise dynamics of the avalanche. For the former, we take the interaction to be of the local electron-phonon type, reflecting the coupling between electrons with molecular vibrational modes of a molecular solid.

We first derive the dynamics due to the low-frequency phonons. We introduce a weakly coupled bath of low-energy, phonons, with electron-phonon interactions given by:

$${H}_{{\rm{bath}}}=\sum _{p,{p}^{{\prime} },\lambda ,\sigma }{g}_{p,{p}^{{\prime} },\lambda }({a}_{q,\lambda }+{a}_{-q,\lambda }^{\dagger }){c}_{p,s}^{\dagger }{c}_{p,\sigma }.$$

(32)

where λ runs over the polarizations of the phonons, ${g}_{p,{p}^{{\prime} },\lambda }$ yields a momentum and polarization-dependent electron-phonon coupling, $q=p-{p}^{{\prime} }$—considering non-Umklapp processes—and σ ∈ {↑, ↓}. Leveraging the assumption that electrons are coupled weakly to the low-lying phonons, we estimate the quasi-particle-phonon scattering times perturbatively using Fermi’s Golden Rule. We delineate between three different equilibration rates: (1) ${\Gamma }_{{\rm{s}}}=\frac{1}{{\tau }_{s}}$, the rate of scattering between Bogolyubov quasi-particles by the acoustic phonons without changing the total number of quasi-particles, (2) ${\Gamma }_{{\rm{r}}}=\frac{1}{{\tau }_{r}}$ the rate at which quasi-particles re-combine into Cooper-pairs (i.e., the number of quasi-particles decreases), and an additional rate: $(3)\,{\Gamma }_{{\rm{g}}}=\frac{1}{{\tau }_{{\rm{g}}}}$, the rate at which quasi-particles are generated due to pair breaking due to phonons (i.e., the number of quasi-particles increases). The typical scale separation, in our setting, that we will find is: Γ_s ≫ Γ_g ≳ Γ_r. This separation enables us to assume that the electronic temperature is chained to the phonon temperature: We are interested primarily in generation and recombination dynamics at a slower scale. To make contact with the “net quasi-particle generation” rate given in the main text, ${\tau }_{{\rm{eq}}}^{-1}={\Gamma }_{{\rm{g}}}-{\Gamma }_{{\rm{r}}}$. Within our mechanism, we find Γ_g ≫ Γ_r at early times, hence focusing on quasi-particle generation in the main text.

We compute the Fermi’s golden rule rate by using H_bath as the perturbation and picking an initial state $\left\vert I\right\rangle$ sampled from a density matrix formed by the Kronecker product of a thermal density matrix of phonons at a temperature T and, for the electrons, an arbitrary quasi-particle occupation function⁵⁷. In thermal equilibrium, this is the Fermi-Dirac distribution; in the quasi-particle trapped steady state, this is given by $f(E)=\frac{1}{\exp \left(\beta (E+\lambda )\right)+1}$. Throughout our discussion, we focus on rates where one of the quasi-particles involved is at the gap Δ. We do this because while, in principle, the rate is frequency-dependent, the density of states of the superconductors is strongly peaked at the gap. Moreover, as we coarse-grain over the time scale over which the electrons thermalize to the phonon temperature, we are mainly concerned with the net influx rate of quasi-particles generated/recombined. As such, a typical scale which provides the correct dynamics is given by Γ_r(Δ) and Γ_g(Δ).

In the ensuing, we focus first on the process (3), the generation of quasi-particles by scattering with bath phonons: the first two processes are discussed in detail in ref. ⁴². We make our discussion concise by computing the generation time for a fixed quasi-particle at the gap energy Δ and with momentum k = 0 and spin ↑. The process whose rate we seek to compute is one which involves the absorption of a phonon at energy Ω and the generation of two quasi-particles, one at energy Δ, the other at energy Ω − Δ ≥ Δ. We write one possible final state as ${\left\vert F\right\rangle }_{q,\lambda }={\gamma }_{k,\uparrow }^{\dagger }{\gamma }_{q,\downarrow }^{\dagger }{a}_{k-q,\lambda }\left\vert I\right\rangle$. To compute the total scattering rate, we sum over quasi-particle momenta q.

We make progress by noting that terms such ${c}_{{p}^{{\prime} },\uparrow }^{\dagger }{c}_{p,\uparrow }+{c}_{-p,\downarrow }^{\dagger }{c}_{-{p}^{{\prime} },\downarrow }$ can be written in terms of Bogolyubov quasi-particle operators as: ${c}_{{p}^{{\prime} },\uparrow }^{\dagger }{c}_{p,\uparrow }+{c}_{-p,\downarrow }^{\dagger }{c}_{-{p}^{{\prime} },\downarrow }=t(p,{p}^{{\prime} })({\gamma }_{p,\uparrow }^{\dagger }{\gamma }_{{p}^{{\prime} },\uparrow }+{\gamma }_{-p,\downarrow }^{\dagger }{\gamma }_{-{p}^{{\prime} },\downarrow })+m(p,{p}^{{\prime} })({\gamma }_{{p}^{{\prime} },\uparrow }^{\dagger }{\gamma }_{-p,\downarrow }^{\dagger }-{\gamma }_{p,\uparrow }{\gamma }_{-{p}^{{\prime} },\downarrow })$, where $t(p,{p}^{{\prime} })$ and $m(p,{p}^{{\prime} })$ are the standard coherence factors: ${m}^{2}(p,{p}^{{\prime} })=\frac{1}{2}(1+\frac{{\epsilon }_{p}{\epsilon }_{{p}^{{\prime} }}+{\Delta }^{2}}{{E}_{p}{E}_{{p}^{{\prime} }}})$ and ${t}^{2}(p,{p}^{{\prime} })=\frac{1}{2}(1+\frac{{\epsilon }_{p}{\epsilon }_{{p}^{{\prime} }}-{\Delta }^{2}}{{E}_{p}{E}_{{p}^{{\prime} }}})$. Using this, we can express the square of our desired matrix elements as: $| \left\langle I\right\vert {H}_{bath}{\left\vert F\right\rangle }_{q,\lambda }{| }^{2}={g}_{k-q,\lambda }^{2}{m}^{2}(k,q)(1-{\nu }_{q,\downarrow })(1-{\nu }_{k,\uparrow }){n}_{ph}(k-q,\lambda )$, where ν_q is the occupation number of a quasi-particle at momentum q and n_ph (k − q, λ) is the occupation number of a phonon at momentum k − q and polarization λ in the initial state $\left\vert I\right\rangle$. Note that while $\left\vert I\right\rangle$ is a pure state, the rate will be averaged over occupation numbers given by the ensemble from which $\left\vert I\right\rangle$ is drawn from, as prescribed above.

Computing the sum over q in the continuum, we introduce the standard Bogolyubov density of states—for a quasi-particle at energy E, the DOS goes as $\rho (E)=\frac{E}{\sqrt{{E}^{2}-{\Delta }^{2}}}$—and phonon spectral density F(Ω), weighted by the square of the matrix element α²(Ω), averaged over the Fermi surface⁴². We note that while taking such an α²(Ω)F(Ω) is appropriate for interactions with a low-frequency bath, given that the electronic density of states changes dramatically at higher frequencies, naively using such an α²(Ω)F(Ω) would be inappropriate in this context.

Using our computation of the matrix element above, we arrive at our result for the rate at which quasi-particles are generated by the scattering of Cooper pairs with low-frequency phonons:

$${\Gamma }_{{\rm{g}}}(\Delta )=\frac{2\pi }{\hslash }\mathop{\int}\nolimits_{2\Delta }^{\infty }d\Omega \left({\alpha }^{2}(\Omega )F(\Omega )\sqrt{\frac{\Omega }{\Omega -2\Delta }}(1-f(\Omega -\Delta ))(1-f(\Delta ))n(\Omega )\right)$$

(33)

The scattering time τ_s, which controls thermal equilibration within each quasi-particle band, is given by:

$${\Gamma }_{{\rm{s}}}(\Delta )=\frac{2\pi }{\hslash }\mathop{\int}\nolimits_{0}^{\infty }d\Omega \left({\alpha }^{2}(\Omega )F(\Omega )\sqrt{\frac{\Omega }{\Omega +2\Delta }}(1-f(\Delta +\Omega ))(1-f(\Delta ))n(\Omega )\right),$$

(34)

Note that Γ_s can be much larger that Γ_g as low-frequency acoustic modes can be significantly thermally populated as arbitrarily low-frequency phonons can participate in number-conserving scattering processes. Our arguments for a fast scattering, τ_s time but a very slow generation time, τ_g, provide justification for our approximation that a superconducting steady state is reached as described by a temperature and a conserved number of quasi-particles.

Finally, for completeness, we provide the rate equations for quasi-particle recombination:

$${\Gamma }_{{\rm{r}}}(\Delta )=\frac{2\pi }{\hslash }\mathop{\int}\nolimits_{2\Delta }^{\infty }d\Omega \left({\alpha }^{2}(\Omega )F(\Omega )\sqrt{\frac{\Omega }{\Omega -2\Delta }}f(\Omega -\Delta )f(\Delta )(1+n(\Omega ))\right).$$

(35)

Having argued for the large discrepancy between scattering rates that thermalize the Bogolyubov quasi-particles and rates for generating new quasi-particles, we now argue that the asymmetry between quasi-particle recombination during driving and quasi-particle generation after driving implies that our long-lived superconductor can be generated by a short pulse, as seen in experiments^13,14. While generating quasi-particles out of the condensate can be slow due to the absence of thermally excited phonons, recombining a pair of quasi-particles requires emitting a phonon, and is therefore not bottlenecked by the phonon population. The recombination bottleneck in traditional “Rothwarf-Taylor” quasi-particle injection experiments arises instead from a dearth of thermally excited quasi-particle partners that are needed for recombining the injected quasi-particle⁴¹: In the quasi-particle injection experiments $f(\Omega -\Delta ) \sim {e}^{-\frac{\Omega -\Delta }{T}}$ at low temperatures. In our context, however, if one rapidly ramps U to U^*, the recombination process is not slowed down due to a lack of quasi-particles: in this situation, initially, there is not a lack but an excess of non-thermally distributed quasi-particles that need to be recombined.

Finally, we arrive at the question of how to modify Eq. (33) and Eq. (35) for the case of the local, vibrational modes. For these—obviating the, in this context, unimportant distinction between inter- and intra-band couplings—we consider a Holstein-type model: H_e-ph = ∑_i,νg_νQ_in_i, summing over modes ν and sites i. Moving to momentum space and performing the same Fermi’s Golden Rule analysis as above—suppressing coherence factors as Ω_ν ≫ Δ—reveals that the proper way to modify α²(Ω)F(Ω) to the high-frequency setting is to write α²(Ω)F(Ω) = ∑_νg²ν_SC(Ω_ν − Δ)δ(Ω − Ω_ν). Considering this rate for Ω_ν ≫ Δ, T yields Eq. (8).

In passing, we note that the dominant dissipative processes considered here are single-phonon relaxation mechanisms. In principle, at sufficiently high temperatures, multi-phonon processes arising from, e.g. thermally populated acoustic modes, could dominate relaxation due to single phonon optical phonons. A precise accounting for this is complicated by the lack of momentum-resolved couplings for acoustic modes. Moreover, it is unclear if they play a significant role in K₃C₆₀ as acoustic modes are believed to not have significant coupling to electrons in the material³⁶. Nevertheless, a quantitative accounting of the relevance of multi-phonon processes should be developed to study the relaxation of driven superconducting systems.

We further note that while Coulomb repulsion may play a role in quasi-particle generation, we do not believe it qualitatively alters our mechanism: whereas phonon-induced quasi-particle is not bottlenecked by the lack of quasi-particles, Coulomb-induced quasi-particle scattering is. Electron-electron scattering, which generates quasi-particle pairs involve the destruction of a high-energy quasi-particle (E ~ 3Δ) and the creation of three low-energy quasi-particles (E ~ Δ). Within the quasi-particle trapping scenario, the non-thermal quasi-particle distribution function at 3Δ is suppressed as $\sim \exp (-(3\Delta +\lambda )/T)$. Immediately after driving, typical λ ≫ Δ, T and the Coulomb scattering process is severely bottlenecked by the lack of high-energy quasi-particles. That this should be the case is easily seen in the extreme limit of “perfect quasi-particle extraction”. In this case, there are no quasi-particles, let alone high-energy ones, to begin with: The Coulomb scattering process is entirely shut off. This is in contrast to the dominant pair-breaking/quasi-particle generating interaction arising from phonons which requires thermal phonons, albeit at high energy, but no pre-existing quasi-particles. As the longevity of the quasi-particle trapping scenario is predicated upon the induction of a low density of quasi-particles, in this regime, Coulomb interactions should not play a significant role and, thereby, are safely neglected. The role of Coulomb interactions in the “avalanche collapse” process, i.e., where quasi-particle densities are higher, is more subtle and deserves attention in future work.

Mapping to K₃C₆₀

In this section, we articulate our microscopic model, describing how it captures essential features of K₃C₆₀. We begin by reviewing the literature relevant to the phonon-pairing based (alternatively, the inverse Hunds) theory of superconductivity K₃C₆₀ and use it to guide an association between our effective two electronic band, single phonon model and the, e.g., three band, five phonon physics of K₃C₆₀. Our goal is to achieve quantitative estimates that dictate how plausible our pictures of longevity are to explain the metastable superconductivity uncovered in K₃C₆₀.

We begin by unpacking the predominant theory regarding the origin of high-T_c equilibrium, s-wave superconductivity in K₃C_60, which implicates an interplay between attraction facilitated by Jahn-Teller Hg modes that are strongly coupled to partially filled t_1u bands and strong electronic correlations that arise from the materials proximity to the Mott transition^36,38,39. The latter leads to a dramatic suppression of charge fluctuations and significant renormalization of both the onsite Coulomb repulsion (in the absence of Tomalchev-Anderson renormalization, due to the large values of ω as compared to E_f) and the bandwidth (W → ZW, where the quasi-particle residue, Z ≪ 1), due to Brinkman-Rice physics³⁶. The Jahn-Teller modes induce an “inverse Hund’s” coupling via the dynamical Jahn-Teller effect that provides the attractive pairing glue for local Cooper pairs. Crucially, as the Jahn-Teller interaction is “traceless” with respect to the charge degrees of freedom, the suppression of charge fluctuations due to Mott repulsion does not effect the attractive inverse Hund’s coupling, as opposed to electron-phonon interactions with Ag modes which couple to the density³⁶: strong electron-phonon interactions and electronic correlations work cooperatively to lead to a T_c ~ 20 K.

In light of the centrality of Mott physics to superconductivity in K₃C₆₀, we carry out the mapping of our minimal model to the electronic physics of K₃C₆₀around E_F from an unconventional but incisive vantage point, starting neither from vanilla DFT models of the electronic structure of K₃C₆₀ nor from the molecular limit but instead interpreting DMFT calculations that account explicitly for Mott effects³⁹. The DMFT-modified spectral function near the Fermi energy contains two sharp quasi-particle peaks—dramatically sharper than in DFT—which we associate with two partially filled, narrow t_1u bands crossing the Fermi surface and one empty, narrow t_1u band, along similar lines to the interpretation of DMFT performed by Capone et al. in ref. ³⁸. As the two peaks in the Mott modified spectral function overlap far from the Fermi energy, we make contact with K₃C₆₀ by identifying the lower c band in our model with the two half-filled t_1u bands crossing the Fermi surface and the upper d band with the empty t_1u band. We map ΔE in our model to the separation of the centers between the two sharp spectral peaks. To summarize, as a crude but comprehensive approximation, we assume that the Mott physics in K₃C₆₀ acts simply to renormalize the repulsive interaction and electronic spectral features such as the bandwidth and band-splitting—beyond this, the superconductivity is determined by local electron-phonon physics. In Fig. 5, we present the DFT bands alongside the DFT and DMFT spectral functions adapted from ref. ³⁹, and illustrate how ΔE can be assigned from the data.

Fig. 5: Ab-initio electronic band structure and DFT-DMFT spectral function in K₃C₆₀.

a DFT electronic band structure of the 1tu bands adapted from ref. ⁶¹, with red color corresponding to the upper unoccupied 1tu band and blue color to the two occupied lower 1tu bands. b Electron spectral functions using DFT and DMFT adapted from ref. ³⁹. Orange-shaded figure corresponds to the DFT spectral function while the DMFT spectral function, which includes renormalization due to electron-electron interaction, is given by the purple curve. Using the above data, we take the gap between occupied and unoccupied 1tu bands to be the distance between the two peaks in the density of states, ΔE_DFT for the DFT spectral function and ΔE_DMFT for the DMFT spectral function. We see that interaction effects can significantly renormalize the band structure.

Having made these identifications on the electronic side, we note that the Jahn-Teller Hg phonons couple to the t_1u bands with different polarizations providing both inter-band and intra-band transitions³⁶. Within our effective two-band model, we take polarizations coupling to intra-band transitions to give rise to the equilibrium pairing attraction U₀ that balances the inverse Hund’s coupling with the Mott renormalized Coulomb interaction to give T_c ~ 20 K, s-wave superconductivity in equilibrium. Inter-band polarizations coupling the half-filled bands to the empty bands, give an additional contribution to attraction, U(Q), as we have shown in our model. We note in passing that virtual inter-orbital Cooper tunneling is already believed to play a small contributing role in equilibrium superconductivity^39,58, underscoring the interpretation of our microscopics as photo-enhancing a (virtual) Suhl-Kondo effect. To determine whether a metastable superconducting state exists in K₃C₆₀ we take the electron-phonon coupling g for each Hg mode to be consistent with ab initio calculations^51,59. We find that the optimal mode for photo-induced metastability in K₃C₆₀—possessing both strong electron-phonon coupling and high-frequency—is the Hg(3) mode at 88 meV: the relevant polarization for this mode has $\frac{g{\ell }_{0}}{\omega }\approx 0.6$, where ℓ₀ is the effective oscillator length of the phonon^51,59. Note that while every mode that can be non-linearly rectified, will be, only the modes whose free-energy landscapes have metastable states can be trapped.

Pair-breaking: an interplay of high-frequency phonons and narrow bands

We begin by reminding the reader that the generation rate for quasi-particles for a superconductor whose charge gap (2Δ) after driving lies in between the intermolecular and intramolecular modes is given by:

$${\tau }_{{\rm{eq}}}^{-1}=\sum _{\nu }{g}_{\nu }^{2}\,{\nu }_{{\rm{SC}}}\left({\Omega }_{\nu }-\Delta (0)\right)\exp \left(-\frac{{\Omega }_{\nu }}{T}\right),$$

(36)

where Ω_ν are the frequencies corresponding to high energy, sharp, local, vibrational phonon modes. In K₃C₆₀, the Hg(3) phonons that are relevant to superconductivity are also the modes that are relevant to dissipation. Moreover, modes that are not of Jahn Teller flavor (e.g., not trace-less in the orbital degrees of freedom) do not couple strongly to the effective delocalized quasi-particles because charge fluctuations are dramatically suppressed due to strong Coulomb repulsion⁶⁰. Beyond the presence of the phonon gap and the importance of the Jahn-Teller Hg modes, there is significant controversy regarding the precise quantitative nature of electron-phonon coupling in the material, although Hg(3) and Hg(8) modes are often implicated³⁶.

To quantitatively attain the nanosecond time-scale at 100K reported in experiments within the quasi-particle trapping mechanism, dissipation due to the lowest lying Hg(1) mode at 33meV is neglected. Such an approximation is supported by ab initio estimates in K₃C₆₀ calculated in the regime that stretching a carbon bond is significantly more energetically costly than bending the bond, corresponding to small β/α within a simplified Keating model for the carbon bonds⁵¹. Thus, we take contributions starting from the Hg(2) phonon at 52meV. To obtain a long lifetime, an interplay of thermal suppression and the (superconducting) density of states must overpower the strong local electron-phonon coupling. The most relevant contribution thus comes from the 52meV mode. Using molecular parameters from ab initio calculations⁵¹ for the electron-phonon coupling, we arrive at a constraint for the effective bandwidth of the electrons (i.e., as is necessary to suppress ν_SC). To get the necessary suppression of the superconducting density of states—and approximating the mobile quasi-particle density of states as a Gaussian—we find that a bandwidth of ~60 meV is sufficient to produce a maximal 20 ns lifetime for the state. Note that while 60 meV is small, it is very much in agreement with seminal DMFT results of Capone et al.³⁸, who find that a quasi-particle residue Z ~ 0.06 is necessary for superconductivity due to the a local, phonon induced inverse Hund’s coupling in the presence of strong repulsive interactions. From this perspective, a reduction of the ~0.5 eV DFT bandwidth by Z ~ 0.06 is roughly half as much as is necessary for the long-lifetime (Fig. 6).

Fig. 6: Electron, phonon density of states in K₃C₆₀.

Schematic of superconducting electron (top) and phonon (bottom) density of states in K₃C₆₀. As discussed in detail, the phonon spectrum contains a significant gap, separating lattice inter-molecular modes of the K₃C₆₀ crystal from the on-ball molecular vibrational modes. In the optimal quasi-particle trapping scenario, strong driving pushes 2Δ into the phonon gap, e.g. above ${\Omega }_{\max }$. Note that while the on-ball vibrations can provide dissipation for the Cooper pairs, a narrow electronic band can suppress resonant electronic scatters: Above the electronic bandwidth, quasi-particle generation is kinematically constrained.