Gapped commensurate antiferromagnetic response in a strongly underdoped model cuprate superconductor

Abstract

It is a distinct possibility that spin fluctuations are the pairing interactions in numerous unconventional superconductors. In the high-transition-temperature (high-T_c) cuprates, superconductivity emerges upon doping antiferromagnetic Mott insulators, and spin fluctuations might furthermore drive unusual pseudogap phenomena. Here we use magnetic neutron scattering to study the highly underdoped cuprate HgBa₂CuO_4+δ (hole concentration p ≈ 0.064). In contrast to prior results for other underdoped cuprates, we find no evidence of incommensurate magnetic order associated with spin-density-wave or stripe correlations. Instead, the antiferromagnetic response in both the superconducting and pseudogap states is gapped below Δ_AF ≈ 6 meV, commensurate over a wide energy range, and disperses above about 55 meV. Given the pristine nature of HgBa₂CuO_4+δ, which exhibits high structural symmetry and minimal point disorder effects, this behavior likely signifies the unmasked response of the underlying CuO₂ planes near the Mott-insulating state. These results serve as a benchmark for a refined theoretical understanding of the cuprates.

Introduction

The cuprate superconductors share a quintessential structural and electronic unit: the copper-oxygen plane. The parent insulating state is characterized by a large Cu 3d-O 2p charge-transfer gap (~1–2 eV)¹, a spin-1/2 Cu moment², and quasi two-dimensional (2D) antiferromagnetic (AF) spin correlations with a large superexchange energy (~130 meV)^3,4. Superconductivity emerges upon doping the planes with about p ~ 0.05 holes per planar Cu. Below optimal doping (p ~ 0.16), where T_c is largest, the superconducting (SC) phase is preceded by the pseudogap (PG) region at higher temperature (Fig. 1); the latter has been the subject of much research activity and found to exhibit myriad ordering phenomena (translational-symmetry-preserving q = 0 magnetism, charge-density-wave, charge-spin stripe, electron-nematic)⁵. Since spin correlations might drive both superconductivity^6,7 and some of the observed PG phenomena^8,9,10, it is imperative to determine the magnetic response of the pristine CuO₂ planes. Indeed, the past four decades have seen tremendous efforts toward this end. Regardless of the nature of the pairing mechanism, a successful theory of the cuprates ought to capture the spin dynamics of these quantum materials.

Fig. 1: Phase diagram.

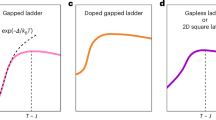
a Phase diagram of Hg1201 (p > 0.04), extended to the undoped insulating state (p = 0) based on data for other cuprates²⁹, with antiferromagnetic (AF), superconducting (SC), pseudogap (PG) and Fermi-liquid (PG + FL) phases/regions. Lines indicate the characteristic pseudogap temperatures T^* and T^** and superconducting transition temperature T_c obtained from charge transport measurements⁴³, and the approximate Néel temperature T_N. Red triangles: temperature T_AF below which the response centered at q_AF is significantly enhanced (present work and refs. ^27,28); purple squares; onset of q = 0 magnetic order from polarized neutron diffraction^35,36,37; brown diamonds: onset of nematic order from torque magnetometry⁵⁹; yellow and orange circles: characteristic temperatures of the onset of short-range charge-density-wave (CDW) order obtained from X-ray²⁹ and optical⁶⁰ measurements. At the doping level of the present study (p $\approx$ 0.064, indicated by the arrow), CDW correlations are weak. b Schematic diagrams of magnetic excitation spectra for Hg1201-UD55 (present work), Hg1201-UD71²⁸, and Hg1201-UD88²⁷ at two temperatures (above and below T_c), showing the characteristics of the magnetic dispersion as a function of energy (vertical) and momentum transfer centered at q_AF (horizontal). The circle indicates the presence of a resonance in Hg1201-UD88, near optimal doping.

Neutron scattering is a powerful probe of the full momentum- and energy-dependent magnetic response of a material, i.e., the scattering cross-section is proportional to the imaginary part of the dynamic magnetic susceptibility, χ″(Q,ω), where Q and ω are the momentum and energy transfer to the scattering system, respectively. Due to limitations in the attainable flux even at the best neutron sources, a measurement of the spin dynamics typically requires sizable crystals, especially in the case of low-dimensional systems and in the extreme quantum limit of spin-1/2, due to sizable quantum fluctuations. For the cuprates, this has largely constrained studies of the magnetic response to two systems for which such crystals have been available^11,12,13,14: La_2-xSr_xCuO₄ (LSCO) and related compounds, as well as YBa₂Cu₃O_6+δ (YBCO). Key features revealed by these studies are: (i) in YBCO, a normal-state excitation gap (Δ_AF) at the antiferromagnetic wave-vector that increases with increasing doping in the SC doping range; (ii) an hourglass-shaped normal-state dispersion that is less pronounced in YBCO than in LSCO; (iii) in the case of YBCO, a resonance upon cooling into the SC state; (iv) near p ~ 1/8, LSCO and the closely related (La,Nd)_2−x(Sr,Ba)_xCuO₄ compounds exhibit a pronounced instability toward stripe order, with incommensurate magnetic correlations, that is stabilized in a low-symmetry structural phase. Incidentally, below p ~ 0.085, YBCO exhibits quasistatic incommensurate spin-density-wave (SDW) correlations¹⁵. Whereas the high-energy response (the upper part of the hourglass) in both compounds resembles the spin-wave dispersion seen in the insulating parent state, the considerable differences observed below about 50 meV have raised questions regarding the nature of the underlying magnetic response of the CuO₂ planes in the absence of compound-specific idiosyncrasies. This issue has not been resolved through more limited neutron scattering studies of several other cuprates^12,13—Bi₂Sr₂CuO_6+x (Bi2201), Bi₂Sr₂CaCu₂O_8+x (Bi2212), and Tl₂Ba₂CuO_6+δ (Tl2201). Note that 50 meV is an important energy scale, as it is comparable to both the PG and SC gap scales near optimal doping¹⁶.

There are good reasons to think that HgBa₂CuO_4+δ (Hg1201) is a model system^17,18,19,20, as it features the highest optimal T_c (nearly 100 K) of all single-CuO₂-layer cuprates (such as LSCO, Bi2201, Tl2201), higher also than the corresponding values for double-layer YBCO and Bi2212²¹. Moreover, unlike YBCO and LSCO, which exhibit low orthorhombic structural symmetry (in the entire SC doping range of YBCO, and up to p ~ 0.22 in the case of LSCO), Hg1201 maintains high tetragonal symmetry²¹. Finally, point disorder effects are rather prominent in LSCO and cause an insulator-like low-temperature resistivity upturn below optimal doping. Such effects have not been observed for Hg1201 in samples with doping levels as low as p ~ 0.055 (T_c ~ 45 K)^22,23, and although less prominent in YBCO, they are present in the doping range where SDW correlations are observed (below p ~ 0.085)²⁴. Notably, in YBCO, both the resistivity upturn²⁵ and the incommensurate magnetic order²⁶ are dramatically enhanced (up to at least p = 0.12) with intentionally introduced point disorder. The degree to which the underlying electronic properties of the CuO₂ planes can be masked by low structural symmetry and/or point disorder effects (e.g., through the stabilization of secondary electronic phases) is exemplified by a study²⁰ that uncovered that: Hg1201 obeys conventional Kohler scaling of the magnetoresistance deep in the PG state, with a Fermi-liquid T² scattering rate; in the case of YBCO, this simple metallic behavior is only seen in de-twinned samples, for charge-current flow perpendicular to the Cu-O chains characteristic of this particular compound; in LSCO, Bi2201 and Bi2212, this simple underlying scaling behavior is masked even more strongly. In this context, it is important to note that theoretical treatments of the cuprates generally avoid consideration of the added complexity due to non-universal disorder effects and deviations from tetragonal symmetry.

In recent years, sizable samples of Hg1201 have become available. Initial neutron scattering work revealed a gapped AF response near optimal doping (p ~ 0.13, T_c = 88 K; sample denoted Hg1201-UD88) similar to YBCO, with a magnetic resonance and an hourglass-shaped dispersion in the SC state²⁷. In stark contrast, a second study at somewhat lower doping (p ~ 0.09, T_c = 71 K; Hg1201-UD71) revealed an unusual, gapped wineglass-shaped response that is hardly altered upon cooling into the SC state²⁸. Since CDW correlations are particularly robust at the doping level of the latter study (Fig. 1), it has remained unclear if the observed behavior is a mere peculiarity associated with the prominence of the CDW phenomenon. It is therefore highly desirable to determine the magnetic response of Hg1201 at lower doping, where CDW order is weak²⁹.

Here, we present a detailed neutron scattering study of a strongly underdoped Hg1201 sample (p ≈ 0.064 and T_c ≈ 55 K; Hg1201-UD55) and uncover the underlying magnetic response of the CuO₂ planes below ~140 meV near the parent insulating state. As in the prior measurements of the AF excitations in Hg1201 at higher doping, we primarily report time-of-flight results^27,28. In order to confirm the magnetic nature of the response, we also present complementary triple-axis data with neutron polarization analysis. We find dynamic, wineglass-shaped AF correlations with little change across T_c, closely similar to the prior result for Hg1201-UD71, but with a much smaller normal-state excitation gap of Δ_AF ≈ 6 meV. Furthermore, we observe no signs of stripe/SDW and q = 0 magnetic order; the former observation is distinct from prior findings for other cuprates near the studied doping level, while the latter result is consistent with prior work for YBCO^30,31,32. Motivated by recent neutron scattering results for LSCO³³, we carry out density-functional theory (DFT) phonon calculations to address the possibility that the spin excitations in Hg1201 are coupled to the lattice dynamics at select energies. We find no evidence of significant intrinsic lattice effects.

Results

Figure 2a shows contour plots of $\chi ^{{\prime} {\prime}} \left({\bf{Q}},{{\upomega }}\right)$ at select energy transfers ω and temperatures T = 5, 70, and 410 K, obtained with incident neutron energies E_i = 70 and 200 meV using the same data analysis method as described previously^27,28 and in the Supplementary Information. We quote the three-dimensional scattering wave-vector Q = Ha* + Kb* + Lc* ≡ (H K L) in reciprocal lattice units, where a* = b* = 1.62 Å⁻¹ and c* = 0.66 Å⁻¹ are the room-temperature values. Given the lamellar nature of the cuprates, we are interested in the 2D magnetic response. Data such as those in Fig. 2a are therefore fit to the heuristic gaussian function χ″(Q) = ${\chi }_{0}^{{\prime} {\prime} }\exp \{-4\mathrm{ln}2R/{\left(2\kappa \right)}^{2}\}$, where R = | [(H − 1/2)² + (K − 1/2)²]^1/2 – δ | ², $2\kappa$ is the intrinsic full-width-at-half-maximum (FWHM) momentum width, and δ parameterizes the incommensurability relative to the 2D AF wave-vector q_AF = (1/2 1/2). Corresponding constant-ω momentum trajectories, averaged over {100} and {010} with lateral momentum-bin range q_⊥ = [0.45, 0.55] r.l.u., are shown in Fig. 2b. The overall response at T = 5 K and 70 K, extracted from the fits up to ~135 meV, is shown in Fig. 2c. $\chi ^{{\prime} {\prime}} \left({\bf{Q}},{{\upomega }}\right)\,$ changes from dispersing to commensurate below ω_c ≈ 55 meV, and becomes immeasurably small below Δ_AF ≈ 6 meV. At 410 K, the response is considerably weaker, yet consistent with these observations.

Fig. 2: Magnetic excitation spectrum featuring gapped commensurate and dispersive components.

a Constant-energy slices of magnetic susceptibility $\chi^{\prime\prime}$ (q) as a function of the 2D in-plane momentum transfer q = (H K) at T = 5 K (left), 70 K (center), and 410 K (right), in units of µ_B² eV⁻¹ f.u.⁻¹ (same color scale as c). Data averaged over indicated energy (ω) ranges. White text indicates that $\chi^{\prime\prime}$ has been multiplied by a factor to highlight more detail. White dots in the lower-left corners indicate momentum resolution. Data with ω < 55 meV (ω > 55 meV) were collected with E_i = 70 meV (E_i = 200 meV). b Corresponding constant-ω cuts across q_AF, averaged over {100} and {010} trajectories. The apparent susceptibility magnitude is slightly lower than the actual values due to the averaging over the binning range q_⊥ = [0.45, 0.55] r.l.u. c Magnetic dispersion extracted from 2D Gaussian fits (see text), as a function of energy transfer (ω) and incommensurability (δ = |q − q_AF | ) at T = 5 K (left) and 70 K (right). The white dotted lines indicate the full-width-half-maximum of the response as a function of energy. White tick marks: ω values in (a, b). See Supplementary Information for data analysis details and additional data.

Figure 3a, b show, respectively, the energy dependence of the amplitude ${\chi }_{0}^{{\prime} {\prime} }\left(\omega \right)$ and the change ${\varDelta \chi }_{0}^{{\prime} {\prime} }\left(\omega \right)$ across T_c and between 5 K and 410 K. Figure 3c, d show the corresponding results for the momentum-integrated local susceptibility, defined as ${\chi }_{\text{loc}}^{{\prime} {\prime} }\left(\omega \right)={\int }_{}{\chi }^{{\prime} {\prime} }\left({\bf{q}},\omega \right){d}^{2}q/{\int d}^{2}q$, and its change ${\Delta}{\chi }_{\text{loc}}^{{\prime} {\prime} }\left(\omega \right).\,$ There is no notable difference between the response at 5 K and 70 K, except for a subtle low-temperature enhancement at ω ~ 30 meV, where ${\chi }_{0}^{{\prime} {\prime} }\left(\omega \right)$ is largest. We notice a spike at ~30 meV in ${\chi }_{\text{loc}}^{{\prime} {\prime} }\left(\omega \right)$ in the 5 K and 70 K data, and broad maxima at ~30 meV and ~50 meV in the 410 K data. Such enhancements were previously observed and ascribed to additional phonon scattering that is not properly removed in the processed data (see Supplementary Information)²⁸. The results in Figs. 2 and 3 reveal that the magnetic response is gapped already in the normal state, with no significant change across T_c. At 5 K and 70 K, ${\chi }_{0}^{{\prime} {\prime} }\left(\omega \right)$ and ${\chi }_{\text{loc}}^{{\prime} {\prime} }\left(\omega \right)\,$ are peaked at ~35 meV and ~50 meV, respectively. Above ω ~ 100 meV, the response is relatively weak and rather similar at all three temperatures.

Fig. 3: Magnetic susceptibility amplitude and local susceptibility.

a Magnetic susceptibility amplitude $\chi^{\prime\prime}_0$, determined from 2D fits to background-subtracted data such as those in Fig. 2a. Filled circles: E_i = 70 meV. Open circles: E_i = 200 meV. b Difference between $\chi^{\prime\prime}_0$ at 5 K, deep in the superconducting state, and at 70 K (black) and 410 K (yellow). c Local (momentum-integrated) susceptibility ${\chi}^{\prime\prime}_{\mathrm{loc}}$ (same colors and symbols as in (a)). d Difference in ${\chi}^{\prime\prime}_{\mathrm{loc}}$, using the same colors and symbols as (c). Black vertical bars in all panels: energies where DFT indicates phonon modes at q_AF. At 410 K, the local maxima in ${\chi}^{\prime\prime}_0$ and ${\chi}^{\prime\prime}_{\mathrm{loc}}$ at ~30 and ~50 meV correspond to phonon crossings and indicate the inability of our analysis to completely remove unwanted phonon contributions and/or to discern an enhanced magnetic response due to nontrivial electron-lattice coupling effects at these energies. The small enhancement in $\chi^{\prime\prime}_0$ near 30 meV across T_c = 55 K is consistent with the existence of a small magnetic resonance, but also coincides with phonon crossings, and hence may be an electron-lattice-coupling effect or spurious. Solid lines: guides to the eye.

In order to obtain data with even better energy resolution and signal-to-noise ratios in the energy range in which the response is commensurate, we carried out measurements with E_i = 50 meV. Figure 4a shows ${\chi }_{0}^{{\prime} {\prime} }\left(\omega \right)$ below 45 meV at seven temperatures in the 10 K to 450 K range. We find again that the magnetic response extrapolates to zero at Δ_AF ≈ 6 meV, both in the normal state and deep in the SC state. As already seen in Fig. 3a for 5 K and 70 K, ${\chi }_{0}^{{\prime} {\prime} }\left(\omega \right)$ exhibits a smooth, non-monotonic energy dependence at all temperatures. The E_i = 50 meV results are consistent with those obtained with higher incident energies (see Fig. 4a inset) within about 15%. Figure 4c shows the same data as a function of temperature. At high-energy transfers, ${\chi }_{0}^{{\prime} {\prime} }$ smoothly increases with decreasing temperature and begins to plateau near T_c. For ω $\le$ 12 meV, ${\chi }_{0}^{{\prime} {\prime} }\,$ eventually decreases at low temperatures, consistent with the opening of a gap.

Fig. 4: Additional time-of-flight results and complementary triple-axis neutron data.

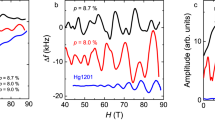
a Energy dependence of $\chi^{\prime\prime}_0$ measured with E_i = 50 meV at seven temperatures. Solid lines: guides to the eye. Inset: $\chi^{\prime\prime}_0$ obtained with E_i = 70 meV at 5 and 70 K (same data as in Fig. 3a). Black vertical bars: energies where DFT indicates phonon crossings at q_AF. b Comparison of energy dependence of $\chi^{\prime\prime}_0$ (at T = 10 K and 72 K; solid lines same as in (a)) with spin-polarized triple-axis neutron scattering results in the spin-flip channel at similar temperatures (squares: data obtained at 5 K and 70 K from momentum scans at select energies; circles: data obtained at 5 K from energy scans at q_AF and two background momentum transfers; see also Figs. S6 and S7 in Supplementary Information). The triple-axis data are scaled to match the time-of-flight result, which is obtained in absolute units. The combined data demonstrate the predominant magnetic nature of the signal, peaked at ~ 35 meV, and are fully consistent with the results in Fig. 3. c Temperature dependence of $\chi^{\prime\prime}_0$ at select energies integrated over ± 1.5 meV obtained with E_i = 50 meV. Solid lines: guides to the eye. Vertical blue lines: T_c = 55 K and T* ~ 370 K (see Fig. 1).

Figure 4b shows the energy dependence of the response at q_AF obtained from triple-axis momentum and energy scans with longitudinal polarization analysis, obtained at 5 K and 70 K. These data agree well with the time-of-flight result and hence confirm the predominant magnetic nature of the scattering and the presence of a gap.

The AF correlation length can be determined from the width of the response in reciprocal space. We define the correlation length as $\xi \,=\,1/2\kappa$, i.e., the reciprocal of the intrinsic FWHM of the response, after correcting for the instrument resolution. In the low-energy range above the AF gap, the length ranges from $\xi \,\approx \,8.8\,\,{\text{\AA }}$ at low temperature to $\xi \approx 6.4\,{\text{\AA}}$ at high temperature, based on the ${E}_{i}=50\,{\rm{meV}}$ data (Fig. 4). An estimate of the instantaneous length ${\xi }_{0}\,$ can be determined from an energy integration of the response. Using the E_i = 70 meV and 200 meV data (Figs. 2 and 3), and integrating over the range from 1.5 to 137.5 meV, this length ranges from ${\xi }_{0}=\,8.3\,\pm \,0.1{\text{\AA }}$ at 5 K to ${\xi }_{0}=\,6.6\,\pm \,0.1{\text{\AA}}$ at 410 K. These lengths of about 2 lattice constants are consistent prior results for other cuprates^12,13,14,15 and comparable to the ~2 nm superconducting coherence length³⁴.

We have tested the possibility of quasi-elastic magnetic scattering, which is seen in other cuprates. Figure 5a shows triple-axis [0 1 0] momentum scans across q_AF at nominally zero energy transfer (1.2 meV FWHM energy resolution). The SC (5 K) and normal (80 K) state data are featureless and statistically indistinguishable. Importantly, unlike for YBCO and LSCO^11,12,13, where strong incommensurate quasi-elastic SDW peaks have been observed at similar doping levels, we observe no such scattering in Hg1201-UD55, consistent with our observation of a gapped response centered at q_AF. Using the known cross-section of the (0 0 4) Bragg peak (which is 4.2 barn) for comparison, we estimate the upper bound of a possible elastic AF signal to be 0.4 mbarn.

Fig. 5: Absence of static SDW/stripe and q = 0 order.

a Triple-axis momentum scan, across q_AF along [0 1 0], at ω = 0 at 5 K (black squares) and 80 K (red circles). Blue crosses: locations where SDW/stripe order is observed at a similar doping level in LSCO (p = 0.06)¹¹. Inset: schematic of the momentum-scan range (blue arrow) and characteristic wave vectors for LSCO (p = 0.06, blue crosses). See Supplementary Information for more details. b Spin-polarized neutron scattering results for the magnetic scattering intensity at the (1 0 0) reflection, determined from the inverse flipping ratio; see Fig. S8 in the Supplementary Information for the full inverse flipping ratio data. The highly underdoped (Hg1201-UD55, blue circles) and optimally doped (Hg1201-OP95, red triangles; data from ref. ³⁷) samples show no detectable static magnetic order, in contrast to the moderately underdoped sample (Hg1201-UD71, yellow squares; data from ref. ³⁷). All data were obtained with the D7 spectrometer at ILL. The gray band corresponds to the 1.7 mbarn upper bound for the magnetic intensity of Hg1201-UD55 (see main text).

Finally, we also investigated the existence of a quasistatic q = 0 magnetic response, which was previously observed in both YBCO^30,31,32 and Hg1201^35,36,37 at higher doping. While this observation was challenged in a subsequent study of YBCO³⁸, it was shown that the samples used in this work were too small to yield meaningful insight³¹. Figure 5b shows the results of polarized neutron diffraction measurements of the magnetic scattering at the (1 0 0) Bragg peak in Hg1201-UD55 compared to earlier results³⁷ for Hg1201-UD71 (moderately underdoped) and Hg1201-OP95 (optimally doped). All data were obtained with the D7 spectrometer at ILL. For Hg1201-UD71, the magnetic scattering (extracted from XYZ longitudinal polarization analysis—see the Supplementary Information) exhibits an order-parameter-like temperature dependence with an onset below T₀ $\sim \,370$ K and a maximum intensity of $\sim \,13$ mbarn at 80 K. Conversely, the highly underdoped and optimally doped samples show no such signature of q = 0 magnetism within the detection limit of the instrument. However, we note that a nonzero q = 0 magnetic response at both the (1 0 0) and (1 0 1) reflections with a magnitude of $\sim \,1.7$ mbarn at 100 K was previously observed for Hg1201-OP95 using a triple-axis neutron spectrometer (4F1 at LLB)³⁷. Due to the thermal drift of the intensities collected in the different measurement channels (see Supplementary Information and ref. ³⁷) and the inability to determine an accurate baseline for the magnetic scattering, the weak q = 0 signal falls below the threshold of detection on D7. One can thus give an upper bound of 1.7 mbarn for the q = 0 magnetism in Hg1201-UD55, as indicated by the shaded area in Fig. 5b. Interestingly, the vanishing of the q = 0 magnetic signal at low doping in Hg1201 is consistent with the significant decrease observed in underdoped YBa₂Cu₃O_6.45 (p = 0.08)³⁹. We note that the present data do not rule out the possibility of significant dynamic q = 0 correlations.

Discussion

At the low doping levels of the present study, the cuprates YBCO, LSCO, and Bi2201 exhibit an ungapped, hourglass-shaped magnetic response in both the normal and SC states^{11,13,15,40,41}. In contrast, our results for Hg1201-UD55 resemble the wineglass-shaped response previously observed for Hg1201-UD71, albeit with a considerably smaller gap (~6 meV vs. ~27 meV). These findings are crucial for two reasons. First, given that the CDW order in Hg1201 is nearly absent at the doping level of the present study²⁹, the prior result for Hg1201-UD71 does not appear to be affected by CDW correlations.

Second, the gapped, wineglass-shaped response must be the intrinsic behavior of the pristine, quintessential CuO₂ planes. Unlike other hole-doped cuprates that have been investigated in this context, Hg1201 exhibits high tetragonal symmetry and minimal disorder effects, as evident from transport measurements, e.g., the observations of Kohler scaling, negligible residual resistivity, and quantum oscillations in the underdoped part of the phase diagram^17,18,19,20. Incommensurate SDW and stripe correlations at low and intermediate hole concentrations^5,15,40, therefore, are not universal features of the cuprates, but rather the result of material-specific interactions. While the high-energy PG energy scale of the cuprates is ~400 meV at the doping level of the present study^16,42,43, the SC gap is expected to be well below the characteristic scale ω_c ≈ 55 meV above which the response of Hg1201-UD55 becomes incommensurate⁴⁴. The present results, which extend to ω ~ 140 meV, thus cover an important energy range and provide pivotal information for tests of SC pairing scenarios, such as spin-fluctuation-driven mechanisms⁶.

At somewhat higher doping levels than in the present work, Hg1201 and several other cuprates exhibit a resonance-like enhancement at q_AF (and characteristic energy ω_r) in the SC state, with a response that is gapped and hourglass- rather than wineglass-shaped (Fig. 1). This can be understood within an itinerant picture, in which the resonance is part of a spin exciton, i.e., a dispersive spin-triplet collective mode bound below the threshold of the Stoner continuum²⁷. Unlike for Hg1201-UD88, which exhibits a resonance at ω_r ≈ 59 meV²⁷, no resonance was observed in Hg1201-UD71²⁸. In the present work, we find an increase in the magnetic response in the 25–35 meV range in the SC state, yet it is unclear if this small, gradual increase is to be thought of as a resonance. From the data in Figs. 3 and 4, we estimate this spectral weight enhancement to be ${{W}}_{{r}}{=}\int {\text{d}}{\omega }\,{\varDelta }{\mbox{''}}{=}{0}{.}{14}{\pm }{0}{.}{07}\,{{\mu }}_{{\text{B}}}^{{2}}{{\text{f.u.}}}^{{-}{1}}$. Additional evidence for a small resonance-like effect from triple-axis scattering data is shown in Fig. S9 in the Supplementary Information. Although the value of the SC gap at the doping level of Hg1201-UD55 is unknown, it is likely not much larger than ω_r ≈ 30 meV⁴⁴, so that W_r is indeed expected to be small²⁷. Moreover, the ratio ω_r/T_c ~ 6.4 is comparable to that for other cuprates⁴⁵. We caution, though, that several phonon modes cross q_AF at about 30 meV, as shown in detail in Fig. 6 and also discussed in refs. ^27,28, which complicates the interpretation of subtle changes in the magnetic response across T_c.

Fig. 6: Comparison of phonon modes with DFT results.

a Scattering intensity without background subtraction as a function of energy and momentum transfer along [1 1 0], integrated over q_⊥ = ± 0.05 (r.l.u.) along [1 -1 0] and over a wide range in L (see Supplementary Information for details). The time-of-flight neutron data were collected at T = 10 K with E_i = 50 meV. Selected calculated phonon modes are overlaid. Red dashed lines indicate spurious scattering from Aluminum in the sample holder. b Calculated phonon intensities in the same momentum range as the data in (a), with all phonon modes below 45 meV overlayed. c–f Select phonon eigenvectors at Q = (0.5 0.5 L), with energies indicated in (a, b).

Our polarized triple-axis neutron scattering data extend up to about 40 meV and confirm that the low-energy commensurate response is predominantly magnetic in nature (Fig. 4b). However, in the time-of-flight data, both the peak and local susceptibilities at 410 K exhibit local maxima at energies (about 30 meV and 50 meV) that correspond to phonon crossings (Fig. 6), and at low temperatures, ${\chi }_{0}^{{\prime} {\prime} }$ is strongest at ~35 meV (Fig. 2–4). This points to the possibility of nontrivial electron-lattice coupling effects. A recent neutron scattering study of LSCO revealed an enhancement of χ′′(ω) in the 16–19 meV range, where the (incommensurate) spin excitations are intersected by optic phonons³³. It was found that this enhancement is present only in SC samples and that, similar to the transition temperature, its magnitude follows a dome-shaped doping dependence. This effect was interpreted as an interplay among spin, charge, and lattice degrees of freedom, with resultant composite excitations: optic phonons stabilize fluctuating, short-range stripe correlations, and thereby enhance the magnetic correlations. Although Hg1201 does not display a tendency toward stripe order, similar electron-lattice coupling effects may be present. Since we lack data for non-SC samples for comparison, we are unable to carry out the same analysis as ref. ³³. Instead, we performed a DFT calculation of the phonon spectrum of stoichiometric, undoped Hg1201. The observed good agreement between experiment and theory (Fig. 6) allows us to identify the approximate energy ranges that are unaffected by phonon crossings at q_AF. For example, only the ω = 30 meV data in Fig. 2a, b are affected, due to the relatively strong dispersion and Q-dependence of a phonon mode crossing q_AF at this energy; this contribution is not fully removed in our data analysis. Similarly, most of the energy transfers for which data are shown in Fig. 4b do not coincide with calculated phonon crossings. From this, we can conclude that, indeed, lattice effects play an overall minor role.

Comparing the present results with those for Hg1201-UD71 and Hg1201-UD88, we find that the low-temperature maximum of the local susceptibility, ${\chi }_{\text{loc}}^{{\prime} {\prime} }\left(\omega \right)$ ~ 4–5 $\mu$_B² eV⁻¹f.u.⁻¹, is approximately independent of doping. Similarly, the strength of the total, energy-integrated response (up to 100 meV) is comparable in Hg1201-UD55 and Hg1201-UD71²⁸, and about 0.25–0.3 ${\mu}_{\mathrm{B}}^{2} {\mathrm{f}}.{\rm{u}}.^{-1}$; extrapolating the available data for Hg1201-UD88²⁷ to 100 meV yields 0.15–0.2 ${\mu}_{\mathrm{B}}^{2} {\mathrm{f}}.{\rm{u}}.^{-1}$. Despite the differences in the structure of the response (wineglass vs. hourglass), this compares rather well with the corresponding strength of the magnetic response of underdoped LSCO (~0.15 ${\mu}_{\mathrm{B}}^{2} {\mathrm{f}}.{\rm{u}}.^{-1}$ for p = 0.085)⁴⁶.

Similar to Hg1201-UD71²⁸, Hg1201-UD88²⁷, and underdoped YBCO^47,48,49, the AF response in Hg1201-UD55 starts to increase below the PG temperature (Figs. 1 and 4c). This observation can be understood within the framework of a recent phenomenological model for the cuprates^42,43, which combines insights from transport measurements with evidence that these complex oxides are inherently inhomogeneous and exhibit local two-component electronic behavior: Mott-localization of one hole per Cu occurs gradually with decreasing doping and/or temperature, in a highly inhomogeneous manner, such that below T* (or, more precisely, the somewhat lower temperature T**), the carrier density has fully crossed over from 1 + p to the nominal value p. In this picture of the phase diagram, the formation of local magnetic moments, loop currents, CDW, SDW and stripe order are all emergent phenomena, and significant (dynamic) AF correlations are expected to develop below T*. While this comprehensive model is phenomenological in nature, the present results pave the way for a microscopic theoretical understanding of the magnetic degrees of freedom of the doped CuO₂ planes near the Mott-insulating parent state.

Methods

Neutron scattering experiments

The neutron scattering measurements were performed on a large co-aligned sample (mass of ~2 g) that consists of approximately 30 single crystals. Neutron diffraction on the full sample shows a FWHM mosaic of 1.7°. Crystals were grown by a flux method⁵⁰ and then annealed to the desired doping level at an elevated temperature in vacuum¹⁷. For each crystal, T_c was determined from a magnetic susceptibility measurement using a Quantum Design, Inc. Magnetic Property Measurement System. The average of these measurements was used to characterize the full sample, resulting in a mean value of T_c = 55 K and a FWHM transition width of ∆T_c = 8 K.

The measurements of the AF response were carried out on the time-of-flight spectrometer ARCS at Oak Ridge National Laboratory (ORNL), Oak Ridge (USA), and on two triple-axis spectrometers: IN20 at the Institute Laue-Langevin (ILL), Grenoble (France), and 2 T at the Laboratoire Léon Brillouin (LLB), Saclay (France). The magnetic dispersion was measured on ARCS, with the sample’s crystalline c-axis aligned along the incident beam, and with three incident neutron energies: E_i = 70 and 200 meV (at 5, 70, and 410 K) and E_i = 50 meV (at 10, 46, 72, 150, 250, 350, and 450 K). As in previous work on Hg1201^27,28, the sample was only measured in one orientation, and the data were integrated along [0 0 1] due to the quasi-2D nature of the magnetic response in the lamellar cuprates. One side effect of this is that for any value of in-plane momentum transfer q = (H K), data with different energy transfer ω correspond to different values of out-of-plane momentum transfer L, as constrained by momentum and energy conservation. The dynamic magnetic susceptibility $\chi ^{{\prime} {\prime}} \left({\bf{Q}},\omega \right)$ was determined from the scattering cross-section by correcting for the anisotropic magnetic form factor^51,52 and the thermal Bose factor of the excitations, as described in previous work^27,28 and detailed in the Supplementary Information. Longitudinal polarization analysis was performed on IN20 to extract the purely magnetic signal. Momentum scans across q_AF at select energies ranging from 9 to 30 meV, and energy scans at q_AF and two background momentum transfers were performed. The detailed temperature dependence of $\chi ^{{\prime} {\prime}} \left({\bf{Q}},\omega \right)$ at $\omega$ = 30 meV (Fig. S9) and the elastic scattering (Fig. 5a) were measured on 2 T.

The q = 0 magnetism measurements were carried out on the D7 diffractometer at ILL, equipped with a cryofurnace, and with an incident neutron wavelength of 3.1 Å. The sample was aligned in the (H 0 L) scattering plane. The temperature dependence of the scattering at (1 0 0) was tracked between 80 K (above the SC transition to avoid the neutron beam depolarization) and 455 K using XYZ longitudinal polarization analysis to search for a possible magnetic signal coincident with the nuclear (1 0 0) Bragg reflection, as detailed in the Supplementary Information.

Density-functional theory calculations

Phonon dispersions and eigenvectors were calculated using the density-functional perturbation theory implementation in the abinit package⁵³. Exchange-correlation was approximated with the PBEsol⁵⁴ version of the generalized-gradient approximation, and norm-conserving pseudopotentials were used for the valence-core interaction⁵⁵. The energy cutoff was 1200 eV, and the k-point grid for ground state and perturbation calculations was 12 × 12 × 6. Dynamical matrices were calculated on a uniform 4 x 4 x 2 q-point grid, corresponding to a 4 × 4 ×2 supercell in real space. The real-space force constants were ported to phonopy⁵⁶ format using abipy⁵⁷ and then used in the euphonic package⁵⁸ to calculate neutron intensities.