Introduction

Superconductivity (SC) is a macroscopic quantum phenomenon stemming from the condensation of paired electrons, which is characterized by a complex pairing order parameter with both amplitude and phase1,2. The superconducting transition temperature Tc is governed by the lower energy scale between Cooper pair formation and phase coherence establishment. In BCS mean-field theory, it is generally assumed that the phase coherence temperature significantly exceeds the Cooper pair formation temperature. Consequently, fluctuations of the order parameter are negligible for determining important physical properties such as transition temperature Tc, which generically holds for SC in many conventional metals3. However, in systems with low superfluid density due to their low charge carrier density, such as unconventional superconductors, including cuprates4,5,6,7, organic superconductors8,9, and twisted bilayer graphene10,11,12,13, this relationship can be reversed. Additionally, superfluid density in conventional superconductors could be heavily suppressed by disorder14,15,16. Even if Cooper pairs form, the system can remain in a non-superconducting state due to the incoherence of the superconducting phases. Therefore, superconducting fluctuations can become significant above the critical temperature Tc. Generally, low-energy physics is governed by superconducting phase fluctuations17, while pairing amplitude fluctuations dominate at higher temperatures18.

When superconducting fluctuations are remarkable, superconducting phase fluctuations can drive many intriguing phenomena19. In the past decades, phase fluctuations in superconductors have been extensively investigated from both theoretical20,21,22,23,24,25,26,27,28,29,30,31,32,33,34,35,36,37,38 and experimental5,39,40,41,42,43,44,45,46,47,48,49,50 perspectives. In unconventional superconductors, the pairing order parameter usually has a more complex structure, such as nodal lines for d-wave pairing. Strong phase fluctuations can lead to the opening of the spectral gap above superconducting Tc19,20,21,22,25,26,27,36. It has been proposed theoretically that phase fluctuations could trigger novel phenomena, such as the Fermi arc26,27,28,29,51 observed in underdoped cuprates52,53,54, and the possibility of charge-4e SC55,56,57,58,59,60,61,62 as a vestigial order. Additionally, the phase fluctuation picture can be employed to explain the light-enhanced superconductivity63.

Nevertheless, a qualitative study of the transport properties arising from superconducting phase fluctuations of a microscopic model in the temperature regime above Tc is rare. Recently, armed with the development of thin-film technology, strange-metal electrical transport behaviors, which were unveiled in underdoped and optimally doped cuprates soon after the discovery of high-Tc superconductors64,65,66, have been observed in a wide doping range of electron-doped cuprates La2−xCexCuO467,68 and iron-pnictide superconductors FeSe69, along with \({{\rm{Ca}}}_{10}\left({{\rm{Pt}}}_{4}{{\rm{As}}}_{8}\right){\left({\left({{\rm{Fe}}}_{0.97}{{\rm{Pt}}}_{0.03}\right)}_{2}{{\rm{As}}}_{2}\right)}_{5}\)70. More remarkably, the coefficient of linear-T resistivity exhibits a quadratic dependence on the superconducting transition temperature Tc68,69,70, which implies the possible relation between anomalous metallic transport and the SC or other ingredients associated with superconducting pairing mechanisms. Therefore, a qualitative investigation of the electrical resistivity driven by superconducting phase fluctuations above the critical temperature Tc is highly desirable. This study could provide valuable insights into the relationship between resistivity and the parameters of superconductivity. Additionally, understanding the role of pairing symmetries in resistivity under phase fluctuations is of significant interest. By considering different pairing symmetries, it could deepen our understanding of the interplay between anisotropic scattering and transport properties in superconducting systems.

In this work, we systematically investigate the properties of electrical transport in a microscopic Bogoliubov-de Gennes (BdG) Hamiltonian that incorporates superconducting pairing and accounts for thermal phase fluctuations above the superconducting critical temperature Tc. As the pairing amplitude fluctuations are insignificant when temperatures are much lower than the pairing temperature, the amplitude is fixed as a spatially independent value. Distinct from the BCS mean-field Hamiltonian, the model under consideration incorporates the spatial fluctuations of phase. The phase fluctuations are governed by a classical XY model, characterizing the thermal fluctuations of the order parameter’s phase with varying temperatures. Employing large-scale Monte Carlo simulation, we study the transport properties of the model at finite temperatures. The numerical results reveal that the electrical resistivity induced by the thermal phase fluctuations in the low-temperature regime above Tc obeys the scaling behavior \(\rho \left(T\right)\propto A\exp (-B/\sqrt{T/{T}_{c}-1})\), which is consistent with the critical scaling relation of the correlation length for the Berezinskii-Kosterlitz-Thouless (BKT) transition71. Thanks to the special form of the BKT correlation length, our results are formally in accord with the phenomenological theory17. However, a notable deviation is revealed by our numerical results, we find that the resistivity is inversely proportional to the BKT correlation length with a power smaller than one, in contrast to the square inverse in the Halperin-Nelson (H-N) framework. We further evaluate the quasiparticle lifetime of electrons versus temperature. Interestingly, we achieve the same scaling behavior as that of electrical resistivity. Hence, our numerical results establish that thermal phase fluctuations yield the anomalous temperature dependence of electrical resistivity in two-dimensional superconductors, which is determined by the BKT critical scaling of the correlation length.

Results

The model

In superconductors characterized by pronounced superconducting fluctuations, such as cuprates, the superconducting transition temperature Tc is often significantly lower than the transition temperature TMF predicted by the mean-field theory. Within the temperature regime above Tc yet substantially below TMF, superconducting coherence is compromised due to phase fluctuations, whose effects can be effectively modeled by the BdG Hamiltonian:

$${{\mathcal{H}}}_{0}\,=\,\sum _{{\boldsymbol{r}},{{\boldsymbol{r}}}^{{\prime} }}\left(\begin{array}{c}{c}_{{\boldsymbol{r}}\uparrow }^{\dagger },{c}_{{\boldsymbol{r}}\downarrow }\end{array}\right)\,\left(\begin{array}{cc}{H}_{0}({\boldsymbol{r}},{{\boldsymbol{r}}}^{{\prime} })&\Delta ({\boldsymbol{r}},{{\boldsymbol{r}}}^{{\prime} })\\ {\Delta }^{* }({\boldsymbol{r}},{{\boldsymbol{r}}}^{{\prime} })&-{H}_{0}({\boldsymbol{r}},{{\boldsymbol{r}}}^{{\prime} })\end{array}\right)\,\left(\begin{array}{c}{c}_{{{\boldsymbol{r}}}^{{\prime} }\uparrow }\\ {c}_{{{\boldsymbol{r}}}^{{\prime} }\downarrow }^{\dagger }\end{array}\right),$$
(1)

where \({c}_{{\boldsymbol{r}}\sigma }^{\dagger }\) is the creation operator of an electron at site r with spin σ, and H0 is the Hamiltonian of non-interacting electrons defined on a square lattice,

$${H}_{0}({\boldsymbol{r}},{{\boldsymbol{r}}}^{{\prime} })=-t{\delta }_{{{\boldsymbol{r}}}^{{\prime} },{\boldsymbol{r}}\pm {\boldsymbol{e}}}-\mu {\delta }_{{\boldsymbol{r}},{{\boldsymbol{r}}}^{{\prime} }},$$
(2)

with t the hopping integral between two nearest-neighboring sites, e = (ex, ey) the two unit lattice vectors, and μ the chemical potential. Variable θ is the phase of the superconducting gap parameter \(\Delta ({\boldsymbol{r}},{{\boldsymbol{r}}}^{{\prime} })\)

$$\Delta ({\boldsymbol{r}},{{\boldsymbol{r}}}^{{\prime} })=\left\vert \Delta ({\boldsymbol{r}},{{\boldsymbol{r}}}^{{\prime} })\right\vert {e}^{i\theta (\bar{{\boldsymbol{r}}})},$$
(3)

where \(\bar{{\boldsymbol{r}}}=({\boldsymbol{r}}+{{\boldsymbol{r}}}^{{\prime} })/2\). In the temperature regime Tc < T ≪ TMF, we assume the gap amplitude to be a constant, \(\left\vert \Delta ({\boldsymbol{r}},{{\boldsymbol{r}}}^{{\prime} })\right\vert =\Delta\), independent of \(({\boldsymbol{r}},{{\boldsymbol{r}}}^{{\prime} })\) and T.

In this work, two kinds of pairing states are considered. One is the s-wave pairing state, and the other is the \({d}_{{x}^{2}-{y}^{2}}\)-wave pairing state. The s-wave pairing state only involves the on-site pairing, whose gap parameter is defined by

$$\Delta ({\boldsymbol{r}},{{\boldsymbol{r}}}^{{\prime} })=\Delta {e}^{i\theta \left({\boldsymbol{r}}\right)}{\delta }_{{\boldsymbol{r}},{{\boldsymbol{r}}}^{{\prime} }}.$$
(4)

The \({d}_{{x}^{2}-{y}^{2}}\)-wave pairing state, on the other hand, arises from the pairing of two electrons on two nearest-neighboring sites r and \({{\boldsymbol{r}}}^{{\prime} }={\boldsymbol{r}}\pm {\boldsymbol{e}}\), and the phase parameter is defined on the corresponding link of the square lattice.

$$\Delta ({\boldsymbol{r}},{{\boldsymbol{r}}}^{{\prime} })=\Delta {e}^{i\theta (\bar{{\boldsymbol{r}}})}\left({\delta }_{{{\boldsymbol{r}}}^{{\prime} },{\boldsymbol{r}}\pm {{\boldsymbol{e}}}_{x}}-{\delta }_{{{\boldsymbol{r}}}^{{\prime} },{\boldsymbol{r}}\pm {{\boldsymbol{e}}}_{y}}\right).$$
(5)

In the temperature range considered here, we assume that the fluctuation of θ is slow in comparison with the quasiparticle excitations so that the dynamics of θ are purely governed by the classical XY model, described by the Hamiltonian

$${{\mathcal{H}}}_{\theta }=-\sum _{\left\langle \bar{{\boldsymbol{r}}},{\bar{{\boldsymbol{r}}}}^{{\prime} }\right\rangle }{J}_{\theta }\cos \left[\theta \left(\bar{{\boldsymbol{r}}}\right)-\theta \left({\bar{{\boldsymbol{r}}}}^{{\prime} }\right)\right],$$
(6)

where 〈 ⋯ 〉 denotes summations over the nearest-neighboring sites for the s-wave pairing state or bond centers for the \({d}_{{x}^{2}-{y}^{2}}\)-wave pairing state.

In the linear response theory, the electromagnetic response function is determined by the current-current correlation function

$${\Lambda }_{\alpha \beta }({\boldsymbol{q}},\omega )=\mathop{\int}\nolimits_{0}^{\infty }dt{e}^{i\omega t}\left[{j}^{\alpha }({\boldsymbol{q}},t),{j}^{\beta }(-{\boldsymbol{q}},0)\right],$$
(7)

where jα(q, t) is the Fourier component of the current operator along the α-direction

$${j}^{\alpha }({\boldsymbol{r}})=it\sum _{\sigma }\left({c}_{{\boldsymbol{r}},\sigma }^{\dagger }{c}_{{\boldsymbol{r}}+{{\boldsymbol{e}}}_{\alpha },\sigma }-{c}_{{\boldsymbol{r}}+{{\boldsymbol{e}}}_{\alpha },\sigma }^{\dagger }{c}_{{\boldsymbol{r}},\sigma }\right).$$
(8)

Using the eigenpairs ψ and ε of \({{\mathcal{H}}}_{0}\), the current-current correlation can be expressed as

$${\Lambda }^{\alpha \beta }({\boldsymbol{q}},\omega )=\frac{1}{N}\sum _{a\ne b}{M}_{ab}({\boldsymbol{q}}){M}_{ba}(-{\boldsymbol{q}})\frac{f({\varepsilon }_{a})-f({\varepsilon }_{b})}{\omega -{\varepsilon }_{a}+{\varepsilon }_{b}+i\eta },$$
(9)

where N = L × L is the lattice size, \(f\left(\varepsilon \right)\) is the Fermi distribution function, η is a positive number that tends to zero in the thermodynamic limit N → ∞, and

$$\begin{array}{rcl}{M}_{ab}\left({\boldsymbol{q}}\right)&=&\mathop{\sum }\limits_{{\boldsymbol{r}}\sigma }\left[{\psi }_{a}^{* }({\boldsymbol{r}},\sigma ){\psi }_{b}({\boldsymbol{r}}+{{\boldsymbol{e}}}_{\alpha },\sigma )\right.\\ &&-\left.{\psi }_{a}^{* }({\boldsymbol{r}}+{{\boldsymbol{e}}}_{\alpha },\sigma ){\psi }_{b}({\boldsymbol{r}},\sigma )\right]{e}^{i{\boldsymbol{q}}\cdot {\boldsymbol{r}}}.\end{array}$$
(10)

Resistivity

The resistivity is the reciprocal of the real part of optical conductivity σ(ω) in the ω→0 limit. The optical conductivity, on the other hand, is determined by the imaginary part of the current-current correlation function in the long-wavelength limit

$${\rm{Re}}\sigma \left(\omega \right)=\frac{{\rm{Im}}{\Lambda }^{xx}\left({\boldsymbol{q}}={\boldsymbol{0}},\omega \right)}{\omega }.$$
(11)

Using the expression (9), it is straightforward to show that

$${\rm{Re}}\sigma \left(\omega \right)=\sum _{a\ne b}{W}_{ab}\delta (\omega -{\varepsilon }_{a}+{\varepsilon }_{b})$$
(12)

in the limit η→0. In this equation,

$${W}_{ab}=-\frac{\pi }{N}{M}_{ab}({\boldsymbol{0}}){M}_{ba}({\boldsymbol{0}})\frac{f({\varepsilon }_{a})-f({\varepsilon }_{b})}{{\varepsilon }_{a}-{\varepsilon }_{b}}.$$
(13)

Hence, only the terms satisfying ω = εa − εb contribute to the conductivity.

In a finite lattice system, the eigenvalues of \({{\mathcal{H}}}_{0}\) are discrete. Therefore, σ(ω) determined using Eq. (12) is also discrete. To extrapolate the value of the conductivity to the thermodynamic limit, we first calculate the total weight of the conductivity for the frequency from 0 to ω

$${S}_{{\rm{tot}}}(\omega )=\sum _{\begin{array}{c}a\ne b\\ 0\le {\varepsilon }_{a}-{\varepsilon }_{b}\le \,\omega \end{array}}{W}_{ab}.$$
(14)

We then determine the conductivity from the numerical derivative of Stot

$$\sigma (\omega )=\frac{{S}_{{\rm{tot}}}(\omega +d\omega )-{S}_{{\rm{tot}}}(\omega -d\omega )}{2d\omega },$$
(15)

where dω is a small parameter that should be taken such that at least one eigenvalue difference εa − εb falls between the interval (ω − dω, ω + dω). Furthermore, we need to do an average of σ(ω) over different phase configurations generated from the Monte-Carlo sampling of the XY model at a given temperature. The resistivity is finally obtained by extrapolating the inverse of the conductivity σ(ω) to the limit ω→0.

Fig. 1 is an illustrative example, demonstrating the variation in optical conductivity with frequency ω at T = 0.1 according to the scheme above. Notably, the outcomes across various system sizes converge onto a single curve for both s- and \({d}_{{x}^{2}-{y}^{2}}\)-wave pairing states. This convergence suggests that the scheme is highly effective in reducing the impact of finite-size effects, thereby enabling accurate extrapolation of resistivity.

Fig. 1: Finite size scaling of optical conductivity.
figure 1

Frequency dependence of the inverse of \({\rm{Re}}\sigma (\omega )\) obtained on five different L × L square lattices at T = 0.1 for the two phase fluctuating states with a s-wave and b \({d}_{{x}^{2}-{y}^{2}}\)-wave pairing states.

Full size image

DC resistivity is determined by extrapolating \(1/{\rm{Re}}\sigma (\omega )\) to the ω = 0 limit. Figure 2 depicts how resistivity varies with temperature for both s- and \({d}_{{x}^{2}-{y}^{2}}\)-wave pairing states. This analysis is based on an average of over 72 independent phase configurations for each system size at a specific temperature. The findings reveal that resistivity stabilizes as system size increases, indicating negligible finite-size effects. Although there are quantitative differences in their absolute values, a universal temperature dependence emerges for both pairing states. Specifically, resistivity escalates with temperature, displaying a downward curvature that contrasts with the T2 behavior characteristic of Fermi liquids.

Fig. 2: Temperature dependence of the DC resistivity.
figure 2

Panels a and b are the reults for s-wave and d-wave pairings in three different lattice systems, respectively. The numerical results are well described by the formula \(\rho \left(T\right)=A\exp (-b/\sqrt{T/{T}_{c}-1})\), depicted by the solid curves. From the fitting, the superconducting transition temperature Tc is found to be Tc = 0.089 (2) in both cases.

Full size image

To delve deeper into the temperature-dependent behavior of resistivity, we conduct a scaling analysis on the numerical data. In the system under study, resistivity results from electron scattering by the fluctuating phase field. Given that the correlation length of the fluctuating pairing phase constitutes the sole length scale in the XY model, we propose that the electron scattering length ls, which is a product of the scattering time τs and the Fermi velocity, is proportional to a power of the correlation length ξ of fluctuating phase, i.e., ls ∝ ξα. As the temperature approaches the BKT critical temperature Tc, the correlation length ξ is expected to diverge, following the theory outlined by Kosterlitz in 197471

$$\xi (T)=a\,\exp \left(\frac{b}{\sqrt{T/{T}_{c}-1}}\right),$$
(16)

where \(b\simeq 1.5\sqrt{{T}_{c}}\) and a is a non-universal coefficient. Any power of the exponential correlation function has the same form. Therefore, if the Fermi velocity remains constant within the considered temperature range, it is anticipated that the resistivity obeys the scaling law

$$\rho (T) \sim {\xi }^{-\alpha }\propto A\exp \left(-\frac{B}{\sqrt{T/{T}_{c}-1}}\right).$$
(17)

The resistivity vanishes at the transition temperature. It is important to note that in realistic systems, there is a complex interaction between the phase field and quasiparticle excitations. Nevertheless, the scaling behavior described by Eq. (16) remains applicable and only the value of Tc is modified by this interaction. This assertion is based on the premise that the interplay between these factors does not significantly alter the underlying mechanisms governing the phase fluctuation and the BKT scaling behavior in Eq. (16) is universal in the phase fluctuating regime of two-dimensional superconductors.

Remarkably, as depicted in Fig. 2a, b, Eq. (17) demonstrates a precise fit to the numerical data for both s- and \({d}_{{x}^{2}-{y}^{2}}\)-wave pairing states. This accurate fitting yields an accurate estimation of the transition temperature Tc = 0.089(2) for both pairing cases, implying that the correlation length of the phase field indeed dictates the electron scattering length. Here, the parameter B is the key parameter that determines the shape of the \(\rho \left(T\right)\) curve. The extracted values of \(B/\sqrt{{T}_{c}}\) by fitting the resistivity are approximately 0.44(1) for s-wave and 0.47(1) for d-wave. According to Eq. (17), the similarity of the scaling parameter B indicates that the scaling exponent α is nearly independent of the pairing symmetries, as the parameter b in Eq. (16) is a universal constant that relates to the vortex core energy of the XY model. Although the s-wave and d-wave pairing symmetries drastically alter the global low-energy fermionic density of states, our numerical results reveal that the fundamental scattering process of a quasiparticle by a local phase gradient emerges as a universal feature of the electron-phase coupling. Therefore, the same scaling of correlation length will give a similar value of the scaling exponent in the two pairings. And the values of B are much smaller than the theoretical prediction of \(b \sim 1.5\sqrt{{T}_{c}}\) based on the correlation length of the XY model. This indicates that the resistivity scales inversely with the correlation length, with a power exponent smaller than one. In the phenomenological theory given by Halperin and Nelson17, it is pointed out that the resistivity results from the scattering by vortices is proportional to the vortex density, namely, ρ ∝ nf, and the density of free vortices scales as the inverse square of the correlation length, thus the resistivity sales as ρ ∝ ξ−2. As the BKT correlation length is an exponential function, and the scaling parameter is an adjustable parameter in fitting the resistivity72,73, the scaling behavior has the same formalism as ours. In our calculations, the resistivity is extracted by directly coupling the entire fluctuating superconducting phase field θ(r) simulated by the XY model to the BdG Hamiltonian. Therefore, the full spectrum of phase fluctuation is encoded in our results. The phase field encompasses not only the free vortices that become prevalent near the critical temperature Tc, but also the long-wavelength smooth twist excitations, along with tightly and loosely bound vortex-antivortex pairs of all sizes up to the correlation length ξ. The formal consistency between our results and the H-N framework implies that the “vortex gas" paradiagram remains valid even if incorporating the full spectrum of thermal phase fluctuations in our model. However, the deviation from the ξ−2 scaling strongly suggests that the resistivity is not solely caused by scattering of a dilute gas of free vortices. Instead, it arises from the scattering of electrons by the continuous, fluctuating phase landscape as a whole. The correlation length ξ is the unique characteristic length scale of this landscape. Our result, ρ ∝ ξ−α with α<1, indicates that the electron scattering time is determined more directly by the correlation length itself, rather than by the density of a specific subset of its thermal topological excitations of the superconducting phases. In essence, our model confirms that the H-N theory correctly identifies vortex unbinding as the driver of the BKT transition, and it refines our understanding of how this complex phase landscape translates into fermionic transport properties. Except for the scaling formalism given by Eq. (17), alternative fitting approaches using a power function or polynomials of \(\left(T/{T}_{c}-1\right)\) fail to consistently describe the resistivity results.

In the above analysis, we find that the scattering lifetime of electrons follows a temperature dependence governed by the correlation length of the fluctuating superconducting order parameters. To gain a deeper understanding of this observation, we calculate the spectral function and the imaginary part of the self-energy for electrons. Selecting the results for L = 70 and ω = 0.1 at temperature T = 0.11 as representations, Fig. 3a, b show stark differences in the spectral functions between the two pairing symmetries. The result for s-wave pairing in Fig. 3a indicates a closed contour. However, the highest spectral weight is heavily suppressed compared to that of the d-wave case. This corroborates the finite pairing gap in the model, and finite phase coherence partially fills the energy gap. We observe a significant enhancement of the spectral weight in s-wave pairing with increasing temperature, which is consistent with progressive gap filling due to increasing phase disorder. Only when the phase becomes completely disordered is the gap-like feature fully destroyed36,74. In contrast, the corresponding d-wave result in Fig. 3b shows a gap along the anti-nodal direction and exhibits Fermi arcs. These Fermi arcs support the assumption of a finite pairing amplitude in our model. Although our model with d-wave pairing reproduces the spectral signature observed in the pseudogap phase, it fails to capture pseudogap physics in the cuprate in regimes of temperature higher than the pairing amplitude. Therefore, while our model captures the emergence of a pairing-fluctuation-driven pseudogap, it is insufficient to describe the full complexity of the phenomenon across all temperature regimes. A complete description would require incorporating other mechanisms, such as competing orders, which are beyond the scope of this study. The self-energy is obtained using the Dyson equation

$$\Sigma (k,\omega )={G}^{-1}(k,\omega )-{G}_{0}^{-1}(k,\omega ),$$
(18)

where \({G}_{0}^{-1}(k,\omega )\) is the single-particle Green’s function of free electrons, described by \({{\mathcal{H}}}_{0}\) without the superconducting pairing. The imaginary part of the self-energy, \({\rm{Im}}\Sigma (k,\omega )\), measures the damping effect induced by the fluctuating phases. Its inverse equals the quasiparticle lifetime τ(q, ω).

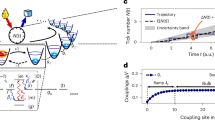
Fig. 3: Quasiparticle properties of s-wave and d-wave pairing states.
figure 3

Momentum-dependent spectral function at T = 0.11 and ω = 0.1 is shown for a s-wave and b d-wave. c, d show the momentum dependence of the imaginary self-energy for the corresponding pairing symmetries under the same parameters as (a) and (b). The spectral function and self-energy are calculated by averaging over 72 samples with L = 70 and the energy broadening η = 0.008. e, f depict the average scattering rate around (π, 0) in the anti-nodal direction of the Brillouin zone and its symmetry-equivalent points obtained by 90∘ rotation around the (π, π) point, where strongest scattering occurs. The solid lines are fitting curves using the formula \(1/\tau \sim \exp (-B/\sqrt{T/{T}_{c}-1})\).

Full size image

Figure 3e, f shows the heat maps of the quasiparticle scattering rate, 1/τ(q, ω), in the Brillouin zone for the s-wave and d-wave pairing states in a square lattice of L = 70 at ω = 0.1, respectively. The result indicates that the quasiparticle scattering rates are the strongest around (π, 0) in the anti-nodal direction and its equivalent points. Under s-wave pairing, the weak anisotropy in spectral function in Fig. 3a reveals degraded quasiparticle coherence near the (±π, 0) and (0, ± π) points. These locations correspond to van Hove singularities in the free-electron band structure. The significantly enhanced density of states around these points strengthens scattering, as evidenced by the large imaginary self-energy in Fig. 3c. For the \({d}_{{x}^{2}-{y}^{2}}\)-wave pairing state, the anisotropy in the quasiparticle scattering rate is more pronounced. Specifically, the near-vanishing scattering rate along the nodal direction of the \({d}_{{x}^{2}-{y}^{2}}\)-wave gap order parameter indicates enhanced quasiparticle coherence in this region. This behavior aligns with the spectral function and reflects the intrinsic anisotropy of the \({d}_{{x}^{2}-{y}^{2}}\)-wave pairing symmetry.

The lower panels of Fig. 3e, f show the temperature dependence of the average scattering rate 1/τ(q, ω) at the points around \(\left(\pi ,0\right)\) in the anti-nodal direction and its symmetry-equivalent points, which exhibit the largest scattering rates. We average over eight equivalent points to obtain the data. Transport scattering rate considering both scattering events and scattering angles. Thus, the quasiparticle lifetime τ is presumably proportional to the scattering time. Therefore, we expect the corresponding scattering rate to share the same temperature dependence as the resistivity

$${\tau }^{-1} \sim \exp \left(-\frac{B}{\sqrt{T/{T}_{c}-1}}\right).$$
(19)

This is indeed the case, as shown in Fig. 3e, f. By fitting the data with the above expression, we estimate the critical temperatures to be Tc = 0.088(2) for both the s-wave and \({d}_{{x}^{2}-{y}^{2}}\)-wave states with L = 70. These values agree with the results of Tc extracted from the resistivity data.

Above the critical temperature, the leading-order contribution to the self-energy, Σ(q, ω), originates from the second-order perturbation of the fluctuating phase fields. Consequently, the primary contribution to the imaginary part of the self-energy is expected to exhibit a quadratic dependence on the gap amplitude Δ such that A ∝ Δ2.

To confirm this quadratic scaling behavior, we evaluated the coefficient of resistivity as a function of temperature for various values of Δ. Figure 4 illustrates the dependence of A on Δ, determined by fitting the numerical data to Eq. (17). Our findings reveal that the equation A = cΔ2, where c is a coefficient independent of Δ, accurately captures the numerical results. It is important to note that this quadratic term solely represents the lowest-order scattering process. The inclusion of higher-order corrections, such as a Δ4 term, further refines the fit. These results demonstrate a correlation between the resistivity coefficient A and the amplitude of the fluctuating field, paving the way for a deeper understanding of the notable relationship between the linear-T coefficient A1 and Tc observed in cuprate68 and other unconventional superconductors69, as reported in previous studies. The coefficient of d-wave is about six times that of s-wave. This observation is consistent with the results in Fig. 2 and indicates that the coefficient A can be significantly influenced by the complex interplay between gapless quasiparticles and vortices. The much larger value of A for the d-wave pairing is consistent with the fact that a higher density of low-energy quasiparticles is available for scattering. It is worth noting that the parameters B and Tc in Eq. (17) are independent of the pairing amplitude within reasonable numerical error in both cases. This indicates that the correlation length of the superconducting phase governs the scaling behavior of the resistivity, while the pairing amplitude determines its magnitude. The superconducting transition is completely determined by the phase coherence energy scale Jθ in our model. Therefore, we can expect that even if there are weak fluctuations in the pairing amplitude, provided that the correlation length of the pairing is much longer than that of the phase, the scattering length is still dominated by the superconducting phase correlations. Considering the BCS temperature dependence of the average pairing amplitude ∣Δ(T)∣, the resistivity should roughly obey \(\rho (T) \sim | \Delta (T){| }^{2}\exp (-B/\sqrt{T/{T}_{c}-1})\). With increasing temperature, the resistivity predicted by this scaling form will be lower than the result obtained here because the pairing amplitude decreases as temperature rises.

Fig. 4: Dependence of the resistivity coefficient A on the pairing gap.
figure 4

The resistivity coefficient A defined in Eq. (17) versus the pairing gap amplitude Δ for a s-wave and b d-wave pairing states with L = 70.

Full size image

Superfluid density

From the current–current correlation function and the expectation value of the diamagnetic current operator, we can also calculate the superfluid density in the superconducting phase:

$${\rho }_{s}=-\langle {K}_{x}\rangle -{\Lambda }^{xx}({q}_{x}=0,{q}_{y}\to 0,\omega =0),$$
(20)

where Kx is the x-component of the diamagnetic current operator

$${K}_{x}=-\frac{t}{N}\sum _{{\boldsymbol{r}},\sigma }\left({c}_{{\boldsymbol{r}},\sigma }^{\dagger }{c}_{{\boldsymbol{r}}+{{\boldsymbol{e}}}_{x},\sigma }+{c}_{{\boldsymbol{r}}+{{\boldsymbol{e}}}_{x},\sigma }^{\dagger }{c}_{{\boldsymbol{r}},\sigma }\right).$$
(21)

The formation of the phase coherence determines the superconducting transition. For the two-dimensional XY model, the superfluid density exhibits a universal jump at the critical point75, where the correlation length diverges. Exactly at the critical point, the superfluid density scales linearly with Tc

$${\rho }_{s}\left({T}_{c},L\right)\simeq \frac{2}{\pi {J}_{\theta }}{T}_{c}.$$
(22)

Figure 5 shows the superfluid density calculated in three different system sizes. With increasing temperature, the superfluid density exhibits a noticeable drop at a temperature close to the BKT transition temperature, TKT ≃ 0.893Jθ, determined by the large-scale Monte-Carlo simulation76,77, indicating that the superconducting coherence is suppressed at high temperatures due to the phase fluctuation. The finite superfluid density above Tc arises from the finite momentum resolution and energy broadening inherent in Green’s function calculations performed on finite-size systems.

Fig. 5: Temperature dependence of superfluid density.
figure 5

The superfluid density as a function of temperature for both s-wave and d-wave pairing states are shown in (a) and (b), respectively. The superfluid density for the two cases is normalized with respect to their values at absolute zero temperature. The black diagonal line represents the universal scaling law \({\rho }_{s}\left(T\right)\simeq 2T/\pi {J}_{\theta }\), with its intersection with the superfluid density curve identifying the superconducting transition temperature Tc, denoted by the gray dashed line. The estimated Tc from the superfluid density of L = 80 is about 0.092(2) for s-wave pairing and 0.095(3) for \({d}_{{x}^{2}-{y}^{2}}\) wave pairing.

Full size image

From the crossing point between the calculated superfluid density and the linear scaling formula (22), we estimate Tc = 0.092(2) and Tc = 0.095(3) when the system size L = 80 for s-wave and d-wave pairing symmetries, respectively. Within the BdG framework, the superfluid density receives dominant contributions from long-wavelength phase gradients. This induces stronger finite-size effects compared to the direct calculation from the XY model, which rounds the transition and accounts for the slight discrepancy between our transition temperatures derived from superfluid density and resistivity fitting. The differences between the two cases are mainly attributed to their distinct density of states at low energy. For d-wave pairing, it is gapless along the nodal directions, while low-energy states are significantly suppressed due to the full gap of s-wave pairing. Consequently, the low-energy states have more pronounced effects on the physics properties in d-wave pairing compared to s-wave pairing, which implies more pronounced finite-size effects for d-wave pairing. And the drop of superfluid density will become sharper and sharper with the increase of system size, thus the finite size effects make the estimated Tc of d-wave is higher than that of s-wave. In fact, accurate determination of the transition point through the superfluid density requires systems of sufficiently large size76,77. Though the jump of superfluid density is rounded by the finite size effects, it does not affect our ability to properly estimate the transition point. The Tc estimated from the cross points agrees with the result given by the XY model on a finite lattice size. The Tc estimated here provides strong support for the scaling of resistivity.

Discussion

In this work, we systematically investigate the electrical resistivity induced by the superconducting thermal phase fluctuation in two dimensions. Employing the Monte Carlo approach, we numerically solve the BdG Hamiltonian in the presence of classical pairing phase fluctuations governed by the ferromagnetic XY model. For both s-wave and \({d}_{{x}^{2}-{y}^{2}}\)-wave pairings, the DC resistivity displays normal metallic behaviors, deviating from the conventional Fermi-liquid scaling properties. The DC resistivity induced by thermal phase fluctuations obeys the universal scaling dependence on the temperature \(\rho \left(T\right)=A\exp (-B/\sqrt{T/{T}_{c}-1})\), which is the same as critical scaling behavior of correlation length for BKT transition. This formally agrees with the Nelson-Halperin phenomenological framework. However, our computational data reveal a nearly pairing-independent resistivity scaling exponent α < 1, contrasting with the value α = 2 predicted by the phenomenological argument of H-N theory. This implies that resistivity originates from scattering by collective thermal fluctuations rather than exclusively from free vortices. The subsequent calculations indicate that the quasi-particle lifetime satisfies the same scaling relation, further substantiating the results of DC resistivity scaling behavior. Further analysis shows that the resistivity under superconducting fluctuations is related to the pairing amplitude, and the coefficient A of the resistivity is a quadratic function of Δ, it encodes the non-universal low-energy states resulting from different pairing symmetries. The quadratic scaling relation potentially provides a direction to understand the interplay between unconventional superconductivity and anomalous dissipation in the normal states.

In the simulations, we focus exclusively on thermal fluctuations while neglecting phase dynamics. For s-wave pairings, the pairing gap suppresses the quasiparticle excitations, rendering the dynamics less important here. d-wave pairing exhibits gapless excitations along the nodal directions, the complex interplays between quasiparticles and vortices may renormalize the transition temperature or even modify the XY model that governs the superconducting phases. However, the transition can remain within the same universality class as the XY model78. Therefore, we neglect the dynamics even for d-wave pairing and use the ferromagnetic XY model to describe the thermal phase fluctuations. These conditions can be true when phase dynamics are much slower than the relaxation rate of quasiparticles. Our model completely ignores the temperature dependence and fluctuations of pairing amplitudes. As a natural result, it can not capture the correlation length behavior predicted by Landau’s theory. Furthermore, the scaling parameter B in Eq. (17) does not account for the information about the temperature distance between the BKT transition Tc and Ginzburg-Landau transition TMF72,73.

Our results show that superconducting thermal phase fluctuations lead to novel transport properties in two dimensions. Since the temperature dependence of DC resistivity arising from pairing phase fluctuation unveiled here is not linear-T, our study cannot directly account for the scaling relation between the strange-metal dissipation and superconducting Tc as observed in experiments. Nonetheless, as aforementioned, our results only apply to the thermal phase fluctuations in two dimensions, where the superconducting transition is a BKT transition. The atomically-thin two-dimensional superconductors, such as twisted bilayer graphene13, single-layer FeSe on SrTiO379, and monolayer NbSe280,81, have low superfluid densities, making them ideal platforms to test our findings. For the most unconventional superconductors, we should consider a three-dimensional system and incorporate the effects of inter-layer coupling. It is intriguing to study the DC resistivity arising from pairing phase fluctuation in a three-dimensional system, and particularly, to investigate whether the strange-metal behavior could emerge or not. Moreover, notice that we only consider the electronic dissipation arising from pairing thermal phase fluctuations. Regarding realistic materials, various scattering mechanisms affect the transport properties above the superconducting transition temperature Tc, including electron-electron scattering, electron-phonon scattering and disorder effects. Considering the cooperative effects on the electronic transport originating from pairing phase fluctuation and these various ingredients is also an interesting direction, which is left for our future study.

Methods

Monte Carlo simulations

In the numerical simulations, we set the hopping integral t = 1 as the unit of energy, the coupling constant Jθ = 0.1, the gap amplitude Δ = 0.3, and the electron filling factor ne = 0.83 (the filling factor is 2 if a band is fully filled) if not explicitly stated. We take these values in our numerical simulations such that there is a relatively wide temperature window above the superconducting transition but lower than the energy scale of pairing amplitude. Furthermore, periodic boundary conditions are assumed.

We use the classical Monte Carlo method to generate a series of configurations of θ in the XY model given by Eq. (6) at a given temperature. To mitigate self-correlation, a single configuration is selected from every 20,000 configurations produced by the Monte Carlo simulation. By inserting each of these phase configurations into the Hamiltonian Eq. (1), it becomes possible to determine the eigenvalues εa and their corresponding eigenvectors ψa of the BdG Hamiltonian Eq. (1) by exact diagonalization.