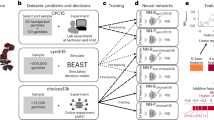
Abstract
Predicting human decisions under risk and uncertainty remains a fundamental challenge across disciplines. Existing models often struggle even in highly stylized tasks like choice between lotteries. Here we introduce BEAST gradient boosting (BEAST-GB), a hybrid model integrating behavioural theory (BEAST) with machine learning. We first present CPC18, a competition for predicting risky choice, in which BEAST-GB won. Then, using two large datasets, we demonstrate that BEAST-GB predicts more accurately than neural networks trained on extensive data and dozens of existing behavioural models. BEAST-GB also generalizes robustly across unseen experimental contexts, surpassing direct empirical generalization, and helps to refine and improve the behavioural theory itself. Our analyses highlight the potential of anchoring predictions on behavioural theory even in data-rich settings and even when the theory alone falters. Our results underscore how integrating machine learning with theoretical frameworks, especially those—like BEAST—designed for prediction, can improve our ability to predict and understand human behaviour.
This is a preview of subscription content, access via your institution
Access options
Access Nature and 54 other Nature Portfolio journals
Get Nature+, our best-value online-access subscription
$32.99 / 30 days
cancel any time
Subscribe to this journal
Receive 12 digital issues and online access to articles
$119.00 per year
only $9.92 per issue
Buy this article
- Purchase on SpringerLink
- Instant access to the full article PDF.
USD 39.95
Prices may be subject to local taxes which are calculated during checkout





Similar content being viewed by others
Data availability
Raw data for CPC18, as well as processed data for analyses of the previously published datasets (Choices13k and HAB22), are publicly available at https://doi.org/10.17605/OSF.IO/VW2SU.
Code availability
Code for all models and analyses reported in this study is publicly available at https://doi.org/10.17605/OSF.IO/VW2SU.
References
Bernoulli, D. Exposition of a new theory on the measurement of risk (original 1738). Econometrica 22, 23–36 (1954).
Tversky, A. & Kahneman, D. Advances in prospect theory: cumulative representation of uncertainty. J. Risk Uncertain. 5, 297–323 (1992).
Kahneman, D. & Tversky, A. Prospect theory: an analysis of decision under risk. Econometrica 47, 263–292 (1979).
von Neumann, J. & Morgenstern, O. Theory of Games and Economic Behavior (Princeton Univ. Press, 1947).
Erev, I., Ert, E., Plonsky, O., Cohen, D. & Cohen, O. From anomalies to forecasts: toward a descriptive model of decisions under risk, under ambiguity, and from experience. Psychol. Rev. 124, 369–409 (2017).
He, L., Analytis, P. P. & Bhatia, S. The wisdom of model crowds. Manag. Sci. 68, 3635–3659 (2022).
Peterson, J. C., Bourgin, D. D., Agrawal, M., Reichman, D. & Griffiths, T. L. Using large-scale experiments and machine learning to discover theories of human decision-making. Science 372, 1209–1214 (2021).
Altman, A., Bercovici-Boden, A. & Tennenholtz, M. Learning in one-shot strategic form games. In European Conference on Machine Learning (eds Fürnkranz, J. et al.) 6–17 (Springer, 2006).
Hartford, J. S., Wright, J. R. & Leyton-Brown, K. Deep learning for predicting human strategic behavior. In Advances in Neural Information Processing Systems (eds Lee, D. et al.) 2424–2432 (2016).
Halevy, A., Norvig, P. & Pereira, F. The unreasonable effectiveness of data. IEEE Intell. Syst. 24, 8–12 (2009).
Silver, D. et al. Mastering the game of Go with deep neural networks and tree search. Nature 529, 484 (2016).
Peysakhovich, A. & Naecker, J. Using methods from machine learning to evaluate behavioral models of choice under risk and ambiguity. J. Econ. Behav. Organ. 133, 373–384 (2017).
Fudenberg, D. & Liang, A. Predicting and understanding initial play. Am. Econ. Rev. 109, 4112–4141 (2019).
Fudenberg, D., Kleinberg, J., Liang, A. & Mullainathan, S. Measuring the completeness of economic models. J. Polit. Econ. 130, 956–990 (2022).
Agrawal, M., Peterson, J. C. & Griffiths, T. L. Scaling up psychology via scientific regret minimization. Proc. Natl Acad. Sci. USA 117, 8825–8835 (2020).
Plonsky, O., Erev, I., Hazan, T. & Tennenholtz, M. Psychological forest: predicting human behavior. In The Thirty-FirstAAAI Conference on Artificial Intelligence Vol. 31, 656–662 (AAAI Press, 2017).
Bourgin, D. D., Peterson, J. C., Reichman, D., Russell, S. J. & Griffiths, T. L. Cognitive model priors for predicting human decisions. In International Conference on Machine Learning (eds Chaudhuri, K. & Salakhutdinov, R.) 5133–5141 (PMLR, 2019).
Plonsky, O., Apel, R., Erev, I., Ert, E. & Tennenholtz, M. When and how can social scientists add value to data scientists? A choice prediction competition for human decision making. Open Science Framework https://doi.org/10.17605/OSF.IO/2X3VT (2018).
Chen, T. & Guestrin, C. XGBoost: a scalable tree boosting system. In Proc. 22nd ACM SIGKDD International Conference on Knowledge Discovery and Data Mining 785–794 (ACM, 2016).
Zhou, K., Liu, Z., Qiao, Y., Xiang, T. & Loy, C. C. Domain generalization: a survey. IEEE Trans. Pattern Anal. Mach. Intell. 45, 4396–4415 (2022).
Savage, L. J. The Foundations of Statistics (John Wiley & Sons, 1954).
Allais, M. Le comportement de l’homme rationnel devant le risque: critique des postulats et axiomes de l’école américaine. Econom. J. Econom. Soc. 21, 503–546 (1953).
Ellsberg, D. Risk, ambiguity, and the Savage axioms. Q. J. Econ. 75, 643–669 (1961).
Breiman, L. Random forests. Mach. Learn. 45, 5–32 (2001).
Dawes, R. M., Faust, D. & Meehl, P. E. Clinical versus actuarial judgment. Science 243, 1668–1674 (1989).
Einhorn, H. J. Expert measurement and mechanical combination. Organ. Behav. Hum. Perform. 7, 86–106 (1972).
Lundberg, S. M. & Lee, S.-I. A unified approach to interpreting model predictions. Adv. Neural Inf. Process. Syst. 30, 4765–4774 (2017).
Thomas, T. et al. Modelling dataset bias in machine-learned theories of economic decision-making. Nat. Hum. Behav. https://doi.org/10.1038/s41562-023-01784-6 (2024).
Shoshan, V., Hazan, T. & Plonsky, O. BEAST-Net: Learning novel behavioral insights using a neural network adaptation of a behavioral model. Open Science Framework https://osf.io/kaeny/ (2023).
Stewart, N., Reimers, S. & Harris, A. J. L. On the origin of utility, weighting, and discounting functions: how they get their shapes and how to change their shapes. Manag. Sci. 61, 687–705 (2015).
Spektor, M. S., Bhatia, S. & Gluth, S. The elusiveness of context effects in decision making. Trends Cogn. Sci. 25, 843–854 (2021).
Heilprin, E. & Erev, I. The relative importance of the contrast and assimilation effects in decisions under risk. J. Behav. Decis. Mak. 37, e2408 (2024).
Blanchard, G., Deshmukh, A. A., Dogan, U., Lee, G. & Scott, C. Domain generalization by marginal transfer learning. J. Mach. Learn. Res. 22, 1–55 (2021).
Andrews, I., Fudenberg, D., Liang, A. & Wu, C. The transfer performance of economic models. Preprint at https://arxiv.org/abs/2202.04796 (2022).
Dwork, C. et al. The reusable holdout: preserving validity in adaptive data analysis. Science 349, 636–638 (2015).
Hofman, J. M. et al. Integrating explanation and prediction in computational social science. Nature 595, 181–188 (2021).
Agassi, O. D. & Plonsky, O. The importance of non-analytic models in decision making research: an empirical analysis using BEAST. In Proc. Annual Meeting of the Cognitive Science Society (eds Goldwater, M. et al.) 45 (2023).
Yarkoni, T. & Westfall, J. Choosing prediction over explanation in psychology: lessons from machine learning. Perspect. Psychol. Sci. 12, 1100–1122 (2017).
Shafir, S., Reich, T., Tsur, E., Erev, I. & Lotem, A. Perceptual accuracy and conflicting effects of certainty on risk-taking behaviour. Nature 453, 917–920 (2008).
Weber, E. U., Shafir, S. & Blais, A.-R. Predicting risk sensitivity in humans and lower animals: risk as variance or coefficient of variation. Psychol. Rev. 111, 430 (2004).
Plonsky, O. & Erev, I. Prediction oriented behavioral research and its relationship to classical decision research. Open Science Framework https://doi.org/10.31234/osf.io/7uha4 (2021).
d’Eon, G., Greenwood, S., Leyton-Brown, K. & Wright, J. R. How to evaluate behavioral models. In AAAI Conference on Artificial Intelligence Vol. 38, 9636–9644 (AAAI Press, 2024).
Agassi, O. D. & Plonsky, O. Beyond analytic bounds: re-evaluating predictive power in risky decision models. Judgm. Decis. Mak. 19, e35 (2024).
Erev, I., Ert, E., Plonsky, O. & Roth, Y. Contradictory deviations from maximization: environment-specific biases, or reflections of basic properties of human learning? Psychol. Rev. 130, 640–676 (2023).
Plonsky, O., Teodorescu, K. & Erev, I. Reliance on small samples, the wavy recency effect, and similarity-based learning. Psychol. Rev. 122, 621–647 (2015).
Erev, I. & Marx, A. Humans as intuitive classifiers. Front. Psychol. 13, 1041737 (2023).
Liu, Y. & Just, A. SHAPforxgboost: SHAP Plots for ‘XGBoost’. R Package Version 0.1.3 (CRAN, 2023).
Ert, E. & Erev, I. On the descriptive value of loss aversion in decisions under risk: six clarifications. Judgm. Decis. Mak. 8, 214–235 (2013).
Thaler, R. H. & Johnson, E. J. Gambling with the house money and trying to break even: the effects of prior outcomes on risky choice. Manag. Sci. 36, 643–660 (1990).
Payne, J. W. It is whether you win or lose: the importance of the overall probabilities of winning or losing in risky choice. J. Risk Uncertain. 30, 5–19 (2005).
Birnbaum, M. H. New paradoxes of risky decision making. Psychol. Rev. 115, 463–501 (2008).
Barron, G. & Erev, I. Small feedback-based decisions and their limited correspondence to description-based decisions. J. Behav. Decis. Mak. 16, 215–233 (2003).
Busemeyer, J. R. & Townsend, J. T. Decision field theory: a dynamic-cognitive approach to decision making in an uncertain environment. Psychol. Rev. 100, 432–459 (1993).
Diederich, A. & Busemeyer, J. R. Conflict and the stochastic-dominance principle of decision making. Psychol. Sci. 10, 353–359 (1999).
Canty, A. & Ripley, B. boot: Bootstrap R (S-Plus) Functions. R Package Version 1.3-28.1 (CRAN, 2022).
Brandstätter, E., Gigerenzer, G. & Hertwig, R. The priority heuristic: making choices without trade-offs. Psychol. Rev. 113, 409–432 (2006).
Stewart, N., Chater, N. & Brown, G. D. A. Decision by sampling. Cogn. Psychol. 53, 1–26 (2006).
Fiedler, S. & Glöckner, A. The dynamics of decision making in risky choice: an eye-tracking analysis. Front. Psychol. 3, 335 (2012).
Rieskamp, J. The probabilistic nature of preferential choice. J. Exp. Psychol. Learn. Mem. Cogn. 34, 1446–1465 (2008).
Stewart, N., Hermens, F. & Matthews, W. J. Eye movements in risky choice. J. Behav. Decis. Mak. 29, 116–136 (2016).
Pachur, T., Schulte-Mecklenbeck, M., Murphy, R. O. & Hertwig, R. Prospect theory reflects selective allocation of attention. J. Exp. Psychol. Gen. 147, 147–169 (2018).
Pachur, T., Mata, R. & Hertwig, R. Who dares, who errs? Disentangling cognitive and motivational roots of age differences in decisions under risk. Psychol. Sci. 28, 504–518 (2017).
Acknowledgements
O.P. thanks O. D. Agassi for help in analysis of some of the curated data. I.E. acknowledges support from the Israel Science Foundation (grant no. 1821/12). M.T. has received funding from the European Research Council (ERC) under the European Union’s Horizon 2020 research and innovation programme (grant agreement number 740435). D.B., J.C.P., D.R. and T.L.G. have received funding from DARPA (cooperative agreement D17AC00004) and the United States National Science Foundation (grant number 1718550). The funders had no role in the study design, data collection and analysis, decision to publish or preparation of the manuscript.
Author information
Authors and Affiliations
Contributions
O.P., R.A., E.E., M.T. and I.E. organized CPC18 (O.P., E.E. and I.E. designed the experiments and collected the experimental data; I.E. developed the first baseline model; O.P., R.A. and I.E. programmed the baseline models; O.P. and E.E. managed submissions). D.B., J.C.P., D.R., T.L.G. and S.J.R. submitted the winning model for the first track of CPC18. E.C.C. and J.F.C. submitted the winning model for the second track of CPC18. O.P. performed all post-competition analyses, including analyses of Choices13k and HAB22. O.P. wrote the manuscript, and all authors commented on it.
Corresponding author
Ethics declarations
Competing interests
One of the authors (D.B.) is affiliated with Adobe Research, but his work on this project was done almost exclusively before he had this affiliation. Adobe Research had no role in this project. We declare no other competing interests.
Peer review
Peer review information
Nature Human Behaviour thanks Pantelis Analytis and the other, anonymous, reviewer(s) for their contribution to the peer review of this work. Peer reviewer reports are available.
Additional information
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Extended data
Extended Data Fig. 1 Comparison of the usefulness of behavioral models as foresight features in CPC18.
In each case, we tuned and trained an XGB algorithm using only the objective features (see Table 1) and the prediction of each foresight on CPC18’s training data and predicted its test data. Data used was restricted to the subset of CPC18’s data that reflects pure decisions under risk (no feedback or ambiguity), implying training on 182 tasks, and testing on 48 tasks. All behavioral models except BEAST were first fitted to the training data independently to provide predictions. BEAST’s (red) predictions used the original parameters from CPC15 (Erev et al., 2017). Ensemble of foresights (rosy-brown) uses all five foresights combined. Bars show the single held-out test-set Mean Squared Error (MSE) per model. Completeness (see Methods) computed relative to a naïve baseline (MSE = 0.05095) and irreducible noise limit (MSE = 0.00113).
Extended Data Fig. 2 Feature importance analyses for Choices13k data.
(a) Test set performance on Choices13k data when removing different sets of features from BEAST-GB. Data was split to 90% training (8848 tasks) and 10% held-out test data (983 tasks), and models were trained on fixed and increasing proportions of the training data. This process was repeated 50 times, and results reflect the average test set MSE over the n = 50 train-test splits. (b) Average absolute SHAP values of BEAST-GB’s features in predicting Choices13k test data, by feature category. “Δ Min payoffs” is both a Naïve and a Psychological feature. For clarity, only top 20 features are shown. Feature names and definitions appear in Table 1.
Extended Data Fig. 3 2D visualization of all 11,666 choice tasks used in this paper.
Each point is a single choice task represented in two dimensions obtained by implementing a t-SNE (t-distributed Stochastic Neighbor Embedding) algorithm on the set of psychological features of each task (see Table 1). Tasks depicted closer together are conceptually more similar than tasks further apart (though the values of the dimensions do not have direct interpretations). Choices13k data appears to cover well the space from which CPC18 data comes from, whereas HAB22 data is different than both.
Extended Data Fig. 4 Feature importance analyses for HAB22 data.
(a) HAB22 test set predictive performance of BEAST-GB (red) and variations of it that remove different feature sets. Bars show mean test-set MSE across the 50 nested cross validation folds (n = 50 fold-MSE values). Grey dots form a horizontal dot-histogram of the n = 50 fold-level MSEs (bin = 0.0005) for each model. Completeness (see Methods) computed relative to a naïve baseline (average MSE = 0.1314) and irreducible noise limit (average MSE = 0.0248), in each fold separately, then averaged. (b) Average absolute SHAP values of BEAST-GB’s features in predicting HAB22’s test set, by feature category. “Δ Min payoffs” is both a Naïve and a Psychological feature. For clarity, only top 20 features are shown. Feature names and definitions in Table 1.
Supplementary information
Supplementary Information
Supplementary text, Fig. 1 and Tables 1–3.
Supplementary Data 1
Trial-by-trial individual raw choice data for experiments 1 and 2 described in the Article.
Rights and permissions
Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.
About this article
Cite this article
Plonsky, O., Apel, R., Ert, E. et al. Predicting human decisions with behavioural theories and machine learning. Nat Hum Behav 9, 2271–2284 (2025). https://doi.org/10.1038/s41562-025-02267-6
Received:
Accepted:
Published:
Version of record:
Issue date:
DOI: https://doi.org/10.1038/s41562-025-02267-6
This article is cited by
-
Feedback-induced attitudinal changes in risk preferences
Nature Communications (2026)
-
Sequence-to-sequence models with attention mechanistically map to the architecture of human memory search
Communications Psychology (2025)